Fabrication of submillimeter-sized spherical self-oscillating gels and control of their isotropic volumetric oscillatory behaviors

Abstract

In this study, we established a fabrication method and analyzed the volumetric self-oscillatory behaviors of submillimeter-sized spherical self-oscillating gels. We validated that the manufactured submillimeter-sized spherical self-oscillating gels exhibited isotropic volumetric oscillations during the Belousov–Zhabotinsky (BZ) reaction. In addition, we experimentally elucidated that the volumetric self-oscillatory behaviors (i.e., period and amplitude) and the oscillatory profiles depended on the following parameters: (1) the molar composition of N-(3-aminopropyl)methacrylamide hydrochloride (NAPMAm) in the gels and (2) the concentration of Ru(bpy)₃–NHS solution containing an active ester group on conjugation. These clarified relationships imply that controlling the amount of Ru(bpy)₃ in the gel network could influence the gel volumetric oscillation during the BZ reaction. These results of submillimeter-sized and spherical self-oscillating gels bridge knowledge gaps in the current field because the gels with corresponding sizes and shapes have not been systematically explored yet. Therefore, our study could be a cornerstone for diverse applications of (self-powered) gels in various scales and shapes, including soft actuators exhibiting life-like functions.

---

1. Introduction

Stimuli-responsive polymer gels have drawn attention due to their intelligent functions, which can sense and respond to external environment changes.^1–3 Specifically, stimuli-responsive gels can undergo mechanical volume phase transition by external stimuli like electricity, temperature, pH, molecules, and light. This responsiveness allows the stimuli-responsive gels to be actively applied in biomedical fields,⁴ including separation and purification technologies,⁵ drug delivery systems, molecular-recognizing systems,⁶ biosensors,⁷ shape memory⁸ and self-healing properties.^9,10 On the other hand, we have developed self-oscillating gels, which have broadened the horizon in stimuli-responsive gels since the gels exhibit autonomous swelling/deswelling volume oscillation without external stimuli.¹¹ The volume oscillations of the self-oscillating gels are driven by a Belousov–Zhabotinsky (BZ) reaction. The BZ reaction is a famous nonlinear oscillatory chemical reaction utilizing a transition metal complex such as tris(2,2′-bipyridine)ruthenium complex (Ru(bpy)₃²⁺) as a catalyst.¹² During the BZ reaction, Ru(bpy)₃ exhibits periodical redox state change (Ru(bpy)₃²⁺ for the reduced state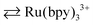 for the oxidized state) by consuming a reductant (e.g., malonic acid (MA)) in the presence of an oxidant (e.g., sodium bromate) in an acidic environment. The self-oscillating gels can be realized by introducing the Ru(bpy)₃ catalyst into the thermoresponsive poly(N-isopropylacrylamide) (PNIPAAm) gel network. If the BZ reaction occurs in the gel network, the hydrophilicity of the gel network periodically changes in synchronization with the periodical redox state change of Ru(bpy)₃. Therefore, water molecules can be diffused in/out of the gel network, which subordinates to the redox state change of Ru(bpy)₃ by the BZ reaction. As a result, the self-oscillating gels periodically and autonomously swell/deswell according to the BZ reaction.

The size of the self-oscillating gels is a major determinant of the volumetric oscillatory behavior during the BZ reaction.^13,14 One of the significant features of the BZ reaction is that it generates a propagating chemical wave with a characteristic wavelength through the medium.^15–21 The chemical wave propagation originates from the diffusion of the HBrO₂ (an activator for the BZ reaction) that leads to an oxidation reaction from Ru(bpy)₃²⁺ to Ru(bpy)₃³⁺. In the self-oscillating gels during the BZ reaction, the chemical wave spreads along the gel if the gels are larger than the wavelength (approximately 1 mm). The gel region where the oxidation wavefront reaches locally swells, and the swollen region moves along the direction of the propagating BZ chemical wave. The millimeter-sized self-oscillating gels have been applied to various biomimetic actuators exploiting the BZ chemical wave, including a self-walking gel,²² an intestine-like motion tubular-self oscillating gel,²³ and a cilia motion actuator.²⁴ If the gels are smaller than the wavelength of the BZ chemical waves, typically 1 mm, the gels exhibit isotropic swelling/deswelling with almost homogeneous redox changes during the BZ reaction. So far, for the self-oscillating microgels with submicrometer-scale, it was reported that they exhibit dispersing-flocculating oscillation and/or high-frequency swelling/deswelling oscillatory behavior.^25–29 However, to the best of our knowledge, for the submillimeter-sized self-oscillating gels, the systematic investigation of the volumetric oscillatory behaviors (i.e., the period and the amplitude) is not yet fully explored, which could hinder expanding the broader applications of the gels in all scales.

In this study, we experimentally verified the changes in the volumetric oscillatory behaviors (the period and the amplitude) of the submillimeter-sized spherical self-oscillating gels by changing the polymer compositions. Furthermore, we adopted the spherical shape because the boundary condition is not affected by shape differences among gels. This would help the researchers evaluate the swelling behaviors without considering geometry effects. The previous studies that theoretically analyzed the swelling kinetics of gels by using spherical coordinate systems^30,31 could support the advantage of the spherical shape. The submillimeter-sized spherical self-oscillating gels were fabricated by the post-polymerization modification of spherical base poly(N-isopropylacrylamide-co-N-(3-aminopropyl)methacrylamide hydrochloride) (poly(NIPAAm-co-NAPMAm)) gels. The base poly(NIPAAm-co-NAPMAm) gels were fabricated by inverse phase suspension polymerization to add the aqueous pre-gel solution dropwise to the stirring silicone oil. The base gels of the same size were categorized, followed by conjugating Ru(bpy)₃ with an active ester group (Ru(bpy)₃–N-hydroxysuccinimide) (Ru(bpy)₃–NHS) to the primary amino groups in the NAPMAm monomer. The effects of (1) the NAPMAm molar composition in the base gels and (2) the concentration of Ru(bpy)₃–NHS solution on the autonomous volumetric oscillatory behavior were systematically investigated and discussed.

2. Experimental section

2.1. Materials

N-Isopropylacrylamide (NIPAAm) was kindly provided by KJ Chemicals (Tokyo, Japan) and recrystallized from toluene/hexane. N-(3-Aminopropyl)methacrylamide hydrochloride (NAPMAm) was purchased by Polyscience (Warrington, PA) and used as received. N,N′-methylenebisacrylamide (MBAAm), ammonium persulfate (APS), N,N,N′,N′-tetramethylethylenediamine (TEMED), hexane, super dehydrated dimethyl sulfoxide (DMSO), sodium bromate (NaBrO₃), 1 M HNO₃ aqueous solution, and malonic acid (CH₂(COOH)₂) (MA) were purchased from Wako Pure Chemical Industries (Osaka, Japan). Silicon oil (KF-96-100CS) was purchased from Shin-Estu Chemical co, Ltd (Tokyo, Japan). Bis(2,2′-bipyridine) (1-(4′-methyl-2,2′-bipyridine-4-carbonyloxy)-2,5-pyrrolidinedione) ruthenium(II) (Ru(bpy)₃–NHS) was purchased from Trylead Chemical (Hangzhou, China).

2.2. Preparation of the spherical base poly(NIPAAm-co-NAPMAm) gels

The spherical base poly(NIPAAm-co-NAPMAm) gels were synthesized by inverse phase suspension polymerization to add the pre-gel solution in a dropwise manner into the silicone oil, which is continuously stirred (Fig. 1(a)). The monomer solution was prepared by dissolving NIPAAm (0.740 g, 6.54 mmol), NAPMAm, MBAAm (0.0347 g, 0.230 mmol), and TEMED (11.2 μl, 0.070 mmol) into the deionized water (4.00 mL, 278 mmol). The amount of NAPMAm was varied as follows: 0.024 g (0.130 mmol, 2.00 mol% (NAPMAm/NIPAAm)), 0.062 g (0.350 mmol, 5 mol% (NAPMAm/NIPAAm)), and 0.137 g (0.770 mmol, 10 mol% (NAPMAm/NIPAAm)). The initiator solution was made by dissolving APS (0.0171 g, 0.070 mmol) in deionized water (1.00 mL, 56.0 mmol). Then, the two solutions were cooled to 0 °C and degassed by Ar bubbling for 10 min. After the Ar bubbling process, the pre-gel solution was prepared by mixing the monomer and the initiator solution and quickly stirring. The pre-gel solution was transferred into the syringe equipped with a syringe needle. The size specification of the syringe needle was a 22 G syringe needle (inner diameter of 0.413 mm and an outer diameter of 0.718 mm). Then the pre-gel solution was added dropwise into the silicone oil with an injection rate of 100 ml h⁻¹. The silicone oil was stirred at various rpm (e.g., 100 rpm, 150 rpm, and 175 rpm) to verify the effect of the stirring speed on the gel size. Note that the silicone oil was purged by Ar bubbling for more than 30 min before the gelation process. The gelation was maintained at 25 °C for 3 h under an Ar atmosphere. After the gelation, the silicone oil was poured into a sieve to collect the spherical base gels. After washing the gels three times with hexane, the gels were dialyzed in deionized water for a week. The deionized water was exchanged every day. After dialysis, the gels with a diameter of 1 mm were carefully classified.

Fig. 1 (a) Schematic illustration of the fabrication of spherical self-oscillating gels. (b) Synthetic scheme of Ru(bpy)₃–NHS conjugation into the gel network.

2.3. Preparation of the spherical self-oscillating gels

Ru(bpy)₃ was introduced into the base gel network by succinimidyl esterification between Ru(bpy)₃–NHS and the primary amines in NAPMAm (Fig. 1(b)).³² Specifically, the fabricated base gels were kept in a super dehydrated DMSO and TEA for 24 h. Then the base gels were put in a super dehydrated DMSO solution (0.5 ml) containing Ru(bpy)₃–NHS and TEA (6.96 μl) for 24 h at 45 °C. The Ru(bpy)₃ conjugated gels were dialyzed by 50% (v/v) DMSO aqueous solutions for the first four days and deionized water for the following three days at 23 °C. The solutions were exchanged every day.

The fabricated samples were abbreviated as NA‘x’_Ru‘y’, where NA means NAPMAm, ‘x’ indicates the NAPMAm molar composition in the gels, Ru signifies Ru(bpy)₃, and ‘y’ denotes the concentration of Ru(bpy)₃–NHS in the conjugation process.

2.4. Measurement of equilibrium swelling ratio

The gels were equilibrated in the solution with 894 mM HNO₃ and 84 mM NaBrO₃ for the oxidized state (Ru(bpy)₃³⁺). For the reduced state (Ru(bpy)₃²⁺), the gels were equilibrated in the solution containing 894 mM HNO₃, 64 mM malonic acid (MA) and 84 mM NaCl. NaCl was added to maintain ionic strength. The gel images were taken using an optical microscope (VHX-970F, Keyence, Osaka, Japan).

2.5. Observation and analysis of self-oscillatory behavior

The gels were immersed in a BZ substrate solution containing 894 mM HNO₃, 84 mM NaBrO₃, and 64 mM MA at 20 °C. The photos of the gels during the BZ reaction were recorded using an optical microscope (VHX-970F, Keyence, Osaka, Japan).

We performed one-way ANOVA with a Tuckey–Krammer post-hoc method to evaluate the statistical significance of the periods and the amplitudes of the gels during the BZ reaction.

3. Results and discussion

3.1. Size distribution of the fabricated spherical poly(NIPAAm-co-NAPMAm) base gels

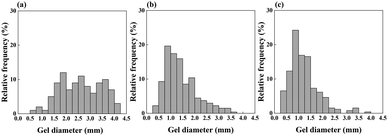
Fig. 2 displays the size distribution of the spherical base poly(NIPAAm-co-NAPMAm) gels with a 5 mol% NAPMAm composition (i.e., the NA5 gels). The stirring speed of the silicon oil was 100 rpm, 150 rpm, and 175 rpm for Fig. 2(a)–(c), respectively. The analyzed parameters of the size histograms are listed in Table 1. The mean values of the gel size were 2.62 mm, 1.42 mm, and 1.23 mm for 100 rpm, 150 rpm, and 175 rpm, respectively. The histograms were right-skewed because each mean value was larger than each median value. In addition, the mean values of the fabricated gel size decreased as the stirring rate of the silicone oil increased. The values of the first and third quartile in each group decreased as the stirring rate became faster, indicating that the size distribution of the gels tended to be smaller.

Fig. 2 Size distribution of the spherical base poly(NIPAAm-co-NAPMAm) gels at 20 °C. The histogram when the pre-gel solution (NAPMAm 5 mol%) was added in a dropwise manner into the silicon oil stirred by (a) 100 rpm (n = 100), (b) 150 rpm (n = 270), and (c) 175 rpm (n = 260). The syringe needle was 22 G.

Table 1 Summary of the size distribution histograms shown in Fig. 2. Note that the NAPMAm molar composition in the base gels was 5 mol%, and the 22 G syringe needle was used

Sample	Mean (mm)	Median (mm)	1st quartile (mm)	3rd quartile (mm)
100 rpm (Fig. 2(a))	2.62	2.57	1.83	3.44
150 rpm (Fig. 2(b))	1.42	1.29	0.93	1.80
175 rpm (Fig. 2(c))	1.23	1.10	0.83	1.46

---

When an aqueous solution droplet was added into the oil-phase solution under stirring, the vortex due to the stirring can induce the added pre-gel solution droplet to be divided into smaller liquid particles.³³ Therefore, if the silicone oil was stirred faster, the size distribution could be wider, and the mean value could become smaller. Furthermore, the larger syringe needle size can allow the larger droplet to be dropped into the silicone oil, which can elevate the mean size values (Fig. S1 and Table S1, ESI†). As the target gel size in this study was 1 mm, 175 rpm (Fig. 2(c)) might be the most efficient fabrication condition to collect the gels. Note that the efficient fabrication conditions, including stirring speed and syringe needle size, can be varied according to the gel target size. These results offer the strategy to produce gels efficiently with desirable sizes.

3.2. Equilibrium swelling behaviors of the spherical self-oscillating gels

In this study, we set two control parameters: (1) the NAPMAm molar composition in the base gels and (2) Ru(bpy)₃–NHS solution concentration during conjugation. Since Ru(bpy)₃ can be conjugated to the primary amine in NAPMAm, the selected parameters would affect the amount of Ru(bpy)₃ in the gel network.³⁴ Specifically, the NAPMAm molar composition can correspond with Ru(bpy)₃ catalyst immobilization sites in the gels. In contrast, the Ru(bpy)₃–NHS solution concentration can mean the amount of an active ester group for the conjugation. Firstly, we fixed the Ru(bpy)₃–NHS solution concentration to 70 mM and varied the NAPMAm molar composition to 2 mol%, 5 mol%, and 10 mol% (i.e., the NA2_Ru70, the NA5_Ru70, and the NA10_Ru70, respectively). The selected concentration of Ru(bpy)₃–NHS (70 mM) could lead all primary amino groups to react with Ru(bpy)₃–NHS molecules.^35,36 We also postulate that a lower concentration of Ru(bpy)₃–NHS than 70 mM might cause unsaturated Ru(bpy)₃ immobilization to the primary amino groups.

Fig. 3(a1)–(c1) exhibit the size change of corresponding self-oscillating gels in each redox state as a function of temperature. Note that the gel size was expressed as an equilibrium swelling ratio that indicates the value of the measured gel diameter divided by the diameter of the base gel before Ru(bpy)₃ conjugation (i.e., 1 mm). All the curves in both redox states decreased with rising temperature. In addition, when comparing the measured values in the same redox state and temperature, the values of the equilibrium swelling ratio decreased as the NAPMAm molar composition increased. The equilibrium swelling ratio in the oxidized state was larger than in the reduced state, and the difference was particularly evident at around 20 °C. Fig. 3(a2) and (a3), (b2) and (b3) and (c2) and (c3) visually display the optical images of the gels in each redox state at 20 °C, which reflect previously described results. To numerically analyze the difference, we fitted the plots of the measured equilibrium swelling ratio to the Boltzmann sigmoidal equation (eqn (s1), ESI†). The details about fitting results are provided in Table S2 (ESI†). The calculated differences in equilibrium swelling ratio between the two redox states at 20 °C were 3.73 × 10⁻², 4.88 × 10⁻², and 7.41 × 10⁻² for the NA2_Ru70 (Fig. 3(a1)), the NA5_Ru70 (Fig. 3(b1)), and the NA10_Ru70 (Fig. 3(c1)), respectively. Considering these results, we determined the temperature to be 20 °C to observe the volumetric self-oscillation behavior during the BZ reaction.

Fig. 3 The equilibrium swelling ratio of (a) the NA2_Ru70, (b) the NA5_Ru70, and (c) the NA10_Ru70 in the redox states. (a1)–(c1) The curves of the equilibrium swelling ratios indicating the measured (the circle marks) and the fitted (dotted line) result as a function of the temperature in each redox state. Optical images of the gels at 20 °C in (a2)–(c2) the oxidized state and (a3)–(c3) the reduced state. The equilibrium swelling ratio was defined as the value of the measured size divided by the gel size before Ru(bpy)₃ conjugation (i.e., 1 mm). The scale bars are 500 μm. The substrate solution for the oxidized state was composed of [HNO₃] = 894 mM and [NaBrO₃] = 84 mM, and [HNO₃] = 894 mM, [NaCl] = 84 mM, and [MA] = 64 mM for the reduced state. NaCl was utilized to maintain the ionic strength of the substrate solution.

We also fixed the NAPMAm molar composition in the base gel as 5 mol% and controlled the Ru(bpy)₃–NHS solution concentration to be 15 mM, 35 mM, and 70 mM (i.e., the NA5_Ru15, the NA5_Ru35, and the NA5_Ru70). Fig. 4(a1)–(c1) display the equilibrium swelling ratio in both redox states as a function of temperature. Note that the result of the NA5_Ru70 in Fig. 4(c) is the same as in Fig. 3(b). The curves were also temperature-dependent in both redox states. When comparing the measure values in the same redox state and temperature, the values decreased as the concentration of Ru(bpy)₃–NHS solution rose. The difference in the equilibrium swelling ratio between the redox states also became most apparent at about 20 °C. Fig. 4(a2) and (a3), (b2) and (b3) and (c2) and (c3) visually illustrate the gel images at 20 °C. We also fitted the measured equilibrium swelling ratio to the Boltzmann sigmoidal equation to mathematically calculate the redox amplitude at 20 °C (see Table S3, ESI† for details of the fitted parameter). The difference in the swelling ratio between redox states at 20 °C were 1.97 × 10⁻², 3.00 × 10⁻², and 4.88 × 10⁻² for the NA5_Ru15 (Fig. 4(a1)), the NA5_Ru35 (Fig. 4(b1)), and the NA5_Ru70 (Fig. 4(c1)), respectively. From these results, we decided on the observation temperature for the volumetric oscillation of the fabricated gels of 20 °C.

Fig. 4 The equilibrium swelling ratio of (a) the NA5_Ru15, (b) the NA5_Ru35, and (c) the NA5_Ru70 in the redox states. (a1, b1 and c1) The curves of the equilibrium swelling ratios signify the measured (the circle marks) and the fitted (dotted line) result as a function of the temperature in each redox state. Optical images of the gels at 20 °C in (a2, b2 and c2) the oxidized state and (a3, b3 and c3) the reduced state. The equilibrium swelling ratio was defined as the value of the measured size divided by the gel size before Ru(bpy)₃ conjugation (i.e., 1 mm). The scale bars are 500 μm. The substrate solution for the oxidized state was composed of [HNO₃] = 894 mM and [NaBrO₃] = 84 mM, and [HNO₃] = 894 mM, [NaCl] = 84 mM, and [MA] = 64 mM for the reduced state. NaCl was utilized to maintain the ionic strength of the substrate solution.

The self-oscillating gels are mainly composed of NIPAAm-based gel networks exhibiting temperature responsiveness.^11,13 Therefore, all analyzed self-oscillating gels displayed temperature-dependent size change trends. In addition, the hydrophobic bipyridine group in the conjugated Ru(bpy)₃ moiety could lead the self-oscillating gels to shrink after the conjugation process.^35,37 Since that hydrophobic effect can increase with the amount of conjugated Ru(bpy)₃ in the gels, the gels with a higher NAPMAm molar composition and Ru(bpy)₃–NHS concentration exhibited smaller sizes after conjugation.

The dependency of the swelling difference on the amount of Ru(bpy)₃ in the gel network was similar to the previous reports.^34,35,37 It has been reported that the oxidation of Ru(bpy)₃ (Ru(bpy)₃²⁺ → Ru(bpy)₃³⁺) induced increased hydrophilicity in the entire gel network, followed by the swelling with flow-in of water molecules. On the contrary, by the reduction (Ru(bpy)₃³⁺ → Ru(bpy)₃²⁺), the gel network becomes relatively less hydrophilic, resulting in the shrinkage with the flow-out of the water molecules. Once again, we note that the hydrophilicity can be manipulated by the amount of Ru(bpy)₃ in the network. Therefore, the NAPMAm molar composition and Ru(bpy)₃–NHS concentration can determine the equilibrium swelling ratio values depending on redox states. Interestingly, the changes in swelling ratio with redox changes were more dramatic when the NAPMAm molar composition varied than when the Ru(bpy)₃–NHS concentration varied. This may be because unreacted amino groups remain after Ru(bpy)₃ conjugation in the latter case. This result implies that manipulating the NAPMAm molar composition of the base gels could be more effective in realizing significant swelling changes, i.e., more practical for causing a large volumetric oscillation of the gels during the BZ reaction.

3.3. Volumetric oscillatory behaviors of the spherical self-oscillating gels

Fig. 5 displays the gel diameter and gray value profiles of (a) the NA2_Ru70 (Movie S1, ESI†), (b) the NA5_Ru70 (Movie S2, ESI†), and (c) the NA10_Ru70 (Movie S3, ESI†), as well as the obtained (d) period and (e) amplitude during the BZ reaction at 20 °C. As shown in Fig. 5(a1)–(c1) and Movies S1–S3 (ESI†), all gels show repetitive isotropic swelling/deswelling oscillation during the BZ reaction. In addition, the two oscillation profiles of gel diameter and the BZ reaction signal expressed as gray values were almost synchronized without a phase difference. The NA2_Ru70 (Fig. 5(a2)) exhibits a relatively small and narrow waveform compared to the NA5_Ru70 (Fig. 5(b2)) and the NA10_Ru70 (Fig. 5(c2)). In particular, the NA10_Ru70 presents the widest waveform. We analyzed the waveform of the diameter profiles by dividing the profile into three regions and measuring the time window of each region; the time window that (1) the gel begins to swell and reaches the peak (t_swell), (2) the gel maintains the volume before shrinkage (t_inter), and (3) the gel rapidly deswells (t_deswell). The measured time windows are sorted in Table 2. The NA2_Ru70 did not exhibit t_inter. All time windows increased as the NAPMAm composition became higher. Fig. 5(d) and (e) display the obtained period and amplitude, respectively. The period and the amplitude were evaluated, as shown in Fig. S2 (ESI†). Similar to the time window analysis, the period and amplitude increased as the NAPMAm composition escalated, and the results were statistically significant.

Fig. 5 Analysis of the volumetric oscillatory behaviors of the self-oscillating gels with modulated NAPMAm compositions, (a) the NA2_Ru70, (b) the NA5_Ru70, and (c) the NA10_Ru70 during the BZ reaction at 20 °C. (a1)–(c1) the gel diameter and the BZ reaction signal profiles (expressed as gray values of the green channel), (a2)–(c2) enlarged representative diameter profile indicating a single waveform. The (d) period and © amplitude obtained from the oscillation profiles. The substrate solution for the BZ reaction was composed of [HNO₃] = 894 mM and [NaBrO₃] = 84 mM, and [MA] = 64 mM. For each NA2_Ru70, NA5_Ru70, and NA10_Ru70, the sample sizes were n = 17, 16, and 7 for the period analysis, and n = 18, 17, and 8 for the amplitude analysis. “n.s.” indicates not statistically significant (p > 0.05) (*, p < 0.05) (**, p < 0.005).

Table 2 The time windows obtained from the oscillation waveform for the fabricated gels

Sample	NAPMAm mol%	Ru(bpy)3–NHS conc. (mM)	t swell (s)	t inter (s)	t deswell (s)
NA2_Ru70	2	70	351 ± 30.6	—	275 ± 41.8
NA5_Ru70	5	70	476 ± 55.5	72.5 ± 29.2	393 ± 62.2
NA10_Ru70	10	70	682 ± 98.6	1124 ± 314	591 ± 78.5
NA5_Ru15	5	15	—	—	—
NA5_Ru35	5	35	380 ± 29.4	50.0± 8.16	308 ± 15.0
NA5_Ru70	5	70	476 ± 55.5	72.5 ± 29.2	393 ± 62.2

---

Fig. 6 shows the gel diameter profiles of (a) the NA5_Ru15 (Movie S4, ESI†), (b) the NA5_Ru35 (Movie S5, ESI†), (c) the NA5_Ru70 (Movie S2, ESI†) (same as in Fig. 5(b)), and the obtained (d) period and (e) amplitude during the BZ reaction at 20 °C. The gels exhibited isotropic periodic volumetric oscillations during the BZ reaction, as illustrated in Fig. 6(a1)–(c1), Movies S4, S5 and S2 (ESI†). Additionally, in each oscillation profile, the oxidation and swelling changes of the gel occurred at almost the same time. The profile of the NA5_Ru15 (Fig. 6(a1) and (a2)) fluctuates compared to the oscillating profiles of the NA5_Ru35 (Fig. 6(b1) and (b2)) and the NA5_Ru70 (Fig. 6(c1) and (c2)). We also analyzed the waveforms by measuring the time window (t_swell, t_inter, and t_dswell), as listed in Table 2. Note that the fluctuating profiles of the NA5_Ru15 prevented analyzing its time windows. The values of the time windows, periods, and amplitude increased with Ru(bpy)₃–NHS concentration (Table 2 and Fig. 6(d) and (e)). When the Ru(bpy)₃–NHS concentration was changed for the fixed NAPMAm molar concentration (5 mol%), the variance in the volumetric oscillatory behaviors was not as dramatic as when the NAPMAm molar composition was controlled for the fixed Ru(bpy)₃–NHS concentration (70 mM). The statistical insignificance shown in Fig. 6(d) and (e) can also support this difference.

Fig. 6 Analysis of the volumetric oscillatory behaviors of the self-oscillating gels with varied Ru(bpy)₃–NHS concentration, (a) the NA5_Ru15, (b) the NA5_Ru35, and (c) the NA5_Ru70 during the BZ reaction at 20 °C. (a1)–d (c1) the gel diameter profiles and the BZ reaction signal profiles (signified as gray values of the green channel); (a2)–(c2) enlarged representative diameter profiles showing a single waveform. The (d) period and (e) amplitude obtained from the oscillation profiles. The substrate solution for the BZ reaction was composed of [HNO₃] = 894 mM and [NaBrO₃] = 84 mM, and [MA] = 64 mM. For each NA5_Ru15, NA5_Ru35, and NA5_Ru70, the sample sizes were n = 33, 16, and 16 for the period analysis, and n = 34, 17, and 17 for the amplitude analysis. “n.s.” indicates not statistically significant (p > 0.05) (*, p < 0.05) (**, p < 0.005).

We also evaluated the volumetric oscillations of the gels with larger diameters; 2 mm (Movie S6, ESI†) and 3 mm (Movie S7 and Fig. S3, ESI†). The NAPMAm molar composition and Ru(bpy)₃–NHS concentration were fixed as 5 mol% and 70 mM, respectively. Contrary to the isotropic oscillations in Movies S1–S5, ESI† Movie S6 displays non-isotropic volumetric oscillatory behavior, while Movie S7 (ESI†) shows non-volumetric oscillation during the BZ reaction. The details are provided in the ESI† 4.

The amount of Ru(bpy)₃ in the gel network could significantly affect the gel diameter and the volumetric oscillatory behaviors (i.e., the period and the amplitude) during the BZ reaction. Firstly, as previously described, the hydrophobicity of the bipyridine group in Ru(bpy)₃ moieties can lead the gels to shrink after Ru(bpy)₃ conjugation.^35,37 Since the NAPMAm molar composition in the base gel and Ru(bpy)₃–NHS concentration can determine the amount of Ru(bpy)₃ conjugated to the gel network, the baselines of the diameter profiles decreased as the NAPMAm molar composition and Ru(bpy)₃–NHS concentration increased (Fig. 5(a1)–(c1) and 6(a1)–(c1)). Secondly, it has been reported that the self-oscillating gels containing larger Ru(bpy)₃ amounts showed a more extended period and a larger amplitude,^14,38 which also corresponds to our results in Fig. 5(d) and (e) and 6(d) and (e). We address that the two described phenomena agree with the equilibrium swelling ratio analysis (Fig. 3 and 4). Because the self-oscillating gels undergo a volumetric change by repeated swelling in the oxidized state and deswelling in the reduced state, the difference in the equilibrium swelling ratio between redox states could potentially correlate to the volumetric amplitude of the gels during the BZ reaction.

We note that the NA5_Ru15 with a short period exhibited large standard deviations in both period and amplitude compared to other gels. In self-oscillating gels, the redox state change of Ru(bpy)₃ by the BZ reaction dominates the volumetric deformation pattern of the gels.^11,13 The mechanical response of the gel network is intrinsically slow; therefore, sometimes, the gel network deformation cannot follow the fast repetitive redox changes by the BZ reaction.^13,34,35 For instance, when Ru(bpy)₃ is oxidized to Ru(bpy)₃³⁺, the gel network will start to swell. However, if the redox change of the corresponding BZ reaction is relatively fast and not balanced with the mechanical response of the gel, Ru(bpy)₃ can be occasionally reduced to Ru(bpy)₃²⁺ before the gel network is completely swollen. Thus, we argue that this delayed mechanical response to the redox change can easily lead the gel diameter profiles to fluctuate, showing large standard deviations.

To clearly discuss the obtained waveform and the time windows, we refer to the Field–Körös–Noyes (FKN) mechanism,¹² which explains the process of the BZ reaction. According to the FKN mechanism, the BZ reaction can be divided into three concurrent processes as follows: process A meaning the consumption of the bromide ion (Br⁻), Process B indicating the catalyst oxidization accompanying the autocatalytic reaction of bromous acid (HBrO₂), and Process C signifying the catalyst reduction by malonic acid.

BrO₃⁻ + 5Br⁻ + 6H⁺ → 3Br₂ + 3H₂O (Process A)

BrO₃⁻ + HBrO₂ + 2M_RED + 3H⁺ → 2HBrO₂ + M_OXI + H₂O (Process B)

2M_OXI + MA + BrMA → 2M_RED + fBr⁻ + other products (Process C)

M_OXI and M_RED indicate oxidized and reduced metal catalysts, respectively. f denotes a stoichiometric factor. Considering this process, we can postulate that Process B is mainly involved in t_swell, while Process C is linked to t_inter and t_deswell. We note again that the three substrates (H⁺, BrO₃⁻ and MA) are required to promote the three processes in the FKN mechanism. Given that Ru(bpy)₃ is immobilized in the gel network, the substrates should diffuse into the gel network and approach the site with immobilized Ru(bpy)₃.^39,40 Thus, the diffusion rate of the BZ substrates could influence the kinetics of the BZ reaction and the self-oscillatory behavior. In this regard, the previous reports can give insight into partially explaining how substrate-diffusion affects self-oscillatory behavior during the BZ reaction.

Here we discuss the possible parameters which can affect the diffusion behavior of the substrates into the gel network, based on the previous reports. Theoretically, the mesh size of the gels or the dynamic free volume void can control the diffusion of the solute and water molecules.^41,42 The former indicates the distance between the neighboring crosslinked point. The latter signifies the micro/nano-sized open space not occupied by molecular substances in the gel network. The size of diffused substances is also a significant consideration. However, here we mainly focus on the gel network because we altered the property of the gel network in this study.

We consider the size of the NIPAAm, NAPMAm, and the Ru(bpy)₃ moiety. The NIPAAm and NAPMAm feature roughly similar backbone lengths of 0.25 nm, while the Ru(bpy)₃ moiety has a spherical shape with approximately 1.3 nm diameter.³⁶ Note that the mesh size of the PNIPAAm-based gels is typically in the nanometer order.^43–46 Considering this, introducing bulky Ru(bpy)₃ into the gel network could lead to a considerably crowded state by the excluded volume effect in the gel network. From this viewpoint, we argue that the excluded volume of conjugated Ru(bpy)₃ can contribute to narrowing the space where the substrate molecules can pass. Note that the space could imply the room between the mesh as well as the dynamic free volume void. It would be reasonable to assume that the increased amount of localized Ru(bpy)₃ in the gel could cause its elevated excluded volume effect. Thus, augmenting the immobilized Ru(bpy)₃ amount can delay the diffusion rate of the BZ substrates from the external solution into the gel network.

From a similar perspective on substrate diffusion, the gel shrinkage after conjugating Ru(bpy)₃ could partially affect the time window. The relatively small gels with a larger amount of Ru(bpy)₃ might provide narrower water channels than those with a small amount of Ru(bpy)₃, contributing to slower diffusion of the BZ substrates. We also assert that the intrinsic hydrophobicity of the bipyridine group can simultaneously contribute to the retarded diffusion of the BZ substrate into the gel network more.

We address that the slow diffusion of the substrates could retard each step of the FKN mechanism.⁴⁷ For instance, delayed diffusion of BrO₃⁻ into the gel network could mainly slow down Process B, inducing a longer t_swell. Similarly, the prolonged diffusion of MA could largely impede Process C, causing a longer t_deswell. Therefore, the time windows and the waveforms in this system could depend on the parameters related to the amount of introduced Ru(bpy)₃ (i.e., NAPMAm molar composition and the concentration of Ru(bpy)₃–NHS solution). In addition, insufficient diffusion of MA can hinder Process C, affecting the existence and length of t_inter. Specifically, t_inter can significantly influence the waveform. For example, the NA2_Ru70 exhibited a sharp waveform without a plateau region (Fig. 5(a)). In contrast, the NA5_Ru70 displayed a plateau region between the increasing and decreasing profile (Fig. 5(b)). Furthermore, the NA10_Ru70 features the widest waveform with a longer plateau region in the interim section (Fig. 5(c)), which can be theorized to be a result of the delayed Process C.

In this study, we fabricated submillimeter-scaled spherical self-oscillating gels by inverse phase suspension polymerization. We also experimentally analyzed the dependency of the period, the amplitude, and the oscillatory waveform during the BZ reaction on (1) the NAPMAm molecular composition in the base gels and (2) Ru(bpy)₃–NHS concentration during conjugation. Both the period and the amplitude increased as the selected parameters elevated. In addition, the waveform of the diameter profiles broadened with increasing the values of the parameters.

We first discuss the fabrication method of the spherical gels. As previously shown, Fig. 1 and Fig. S1 (ESI†) provided the size distribution of the fabricated spherical gels. Here we introduced practical strategies to control the size distribution. We address some candidates to narrow the size distribution, which could help produce the target-sized gels. One possible strategy is to control the droplet size falling from the syringe needle. Surfactants, such as Tween (non-ionic), cetrimonium bromide (CTAB), or sodium dodecyl sulfate (SDS) (anionic), might be adopted.^48–50 We note that surfactant can affect the surface tension, which changes the droplet size from the syringe needle tip. Simultaneously, increasing the droplet viscosity with a thickener (e.g., carboxymethyl cellulose) can be considered because it may prevent the droplet breaking in the stirring oil phase. Exploiting a more viscous oil phase could also be a significant candidate to hinder the breakage of the droplet during the agitation, inducing the narrowed size distribution. Controlling the size of the syringe needles and stirring speed adopted in this study also needs to be considered. At any level, we assert that our result will be a definite reference point to produce target-sized spherical gels efficiently.

For the volumetric oscillation of the gels during the BZ reaction, various factors such as the ionic effect of the residual ionic monomers; the frictional effect of solvent and monomers; and the elasticity of the gel network, which may also affect the BZ reaction, are intertwined. This complexness could hinder forecasting the volumetric oscillatory behavior of the self-oscillating gels. Therefore, direct experimental verification will be important in understanding the volume oscillations of the gel. Significantly, here we experimentally verified the behaviors of submillimeter-scaled spherical self-oscillating gels, including the fabrication process and detailed strategy to control the volumetric oscillatory behaviors. This study can fill the knowledge gap between the nano/micro-scaled and millimeter-scaled systems which have been reported so far, leading to an insight encompassing the overall scale systems.

Our experimental studies on the spherical self-oscillating gel can promote a comprehensive understanding and advance of the BZ system. From a geometrical perspective, a spherical shape can offer almost the same boundary conditions depending on the gel shape compared to other designs (e.g., cylinder⁵¹). Thus we may discuss the swelling behaviors of the various-sized spherical gels without considering geometry effects. Notably, the kinetics of the volume phase transition of the gels has been theoretically analyzed using spherical coordinate systems.^30,31 The results of isotropic oscillations in the spherical gels obtained here might apply to compare and theoretically forecast the self-oscillatory behaviors in various gels. Furthermore, the self-oscillating gels can be fused with previous studies, including surface modification.^52–54 This is because the spherical form is a representative geometrical model for surface modification of the substrate. These applications may lead to new self-oscillatory functions. We emphasize that those emergent functions might also be studied with theoretical and simulation approaches that benefit from the spherical shape-based analysis.

Although detailed quantitative evaluations of the introduced Ru(bpy)₃ amount and the analysis of the influence of the residual ionic monomers on the gel swelling may be required in the future, we believe that the experimentally accumulated knowledge obtained in this study will be a more concrete foundation for functional control and application of the self-oscillating gels.

4. Conclusion

In this study, we established a fabrication process to produce submillimeter-sized spherical self-oscillating gels. The fabricated self-oscillating gels exhibited a clear isotropic swelling/deswelling volume change during the BZ reaction. In addition, we varied the conjugated Ru(bpy)₃ amount in the gel network by varying (1) the NAPMAm molar composition in the base gels and (2) the concentration of Ru(bpy)₃–NHS solution in the conjugation process. We experimentally proved that controlling the selected parameters, which could cause a changed Ru(bpy)₃ amount in the gel network, can determine the volumetric oscillatory behavior (i.e., the period and the amplitude). The results provide unexplored fundamental knowledge in the current research of the self-oscillating gels regarding scale (i.e., submillimeter-sized) and shape design (i.e., spherical). This study could be a versatile milestone for broadening the applications of self-oscillating gels such as biomimetic actuators.

Author contributions

W.S. Lee contributed to designing the system, collecting the data, performing the analysis, and writing the paper. T. Enomoto, A. M. Akimoto, and R. Yoshida contributed to analyzing and organizing the data. All authors contributed to conceiving and designing the analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by the Grants-in-Aid for Science Research (No. 20H00388 to R.Y.) from the Ministry of Education, Culture, Sports, Science, and Technology of Japan. We would like to thank Ms Su-wen Lee for the English language editing.

References

1. I. Galaev and B. Mattiasson, Smart polymers: applications in biotechnology and biomedicine, CRC Press, Boca Raton, FL, 2nd edn, 2008.
2. A. S. Hoffman, Adv. Drug Delivery Rev., 2013, 65, 10–16.
3. F. Liu and M. W. Urban, Prog. Polym. Sci., 2010, 35, 3–23.
4. M. J. Majcher and T. Hoare, in Functional Biopolymers, ed. M. A. Jafar Mazumder, H. Sheardown and A. Al-Ahmed, Springer International Publishing, Cham, 2019, pp. 453–490.
5. C. N. Kotanen, A. N. Wilson, A. M. Wilson, K. Ishihara and A. Guiseppi-Elie, Biomed. Microdevices, 2012, 14, 549–558.
6. F. Lancia, A. Ryabchun and N. Katsonis, Nat. Rev. Chem., 2019, 3, 536–551.
7. S. Bauer, S. Bauer-Gogonea, I. Graz, M. Kaltenbrunner, C. Keplinger and R. Schwödiauer, Adv. Mater., 2014, 26, 149–162.
8. R. Geryak and V. v Tsukruk, Soft Matter, 2014, 10, 1246–1263.
9. P. Cordier, F. Tournilhac, C. Soulié-Ziakovic and L. Leibler, Nature, 2008, 451, 977–980.
10. A. C. Daly, M. D. Davidson and J. A. Burdick, Nat. Commun., 2021, 12, 753.
11. R. Yoshida, T. Takahashi, T. Yamaguchi and H. Ichijo, J. Am. Chem. Soc., 1996, 118, 5134–5135.
12. R. J. Field and R. M. Noyes, J. Chem. Phys., 1974, 60, 1877–1884.
13. R. Yoshida, Polym. J., 2022, 54, 827–849.
14. R. Yoshida, M. Tanaka, S. Onodera, T. Yamaguchi and E. Kokufuta, J. Phys. Chem. A, 2000, 104, 7549–7555.
15. L. Howell, E. Osborne, A. Franklin and E. Hébrard, J. Phys. Chem. B, 2021, 125, 1667–1673.
16. R. Teng, L. Ren, L. Yuan, L. Wang, Q. Gao and I. R. Epstein, J. Phys. Chem. A, 2019, 123, 9292–9297.
17. R. Toth and A. F. Taylor, Prog. React. Kinet., 2006, 31, 59–115.
18. L. Ren, M. Wang, C. Pan, Q. Gao, Y. Liu and I. R. Epstein, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8704–8709.
19. T. Masuda, A. M. Akimoto, K. Nagase, T. Okano and R. Yoshida, Sci. Adv., 2016, 2, e1600902.
20. L. Ren, L. Yuan, Q. Gao, R. Teng, J. Wang and I. R. Epstein, Sci. Adv., 2020, 6, eaaz9125.
21. X. Li, J. Li, Z. Zheng, J. Deng, Y. Pan and X. Ding, Soft Matter, 2022, 18, 482–486.
22. S. Maeda, Y. Hara, T. Sakai, R. Yoshida and S. Hashimoto, Adv. Mater., 2007, 19, 3480–3484.
23. Y. Shiraki and R. Yoshida, Angew. Chem., Int. Ed., 2012, 51, 6112–6116.
24. O. Tabata, H. Hirasawa, S. Aoki, R. Yoshida and E. Kokufuta, Sens. Actuators, A, 2002, 95, 234–238.
25. S. Matsui, K. Inui, Y. Kumai, R. Yoshida and D. Suzuki, ACS Biomater. Sci. Eng., 2019, 5, 5615–5622.
26. K. Inui, I. Saito, R. Yoshida, H. Minato and D. Suzuki, ACS Appl. Polym. Mater., 2021, 3, 3298–3306.
27. D. Suzuki and R. Yoshida, Macromolecules, 2008, 41, 5830–5838.
28. D. Suzuki, T. Sakai and R. Yoshida, Angew. Chem., Int. Ed., 2008, 47, 917–920.
29. D. Suzuki, H. Taniguchi and R. Yoshida, J. Am. Chem. Soc., 2009, 131, 12058–12059.
30. T. Tanaka, E. Sato, Y. Hirokawa, S. Hirotsu and J. Peetermans, Phys. Rev. Lett., 1985, 55, 2455–2458.
31. T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218.
32. T. Ueki, M. Onoda, R. Tamate, M. Shibayama and R. Yoshida, Chaos, 2015, 064605.
33. H. Tokuyama and N. Yazaki, React. Funct. Polym., 2010, 70, 967–971.
34. W. S. Lee, T. Enomoto, A. M. Akimoto and R. Yoshida, NPG Asia Mater., 2022, 14, 12.
35. T. Masuda, A. Terasaki, A. M. Akimoto, K. Nagase, T. Okano and R. Yoshida, RSC Adv., 2015, 5, 5781–5787.
36. T. Geher-Herczegh, Z. Wang, T. Masuda, R. Yoshida, N. Vasudevan and Y. Hayashi, Macromolecules, 2021, 54, 6430–6439.
37. R. Mitsunaga, K. Okeyoshi, R. Yoshida and T. Li, Chem. Commun., 2013, 49, 4935–4937.
38. I. C. Chen, O. Kuksenok, V. V. Yashin, R. M. Moslin, A. C. Balazs and K. J. van Vliet, Soft Matter, 2011, 7, 3141–3146.
39. D. Suzuki and R. Yoshida, J. Phys. Chem. B, 2008, 112, 12618–12624.
40. R. Yoshida, S. Onodera, T. Yamaguchi and E. Kokufuta, J. Phys. Chem. A, 1999, 103, 8573–8578.
41. T. Fujiyabu, X. Li, U. il Chung and T. Sakai, Macromolecules, 2019, 52, 1923–1929.
42. E. Axpe, D. Chan, G. S. Offeddu, Y. Chang, D. Merida, H. L. Hernandez and E. A. Appel, Macromolecules, 2019, 52, 6889–6897.
43. E. Parrish, S. C. Seeger and R. J. Composto, Macromolecules, 2018, 51, 3597–3607.
44. X. Lin, R. Huang and M. Ulbricht, J. Mater. Chem. B, 2016, 4, 867–879.
45. N. Adrus and M. Ulbricht, J. Mater. Chem., 2012, 22, 3088–3098.
46. A. M. Gajda and M. Ulbricht, J. Mater. Chem. B, 2014, 2, 1317–1326.
47. T. Masuda, A. M. Akimoto, M. Furusawa, R. Tamate, K. Nagase, T. Okano and R. Yoshida, Langmuir, 2018, 34, 1673–1680.
48. P. Zaheri, H. Abolghasemi and M. Zaheri, Chem. Eng. Res. Des., 2013, 91, 396–402.
49. A. Bak and W. Podgórska, Chem. Eng. Sci., 2012, 74, 181–191.
50. A. J. G. Zarbin, Mater. Horiz., 2021, 8, 1409–1432.
51. X. J. Lu, L. Ren, Q. Y. Gao, Y. Y. Yang, Y. M. Zhao, J. Huang, X. L. Lv and I. R. Epstein, J. Phys. Chem. Lett., 2013, 4, 3891–3896.
52. K. Matsukawa, T. Masuda, A. M. Akimoto and R. Yoshida, Chem. Commun., 2016, 52, 11064–11067.
53. K. Zhang, W. Yan, R. Simic, E. M. Benetti and N. D. Spencer, ACS Appl. Mater. Interfaces, 2020, 12, 6761–6767.
54. K. Zheng, B. Sui, K. Ilyas and A. R. Boccaccini, Mater. Horiz., 2021, 8, 300–335.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01604d

---