Open Access Article
Open Access ArticleDynamics of the axon plasma membrane skeleton†
Zhaojie
Chai
 a,
Shiju
Gu
a,
Shiju
Gu
 b and
George
Lykotrafitis
b and
George
Lykotrafitis
 *ab
*ab
aDepartment of Mechanical Engineering, University of Connecticut, Storrs, CT 06269, USA. E-mail: george.lykotrafitis@uconn.edu
bDepartment of Biomedical Engineering, University of Connecticut, Storrs, Connecticut, USA
First published on 13th March 2023
Abstract
It was recently revealed via super-resolution microscopy experiments that the axon plasma membrane skeleton (APMS) comprises a series of periodically arranged azimuthal actin rings connected via longitudinal spectrin filaments forming an orthotropic network. The common perception is that APMS enhances structural stability of the axon but its impact on axon deformation is unknown. To investigate the response of the APMS to extension, we introduce a coarse-grain molecular dynamics model consisting of actin particles forming rings and chains of particles representing spectrin tetramers with repeats than can unfold. We observe that the shape of force–extension curve is initially linear and the force level depends on the extension rate. Even during the initial deformation stage, unfolding of spectrin repeats occurs, but the saw-tooth shape of the corresponding force–extension curve observed in the case of one spectrin tetramer does not appear in the case of the entire APMS. The reason is that spectrin unfolding is not synchronized across filaments during extension. If actin–spectrin associations remain intact, the force–extension response reaches a perfectly plastic region because of increased spectrin unfolding frequency. However, when actin–spectrin links dissociate, which can happen at moderate and high extension rates, APMS softens and the resistance force decreases linearly as the axon elongates until it reaches a point where the APMS is completely severed. Furthermore, when the ring-to-ring distance is maintained fixed under stretch, the resistance force relaxes exponentially as a function of time due to additional unfolding of spectrin tetramers following the Kelvin–Voigt representation of the Zener model.
1. Introduction
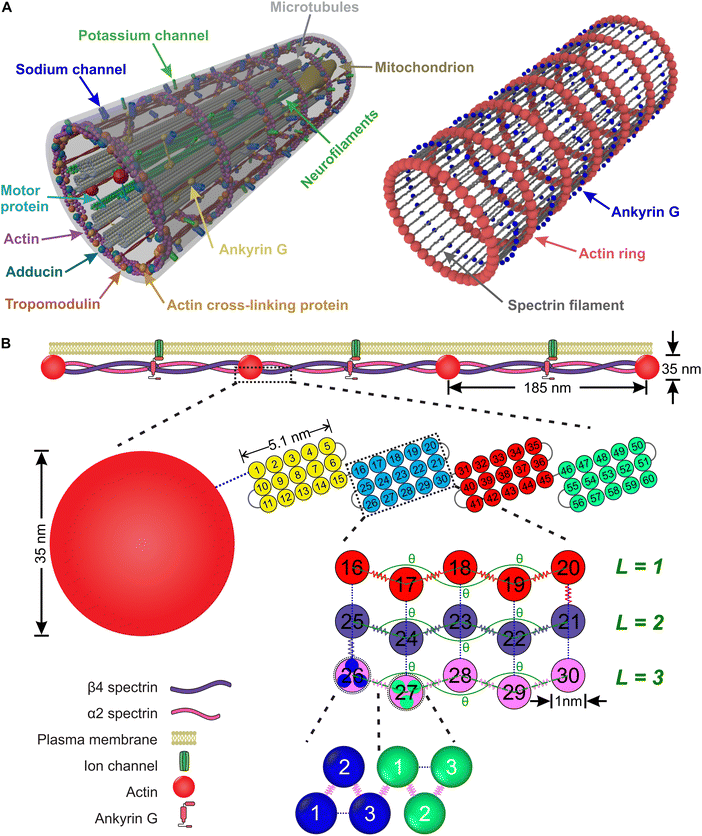
An axon is typically a long cylindrical neuronal projection whose main function is to integrate electrical signals and transmit them as a single or a sequence of action potentials. It consists of the plasma membrane and several endoplasmic filaments and organelles including microtubules, neurofilaments, and mitochondria. The axon plasma membrane (APM) is formed by two main substructures: the phospholipid bilayer and the membrane skeleton.1,2 In recent years, significant progress has been made in relation to the structural characterization of the axon plasma membrane skeleton (APMS). Importantly, in 2013 it was revealed via super-resolution microscopy that the APMS comprises a series of periodically arranged azimuthal actin rings connected via longitudinal spectrin tetramer filaments and other associated molecules with an approximately 190 nm periodicity of the actin rings (Fig. 1A).3 In mature neurons (DIV > 10), the lipid bilayer is anchored to the APMS via ankyrin G, in the axon initial segment (AIS) and proximal axon, and via ankyrin B in the distal axon.4,5 Ankyrin links the membrane skeleton and the endoplasmic filamentous axon skeleton by binding to the carboxyl terminus of beta IV-spectrin, which is located near the middle area of a spectrin tetramer, and to a microtubule via microtubule-associated proteins.6,7 The distribution of ankyrin along the axon is thus highly periodic and in an out-of-phase arrangement with respect to actin. We note that voltage-gated sodium (Nav) channels are associated to ankyrin G in the AIS and as a result their plasma membrane distribution is also periodic and out-of-phase with respect to actin rings.3It is important for axons to maintain their morphology and integrity during deformations which can be significant even during normal daily activities. It had been routinely hypothesized that stability of the axon is mainly due to endoplasmic filaments and specifically to bundles of microtubules because of their large stiffness compared to plasma membrane.1,8–11 However, the recent discovery of the unique periodic structure of the APMS and its connectivity to endoplasmic filaments via Ankyrin, offers new possibilities in understanding neuronal axons durability. It was recently shown that the APMS can significantly shield microtubules during applied tissue stress.12 Additionally, it has been demonstrated that the loss of beta-spectrin, one of the main components of APMS, in C. elegans leads to spontaneous breaking of axons, which is caused by mechanical strains generated by mere animal movement, and that such axon breaking phenotype can be prevented by paralyzing the animal to reduce movement induced mechanical strains.13,14 It was also recently shown that actin rings are required to maintain microtubule organization.15 Due to those findings it is now accepted that the APMS in coordination with microtubules and other axonal filaments such as neurofilaments contributes in maintaining integrity and mechanical stability of the axon.16–18
Axonal extension has attracted a significant interest due to its relation to traumatic axonal injury, which is an important type of traumatic brain injury leading to localized axon damage, partial disruption of intracellular transport, and subsequent degeneration.10,19 It has also been shown that it is related to neurotransmission because it interferes with clustering of neurotransmitter vesicles.20 There is significant experimental evidence that an observable interaction between the endoplasmic cytoskeleton and the APMS during axon extension experiments occurs.21 However, it is important to clarify the mechanical behavior of the APMS separately from the endoplasmic cytoskeleton. While there exists a significant amount of work on modeling of the behavior of the entire axon during extension22–26 and in particular of the microtubules network,11,27 there is a very limited work on modelling extension of the APMS. In this paper, we focus on just that, the mechanical behavior of the APMS during extension and during relaxation.
One of the main filaments comprised in the APMS is the spectrin tetramer, which is formed by two antiparallel heterodimers consisting of α- and β-subunits with 22 and 17-triple-helical domains, respectively.28 Single molecule atomic force microscopy experiments demonstrated that an individual spectrin repeat mechanically unfolds in an all-or-none process when it is subjected to 25 to 35 pN force and it refolds when it is relaxed.29 Under tension the alternative topologies could gain mechanical stability. These distinct properties of spectrin filaments critically determine the behavior of the APMS and most likely of the entire axon during extension.30 Actin rings are formed by actin filaments and the associated actin-capping protein adducin and are stable after 7 days in vitro (DIV). Actin and spectrin are cross-linked to form the APMS in the presence of ankyrin. Maturation of the axon is dynamic and it is evolved during the early stages before it reaches its final structure at approximately DIV 10.5,31
In this paper, we investigate the mechanical behavior of the APMS under extension and relaxation. To this end, we develop a spring chain model for spectrin tetramers allowing unfolding of spectrin repeats under extension and refolding when no force is applied. We validate the model by comparing numerical and experimental results.29 We also implement a model for actin rings, which can reproduce the axon's stiffness as measured via atomic force microscopy.32 By combining the two models and with the addition of a particle representation of ankyrin, we build a particle-based model for the APMS. We note that we implement dynamic association between actin and spectrin allowing, in principle, dissociation and re-forming of actin–spectrin links. Then, we use the model to investigate the mechanical behavior of the APMS during extension and relaxation taking into consideration possible unfolding of spectrin filaments and dissociation of actin–spectrin links.
2. Model and methods
In this section, we introduce a coarse-grain molecular dynamics (CGMD) model for the APMS comprising azimuthal actin rings connected to longitudinal foldable spectrin filaments, which are connected to ankyrin particles (Fig. 1).2.1. Computational model for the axonal actin rings
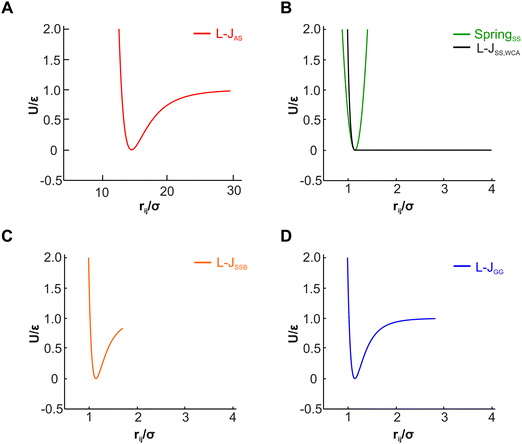
The actin rings consist of short actin filaments arranged along the circumference of the axon.3 Because the exact molecular structure of the actin rings is not known and whether actin filaments are connected side by side or they are in an end-to-end arrangement has not been determined, we adopted a coarse-grain particle model that produces stable actin rings but it does not consider their specific molecular structure.32 In this coarse-grain particle model, an actin ring contains 39 actin beads (Fig. 1A) with a bead diameter of approximately 35 nm, which is close to the size of actin junctions in red blood cells (RBCs).33 These beads form a circle with a diameter of approximately 434 nm, which is within the range of an actual axon diameter.3,5Adjacent actin particles i and j in the same ring are connected via a spring potential UAAspring(rAAij) = 1/2kA(rAAij − rAAeq)2 and the purely repulsive L-J, or as it is sometime called Weeks–Chandler–Andersen (WCA)34 potential
 | (1) |
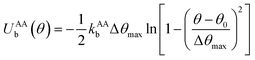 to maintain the circular configuration of the actin rings. In the FENE bending potential, kAAb = 3500kBT determine the bending stiffness of the actin filament. This value of kAAb resulted in actin filament bending rigidity κbend = 7.1 × 10−26 N m2, which is consistent with a reported experimental value of 7.3 × 10−26 N m2.35,36θ is the angle formed by three consecutive actin beads in the same actin ring,
to maintain the circular configuration of the actin rings. In the FENE bending potential, kAAb = 3500kBT determine the bending stiffness of the actin filament. This value of kAAb resulted in actin filament bending rigidity κbend = 7.1 × 10−26 N m2, which is consistent with a reported experimental value of 7.3 × 10−26 N m2.35,36θ is the angle formed by three consecutive actin beads in the same actin ring,  is the equilibrium angle, and Δθmax = 0.3θ0 is the maximum allowed bending angle (Table S1, ESI†). We note that the combination of kAAb and Δθmax in the bending potential equation determines the stiffness of the structure. The angle Δθmax defines the maximum local deformation of the actin rings but its exact value does not affect the behavior of the system near equilibrium. Because of this, we chose to use Δθmax = 0.3θ0.32
is the equilibrium angle, and Δθmax = 0.3θ0 is the maximum allowed bending angle (Table S1, ESI†). We note that the combination of kAAb and Δθmax in the bending potential equation determines the stiffness of the structure. The angle Δθmax defines the maximum local deformation of the actin rings but its exact value does not affect the behavior of the system near equilibrium. Because of this, we chose to use Δθmax = 0.3θ0.32
2.2. Computational model for spectrin filaments
A spectrin filament is a tetramer comprised of two identical, intertwined antiparallel heterodimers. Each dimer in a mature neuron after DIV 10 comprises an αII-spectrin filament consisting of 22 homologous triple-helical repeats, and a βIV-spectrin filament in the AIS and proximal axon or a βII-spectrin filament in the distal axon, consisting of 17 homologous triple-helical repeats.28,31,37 In this work, we represent a spectrin tetramer as a chain of 39 repeats. The length of a repeat is Lc/39 = 5.1 nm with Lc ≃ 200 nm being the contour length of a spectrin tetramer (Fig. 1B). It has been shown that the repeats are mostly 106 amino-acids long, which are arranged in three antiparallel stranded α-helical coils.38 Considering that the length of each amino acid is approximately 0.15 nm,39 the length of each repeat is estimated to approximately be 106/3 × 0.15 nm = 5.3 nm, which matches the repeat length implemented in the spectrin filament model here.39 For α-helical segments, the length of the residue is 0.15 nm, whereas, for non-helical segments, the length is 0.37 nm per residue.40 To obtain the same characteristics of α-helical segments, we use a virtual ball structure containing 3 beads successively connected via a spring potential (Fig. 1B). The center of a virtual ball is the center of mass of the three corresponding spectrin beads.All three beads in a virtual ball interact via the WCA potential
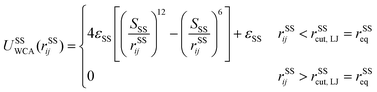 | (2) |
 | (3) |
A completely unfolded repeat contains not only the non-helical segments, which comprise elongated residues, but unfolded segments as well.39 The length of a fully unfolded repeat is approximately 31.7 nm based on force–extension AFM measurements obtained by Rief et al.29,41 In order for our model to represent unfolded segments, we use a three-segment structure. Virtual balls in the same repeat but in different segments interact via their corresponding spectrin beads through the Lennard-Jones (L-J) potential (Fig. 2D)
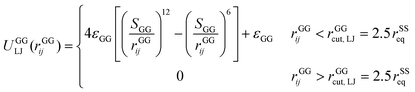 | (4) |
 | ||
| Fig. 3 Representation of a spectrin repeat. There are 3 segments in one repeat. The same color beads are within one segment of a repeat. (A) Folded spectrin repeat. (B) Unfolded spectrin repeat. | ||
Overall, in our spectrin filament model, we use a chain of 1755 beads connected by a spring potential USSspring(rSSij) = 1/2kS(rSSij − rSSeq)2 in series (Table S2, ESI†). The equilibrium distance between two consecutive virtual balls is rBBeq ≅ Lc/(5 × 39) ≅ 1.03 nm, where Lc ≅ 200 nm. Two consecutive repeats contain 10 virtual balls or 15 beads along their length (see Fig. 1B) resulting to an equilibrium distance between two beads within a virtual ball rSSeq ≅ rBBeq × 10/15 ≅ 0.685 nm. A spectrin tetramer is a chain comprising 39 repeats. Each repeat contains 45 beads grouped in 15 virtual balls, which are arranged in 3 segments of 5 virtual balls per segment. Furthermore, all spectrin beads interact via the WCA potential (eqn (2)), where the equilibrium distance is rSSeq = 21/6σ = 0.685 nm yielding a unit length of σ ≅ 0.61 nm.
Finally, in each segment we apply the FENE bending potential of  between consecutive virtual balls to stabilize the shape of the spectrin repeat (Table S2, ESI†), where kBBb = 5kBT is the stiffness that directly controls the bending rigidity of segments. The angle formed by the three consecutive spectrin virtual balls of the same segment is θ with an equilibrium angle θ0 = 180°, which means that the consecutive virtual balls are initially located along a straight line (Fig. 1B). The maximum allowed deformation angle is Δθmax = 0.3θ0. We note that, similar to actin rings, the combination of kBBb and Δθmax determines the stiffness of the structure. However, the value of Δθmax does not affect the behavior of a spectrin filament at small deformations near thermal equilibrium. Because of this, we choose to use Δθmax = 0.3θ0, which gives margin for flexibility to the bending potential.42
between consecutive virtual balls to stabilize the shape of the spectrin repeat (Table S2, ESI†), where kBBb = 5kBT is the stiffness that directly controls the bending rigidity of segments. The angle formed by the three consecutive spectrin virtual balls of the same segment is θ with an equilibrium angle θ0 = 180°, which means that the consecutive virtual balls are initially located along a straight line (Fig. 1B). The maximum allowed deformation angle is Δθmax = 0.3θ0. We note that, similar to actin rings, the combination of kBBb and Δθmax determines the stiffness of the structure. However, the value of Δθmax does not affect the behavior of a spectrin filament at small deformations near thermal equilibrium. Because of this, we choose to use Δθmax = 0.3θ0, which gives margin for flexibility to the bending potential.42
 ,44 and the contour length of spectrin filament is approximately 200 nm.37,45 Based on the above quantities, we compute the persistence length of a spectrin filament to be 16.6 nm, which is close to the reported experimental values of 10 nm46 and 20 nm.43
,44 and the contour length of spectrin filament is approximately 200 nm.37,45 Based on the above quantities, we compute the persistence length of a spectrin filament to be 16.6 nm, which is close to the reported experimental values of 10 nm46 and 20 nm.43
2.3. Computational model of the APMS
We combine the actin ring and spectrin filament models described above along with a particle representation of ankyrin to simulate the APMS (Fig. 5). The spectrin filaments in a normal neuronal axons are extended to approximately their contour length. The APMS behaves as an orthotropic material with different mechanical properties in the azimuthal direction compared to longitudinal direction. We note that the main difference between the current work and the work by Zhang et al.32 is that here the spectrin filaments are extendable while in the previous work they were not. This difference allows us to study extension of the APMS axons beyond the artificial limit set by the spectrin contour length and to also study relaxation of the APMS. . The equilibrium distance between the centers of the two actin rings is set to dRReq = 185 nm, the maximum allowed deformation is Δdmax = 0.3dRReq, and the distance between two consecutive actin rings is d, which is calculated by measuring the mean value of the corresponding coordinate of particles belonging to the same ring. Finally, we determine that kmt ≃ 239kBT/σ ≃ 19
. The equilibrium distance between the centers of the two actin rings is set to dRReq = 185 nm, the maximum allowed deformation is Δdmax = 0.3dRReq, and the distance between two consecutive actin rings is d, which is calculated by measuring the mean value of the corresponding coordinate of particles belonging to the same ring. Finally, we determine that kmt ≃ 239kBT/σ ≃ 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822kBT/dRReq at T = 300 K based on the longitudinal Young's modulus of the axon EL ≃ 10 kPa.55 The parameters of this FENE potential can be found in Table S1 (ESI†).32
822kBT/dRReq at T = 300 K based on the longitudinal Young's modulus of the axon EL ≃ 10 kPa.55 The parameters of this FENE potential can be found in Table S1 (ESI†).32
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085 particles. We use the Beeman's algorithm to integrate the equations of motion. The temperature of the system is controlled by the Nose–Hoover thermostat at kBT/ε = 0.22. The model is implemented in the NVT ensemble with a timescale of
085 particles. We use the Beeman's algorithm to integrate the equations of motion. The temperature of the system is controlled by the Nose–Hoover thermostat at kBT/ε = 0.22. The model is implemented in the NVT ensemble with a timescale of 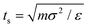 and time step of Δt = 0.01ts. We first equilibrate the models for 106 time steps and then run it for 10 × 106 time steps after equilibration. We performed the simulations on a high-performance computing cluster at the University of Connecticut and on the San Diego Supercomputer Center supported by the Extreme Science and Engineering Discovery Environment.56
and time step of Δt = 0.01ts. We first equilibrate the models for 106 time steps and then run it for 10 × 106 time steps after equilibration. We performed the simulations on a high-performance computing cluster at the University of Connecticut and on the San Diego Supercomputer Center supported by the Extreme Science and Engineering Discovery Environment.56
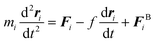 | (5) |
| 〈FBi〉 = 0 | (6) |
 | (7) |
3. Results and discussion
We first simulate the behavior of a single spectrin filament during extension and validate our model using published experimental data, which show that spectrin tetramers unfold when the extension force reaches a critical value. Then, we study how the APMS behaves during large extensions at different extension rates and for different actin–spectrin association energies. We also examine how unfolding of spectrin tetramers influences resistance of APMS during extension. Additionally, we explore possible actin–spectrin dissociation and resulting partial or complete axon rupture. Finally, we study relaxation of the APMS model when the axon's length is held fixed after extension.3.1. Unfolding of the spectrin filament
To study extension of a spectrin tetramer, we first equilibrate the filament for 106 time steps and then stretch one of its ends at the constant speed of 0.05σ/ts while the other end is fixed. As the distance between the two ends of the filament increases, the extension force increases up to the point where a repeat unfolds and the extension force abruptly decreases (Fig. 6). We note that a spectrin repeat unfolds in an all-or-none process. Hence, the peak force marks the unfolding force of a repeat whereas a distance between two consecutive peaks reflects the length increase (ΔL) of the spectrin filament due to unfolding of one of the spectrin repeats. The sequential unfolding of spectrin repeats exhibits a clear saw-tooth pattern. The peak of the extension force leading to repeat unfolding lies between 33 pN to 41 pN (Fig. 6), which is close to reported experimental values of 25 pN to 35 pN.29 Our model predicts that the average distance between two adjacent unfolding peaks is ΔL = 32.2 ± 0.8 nm at an extension speed of 0.05σ/ts. This result is close to the experimental value of ΔL = 31.7 ± 0.5 nm.29,41 The elongation speed of the AFM experiments, which produced a result very similar to our simulations, was 0.3 μm s−1.29 This corresponds to a characteristic time ts ≅ 1.0 × 10−4 s. We note that at higher extension rates the pick unfolding forces are higher. Specifically, at 0.10σ/ts, 0.20σ/ts, and 0.40σ/ts the maximum forces are 38 pN, 44 pN, and 56 pN respectively. | ||
| Fig. 6 Force–extension curves for a section of a spectrin filament. Each unfolding event increases the length of the spectrin filament by L = 32.2 ± 0.8 nm at an extension speed of 0.05σ/ts. | ||
3.2. Extension of the periodic APMS
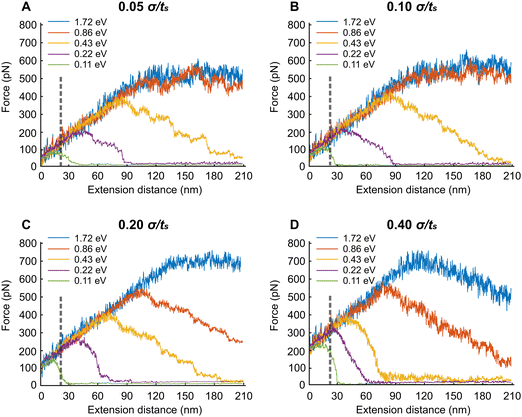
In this section, we extend the APMS model at different extension rates and actin–spectrin association energies and illustrate how spectrin unfolding and actin–spectrin dissociation impact the corresponding force–extension curves. The results are shown in Fig. 7. We chose the association energies 1.72 eV, 0.86 eV, 0.43 eV, 0.22 eV, and 0.11 eV, which range from stable to unstable configurations for the extension rates of 0.05σ/ts, 0.10σ/ts, 0.20σ/ts, and 0.40σ/ts. Considering that σ = 0.61 nm the actual extension rates are 0.3 μm s−1, 0.6 μm s−1, 1.2 μm s−1, and 2.4 μm s−1 respectively. The original distance between actin rings at initiation of stretching is 160 nm, which is smaller than the contour length Lc of a spectrin filament. The corresponding actual strain rates are 1.87 s−1, 3.75 s−1, 7.5 s−1 and 15 s−1.We found that at the low extension rates of 0.05σ/ts and 0.10σ/ts and at association energies of 1.72 eV and 0.86 eV there is no dissociation between actin and spectrin meaning that the entire force–extension curve is the result of spectrin unfolding. Specifically, extension brings spectrin filaments to their contour length followed by random unfolding (see Movie S1, ESI†). The force–extension curves have two clearly distinct regions. Initially, the force–extension curve is linear. In the second region the average extension force does not increase meaning that the structure behaves as a perfectly plastic material. In both regions, the linear response region and perfect plasticity behavior region, we observe unfolding of filaments. The only difference between the two regions is that the frequency of unfolding is much higher in the plastic region compared to linear response region as it is shown in the case of 0.05σ/ts extension rate and 0.86 eV (Fig. S1, ESI†). Unfolding events are marked with vertical arrows. To better characterize the deformation mechanisms, we next gradually reduce the extension starting at 180 nm displacement, after reaching the plastic region, and at the same rates (0.05σ/ts and 0.10σ/ts) and association energies (0.86 eV and 1.72 eV) as with the extension simulations (Fig. S2, ESI†). We find that there is permanent deformation when the resisting force reaches its initial value. We observe that the permanent extension is due to the fact that unfolded sections of spectrin tetramers fold back only partially, at least during our simulations time range.
To further clarify the linear force–extension increase, we perform axon extension simulations when 1, 2, 6, 12, and 24 spectrin filaments are attached to each pair of actin rings. In Fig. S3 (ESI†), we plot the extension force vs. the displacement for all cases above for 0.05σ/ts extension rate and 0.86 eV and we mark unfolding events with vertical arrows. We observe that in the case of one filament, the unfolding events are associated with characteristic abrupt drops in the extension force. However, in the case of two filaments we observe cases where unfolding is not associated with a clear drop of the resisting force (Fig. S3, ESI†). As the number of spectrin filaments increases to 6, 12, and 24, the force–extension curve has an initial linear increase section despite the occurrence of unfolding events (Fig. S3, ESI†). This is due to non-synchronized unfolding events.
At the lower association energies of 0.43 eV, 0.215 eV, and 0.11 eV and at the extension rates of 0.05σ/ts and 0.10σ/ts, in addition to unfolding, we encounter actin–spectrin dissociation causing a softening of the APMS after the extension force reaches a critical value (see Fig. 7A, B and Table S3, Movie S2, ESI†). As we can see in Fig. 7A, at 0.11 eV association energy, the critical force is about 100 pN after which the stiffness of the APMS decreases and becomes gradually almost zero because of extensive dissociation resulting in a final APMS configuration, which cannot sustain any load. The small resisting force is due to viscous resistance. The same trend is apparent for both 0.22 eV and 0.43 eV association energies (Fig. 7A). The difference between 0.05σ/ts and 0.10σ/ts extension rates is that actin–spectrin dissociation occurs at larger extension forces for the higher extension rate of 0.10σ/ts compared to the lower rate of 0.05σ/ts (Fig. 7A and B). We indeed show in Fig. S4 (ESI†) that at 0.43 eV and 0.05σ/ts actin–spectrin dissociation starts at approximately 380 pN force and increases gradually to almost complete actin–spectrin disruption at very large extension. The numbers above the arrows in the graph of Fig. S4 (ESI†) indicate the cumulative dissociated actin–spectrin junctions at the corresponding time point. As the extension increases, the number of dissociated junctions tends to 39, which is the total number of actin–spectrin associations per actin ring in our model, and the total resisting force decreases to viscous resistance. We note that increment of decrease is not one because we output configurations every 104 time steps. At 0.43 eV and 0.1σ/ts actin–spectrin dissociation starts at approximately 420 pN force and it similarly increases gradually to almost complete actin–spectrin disruption at approximately 200 nm extension. It is important to point out that at 0.10σ/ts extension rate and for 0.11 eV there is no spectrin unfolding during extension but only actin–spectrin dissociation illustrated by a sharper force–extension decrease curve – from ≅100 pN resisting force at ≅20 nm extension to ≅0 pN resisting force at ≅30 nm extension – than in the corresponding case at 0.05σ/ts extension rate – from ≅90 pN resisting force at ≅20 nm extension to ≅0 pN resisting force at ≅40 nm extension – where in addition to actin–spectrin dissociation spectrin unfolding occurs as well (Table S3, ESI† and Fig. 7B).
Next, we describe the behavior of the APMS at the extension rate of 0.20σ/ts for different actin–spectrin association energies. At 1.72 eV association energy, we did not observe actin–spectrin dissociation but only spectrin unfolding. The force–extension curve increases linearly until the yield point is reached at approximately 120 nm extension where considerable spectrin unfolding occurs. At larger strains APMS behaves as a perfectly plastic material without further increase in load bearing capacity (Fig. 7C). At association energies 0.86 eV and 0.43 eV both spectrin unfolding and actin–spectrin dissociation occur after approximately 110 nm and 70 nm extension respectively resulting in a decreasing load bearing capacity as it is shown by the negative slope of the force–extension curves (Fig. 7C). At 0.43 eV and at approximately 190 nm extension APMS completely ruptures and it cannot support any load. Fig. S4C (ESI†) shows the cumulative number of disrupted actin–spectrin junctions during extension. Complete disruption occurs at approximately 190 nm extension. We finally note that at 0.22 eV and 0.11 eV actin–spectrin association energies, we do not observe unfolding of spectrin repeats but only actin–spectrin dissociation resulting in an abrupt decrease of the extension force to almost zero at approximately 40 nm and 20 nm extension respectively corresponding to a complete rupture of the axon.
When the extension rate is 0.40σ/ts at 1.72 eV and 0.86 eV actin–spectrin association energies, the force resistance increases linearly until extensions reach approximately 120 nm and 80 nm respectively, where actin–spectrin links rupture and extensive spectrin unfolding occur. At larger extensions force decreases because of actin–spectrin dissociations, which weaken the APMS. An extension larger than 210 nm is required for complete collapse of APMS (Fig. 7D). At the association energies of 0.43 eV, 0.215 eV, and 0.108 eV, we did not observe spectrin unfolding but only actin–spectrin dissociation resulting in an abrupt decrease of the extension force to almost zero at approximately 50, 30, and 15 nm extensions respectively corresponding to a complete axon rupture (see Table S3 and Movie S3, ESI†). Fig. S4D (ESI†) clearly shows that the rate of actin–spectrin disruption for 0.43 eV association energy and 0.40σ/ts extension rate is higher than in the case of 0.43 eV association energy and 0.20σ/ts. In this case complete disruption occurs at only 90 nm extension.
Finally, we investigate the force required to initiate extension at different extension rates. We observe that this force increases from approximately 44 pN at 0.05σ/ts extension rate to 69 pN at 0.10σ/ts, 118 pN at 0.20σ/ts, and 220 pN at 0.40σ/ts extension rate (Fig. 8). The reason for this increase is the viscous resistance of the lipid bilayer to the relative motion of the actin rings and ankyrin G particles during extension. This resistance is represented by the Langevin equation (eqn (5)). We also note that the fitted straight line intersects the force axis not at zero force but at ∼20 pN at zero elongation. This is because the distance between the actin rings is not equal to the equilibrium end-to-end distance of spectrin, which is approximately 81.5 nm, but it is 165 nm. As a result, a force is required to maintain this distance. To confirm this hypothesis, we perform a simple calculation of the required force, using the worm-like-chain (WLC) model expression  , where x = 130 nm is the spectrin filament initial length, which is obtained by subtracting the actin diameter of 35 nm from the distance of 165 nm between two actin rings. Lc ≃ 190 nm is the contour length, lp ≃ 16.6 nm is the spectrin persistence length, T ≅ 300 K, and kB ≅ 1.38 × 10−23 J K−1 is the Boltzmann's constant. The required force to maintain the length of each spectrin filament to 130 nm is approximately 0.73 pN and since the number of spectrin filaments between two actin rings is 39, the required overall force is predicted to approximately be 28.6 pN which is close to our observed value (see Fig. 8).
, where x = 130 nm is the spectrin filament initial length, which is obtained by subtracting the actin diameter of 35 nm from the distance of 165 nm between two actin rings. Lc ≃ 190 nm is the contour length, lp ≃ 16.6 nm is the spectrin persistence length, T ≅ 300 K, and kB ≅ 1.38 × 10−23 J K−1 is the Boltzmann's constant. The required force to maintain the length of each spectrin filament to 130 nm is approximately 0.73 pN and since the number of spectrin filaments between two actin rings is 39, the required overall force is predicted to approximately be 28.6 pN which is close to our observed value (see Fig. 8).
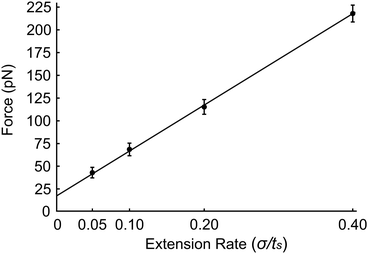 | ||
| Fig. 8 Force required to initiate extension at extension rates 0.05σ/ts, 0.10σ/ts, 0.20σ/ts and 0.40σ/ts. | ||
3.3. APMS relaxation properties
In this section, we examine how the force required to keep APMS stretched at a constant displacement changes as a function of time. APMS relaxation behavior depends on the initial extension, on the extension rate, and on the actin–spectrin association energy since these factors determine the degree of spectrin unfolding and actin–spectrin dissociation. We first investigate APMS relaxation for 0.05σ/ts extension rate and 0.86 eV association energy. In this case, there is no actin–spectrin dissociation, which would have changed the structure of the APMS at different extensions. The numerical experiment is designed as follows. First, we run the simulation for 2 × 105 time steps to reach thermal equilibrium and then extend the APMS model. During extension, some of the spectrin repeats unfold. When the extension distance reaches a chosen value, we fix the position of the two actin rings. At this point, the required applied force sharply drops (Fig. 9) because the resistance to the movement of the actin rings by the solution and the plasma membrane ceases, since it depends on the axon extension speed, and because of additional rapid spectrin repeats unfolding as it is illustrated in Fig. S5 (ESI†). Keeping the APMS at fixed extension, more spectrin repeats unfold (see Movie S4, ESI†) resulting in an increase of the contour length of the corresponding spectrin tetramers and a further decrease of the applied force required to maintain the spectrin filaments extended. Repetition of the relaxation experiment, for different degrees of extension, results in a reduction of the extension force with time in all cases (Fig. 9). The viscoelastic behavior of the APMS during relaxation is due to particle-particle interactions during repeat unfolding. To model relaxation of the APMS, we adopt the three-element viscoelastic or Zener model comprising a Voigt element (k2,η2) connected in series with a spring k1 (Fig. S6, ESI†). η2 is the viscosity of the material represented as a dashpot viscosity. The governing equation of the Zener model is: | (8) |
 , where tc = η2/(k1 + k2) is the displacement relaxation time.61 Using least squares and nonlinear curve-fitting in Matlab, we find that the numerical data fit the analytical solution of the Zener model for the values shown in Table S4 (ESI†). The average k1 ≅ 0.94 mN m−1 and the average k2 ≅ 0.255 mN m−1 whereas η2 is smaller at low extension (time step ≅ 0.6 × 106) when unfolding during relaxation is limited and has a higher average value of η2 ≅ 0.23 mN s m−1 at larger initial extensions when unfolding is more widespread. k1 determines the elastic resistance of the APMS at the initiation of relaxation and corresponds to a Young's modulus similar to the one produced by the model. k2 is connected in series with k1 and determine the final decrease in stiffness of the APMS because of spectrin tetramers unfolding. η2 is an indicator of unfolding frequency during relaxation.
, where tc = η2/(k1 + k2) is the displacement relaxation time.61 Using least squares and nonlinear curve-fitting in Matlab, we find that the numerical data fit the analytical solution of the Zener model for the values shown in Table S4 (ESI†). The average k1 ≅ 0.94 mN m−1 and the average k2 ≅ 0.255 mN m−1 whereas η2 is smaller at low extension (time step ≅ 0.6 × 106) when unfolding during relaxation is limited and has a higher average value of η2 ≅ 0.23 mN s m−1 at larger initial extensions when unfolding is more widespread. k1 determines the elastic resistance of the APMS at the initiation of relaxation and corresponds to a Young's modulus similar to the one produced by the model. k2 is connected in series with k1 and determine the final decrease in stiffness of the APMS because of spectrin tetramers unfolding. η2 is an indicator of unfolding frequency during relaxation.
We also examine the relaxation behavior of the APMS when the extension rate is 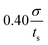 and the actin–spectrin association energy is 0.86 eV. In this case, in addition to spectrin unfolding actin–spectrin dissociation and softening of the APMS occurs (Fig. 10). Dissociation occurs for time larger than 2.5 × 105ts when the stress curve starts decreasing with time. We again note that at the beginning of relaxation the resistance force drops sharply because the viscous resistance to actin rings becomes zero when the extension stops and because of additional rapid repeat unfolding (Fig. S7, ESI†). Using the Zener model, we determine the parameters k1, k2, and η2 (see Table S5, ESI†). For the case of maximum extension without actin–spectrin dissociation (magenta curve in Fig. 10), we find that k1 ≅ 1.18 mN m−1, k2 ≅ 0.101 mN m−1, and η2 ≅ 0.163 mN s m−1. We observe that the spring constants k1 and k2 are at the same order as in the first case since there is no actin–spectrin dissociation. For larger extensions the average k1 ≅ 0.63 mN m−1 and the average k2 ≅ 0.07 mN m−1 whereas η2 ≅ 0.11 mN s m−1. We observe that k1 is lower than the corresponding value when actin–spectrin dissociation has not occurred as it is expected. The value of k2 and η2 are also lower because actin–spectrin dissociation results to a lower degree of actual unfolding since only the connected spectrin tetramers unfold. We note that literature values for the viscosity of the RBC membrane, measured via micropipette experiments vary between 0.6 and 2.7 μN s m−1,62 which is approximately 100 times smaller than the value measured here. We compare to the RBC membrane because its membrane skeleton comprises spectrin filaments connected to actin junctions as in the APMS. However, in the RBC membrane skeleton spectrin filaments form an isotropic hexagonal network when stretched.1,63 The difference in the viscosities is expected because in the RBC at equilibrium the spectrin filaments have a junction-to-junction distance of ∼80 nm and even at very large deformations relaxation does not involve unfolding but mostly reduced entropic entanglement.64 In the case of the neuronal axon on the other hand, spectrin filaments are near their contour length and extension and relaxation involves unfolding which is determined by spectrin–spectrin interactions between spectrin-repeats.
and the actin–spectrin association energy is 0.86 eV. In this case, in addition to spectrin unfolding actin–spectrin dissociation and softening of the APMS occurs (Fig. 10). Dissociation occurs for time larger than 2.5 × 105ts when the stress curve starts decreasing with time. We again note that at the beginning of relaxation the resistance force drops sharply because the viscous resistance to actin rings becomes zero when the extension stops and because of additional rapid repeat unfolding (Fig. S7, ESI†). Using the Zener model, we determine the parameters k1, k2, and η2 (see Table S5, ESI†). For the case of maximum extension without actin–spectrin dissociation (magenta curve in Fig. 10), we find that k1 ≅ 1.18 mN m−1, k2 ≅ 0.101 mN m−1, and η2 ≅ 0.163 mN s m−1. We observe that the spring constants k1 and k2 are at the same order as in the first case since there is no actin–spectrin dissociation. For larger extensions the average k1 ≅ 0.63 mN m−1 and the average k2 ≅ 0.07 mN m−1 whereas η2 ≅ 0.11 mN s m−1. We observe that k1 is lower than the corresponding value when actin–spectrin dissociation has not occurred as it is expected. The value of k2 and η2 are also lower because actin–spectrin dissociation results to a lower degree of actual unfolding since only the connected spectrin tetramers unfold. We note that literature values for the viscosity of the RBC membrane, measured via micropipette experiments vary between 0.6 and 2.7 μN s m−1,62 which is approximately 100 times smaller than the value measured here. We compare to the RBC membrane because its membrane skeleton comprises spectrin filaments connected to actin junctions as in the APMS. However, in the RBC membrane skeleton spectrin filaments form an isotropic hexagonal network when stretched.1,63 The difference in the viscosities is expected because in the RBC at equilibrium the spectrin filaments have a junction-to-junction distance of ∼80 nm and even at very large deformations relaxation does not involve unfolding but mostly reduced entropic entanglement.64 In the case of the neuronal axon on the other hand, spectrin filaments are near their contour length and extension and relaxation involves unfolding which is determined by spectrin–spectrin interactions between spectrin-repeats.
4. Discussion
The discovery of the periodic APMS and the related periodic arrangement of ankyrin G and sodium channels in the AIS is a major development in our understanding of axonal mechanics and functionality. Before this discovery, it was commonly thought that parallel longitudinal bundles of microtubules are not only the substrate for vesicular transport but they are the structural backbone of the axon as well.6,15 Since then, it has been acknowledged that the APMS provides lateral stiffness to the axon via the actin rings32 and that it shields microtubules from axial stress.12 It has also been shown that the APMS can act as a tensile shock absorber.21Besides its role in the mechanical behavior of axons, the APMS is very important for the stability of microtubules, and consequently, the stability of the axon, as well since APMS-dependent polymerization of microtubules is required for their maintenance.15 An important structural element of the APMS is ankyrin G, which is an AIS scaffold protein acting as a master organizer, as it is responsible for the recruitment of most AIS-enriched proteins.65,66 In relation to its structural function, the amino terminus of ankyrin G binds to βIV-spectrin47 and the C terminus binds to microtubule fascicles via plus-end-binding proteins EB1 and EB37 and via Ndel1.6,67 In a similar fashion, in the distal axon ankyrin-B binds to βII-spectrin3,68 and to microtubules.5 These associations in both cases establish anchoring of the APMS to the endoplasmic microtubules network and subsequent mechanical stability of the axon. In addition, ankyrin G is associated with Nav channels resulting in a periodic distribution of Nav in the AIS and proximal axon. Nav channels then assist tethering of the lipid bilayer to the APMS. It has also been shown that periodicity of Nav does not affect the action potential but it only localizes ionic currents.69
It is known that axonal extension and torsion caused by mechanical forces can directly alter the structure of an axon and/or trigger biochemical degradation.14,17,70,71 Force experiments usually involve extension of an entire axon via a microneedle21,22,72 and it has been observed that axon typically have a viscoelastic response to extension.21,22 Modeling of the mechanical behavior of axons during stretching or torsion, usually including growth or injury, typically involves discrete representation of microtubules cross-linked by tau proteins.11,21,27,71,73–76 Finite elements approaches are used to solve the resulting governing equations including viscoelastic responses.25,71 A similar finite element-based approach uses a homogenized representation of the axon and it often is part of brain tissue modelling.77–79
A very significant question is if the APMS directly influences axonal mechanics. It has been shown that treatment of rat hippocampal neurons with latrunculin B, which inhibits actin polymerization, reduces lateral Young's modulus from 4.6 ± 1.5 kPa to 2.2 ± 0.6 kPa32 indicating that actin rings are important for the mechanical behavior of the axon. It has also been shown recently that APMS plays a prominent mechanical role acting as a tension buffer in tensile experiments and that chick dorsal root ganglion axons have a strain softening response.21 Treatment of neurons with F-actin stabilizer drug Jasplakinolide results in a significant increase of axonal stiffness at least at the same level as caused by treatment with the microtubule stabilizer drug taxol. Treatment of neurons with nocodazole, which is a microtubule disrupting drug, or with latrunculin-A, which is an F-actin disrupting drug, made the axons fragile in tensile experiments.21 Furthermore, it has been demonstrated, exploiting mutations in β-spectrin and microtubule network, that APMS in combination with the microtubule network protects axons during extension and torsion.14,17 All those results illustrate the importance of the APMS in axonal extension experiments.
In this work, we developed a CGMD model of the APMS to investigate its response to extension taking into consideration that, while actin rings are stable, spectrin repeats can unfold under tension. We note that we modeled the microtubule network implicitly considering only its effect on maintaining the distance of actin rings at approximately 190 nm at equilibrium. One question is then if the force–extension curve of the entire APMS exhibits the characteristic saw-tooth pattern observed in single spectrin filament extension experiments.29 Another important question is about the effect of extension rate to the force response. Finally, we examine the behavior of the APMS model during relaxation.
The APMS model comprises longitudinal spectrin tetramers, which connect azimuthal rings. We validated our CGMD model of spectrin tetramers by using experimental results that confirm the persistence length of our model.43,46 The saw-tooth shape of the force–extension curve caused by unfolding of spectrin repeats during extension simulations were also validated via experimental results in terms of the maximum resistance forces and the overall shape of the force–extension curve.29,41 The model of the actin rings follows closely the model used in our previous publication which has been validated against AFM experiments.32 One important consideration is the actin–spectrin association energy. Because its value for the axon is not known, we used values 0.11, 0.22, 0.43, 0.86, and 1.72 eV, which are in the same order of magnitude as the actin junction–spectrin association energy observed in wild-type human RBCs, which is approximately 0.74 eV.49 Another important point is that we implemented the Langevin equation for the motion of the actin rings and ankyrin particles because actin rings and ankyrin directly and indirectly through their associated proteins interact with the lipid bilayer during extension.
The results provide a clear picture of how the APMS responds to extension. We observed that during extension, even at moderate displacements and at low extension rates, unfolding of spectrin repeat is common (Fig. S1, ESI†). We also noticed that actin–spectrin dissociation, which results to APMS softening, depends on the association energy level, as expected, and on the extension rate, with faster extension rates making the network more brittle (Fig. 7 and Fig. S4, ESI†). The resisting force during extension is on the order of 0.5 nN, which is one order of magnitude lower than forces developed during extension experiments.21,72 This is justified since in those experiments the entire axon, including the microtubule network, was resisting to extension.
The force–extension relationship is initially linear despite unfolding or spectrin filaments. To clarify if this is due to the viscous effect of the Langevin equation, which is involved in the motion of the actin rings and the ankyrin particles, or it is due to not synchronized unfolding of spectrin filaments, we investigated several cases. In particular, we built APMS models with 1, 2, 6, 12, and 24 spectrin filaments with and without implementing the Langevin equations for the actin rings and the corresponding ankyrin particles for the case of 0.05σ/ts extension rate and 0.86 eV actin–spectrin association energy. We observed that the viscous forces did not affect the overall shape of the force–extension curves but they shifted the overall force to higher values (Fig. S3, S8 and S9, ESI†). We can clearly see that in both cases – with and without viscous forces – abrupt changes in the force–extension curve are observed only in the case of one filament between each pair of rings (Fig. S3 and S8, ESI†). We also note that the average load bearing is constant after an initial increase similarly to the complete APMS model force–extension curve. In the case of two spectrin filaments, we can still see a saw-tooth resembling pattern, which is correlated with multiple repeats unfolding occurring in a distance much smaller than 32.2 ± 0.8 nm, which is the characteristic distance for single spectrin filament unfolding.29 As the number of filaments increases multiple repeats unfold in very short distances, compared to the characteristic length of 32.2 ± 0.8 nm, obscuring individual saw-tooth shapes independently if we consider the Langevin equation.
It is interesting to explore how our results compare to experimental results with respect to a combination of strain and strain rates. As we mentioned at the beginning of the “results” section the corresponding actual strain rates are 1.87 s−1, 3.75 s−1, 7.5 s−1 and 15 s−1, while the strain reaches up to 100%. It is known that strain rates exceeding 10 s−1 cause diffuse axonal injury.80 It has been found that during mild to severe traumatic brain injury (TBI) events caused by blunt-force, brain tissue is subjected to 10–50% strains and up to 50 s−1 strain rates.73,81 It is also known that brain tissue deformations caused by electromagnetic or sonic-based directed energy can occur at high strain rates >100 s−1 and approach 1000 s−1.82,83 Clearly our simulations are in the range of low and moderate strain rates.82 Because of this, we ran an additional simulation at 30 s−1 strain rate for the highest assumed actin–spectrin association energy of 1.72 eV. We observed that at this strain rate all actin–spectrin junctions were dissociated at the very beginning of the simulation. This means that the actin–spectrin membrane skeleton is very brittle at strain rates higher than 15 s−1 and it cannot sustain fast impact loading. This finding is in agreement with experimental results, which show that at low strain rates axons can accommodate even up to 100% strain without microstructural defects including defects in microtubules.9 However, at moderate and high strain rates axons sustain significant injury leading to swelling, degeneration, and cell death.10,73 Axonal injury in those cases has mainly been attributed to microtubule rupture, detachment of tau proteins, and disruption of microtubules organization.10,73,83 Here, we propose that dissociation of actin–spectrin junctions and subsequent compromise of the APMS is an additional factor, which plays an important role in axon degeneration under large strains and high strain rates.
At large extensions, the behavior of the APMS is perfectly plastic as long as actin–spectrin dissociation does not occur (Fig. 7A and B). When actin–spectrin dissociation occurs, because of reduced actin–spectrin association energy and/or because of increased extension rate, the APMS softens. This results in a decreasing resisting force as extension increases because of accumulated defects in the membrane skeleton. At the final stages, the APMS is completely ruptured and the force resisting to extension approaches zero (Fig. 7). We note that when actin–spectrin dissociation occurs but not spectrin repeats unfolding takes place, the force–extension curve abruptly drops close to zero at large extension rates (0.2 and 0.4σ/ts) and at low actin–spectrin association energies (0.11 and 0.22 eV) (Fig. 7C and D). We also confirmed that rupture of the APMS at actin–spectrin binding sites is not reversible not only during extension but also at equilibrium because spectrin filaments are at entropic tension and after dissociation they recoil from their original configuration with a 190 nm end-to-end distance to their equilibrium free-end configuration with a 81.5 nm end-to-end distance.
Finally, we investigated the behavior of the APMS model during relaxation which is due to additional spectrin unfolding when the extension is held constant for a large number of time steps. To analytically model the process, we used the Kelvin–Voigt representation of the Zener model which comprises two spring elements (k1, k2) and one dashpot element η2. The viscous response is due to sliding interactions between repeats during the process of unfolding. We note that when extension stops and relaxation response starts, we observed a sharp drop to the resisting force. This drop was due to discontinuation of the drag force applied to actin rings and to rapid unfolding of actin repeats. This is clearly illustrated in Fig. S7, S9, and S10 (ESI†) which correspond to 0.86 eV and 0.05σ/ts (Fig. S9, ESI†) and 0.4σ/ts (Fig. S7 and S10, ESI†) cases. The arrows, which indicate when a repeat unfolding happens, clearly show that at the sharp drops of the resisting forces, rapid spectrin unfolding occurs.
5. Conclusion
We investigated how the recently discovered periodic APMS endows the axon with structural stability during extension, which can be significant even in everyday activities. Specifically, we introduced a coarse-grain molecular dynamics model for the APMS consisting of actin rings connected by extendable longitudinal spectrin filaments and implemented breakable actin–spectrin protein associations. We showed that APMS protects an axon from catastrophic collapse during large extensions by acting as a series of molecular dashpots buffering tension. We predicted that during extension the force response is initially linear despite limited unfolding of spectrin repeats. However, at larger deformations unfolding spreads out and the APMS becomes perfectly plastic protecting the membrane skeleton from disruption. We also showed that reduction of extension of the APMS until the resisting force reaches its initial value results in a permanent APMS displacement because spectrin filaments only partially folded back to their original configuration. Overall, at low extension rates, spectrin unfolding and ensuing reduction of the force resisting to axon extension shield APMS from actin–spectrin dissociation and fragmentation. At higher extension rates, in addition to unfolding, rupture of actin–spectrin links occurs softening and finally severing the axon. Finally, during relaxation simulations, the required extension force decreases exponentially, due to continuous unfolding of spectrin filaments.Author contributions
Z. C. wrote the code and ran the simulations. G. L. conceptualized the study and interpreted the results. All authors wrote and edited the paper. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation Division of Physics, Physics of Living Systems 2210535 and by the Division of Civil, Mechanical and Manufacturing Innovation Career Award 1351363 to G. Lykotrafitis. This work used the San Diego Supercomputer Center (SDSC) supported by the Extreme Science Engineering and Discovery Environment (XSEDE).References
- B. Alberts, J. H. Wilson and T. Hunt, Molecular biology of the cell, Garland Science, Taylor and Francis Group, New York, NY, 6th edn, 2015 Search PubMed.
- C. Leterrier, P. Dubey and S. Roy, Nat. Rev. Neurosci., 2017, 18, 713–726 CrossRef CAS PubMed.
- K. Xu, G. Zhong and X. Zhuang, Science, 2013, 339, 452–456 CrossRef CAS PubMed.
- M. R. Galiano, S. Jha, T. S.-Y. Ho, C. Zhang, Y. Ogawa, K.-J. Chang, M. C. Stankewich, P. J. Mohler and M. N. Rasband, Cell, 2012, 149, 1125–1139 CrossRef CAS PubMed.
- G. Zhong, J. He, R. Zhou, D. Lorenzo, H. P. Babcock, V. Bennett and X. Zhuang, eLife, 2014, 3, e04581 CrossRef PubMed.
- C. Leterrier, J. Neurosci., 2018, 38, 2135–2145 CrossRef CAS PubMed.
- C. Leterrier, H. Vacher, M.-P. Fache, S. A. d'Ortoli, F. Castets, A. Autillo-Touati and B. Dargent, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 8826–8831 CrossRef CAS PubMed.
- C. P. Brangwynne, F. C. MacKintosh, S. Kumar, N. A. Geisse, J. Talbot, L. Mahadevan, K. K. Parker, D. E. Ingber and D. A. Weitz, J. Cell Biol., 2006, 173, 733–741 CrossRef CAS PubMed.
- M. D. Tang-Schomer, A. R. Patel, P. W. Baas and D. H. Smith, FASEB J., 2010, 24, 1401–1410 CrossRef CAS PubMed.
- M. D. Tang-Schomer, V. E. Johnson, P. W. Baas, W. Stewart and D. H. Smith, Exp. Neurol., 2012, 233, 364–372 CrossRef PubMed.
- S. J. Peter and M. R. Mofrad, Biophys. J., 2012, 102, 749–757 CrossRef CAS PubMed.
- A. Kant, V. E. Johnson, J. D. Arena, J.-P. Dollé, D. H. Smith and V. B. Shenoy, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024961118 CrossRef CAS PubMed.
- M. Hammarlund, E. M. Jorgensen and M. J. Bastiani, J. Cell Biol., 2007, 176, 269–275 CrossRef CAS PubMed.
- M. Krieg, A. R. Dunn and M. B. Goodman, Nat. Cell Biol., 2014, 16, 224–233 CrossRef CAS PubMed.
- Y. Qu, I. Hahn, S. E. Webb, S. P. Pearce and A. Prokop, Mol. Biol. Cell, 2017, 28, 296–308 CrossRef CAS PubMed.
- C. Leterrier and P. A. Pullarkat, J. Cell Sci., 2022, 135, jcs259356 CrossRef CAS PubMed.
- M. Krieg, J. Stuhmer, J. G. Cueva, R. Fetter, K. Spilker, D. Cremers, K. Shen, A. R. Dunn and M. B. Goodman, eLife, 2017, 6, e20172 CrossRef PubMed.
- S. Coakley, F. K. Ritchie, K. M. Galbraith and M. A. Hilliard, Nat. Commun., 2020, 11, 133 CrossRef CAS PubMed.
- C. S. Hill, M. P. Coleman and D. K. Menon, Trends Neurosci., 2016, 39, 311–324 CrossRef CAS PubMed.
- S. Siechen, S. Yang, A. Chiba and T. Saif, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 12611–12616 CrossRef CAS PubMed.
- S. Dubey, N. Bhembre, S. Bodas, S. Veer, A. Ghose, A. Callan-Jones and P. Pullarkat, eLife, 2020, 9, e51772 CrossRef CAS PubMed.
- T. J. Dennerll, P. Lamoureux, R. E. Buxbaum and S. R. Heidemann, J. Cell Biol., 1989, 109, 3073–3083 CrossRef CAS PubMed.
- R. Bernal, P. A. Pullarkat and F. Melo, Phys. Rev. Lett., 2007, 99, 018301 CrossRef PubMed.
- R. de Rooij, E. Kuhl and K. E. Miller, Biophys. J., 2018, 115, 1783–1795 CrossRef CAS PubMed.
- R. de Rooij and E. Kuhl, Biophys. J., 2018, 114, 201–212 CrossRef CAS PubMed.
- L. M. Wang and E. Kuhl, Semin. Cell Dev. Biol., 2023, 140, 13–21 CrossRef CAS PubMed.
- C. Lazarus, M. Soheilypour and M. R. Mofrad, Biophys. J., 2015, 109, 231–239 CrossRef CAS PubMed.
- V. Bennett and A. J. Baines, Physiol. Rev., 2001, 81, 1353–1392 CrossRef CAS PubMed.
- M. Rief, J. Pascual, M. Saraste and H. E. Gaub, J. Mol. Biol., 1999, 286, 553–561 CrossRef CAS PubMed.
- S. M. Altmann, R. G. Grünberg, P.-F. Lenne, J. Ylänne, A. Raae, K. Herbert, M. Saraste, M. Nilges and J. K. H. Hörber, Structure, 2002, 10, 1085–1096 CrossRef CAS PubMed.
- D. N. Lorenzo, A. Badea, R. Zhou, P. J. Mohler, X. Zhuang and V. Bennett, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 15686–15695 CrossRef CAS PubMed.
- Y. Zhang, K. Abiraman, H. Li, D. M. Pierce, A. V. Tzingounis and G. Lykotrafitis, PLoS Comput. Biol., 2017, 13, e1005407 CrossRef PubMed.
- S.-C. Liu, L. H. Derick and J. Palek, J. Cell Biol., 1987, 104, 527–536 CrossRef CAS PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- F. Gittes, B. Mickey, J. Nettleton and J. Howard, J. Cell Biol., 1993, 120, 923–934 CrossRef CAS PubMed.
- H. Isambert, P. Venier, A. C. Maggs, A. Fattoum, R. Kassab, D. Pantaloni and M. F. Carlier, J. Biol. Chem., 1995, 270, 11437–11444 CrossRef CAS PubMed.
- D. M. Shotton, B. E. Burke and D. Branton, J. Mol. Biol., 1979, 131, 303–329 CrossRef CAS PubMed.
- D. W. Speicher and V. T. Marchesi, Nature, 1984, 311, 177–180 CrossRef CAS PubMed.
- Q. Zhu and R. J. Asaro, Biophys. J., 2008, 94, 2529–2545 CrossRef CAS PubMed.
- C. I. Branden and J. Tooze, Introduction to protein structure, Garland Science, 2012 Search PubMed.
- M. Rief, M. Gautel, F. Oesterhelt, J. M. Fernandez and H. E. Gaub, Science, 1997, 276, 1109–1112 CrossRef CAS PubMed.
- H. Li, V. Ha and G. Lykotrafitis, J. Biomech., 2012, 45, 1947–1951 CrossRef PubMed.
- B. T. Stokke, A. Mikkelsen and A. Elgsaeter, Biochim. Biophys. Acta, Biomembr., 1985, 816, 102–110 CrossRef CAS PubMed.
- P. J. Flory and M. Volkenstein, Biopolymers, 1969, 8, 699–700 CrossRef.
- J. R. Glenney Jr., P. Glenney, M. Osborn and K. Weber, Cell, 1982, 28, 843–854 CrossRef CAS PubMed.
- K. Svoboda, C. F. Schmidt, D. Branton and S. M. Block, Biophys. J., 1992, 63, 784–793 CrossRef CAS PubMed.
- C. Leterrier, J. Potier, G. Caillol, C. Debarnot, F. Rueda Boroni and B. Dargent, Cell Rep., 2015, 13, 2781–2793 CrossRef CAS PubMed.
- T. J. Byers and D. Branton, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6153–6157 CrossRef CAS PubMed.
- V. Bennett, Biochim. Biophys. Acta, 1989, 988, 107–121 CrossRef CAS PubMed.
- E. Kordeli, S. Lambert and V. Bennett, J. Biol. Chem., 1995, 270, 2352–2359 CrossRef CAS PubMed.
- P. M. Jenkins, N. Kim, S. L. Jones, W. C. Tseng, T. M. Svitkina, H. H. Yin and V. Bennett, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 957–964 CrossRef CAS PubMed.
- C. F. Kline, J. Scott, J. Curran, T. J. Hund and P. J. Mohler, J. Biol. Chem., 2014, 289, 5285–5295 CrossRef CAS PubMed.
- M. H. P. Kole and G. J. Stuart, Neuron, 2012, 73, 235–247 CrossRef CAS PubMed.
- E. Bamberg and H. Passow, The band 3 proteins: anion transporters, binding proteins and senescent antigens, Elsevier, Amsterdam, Oxford, 1992 Search PubMed.
- S. Javid, A. Rezaei and G. Karami, J. Mech. Behav. Biomed. Mater., 2014, 30, 290–299 CrossRef PubMed.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkins-Diehr, Comput. Sci. Eng., 2014, 16, 62–74 Search PubMed.
- Y. Zhang, A. V. Tzingounis and G. Lykotrafitis, PLoS Comput. Biol., 2019, 15, e1007003 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- F. Reif, Fundamentals of statistical and thermal physics, Waveland Press, 2009 Search PubMed.
- H. Noguchi and G. Gompper, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 021903 Search PubMed.
- F. Mainardi and G. Spada, Eur. Phys. J.: Spec. Top., 2011, 193, 133–160 CAS.
- R. M. Hochmuth and R. E. Waugh, Annu. Rev. Physiol., 1987, 49, 209–219 CrossRef CAS PubMed.
- S. E. t Lux, Blood, 2016, 127, 187–199 CrossRef CAS PubMed.
- L. Pan, R. Yan, W. Li and K. Xu, Cell Rep., 2018, 22, 1151–1158 CrossRef CAS PubMed.
- M. N. Rasband, Nat. Rev. Neurosci., 2010, 11, 552–562 CrossRef CAS PubMed.
- C. Leterrier, N. Clerc, F. Rueda-Boroni, A. Montersino, B. Dargent and F. Castets, Front. Cell. Neurosci., 2017, 11, 6 Search PubMed.
- M. Kuijpers, D. van de Willige, A. Freal, A. Chazeau, M. A. Franker, J. Hofenk, R. J. Rodrigues, L. C. Kapitein, A. Akhmanova, D. Jaarsma and C. C. Hoogenraad, Neuron, 2016, 89, 461–471 CrossRef CAS PubMed.
- V. Bennett and D. N. Lorenzo, in Current Topics in Membranes, ed. V. Bennett, Academic Press, 2013, vol. 72, pp. 1–37 Search PubMed.
- Z. Chai, A. V. Tzingounis and G. Lykotrafitis, Biophys. J., 2022, 121, 3334–3344 CrossRef CAS PubMed.
- V. E. Johnson, W. Stewart and D. H. Smith, Exp. Neurol., 2013, 246, 35–43 CrossRef CAS PubMed.
- H. Ahmadzadeh, D. H. Smith and V. B. Shenoy, Biophys. J., 2014, 106, 1123–1133 CrossRef CAS PubMed.
- J. Rajagopalan, A. Tofangchi and A. S. MT, Biophys. J., 2010, 99, 3208–3215 CrossRef CAS PubMed.
- H. Ahmadzadeh, D. H. Smith and V. B. Shenoy, Biophys. J., 2015, 109, 2328–2337 CrossRef CAS PubMed.
- R. de Rooij, K. E. Miller and E. Kuhl, Comput. Mech., 2017, 59, 523–537 CrossRef CAS PubMed.
- A. Montanino and S. Kleiven, Front. Neurol., 2018, 9, 643 CrossRef PubMed.
- N. Liu, P. Chavoshnejad, S. Li, M. J. Razavi, T. Liu, R. Pidaparti and X. Wang, Biophys. J., 2021, 120, 3697–3708 CrossRef CAS PubMed.
- L. M. Wang and E. Kuhl, Comput. Mech., 2020, 65, 587–595 CrossRef.
- H. Oliveri, R. de Rooij, E. Kuhl and A. Goriely, Phys. Rev. Res., 2022, 4, 033125 CrossRef CAS.
- M. A. Holland, K. E. Miller and E. Kuhl, Ann. Biomed. Eng., 2015, 43, 1640–1653 CrossRef PubMed.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2013, 28, 71–85 CrossRef PubMed.
- J. P. Dollé, B. Morrison, 3rd, R. S. Schloss and M. L. Yarmush, Lab Chip, 2013, 13, 432–442 RSC.
- J. B. Estrada, H. C. Cramer, M. T. Scimone, S. Buyukozturk and C. Franck, Brain Multiphys., 2021, 2, 100034 CrossRef.
- N. J. Braun, K. R. Yao, P. W. Alford and D. Liao, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 29069–29079 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01602h |
| This journal is © The Royal Society of Chemistry 2023 |