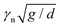Open Access Article
Open Access ArticleMachine learning approaches for the optimization of packing densities in granular matter
Adrian
Baule
 *a,
Esma
Kurban
*a,
Esma
Kurban
 a,
Kuang
Liu
b and
Hernán A.
Makse
b
a,
Kuang
Liu
b and
Hernán A.
Makse
b
aSchool of Mathematical Sciences, Queen Mary University of London, London E1 4NS, UK. E-mail: a.baule@qmul.ac.uk
bLevich Institute and Physics Department, The City College of New York, NY 10031, USA
First published on 20th July 2023
Abstract
The fundamental question of how densely granular matter can pack and how this density depends on the shape of the constituent particles has been a longstanding scientific problem. Previous work has mainly focused on empirical approaches based on simulations or mean-field theory to investigate the effect of shape variation on the resulting packing densities, focusing on a small set of pre-defined shapes like dimers, ellipsoids, and spherocylinders. Here we discuss how machine learning methods can support the search for optimally dense packing shapes in a high-dimensional shape space. We apply dimensional reduction and regression techniques based on random forests and neural networks to find novel dense packing shapes by numerical optimization. Moreover, an investigation of the regression function in the dimensionally reduced shape representation allows us to identify directions in the packing density landscape that lead to a strongly non-monotonic variation of the packing density. The predictions obtained by machine learning are compared with packing simulations. Our approach can be more widely applied to optimize the properties of granular matter by varying the shape of its constituent particles.
1. Introduction
Granular matter is ubiquitous in science and nature representing one of the most common states of matter. While granular matter seems conceptually simple, consisting of hard particles interacting solely by steric repulsion and friction, understanding its properties from first principles has been a major challenge.1,2 Already the fundamental and seemingly simple question of how densely granular matter can pack has a long and illustrious history in mathematics and the sciences.3 Considering a bulk region away from any confining boundaries and a large number of hard particles, the packing density of the aggregate depends sensitively on (i) particle shape; (ii) friction; and (iii) details of the preparation protocol which could lead to (partial) structural order. Much work has been devoted to the study of packings of hard spheres, for which the effect of (ii and iii) has been investigated in great detail.1,4–6 On the other hand, the effect of particle shape on packing densities is still only relatively poorly understood, owing to the complexity and high-dimensionality of the shape space, which makes any empirical work based on simulations computationally costly.Systematic explorations of the mapping between particle shape and the associated packing density are usually constrained to a specific category of shapes with high symmetry so that the shape parameter space is limited and can be fully explored. One then finds, for example, that disordered monodisperse packings of hard frictionless particles in the shape of ellipsoids, spherocylinders, and dimers, can pack considerably denser than spheres, achieving packing densities ϕ > 0.7, while spheres pack up to ϕ ≈ 0.64.7 Moreover, for these shapes one observes a characteristic peak in the packing density for aspect ratios of around 1.5 upon deforming from the spherical shape indicating the existence of particular optimally dense packings for these shape categories.8–19 The densest disordered packings that have been reported for these shapes have ϕ ≈ 0.740 (ellipsoids20), ϕ ≈ 0.722 (spherocylinders16), and ϕ ≈ 0.707 (dimers19). Regular polyhedra such as tetrahedra and other platonic solids also pack denser than spheres21,22 and can reach densities as high as ϕ ≈ 0.78 in disordered arrangements.21
In order to go beyond the constraint of a specific shape category, a much larger parameter-space of shapes has been considered by introducing a shape representation consisting of overlapping spheres of varying diameters.17,23–25 Applying black-box optimization methods based on evolutionary algorithms in this high-dimensional shape space has identified a symmetric trimer, see Fig. 1 as densest packing shape25 achieving ϕ = 0.729 ± 0.003, above the density of the densest packing ellipsoid20 packed with the same protocol.
 | ||
| Fig. 1 The symmetric trimer identified in ref. 25 as densest packing shape. | ||
For comparison, crystalline packings of non-spherical particles typically achieve higher packing densities than in disordered arrangements with maximal densities of ϕ = 0.770… for ellipsoids,26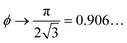 for spherocylinders,27
for spherocylinders,27 for dimers,27 and ϕ = 0.856… for tetrahedra.28
for dimers,27 and ϕ = 0.856… for tetrahedra.28
Here, we revisit the question of “which shape packs the densest” in a disordered arrangement. Instead of using simulations or mean-field theory,2,17 we employ an approach based on machine learning to identify novel dense packing shapes. Machine learning is increasingly used in materials discovery29–31 and has the particular benefit that insight can be gained from “failures”, since such data is still useful as training data.32 In the context of granular matter, machine learning has, e.g., helped to identify flow defects from structural data,33 to optimally characterize permeability,34 to predict the formation of crystalline phases,35 and to identify force chains.36 In our approach, we first employ principal component analysis to reduce the high-dimensional shape space to a lower-dimensional representation and then apply random forests and neural networks to construct regression functions on this space. Optimizing the regression functions yields predictions of new shapes, which we test using the same protocol used for the training data. All shapes predicted by this approach are different from the symmetric trimer, but pack slightly denser with ϕ ≈ 0.733. We also investigate the packing density landscape that results from the regression in the dimensionally reduced space and identify directions with strongly non-monotonic variation of the packing density.
2. Methods
The optimization of packing densities in the space of particle shapes requires the following steps:1. A suitable representation model of particle shapes captured in a vector α
2. A method to determine the (protocol-specific) packing density ϕ for a given α
3. An optimization method to find the maximum of ϕ(α)
| α* = argmaxαϕ(α). |
Clearly, exploring a sufficiently general shape space α requires a high-dimensional representation, which, in turn, makes the optimization step 3 challenging, since ϕ(α) is not guaranteed to be a convex function. In terms of computational cost, step 2 is the main problem, because for every query of a new function value ϕ(α) a whole simulation of the packing needs to be performed, which requires a sufficiently large number of particles to reduce any effects due to boundaries and initial conditions. The fact that the function to be optimized is in itself a complex “procedure” limits the choice of possible optimization algorithms to gradient-free black-box optimizers. An additional challenge is to constrain the optimization to physical shapes only. For example, if we consider the space of shapes consisting of two overlapping spheres with different diameters (dimers), α is two-dimensional, but valid shapes are constrained to the range of values for which the two spheres overlap, imposing a nonlinear constraint. In higher dimensions, this becomes increasingly difficult to implement.
In order to improve on this approach, we use machine learning including dimensional reduction and regression to replace step 2. Since we now optimize the regression function instead of the actual ϕ, we also need to verify the predicted packing density at the end. Overall, our optimization approach thus requires the following:
1. A set of training data (ϕ1, α1), …, (ϕN, αN) based on the real-space shape representation α
2. A suitable dimensional reduction method α → ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) to simplify both regression and optimization
to simplify both regression and optimization
3. A regression function ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) (
(![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) ) fitted to the training data
) fitted to the training data
4. An optimization method to find the maximum of ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) (
(![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) )
)
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) * = argmax * = argmax![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ( (![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) ). ). | (1) |
5. The inverse dimensional reduction ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) * → α*
* → α*
6. A test of the new shape with the same simulation algorithm as the training data
Further details on the different steps are given below. Machine learning algorithms are implemented with the software platform Mathematica, while packing simulations are performed with the molecular dynamics solver LAMMPS.37,38 All code and data generated for this work are publicly available.39
2.1 Shape representation model
We represent shapes in terms of a large number of overlapping spheres (the upper limit of components is essentially set by computational tractability), as used in the mean-field theory of ref. 17 and the optimization approaches of ref. 23–25 It is natural that the first sphere sets both the origin of the coordinate system and the length scale of the shape representation. The vector α thus contains the positions and radii of all other spheres relative to the first sphere. For a trimer consisting of three spheres as an example, α is expressed as , where ri and ai denote the position and radius of the ith sphere. In 3D, the trimer is thus represented by an 8-dimensional vector α and for a general shape consisting of n spheres, the dimensionality of α is p = 4(n − 1). We note that the mapping between such a vector and a shape is not unique: the same trimer shape can be parametrized, e.g., aligned with the
, where ri and ai denote the position and radius of the ith sphere. In 3D, the trimer is thus represented by an 8-dimensional vector α and for a general shape consisting of n spheres, the dimensionality of α is p = 4(n − 1). We note that the mapping between such a vector and a shape is not unique: the same trimer shape can be parametrized, e.g., aligned with the ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) -axis or with the ŷ-axis, leading to different vectors α even though the shape is the same. In fact, three degrees of freedom can in principle be further reduced by rotation of each shape such that their vectors r1 − r0 are all parallel (reducing dimensionality by two) and the vectors r2 − r0 are all in the same plane (reducing dimensionality by one).
-axis or with the ŷ-axis, leading to different vectors α even though the shape is the same. In fact, three degrees of freedom can in principle be further reduced by rotation of each shape such that their vectors r1 − r0 are all parallel (reducing dimensionality by two) and the vectors r2 − r0 are all in the same plane (reducing dimensionality by one).
Such a shape representation is able to approximate a large variety of convex and non-convex shapes.17,23–25 In addition, the representation model has the advantages: (i) it simplifies overlap detection in simulations; (ii) it can be easily implemented in LAMMPS to simulate granular aggregates of such particles; and (iii) it allows for the fully analytical description of the Voronoi boundary between two particles, which facilitates a structure and void analysis in terms of a Voronoi tessellation.2,17,40 Even though this model does not strictly reproduce shapes with flat sides or smooth non-spherical surfaces, it can provide good approximations with large sphere numbers. In the following, we also refer to particles consisting of overlapping spheres as “molecules”.
2.2 Dataset of Roth & Jaeger
As underlying dataset for our machine learning approach, we use the data generated by Roth & Jaeger in ref. 25 for particle shapes consisting of n = 5 overlapping spheres. The dataset consists of N = 5800 distinct packings, i.e., {ϕi, αi} pairs, whereby the dimensionality of α is p = 4(n − 1) = 16 (the global rotations are ignored). While ref. 25 also considered shapes consisting of 10 and 25 spheres, their result of the optimization did not vary significantly. Moreover, the number of packings generated for 5, 10, 25 spheres is of the same order, thus the 5-sphere data is the least sparse, while still not ideal for the high dimensionality of α. We further improve on the “curse of dimensionality” problem by using dimensional reduction techniques based on principal component analysis, see below.Ref. 25 used a pouring protocol under gravity implemented in LAMMPS to generate dense disordered packings of each shape. For the symmetric trimer of Fig. 1, which has been identified as the densest packing shape, it was further confirmed that the high packing density is not related to significantly increased positional or orientational ordering in the packing. For further details on the data generation and their analysis, we refer to ref. 25.
A caveat of the dataset is that it is itself the output of an optimization algorithm (covariance matrix adaptive evolutionary strategy or CMA-ES), which means that shapes in the training data are not uniformly distributed in α space, but already clustered in the region of high ϕ values. As we will see below, our machine learning approach thus leads to different but quite similar shapes as those identified in ref. 25.
2.3 Machine learning implementations
We apply principal component analysis in order to reduce the dimensionality of the shape space α. We then perform regression in the reduced![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) space using two common machine learning techniques: random forests as a non-parametric regression method and artificial neural networks as a parametric method.41 The regression functions are subsequently numerically optimized and the maxima mapped back to the full shape space to identify novel dense packing shapes.
space using two common machine learning techniques: random forests as a non-parametric regression method and artificial neural networks as a parametric method.41 The regression functions are subsequently numerically optimized and the maxima mapped back to the full shape space to identify novel dense packing shapes.
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) a matrix that contains as columns the first m PCs, we can transform every original shape in the p-dimensional representation αi into a new m-dimensional representation
a matrix that contains as columns the first m PCs, we can transform every original shape in the p-dimensional representation αi into a new m-dimensional representation ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) i
i![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) i = αi i = αi![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) , , | (2) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is a p × m matrix. For example, for our dataset p = 16, but the first 6 PCs already contain around 80% of the total variance in the data. We will separately perform the analysis considering a reduced feature space
is a p × m matrix. For example, for our dataset p = 16, but the first 6 PCs already contain around 80% of the total variance in the data. We will separately perform the analysis considering a reduced feature space ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) of m = 2,3, …, 6 dimensions corresponding to the number of PCs used.
of m = 2,3, …, 6 dimensions corresponding to the number of PCs used.
Due to the linearity of the transformation, any new data point in the reduced space can be easily transformed back to the original space by inverting eqn (2), which allows us to determine the corresponding shape in the original representation. We implement PCA in Mathematica with the DimensionalReduction[] routine using the option Method → “PrincipalComponentsAnalysis”.
• Fraction of features randomly selected to train each tree: 1/3
• Maximum number of data points in each leaf of the tree: 4
• Number of trees in the forest: 100
Overfitting is automatically controlled in random forests since the trees in the ensemble are trained independently on different subsets of the features and the data.
• Size of training set: 4930 (85% of the dataset)
• Size of validation set: 870 (15% of the dataset)
• Number of layers: 8
• Nodes per layer: 50
• Activation function: scaled exponential linear units (SELUs)
• Loss function: mean cross entropy
• Maximal training rounds: 10
The Predict[] routine with Method → “NeuralNetwork” is able to control overfitting by (i) using a validation set; (ii) early stopping of the training; (iii) regularization of the weights; (iv) introducing dropout layers. For our data, Predict[] implements (i and ii).
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) (
(![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) ) in the case of non-parametric RF requires gradient-free methods to find the maximum
) in the case of non-parametric RF requires gradient-free methods to find the maximum ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) *. We use Mathematica's NMaximize[] routine, which has built-in gradient-free options Method → “NelderMead”, “RandomSearch”, “SimulatedAnnealing”, “DifferentialEvolution”. None of these four methods is guaranteed to converge to a global maximum, since the search landscape is non-convex, but the risk of obtaining a local maximum is mitigated by starting from an initial random configuration and due to the fact that we select the maximum from the outputs of these distinct methods.
*. We use Mathematica's NMaximize[] routine, which has built-in gradient-free options Method → “NelderMead”, “RandomSearch”, “SimulatedAnnealing”, “DifferentialEvolution”. None of these four methods is guaranteed to converge to a global maximum, since the search landscape is non-convex, but the risk of obtaining a local maximum is mitigated by starting from an initial random configuration and due to the fact that we select the maximum from the outputs of these distinct methods.
2.4 Packing simulations
We apply the same gravitational packing protocol as used in ref. 25 to verify the predicted packing densities with simulations. In this protocol, N monodisperse particles are poured under gravity into a three-dimensional box of side length ≈20d, where d = 1 is the diameter of the first sphere in the molecule that sets the length scale. The box is constrained in the ẑ-direction by a rough surface at the bottom and an open top with periodic boundary conditions in the![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) –ŷ-plane. Initially the molecules are placed at random positions and with random orientations within a specified insertion region 30–40d above the bottom and then released to settle in the box under gravity.
–ŷ-plane. Initially the molecules are placed at random positions and with random orientations within a specified insertion region 30–40d above the bottom and then released to settle in the box under gravity.
In order to perform the time-integration of the dynamical evolution of the molecules, we use LAMMPS,37,38 which allows the definition of rigid bodies consisting of overlapping spheres (using the fix rigid/small command). Running a packing simulation for a given molecule shape requires as input the positions and diameters of each sphere, molecule volume, molecule mass (following directly from the volume since we consider a mass density of 1), center of mass, and moment of inertia. The molecule volume, center of mass, and moment of inertia are calculated by Monte-Carlo integration. LAMMPS assumes that the interaction between two rigid composite particles is equal to the sum of the pairwise interactions between its constituent spheres. The time-integration for a rigid molecule then proceeds as follows:42 (1) the forces and torques acting on all constituent spheres are computed. (2) Within each molecule, the forces and torques on the constituent spheres are added. (3) For each molecule the position, orientation, and translational/rotational velocity are updated. (4) The position and velocity of each constituent sphere are reset.
If a sphere is fully inside a molecule, then we exclude it when defining the molecule before running the simulations. Intramolecular forces and torques in the simulations are also excluded, since they do not contribute to the external forces and torques on the molecules. This prevents any possible numerical issues due to the presence of large overlaps.
In order to compute the pairwise contact interaction between spheres, we assume a spring-dashpot model, where two contacting spheres i of radius ai and j of radius aj having positions ri and rj, respectively experience a relative normal compression with overlap δ = ai + aj − rij, where rij = ri − rj and rij= |rij|. The resulting force on sphere i is Fij = Fnij + Ftij, where Fn,tij are the normal and tangential contact forces, respectively, given as:43
 | (3) |
 | (4) |
 . We note that the masses of the constituent spheres mi, mj are calculated from the sphere volumes and the mass density. The quantities Δst, Kn,t and γn,t are the elastic tangential displacement, and the elastic and viscoelastic constants, respectively.43 In a gravitational field g = −gẑ, the total force Ftoti and torque τtoti on sphere i is then given as:
. We note that the masses of the constituent spheres mi, mj are calculated from the sphere volumes and the mass density. The quantities Δst, Kn,t and γn,t are the elastic tangential displacement, and the elastic and viscoelastic constants, respectively.43 In a gravitational field g = −gẑ, the total force Ftoti and torque τtoti on sphere i is then given as: | (5) |
 | (6) |
Simulations are run until a static equilibrium is achieved when the kinetic energy per particle is less than 10−9mgd, where m is the mass of the first sphere in the molecule. The number of particles, material parameter values, and time step used in the simulations are given in Table 1. We run 10 independent simulations for each shape and average packing densities, with error bars given as the standard deviation of the sample.
2.5 Packing density calculation
Since our packing protocol can result in some crystallization at the bottom of the box, depending on many factors such as the box width, the time step and the pouring height, we define a bulk region by excluding particles within 5d from the boundaries in the ẑ-direction. This definition of bulk region is consistent with that used in ref. 25, where an investigation of the radial distribution function and an orientational correlation function of the trimer packing has confirmed that such a distance from the boundaries ensures that no significant ordering effects occur.We then determine the packing density in the bulk, which is generally given as the number of particles Nb within the bulk times the volume of a single molecule, divided by the bulk volume Vb:
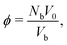 | (7) |
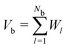 . The superposition is due to the fact that the Voronoi cells of the molecules provide a tessellation of the total volume. To consider a molecule as part of the bulk, the centres of all constituent spheres should be within the bulk, which leads to a straightforward calculation of Nb. The Voronoi cell of a molecule is given as superposition of the Voronoi cells of the constituent spheres. These in turn can be directly calculated in LAMMPS using the Voro++ package, which implements a Voronoi tessellation, i.e., it determines the Voronoi boundaries between all the spheres in the packing and outputs the corresponding cell volumes. Since spheres that are fully inside a molecule are excluded, the tessellation is exact.
. The superposition is due to the fact that the Voronoi cells of the molecules provide a tessellation of the total volume. To consider a molecule as part of the bulk, the centres of all constituent spheres should be within the bulk, which leads to a straightforward calculation of Nb. The Voronoi cell of a molecule is given as superposition of the Voronoi cells of the constituent spheres. These in turn can be directly calculated in LAMMPS using the Voro++ package, which implements a Voronoi tessellation, i.e., it determines the Voronoi boundaries between all the spheres in the packing and outputs the corresponding cell volumes. Since spheres that are fully inside a molecule are excluded, the tessellation is exact.
We also employ (2) a centroid method, for which the bulk region is fixed as a rectangular volume of height 8d, i.e., Vb = 20d × 20d × 8d, which is at least 5d away from the boundaries in ẑ-direction. The number Nb is determined by counting all molecules whose centroid is within the bulk region. Here, the fact that molecules are overlapping at the boundaries generates some uncertainty in the count of Nb, which varies depending on the precise location of the bulk region in the packing. In order to minimize the effect of this variation, we shift the rectangular volume stepwise in the vertical direction starting at 5d from the bottom, determine for each step Nb and the packing density viaeqn (7), and then average the packing densities over all steps (which are taken as 50).
3. Results
We first confirm that our packing protocol is consistent with that used in ref. 25 by comparing packing density measurements for five randomly selected shapes across different packing density regimes, see Fig. 2. For all shapes, our packing density measurements using the two different methods of Section 2.5 agree with that of the dataset within errorbars.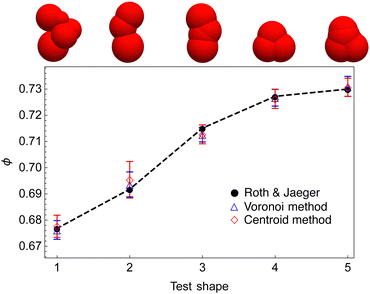 | ||
| Fig. 2 Comparison of our packing simulation with that of ref. 25. We randomly select 5 shapes across different packing density regimes from the dataset and use the packing protocol outlined in Section 2.4. For all shapes, our packing density measurements using two different methods (see Section 2.5) agree with that of the dataset within errorbars. Note that the dashed line only serves to guide the eye. | ||
The results from the PCA dimensional reduction are shown in Fig. 3. In Fig. 3(a) we plot the cumulative variance of the PCs for all 20 dimensions. Of these, 4 dimensions are trivially redundant, since the first sphere sets the origin of the coordinate system and the length scale. There is no variance due to these features, as evident in Fig. 3(a), but PCA is not able to pick up the additional 3 redundant features that result from rotations. Since we anyways only consider up to the first 6 PCs, which capture 80.8% of the total variance, we do not impose a further reduction by these 3 degrees of freedom by hand. Fig. 3(b and c) then show scatter plots of ϕ(![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2)) (here the superscript in
(2)) (here the superscript in ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2) denotes that the first two PCs are considered as reduced shape representation), which indicates that the densest packings are clustered within a region of small PC1–PC2 values.
(2) denotes that the first two PCs are considered as reduced shape representation), which indicates that the densest packings are clustered within a region of small PC1–PC2 values.
Fig. 4 shows plots of the regression functions ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) (
(![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2)) for RF and ANN fitted to the data. We also fitted regression functions to dimensionally reduced shape data with more PCs up to 6. The accuracy of the regression functions is measured by evaluating the root-mean-square error between the packing density predictions and the true values of a 15% testset, see Table 2. As the dimensionality increases, the accuracy also slightly increases, but the error remains approximately twice as large as the error measured in the simulations due to the run-to-run variability.
(2)) for RF and ANN fitted to the data. We also fitted regression functions to dimensionally reduced shape data with more PCs up to 6. The accuracy of the regression functions is measured by evaluating the root-mean-square error between the packing density predictions and the true values of a 15% testset, see Table 2. As the dimensionality increases, the accuracy also slightly increases, but the error remains approximately twice as large as the error measured in the simulations due to the run-to-run variability.
 | ||
Fig. 4 Regression surfaces ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ( (![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2)). (a) Random forest regression. (b) Artificial neural network regression leading to a smooth regression surface. (2)). (a) Random forest regression. (b) Artificial neural network regression leading to a smooth regression surface. | ||
| PCs | RMSE (RF) (×10−3) | RMSE (ANN) (×10−3) |
|---|---|---|
| 2 | 8.13 | 7.88 |
| 3 | 6.95 | 6.81 |
| 4 | 6.64 | 6.29 |
| 5 | 6.43 | 6.31 |
| 6 | 6.47 | 6.76 |
Results from the optimization of the various regression functions for different PCs, the resulting densest packing shapes and the corresponding actual packing densities obtained from LAMMPS simulations are summarized in Table 3 and displayed in Fig. 5. We note that the numerical optimization in the reduced shape space does not require any additional constraint equivalent to the overlap constraint in physical space and always leads to overlapping molecules. The numerical optimization highlights that, at every level of PC retained in the regression, the RF regression function combined with the differential evolution optimization yields the densest predicted packing density, which, if rounded to the third digit, is ϕ = 0.734 throughout. Comparing with the actual simulated values, the ML prediction is systematically above the measured mean value, but well within the error bars, see Fig. 5. The densest packing molecule shape that we find packs slightly denser than the symmetric trimer with up to ϕ = 0.733 ± 0.003, while the symmetric trimer packs with ϕ = 0.729 ± 0.003.25
 | ||
| Fig. 5 Plot of the densest packing shapes found by numerical optimization of the regression function for the indicated number of PCs. The ϕ values and molecule shapes are shown in Table 3. The shaded region indicates the packing density of the symmetric trimer of ref. 25 with ϕ = 0.729 ± 0.003. Note that the displayed ϕ-values for the ML prediction are not rounded and thus slightly vary compared with Table 3. | ||
The fact that the predictions do not improve with increasing the number of PCs used indicates that already the first two PCs, which capture around 40% of the variance in the data (see Fig. 3a), provide a good representation of the densest packing shapes. The PC1–PC2 representation of all the new shapes of Table 3 is shown in Fig. 6a) together with the corresponding PCs of all the molecules in the dataset that pack with ϕ > 0.73. All these shapes occur in a narrow range of PC values with approximately PC1 ∈ [−2,0] and PC2 ∈ [−1,1] and are also visually very similar, see Table 3, forming a family of asymmetric shapes that pack slightly denser than the symmetric trimer.
 | ||
Fig. 6 (a) The PC1–PC2 coordinates of all the shapes in the dataset with ϕ > 0.73 and the new shapes of Table 3. Symbols correspond to PCs as follows: circle (2 PCs), square (3 PCs), diamond (4 PCs), up triangle (5 PCs), down triangle (6 PCs). (b) Density plot of the ANN regression function ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ( (![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2)). (c) Plot of the ANN regression function (2)). (c) Plot of the ANN regression function ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ( (![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2)) along the PC1 = 4 path (indicated by a dashed line in (b)), which exhibits strongly non-monotonic behaviour confirmed in the simulations. The simulated ϕ-values shown are determined by the Voronoi method. (2)) along the PC1 = 4 path (indicated by a dashed line in (b)), which exhibits strongly non-monotonic behaviour confirmed in the simulations. The simulated ϕ-values shown are determined by the Voronoi method. | ||
We further investigate the packing density landscape of the ANN regression function ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) (
(![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2)), displayed in Fig. 6b). The landscape clearly reveals the region of densest packing shapes, but also indicates areas with non-monotonic behaviour. Focusing on the PC1 = 4 path, indicated by a dashed line in Fig. 6b), the packing density exhibits strongly non-monotonic behaviour with a double peak structure, confirmed in the simulations, see Fig. 6c). Visual inspection of the corresponding molecule shapes reveals that the PC2 direction captures roughly the elongation of the shapes, with the local minimum at PC2 ≈ 0 associated with a sphere-like molecule. The plot in Fig. 6c) is thus reminiscent of the variation in packing density of monodisperse ellipsoid packings when the shape is changed from oblate to prolate ellipsoids, which also exhibits a double-peak structure with the perfect sphere as local minimum.10 Varying the two PCs over a wider range shows that the inverse mapping
(2)), displayed in Fig. 6b). The landscape clearly reveals the region of densest packing shapes, but also indicates areas with non-monotonic behaviour. Focusing on the PC1 = 4 path, indicated by a dashed line in Fig. 6b), the packing density exhibits strongly non-monotonic behaviour with a double peak structure, confirmed in the simulations, see Fig. 6c). Visual inspection of the corresponding molecule shapes reveals that the PC2 direction captures roughly the elongation of the shapes, with the local minimum at PC2 ≈ 0 associated with a sphere-like molecule. The plot in Fig. 6c) is thus reminiscent of the variation in packing density of monodisperse ellipsoid packings when the shape is changed from oblate to prolate ellipsoids, which also exhibits a double-peak structure with the perfect sphere as local minimum.10 Varying the two PCs over a wider range shows that the inverse mapping ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2) → α leads to a range of shapes from highly asymmetric elongated ones to more symmetric compact ones, see Fig. 7. In general, PC2 seems to be approximately associated with the elongation of the shape, whereby for each PC1 the most compact shapes occur in the regime PC2 ≈ 0.
(2) → α leads to a range of shapes from highly asymmetric elongated ones to more symmetric compact ones, see Fig. 7. In general, PC2 seems to be approximately associated with the elongation of the shape, whereby for each PC1 the most compact shapes occur in the regime PC2 ≈ 0.
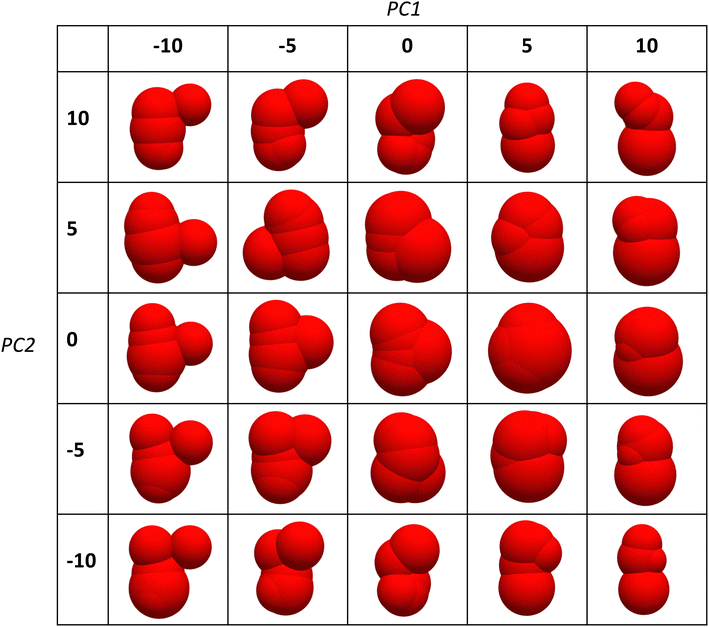 | ||
Fig. 7 Shapes obtained by performing the inverse mapping ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0dc.gif) (2) → α and varying PC1 and PC2 over a range of values. (2) → α and varying PC1 and PC2 over a range of values. | ||
We note that the simulated ϕ values in Fig. 6c) do not agree well with the ANN regression function away from the central region. We believe that the underlying reason is the sparsity of datapoints for large PC1 and PC2 values, which leads to a systematic error in the regression.
4. Conclusions
Using a combination of dimensional reduction, regression, and numerical optimization we have identified shapes that pack slightly denser than the symmetric trimer of ref. 25. We note that these new shapes are only slight variations of shapes that are already in the dataset and represent a family of asymmetric shapes that pack with ϕ ≈ 0.733. Our results show that reducing the shape representation to the first two PCs already allows for a classification of these dense packing shapes, which occur in a narrow range of PC1 ∈ [−2,0] and PC2 ∈ [−1,1]. Further investigation of the ANN regression function has identified a range of PC values, where a strong non-monotonic variation of the packing density occurs, akin to that found in the variation of ellipsoidal shapes.One caveat of the dataset is that it does not provide a uniform sampling of the shape space, but is the output of a CMA-ES optimization algorithm. As a consequence, the datapoints are already clustered around the densest packing shapes and our regression functions yield maxima within the same region. It would thus be interesting to apply our methodology to a less biased dataset.
A crucial question is of course why this particular class of shapes (Table 3) packs the densest? At this point we can only speculate. It seems that these shapes combine several features that are empirically known to pack dense: 1. They are slightly elongated. Approximating the aspect ratio by dividing the longest axis by the next longest one perpendicular to it, indicates an aspect ratio of ≈1.2. For comparison, the densest packings of ellipsoids, spherocylinders, and dimers are found at an aspect ratio of ≈1.4–1.5. 2. They are slightly tetrahedral. The projection of these shapes onto the plane is triangular, but the largest sphere in the shape gives it a tetrahedral appearance. Tetrahedra with flat sides are the densest packing shapes known so far21 with ϕ ≈ 0.78. 3. They are asymmetric. Leaving polyhedral shapes aside, high symmetry of rounded shapes seems to be associated with lower packing density. Examples are: spheres represent a local minimum in the packing density;44 asymmetric ellipsoids pack denser than rotationally symmetric ones;10 cubic-like superellipsoids pack denser than ellipsoid-like ones.46
Our approach could be extended to a variety of other dimensional reduction and regression techniques. Conceptual questions concern, e.g., whether one should a priori restrict the choice of base representation used in the regression based on physical constraints. After all, a non-parametric form like RF leads to a piecewise functional form of ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) (α), which can not represent the “true” (physical) ϕ(α) relationship. On the other hand the physical ϕ(α) function is also not perfectly smooth, since empirical studies indicate that shape variations around the sphere point lead to a cusp singularity in the resulting ϕ as shown, e.g., for ellipsoids at the transition between oblate and prolate ellipsoids of revolution.10 For ANNs this would actually imply that the activation functions should not be chosen as smooth functions like the widely used sigmoid form.
(α), which can not represent the “true” (physical) ϕ(α) relationship. On the other hand the physical ϕ(α) function is also not perfectly smooth, since empirical studies indicate that shape variations around the sphere point lead to a cusp singularity in the resulting ϕ as shown, e.g., for ellipsoids at the transition between oblate and prolate ellipsoids of revolution.10 For ANNs this would actually imply that the activation functions should not be chosen as smooth functions like the widely used sigmoid form.
In ref. 7 a phase diagram of packings of non-spherical particles has been suggested that provides a phase boundary for disordered packings in the ϕ–z plane, where z denotes the average number of contacts of a particle in the packing. General considerations of mechanical stability5 would suggest that the asymmetric shapes found here have z = 12, which locates our packings just inside the phase boundary. We note that evaluating z in simulations can be challenging for molecules with strongly overlapping constituent spheres. In this case, the sphere that is partially inside another one can create an unphysical contact signal due to the soft sphere model used. This issue has been investigated in detail for packings of dimer-shaped particles generated by the same packing protocol.19
We highlight that our machine learning approach to find maximally dense packing shapes can be applied in a straightforward way to other observables of granular matter that are tuned by varying particle shape such as stiffness or diffusivity.23,45 ML can thus be an important tool to address general tasks in granular materials design by identifying shapes that yield aggregates with optimal or tailored properties.47
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully thank Leah K. Roth and Heinrich M. Jaeger for sharing their dataset with us. This research was performed with funding from NSF DMR-1945909. We acknowledge the use of Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT http://doi.org/10.5281/zenodo.438045 and the assistance of the ITS Research team at QMUL.Notes and references
- S. Torquato and F. Stillinger, Rev. Mod. Phys., 2010, 82, 2633–2672 CrossRef.
- A. Baule, F. Morone, H. J. Herrmann and H. A. Makse, Rev. Mod. Phys., 2018, 90, 015006 CrossRef CAS.
- D. Weaire and T. Aste, The pursuit of perfect packing, CRC Press, 2008 Search PubMed.
- L. E. Silbert, Soft Matter, 2010, 6, 2918–2924 RSC.
- M. van Hecke, J. Phys. Cond. Mat., 2010, 22, 033101 CrossRef CAS PubMed.
- P. Charbonneau, J. Kurchan, G. Parisi, P. Urbani and F. Zamponi, Annu. Rev. Cond. Matt. Phys., 2017, 8, 265–288 CrossRef.
- A. Baule and H. A. Makse, Soft Matter, 2014, 10, 4423–4429 RSC.
- S. R. Williams and A. P. Philipse, Phys. Rev. E, 2003, 67, 051301 CrossRef CAS PubMed.
- C. Abreu, F. Tavares and M. Castier, Powder Technol., 2003, 134, 167–180 CrossRef CAS.
- A. Donev, I. Cisse, D. Sachs, E. Variano, F. Stillinger, R. Connelly, S. Torquato and P. Chaikin, Science, 2004, 303, 990–993 CrossRef CAS PubMed.
- X. Jia, M. Gan, R. A. Williams and D. Rhodes, Powder Technol., 2007, 174, 10 CrossRef CAS.
- M. Bargiel, Comput. Sci., 2008, 5102, 126 Search PubMed.
- A. Wouterse, S. Luding and A. P. Philipse, Granular Matter, 2009, 11, 169–177 CrossRef.
- S. Faure, A. Lefebvre-Lepot and B. Semin, ESAIM: Proceedings, 2009, 28, 13–32 CrossRef.
- A. V. Kyrylyuk, M. A. van de Haar, L. Rossi, A. Wouterse and A. P. Philipse, Soft Matter, 2011, 7, 1671–1674 RSC.
- J. Zhao, S. Li, R. Zou and A. Yu, Soft Matter, 2012, 8, 1003–1009 RSC.
- A. Baule, R. Mari, L. Bo, L. Portal and H. A. Makse, Nat. Commun., 2013, 4, 2194 CrossRef PubMed.
- K. Shiraishi, H. Mizuno and A. Ikeda, J. Phys. Soc. Jpn., 2020, 89, 074603 CrossRef.
- E. Kurban and A. Baule, Soft Matter, 2021, 17, 8877–8890 RSC.
- W. Man, A. Donev, F. H. Stillinger, M. T. Sullivan, W. B. Russel, D. Heeger, S. Inati, S. Torquato and P. M. Chaikin, Phys. Rev. Lett., 2005, 94, 198001 CrossRef PubMed.
- A. Haji-Akbari, M. Engel, A. S. Keys, X. Zheng, R. G. Petschek, P. Palffy-Muhoray and S. C. Glotzer, Nature, 2009, 462, 773 CrossRef CAS PubMed.
- Y. Jiao and S. Torquato, Phys. Rev. E, 2011, 84, 041309 CrossRef PubMed.
- M. Z. Miskin and H. M. Jaeger, Nat. Mater., 2013, 12, 326–331 CrossRef CAS PubMed.
- M. Z. Miskin and H. M. Jaeger, Soft Matter, 2014, 10, 3708–3715 RSC.
- L. K. Roth and H. M. Jaeger, Soft Matter, 2016, 12, 1107–1115 RSC.
- A. Donev, F. H. Stillinger, P. M. Chaikin and S. Torquato, Phys. Rev. Lett., 2004, 92, 255506 CrossRef PubMed.
- S. Torquato and Y. Jiao, Phys. Rev. E, 2012, 86, 011102 CrossRef PubMed.
- E. R. Chen, M. Engel and S. C. Glotzer, Discrete Comput. Geom., 2010, 44, 253–280 CrossRef.
- N. E. Jackson, M. A. Webb and J. J. de Pablo, Curr. Opin. Chem. Eng., 2019, 23, 106–114 CrossRef.
- T. Qu, S. Di, Y. Feng, M. Wang and T. Zhao, Int. J. Plast., 2021, 144, 103046 CrossRef.
- X. Sun, B. Bahmani, N. N. Vlassis, W. Sun and Y. Xu, Granular Matter, 2021, 24, 1 CrossRef.
- P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76 CrossRef CAS PubMed.
- E. D. Cubuk, S. S. Schoenholz, J. M. Rieser, B. D. Malone, J. Rottler, D. J. Durian, E. Kaxiras and A. J. Liu, Phys. Rev. Lett., 2015, 114, 108001 CrossRef CAS PubMed.
- J. H. van der Linden, G. A. Narsilio and A. Tordesillas, Phys. Rev. E, 2016, 94, 022904 CrossRef PubMed.
- Y. Zhang, G. Ma, L. Tang and W. Zhou, Granular Matter, 2021, 24, 18 CrossRef.
- R. Mandal, C. Casert and P. Sollich, Nat. Commun., 2022, 13, 4424 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- LAMMPS, http://lammps.sandia.gov.
- https://github.com/adrian-baule/granularAI.git, https://github.com/makselab/granularAI.git.
- M. Danisch, Y. Jin and H. A. Makse, Phys. Rev. E, 2010, 81, 051303 CrossRef PubMed.
- T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Springer New York, 2013 Search PubMed.
- T. D. Nguyen and S. J. Plimpton, Comput. Phys. Commun., 2019, 243, 12–24 CrossRef CAS.
- L. E. Silbert, D. Ertas, G. S. Grest, T. C. Halsey and D. Levine, Phys. Rev. E, 2002, 65, 031304 CrossRef PubMed.
- Y. Kallus, Soft Matter, 2016, 12, 4123–4128 RSC.
- M. Roding, Soft Matter, 2017, 13, 8864–8870 RSC.
- G. W. Delaney and P. W. Cleary, EPL, 2010, 89, 34002 CrossRef.
- H. M. Jaeger, Soft Matter, 2015, 11, 12–27 RSC.
| This journal is © The Royal Society of Chemistry 2023 |