Open Access Article
Open Access ArticlePositive, negative and controlled durotaxis†
P.
Sáez
 *abc and
C.
Venturini
a
*abc and
C.
Venturini
a
aLaboratori de Càlcul Numèric (LaCaN), Universitat Politècnica de Catalunya, Barcelona, Spain. E-mail: pablo.saez@upc.edu
bE.T.S. de Ingeniería de Caminos, Universitat Politècnica de Catalunya, Barcelona, Spain
cInstitut de Matemàtiques de la UPC-BarcelonaTech (IMTech), Universitat Politècnica de Catalunya, Barcelona, Spain
First published on 29th March 2023
Abstract
Cell migration is a physical process central to life. Among others, it regulates embryogenesis, tissue regeneration, and tumor growth. Therefore, understanding and controlling cell migration represent fundamental challenges in science. Specifically, the ability of cells to follow stiffness gradients, known as durotaxis, is ubiquitous across most cell types. Even so, certain cells follow positive stiffness gradients while others move along negative gradients. How the physical mechanisms involved in cell migration work to enable a wide range of durotactic responses is still poorly understood. Here, we provide a mechanistic rationale for durotaxis by integrating stochastic clutch models for cell adhesion with an active gel theory of cell migration. We show that positive and negative durotaxis found across cell types are explained by asymmetries in the cell adhesion dynamics. We rationalize durotaxis by asymmetric mechanotransduction in the cell adhesion behavior that further polarizes the intracellular retrograde flow and the protruding velocity at the cell membrane. Our theoretical framework confirms previous experimental observations and explains positive and negative durotaxis. Moreover, we show how durotaxis can be engineered to manipulate cell migration, which has important implications in biology, medicine, and bioengineering.
1 Introduction
Cell migration is central to life.1–3 It determines fundamental biological processes such as embryonic development, tissue regeneration, wound healing or tumor invasion. Cells move guided by exogenous chemical,4,5 electrical6,7 and mechanical signals in vivo and in vitro,3,8–10 known as chemotaxis, electrotaxis and durotaxis. For decades, there have been tremendous efforts to understand how cells organize themselves to follow these stimuli. There is also an increasing interest in controlling cell migration through external cues because it may allow us to propose strategies to arrest tumor progression,11–13 boost tissues regeneration1,14 and to design biomimetic materials.15,16Durotaxis8,9,17 represents a universal mode of directed cell migration across cell types. Among others, fibroblasts,18 some cancer cells24 and smooth muscle cells19 migrate toward positive gradients of the extracellular matrix (ECM), while certain types of cancer cells21,25 migrate toward negative gradients. These are referred to as positive and negative durotaxis, respectively. A stiffness gradient in the ECM exposes cells to a differential rigidity that they sense, transduce and integrate into intracellular responses. Experimental evidence showed dependences on the stiffness gradient20,22,23 and on the absolute stiffness value in which cells migrate.23,24 However, there is a lack of physical understanding of durotaxis across cell scales that could help us to rationalize durotaxis. Among other insights, this could allow us to understand why some cells express positive durotaxis while others migrate down the stiffness gradient. Recent experimental work, in combination with clutch models, has shown the first pieces of evidence of how cell adhesion is implicated in these opposed durotactic responses.25
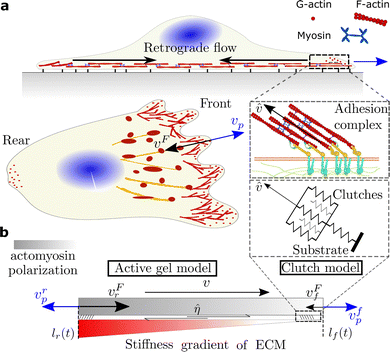
As for any cell migration mode,26,27 durotaxis should be driven by competition of a continuous polymerization of actin filaments that protrudes the cell membrane forward28–30 and an inward retrograde flow generated by the contractile forces that myosin motors exert on the F-actin network31,32 (Fig. 1). Balancing these two forces, adhesion complexes (ACs) establish cell attachments to their surroundings through a large number of cell adhesion molecules (CAMs).33,34 At some point during the motility process, the formation of a cell front orients the cell toward positive or negative stiffness gradients.
Here, we integrate active gel models with stochastic clutch models for cell adhesion to reveal how durotaxis works. Cells read differences in the ECM stiffness through CAMs and regulate the ACs dynamics accordingly.33–36 Therefore, durotaxis must be first activated by the mechanotransduction of the substrate stiffness. Then, the striking durotactic modes found across cell types must be due to a differential expression of adhesion dynamics. Under this rationale, we explore how the cell adhesion can be manipulated to arrest or enhance durotaxis, and to switch from positive to negative durotaxis, and vice versa.
2 Model
To explore the role of adhesion mechanics in cell migration, we build a minimal active gel model for cell migration.40 We consider a 1D domain, Ω, with moving coordinates x(t) ∈ [lr(t),lf(t)]. lr(t) and lf(t) represent the rear and front boundaries of the cell and, therefore, the cell length is determined as L(t) = lf(t) − lr(t) (Fig. 1), where f and r indicate the front and rear of the cell.We take into account three actin structures (the mathematical model for each network is specified in the following section). First, an actomyosin structure that is activated by the action of myosin motors (mostly myosin motors IIA (MMIIA)). This network is distributed along the entire cell domain Ω and flows from the cell front toward the cell center, which constitutes the retrograde flow of the cell, vF. We consider a second actin structure, which represents the actin filaments at the cell front that polymerize against the cell membrane with velocity vp, as described in ref. 47. We decouple these two regions because they are spatially and functionally different (see, e.g., ref. 44 and 49). This cell region is small compared with the cell length and, therefore, we assume no length dependence on vp. The actomyosin network is rich in myosin motors and responsible for retrograde flow. Indeed, if MMIIA is inhibited, the retrograde flow is dramatically reduced.45 The other, which polymerizes actin against the cell membrane, does not depend on myosin activity46 but it is rich in Arp2–3, which is responsible for actin polymerization. These two models directly control cell migration (see Section 2.2). We have included a third actomyosin network, a stress fiber-like structure that forms on top of adhesion complexes. This network is activated by both myosin motors IIA and IIB and it exerts traction forces on the substrate. To model this network, we apply the clutch model to compute the tractions and actin velocity, ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) , of this structure, instead of the classical use of the clutch model where the retrograde flow vF is obtained. To account for durotaxis, we coarse-grain the interaction of the retrograde flow with the adhesion complexes through a friction parameter, η, that directly enters the active gel model (see Section 2.1 and 2.3).
, of this structure, instead of the classical use of the clutch model where the retrograde flow vF is obtained. To account for durotaxis, we coarse-grain the interaction of the retrograde flow with the adhesion complexes through a friction parameter, η, that directly enters the active gel model (see Section 2.1 and 2.3).
2.1 Clutch model of cell adhesion
To model the adhesion dynamics, we adopt previous clutch models (see ref. 37–39 and ESI† for details). The clutch hypothesis considers a contractile acto-myosin network that pulls on the CAMs bound to the ECM. Different cell types respond to the intracellular pulling forces in different ways because cells express specific types of CAMs. Some cells, e.g. neurons,37 express slip bonds: the lifetime of the bond decreases exponentially as the force increases. Other cells, such as fibroblasts, express catch bonds, that is the lifetime first increases and then decreases exponentially with force. To consider these differences and the specific adhesion dynamics, the clutch model considers that a number of molecular clutches bind to the ECM with a constant rate kon, and unbinds with a dissociation rate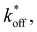 that depends on force as
that depends on force as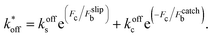 | (1) |
Previous clutch models solve the velocity of the retrograde flow. In our interpretation of the clutch, we compute the tractions, P, and an actin velocity, ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) , of the actin fibers that form upon the adhesion complexes (see Fig. 1). We also assume that the density of myosin motors within the actin fibers is constant in time and space. We compute the retrograde flow through an active gel model, as described in the following section. We focus here on cells expressing slip bonds, as a case of non-reinforced bonds, and cells expressing reinforced catch bonds (all model parameters are in Table S1, ESI†) as a function of the ECM stiffness (Fig. 2).
, of the actin fibers that form upon the adhesion complexes (see Fig. 1). We also assume that the density of myosin motors within the actin fibers is constant in time and space. We compute the retrograde flow through an active gel model, as described in the following section. We focus here on cells expressing slip bonds, as a case of non-reinforced bonds, and cells expressing reinforced catch bonds (all model parameters are in Table S1, ESI†) as a function of the ECM stiffness (Fig. 2).
2.2 Minimal active gel model for cell migration
We model the mechanics of the acto-myosin network as a contractile viscous gel, that represents the retrograde flow parallel to the contact plane between the cell and the ECM.40–44 We assume that viscous forces dominate the elastic forces and that inertial forces are negligible. Therefore, the balance of linear momentum for the active gel is| ∂xσF = ηvF, where σF = μF∂xvF + ζρFρM | (2) |
A second differentiated actin network polymerizes against the membrane,32,46 which increases the membrane tension and, in turn, reduces the polymerization velocity.28,29 Filaments grow freely with velocity vp0 = kponδ if there is no opposing force to it ref. 47. kpon is the rate of actin assembly and δ is the size of one single monomer at the tip of the filament. When the membrane tension increases, the actin polymerization decreases as vp = vp0[1 − τ(L(t))/τstall]z,47,48 where τstall is a tension required to stall the polymerization of the actin network and z is a model parameter that controls the velocity decay. We assume that actin polymerization is symmetric and vp is equal at both sides of the cell. The membrane tension, τ, follows a simple Hookean law such that τ(L(t)) = k(L(t) − Lb), where k is the spring constant and Lb = L0 + Lr accounts for the resting length, L0, and the buffer membrane length Lr in reservoirs and foldings of the cell membrane. Therefore, membrane tension starts to increase once all reservoirs and membrane folds have flattened, i.e. L(t) > Lb. We assume zero compressive stresses when L(t) < Lb.
The outward polymerization velocities, vpr,f, compete against the cell membrane with the inward retrograde flow velocities vFr,f. Then, the rear and front of the cell expand or retract with velocity
![[l with combining dot above]](https://www.rsc.org/images/entities/i_char_006c_0307.gif) r,f(t) = vpr,f − vFr,f, r,f(t) = vpr,f − vFr,f, | (3) |
![[l with combining dot above]](https://www.rsc.org/images/entities/i_char_006c_0307.gif) r(t) +
r(t) + ![[l with combining dot above]](https://www.rsc.org/images/entities/i_char_006c_0307.gif) f(t))/2.
f(t))/2.
The distribution of the F-actin density, ρF(x,t), is modeled as
| ∂tρF + ∂x(wρF − DF∂xρF) = kp − kdρF | (4) |
| ∂tρM + ∂x(wρM − D∂xρM) = 0. | (5) |
2.3 Coupling the clutch and the active gel model
The friction η between the actin network flow has two components, η = η0 +![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) . η0 = 0.05 kPa s μm−2 is a baseline friction of the retrograde flow with the membrane and the surrounding cytoskeletal structures.
. η0 = 0.05 kPa s μm−2 is a baseline friction of the retrograde flow with the membrane and the surrounding cytoskeletal structures. ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) is an effective friction parameter that coarse-grains the friction created between the retrograde flow and the actin network that is connected to the adhesion complexes. If adhesion complexes form, these structures create friction with the surrounding retrograde flow. Large and stable adhesion complexes should induce high friction in comparison with small nascent adhesions. Indeed, large adhesion complexes, such as focal adhesions, create large tractions in the ECM and show slow velocity values
is an effective friction parameter that coarse-grains the friction created between the retrograde flow and the actin network that is connected to the adhesion complexes. If adhesion complexes form, these structures create friction with the surrounding retrograde flow. Large and stable adhesion complexes should induce high friction in comparison with small nascent adhesions. Indeed, large adhesion complexes, such as focal adhesions, create large tractions in the ECM and show slow velocity values ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) of the actin structures connected to them. On the other hand, small adhesion complexes impose low friction forces of the retrograde flow within the ECM. We compute this friction as
of the actin structures connected to them. On the other hand, small adhesion complexes impose low friction forces of the retrograde flow within the ECM. We compute this friction as ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) = P/
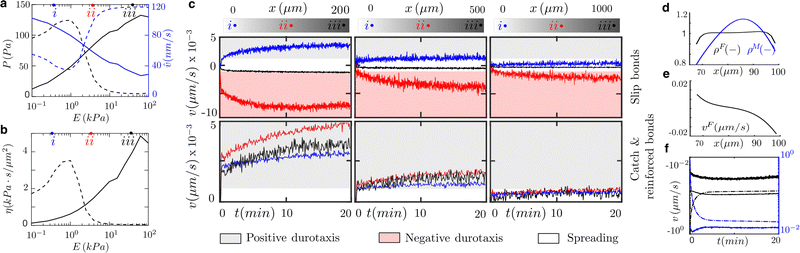
= P/![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) ,42 which reproduces large friction for large and stable adhesion complexes and small friction values for small nascent adhesions. For cells expressing pure slip and catch bonds, there is a maximum traction force at a stiffness value, E ≈ 1 kPa, called optimum stiffness (Fig. 2a). Below and above the optimum stiffness, the traction forces increase and decrease with an increasing value of the substrate rigidity, respectively. However, reinforced bonds show that the traction forces increase as the stiffness of the ECM increases. For the slip case, the effective friction has also a maximum of ≈4 kPa s μm−2 at the optimum rigidity (Fig. 2b). The friction is ≈2 kPa at 0.1 kPa and vanishes for substrate rigidities larger than 10 kPa. Friction increases monotonically from zero to ≈4.5 kPa s μm−2 in the reinforced case. Because ACs only exert tractions where they form, we weight these friction values by an averaged ACs density of 0.1, meaning that ACs occupy the 10% of the contact area. These differences in the cell adhesion behavior could explain the opposite durotactic modes found across cell types. We solve a clutch model along the entire length of the cell (at each integration point of the finite element mesh, see next section for details). All clutch variables, including traction force, P, and actin velocity,
,42 which reproduces large friction for large and stable adhesion complexes and small friction values for small nascent adhesions. For cells expressing pure slip and catch bonds, there is a maximum traction force at a stiffness value, E ≈ 1 kPa, called optimum stiffness (Fig. 2a). Below and above the optimum stiffness, the traction forces increase and decrease with an increasing value of the substrate rigidity, respectively. However, reinforced bonds show that the traction forces increase as the stiffness of the ECM increases. For the slip case, the effective friction has also a maximum of ≈4 kPa s μm−2 at the optimum rigidity (Fig. 2b). The friction is ≈2 kPa at 0.1 kPa and vanishes for substrate rigidities larger than 10 kPa. Friction increases monotonically from zero to ≈4.5 kPa s μm−2 in the reinforced case. Because ACs only exert tractions where they form, we weight these friction values by an averaged ACs density of 0.1, meaning that ACs occupy the 10% of the contact area. These differences in the cell adhesion behavior could explain the opposite durotactic modes found across cell types. We solve a clutch model along the entire length of the cell (at each integration point of the finite element mesh, see next section for details). All clutch variables, including traction force, P, and actin velocity, ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) , change point-wise along the cell–surface interface if there is a difference in the stiffness of the matrix. Therefore, the effective friction is space and time-dependent.
, change point-wise along the cell–surface interface if there is a difference in the stiffness of the matrix. Therefore, the effective friction is space and time-dependent.
2.4 Numerical solution of the system of equations and model parameters
We solve computationally the system above in a staggered approach. We use the finite element method to discretize the system in space, and an implicit second-order Crank–Nicholson method to discretize the parabolic equations in time.51,52 The numerical solution of the parabolic equations can present undesired oscillations if the problem becomes convective dominant, i.e. Pe > 1. The Peclet numbers for the actin and myosin transport problems are PeF = hw/2DF and PeM = hw/2D respectively. We use finite elements of constant size h = L(t)/N, where N is the number of elements. As the convective velocity is the solution to the problem, we cannot guarantee a priori that the problem will remain in the limit case of Pe < 1. Because we want to keep the number of elements of our domain constant and avoid re-meshing strategies in the case that the element size needs to be decreased to keep Pe < 1, we include the Stream-Upwind Petrov Galerkin (SUPG) stabilization term to overcome possible numerical oscillations in our solution.52 The complete finite element and time discretization procedure is presented in ESI.† The model parameters of the clutch and active gel model are summarized in Tables S1 and S2 (ESI†).3 Results
3.1 Cell adhesion explains positive and negative durotaxis
To analyze the exposure of cells to exogenous stimuli in the form of shallow or highly localized stiffness gradients, we use samples of varying length (200, 500, and 1000 μm) with substrate stiffnesses between 0.1 and 100 kPa39 (Fig. 2a). The clutch model predicts traction stresses and retrograde flow as a function of the ECM rigidity and bond behavior (see Fig. 2a and Materials and methods). Then, effective friction![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) can be obtained to inform an active gel model for cell migration (see Materials and methods) about the asymmetry that the stiffness gradient induces in the cell–ECM friction.
can be obtained to inform an active gel model for cell migration (see Materials and methods) about the asymmetry that the stiffness gradient induces in the cell–ECM friction.
We simulate cells initially placed at three different locations of the sample to study how the absolute value of the substrate stiffness, and not only its gradient, may regulate the durotactic response. We consider that cells undergo durotaxis if the migration velocity is larger than v = 1 nm s−1, otherwise, we assume that they spread and remain stationary. We analyze the process during the first 20 min. when the durotactic response is already apparent.
Simulations of cells placed in the sample of 1000 μm in length do not express durotaxis. However, there is a strong durotactic response in the 200 μm-length sample. Cells simulated in the 500 μm-length sample also sustain durotaxis but at a lower degree. In the three samples (200, 500, and 1000 μm), the strongest durotactic response is obtained for cells located at the center of the sample (E ≈ 1–10 kPa). This is due to a large friction gradient (Fig. 2b) and absolute friction that enables intracellular polarization.
In terms of migration direction (Fig. 2c), all cells with reinforced adhesions move toward the positive stiffness gradient of the ECM with similar migration velocities that peak for substrate rigidities between 0.1–1 kPa. However, without reinforcement, cells can migrate toward positive or negative stiffness gradients of the ECM. Cells located on the left of the optimal rigidity (E = 0.1–1 kPa) undergo positive durotaxis. Cells located at the stiffest region of the samples, above 10 kPa, and where no friction gradient exists, show a weak durotactic response and stay mostly stationary. However, cells located just on the right of the optimal rigidity, E ≈ 1–10 kPa, express negative durotaxis. This is because of a negative friction gradient. For the strongest durotactic expression, in the 200 μm-length sample and for cells placed on the right of the optimal rigidity, the maximum migration velocity is v ≈ 8 nm s−1. Cells placed on the left of the optimal rigidity migrate with v ≈ 4.5 nm s−1. However, cells placed on E ≈ 10–100 kPa show a weak durotactic response.
To understand the physical mechanisms behind durotaxis, we further analyze the model results for the strongest durotactic response (right of the optimal rigidity, 200 μm sample) of cells expressing slip bonds (Fig. 2a and c). We analyze the model for 20 min when the migration velocity is maximum. The actomyosin network polarizes (Fig. 2d) because of an asymmetric retrograde flow (Fig. 2e) that results from asymmetric adhesion forces. The asymmetric retrograde flow and the constant polymerization velocity at both cell edges make one side of the cell protrude faster than the other, which establishes the cell front (Fig. 2f). Cells elongate 4-fold from the initial length and the cell membrane reaches a tension of ≈60 pN nm−1 (Fig. S1, ESI†), similar to previous experimental data.53 The stress of the actomyosin network is mostly symmetric with a maximum at the cell center of 50 Pa (Fig. S1, ESI†). This result indicates that the actomyosin network imposes traction on the nuclear region of the cell, which is also in agreement with previous results on the mechanosensitivity of the cell nucleus.54 All other cases of durotaxis shown in Fig. 2 exhibit similar results, with the model variables polarized towards the positive or negative direction, depending on the direction of the friction polarization, and a smaller or larger polarization depending on the strength of the durotaxis response (Fig. S2, ESI†). All cases with spreading signatures (see Fig. 2) show an almost symmetric distribution of all models' variables (Fig. S3, ESI†).
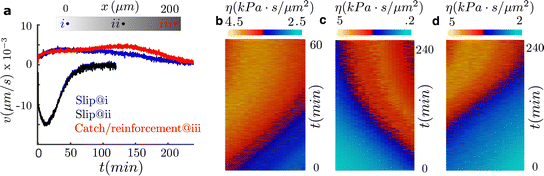
At steady state (Fig. 3), the friction values are symmetric and large enough to significantly reduce the retrograde flow, which reduces the front-rear differences between the inward flow and the outward actin polymerization velocity and, consequently, cells get into a stationary spreading-like phase.
To further analyze the durotaxis dynamics as cells travel along the sample until they reach a steady state (reached when cells stop and no longer migrate), we focus on three cases (Fig. S3, ESI†): the two slip cases of cells initially placed on the left and right of the optimum rigidity in the 200 μm-length sample (strong positive and negative durotaxis expression, respectively, Fig. 2c) and the reinforced case with cells located on the stiff side, E ≈ 30 kPa, of the 200 μm-length sample (positive durotaxis expression, Fig. 2c). As cells migrate, they travel through regions of different stiffnesses (Fig. S3b–d, ESI†) and, therefore, the friction computed through the clutch model also changes in space and time (Fig. 3b–d). In the slip cases, cells migrate toward the optimal rigidity location and stop when they reach it (Fig. 3b and a). Cells stall at the optimal rigidity because they reach a symmetric distribution of the adhesion forces, which reverses the durotactic mode into the symmetric spreading phase (Fig. 3a–c). The non-motile steady state is reached at ≈1 and 4 hors. for cells expressing negative and positive durotaxis, respectively (Fig. 3). For the reinforced case, where no optimal rigidity exists, cells stall when they reach a friction of ≈4.5 kPa s μm−2 at a stiffness of ≈60 kPa.
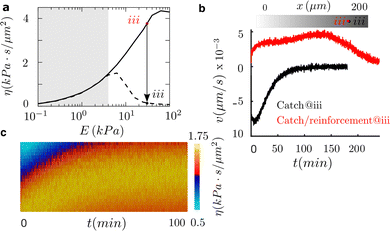
3.2 Durotaxis response to talin knockout: switching to negative durotaxis
Then, we look into the effect of talin knockout, because we know that it changes the cell adhesion behavior remarkably39 and, ask ourselves if it could reverse positive durotaxis. By talin depletion, talin reinforcement is canceled and, therefore, the adhesion behaves as a pure catch bond. This inhibition of the adhesion reinforcement induces a drastic reduction in cell traction and, consequently, in cell friction above a new optimal rigidity that forms at E ≈ 7 kPa (Fig. 4a).To analyze this idea, we use again a sample of 200 μm in length and simulate cells initially placed at E ≈ 30 kPa. We choose this location to analyze substrate regions where the catch and the talin reinforced cases differ (white region, Fig. 4a). Our results show that we are able to shift the direction of durotaxis by inhibiting adhesion reinforcement (Fig. 4b). Furthermore, the motility of the cell is enhanced, and the maximum migration velocity doubles in the knockout case to ≈8 nm s−1. These cells reach the target optimal rigidity in ≈90 min (Fig. 4b). At the optimal rigidity, the cell reaches a state of symmetric friction, which makes it depolarize and stall. Therefore, the talin knockout allows us to switch the directed durotaxis. Moreover, we could tune the location where the motility of the cell stalls and, therefore, we could design matrices to precisely control the target locations in cell migration.
3.3 Engineering durotaxis
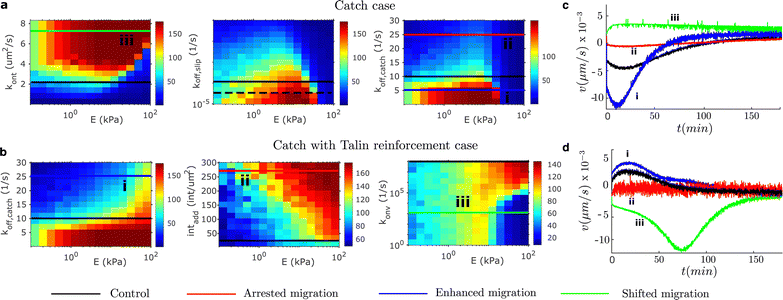
Finally, we further explore possibilities for engineering durotaxis other than the matrix features where cells are placed. Specifically, we are interested in physical quantities that may enhance, arrest or shift durotaxis. Our results above indicate that cell adhesion, in particular the asymmetric distribution of the adhesion strength, controls durotaxis. Therefore, we should arrest durotaxis when the traction force vanishes, is too high or there are no friction gradients. We would enhance durotaxis when the friction gradient increases, in combination with placing cells in specific stiffnesses. Finally, we would shift the durotactic direction if the friction gradient changes sign. We focus on adhesion parameters that can clearly induce these changes in the adhesion behavior and that are prone to be manipulated in vitro and in vivo. To do so, we performed a parametric analysis of different adhesion model parameters (the binding rate kont, the slip part of the off-rate in all the unbinding models koff,slip, the catch part of the unbinding rate, koff,catch, the number of integrins added to the system intadd and the rate of vinculin attachment konv). We show in Fig. 5 the specific values of the model parameters and the resulting traction.Among the different possibilities prone to change durotaxis, we present one case of enhancement, arrest and direction shifting of durotaxis for each adhesion case. We show that in the pure catch case, where the maximum migration velocity in the control case is ≈5 nm s−1, we can enhance durotaxis by decreasing the off-rate of the catch bond (Fig. 5a and c). We show that the migration velocity increases to 12 nm s−1 (Fig. 5c). We also demonstrate a shift in the migration direction when the off-rate of the integrin increases. These two modifications are enabled by increasing and decreasing the rigidity gradient, respectively. To shift the direction of migration, i.e. to shift the gradient sign, we increase the binding rate of the integrin. Similar to the reinforced case (Fig. 5b), we can foster durotaxis by increasing the off-rate of the catch part of the bond. In this case, the migration velocity increases from ≈5 nm s−1 in the control case to ≈7 nm s−1 (Fig. 5d). We can arrest durotaxis by increasing the recruitment of integrins to the AC, which creates a friction large enough to significantly reduce the retrograde flow. Finally, we can also shift the durotaxis direction, with a remarkable enhancement in the migration velocity up to ≈12 nm s−1 (Fig. 5d), by reducing the on rate of vinculin to talin. This inhibition of vinculin binding cancels the adhesion reinforcement and, at the same time, increases the friction gradient (see also Fig. 4).
3.4 Haptotaxis
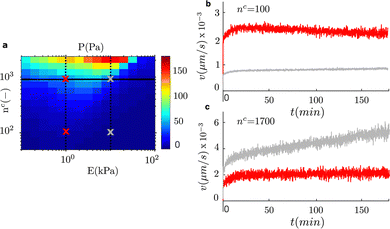
To take advantage of the engineered approach that we discuss in the previous section, and provide an application of our model to a similar system, we focus now on haptotaxis. Haptotaxis refers to the migration of cells toward gradients of ligands density.55,56 We vary the ligands number, nc, for fixed adhesion lengths, while we also vary the stiffness gradient of the matrix. We first use the clutch model to compute the cell traction for the combination of these two features of the matrix (Fig. 6a). As we discussed previously, we can anticipate that a cell traction gradient along with an increase in ligands density will activate a directed cell migration. We compute the migration velocity for two values of the matrix stiffness (E = 1 kPa and E = 10 kPa) while we increase the number of ligands under the adhesion complexes in a domain of length 200 μm (Fig. 6). We compute the migration velocity in time for four cases. For each value of the matrix stiffness, we simulate cells that start to migrate at locations of low ligands density (nc ≈ 100) and in the default density from all previous cases (nc ≈ 1700). The results show that cell migration is always activated toward the positive gradient of ligands density. Therefore, we cannot demonstrate negative haptotaxis. Our results show that on average a low ligands density induces weak haptotaxis compared with a higher density (Fig. 6b and c). Similar to durotaxis, the cell traction, and equivalently friction gradient, has also an important role in the migration velocity. A large traction gradient at E = 10 kPa and nc ≈ 1700 results in a higher migration velocity than in the shallow gradient at E = 10 kPa, nc ≈ 100 and at E = 1 kPa, nc ≈ 1700. Our results show that not only does the gradient of ligands density matter, but the stiffness of the matrix to which those ligands are attached has also a significant effect on the migration velocity in haptotaxis.4 Discussion
Durotaxis represents a universal mode of directed cell migration. Although it manifests across most cell types, fibroblasts18 and smooth muscle cells19 express positive durotaxis, while other cell types present negative durotaxis.19,24 Similarly, axons also move toward soft regions of the ECM,20 although they do not really test migration. How the physical mechanisms that enable cell motility cooperate to activate these remarkable and reversed modes of durotaxis were hindered behind complex in vivo and in vitro tests.Different theoretical and computational models have explained positive and negative durotaxis individually (see, e.g., ref. 57–59). Recently, a clutch model with a number of modules that moves forward and enables cell migration showed, in cooperation with experimental data, the role of adhesion mechanics in durotaxis.60 Here, we coarse-grained the effect of ACs in the retrograde flow through an effective friction parameter that results from clutch models. This friction parameter directly enters in our cell migration model, which we solve through classical active gel models for cell migration, from where we can recover actin retrograde flows. Our theory also explains positive and negative durotaxis by the mechanics of cell adhesion. Our results suggest that cells that express bonds with talin reinforcement follow positive durotaxis while those that express negative durotaxis are crowded by either pure slip or catch bonds. This is the case, e.g., of fibroblasts18,39 and neurons,37 respectively. In other words, reinforcement seems to control the durotactic response.
Our results also support and validate previous experimental data. Focal adhesions induce high friction between the retrograde flow and the ECM in comparison with small nascent adhesion, or other types of cell adhesion. This is reproduced by our model. We showed that low friction values are associated with larger retrograde flows and reduced protrusion velocities. However, large friction values reduce the velocity of the retrograde flow and increase the protrusion velocity of the cell fronts (see eqn (3)), which is in agreement with previous data on spreading cells72,73 and on how adhesion forces are transmitted to the nucleus.54 We also show that cells need a strong stiffness gradient (and friction gradient) in order to express durotaxis and that they prefer intermediate stiffnesses rather than soft or stiff substrates.20,22,23,61,62 Indeed, there is a sweet spot at 1–5 kPa that favors durotaxis. Conversely, lower and higher stiffnesses reduce cell motility and arrest durotaxis, respectively, which are aligned with low and high friction forces. These results may also explain differences between weakly and strongly adherent cancer cells.63 Interestingly, our results also show that cells migrate through the extracellular space guided by the stiffness gradient up to regions of large and symmetric adhesion forces, where the asymmetry of the motile forces stalls and cells stop. These results indicate that cells migrate towards the optimal rigidity location, when it exists, or up to a location of friction large enough to stall the polarization of the cell.
Friction has a central role in our durotaxis model. As we discussed in Section 2.3, the friction between the retrograde flow and the ECM, η, is due to the formation of ACs. The retrograde flow couples with the stable ACs through a continuum actin network. When ACs are present, the friction coefficient accounts for the reduction in fluid flow velocity as the ACs become larger and more stable. Although our model doesn't tackle explicitly such interactions, and just coarse-grained them through a friction parameter. How the interaction between these differentiated, but also structurally connected actin networks mechanically communicates to regulate cell function is a fundamental research question that should be carefully addressed in the future.
We also show specific aspects of the adhesion complex that can be pinpointed to control the strength and the direction of durotaxis. Future experimental work should confirm these predictions and further interact with computational models to exploit the control of cell migration. Because mechanical cues usually coexist with other exogenous signals, our theory can be extended to incorporate, e.g., chemotaxis and investigate the competition between these two prevalent migrating cues. In our model, if we do not establish a stiffness gradient, the cell would never migrate and it would just spread. Symmetric spreading occurs when cells are seeded in matrices of constant stiffness. However, there are always other signals in in vivo and in vitro systems, that may also cohabitate with the mechanical gradients. These signals can trigger downstream polarization of GTPases.66 GTPases may self-polarize because of the noise of stimuli and induce cell migration.67,69 Even changes in the cell membrane tension may induce polarization of GTPases, which eventually would polarize the downstream signals to enhance actin and myosin activity and aid in the formation of a clear cell front and rear.68,69 Eventually, cells migrate even though no stiffness gradient exists. How chemotaxis and durotaxis compete when they coexist is an interesting research question to be addressed.
The viscoelastic properties of the ECM may also mediate cell motility. Viscoelasticity of the ECM is involved in the formation of adhesion complexes70,71,73 and spreading.70,71,73 Previous studies have used constant viscous properties. However, whether a viscoelastic gradient can also induce directed cell migration or not is still widely unknown.74
A deep understanding and precise control of the mechanisms in cell motility may allow us not only to understand how tumor cells invade healthy tissues and metastasize11,12 or how cells orchestrate the regeneration of the tissues,1,14 but also provide tools to arrest tumor progression13 and to engineer cell migration for better biomimetic tissue designs.64,65
Author contributions
P. S. designed the work and performed full simulations. C. V. performed the clutch model simulation. P. S. wrote the paper. All authors analyzed the data and critically reviewed the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. S. acknowledges support from the Spanish Ministry of Economy and Competitiveness (Grant No.: PID2019-110949GB-I00) and the Generalitat de Catalunya (Grant No.: 2017-SGR-1278). C. V. was supported by the Generalitat de Catalunya (FI grant). P. S. and C. V. acknowledge support from the European Commission (Grant No. H2020-FETPROACT-01-2016-731957). We also thank W. Mirza, J. J. Muñoz, and M. Arroyo for discussion.References
- P. Friedl and D. Gilmour, Nat. Rev. Mol. Cell Biol., 2009, 10, 445–457 CrossRef CAS PubMed.
- R. Mayor and S. Etienne-Manneville, Nat. Rev. Mol. Cell Biol., 2016, 17, 97–109 CrossRef CAS PubMed.
- S. Van Helvert, C. Storm and P. Friedl, Nat. Cell Biol., 2018, 20, 8–20 CrossRef CAS PubMed.
- P. J. M. Van Haastert and P. N. Devreotes, Nat. Rev. Mol. Cell Biol., 2004, 5, 626–634 CrossRef CAS PubMed.
- R. R. Kay, P. Langridge, D. Traynor and O. Hoeller, Nat. Rev. Mol. Cell Biol., 2008, 9, 455–463 CrossRef CAS PubMed.
- C. D. McCaig, A. M. Rajnicek, B. Song and M. Zhao, Physiol. Rev., 2005, 85, 943–978 CrossRef.
- B. Cortese, I. E. Palamà, S. D'Amone and G. Gigli, Integr. Biol., 2014, 6, 817–830 CrossRef CAS PubMed.
- A. Shellard and R. Mayor, Dev. Cell, 2021, 56, 227–239 CrossRef CAS PubMed.
- R. Sunyer and X. Trepat, Curr. Biol., 2020, 30, R383–R387 CrossRef CAS PubMed.
- G. Charras and E. Sahai, Nat. Rev. Mol. Cell Biol., 2014, 15, 813–824 CrossRef CAS PubMed.
- P. Friedl and K. Wolf, Nat. Rev. Cancer, 2003, 3, 362–374 CrossRef CAS PubMed.
- H. Yamaguchi, J. Wyckoff and J. Condeelis, Curr. Opin. Cell Biol., 2005, 17, 559–564 CrossRef CAS.
- D. T. Butcher, T. Alliston and V. M. Weaver, Nat. Rev. Cancer, 2009, 9, 108–122 CrossRef CAS PubMed.
- F. Qu, F. Guilak and R. L. Mauck, Nat. Rev. Rheumatol., 2019, 15, 167–179 CrossRef.
- R. Langer and D. A. Tirrell, Nature, 2004, 428, 487–492 CrossRef CAS PubMed.
- U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2014, 14, 23–36 CrossRef PubMed.
- J. A. Espina, C. L. Marchant and E. H. Barriga, FEBS J., 2021, 289(10), 2736–2754 CrossRef PubMed.
- C. M. Lo, H. B. Wang, M. Dembo and Y. L. Wang, Biophys. J., 2000, 79, 144–152 CrossRef PubMed.
- J. Y. Wong, A. Velasco, P. Rajagopalan and Q. Pham, Langmuir, 2003, 19, 1908–1913 CrossRef CAS.
- D. E. Koser, A. J. Thompson, S. K. Foster, A. Dwivedy, E. K. Pillai, G. K. Sheridan, H. Svoboda, M. Viana, L. D. F. Costa, J. Guck, C. E. Holt, K. Franze, L. D. F. Costa, J. Guck and Others, Nat. Neurosci., 2016, 19, 1592–1598 CrossRef CAS PubMed.
- S. P. Singh, M. P. Schwartz, J. Y. Lee, B. D. Fairbanks and K. S. Anseth, Biomater. Sci., 2014, 2, 1024–1034 RSC.
- B. C. Isenberg, P. A. DiMilla, M. Walker, S. Kim and J. Y. Wong, Biophys. J., 2009, 97, 1313–1322 CrossRef CAS PubMed.
- R. Sunyer, V. Conte, J. Escribano, A. Elosegui-Artola, A. Labernadie, L. Valon, D. Navajas, J. M. García-Aznar, J. J. Muñoz, P. Roca-Cusachs and X. Trepat, Science, 2016, 353, 1157–1161 CrossRef CAS PubMed.
- B. J. DuChez, A. D. Doyle, E. K. Dimitriadis and K. M. Yamada, Biophys. J., 2019, 116, 670–683 CrossRef CAS PubMed.
- A. Isomursu, K.-Y. Park, J. Hou, C. Bo, G. Shamsan, B. Fuller, J. Kasim, M. M. Mahmoodi, T. J. Lu, G. M. Genin and Others, Nat. Mater., 2022, 21, 1081–1090 CrossRef CAS PubMed.
- K. M. Yamada and M. Sixt, Nat. Rev. Mol. Cell Biol., 2019, 20, 738–752 CrossRef CAS PubMed.
- J. E. Bear and J. M. Haugh, Curr. Opin. Cell Biol., 2014, 30, 74–82 CrossRef CAS PubMed.
- M. J. Footer, J. W. Kerssemakers, J. A. Theriot and M. Dogterom, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2181–2186 CrossRef CAS PubMed.
- C. H. Schreiber, M. Stewart and T. Duke, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9141–9146 CrossRef CAS.
- S. Wong, W. H. Guo and Y. L. Wang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17176–17181 CrossRef CAS PubMed.
- D. Pantaloni, C. Le Clainche and M. F. Carlier, Science, 2001, 292, 1502–1506 CrossRef CAS PubMed.
- T. D. Pollard and G. G. Borisy, Cellular motility driven by assembly and disassembly of actin filaments, 2003 Search PubMed.
- J. T. Parsons, A. R. Horwitz and M. A. Schwartz, Nat. Rev. Mol. Cell Biol., 2010, 11, 633–643 CrossRef CAS PubMed.
- M. Vicente-Manzanares, C. K. Choi and A. R. Horwitz, J. Cell Sci., 2009, 1473, 199–206 CrossRef PubMed.
- B. Pontes, P. Monzo, L. Gole, A. L. Le Roux, A. J. Kosmalska, Z. Y. Tam, W. Luo, S. Kan, V. Viasnoff, P. Roca-Cusachs, L. Tucker-Kellogg and N. C. Gauthier, J. Cell Biol., 2017, 216, 2959–2977 CrossRef CAS PubMed.
- J. Z. Kechagia, J. Ivaska and P. Roca-Cusachs, Nat. Rev. Mol. Cell Biol., 2019, 20, 457–473 CrossRef CAS PubMed.
- C. E. Chan and D. J. Odde, Science, 2008, 322, 1687–1691 CrossRef CAS PubMed.
- G. Giannone, R. M. Mège and O. Thoumine, Trends Cell Biol., 2009, 19, 475–486 CrossRef CAS.
- A. Elosegui-Artola, R. Oria, Y. Chen, A. Kosmalska, C. Pérez-gonzález, N. Castro, C. Zhu, X. Trepat and P. Roca-Cusachs, Nat. Cell Biol., 2016, 18, 540 CrossRef CAS.
- T. Putelat, P. Recho and L. Truskinovsky, Phys. Rev. E, 2018, 97, 1–11 CrossRef PubMed.
- J. Prost, F. Jülicher and J. F. Joanny, Nat. Phys., 2015, 11, 111–117 Search PubMed.
- B. Rubinstein, M. F. Fournier, K. Jacobson, A. B. Verkhovsky and A. Mogilner, Biophys. J., 2009, 97, 1853–1863 CrossRef CAS PubMed.
- A. Mogilner and A. Manhart, Annu. Rev. Fluid Mech., 2018, 50, 347–370 CrossRef.
- E. Barnhart, K.-C. C. Lee, G. M. Allen, J. A. Theriot and A. Mogilner, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5045–5050 CrossRef CAS PubMed.
- Y. Cai, N. Biais, G. Giannone, M. Tanase, G. Jiang, J. M. Hofman, C. H. Wiggins, P. Silberzan, A. Buguin, B. Ladoux and M. P. Sheetz, Biophys. J., 2006, 91(10), 3907–3920 CrossRef CAS PubMed.
- A. Ponti, M. Machacek, S. L. Gupton, C. M. Waterman-Storer and G. Danuser, Science, 2004, 305, 1782–1786 CrossRef CAS PubMed.
- A. Mogilner and G. Oster, Biophys. J., 1996, 71, 3030–3045 CrossRef CAS PubMed.
- K. Keren, Z. Pincus, G. M. Allen, E. L. Barnhart, G. Marriott, A. Mogilner and J. A. Theriot, Nature, 2008, 453, 475–480 CrossRef CAS PubMed.
- E. L. Barnhart, K. C. Lee, K. Keren, A. Mogilner and J. A. Theriot, PLoS Biol., 2011, 9(5), e1001059 CrossRef CAS PubMed.
- N. Ofer, E. Abu-Shah, J. Allard, O. Krichevsky, A. Mogilner and K. Keren, Curr. Biol., 2017, 27(19), 2963–2973.e14 CrossRef PubMed.
- O. C. Zienkiewicz and R. L. Taylor, The Finite Element Method, Fluid Dynamics, Vol. 3, 2000 Search PubMed.
- J. Donea and A. Huerta, Finite Element Methods for Flow Problems, Wiley, 2003 Search PubMed.
- Z. Shi, Z. T. Graber, T. Baumgart, H. A. Stone and A. E. Cohen, Cell, 2018, 175, 1769–1779.e13 CrossRef CAS PubMed.
- A. Elosegui-Artola, I. Andreu, A. E. Beedle, A. Lezamiz, M. Uroz, A. J. Kosmalska, R. Oria, J. Z. Kechagia, P. Rico-Lastres, A. L. Le Roux, C. M. Shanahan, X. Trepat, D. Navajas, S. Garcia-Manyes and P. Roca-Cusachs, Cell, 2017, 171, 1397–1410.e14 CrossRef CAS PubMed.
- S. B. C. Carter, Nature, 1967, 213, 256–260 CrossRef CAS PubMed.
- S. G. Ricoult, T. E. Kennedy and D. Juncker, Front. Bioeng. Biotechnol., 2015, 3, 40 Search PubMed.
- E. A. Novikova, M. Raab, D. E. Discher and C. Storm, Phys. Rev. Lett., 2017, 118, 1–5 CrossRef PubMed.
- Y. Kim, S. M. Meade, K. Chen, H. Feng, J. Rayyan, A. Hess-Dunning and E. S. Ereifej, Front. Neurosci., 2018, 12, 1–20 CAS.
- H. Oliveri, K. Franze and A. Goriely, Phys. Rev. Lett., 2021, 126, 118101 CrossRef CAS PubMed.
- B. L. Bangasser, G. A. Shamsan, C. E. Chan, K. N. Opoku, E. Tuzel, B. W. Schlichtmann, J. A. Kasim, B. J. Fuller, B. R. McCullough, S. S. Rosenfeld and D. J. Odde, Nat. Commun., 2017, 8, 15313 CrossRef CAS PubMed.
- D. Joaquin, M. Grigola, G. Kwon, C. Blasius, Y. Han, D. Perlitz, J. Jiang, Y. Ziegler, A. Nardulli and K. J. Hsia, Biotechnol. Bioeng., 2016, 113, 2496–2506 CrossRef CAS PubMed.
- W. J. Hadden, J. L. Young, A. W. Holle, M. L. McFetridge, D. Y. Kim, P. Wijesinghe, H. Taylor-Weiner, J. H. Wen, A. R. Lee, K. Bieback, B. N. Vo, D. D. Sampson, B. F. Kennedy, J. P. Spatz, A. J. Engler and Y. S. Cho, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5647–5652 CrossRef CAS PubMed.
- B. Yeoman, G. Shatkin, P. Beri, A. Banisadr, P. Katira and A. J. Engler, Cell Rep., 2021, 34, 2021 Search PubMed.
- D. E. Ingber, V. C. Mow, D. Butler, L. Niklason, J. Huard, J. Mao, I. Yannas, D. Kaplan and G. Vunjak-Novakovic, Tissue Eng., 2006, 12, 3265–3283 CrossRef CAS PubMed.
- B. Zhang, A. Korolj, B. F. L. Lai and M. Radisic, Nat. Rev. Mater., 2018, 3, 257–278 CrossRef.
- A. J. Ridley, M. A. Schwartz, K. Burridge, R. A. Firtel, M. H. Ginsberg, G. Borisy, J. T. Parsons and A. R. Horwitz, Science, 2003, 302, 1704–1709 CrossRef CAS PubMed.
- A. Jilkine and L. Edelstein-Keshet, A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues, PLoS Comput. Biol., 2011, 7(4), e1001121 CrossRef CAS PubMed.
- A. R. Houk, A. Jilkine, C. O. Mejean, R. Boltyanskiy, E. R. Dufresne, S. B. Angenent, S. J. Altschuler, L. F. Wu and O. D. Weiner, Cell, 2012, 148, 175–188 CrossRef CAS PubMed.
- A. Huttenlocher, Nat. Cell Biol., 2005, 7, 336–337 CrossRef CAS PubMed.
- E. E. Charrier, K. Pogoda, R. G. Wells and P. A. Janmey, Nat. Commun., 2018, 9, 1–13 CrossRef CAS PubMed.
- Z. Gong, S. E. Szczesny, S. R. Caliari, E. E. Charrier, O. Chaudhuri, X. Cao, Y. Lin, R. L. Mauck, P. A. Janmey, J. A. Burdick and V. B. Shenoy, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E2686–E2695 CAS.
- T. Yeung, P. C. Georges, L. A. Flanagan, B. Marg, M. Ortiz, M. Funaki, N. Zahir, W. Ming, V. Weaver and P. A. Janmey, Cell Motil. Cytoskeleton, 2005, 60(1), 24–34 CrossRef PubMed.
- O. Chaudhuri, L. Gu, M. Darnell, D. Klumpers, S. A. Bencherif, J. C. Weaver, N. Huebsch and D. J. Mooney, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- P. U. Shirke, H. Goswami, V. Kumar, D. Shah, S. Beri, S. Das, J. Bellare, S. Mayor, K. Venkatesh, J. R. Seth and A. Majumder, Acta Biomater., 2021, 135, 356–367 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01326f |
| This journal is © The Royal Society of Chemistry 2023 |