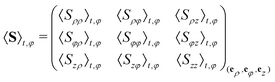Three-dimensional liquid foam flow through a hopper resolved by fast X-ray microtomography

Abstract

We probe the complex rheological behaviour of liquid foams flowing through a conical constriction. With fast X-ray tomographic microscopy we measure in situ the displacement and deformation of up to fifty thousand bubbles at any single time instance while varying systematically the foam liquid fraction, the bubble size and the flow direction – convergent vs. divergent. The large statistics and high spatio-temporal resolution allows to observe and quantify the deviations from a purely viscous flow. We indeed reveal an asymmetry between the convergent and divergent flows associated to the emergence of elastic stresses in the latter case, and enhanced as the liquid fraction is reduced. Such effect is related to the reorientation of the deformed bubbles flowing out of the constriction, from a prolate to an oblate shape in average, while they pass through the hopper waist.

---

1 Introduction

Liquid foams are dispersions of gas bubbles in close contact inside a liquid phase.¹ They are found in various industrial applications including food, cosmetics, soil remediation, oil recovery, and ore flotation,² and mainly used for their particular structure and mechanical behaviour. Liquid foams belong to the class of soft glassy materials which present particular rheological properties in volume with visco-elasto-plastic behaviors.^3,4 This behavior is linked to mechanisms occurring at various scales within their multiscale structure. Elasticity is associated with bubble deformation and the elastic stress tensor is thus directly correlated to tensor quantities that describe the internal deformation state of the bubbles.⁵ Elastic effects saturate through plastic rearrangements that relax the bubble deformation, whose maximal value is strongly correlated to the liquid fraction.⁶ Dissipation in bulk occurs inside the films separating bubbles or at their surface.⁷ While all these various mechanisms were studied separately with model experiments or in simulations, all in simple geometries, it remains difficult to explain how these mechanisms interact to give rise to more complex flow in 3D geometries. One of the experimental challenges is related to the fact that liquid foams are highly dispersive to optical wavelengths and therefore difficult to image in 3D. Full characterizations of the bubble deformations inside a 3D foam flows are scarce.⁸ It is only recently that it has been possible to combine a complete characterization of the bubble deformation with their displacement⁹ for 3D flowing foams. As a consequence, liquid foam flows were mainly studied in 2D^10–16 with a monolayer of foam confined between plates. However, the friction induced by the confinement induces strong effects, such as shear banding,¹¹ that should not be so significant for 3D foam flows. Using X-ray tomographic microscopy we previously succeeded in extracting the deformation and displacement fields of bubbles while flowing around an obstacle,⁹ suggesting this modality as a new tool to describe 3D liquid foam rheology. Our research continues along this work-path by characterizing the flow and bubble elastic deformation inside a liquid foam flowing through a constriction geometry, previously studied in 2D,^17,18i.e. a 3D hourglass-like constriction. Compared to previous studies,⁹ from the perspective of methodology, we improved the bubble statistics by a factor of 100 to 1000 per time series by decreasing the bubble volume (up to a factor of 300) and the voxel size. In addition, we developed an open source 3D quantification toolbox to reconstruct the individual bubble geometry with improved accuracy, and to extract their displacements and deformations.¹⁹ We compare velocity fields acquired in experiments to standard models and we show the interplay between bubble elastic deformations, the local liquid fraction and the boundary conditions at the solid walls on the macroscopic flow. We show that the bubble elastic deformation asymmetry between the convergent and divergent flows was not sufficient to induce significant flow asymmetry at high liquid fractions. Elastic effects are observed only in the divergent geometry when the value of liquid fraction is lowered, typically below 0.15, in agreement with the characterization of the internal bubble strain as a function of the liquid fraction. The effects are finally compared with 2D experiments.

2 Methods

2.1 Liquid foam production and properties

The nature of the foaming solution and of the gas composing the foam has been chosen to minimize aging and modification of the properties at the time scales of the image acquisition (several minutes). The foaming solution was prepared following the protocol of Golemanov et al.²⁰: first 6.6% sodium lauryl ether sulfate (SLES) and 3.4% cocamidopropyl betaine (CAPB) in mass were mixed in ultrapure water; then 0.4% of myristic acid (MAc) was dissolved into the solution by stirring and heating at 60 °C for one hour; this solution was finally diluted 20 times with a glycerol/water mixture with a mass ratio of 90/10 to obtain the foaming solution. Liquid foams were formed inside a co-flow microfluidic device²¹ by simultaneously injecting the foaming solution and a gas composed of perfluorohexane-saturated air. The flow rate of the solution and the pressure of the gas at the device inlets were controlled using a syringe pump (Harvard Apparatus, PHD Ultra) and a pressure controller (MFCS-FLEX, Fluigent), respectively. Two bubble size distribution, denoted “Large” and “Small” were studied with an equivalent bubble radius of about 150 ± 20 μm and 70 ± 15 μm, respectively. The liquid fraction was systematically varied between 12 and 27%. All these quantities are measured in situ in 3D directly from the tomographic images as described in Section 2.3. We verified that the bubble size distribution remained constant and spatially homogeneous over the time scale of each experiment, while the liquid fraction exhibits a small spatial gradient due to gravity-induced drainage (Appendix A).

2.2 Flow geometry, control and imaging

The flow cell is sketched in Fig. 1(A). It was made of acrylic and has the shape of a cylindrical hopper, with an inner diameter of 10 mm outside the constriction and a total height of 50 mm. The constriction is in the middle of the cell, and has the shape of two connected truncated cones with the same opening half-angle α = 35°. Its waist has a diameter of 2.44 mm and a radius of curvature of 0.4 mm. Only the upper part is imaged (Fig. 1(B)) and the measurement region inside the conical part spans between R₀ = 2.45 mm and R₁ = 4.64 mm in spherical coordinates (see Fig. 1(C) for the definition of the coordinate systems). Once a liquid foam is placed inside the cell, a perforated cover closes the upper part of the cell to minimize evaporation while maintaining the ambient pressure. The lower part of the cell is closed by a piston that can move at about 5 μm s⁻¹ in both directions and imposes a constant flow rate Q ≃ 0.39 mm³ s⁻¹ in the cell. Since only the upper part of the constriction was imaged, the flow is divergent, respectively convergent, when the foam is moved upwards, respectively downwards. The tomographic imaging was performed at the TOMCAT beamline of the Paul Scherrer Institute in Switzerland. The photon energy of the monochromatic X-ray beam was set to 16 keV. For each time series, we recorded continuously high-resolution angular projections at 0.7 ms exposure time while rotating the sample at a speed of 14.7 rad s⁻¹. Images were acquired with a dedicated fast X-ray detector system²² placed 25 cm downstream the sample. As a result we reconstruct one 3D image every 0.214 s for a maximum of 28 s covering a volume of 5.3 × 5.8 × 5.8 mm³ with a voxel size equal to 2.92 μm. Before the tomographic reconstruction, we processed the phase contrast projections using a phase retrieval approach assuming that the sample consists of only one material interface (true for a liquid foam). This is a well established method for contrast enhancement to enable better phase separation by thresholding.²³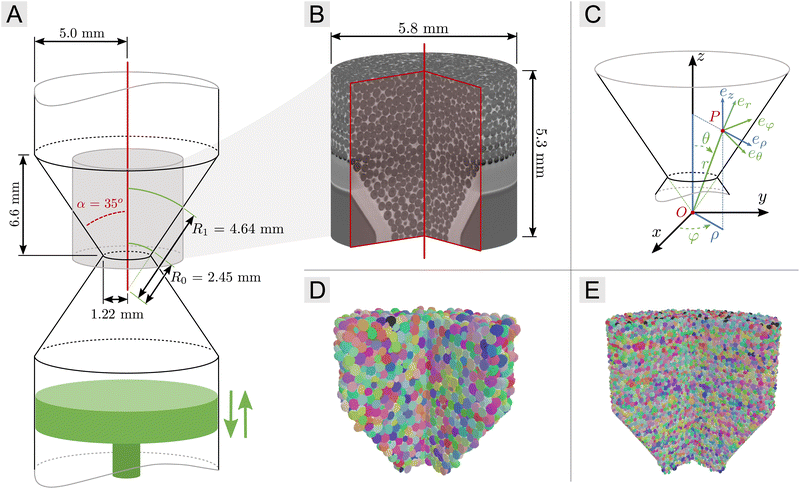

Fig. 1 (A) Sketch of the hourglass-like constriction with the piston in green and the acquired field of view in grey. (B) Typical 3D image with a vertical red cut showing the bubbles inside the constriction. (C) Definition of the Cartesian, cylindrical and spherical basis, (O, e_x, e_y, e_z), (O, e_ρ, e_φ, e_z) and (O, e_r, e_θ, e_φ) respectively, with the tip of the cone O. (D) Segmented image from the CL13 series with an average equivalent radius 〈r_eq〉 = 154 μm and bubbles labeled by arbitrary colors (bubbles in contact with the solid wall are not represented). (E) Same as in (D) with an image from the DS28 series and 〈r_eq〉 = 68 μm. The ESI† includes 3D images after the labeling process and time-lapse sequences of successive 2D slices showing the flow inside the cell.

Our study involved 8 time series presented in Table 1. Each of them is named following the example: the series “DL12” represents a divergent flow “D” with large bubbles “L” and a 12% liquid fraction. Each 3D image contained approximately 5000 and 50 000 bubbles for the large and small bubbles series, respectively. We have checked that the number of bubbles does not significantly change between two successive time steps highlighting the stability of our foams. For instance for large bubbles, changes in number is less than 0.2% and is associated to the difference between bubbles entering/leaving the region of visualization.

Table 1 Selected time series with detailed foam and flow parameters: equivalent radius r_eq and liquid fraction ϕ_l (see Section 2.3 for details)

Name	r eq (μm)	ϕ l	Flow
DL12	150 ± 19	0.12 ± 0.02	Divergent
CL12	154 ± 21	0.12 ± 0.02	Convergent
DL15	154 ± 22	0.15 ± 0.02	Divergent
CL16	154 ± 22	0.16 ± 0.03	Convergent
DL22	153 ± 22	0.22 ± 0.04	Divergent
CL23	155 ± 23	0.23 ± 0.05	Convergent
DS25	68 ± 19	0.25 ± 0.03	Divergent
CS27	68 ± 13	0.27 ± 0.03	Convergent

---

2.3 Image analysis

The 3D images were binned by joining four neighboring voxels, homogenized in the background with a top-hat filter,²⁴ and phase-segmented with an Otsu threshold.²⁴ In this state, the images consist of binary values (0 and 1), corresponding to the gas and liquid phases respectively. Then, each individual bubble volume was segmented with a standard watershed algorithm²⁴ using a Gaussian filtered distance map and an imposed minimum distance between seeds equal to half the average equivalent radius of the bubbles. Bubbles on the top and bottom edges of the image were ignored and removed from the labeling process. Two examples of these segmented and bubble-labeled images are shown in Fig. 1(D and E).

Physical properties at the scale of the foam were extracted from these images. The liquid fraction ϕ_l = n_liquid/(n_liquid + n_gas) is defined as the ratio of the number of voxels in the liquid phase to the total number of voxels in a phase segmented image, with n_liquid and n_gas the number of voxels in the liquid and gas phases respectively. We measured the liquid fraction first globally and also divided the image into sub-volumes along the vertical axis to characterize the liquid fraction profile associated to gravity drainage as shown in Fig. 8 (Appendix A). The higher the position, the drier the foam and the difference between the lowest and highest values of the liquid fraction is used to quantify the dispersion given in Table 1. The bubble volumes were extracted from the bubble segmented images. From the distribution of the bubble volume, we extract the equivalent radius r_eq = 〈(3V_i/4π)^1/3〉_N with 〈⋯〉_N the average over the N bubbles and V_i the volume of the bubble i.

2.4 Velocity fields

The displacement of bubbles between two successive images is obtained by Discrete Digital Volume Correlation (Discrete DVC) as implemented by the SPAM (Software for the Practical Analysis of Materials) package.²⁵ DVC is a well-established and robust approach that uses both the labeled and grayscale images at one time and the grayscale image at the next. The ESI† includes a typical velocity map between two successive time steps to show the quality of the measurements: only a few defects highlighted by very large and randomly oriented arrows are observed among 50 000 bubbles.

Given the geometry, we define a Cartesian coordinate system (O, e_x, e_y, e_z) whose origin O lies at the apex of the conical shape extrapolated from the constriction geometry (black coordinate system in Fig. 1(C)), and where (Oz) is the axis of symmetry. In this system, each point P can be expressed with the cylindrical (ρ, φ, z) or spherical coordinates (r, θ, φ) using the unit vectors (e_ρ, e_φ, e_z) or (e_r, e_θ, e_φ) (blue and green coordinate systems in Fig. 1(C), respectively). The velocity of each bubble was expressed in spherical coordinates (v_r, v_θ, v_φ). The averaged velocity components in the spherical coordinate system (〈v_r〉_t,φ, 〈v_θ〉_t,φ, 〈v_φ〉_t,φ) were obtained by averaging each of the three components in time and space over all bubbles, whose centers of mass are found within tori obtained by sweeping φ between 0 and 360°. For large bubbles, there are typically 400 bubbles in the smallest tori (the closest to the axis of symmetry) and 8000 in the largest (the farthest from the axis of symmetry) after averaging. For small bubbles, these numbers become 4000 and 70 000 respectively. Note that these number reduces to 90 and 1500 for the CL23 series due to a shorter acquisition time.

Given the geometry of our experiment, the 〈v_φ〉_t,φ component is expected to be negligible, as checked afterwards (see Section 3.1); this justifies our choice to average over φ, to improve the statistics. We define the velocity v₀ = Q/[2π(1 − cos α)R₀²] as the velocity of a radially symmetric flow field of the same flow rate measured at radius R₀. With our parameters, we expect v₀ ≃ 58 μm s⁻¹. In what follows, all velocity components are divided by this reference velocity to obtain dimensionless quantities.

2.5 Internal strain fields

Each bubble i is characterized by the set of coordinates {r} of all voxels defining the bubble region. This allows to define the center of mass position 〈r〉_i and a shape tensor, to characterize the bubble geometry, defined as S = 〈(r − 〈r〉_i) ⊗ (r − 〈r〉_i)〉_i^1/2 with 〈⋯〉_i the average operation over all the pixels of the bubble i.⁹ We then consider an average shape tensor obtained by averaging each of the nine components, in cylindrical coordinates, in time and space over all the bubbles present in the aforementioned tori:
Bubbles in contact with solid walls are discarded from the statistics because they may have specific geometries due to contact with the walls or a lack of precision in the location of bubble-wall boundaries. By construction the averaged shape tensor is symmetric and can be diagonalized in an orthogonal eigenbasis. As expected by the symmetry, the four components 〈S_ρφ〉_t,φ, 〈S_φρ〉_t,φ, 〈S_zφ〉_t,φ and 〈S_φz〉_t,φ can be neglected with respect to the other components, and 〈S_φφ〉_t,φ, noted S_φ, is an eigenvalue of 〈S〉_t,φ with e_φ as eigenvector. The two remaining eigenvectors (e₊, e₋) are thus in the azimuthal plane (e_ρ, e_z) with eigenvalues S₊ and S₋ for the largest and smallest value, respectively. The obtained expression of the diagonalised averaged shape tensor writes
The average shape tensor representation is an ellipsoid with (S₊e₊, S₋e₋, S_φe_φ) as the principal semi-axes. The average bubble shape anisotropy can be characterized by the difference with a sphere of the same volume whose radius is S₀ = (S₊S₋S_φ)^1/3. In the spirit of Graner et al.,²⁶ this anisotropy can be quantified by the internal strain tensor U_S defined as the comparison between the current structure (a set of bubbles deformed on average) and a reference one (the same set of bubbles undeformed on average), i.e. as U_S = log(〈S〉_t,φ) − log(S₀), with S₀ = S₀Id an isotropic tensor, proportional to the identity tensor Id, whose three eigenvalues are equal to S₀. The tensor U_S has the three eigenvalues U₊ = log(S₊/S₀), U₋ = log(S₋/S₀) and U_φ = log(S_φ/S₀) in the eigenbasis (e₊, e₋, e_φ). This tensor assumes that the structure is incompressible, which is provided by the relation U₊ + U₋ + U_φ = 0. In other words, if the structure is stretched in one direction, it is compressed in at least one of the two other directions. This will be further discussed and illustrated in Section 3.2 and Fig. 5.

Finally, we can compute the second invariant of the internal strain tensor as a scalar, named internal strain U, to quantify the distortion of the structure with respect to its undeformed and isotropic reference:

Note that we have tested another method to characterize the deformation and anisotropy of the inner foam structure. We have computed the texture tensor based on the links between adjacent bubbles.^26,27 Both methods give comparable results which show the robustness of the tool chosen to characterize the bubble shape and anisotropy (Appendix B).

3 Results and discussion

3.1 Velocity fields

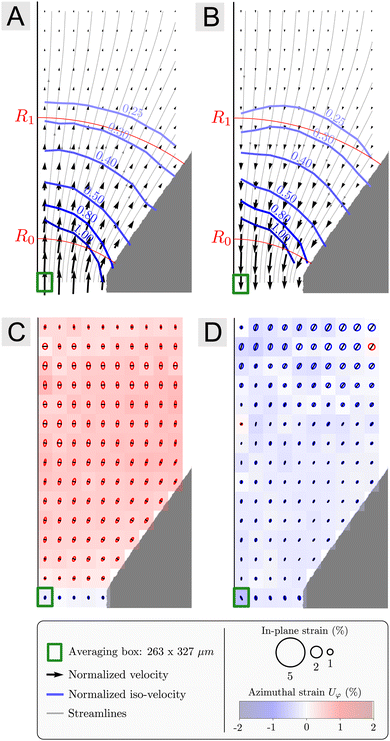
In Fig. 2, the radial velocity component v_r of each bubble is plotted as a function of r for DL22 series. Despite the large dispersion, one can clearly observe that v_r decreases with r. The average 〈v_r〉_t,θ,φ(r) over time, θ and φ for a given r is superimposed and is a decreasing function of r too. Inside the conical part of the constriction we obtain 〈v_r〉_t,θ,φ(r) ∝ 1/r². This result is a strong validation of the velocity measurements since we expect 〈v_r〉_t,θ,φ(r) = v₀(R₀/r)² for r between R₀ and R₁ from the mass balance equation for an incompressible flow. The v₀ value obtained from the best fit, 62 μm s⁻¹, is in very good agreement with the value expected from the imposed flow rate, approximately 58 μm s⁻¹ (Section 2.2). The quantities 〈v_θ〉_t,θ,φ(r) and 〈v_φ〉_t,θ,φ(r) are represented in the same figure. The component 〈v_φ〉_t,θ,φ(r) is almost null whatever r, as expected by symmetry. The component 〈v_θ〉_t,θ,φ(r) is always smaller than 〈v_r〉_t,θ,φ(r) before the entrance of the conical part (r < R₀) and it can be neglected inside the conical part of the constriction, as expected for a radial flow.

Fig. 2 The averaged velocity components (〈v_r〉_t,θ,φ, 〈v_θ〉_t,θ,φ, 〈v_φ〉_t,θ,φ) as functions of r for the DL22 series. In addition the local v_r components are showed by grey points (each one corresponding to one bubble at a given time step, around 1 15 000 points in total). Inset: 〈v_r〉_t,θ,φ(r) as a function of r in a log–log scale. The red line is the best fit of the data in the conical part, between R₀ and R₁, with the function v_r = v₀(R₀/r)², and v₀ = (62 ± 1) μm s⁻¹ as the best fit parameter.

Fig. 3 shows typical average velocity maps in the (e_ρ, e_z) plane, allowing an easy comparison between experiments and viscous flow simulations (Appendix C), between convergent and divergent flows, as well as between several values of the liquid fraction. If we compare the positions of the iso-value curves of the speed, i.e. the norm of the local velocity vector, inside the region of interest, we observe qualitatively that all experiments are close to the viscous model prediction (Appendix C). Flow fields for the smallest bubble size are also provided in Appendix D. They are comparable to those obtained for the largest values of liquid fraction and there are no significant differences between the convergent and divergent flows considering the transformation v → −v.

Fig. 3 Averaged flow field maps in the (e_ρ, e_z) plane obtained with large bubbles. Two flow directions (divergent/convergent) and two liquid fractions (0.12 and 0.22) are probed: (A) DL12, (B) CL12, (C) DL22, (D) CL22. The flow fields are normalized by v₀.

Nevertheless, a finer analysis reveals quantitative deviations to the viscous model in the case of divergent flows that increase as the liquid fraction is lowered. To quantify these deviations, we have observed that each flow field can be reasonably well approximated with a parabolic function of θ for a given r (Fig. 4(A)),

where v_c(r) and v_w(r) are the fitted center and solid wall velocity at a given r. In Fig. 4(B and C), the ratio v_w/v_c is plotted as a function of r in experiments and in simulations. For convergent flows, the trend is independent of the liquid fraction and well described by the viscous flow model. Inside the conical part of the constriction, this ratio increases from 0.5–0.6 to 0.75–0.85 approximately for large bubbles as r increases from R₀ to R₁ (bounds of the measurement regions). Note that the velocity profile for the small bubble size gives slightly larger values, up to 25%, than the ones obtained with the large bubble size and with the viscous flow model. For the case of divergent flows at large values of the liquid fraction, whatever the bubble size, the velocity profiles are the same within 10% (corresponding to the standard deviation of the measurements) to those of convergent flows. However, as the liquid fraction is decreased, the ratio v_w/v_c becomes larger, up to 40%, than for the viscous flow model for a given r. Moreover, for the smallest values of the liquid fraction, the velocity at the contact with the solid wall can even be larger than that found at the center of the constriction (v_w/v_c > 1), which is not possible in the viscous flow model.

Fig. 4 (A) Normalized radial velocity 〈v_r〉_t,φ(r,θ)/v₀ (noted v_r/v₀ for simplicity) as a function of θ and at various radial r positions, for the DL12 series. For all the series and all the r values, the data were fitted with a parabolic function by finding the best v_w and v_c values in eqn (2). (B) v_w/v_c as a function of r inside the conical part in experiments (four series) and in simulations for convergent flows. The error bars are represented by shaded regions and are obtained from the standard deviation of the fitting parameters when fitting the normalized radial velocity profiles with eqn (2). (C) Same as in (B) for divergent flows.

This set of results shows that there is no difference between convergent and divergent flows at high values of liquid fraction whatever the bubble size. At these values, the bubble deformations are expected to be small and so are the elastic stresses. As a consequence the flow is time-reversible explaining the same speed values for a given position inside convergent and divergent flows. Finally, the deviations up to 40% measured at low liquid fractions in the case of divergent flows suggests that the combination of both a specific geometry and of large enough deformations is required to observe specific features associated to elastic effects. These results call for a full characterization of the bubble deformations inside the flow cell as provided by internal strain measurements.

3.2 Internal strain fields

Fig. 5(B–E) displays maps of the internal strain field for the four series DL12, CL12, DL22 and CL22. For simplicity the averages over time and φ of the eigenvalues (〈U₊〉_t,φ(r, θ), 〈U₋〉_t,φ(r, θ), 〈U_φ〉_t,φ(r, θ)) are henceforth noted (U₊, U₋, U_φ). The internal strain in the azimuthal plane (e_ρ, e_z) is shown as ellipses with semi-axes |U₊| and |U₋| in the e₊ and e₋ directions, respectively. Information about the sign of the eigenvalues is indicated by a line segment along the positive axes if any. With this definition, ellipses can have 0, 1 or 2 line segments. The strain U_φ in the third dimension is coded by the background color with a scale from dark blue (strongly negative) to dark red (strongly positive). The color of the ellipse contour (blue or red) is associated to the sign of this eigenvalue (negative or positive) too. Given that U₊ + U₋ + U_φ = 0 by construction of the internal strain tensor, four different cases can be encountered as summarized in Fig. 5(A). As examples, case 1 corresponds to prolate bubbles that are stretched along e₊ and compressed along e₋ and e_φ (U₊ > 0, U₋ < 0 and U_φ < 0); case 2 corresponds to oblate bubbles that are stretched along e₊ and e_φ and compressed along e₋ (U₊ > 0, U₋ < 0 and U_φ > 0).

Fig. 5 (A) Representation of the averaged shape tensor as an ellipsoid, which is compared to the sphere of the same volume to identify the magnitude and orientation of dilation/compression, and to the internal strain tensor as ellipses in the (e_ρ, e_z) plane (see (B–E) or main text for explanations). Based on the signs of the internal strain eigenvalues, four cases are possible and detailed. Internal strain maps for the series (B) DL12, (C) CL12, (D) DL22 and (E) CL22. The ellipses in the (e_ρ, e_z) plane have semi-axes |U₊| and |U₋| and a line segment for positive eigenvalues. The third eigenvalue U_φ representing the deformation in the third dimension is coded by the background color. See the main text for additional explanations. Note that the data in (E) are noisier, especially near the axis of symmetry, due to worse statistics (Section 2.4).

For the various experiments performed, we have only measured bubble deformations corresponding to the cases 1 and 2. Convergent flows display quasi exclusively an internal strain of the first case. The averaged bubble shape is mainly prolate (“cigar-like”): bubbles are mostly elongated in a direction close to the one given by the local velocity (U₊ > 0) while they are compressed in the two other directions (U₋ < 0 and U_φ < 0). On the opposite, divergent flows display quasi exclusively an internal strain of the second case. The averaged bubble shape is mainly oblate (“disk-like”): bubbles are mostly compressed in a direction close to the one given by the local velocity (U₋ < 0) while they are elongated in the two other directions (U₊ > 0 and U_φ > 0). This observation constitutes the main difference between convergent and divergent flows characterized by opposite signs of the eigenvalues for a given position inside the cell. It is important to note that the averaged bubble shape is mostly prolate within the waist (see bottom of maps), regardless of the series, associated with the need for the bubble to elongate along the flow to pass through the narrowest part of the constriction. Comparing Fig. 5(B and C) with Fig. 5(D and E) respectively shows that the same features are observed whatever the liquid fraction with the difference that the larger the liquid fraction, the smaller the absolute values of the internal strain eigenvalues. For instance, for the driest foams, the internal strain eigenvalues saturate around 3–4% in absolute value (Fig. 5(B and C)), while they barely reach 1% for the wettest foams (Fig. 5(D and E)). In addition, we observe that the higher the position inside the cell, the larger the eigenvalues in absolute values. In fact, values in Table 1 are averages over all the cell volume but there is a gradient of liquid fraction due to gravity and the higher the position inside the cell, the lower the liquid fraction is for a given series as described in Appendix A. In Appendix D, the internal strain maps are plotted for the two series with the smallest bubbles (DS25 and CS27). We do not observe any specific effect associated with the bubble size, except that those fields are smoother due to a better statistics associated to a larger number of bubbles. These series have relatively high values of liquid fraction and display the same features than the series with larger bubbles and similar liquid fractions (DL22 and CL22 in Fig. 5(D and E)).

To show quantitatively the difference between the convergent and the divergent flows, Fig. 6(A–C) displays respectively the internal strain spherical components U_r, U_θ and U_φ, averaged over time, θ and φ, as a function of r for all the series. Despite a significant data scatter for the series with large bubbles, the internal strain asymmetry between convergent and divergent flows is directly observable, even for the large liquid fraction series CS27 and DS25. Indeed, in the conical part of the hopper (R₀ ≤ r ≤ R₁), the sign of all components are reversed between the convergent geometry (for which U_r > 0, U_θ < 0 and U_φ < 0) and the divergent geometry (for which U_r < 0, U_θ > 0 and U_φ > 0). Moreover, the amplitude of the deformations is gradually larger as the liquid fraction becomes smaller. The absolute values of the components U_r and U_φ show a slight increase with r for the two series at largest average liquid fraction, especially in the divergent geometry. Once again, we ascribe this drift to the gradient of liquid fraction induced by gravity and quantified in Appendix A. For r ≤ R₀, i.e. in the waist region, Fig. 6 reveals an interesting difference between the convergent and divergent cases. In the convergent cases, the values of all components remain similar to their values in the conical region R₀ ≤ r ≤ R₁. In the divergent cases, the situation is markedly different: there is a sign reversal of all components between r = 1.8 mm, where we are very close to the center of the waist, to r = R₀, where we enter the divergent part, after which the components almost saturate (except for the aforementioned drift). We believe that this interesting reversal is a manifestation of the time reversal asymmetry in foam yielding previously evidenced by Rouyer et al.²⁸ and modelled by Marmottant & Graner.²⁹ The scenario as follows: at the exit of the convergent region, the bubbles are prolate, but they start evidencing a divergent flow. The latter first elastically reverses the strain components of the bubbles, leading to oblate shapes, in a region of small but finite extent close to the waist; then the foam yields, and in the rest of the divergent region, the strain components (and the oblate average shape of the bubbles) saturate.

Fig. 6 Internal strain tensor spherical components (A) U_r, (B) U_θ and (C) U_φ averaged over time and the spherical coordinates θ and φ, as a function of the spherical radius r. Notice the sign differences between the convergent cases (in blue) and the divergent cases (in red).

To be more quantitative on the effect of the liquid fraction, we use the internal strain U as defined in eqn (1) to quantify with a single scalar the local deformation of the structure. In Fig. 7, U is plotted as a function of ϕ_l for the eight series. Each point of the 2D map gives one point in this figure and we use the local values of liquid fraction for each of them. Here, we take advantage of the aforementioned gravity-induced gradient of liquid fraction quantified in Appendix A to scan different values of the liquid fraction within each series. In Fig. 7, we observe that all data points are found within a band that has a certain height for a given liquid fraction. The largest values, around 4%, are obtained for the driest foams. Note that this scalar does not characterize the deformation of individual bubbles but is by definition an averaged deformation state of the local structure composed of many bubbles. Typical values of U obtained with individual bubbles can be up to ten times larger. All series overlap, meaning that we characterize the same features regardless of the bubble size or flow direction. There is a clear trend that U is a decreasing function of ϕ_l, which can be explained as follows. In foams, the liquid-like behavior is associated to plastic rearrangements that limit the maximum deformation of bubbles, and thus of the structure.¹ This results in a yield strain which has been found to decrease with increasing liquid fraction in conventional rheological studies of foams or similar materials like emulsions.^6,30Fig. 7 provides the first in situ measurements at the bubble scale of such a behavior in 3D flow and deserve several comments. First, the dispersion in U for a given ϕ_l can be associated to spatial heterogeneities. In fact the flow inside the cell geometry is not homogeneous and some regions in the cell are probably deformed quasi-elastically with little or no plastic rearrangement, while other regions exhibit yielding with probably numerous plastic rearrangements at the bubble scale and an internal strain that should saturate. These regions should constitute the upper bound of the internal strain values displayed in Fig. 7.

Fig. 7 U as a function of the local liquid fraction ϕ_l, characterized in Appendix A, for all the data points of the internal strain field maps and the eight series.

3.3 Comparison with 2D flows

2D flows confined between plates can be a relevant source of comparison in particular because local deformations, and thus elastic effects, are often exacerbated by the confinement. Quasistatic experiments in a 2D convergent flow geometry (i.e. experiments where friction is small enough that while flowing, the bubble retain a quasi-static geometry) do not reveal any deviation from a viscous flow,¹⁸ as observed in 3D. In this case, the deformation saturates everywhere in the flow cell due to plastic rearrangements occurring at any point. This deformation has roughly the same orientation characteristics resulting in constant elastic stresses.¹⁸ Non-quasistatic effects can nevertheless be observed in these 2D experiments if friction with the confining plates cannot be neglected. In this case, larger deformations can be observed due to a delay in the relaxation of bubbles following plastic rearrangements where the flow is fastest, mainly in the waist of the constriction, resulting in a deviation from a radial flow due to elastic effects.¹⁸ In 3D, such effects are not present and the flow can be considered as quasistatic in the eight series.

A direct comparison between convergent and divergent 2D confined flows was reported for an abrupt contraction.³¹ Again, the convergent flow at the entrance of the contraction shares the same characteristics as a viscous flow, while the divergent flow at the exit of the contraction displays striking features: a velocity undershoot along the axis of symmetry and a re-focussing of the streamlines due to elastic effects. A simple explanation was provided in terms of reorientation of the bubble deformation. In these 2D experiments, bubbles elongated streamwise inside the contraction become elongated spanwise once outside to accommodate channel enlargement. The elastic stresses generated by the spatial heterogeneities in the deformation orientation lead to higher velocities at the edges than expected for a viscous flow. The similarities with the features of the 3D flows are striking. In Fig. 5(B and D), prolate and oblate shapes are observed inside and after the narrowest part of the constriction respectively. Although this effect is less pronounced in 3D due to smaller deformations, approximately 10 times smaller in comparison to the ones reported for the 2D foam flows in ref. 18, it exists and the flow is also faster than expected at the edges for the 3D divergent flow case, provided the magnitude of the deformations is large enough (Fig. 4(C)). In summary, 2D and 3D foam flows appear to share many similarities. Nevertheless, the fore-aft asymmetry of the velocity field through the constriction is much less marked in 3D. This suggests that elastic effects are weaker in our 3D study than in existing 2D studies, because yielding appears at much lower bubble deformation.

4 Conclusion

In conclusion, we have provided experimental measurements of a set of 3D time- and space-resolved foams flow measured directly from individual bubble tracking, allowing a systematic analysis of the flow as a function of liquid fraction, mean radius, and convergent vs. divergent constrictions. The main liquid foam properties were extracted: elastic deformation and flow. Several limitations in our previous studies^9,32 were overcome. New image analysis tools specifically dedicated to liquid foams were developed to capture smaller bubble deformations in wet liquid foams. The overall statistics were improved, with 100 to 1000 times more bubbles. This allowed a detailed quantification of the elastic storage and release of the foam flowing through the constriction. The significant internal strain asymmetry measured between the convergent and divergent flow towards the hopper waist did not induce a correspondingly large asymmetry in the foam flow. The wall-center velocity ratio typically increased with the spherical radius r, a trend captured by the viscous flow simulations. The convergent flow showed less deviation from the viscous model than the divergent flow. This can be explained by the different nature of the elastic state of the ingoing and outgoing flows observed in the deformation maps. The liquid foam is elastically loaded when converging; this stored energy is then released in the diverging part of the cone, generating elastic stresses that alter the flow.

A promising perspective of the technique presented in this article is in foam rheometry. It opens the possibility to simultaneously measure the macroscopic response of a 3D foam (e.g. a stress–strain curve) in a well-controlled rheometric geometry, while simultaneously imaging the response of the foam at the bubble scale and get all individuals displacements, deformations and rearrangements. This simultaneous characterization has, to our knowledge, never been done. The automated and unambiguous detection of all plastic rearrangements in 3D, in particular, is an interesting but challenging technical development which requires a dedicated study. These new 3D tools would allow to answer some exciting long-standing open questions, for instance: (i) whether the flow is homogeneous in terms of velocity and bubble deformations; (ii) whether plastic rearrangements occur as isolated “hot spots”³³ or as large-scale avalanches; (iii) the correspondence between the macroscopic foam response measured by the rheometer and the bubble-resolved elastic stress field; (iv) the difference between the deformation values in 3D with that in 2D, which are much higher. We are currently addressing these questions with recently acquired rheometric datasets.

Author contributions

All authors designed and performed the research, analyzed the results and wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Appendix

A Liquid fraction profiles

The foam liquid fraction exhibits a slight vertical gradient associated to gravity drainage. The liquid fraction was measured locally within non-overlapping rectangular cuboid (1.77 mm × 1.77 mm for horizontal dimensions and 0.66 mm in height) centered along the symmetry axis to avoid artefacts at the contact with walls. The liquid fraction profiles are given in Fig. 8. The higher the position inside the foam, the drier the foam. The difference between the lowest and highest values of the liquid fraction is used to quantify the dispersion given in Table 1.

Fig. 8 Profiles of the liquid fraction obtained for the 8 series.

B Internal strain measurements

We have tested another method to characterize the deformation and anisotropy of the inner foam structure and check the robustness of our results. While the shape tensor is based on the pixels defining a bubble region, the texture tensor is based on the links between adjacent bubbles.^26,27 Each bubble is characterized by the set of link vectors {l} between its bubble center and the neighboring bubble centers. For each bubble, the texture tensor is defined as M = 〈l⊗l〉 (with 〈⋯〉 the average over the set of neighboring bubbles) and we followed the same protocol as the one applied to the shape tensor S. First, the texture tensor is expressed in cylindrical coordinates. Second, the averaged texture tensor is obtained by averaging each of the 9 components in time and space over all the bubbles present in tori. The averaged texture tensor is then diagonalized: it has one eigenvalue M_φ with e_φ as eigenvector; the two remaining eigenvectors (e₊, e₋) are in the azimuthal plane (e_ρ, e_z) with eigenvalues M₊ and M₋ for the largest and smallest value, respectively.
Again we can defined the internal strain tensor based on the averaged texture tensor as , with M₀ = M₀Id and M₀ = (M₊M₋M_φ)^1/3. Id is the identity tensor. The factor takes into account the fact that the 〈M〉 components have dimensions of length squared while the 〈S〉 components have dimensions of length.

In Fig. 9(A), the eigenvalues of U_M are plotted as functions of the eigenvalues of U_S for all series (each data point corresponds to one torus within one series). There is a clear correlation characterized by a proportionality relation between the U_M and U_S eigenvalues with a factor equal to 1.1 ± 0.1. The proportionality factor around unity shows that the deformation and anisotropy of the internal foam structure can be quantified by either method. In Fig. 9(B and C), the same quantities are plotted without averaging in time and space, so that each data point corresponds to a bubble at a given time. We observed a dispersion of the data with a very high density of points near the line U_M = 1.1U_S, consistent with the factor obtained from the averaged quantities. Although the two quantities are not identical at the scale of individual bubbles, they are almost identical at the scale of sets of numerous bubbles. We have thus noticed that the higher the number of bubbles in the statistics, the lower the dispersion while comparing the eigenvalues obtained with the two methods (Fig. 9(A–C)) and the smoother the fields (Fig. 5(B–E) and 11(C and D)). The wetter foams composed of the smallest bubbles give the best quality fields: the gain in the statistics largely dominates the fact that the values of the internal strain are smaller compared to the ones of the other foams.

Fig. 9 The U_M eigenvalues as functions of the corresponding U_S eigenvalues with the following color code: the eigenvalues along (e₊, e₋, e_φ) are displayed in blue, green and red, respectively: (A) data averaged in tori (8 series) and (B) data for each bubble (6 series with large bubbles, about 150 μm in radius). (C) Density map obtained from the data of (B) by counting the number of data points (logarithmic scale) inside boxes (300 × 300 boxes in total). The solid lines represent the best proportionality relation with a proportionality factor equal to 1.1.

C Simulation of a newtonian flow

In order to compare our measured velocity fields to a reference, we have simulated a steady viscous flow at vanishing inertia (Stokes flow) with the software COMSOL. The same geometry and flow conditions were implemented, including free-slip (no tangential stress) boundary conditions at the solid wall.^34,35 The flow fields obtained for a divergent and convergent flows are plotted in Fig. 10. The Stokes equation being time reversible, one field can be obtained from the other field by the transformation v → −v.

Fig. 10 Flow map through the constriction from the COMSOL simulations for the two flow directions, i.e. divergent (A) and convergent (B) boundary conditions.

D Results with small bubbles

In Fig. 11, we plot the average flow field and internal strain maps obtained with small bubbles for comparison with data obtained with large bubbles (Fig. 3 and 5). As a reminder, the small and large bubbles had an equivalent bubble radius of about 150 ± 20 μm and 70 ± 15 μm, respectively. The maps seem smoother than the ones obtained with large bubbles, a fact that we attribute to the larger number of bubbles in the statistics. We observed the same characteristics highlighted with the large bubbles, for instance the prolate bubble shape inside the waist whatever the flow direction.

Fig. 11 Average flow field maps obtained with small bubbles in a divergent (A) and convergent (B) flow geometry with foams DS25 and CS27 respectively. (C and D) Internal strain maps for the same foams and flow geometries.

Acknowledgements

We would like to thank the Swedish Research Council for funding this project (grant no. 2019-03742). We are grateful to Gordan Mikuljan for designing and building the flow cell, and would like to thank Edward Andò, Sara Johansson, Stephen Hall and Emanuel Larsson for their helpful image analysis advises. We acknowledge the Paul Scherrer Institute, Villigen, Switzerland for provision of synchrotron radiation beamtime 20150185 at beamline X02DA TOMCAT and the support of the CNRS, through the International Research Project (IRP) D-FFRACT. A special thank to Jason Brudvik and Zdenek Matej for their IT support with the MAX IV HPC and their help for creating the Github. Finally, we would like to have a general thank to Scikit-Image and SPAM communities without which the presented analysis would not have been possible.

Notes and references

1. I. Cantat, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, F. Rouyer and A. Saint-Jalmes, Foams: Structure and Dynamics, Oxford University Press, 2013.
2. Foam Engineering: Fundamentals and Applications, ed. P. Stevenson, Wiley-Blackwell, Chichester, 1st edn, 2012.
3. S. Cohen-Addad, R. Höhler and O. Pitois, Annu. Rev. Fluid Mech., 2013, 45, 241–267.
4. B. Dollet and C. Raufaste, C. R. Phys., 2014, 15, 731–747.
5. D. A. Reinelt and A. M. Kraynik, J. Fluid Mech., 1996, 311, 327–343.
6. A. Saint-Jalmes and D. J. Durian, J. Rheol., 1999, 43, 1411–1422.
7. A. Bussonnière and I. Cantat, J. Fluid Mech., 2021, 925, A25.
8. I. T. Davies, S. J. Cox and J. Lambert, Colloids Surf., A, 2013, 438, 33–40.
9. C. Raufaste, B. Dollet, K. Mader, S. Santucci and R. Mokso, EPL, 2015, 111, 38004.
10. G. Debrégeas, H. Tabuteau and J. M. di Meglio, Phys. Rev. Lett., 2001, 87, 178305.
11. Y. Wang, K. Krishan and M. Dennin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031401.
12. B. Dollet and F. Graner, J. Fluid Mech., 2007, 585, 181–211.
13. C. Raufaste, B. Dollet, S. Cox, Y. Jiang and F. Graner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 217–228.
14. G. Katgert, M. E. Möbius and M. van Hecke, Phys. Rev. Lett., 2008, 101, 058301.
15. T. Chevalier, J. Koivisto, N. Shmakova, M. J. Alava, A. Puisto, C. Raufaste and S. Santucci, J. Phys.: Conf. Ser., 2017, 925, 012025.
16. N. Shmakova, T. Chevalier, A. Puisto, M. Alava, C. Raufaste and S. Santucci, Phys. Rev. Fluids, 2020, 5, 093301.
17. Y. Bertho, C. Becco and N. Vandewalle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 056309.
18. B. Dollet and C. Bocher, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 123.
19. https://foamquant.readthedocs.io/ .
20. K. Golemanov, N. D. Denkov, S. Tcholakova, M. Vethamuthu and A. Lips, Langmuir, 2008, 24, 9956–9961.
21. E. Lorenceau, Y. Y. C. Sang, R. Höhler and S. Cohen-Addad, Phys. Fluids, 2006, 18, 097103.
22. R. Mokso, C. M. Schlepütz, G. Theidel, H. Billich, E. Schmid, T. Celcer, G. Mikuljan, L. Sala, F. Marone, N. Schlumpf and M. Stampanoni, J. Synchrotron Radiat., 2017, 24, 1250–1259.
23. R. Mokso, F. Marone, S. Irvine, M. Nyvlt, M. Skeren, D. Schwyn, H. Krapp, G. Taylor and M. Stampanoni, J. Phys. D: Appl. Phys., 2013, 46, 494004.
24. S. van der Walt, J. L. Schönberger, J. Nunez-Iglesias, F. Boulogne, J. D. Warner, N. Yager, E. Gouillart, T. Yu and the scikit-image contributors, PeerJ, 2014, 2, e453.
25. E. Andò, G. Viggiani, S. A. Hall and J. Desrues, Géotechnique Lett., 2013, 3, 142–146.
26. F. Graner, B. Dollet, C. Raufaste and P. Marmottant, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 25, 349–369.
27. P. Marmottant, C. Raufaste and F. Graner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 25, 371–384.
28. F. Rouyer, S. Cohen-Addad, R. Höhler, P. Sollich and S. M. Fielding, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 27, 309–321.
29. P. Marmottant and F. Graner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 337–347.
30. T. Mason, J. Bibette and D. Weitz, J. Colloid Interface Sci., 1996, 179, 439–448.
31. B. Dollet, J. Rheol., 2010, 54, 741–760.
32. K. Mader, R. Mokso, C. Raufaste, B. Dollet, S. Santucci, J. Lambert and M. Stampanoni, Colloids Surf., A, 2012, 415, 230–238.
33. A. Amon, V. B. Nguyen, A. Bruand, J. Crassous and E. Clément, Phys. Rev. Lett., 2012, 108, 135502.
34. S. Marze, D. Langevin and A. Saint-Jalmes, J. Rheol., 2008, 52, 1091–1111.
35. M. Marchand, F. Restagno, E. Rio and F. Boulogne, Phys. Rev. Lett., 2020, 124, 118003.

---

Footnote

† Electronic supplementary information (ESI) available: 3D images after the labeling process, time-lapse sequences of successive 2D slices showing the flow inside the cell and a typical 3D velocity map between two successive time steps. See DOI: https://doi.org/10.1039/d2sm01299e

---