DOI:
10.1039/D2SM01261H
(Paper)
Soft Matter, 2023,
19, 436-450
The permeability of pillar arrays in microfluidic devices: an application of Brinkman's theory towards wall friction†
Received
16th September 2022
, Accepted 6th December 2022
First published on 13th December 2022
Abstract
Darcy's law describes the flow of Newtonian fluids through bulk porous media as the product of the applied pressure difference, the fluid's viscosity and the medium's permeability. Brinkman extended Darcy's law with a viscous stress term, thereby enabling boundary conditions to the flow field at the surface of the medium. The validity of Brinkman's term, and the value of its effective viscosity, have been heavily debated since their introduction nearly 75 years ago. We use experiments and Multibody Dissipative Particle Dynamics (MDPD) simulations to study flows through ordered and disordered pillar arrays in microfluidic channels of limited height. We find that the simulated velocity profiles are well described by an expedient interpretation of Brinkman's theory. Depending on the solid volume fraction and pillar arrangement, the effective viscosity varies between two and three times the bulk fluid viscosity. The calculated effective permeabilities of the flow devices, combining the flow resistances due to the pillars and the walls by Brinkman's theory, agree well with the experimental data. This approach enables fast and accurate estimates of the effective permeability of micropillared chips. The simulated force distributions over the walls and pillars require an effective viscosity equal to the bulk viscosity and an elevation-dependent permeability of the pillar array.
1 Introduction
Flow through porous media is a research theme with many applications.1,2 Examples include the flow of water through a packed coffee-bed,3,4 fluidized bed,5,6 the recovery of oil from natural deposits,1 flows in filtration membranes,7–9 adsorption/chromatography columns10,11 and flows in fuel cells.12,13 The flow of fluids through porous media is often successfully described by Darcy's theory14 as plug flow with a flux proportional to both the pressure gradient and the permeability of the medium, and inversely proportional to the viscosity of the fluid. We are interested in the flow through ordered and disordered arrays of impermeable pillars etched in microfluidic chips, with channel heights comparable to the pillar diameter. These chips are used in liquid chromatography separations15 and can provide extremely high separation efficiencies.16 Because of the extreme area to volume ratios of these micro-channels, the drag at the floor and ceiling of the channel is expected to affect the flow. Darcy's law, by assuming a homogeneous flow field, evidently does not allow for boundary conditions. Brinkman17 proposed a phenomenological equation that alleviates this deficiency by complementing Darcy's description with a viscous stress term accounting for the velocity gradient perpendicular to the flow in the vicinity of a boundary. Because this term applies to the average local flow velocity of the fluid in the medium, it contains an effective viscosity μeff that need not be identical to the bulk viscosity of the fluid μ.17 We use experiments and Multibody Dissipative Particle Dynamics (MDPD) simulations to explore the effective permeabilities of microfluidic channels in relation to the permeability of the pillar arrays and the flow resistance due to the walls.
Brinkman's theory has been investigated by many authors using theoretical methods, computational techniques and experiments. Originally, Brinkman17 was interested in the viscous force on a spherical particle surrounded by a stationary swarm of spherical particles. He considered equating the effective viscosity to the Einstein viscosity of this suspension, 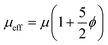 with ϕ the solid volume fraction, but argued that the swarm's immobility hindered momentum transport and hence settled for the fluid's bulk viscosity instead, μeff = μ. Tam18 derived the Darcy–Brinkman theory, obtaining a drag force in agreement with the experimental data of Happel and Epstein.19 Lundgren20 obtained an effective viscosity that matches the Einstein viscosity for low volume fraction, peaks 20% above the bulk viscosity and drops below the latter for solid volume fractions exceeding 0.25. Neale and Nader21 re-interpreted in terms of Brinkman's theory the slip velocity at the interface between bulk flow and flow in a fluid-infused porous medium, as measured by Beavers and Joseph,22 arriving at viscosity ratios μeff/μ ranging from 0.01 to 16. Freed and Muthukumar23 obtained an effective viscosity that follows Einstein's relation for low particle volume fraction. Nield24 and Kim and Russel25 emphasized that Brinkman's equation breaks down for higher solid fraction. Simulations by Durlofksy and Brady26 confirmed Brinkman, with μeff = μ, for particle volume fractions below 0.05. Koplik et al.27 argued that the medium induces a renormalization of the viscosity, yielding an effective viscosity below the bulk viscosity that decreases with increasing solid volume fraction. Larson and Higdon28 reported viscosity ratios close to unity, but also noted the limited validity of Brinkman's theory. Martys et al.29 used Brinkman's theory to fit calculated flow profiles in a random porous medium, obtaining viscosity ratios steadily increasing from 1.9 to 4.2 with decreasing porosity, ε = 1 − ϕ. Givler and Altobelli30 measured the flow field in a coarse foam, thereby deducing μeff/μ ≈ 7.5. Ochoa-Tapia and Whitaker31,32 derived a volume-averaged flow equation, with an apparent viscosity μ/ε. Starov and Zhdanov33 arrived at an effective viscosity that follows the Einstein viscosity to first order in the volume fraction. Liu et al.34 solved the flow in a channel and extracted a viscosity ratio close to unity. Valdes-Parada et al.35 showed that the effective viscosity varies with the chosen boundary conditions for flow over a fluid-infused medium. Levy36 and Auriault37 limited the validity of Brinkman's theory to arrays of spheres and fibers. Kołodziej et al.38 numerically solved the flow between a mobile and an immobile wall sandwiching an array of cylinders, obtaining a viscosity ratio of 0.9 at ε = 10−8 and a rapid decay to 0.4 at ε = 0.1. Zaripov et al.39 reported viscosity ratios spanning several orders of magnitude.
with ϕ the solid volume fraction, but argued that the swarm's immobility hindered momentum transport and hence settled for the fluid's bulk viscosity instead, μeff = μ. Tam18 derived the Darcy–Brinkman theory, obtaining a drag force in agreement with the experimental data of Happel and Epstein.19 Lundgren20 obtained an effective viscosity that matches the Einstein viscosity for low volume fraction, peaks 20% above the bulk viscosity and drops below the latter for solid volume fractions exceeding 0.25. Neale and Nader21 re-interpreted in terms of Brinkman's theory the slip velocity at the interface between bulk flow and flow in a fluid-infused porous medium, as measured by Beavers and Joseph,22 arriving at viscosity ratios μeff/μ ranging from 0.01 to 16. Freed and Muthukumar23 obtained an effective viscosity that follows Einstein's relation for low particle volume fraction. Nield24 and Kim and Russel25 emphasized that Brinkman's equation breaks down for higher solid fraction. Simulations by Durlofksy and Brady26 confirmed Brinkman, with μeff = μ, for particle volume fractions below 0.05. Koplik et al.27 argued that the medium induces a renormalization of the viscosity, yielding an effective viscosity below the bulk viscosity that decreases with increasing solid volume fraction. Larson and Higdon28 reported viscosity ratios close to unity, but also noted the limited validity of Brinkman's theory. Martys et al.29 used Brinkman's theory to fit calculated flow profiles in a random porous medium, obtaining viscosity ratios steadily increasing from 1.9 to 4.2 with decreasing porosity, ε = 1 − ϕ. Givler and Altobelli30 measured the flow field in a coarse foam, thereby deducing μeff/μ ≈ 7.5. Ochoa-Tapia and Whitaker31,32 derived a volume-averaged flow equation, with an apparent viscosity μ/ε. Starov and Zhdanov33 arrived at an effective viscosity that follows the Einstein viscosity to first order in the volume fraction. Liu et al.34 solved the flow in a channel and extracted a viscosity ratio close to unity. Valdes-Parada et al.35 showed that the effective viscosity varies with the chosen boundary conditions for flow over a fluid-infused medium. Levy36 and Auriault37 limited the validity of Brinkman's theory to arrays of spheres and fibers. Kołodziej et al.38 numerically solved the flow between a mobile and an immobile wall sandwiching an array of cylinders, obtaining a viscosity ratio of 0.9 at ε = 10−8 and a rapid decay to 0.4 at ε = 0.1. Zaripov et al.39 reported viscosity ratios spanning several orders of magnitude.
The discrepancies in the aforementioned results reflect the limited validity of Brinkman's theory, as well as the dependence of the effective viscosity on the structural details of the porous medium and the type of boundary condition. Especially the common application to flow over a fluid-infused medium is problematic, because this interface combines fluid–fluid and fluid–solid contacts with differing boundary conditions.40 This situation does not arise in the microfluidic devices studied here, with pillars running from the floor to the ceiling of the flow channel. Consequently, the floor and ceiling of the channel force the fluid to flow around rather than over the impermeable pillars, making the flow more suitable to the application of Brinkman's theory. Our aim here is to explore whether this theory can be used to combine the Darcy permeability of the pillar array – in the absence of wall friction – with an effective Stokesian drag accounting for all changes to the flow upon the introduction of channel walls, to yield the effective permeability of the pillared channel. This differs from analytic studies36,41 in which the effective permeability is obtained by formally solving the flow to lowest order, including all boundary conditions, with the Brinkman term emerging as a higher order correction. We furthermore note that the micro-pillared devices do not meet the separation of length scales required in theoretical studies. Nevertheless, using Brinkman's theory as an expedient provides a useful prediction of the flow field in these channels. The physical reality of this approach will be discussed.
A number of groups studied flow through arrays of pillars spanning the height of a channel. Lee and Fung42 and Lee43 used regularly spaced posts between two walls as a model for blood flow in long alveoli, deriving an approximate solution to Stokes flow in substantial agreement with experimental measurements. Tsay and Weinbaum44 solved the Stokes equation for a square array of wall-to-wall cylindrical fibers; they noted that Brinkman's theory with μeff = μ is a remarkably good approximation for fibers with aspect ratios larger than five, but breaks down for aspect ratios less than unity. Yeom et al.45 corrected their experimental data with a baseline control, i.e. the pressure drop for flow through the microchannel in the absence of pillars, thereby tacitly assuming μeff = μ. Tamayol et al.46 made square arrays of microcylinders in polydimethylsiloxane (PDMS), yielding a reasonable agreement with theoretical calculations at μeff = μ/ε, but also noted the potential impact of the material's softness. The experiment was therefore repeated with micro-channels etched in silicon by Gunda,47 who ‘concluded that the existing theoretical models in [the] literature fail to accurate[ly] represent the permeabilities of structured porous media’, again using μeff = μ/ε. Wang and Wang48 used micro-particle image velocimetry to measure the velocity distribution in the midplane of the cell; assuming μeff = μ, they fitted the permeabilities with Kozeny–Carman theory and suggested that the permeability varies with elevation. Wagner et al.49 reported quantitative agreement across a number of numerical techniques for the permeability of a square array of wall-to-wall cylinders; the comparison with an experimental set-up of 10 × 14 pillars revealed the impact of the inlet and outlet in their microfluidic device.
Flow through arrays of infinitely long parallel cylinders – in the absence of bounding walls – were studied by various authors using theory and simulations, for both regular and irregular distributions of the cylinders.50–62 These will be discussed in more detail below. An extensive collection of references was presented by Khalifa et al.63
This paper is organized as follows: in the section Theory and methods we briefly discuss Darcy's law and Brinkman's theory, followed by a description of the experimental and simulation methodologies used here to study the flow through four distinct arrangements of cylindrical pillars in microfluidic channels. The section Results and discussion presents the experimental and simulation results, i.e. the (effective) permeabilities and effective viscosities for the four pillar arrangements over a wide range of porosities, ending with a comparison of these results. The main conclusions are summarized in the section Conclusions.
2 Theory and methods
In this section, we revisit Darcy's law, apply Brinkman's law to pillars confined between two parallel walls, and detail the experimental and simulation techniques employed in this study.
2.1 Darcy's law
Darcy's law describes the volumetric flow rate Q of a viscous liquid through a porous medium as14| | 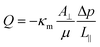 | (1) |
where Δp denotes the drop in pressure over the length L‖ of the medium in the flow direction, A⊥ is the cross-section of the medium perpendicular to the flow direction, μ is the dynamic viscosity of the fluid and κm is the permeability of the porous medium. The permeability measures how easily (reverse of resistance) a fluid flows through the porous medium. It is related to the medium's porosity ε, but not fully determined by the porosity: the microstructural details, like the distribution of pore sizes and the inter-connectivity of the voids, also contribute to the permeability. The global superficial velocity or flux of the fluid reads as| | 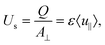 | (2) |
where 〈u‖〉 is the mean velocity of the fluid in the flow direction, i.e. averaged with respect to the total fluid volume in the medium. Henceforth, we are concerned with porous media composed of identical parallel cylindrical pillars or fibers of diameter d, with their long axes oriented perpendicular to the main flow direction, see Fig. 1. The permeabilities of these pillar arrays, κp, can be measured using Darcy's law, provided one may ignore the boundary effects. Under the same conditions, the permeability may also be obtained from the total drag force on the pillars per unit length,64,65| | 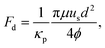 | (3) |
where ϕ= 1 − ε is the solid volume fraction.
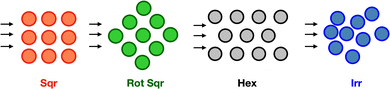 |
| | Fig. 1 Schematics of the four arrangements of cylindrical pillars employed in this article. The arrows indicate the direction of flow relative to the pillar assembly. The abbreviations Sqr, Rot Sqr, Hex and Irr correspond to a square lattice, a rotated square lattice, an hexagonal lattice and an irregular array, respectively. The colour-coding of pillar arrangements is used in all figures. | |
2.2 Brinkman's theory
Darcy's law can also be applied to flow through pillar arrays in a channel, see Fig. 2. Inserting the flow rate, pressure drop and device dimensions in eqn (1) then yields an effective permeability, κeff, combining contributions from the pillars and the walls, dp/dx = −(μ/κeff)Us. Brinkman's equation can be used as an expedient to decouple these two contributions by expressing the pressure gradient as a superposition of Stokesian drag due to the pillars and viscous friction due to the walls,17,46–48| | 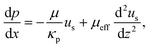 | (4) |
where us(z) = ε〈ux〉z defines the superficial fluid velocity in the flow direction x as a function of the elevation z, and μeff denotes Brinkman's effective viscosity. Whereas in the (Navier–)Stokes equation the viscous shear stress is calculated from the local velocity, Brinkman's equation uses the averaged superficial velocity. The effective viscosity here represents the friction due to the walls, as well as the impact of the wall-altered flow on the forces exerted by the pillars. As discussed in the introduction, this effective viscosity is to be solved for a particular application. In the current configuration, the walls at the top and bottom of the channel impose no-slip boundaries conditions, ux(±H/2) = 0, where z = 0 defines the mid-plane of the flow cell. Because the widths of our channels far exceed their heights, the friction with the floor and ceiling will be far larger than the friction with the two side walls; the contribution by the latter will therefore be ignored. Solving Brinkman's equation yields| | 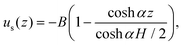 | (5) |
with amplitude B = (κp/μ)(Δp/L‖) and decay parameter (or reciprocal length scale) 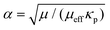 . The total flow rate is obtained by integration of the velocity profile,
. The total flow rate is obtained by integration of the velocity profile,| | 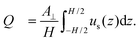 | (6) |
Inserting this flow rate in Darcy's law, see eqn (1), yields an effective permeability of the channel (including wall contributions), κeff, that is related to the permeability of the pillars (excluding wall contributions), κp, by| | 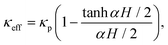 | (7) |
where the pressure gradient has been assumed constant along the medium. This expression indicates that the permeability of a pillar array between walls can be calculated by combining the permeability of the pillar array (for pillars of infinite length) with a contribution arising from the walls. Below, we will use simulations and experiments to explore the validity of this relation, and the underlying velocity profile, for flow through several pillar arrangements in microfluidic channels. An alternative route to eqn (5) by accounting for the walls with an elevation-dependent permeability, usually reserved for media of variable porosity,66–69 is presented in the Appendix.
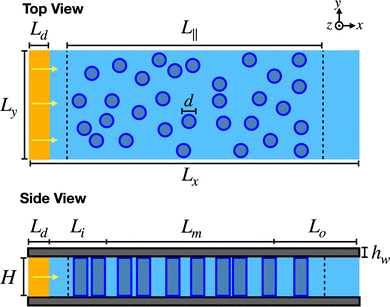 |
| | Fig. 2 Schematic of the 3D simulation set-up for fluid (light blue) flowing through a disordered array of pillars in a microfluidic chip. All pillars (dark blue) have the same diameter d and span the height H between the two flat walls bounding the flow cell at the top and bottom (dark gray). Periodic boundary conditions apply in the x and y directions. In the driving region of length Ld (yellow), the fluid experiences a body force fb in the x direction (arrows). Consequently, the fluid in the measurement region Lm experiences a pressure-driven flow. The lengths L‖ and Ly of the pillared region match the box dimensions used in the Monte Carlo simulation generating the random pillar configuration. The measurement region is separated from the driving region by the in-flow and out-flow regions of lengths Li and Lo, respectively. | |
2.3 Generating pillar configurations
The disordered configurations of parallel non-overlapping pillars were created using two-dimensional (2D) hard-disk Monte Carlo (MC) simulations.61 Disks of equal diameter d* were placed on a square lattice in a square box with periodic boundary conditions, representing a two-dimensional cross-section of the unit cell of the pillared system. The diameters of the disks were slightly larger than the diameters of the pillars, d* = 1.2d, to create small gaps between the pillars in the final configurations. These gaps were required in the production of the microfluidic chips, with the smallest structural features - pillar or gap – measuring about 1 μm. The gaps were also convenient in the simulations, as they ensured that the distances between pillar surfaces were well beyond the mean nearest particle distance in the MDPD fluid, thereby avoiding discretization effects arising in particle-based simulations.70 Each MC step consisted of generating a small random displacement of a randomly selected disk, while rejecting any moves that resulted in overlapping disks. For the experimental systems, ‘large’ irregular configurations of 800 disks were created at porosities (based on the pillar diameter d) of 55%, 60%, 70% and 85%, by runs of 107 MC steps to ensure that the resulting pillar configurations were randomly disordered. These four configurations were also used in the 2D simulations of pillar permeabilities, κp. Additional sets of 25 random ‘small’ configurations of 28 to 45 pillars in rectangular unit cells were generated for 2D simulations of κp and 3D simulations of κp and κeff at porosities from 0.55 to 0.85, in steps of 0.05.
2.4 Experimental
2.4.1 Fabrication of microfluidic structures.
The random configurations of 800 disks generated by the MC algorithm were treated as square unit cells of 500 × 500 μm to design the masks of microfluidic chips in the layout editor CleWin 5 (WieWeb software, The Netherlands). This unit cell was repeated 10 × 5 in the planar directions, creating an array of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pillars covering an area of 5 × 2.5 mm. The pillar configuration was fabricated in silicon using standard photolithography and reactive ion etching, creating pillars with a height of H = 20 μm; the detailed fabrication procedure is described in the ESI,† Section S1.1. The fabricated chips were inspected using an inverted optical microscope (Zeiss Axiovert 40 MAT) with an objective of 5× magnification (Zeiss EC Epiplan 5×/0.13, working distance of 19.8 mm). The actual diameters of the pillars were measured for at least 35 pillars on each chip, using image analysis software (HoKaWo 3.00). The pillars were also observed using a scanning electron microscope (SEM, JEOL JSM 5610), see Fig. 3 and 4 and Fig. S1 through S3 in Section S1.2 (ESI†). After pillar fabrication and inspection, the microfluidic chip was finalized by anodic bonding a glass wafer to the silicon. All chips were used as received from the clean room with no further cleaning or treatment, and hence were hydrophilic.
000 pillars covering an area of 5 × 2.5 mm. The pillar configuration was fabricated in silicon using standard photolithography and reactive ion etching, creating pillars with a height of H = 20 μm; the detailed fabrication procedure is described in the ESI,† Section S1.1. The fabricated chips were inspected using an inverted optical microscope (Zeiss Axiovert 40 MAT) with an objective of 5× magnification (Zeiss EC Epiplan 5×/0.13, working distance of 19.8 mm). The actual diameters of the pillars were measured for at least 35 pillars on each chip, using image analysis software (HoKaWo 3.00). The pillars were also observed using a scanning electron microscope (SEM, JEOL JSM 5610), see Fig. 3 and 4 and Fig. S1 through S3 in Section S1.2 (ESI†). After pillar fabrication and inspection, the microfluidic chip was finalized by anodic bonding a glass wafer to the silicon. All chips were used as received from the clean room with no further cleaning or treatment, and hence were hydrophilic.
 |
| | Fig. 3 Sections of the fabricated pillar arrays as visualized by scanning electron microscopy (SEM, left), compared against the corresponding configuration as generated by the Monte Carlo scheme (MC, right), at porosities of (a) 0.58, (b) 0.65, (c) 0.73 and (d) 0.87, respectively. The thick black line corresponds to 100 μm, while the length scale of the MC figures are expressed in arbitrary units. The pillars inked in red are guides to facilitate visual comparison. | |
 |
| | Fig. 4 Scanning electron microscopy images showing tilted views of the pillared microfluidic chips at four porosities: 0.58 (top left), 0.65 (top right), 0.73 (bottom left) and 0.87 (bottom right). Scale bars are in the bottom-right corner of every picture. | |
2.4.2 Permeability by experiments.
The measurements of the permeability were performed at room temperature using the set-up illustrated in Fig. 5. The fluids used were water (Milli-Q grade) with a viscosity of 1 mPa s and hexadecane (ReagentPlus 99% from Sigma-Aldrich, The Netherlands) with a viscosity of 3.2 mPa s, both at room temperature, 20 °C. The pressure driving the fluids was increased from 100 mbar to 1000 mbar in steps of 100 mbar, using a pressure controller (OB1 Mk3+ from ElveFlow, France). The corresponding flow rates were measured simultaneously using a flow meter (Bronkhorst mini Cori flow M12) with an accuracy of 2% in the working range of 0.1–200 g h−1. At each step, the pressure was kept constant for 20 s during which the flow was measured every one-tenth of a second. The average flow and pressure values at each step, excluding the first five data points, were collected. In the stabilisation runs, the first pressure step (100 mbar) was kept for 1 minute to allow the permeating liquid sufficient time to fill the chip and connection tubing, as well as to ensure the removal of air bubbles. The measurement runs were performed twice, to verify consistency. Details on the various experiments are provided in the ESI,† see Fig. S4.
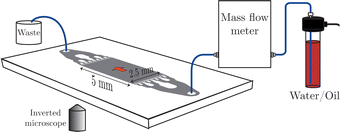 |
| | Fig. 5 Schematic of the experimental set-up for permeability measurements of random pillared microstructures etched in a microfluidic chip. The fluid entering the chip is pressure controlled, the resulting flux is measured. | |
2.5 Simulations
2.5.1 Multibody dissipative particle dynamics.
The flow through the pillar array was simulated using Multibody Dissipative Particle Dynamics (MDPD). Over the years, MDPD has gained prominence as a flow solver for complex geometries.71–73 In this particle-based simulation technique, the force on particle i is expressed as a sum of pair forces due to its neighbours j,74–79| | 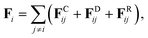 | (8) |
with the conservative, dissipative and random contributions, marked with the superscripts C, D and R, respectively, given by| | FCij = AijwA(rij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij + Bij( ij + Bij(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) i + i + ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) j)wB(rij) j)wB(rij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (9a) |
| | FDij = −DijwD(rij)(vij·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij) ij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (9b) |
| | 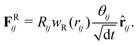 | (9c) |
The conservative force combines a pairwise additive attraction with strength parameter Aij and a density dependent repulsion with strength parameter Bij, where the latter is identical for all particle pairs in a conservative potential.80 The force acts along the unit vector between the two particles, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = (ri − rj)/rij, with ri the position of particle i and rij the inter-particle distance. The weight-functions wA(rij) = 1 − rij/rA and wB(rij) = 1 − rij/rB decay linearly with the distance and are identically zero beyond their cut-off distances rA and rB, respectively. The multibody density at particle i is calculated as
ij = (ri − rj)/rij, with ri the position of particle i and rij the inter-particle distance. The weight-functions wA(rij) = 1 − rij/rA and wB(rij) = 1 − rij/rB decay linearly with the distance and are identically zero beyond their cut-off distances rA and rB, respectively. The multibody density at particle i is calculated as 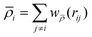 , with the normalized weight function w
, with the normalized weight function w![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (rij) = (15/2πrB3)wB2(rij). Dij and Rij are the strength parameters of the dissipative and random forces, respectively, with wD(rij) = wR2(rij) and wR(rij) = 1 − rij/rA the corresponding weight functions. The friction forces are proportional to the velocity difference vij = ṙi − ṙj. The random numbers θij have zero mean and unit variance, are uncorrelated in time and are uncorrelated between particle pairs. The stochastic nature of the random force also gives rise to its scaling with the time step dt, see eqn (9c). Finally, the dissipative and random forces are related by the fluctuation-dissipation theorem81
(rij) = (15/2πrB3)wB2(rij). Dij and Rij are the strength parameters of the dissipative and random forces, respectively, with wD(rij) = wR2(rij) and wR(rij) = 1 − rij/rA the corresponding weight functions. The friction forces are proportional to the velocity difference vij = ṙi − ṙj. The random numbers θij have zero mean and unit variance, are uncorrelated in time and are uncorrelated between particle pairs. The stochastic nature of the random force also gives rise to its scaling with the time step dt, see eqn (9c). Finally, the dissipative and random forces are related by the fluctuation-dissipation theorem81| | | 2kBTDijwD(rij) = Rij2wR2(rij), | (10) |
where kB is Boltzmann's constant and T is the desired temperature of the system. The Newtonian equations of motion are integrated numerically over time steps dt using the Verlet leap-frog scheme.82,83 The appealing aspect of MDPD is its ability to simulate hydrodynamic flow under complex conditions, which emerges from the conservation of momentum by the above forces.
The cut-off distance rA, the particle's mass m and the thermal energy kBT were selected as the unit of length σ, the unit of mass m and the unit of energy ε, respectively. These implicitly define the unit of time as τ = m1/2σε−1/2. The number density was fixed at ρ = 6σ−3, the time step at dt = 0.01τ. In all simulations and for all particle pairs, A = −40ε/σ, B = 25εσ2, rB = 0.75σ, and R = 12ετ1/2/σ. The determination of the fluid's viscosity, following a procedure outlined elsewhere,73 yielded μ = 17.5ετ/σ3. Henceforth, most numerical results will be presented in dimensionless ratios to facilitate the comparison between simulations, theory and experiments.
All solid structures – walls and pillars – were made of MDPD particles restrained to fixed positions by means of Hookean springs with spring constants kS = 12.5ε/σ2, acting on top of the aforementioned interactions. Due to the softness of the conservative repulsive potential, the liquid particles occasionally diffused into the solid structures; to prevent these particles from penetrating too deeply, a purely repulsive Weeks-Chandler-Andersen (WCA) potential82,83 was introduced between fluid particles and solid particles more than 1.2σ below the surface of the solid. All pillars and walls were carved from snapshots of the equilibrated quiescent bulk fluid. The pillars left standing were either positioned following 2D regular grids, or distributed irregularly following patterns generated by the MC routine. In both cases, the length L‖ and width Lw of the porous region corresponded with the periodic rectangular box employed in the generation of the pillar configuration. Periodic boundary conditions apply in the x and y directions, see Fig. 2, while the fluid is confined along the z axis by walls. The pillar diameter was fixed at 5σ, thereby ensuring that the pillars were always substantially larger than the fluid particles. The 3D disordered systems contained one copy of a ‘small’ random unit cell, for a total of 25 configurations at every porosity, while system size dependence was tested by rerunning one configuration per porosity with two unit cells back-to-back.
In simulations focussing on the permeability of pillars arrays, i.e. without the limiting walls, the 3D simulation box was periodically continued in all three directions. The resulting translation symmetry along z rendered this system effectively two dimensional. Hence, we repeatedly resorted to computationally less demanding 2D simulations to obtain the permeabilties due to the pillars. In the 2D simulations all parameters were kept at their aforementioned values, except ρ = 6σ−2 and B = 30εσ2, while the 3D normalized weight function w![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) was replaced by its 2D equivalent, w
was replaced by its 2D equivalent, w![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (rij) = (6/πrB2)wB2(rij). The viscosity of the resulting 2D fluid was determined as μ = 26.1ετ/σ2. The 2D simulations of disordered pillar configurations employed the same configurations as the 3D simulations. In this case, however, the boxes contained two copies of the unit cell back to back, while system size dependence was tested by rerunning one configuration per porosity using one unit cell. The experimental disordered systems were simulated in 2D only, using one copy of the ‘large’ unit cell.
(rij) = (6/πrB2)wB2(rij). The viscosity of the resulting 2D fluid was determined as μ = 26.1ετ/σ2. The 2D simulations of disordered pillar configurations employed the same configurations as the 3D simulations. In this case, however, the boxes contained two copies of the unit cell back to back, while system size dependence was tested by rerunning one configuration per porosity using one unit cell. The experimental disordered systems were simulated in 2D only, using one copy of the ‘large’ unit cell.
2.5.2 Permeability by simulations.
For the permeability calculations, the 2D and 3D simulated systems were divided into several regions, see Fig. 2. The flow is maintained by a body force fbêx acting on all particle in the driving region of length Ld, thus inducing a pressure difference Δp = −fbρLd over the pillared region. In all simulations, the length of the driving region was kept constant at Ld = 5σ. For the smaller systems, the driving forces were set at fb = 0.1, 0.2 and 0.3ε/σ in 2D and at fb = 0.25, 0.3 and 0.35ε/σ in 3D. In the 2D simulations of the experimental system, owing to the considerably larger number of pillars, the driving force was varied from fb = 0.5 to 2.0ε/σ in steps of 0.5. Equilibration phases lasted for t = 103τ, followed by production phases of 5 × 103τ. Details on the various simulations are provided in the ESI,† see Section S2, Tables S1 through S2 and Fig. S5 through S11. We note that maintaining the flow by applying a body force to all fluid particles, as opposed to the localized body force in the current study, produces a markedly different flow problem to which Darcy's law does not apply.62
Following a transient phase at the start of the simulation, the system achieves a steady state characterized by a stationary velocity field. The mean flow velocity 〈ux〉 is determined as the average velocity along the flow direction of all fluid particles in the monitoring region of length Lm around the center of the pillar configuration, excluding regions at either end to minimize the impact of in-flow and out-flow. Combination of eqn (1) and (2) then yields the permeability. The 3D simulations with bounding walls establish an effective permeability κeff combining contributions from pillars and walls. The 3D simulations with periodic boundary conditions along z, as well as the 2D simulations, yield the permeability of the pillar configuration κp. For the latter systems without walls, the permeability κp is also calculated from the drag forces on the pillars, using eqn (3), where the drag force is obtained by summing all fluid–solid interactions in the monitoring region Lm.
To assess the suitability of Brinkman's theory in relating κeff to κp, see eqn (7), one needs to determine the shape of the simulated velocity profile us(z) and the single unknown variable in that theory, μeff. This is realized by sampling the velocity profile of the fluid particles in the monitoring region, using a bin width of 0.5σ along the z direction. A least-squares fit with the theoretical prediction of eqn (5) yields two fit parameters, namely the amplitude of the velocity profile Bfit and the coefficient αfit determining the curvature of the velocity profile; the latter is readily converted to yield the desired effective viscosity. Simulations with walls but no pillars recover Poiseuille's quadratic velocity distribution, with negligible slip velocities at the walls (data not shown); these simulations recover the theoretical permeability due to the walls, κw = H2/12.
3 Results and discussion
We here present the results of the experiments and simulations, and explore whether the latter – using Brinkman's theory – recovers the experimental effective permeabilities for the microfluidic devices.
3.1 Experiments
The effective permeabilities of all pillared microfluidic chips are obtained by interpreting the experimental data in terms of Darcy's description, see eqn (1) and Fig. S4 (ESI†). Fig. 6(a) shows the measured normalized fluxes as functions of the applied pressure gradient, for both water and hexadecane flowing through the four pillared microstructures with differing porosities. Linear relationships are observed, indicative of viscosity-dominated flows obeying Darcy's law. The effective permeabilities of the microfluidic chips, as deduced from the slopes, are collected in Table 1 and Fig. 6(b). For comparison purposes, a Poiseuille flow (in the absence of pillars) between the bounding walls of the chip results in a permeability κw = H2/12 of 33 μm2. It follows that the flow resistances (or inverse permeabilities) of the chips vary between 6 and 25 times the flow resistance due to the walls. The walls can therefore not be ignored in the current set-up, and they gain importance with increasing porosity. We do not observe significant differences between the permeabilities obtained with the two fluids, confirming that κeff is independent of fluid.
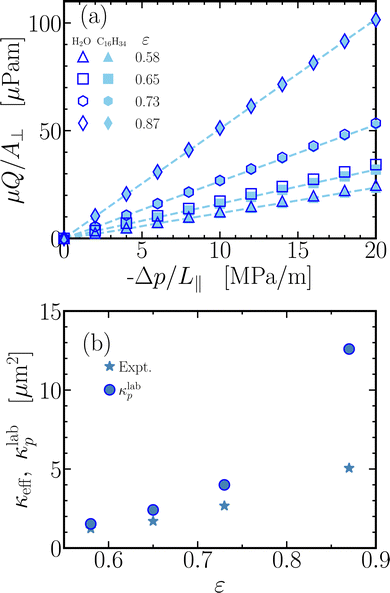 |
| | Fig. 6 Experimental measurements of the fluxes and permeabilities for disordered configurations of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cylindrical pillars, i.e. a unit cell of 800 pillars repeated 10 × 5 on the microfluidic chip, bound between two flat walls separated by H = 20 mm. (a) Normalized fluxes as functions of the applied pressure gradient for four microfluidic chips with differing porosities, for water (dark blue open markers) and hexadecane (light blue solid markers). Dashed lines represent linear fits to the data points at a given porosity. (b) Effective permeabilities of the microfluidic chips, κeff (stars), obtained as the slopes of the linear fits in (a), plotted against the measured porosity. Also shown are permeabilities κlabp (circles) extracted from 2D MDPD simulations (i.e. infinitely long pillars without bounding walls, see Table 1) for disordered arrays identical in configuration and pillar radius to those on the chips. For comparison, the permeability expected from the walls of the device in the absence of pillars amounts to κw = 33 μm2. 000 cylindrical pillars, i.e. a unit cell of 800 pillars repeated 10 × 5 on the microfluidic chip, bound between two flat walls separated by H = 20 mm. (a) Normalized fluxes as functions of the applied pressure gradient for four microfluidic chips with differing porosities, for water (dark blue open markers) and hexadecane (light blue solid markers). Dashed lines represent linear fits to the data points at a given porosity. (b) Effective permeabilities of the microfluidic chips, κeff (stars), obtained as the slopes of the linear fits in (a), plotted against the measured porosity. Also shown are permeabilities κlabp (circles) extracted from 2D MDPD simulations (i.e. infinitely long pillars without bounding walls, see Table 1) for disordered arrays identical in configuration and pillar radius to those on the chips. For comparison, the permeability expected from the walls of the device in the absence of pillars amounts to κw = 33 μm2. | |
Table 1 The measured porosities, pillar diameters and effective permeabilities of the microfluidic devices. The last column shows simulation results on the permeabilities of arrays of infinitely long pillars arranged by the etched patterns, κp, where the pillar diameters were used to convert the simulated permeabilities into laboratory units, κlabp. As discussed in the main text, the differences between κeff and κlabp are due to the walls of the flow channels
|
ε
|
d (μm) |
κ
eff (μm2) |
κ
labp (μm2) |
| 0.58 |
12.93 ± 0.30 |
1.23 |
1.53 |
| 0.65 |
11.84 ± 0.26 |
1.70 |
2.42 |
| 0.73 |
10.40 ± 0.27 |
2.67 |
4.00 |
| 0.87 |
7.16 ± 0.26 |
5.06 |
12.58 |
As a first comparison of the experimental permeabilities with their numerical counterparts, it appears reasonable to assume that the flow resistance is predominantly due to the pillars. Upon ignoring the wall contributions altogether, a 2D simulation suffices to calculate the permeability of an array of pillars, κp. The results from simulations employing the four experimental pillar configurations, converted to laboratory values κlabp using the ratio of the simulated and experimental pillar diameters, are presented in Table 1 and Fig. 6(b). The agreement with the measured effective permeabilities is reasonable at the lower porosities, confirming that the flow resistances of these denser arrays are dominated by the pillars with relatively minor contributions from the walls. A significant deviation is observed at the highest porosity, ε = 0.87, indicating that the walls can not be neglected for non-dense arrays of pillars. A more detailed discussion of the simulation results will be presented in the next section.
3.2 Simulations
The discussion of the simulations of flow through ordered and disordered pillar arrays will focus first on pillar arrays without bounding walls, next on pillar arrays with bounding walls, and finally on the experimental devices.
3.2.1 Arrays of pillars (without walls).
We begin by validating the simulations against benchmark cases. A number of expressions have been derived in the literature for the classical problem of a pressure driven flow transverse to an array of infinitely long cylindrical pillars arranged on a square lattice,50–59 as collected in Table S13 (ESI†). The permeability of these arrays are efficiently obtained by 2D simulations of flow across a lattice of circular obstacles, with the lattice vectors of equal length oriented parallel and perpendicular to the flow, respectively, see Fig. 1 (Sqr). Fig. 7(a) shows the calculated flux as a function of the applied pressure gradient for two porosities. The data are well fitted by straight lines following Darcy's law, with the slopes providing the permeabilities; extrapolations of the fits agree with vanishing fluxes in the absence of a pressure gradient. The permeabilities, normalized by the square pillar diameter, are plotted as a function of porosity in Fig. 7(b), along with four theoretical expressions; a plot with six additional theoretical curves is provided in Fig. S6 (ESI†). At low porosities we find excellent agreement with the expressions derived from lubrication theory by Gebart,55 with the interpolation formula by the ‘least-squares solution’ of creeping flow by Sangani and Acrivos,53 and with the scaling theory of Tamayol and Bahrami.59 At high porosities, the simulation data agree well with the infinite series expansion of the Stokes equation by Drummond and Tahir,54 the ‘least-squares solution’ of creeping flow by Sangani and Acrivos,53 and the scaling theory of Tamayol and Bahrami.59 Sangani and Acrivos considered the low and high porosity limits separately, while the plot shows the merging formula by Tsay and Weinbaum.44 As shown in Fig. S6 (ESI†), a number of other expressions in the literature also agree reasonably well with the simulation data.50–54,56–58 Note that the creeping flow condition becomes problematic for arrays of long cylinders at high dilution,52 a.k.a. Stokes' paradox, resulting in the divergence of the permeability for porosities approaching unity. This complication does not arise for the porosities studied here.
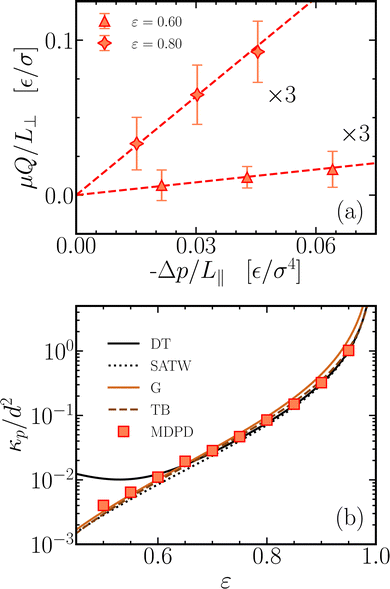 |
| | Fig. 7 Transverse flow through assemblies of cylindrical pillars arranged on two-dimensional square lattices. (a) The flux is linear in the applied pressure gradient, in agreement with Darcy's law, with the slope yielding the permeability. The error bars represent standard deviations, multiplied by a factor three for clarity. (b) Permeabilities extracted from the simulations (markers) plotted against porosity. The confidence intervals of the simulation results are smaller than the markers. The lines represent theoretical expressions by Drummond and Tahir54 (DT), the merger by Tsay and Weinbaum44 of two theories by Sangani and Acrivos53 (SATW), Gebart55 (G) and Tamayol and Bahrami59 (TB). Their expressions are collected in in Table S13 (ESI†). Fig. S6 (ESI†) presents a comparison of the numerical results with six additional theoretical curves. The various theories differ in the details of the flow problem being solved, the series expansion being used, and the truncation of this series. | |
The close adherence of the simulated flow in square lattices to the theory by Tamayol and Bahrami59 is highlighted in Fig. 8, where the ratio of simulated and theoretical permeabilities is plotted against porosity. Note that the ratio deviates from unity by less than 20%, except at the lowest porosity, while the permeabilities vary over nearly three orders of magnitude. We attribute the differences to the approximations made in the simulations and theory; e.g. with decreasing porosity we expect an increasing impact of the relatively large size of the fluid particles in comparison to the gaps between the pillars. Besides employing the flux, we also use the average drag force on the pillars to determine the permeability, see eqn (3). The two methods typically agree to within 1%. Simulation results are also collected for flow through square lattices rotated over 45°, i.e. with both equal length lattice vectors at the same angle relative to the flow direction, see Fig. 1 (Rot sqr). Theoretical arguments indicate that this rotation does not affect the permeability.54,60 The simulated permeabilities for the rotated lattice indeed closely follow those of the non-rotated lattice, as shown in Fig. 8.
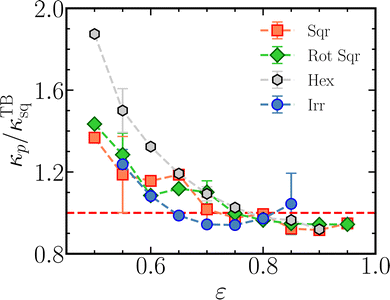 |
| | Fig. 8 The permeabilities of transverse flow though ordered and disordered assemblies of cylindrical pillars, as illustrated in Fig. 1, normalized by the theoretical values for square lattices of the same porosities by Tamayol and Bahrami,59 plotted against porosity. The error bars for the three ordered arrays are similar in size, and become smaller with increasing porosity. The error bars for the irregular arrays reflect standard deviations across 25 configurations per porosity. | |
Flow through hexagonal lattices serves as a further test. The pillars are ordered in rows along the flow direction, with a nearest neighbour distance between the pillar centers, as illustrated in Fig. 1 (Hex). For high porosities, above 0.70, the permeability of the hexagonal lattice is very close to that of the square lattices, see Fig. 8. The difference between the two sets of simulations steadily increases with decreasing porosity, but stays within ∼40% over the range covered. The expressions for the permeability derived by Sangani and Acrivos,53 Drummond and Tahir,54 and Gebart,55 as collected in Table S14 (ESI†), provide accurate descriptions of the simulation data, see Fig. S7 (ESI†). The close agreements between simulations and theories indicates that the MDPD simulation method is well suited for these kind of simulations, with the pillars providing near-stick boundary conditions to the flow.
Having established the suitability of our simulation method, we now advance to the disordered pillar configurations. At each porosity studied, the permeability is calculated for 25 ‘small’ random configurations, see Table S6 (ESI†). The resulting average permeabilities are close to those of the square and hexagonal lattices at the same porosity, see Fig. 8, while the values for individual configurations both undershoot and overshoot those of the ordered lattices, see Fig. S8 (ESI†). Akin to the ordered configurations, the permeability grows nearly exponentially with porosity up to ε ∼ 0.75, followed by a steeper growth for higher porosities. Yazdchi et al.61 present permeabilities for ordered and disordered pillar arrays, obtained by Finite Element simulations, as a function of the mean next-nearest pillar distance, non-dimensionalized with the pillar diameter as γ2, which in turn is a function of porosity. We follow the same procedure in Fig. S12 (ESI†), obtaining good agreement with their data and fit functions. The clustering of the data points along clearly separated lines in Fig. 8 and Fig. S12(b) (ESI†) indicates that the permeability is not fully determined by ε or by γ2, but is also a function of the finer details of the configuration like its (lack of) regularity. The variation in κp across the irregular arrays at the same porosity is expected to gradually disappear upon increasing the system size to include more pillars at constant porosity and pillar diameter. The difference in κp between ordered and disordered arrays at the same porosity is unlikely to vanish, however, just like there exists a systematic difference in κp between square and hexagonal arrays with the same porosity.
Permeability calculations are also performed in 3D simulations for several porosities and pillar configurations, using periodic boundary conditions along the z direction and pillars spanning the entire height of the box. These 3D permeabilities agree well with their 2D counterparts, as illustrated in Fig. S11 (ESI†). These results validate the applied methodology, which will next be applied to pillars between walls.
3.2.2 Arrays of pillars between walls.
Effective permeabilities κeff of simulated flows through a rotated square array of pillars placed between two parallel flat walls, separated by H = 7.5σ, are presented in Fig. 9. At the highest porosity, for ε = 1, the resistance to the flow is solely due to the walls and the simulations recover the permeability associated with Poiseuille flow, κw = H2/12. The effective permeability rapidly drops with decreasing porosity, as expected for dense arrays of pillars. Normalization of the effective permeabilities with the above calculated permeabilities due to the pillars at the same porosity, see Fig. 9(b), highlights that the effective permeability at low porosities is dominated by the pillars' resistance to the flow. Tsay and Weinbaum,44 building on the work by Lee and Fung,42 derived an infinite series solution for Stokesian flow through the simulated configuration. These authors also obtained a compact approximate expression (TW) by interpolating between an extrapolation of a theory by Lee43 for a dilute rotated square pillar arrays between walls (LTW) and a fit to the equations by Sangani and Acrivos53 for 2D flow through square pillar arrays (SATW); these expressions are collected in Table S16 (ESI†). The simulation results follow the theoretically predicted trends, see Fig. 9, though the simulated ratio κeff/κp increases less with decreasing porosity than its theoretical counterpart. The deviations of up to 20% at the lower porosities are just within the accuracy attributed by Tsay and Weinbaum to their interpolation formula. To put this deviation in perspective, note that both κeff and κp decrease by approximately an order of magnitude between ε = 0.8 and 0.6, see Fig. S14 (ESI†). Although the pillars are the dominant resistance to the flow at the lower porosities, the contributions due to the walls can not be ignored and result in κeff remaining smaller than κp.
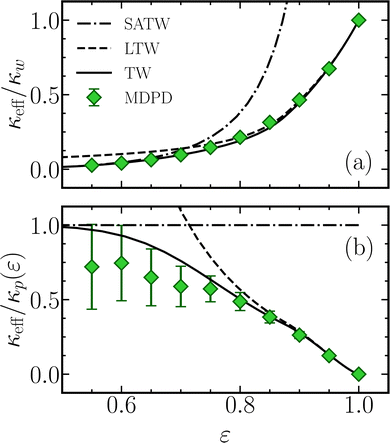 |
| | Fig. 9 Effective permeabilities of flow through assemblies of cylindrical pillars, arranged on a rotated two-dimensional square lattice and confined between two parallel flat walls. The permeabilities are normalized (a) by the permeability of a Poiseuille flow between two flat walls at the same perpendicular distance H, namely κw = H2/12, and (b) by the permeability of the pillar assembly κp, i.e. the permeability in the limit H → ∞. Markers show simulation results, with their standard deviations. The lines represent theoretical expressions by Tsay and Weinbaum:44 an extension of earlier work by Lee43 on the wall-dominated asymptotic regime (LTW), a fit of the expression by Sangani and Acrivos53 for the pillar-dominated asymptotic regime (SATW), and an interpolation formula between these extremes (TW). | |
Superficial velocity profiles are obtained by averaging over the fluid particles in slabs parallel to the walls. The three typical profiles shown in Fig. 10 vary from a Pouiseille-like quadratic curve at high porosity, to a nearly uniform velocity with relatively thin boundary layers at low porosity. All are fitted well with the velocity field solved from Brinkman's theory, see eqn (5). The parameters obtained by these fits are collected in Fig. 11. We focus first on the square lattice and the rotated square lattice. Since this rotation affects neither the flow resistance due to the pillars nor the flow resistance due to the walls, we expect to find agreement between both lattices. The fitted amplitudes, Bfit, as well as the theoretical predictions B = (κp/μ)(Δp/L‖) based on the corresponding 2D permeabilities, κp, vary by nearly three orders of magnitude over the simulated range of porosities. Hence, to facilitate the comparison, their ratio is shown in Fig. 11(a). This reveals that the simulation results for both lattices lie below the theoretical values for most porosities, by up to 25%, but exceed the theory by 20% at the highest porosity. In Fig. 11(b) the fit parameters αfit determining the shapes of the velocity profiles are converted into normalized effective viscosities following μeff/μ = 1/(κpαfit2), where again use is made of the permeabilities established in the matching 2D simulations. The resulting effective viscosities fluctuate around μfiteff ≈ 2.1μ, with the exception of the simulations at the lowest and highest porosity. We note that the velocity fitting procedure approaches its innate limitations at the highest porosity, where a Poiseuille-like velocity profile is fitted with eqn (5): the latter only converges to a quadratic profile with stick boundary conditions us(±H/2) = 0 under the combined limits of α → 0 and B → ∞, while their product must remain finite since it determines the midplane velocity, Bα2 = 2us(0). It then follows that the correct Poiseuille profile is recovered only for μeff = μ.
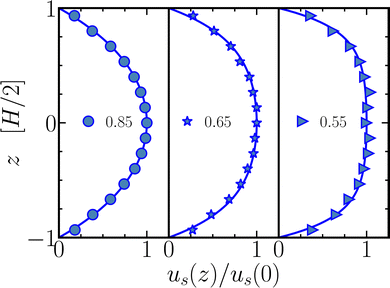 |
| | Fig. 10 The simulated superficial velocity us as function of the distance from the midplane, z, for irregular arrays at three porosities in channels of height H = 7.5σ. All three velocity profiles are normalized by their respective simulated mid-plane velocities, to highlight the transition from a wall-dominated nearly quadratic profile at ε = 0.85 to a pillar-dominated nearly uniform profile at ε = 0.55. Solid lines show the fitted velocity profiles following Brinkman's theory, eqn (5). The fitted values of α are 0.4 (ε = 0.85), 0.9 (ε = 0.65); and 1.4 (ε = 0.55). | |
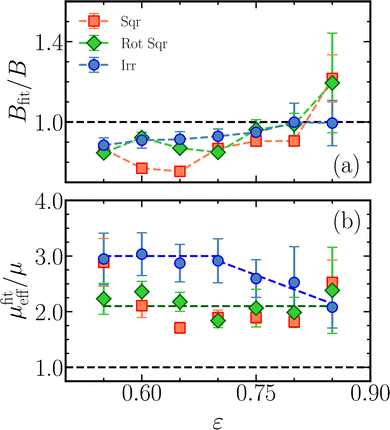 |
| | Fig. 11 (a) The amplitudes Bfit and (b) the effective viscosities μfiteff as obtained by fitting the superficial velocity profiles in the simulations, see Fig. 10, with the theoretical profile following Brinkman's theory, see eqn (5). The amplitudes are normalized by the theoretical prediction, the effective viscosity is scaled by the fluid's viscosity. Both are plotted as functions of porosity for the square lattice, the square lattice rotated over 45° and irregular pillar configurations, for a channel height H = 7.5σ. The error bars for the regular arrays denote standard deviations across three driving forces, while those for the irregular arrays represent standard deviations over 25 configurations at one driving force. | |
Irregular pillar arrays bound between walls are simulated for a range of porosities, using 25 independently generated ‘small’ configuration at every porosity. Their velocity profiles are fitted to obtain the amplitudes and effective viscosities, presented in Fig. 11 by circular markers. The amplitudes are again less than their theoretical value, though the deviations are smaller and show less variation than those of the regular lattices. The effective viscosity has an approximately constant value of μeff ≈ 3.0μ for low porosities, ε ≲ 0.7, while a nearly linear decline is observed for higher porosities, μfiteff/μ = 6.52 − 5.14ε. The extrapolation of this fitted line crosses μfiteff/μ = 1 at ε = 1.06, whereas – as discussed above – Poiseuille flow requires the effective viscosity to match the fluid viscosity at ε = 1. It is therefore likely that the observed linear decrease is followed by an even steeper decrease for porosities approaching unity, or that the observed decay underestimates the actual slope. We note that simulations at these high porosities are excessively time consuming, because of the large system sizes required. Refitting the effective viscosities at the four highest porosities with a straight line crossing μeff/μ = 1 at ε = 1 yields μfiteff/μ = 1 + 6.70(1 − ε). From the close agreement of the simulated velocity profile with the theoretical profile of eqn (5), it follows that eqn (7) provides an accurate relation between the effective permeability of a pillar array in a channel and the 2D permeability of that array.
The height dependence of the effective viscosity is explored by simulating pillars on a square lattice and on a rotated square lattice at two channel heights, H = 7.5σ and 10σ. For the disordered arrays, at every porosity one randomly selected configuration per porosity is simulated at three channel heights, H = 7.5σ, 10σ and 12.5σ. The results over the range of porosities, see Fig. 12, suggest that the effective viscosity is insensitive to the height within the accuracy and range of the current simulations. The fluctuations are of similar sizes as the error bars in Fig. 11(b).
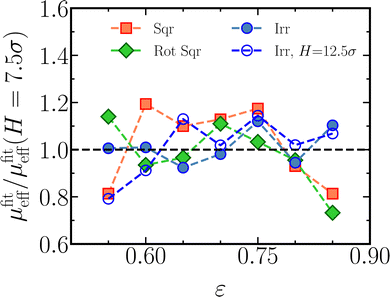 |
| | Fig. 12 The fitted effective viscosities μfiteff at the elevated heights of H = 10σ (all configurations) and H = 12.5σ (disordered configurations only), divided by their counterparts for the same configurations at H = 7.5σ. | |
The deviation of the effective viscosity from the fluid's viscosity highlights the interference of walls and pillars in determining the overall flow field in Brinkman's theory. We have thus far assumed that the direct and indirect effects of the wall can be accounted for by a viscous shear term with an effective viscosity, and thereby obtained a useful function describing the superficial velocity profile. The simulations permit an exploration of this assumption, by calculating the actual forces acting on the walls and pillars. We find that the viscous force Fw,± by the liquid on an area of the wall parallel to the flow, say A‖, is related to the superficial velocity by
| | 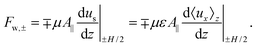 | (11) |
On the r.h.s., 〈
ux〉
z =
us(
z)/
ε represents the actual velocity of the fluid particles near the wall and
εA‖ denotes the area of the wall in contact with these fluid particles. Note that the regular fluid viscosity, rather than the effective viscosity of Brinkman's equation, yields a match. The simulations also provide the force on the pillars by the liquid, which is about four times as high as the combined forces by the walls for
ε = 0.75 and grows in relative importance with decreasing porosity. The pillar force density is calculated as
fp =
Fp/
V‖, where
Fp is the total force between pillars and fluid in a slab of thickness Δ
h and volume
V‖ =
A‖Δ
h.
Fig. 13(a) shows that this force density is fairly constant in the middle of the channel, where the velocity distribution is nearly flat, and drops to a low value near the walls, where the flow velocity is small. Contrary to the assumption in
eqn (4), however, this force density is not proportional to the velocity profile. Dividing the force density by the fitted superficial velocity profile yields the elevation-dependent permeability
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) p
p =
fp/
us shown in
Fig. 13(b). This permeability is in agreement with the bulk pillar permeability
κp in the center of the channel, but drops below halve that value near the walls. It should be noted that the signal to noise ratio deteriorates for the small average forces in the vicinity of the wall. Assuming, inspired by
eqn (11), that the viscosity of the superficial flow field is identical to the bulk viscosity
μ throughout the entire channel height, we find that the sum of the pillar and shear force densities matches the force density due to the imposed pressure difference, except for the bin nearest the wall (data not shown). This suggests that the velocity profile of
eqn (5) and the above force distributions agree with Brinkman's
eqn (4), provided
μeff =
μ and the pillar permeability is elevation dependent,
| | 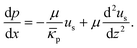 | (12) |
Insertion of the superficial velocity then yields
| | 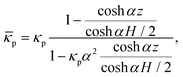 | (13) |
in reasonable agreement with the elevation-dependent permeability deduced from the force distribution on the pillars, see
Fig. 13(b). A more detailed exploration of the force distribution is a topic of ongoing work.
 |
| | Fig. 13 (a) The force density fp by the liquid on the pillars as a function of elevation, normalized by the area parallel to the flow, for an irregular array at a porosity of 0.70. (b) The corresponding elevation dependent permeability, as deduced from the simulations (markers) and the profile derived in eqn (13) (line). | |
3.2.3 Simulations of the experimental configurations.
We are now in a position to compare simulation results with experimental data. The unit cells of 800 pillars etched in the microfluidic chip are computationally too demanding for full-blown 3D simulations including walls, but they are amenable to 2D simulations yielding the permeabilities due to the pillars. The simulations employ the pillar configurations etched in the chips, adjusted to match the actual porosities of the fabricated devices, while maintaining a pillar diameter of 5σ. As shown in Fig. 6 and Table 1, the simulated permeabilities of the pillar arrays κp approach the effective permeability of the devices at low porosity but deviate significantly at high porosities. Their conversion into effective permeabilities for pillars arrays between walls is achieved by Brinkman's theory, which in Fig. 10 and 11 was found to hold true for the 3D simulations – provided one uses the effective viscosities of Fig. 11(b). Upon assuming that these effective viscosities also apply to the microfluidic device, eqn (7) yields the effective permeabilities presented in Fig. 14. We observe a nice agreement with the experimental data, much better than in Fig. 6, indicating once more that the friction at the walls plays an important role in these microfluidic experiments. The plotted standard deviations are mostly due to the uncertainty in the effective viscosity, estimated from Fig. 11(b) as 0.4μ. For comparison purposes, the plot also shows the effective permeability following the common assumption μeff = μ, which clearly overestimates the experimental values by underestimating the drag forces at the walls. The effective permeability obtained by combining the random pillar permeability of Yazdchi et al.61 with Brinkman's theory for μeff = 3μ produces a good agreement with the experimental data.
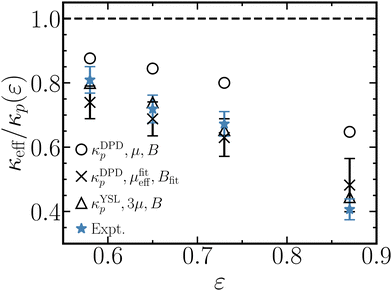 |
| | Fig. 14 Comparison of the effective permeabilities measured using microfluidic chips with their numerically calculated counterparts. All permeabilities are normalized by the permeabilities of the pillar configurations, κp(ε), as determined by 2D simulations of flow through the unit cell of 800 pillars. The calculated 3D effective permeabilities are obtained with Brinkman's theory, see eqn (7), using the pillar permeability, effective viscosity and amplitude listed in the legend. The effective permeability based on the simulation results (×) matches the experimental results (*) nicely. An equally satisfactory agreement is found (Δ) when combining the permeability of random pillars by Yazdchi et al.61 (YSL) with μeff = 3μ and the theoretical expression for the amplitude B. An effective viscosity matching the bulk fluid viscosity (°) underestimates the wall contributions to the flow. Additional comparisons are presented in Fig. S15 (ESI†). | |
3.2.4 Square lattices from the literature.
The above permeabilities and effective viscosities also enable comparisons with data from earlier studies on regular arrays of cylinders between walls. Gunda et al.47 report experimental effective permeabilities of square arrays of cylindrical pillars etched in silicon microchannels. As detailed in Section S4.2 of the ESI,† these data are reasonably well-described by combining the expression by Tamayol and Bahrami59 for square arrays of pillars with Brinkman's theory accounting for the walls, where μeff = 2.1μ following Fig. 11. Wagner et al.49 present benchmark calculations of flow around a square array of cylindrical pillars between two flat walls, using a range of semi-analytical and simulation techniques. These included two mathematical homogenization theories, namely the classical 3D approach (H3D) and the Very Thin Porous Medium approach (VTPM), a Finite Element Method for incompressible Navier-Stokes equations (FEM), Smooth Particle Hydrodynamics (SPH) and the Lattice-Boltzmann Method (LBM). The numerical results obtained with these methods are reproduced in Fig. 15. We note that the range of porosities in their work, from 0.25 to 0.62, hardly overlaps with that in the current work, from 0.55 to 0.95. Furthermore, their pillars have aspect ratios H/d between 0.09 and 0.13, whereas our simulations are in the range from 1.5 to 2.5. Nevertheless, repeating the above approach of estimating the permeabilities of square arrays between walls by combining the Tamayol and Bahrami59 expression for square arrays of pillars with Brinkman's theory accounting for the walls gives a good agreement for μeff = 2.1μ, see Fig. 15. Using the higher effective viscosity μeff = 3μ of irregular arrays also gives a good match, while the lower value μeff = μ overestimates the effective permeability at the higher porosity. The viscosity μeff = μ/ε performs quite well (data not shown), possibly helped by 1/ε having a value comparable to 2–3 in the region of the plot 0.35 ≤ ε ≤ 0.65 where the wall effects are important.
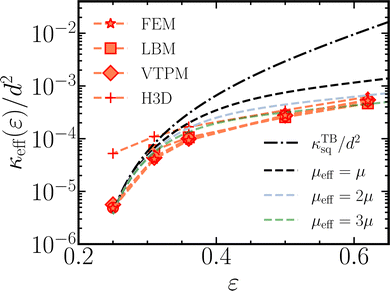 |
| | Fig. 15 The effective permeability of square arrays of pillars between walls as calculated by Wagner et al.49 using various numerical methods (red markers, see main text for abbreviations in legend) compared against the theory by Tamayol and Bahrami59 for a square lattice of pillars (black dashed-dotted line) and the combination of the latter with wall contributions using Brinkman's theory (dashed lines). | |
4 Conclusions
Computer simulations and experiments are used to study the flow through irregular pillar configurations etched in a microfluidic chip, for channel heights two to three times the pillar diameter. The simulations indicate that the velocity profile between the walls is well-described by an expedient interpretation of Brinkman's theory, which solves the stationary flow by replacing the non-slip boundary conditions at the pillars by an effective Darcy permeability while retaining the non-slip boundary conditions at the walls with an effective viscosity. We extract effective viscosities of twice the bulk viscosity for square and rotated square pillar arrays and thrice the bulk viscosity for irregular configurations, for porosities up to ∼0.8. From the subsequent calculations, the choice μeff = 3μ emerges as a generic estimate for cross-channel pillar arrays. It is then straightforward to convert permeabilities of pillar arrays – from a relatively cheap 2D calculation or using an expression from the literature, see ESI† – into the effective permeability of the microfluidic device. The results obtained are in good agreement with experimental data and elaborate 3D benchmark calculations. We therefore conclude that Brinkman's theory works well for arrays of wall-to-wall pillars in microfluidic channels, enabling fast and accurate estimates of the superficial flow field and effective permeability. The accompanying force distribution on walls and pillars requires an alternative interpretation of Brinkman's equation, with an effective viscosity equal to the fluid's bulk viscosity and the walls inducing an elevation-dependent pillar permeability.
Author contributions
THC developed the simulation code, performed simulations, analyzed the data and participated in the conceptualization of the research. HB designed and performed the experiments and analyzed the data. THC and HB co-wrote the original draft. RGHL and SL initiated and directed the research, acquired funding and resources, and reviewed the manuscript. WKdO conceptualized and supervised the research, provided the computational resources, co-wrote and reviewed the manuscript.
Conflicts of interest
There are no conflicts to declare.
Appendix
Inspired by numerous decay processes in physics, one may guess that the flow field through an array of infinitely tall pillars bound by a flat wall at z ≤ 0 decays exponentially from a Darcy velocity for z ≫ 0 to a vanishing velocity at the wall,| | 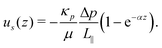 | (14) |
This flow field can be considered as the solution to Darcy's equation dp/dx = −[μ/![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff]us with an elevation-dependent effective permeability,
eff]us with an elevation-dependent effective permeability, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff = κp(1 − e−αz). In this view, the decay parameter α characterizing the impact of the wall is no longer related to an effective viscosity. For pillars confined between two walls, this approach leaves two alternatives,
eff = κp(1 − e−αz). In this view, the decay parameter α characterizing the impact of the wall is no longer related to an effective viscosity. For pillars confined between two walls, this approach leaves two alternatives,| | ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff = 1 − βe−αz − γeαz, eff = 1 − βe−αz − γeαz, | (15) |
| | ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff = (1 − βe−αz)(1 − γeαz). eff = (1 − βe−αz)(1 − γeαz). | (16) |
The values of β and γ are determined by inserting the boundary conditions ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff(±H/2) = 0, yielding β = γ. In the former case, β = 2/cosh(αH/2) and one recovers Brinkman's solution. The latter case offers two solutions, β± = cosh(αH/2)±sinh(αH/2), resulting in flow fields identical to Brinkman's except for a multiplication factor,
eff(±H/2) = 0, yielding β = γ. In the former case, β = 2/cosh(αH/2) and one recovers Brinkman's solution. The latter case offers two solutions, β± = cosh(αH/2)±sinh(αH/2), resulting in flow fields identical to Brinkman's except for a multiplication factor,| | 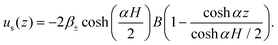 | (17) |
Using β+ does not recover the Darcy flow velocity us(0) ≈ B in the center of the channel, thereby leaving β− as the only solution. Fitting the flow field recovers the decay parameters αfit in the main text; the only difference is in the Bfit. For the current values of αH/2 ≥ 1.5, the multiplication factor 2β−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh(αH/2) hardly differs from unity and there is little to choose. For a typical viscosity ratio of three, see Fig. 11, the decay parameter and the pillar permeability are related by α ≈ (3κp)−1/2.
cosh(αH/2) hardly differs from unity and there is little to choose. For a typical viscosity ratio of three, see Fig. 11, the decay parameter and the pillar permeability are related by α ≈ (3κp)−1/2.
Acknowledgements
THC acknowledges the Industrial Partnership Programme of the Foundation for Fundamental Research on Matter (FOM, project code:i43), which is financially supported by The Netherlands Organisation for Scientific Research (NWO). This research program was co-financed by Canon Production Printing (Venlo, The Netherlands). HB acknowledges the Netherlands Organisation for Scientific Research (NWO) for a Vici grant (project code: STW 016.160.312). This work was performed in the cooperation framework of Wetsus, the European Centre of Excellence for Sustainable Water Technology (http://www.wetsus.nl). Wetsus is co-funded by the Dutch Ministry of Economic Affairs, the Ministry of Infrastructure and Environment, the European Union Regional Development Fund, the Province of Fryslân and the Northern Netherlands Provinces. We thank Jan W. van Nieuwkasteele (University of Twente) for the fabrication of the chips.
Notes and references
-
M. J. Blunt, Multiphase flow in permeable media: A pore-scale perspective, Cambridge University Press, Cambridge, U.K., 2017 Search PubMed.
- J. Hommel, E. Coltman and H. Class, Transp. Porous Med., 2018, 124, 589–629 CrossRef.
- W. D. King, Am. J. Phys., 2008, 76, 558–565 CrossRef.
- F. B. Wadsworth, C. E. J. Vossen, M. J. Heap, A. Kushnir, J. I. Farquharson, D. Schmid, D. B. Dingwell, L. Belohlavek, M. Huebsch, L. Carbillet and J. E. Kendrick, Am. J. Phys., 2021, 89, 769–775 CrossRef.
- P. Foscolo, L. Gibilaro and S. Waldram, Chem. Eng. Sci., 1983, 38, 1251–1260 CrossRef CAS.
- D. Mandal, Powder Technol., 2015, 276, 18–25 CrossRef CAS.
- V. Nassehi, Chem. Eng. Sci., 1998, 53, 1253–1265 CrossRef CAS.
- N. Hanspal, A. Waghode, V. Nassehi and R. Wakeman, Chem. Eng. J., 2009, 149, 132–142 CrossRef CAS.
- H. Bazyar, P. Lv, J. A. Wood, S. Porada, D. Lohse and R. G. H. Lammertink, Soft Matter, 2018, 14, 1780–1788 RSC.
- D. Grolimund and M. Borkovec, Environ. Sci. & Technol., 2005, 39, 6378–6386 CrossRef CAS PubMed.
- F. He, M. Zhang, T. Qian and D. Zhao, J. Colloid Interface Sci., 2009, 334, 96–102 CrossRef CAS PubMed.
- D. Natarajan and T. V. Nguyen, J. Electrochem. Soc., 2001, 148, A1324 CrossRef CAS.
- K. Jiao and X. Li, Prog. Energy Combustion Sci., 2011, 37, 221–291 CrossRef CAS.
-
H. Darcy, Les fontaines publiques de la ville de Dijon, Victor Dalmont, Paris, France, 1856 Search PubMed.
- W. De Malsche, S. De Bruyne, J. Op De Beek, P. Sandra, H. Gardeniers, G. Desmet and F. Lynen, J. Chromatogr. A, 2012, 1230, 41–47 CrossRef CAS PubMed.
- W. D. Malsche, J. O. D. Beeck, S. D. Bruyne, H. Gardeniers and G. Desmet, Anal. Chem., 2012, 84, 1214–1219 CrossRef PubMed.
- H. C. Brinkman, Appl. Sci. Res., 1949, 1, 27–34 Search PubMed.
- C. K. W. Tam, J. Fluid Mech., 1969, 38, 537–546 CrossRef.
- J. Happel and N. Epstein, Ind. Eng. Chem. Res., 1954, 46, 1187–1194 CrossRef CAS.
- T. S. Lundgren, J. Fluid Mech., 1972, 51, 273–299 CrossRef.
- G. Neale and W. Nader, Can. J. Chem. Eng., 1974, 32, 475–478 CrossRef.
- G. S. Beavers and D. D. Joseph, J. Fluid Mech., 1967, 30, 197–207 CrossRef.
- K. F. Freed and M. Muthukumar, J. Chem. Phys., 1978, 68, 2088–2096 CrossRef CAS.
- D. A. Nield, J. Fluid Mech., 1983, 128, 37–46 CrossRef.
- S. Kim and W. B. Russel, J. Fluid Mech., 1985, 154, 269–286 CrossRef CAS.
- L. Durlofsky and J. F. Brady, Phys. Fluids, 1987, 30, 3329–3341 CrossRef.
- J. Koplik, H. Levine and A. Zee, Phys. Fluids, 1983, 26, 2864–2870 CrossRef.
- R. E. Larson and J. J. L. Higdon, J. Fluid Mech., 1986, 166, 449–472 CrossRef CAS.
- N. Martys, D. P. Bentz and E. J. Garboczi, Phys. Fluids, 1994, 6, 1434–1439 CrossRef CAS.
- R. C. Givler and S. A. Altobelli, J. Fluid Mech., 1994, 258, 355–370 CrossRef CAS.
- J. A. Ochoa-Tapia and S. Whitaker, Int. J. Heat Mass Transfer, 1995, 38, 2635–2646 CrossRef CAS.
- J. A. Ochoa-Tapia and S. Whitaker, Int. J. Heat Mass Transfer, 1995, 38, 2647–2655 CrossRef CAS.
- V. M. Starov and V. G. Zhdanov, Colloids Surf., A, 2001, 192, 363–375 CrossRef CAS.
- H. Liu, P. R. Patil and U. Narusawa, Entropy, 2007, 9, 118–131 CrossRef.
- F. J. Valdes-Parada, J. A. Ochoa-Tapia and J. Alvarez-Ramirez, Physica A, 2007, 385, 69–79 CrossRef.
- T. Lévy, Int. J. Eng. Sci., 1983, 21, 11–23 CrossRef.
- J.-L. Auriault, Transp. Porous Med., 2009, 79, 215–223 CrossRef.
- J. Kołodziej, M. Mierzwiczak and J. Grabski, J. Mech. Mater. Struct., 2017, 12, 93–106 CrossRef.
- S. K. Zaripov, R. F. Mardanov and V. F. Sharafutdinov, Transp. Porous Media, 2019, 130, 529–557 CrossRef CAS.
- D. A. Nield, Int. J. Heat Fluid Flow, 1991, 12, 269–272 CrossRef CAS.
- J.-L. Auriault, C. Geindreau and C. Boutin, Transp. Porous Med., 2005, 60, 89–108 CrossRef.
- J. S. Lee and Y. C. Fung, J. Fluid Mech., 1969, 37, 657–670 CrossRef.
- J. S. Lee, J. Biomech., 1969, 2, 187–198 CrossRef CAS PubMed.
- R.-Y. Tsay and S. Weinbaum, J. Fluid Mech., 1991, 226, 125–148 CrossRef CAS.
- J. Yeom, D. D. Agonafer, J.-H. Han and M. A. Shannon, J. Micromech. Microeng., 2009, 19, 065025 CrossRef.
- A. Tamayol, A. Khosla, B. L. Gray and M. Bahrami, Int. J. Heat Mass Transfer, 2012, 55, 3900–3908 CrossRef CAS.
- N. S. K. Gunda, J. Joseph, A. Tamayol, M. Akbari and S. K. Mitra, Microfluid. Nanofluid., 2013, 14, 711–721 CrossRef CAS.
- H. Wang and P. Wang, J. Fluids Eng., 2017, 139, 021108 CrossRef.
- A. Wagner, E. Eggenweiler, F. Weinhardt, Z. Trivedi, D. Krach, C. Lohrmann, K. Jain, N. Karadimitriou, C. Bringedal and P. Voland,
et al.
, Transp. Porous Media, 2021, 1–23 Search PubMed.
- J. Happel, AIChE J., 1959, 5, 174–177 CrossRef CAS.
- H. Hasimoto, J. Fluid Mech., 1959, 5, 317–328 CrossRef.
- S. Kuwabara, J. Phys. Soc. Japan, 1959, 14, 527–532 CrossRef.
- A. S. Sangani and A. Acrivos, Int. J. Multiphase Flow, 1982, 8, 193–206 CrossRef CAS.
- J. E. Drummond and M. I. Tahir, Int. J. Multiphase Flow, 1984, 10, 515–540 CrossRef CAS.
- B. R. Gebart, J. Compos. Mater., 1992, 26, 1100–1133 CrossRef CAS.
- M. V. Bruschke and S. G. Advani, J. Rheol., 1993, 37, 479–498 CrossRef CAS.
- M. Sahraoui and M. Kaviany, Int. J. Heat Mass Transfer, 1994, 35, 927–943 CrossRef.
- S. Lee and J. Yang, Int. J. Heat Mass Transfer, 1997, 40, 3149–3155 CrossRef CAS.
- A. Tamayol and M. Bahrami, Phys. Rev. E, 2011, 83, 046314 CrossRef PubMed.
- K. Yazdchi, S. Srivastava and S. Luding, Int. J. Multiphase Flow, 2011, 37, 956–966 CrossRef CAS.
- K. Yazdchi, S. Srivastava and S. Luding, Composites A, 2012, 43, 2007–2020 CrossRef CAS.
- A. Narváez, K. Yazdchi, S. Luding and J. Harting, J. Stat. Mech., 2013, 2013, P02038 CrossRef.
- Z. Khalifa, L. Pocher and N. Tilton, Int. J. Heat Mass Transfer, 2020, 159, 120072 CrossRef.
- J. J. L. Higdon and G. D. Ford, J. Fluid Mech., 1996, 308, 341–361 CrossRef CAS.
- D. S. Clague and R. J. Phillips, Phys. Fluids, 1997, 9, 1562–1572 CrossRef CAS.
- A. H.-D. Cheng, Water Resour. Res., 1984, 20, 980–984 CrossRef.
- S. M. White and C. L. Tien, Heat Mass Transfer, 1987, 21, 291–296 CAS.
- D. A. S. Rees and I. Pop, Int. J. Heat Mass Transfer, 2000, 43, 2565–2571 CrossRef.
- M. S. Abu Zaytoon, T. L. Alderson and M. H. Hamdan, J. Appl. Math. Phys., 2016, 4, 86–99 CrossRef.
- E. S. Boek and P. Van Der Schoot, Int. J. Mod. Phys. C, 1998, 09, 1307–1318 CrossRef.
- Y. Xia, J. Goral, H. Huang, I. Miskovic, P. Meakin and M. Deo, Phys. Fluids, 2017, 29, 056601 CrossRef.
- Z. Li, X. Bian, Y.-H. Tang and G. E. Karniadakis, J. Comp. Phys., 2018, 355, 534–547 CrossRef CAS.
- T. Hulikal Chakrapani and W. K. den Otter, Langmuir, 2020, 36, 12712–12722 CrossRef CAS PubMed.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, EPL, 1992, 19, 155–160 CrossRef.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- I. Pagonabarraga and D. Frenkel, Mol. Simul., 2000, 25, 167–175 CrossRef CAS.
- I. Pagonabarraga and D. Frenkel, J. Chem. Phys., 2001, 115, 5015–5026 CrossRef CAS.
- S. Y. Trofimov, E. L. F. Nies and M. A. J. Michels, J. Chem. Phys., 2002, 117, 9383–9394 CrossRef CAS.
- P. B. Warren, Phys. Rev. E, 2003, 68, 066702 CrossRef CAS PubMed.
- P. B. Warren, Phys. Rev. E, 2013, 87, 045303 CrossRef PubMed.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
-
M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, Ofxord, UK, 2nd edn, 2017 Search PubMed.
-
D. Frenkel and B. Smit, Understanding molecular simulation, Academic Press, San Diega, CA, USA, 2nd edn, 2002 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01261h |
| ‡ Present address: Engineering Thermodynamics, Process & Energy Department, Faculty of Mechanical, Maritime and Materials Engineering, Delft University of Technology, Leeghwaterstraat 39, 2628CB Delft, The Netherlands. |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Hanieh
Bazyar‡
a,
Hanieh
Bazyar‡
 b,
Rob G. H.
Lammertink
b,
Rob G. H.
Lammertink
 b,
Stefan
Luding
b,
Stefan
Luding
 a and
Wouter K.
den Otter
a and
Wouter K.
den Otter
 *a
*a
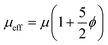 with ϕ the solid volume fraction, but argued that the swarm's immobility hindered momentum transport and hence settled for the fluid's bulk viscosity instead, μeff = μ. Tam18 derived the Darcy–Brinkman theory, obtaining a drag force in agreement with the experimental data of Happel and Epstein.19 Lundgren20 obtained an effective viscosity that matches the Einstein viscosity for low volume fraction, peaks 20% above the bulk viscosity and drops below the latter for solid volume fractions exceeding 0.25. Neale and Nader21 re-interpreted in terms of Brinkman's theory the slip velocity at the interface between bulk flow and flow in a fluid-infused porous medium, as measured by Beavers and Joseph,22 arriving at viscosity ratios μeff/μ ranging from 0.01 to 16. Freed and Muthukumar23 obtained an effective viscosity that follows Einstein's relation for low particle volume fraction. Nield24 and Kim and Russel25 emphasized that Brinkman's equation breaks down for higher solid fraction. Simulations by Durlofksy and Brady26 confirmed Brinkman, with μeff = μ, for particle volume fractions below 0.05. Koplik et al.27 argued that the medium induces a renormalization of the viscosity, yielding an effective viscosity below the bulk viscosity that decreases with increasing solid volume fraction. Larson and Higdon28 reported viscosity ratios close to unity, but also noted the limited validity of Brinkman's theory. Martys et al.29 used Brinkman's theory to fit calculated flow profiles in a random porous medium, obtaining viscosity ratios steadily increasing from 1.9 to 4.2 with decreasing porosity, ε = 1 − ϕ. Givler and Altobelli30 measured the flow field in a coarse foam, thereby deducing μeff/μ ≈ 7.5. Ochoa-Tapia and Whitaker31,32 derived a volume-averaged flow equation, with an apparent viscosity μ/ε. Starov and Zhdanov33 arrived at an effective viscosity that follows the Einstein viscosity to first order in the volume fraction. Liu et al.34 solved the flow in a channel and extracted a viscosity ratio close to unity. Valdes-Parada et al.35 showed that the effective viscosity varies with the chosen boundary conditions for flow over a fluid-infused medium. Levy36 and Auriault37 limited the validity of Brinkman's theory to arrays of spheres and fibers. Kołodziej et al.38 numerically solved the flow between a mobile and an immobile wall sandwiching an array of cylinders, obtaining a viscosity ratio of 0.9 at ε = 10−8 and a rapid decay to 0.4 at ε = 0.1. Zaripov et al.39 reported viscosity ratios spanning several orders of magnitude.
with ϕ the solid volume fraction, but argued that the swarm's immobility hindered momentum transport and hence settled for the fluid's bulk viscosity instead, μeff = μ. Tam18 derived the Darcy–Brinkman theory, obtaining a drag force in agreement with the experimental data of Happel and Epstein.19 Lundgren20 obtained an effective viscosity that matches the Einstein viscosity for low volume fraction, peaks 20% above the bulk viscosity and drops below the latter for solid volume fractions exceeding 0.25. Neale and Nader21 re-interpreted in terms of Brinkman's theory the slip velocity at the interface between bulk flow and flow in a fluid-infused porous medium, as measured by Beavers and Joseph,22 arriving at viscosity ratios μeff/μ ranging from 0.01 to 16. Freed and Muthukumar23 obtained an effective viscosity that follows Einstein's relation for low particle volume fraction. Nield24 and Kim and Russel25 emphasized that Brinkman's equation breaks down for higher solid fraction. Simulations by Durlofksy and Brady26 confirmed Brinkman, with μeff = μ, for particle volume fractions below 0.05. Koplik et al.27 argued that the medium induces a renormalization of the viscosity, yielding an effective viscosity below the bulk viscosity that decreases with increasing solid volume fraction. Larson and Higdon28 reported viscosity ratios close to unity, but also noted the limited validity of Brinkman's theory. Martys et al.29 used Brinkman's theory to fit calculated flow profiles in a random porous medium, obtaining viscosity ratios steadily increasing from 1.9 to 4.2 with decreasing porosity, ε = 1 − ϕ. Givler and Altobelli30 measured the flow field in a coarse foam, thereby deducing μeff/μ ≈ 7.5. Ochoa-Tapia and Whitaker31,32 derived a volume-averaged flow equation, with an apparent viscosity μ/ε. Starov and Zhdanov33 arrived at an effective viscosity that follows the Einstein viscosity to first order in the volume fraction. Liu et al.34 solved the flow in a channel and extracted a viscosity ratio close to unity. Valdes-Parada et al.35 showed that the effective viscosity varies with the chosen boundary conditions for flow over a fluid-infused medium. Levy36 and Auriault37 limited the validity of Brinkman's theory to arrays of spheres and fibers. Kołodziej et al.38 numerically solved the flow between a mobile and an immobile wall sandwiching an array of cylinders, obtaining a viscosity ratio of 0.9 at ε = 10−8 and a rapid decay to 0.4 at ε = 0.1. Zaripov et al.39 reported viscosity ratios spanning several orders of magnitude.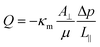
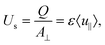
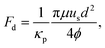
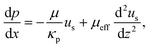
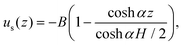
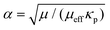 . The total flow rate is obtained by integration of the velocity profile,
. The total flow rate is obtained by integration of the velocity profile,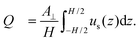
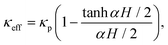
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pillars covering an area of 5 × 2.5 mm. The pillar configuration was fabricated in silicon using standard photolithography and reactive ion etching, creating pillars with a height of H = 20 μm; the detailed fabrication procedure is described in the ESI,† Section S1.1. The fabricated chips were inspected using an inverted optical microscope (Zeiss Axiovert 40 MAT) with an objective of 5× magnification (Zeiss EC Epiplan 5×/0.13, working distance of 19.8 mm). The actual diameters of the pillars were measured for at least 35 pillars on each chip, using image analysis software (HoKaWo 3.00). The pillars were also observed using a scanning electron microscope (SEM, JEOL JSM 5610), see Fig. 3 and 4 and Fig. S1 through S3 in Section S1.2 (ESI†). After pillar fabrication and inspection, the microfluidic chip was finalized by anodic bonding a glass wafer to the silicon. All chips were used as received from the clean room with no further cleaning or treatment, and hence were hydrophilic.
000 pillars covering an area of 5 × 2.5 mm. The pillar configuration was fabricated in silicon using standard photolithography and reactive ion etching, creating pillars with a height of H = 20 μm; the detailed fabrication procedure is described in the ESI,† Section S1.1. The fabricated chips were inspected using an inverted optical microscope (Zeiss Axiovert 40 MAT) with an objective of 5× magnification (Zeiss EC Epiplan 5×/0.13, working distance of 19.8 mm). The actual diameters of the pillars were measured for at least 35 pillars on each chip, using image analysis software (HoKaWo 3.00). The pillars were also observed using a scanning electron microscope (SEM, JEOL JSM 5610), see Fig. 3 and 4 and Fig. S1 through S3 in Section S1.2 (ESI†). After pillar fabrication and inspection, the microfluidic chip was finalized by anodic bonding a glass wafer to the silicon. All chips were used as received from the clean room with no further cleaning or treatment, and hence were hydrophilic.
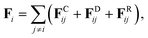
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij + Bij(
ij + Bij(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) i +
i + ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) j)wB(rij)
j)wB(rij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij,
ij,![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij)
ij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij,
ij,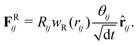
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = (ri − rj)/rij, with ri the position of particle i and rij the inter-particle distance. The weight-functions wA(rij) = 1 − rij/rA and wB(rij) = 1 − rij/rB decay linearly with the distance and are identically zero beyond their cut-off distances rA and rB, respectively. The multibody density at particle i is calculated as
ij = (ri − rj)/rij, with ri the position of particle i and rij the inter-particle distance. The weight-functions wA(rij) = 1 − rij/rA and wB(rij) = 1 − rij/rB decay linearly with the distance and are identically zero beyond their cut-off distances rA and rB, respectively. The multibody density at particle i is calculated as 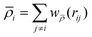 , with the normalized weight function w
, with the normalized weight function w![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (rij) = (15/2πrB3)wB2(rij). Dij and Rij are the strength parameters of the dissipative and random forces, respectively, with wD(rij) = wR2(rij) and wR(rij) = 1 − rij/rA the corresponding weight functions. The friction forces are proportional to the velocity difference vij = ṙi − ṙj. The random numbers θij have zero mean and unit variance, are uncorrelated in time and are uncorrelated between particle pairs. The stochastic nature of the random force also gives rise to its scaling with the time step dt, see eqn (9c). Finally, the dissipative and random forces are related by the fluctuation-dissipation theorem81
(rij) = (15/2πrB3)wB2(rij). Dij and Rij are the strength parameters of the dissipative and random forces, respectively, with wD(rij) = wR2(rij) and wR(rij) = 1 − rij/rA the corresponding weight functions. The friction forces are proportional to the velocity difference vij = ṙi − ṙj. The random numbers θij have zero mean and unit variance, are uncorrelated in time and are uncorrelated between particle pairs. The stochastic nature of the random force also gives rise to its scaling with the time step dt, see eqn (9c). Finally, the dissipative and random forces are related by the fluctuation-dissipation theorem81![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) was replaced by its 2D equivalent, w
was replaced by its 2D equivalent, w![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (rij) = (6/πrB2)wB2(rij). The viscosity of the resulting 2D fluid was determined as μ = 26.1ετ/σ2. The 2D simulations of disordered pillar configurations employed the same configurations as the 3D simulations. In this case, however, the boxes contained two copies of the unit cell back to back, while system size dependence was tested by rerunning one configuration per porosity using one unit cell. The experimental disordered systems were simulated in 2D only, using one copy of the ‘large’ unit cell.
(rij) = (6/πrB2)wB2(rij). The viscosity of the resulting 2D fluid was determined as μ = 26.1ετ/σ2. The 2D simulations of disordered pillar configurations employed the same configurations as the 3D simulations. In this case, however, the boxes contained two copies of the unit cell back to back, while system size dependence was tested by rerunning one configuration per porosity using one unit cell. The experimental disordered systems were simulated in 2D only, using one copy of the ‘large’ unit cell.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cylindrical pillars, i.e. a unit cell of 800 pillars repeated 10 × 5 on the microfluidic chip, bound between two flat walls separated by H = 20 mm. (a) Normalized fluxes as functions of the applied pressure gradient for four microfluidic chips with differing porosities, for water (dark blue open markers) and hexadecane (light blue solid markers). Dashed lines represent linear fits to the data points at a given porosity. (b) Effective permeabilities of the microfluidic chips, κeff (stars), obtained as the slopes of the linear fits in (a), plotted against the measured porosity. Also shown are permeabilities κlabp (circles) extracted from 2D MDPD simulations (i.e. infinitely long pillars without bounding walls, see Table 1) for disordered arrays identical in configuration and pillar radius to those on the chips. For comparison, the permeability expected from the walls of the device in the absence of pillars amounts to κw = 33 μm2.
000 cylindrical pillars, i.e. a unit cell of 800 pillars repeated 10 × 5 on the microfluidic chip, bound between two flat walls separated by H = 20 mm. (a) Normalized fluxes as functions of the applied pressure gradient for four microfluidic chips with differing porosities, for water (dark blue open markers) and hexadecane (light blue solid markers). Dashed lines represent linear fits to the data points at a given porosity. (b) Effective permeabilities of the microfluidic chips, κeff (stars), obtained as the slopes of the linear fits in (a), plotted against the measured porosity. Also shown are permeabilities κlabp (circles) extracted from 2D MDPD simulations (i.e. infinitely long pillars without bounding walls, see Table 1) for disordered arrays identical in configuration and pillar radius to those on the chips. For comparison, the permeability expected from the walls of the device in the absence of pillars amounts to κw = 33 μm2.




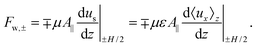
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) p = fp/us shown in Fig. 13(b). This permeability is in agreement with the bulk pillar permeability κp in the center of the channel, but drops below halve that value near the walls. It should be noted that the signal to noise ratio deteriorates for the small average forces in the vicinity of the wall. Assuming, inspired by eqn (11), that the viscosity of the superficial flow field is identical to the bulk viscosity μ throughout the entire channel height, we find that the sum of the pillar and shear force densities matches the force density due to the imposed pressure difference, except for the bin nearest the wall (data not shown). This suggests that the velocity profile of eqn (5) and the above force distributions agree with Brinkman's eqn (4), provided μeff = μ and the pillar permeability is elevation dependent,
p = fp/us shown in Fig. 13(b). This permeability is in agreement with the bulk pillar permeability κp in the center of the channel, but drops below halve that value near the walls. It should be noted that the signal to noise ratio deteriorates for the small average forces in the vicinity of the wall. Assuming, inspired by eqn (11), that the viscosity of the superficial flow field is identical to the bulk viscosity μ throughout the entire channel height, we find that the sum of the pillar and shear force densities matches the force density due to the imposed pressure difference, except for the bin nearest the wall (data not shown). This suggests that the velocity profile of eqn (5) and the above force distributions agree with Brinkman's eqn (4), provided μeff = μ and the pillar permeability is elevation dependent,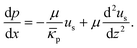
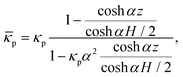



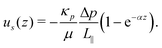
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff]us with an elevation-dependent effective permeability,
eff]us with an elevation-dependent effective permeability, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff = κp(1 − e−αz). In this view, the decay parameter α characterizing the impact of the wall is no longer related to an effective viscosity. For pillars confined between two walls, this approach leaves two alternatives,
eff = κp(1 − e−αz). In this view, the decay parameter α characterizing the impact of the wall is no longer related to an effective viscosity. For pillars confined between two walls, this approach leaves two alternatives,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff = 1 − βe−αz − γeαz,
eff = 1 − βe−αz − γeαz,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff = (1 − βe−αz)(1 − γeαz).
eff = (1 − βe−αz)(1 − γeαz).![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/char_e0cb.gif) eff(±H/2) = 0, yielding β = γ. In the former case, β = 2/cosh(αH/2) and one recovers Brinkman's solution. The latter case offers two solutions, β± = cosh(αH/2)±sinh(αH/2), resulting in flow fields identical to Brinkman's except for a multiplication factor,
eff(±H/2) = 0, yielding β = γ. In the former case, β = 2/cosh(αH/2) and one recovers Brinkman's solution. The latter case offers two solutions, β± = cosh(αH/2)±sinh(αH/2), resulting in flow fields identical to Brinkman's except for a multiplication factor,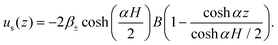
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh(αH/2) hardly differs from unity and there is little to choose. For a typical viscosity ratio of three, see Fig. 11, the decay parameter and the pillar permeability are related by α ≈ (3κp)−1/2.
cosh(αH/2) hardly differs from unity and there is little to choose. For a typical viscosity ratio of three, see Fig. 11, the decay parameter and the pillar permeability are related by α ≈ (3κp)−1/2.






