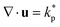Open Access Article
Open Access ArticleActivity-driven tissue alignment in proliferating spheroids†
Liam J.
Ruske
 * and
Julia M.
Yeomans
* and
Julia M.
Yeomans

Rudolf Peierls Centre For Theoretical Physics, University of Oxford, UK. E-mail: liam.ruske@physics.ox.ac.uk
First published on 24th December 2022
Abstract
We extend the continuum theory of active nematic fluids to study cell flows and tissue dynamics inside multicellular spheroids, spherical, self-assembled aggregates of cells that are widely used as model systems to study tumour dynamics. Cells near the surface of spheroids have better access to nutrients and therefore proliferate more rapidly than those in the resource-depleted core. Using both analytical arguments and three-dimensional simulations, we find that the proliferation gradients result in flows and in gradients of activity both of which can align the orientation axis of cells inside the aggregates. Depending on environmental conditions and the intrinsic tissue properties, we identify three distinct alignment regimes: spheroids in which all the cells align either radially or tangentially to the surface throughout the aggregate and spheroids with angular cell orientation close to the surface and radial alignment in the core. The continuum description of tissue dynamics inside spheroids not only allows us to infer dynamic cell parameters from experimentally measured cell alignment profiles, but more generally motivates novel mechanisms for controlling the alignment of cells within aggregates which has been shown to influence the mechanical properties and invasive capabilities of tumors.
I. Introduction
Many biological systems such as epithelial tissues, bacterial colonies or three-dimensional organoids are active systems; they continuously consume chemical energy from their environment to perform tasks such as growth or migration, both of which involve the generation of mechanical stresses by the cells through a variety of biochemical processes.1–3 A prominent 3D example of an active tissue is multicellular spheroids. These are spherical, self-assembled aggregates of cells which provide important model systems for investigating the behaviour of 3D cell aggregates, for example, the effects of mechanical stress, or for screening of anti-cancer drugs.Multicellular spheroids are typically studied in a suitable environment which provides cells with all the needed metabolites such as oxygen and nutrients. The metabolite concentration within cellular aggregates therefore normally decreases towards the core since the supply of metabolites in spheroids and avascular tumors is limited by diffusive transport from the surface. While cells close to the surface show a high rate of cell division, cells located close to the core do not have sufficient access to metabolites and die, thereby forming a necrotic core.4,5 Hence the outer shell of spheroids is dominated by cell growth while the core is dominated by cell death. This has two consequences. The first is that a radial flow of cells is set up from the surface to the centre of the spheroid. The second is a gradient of activity which is a consequence of the gradient in the number of cell divisions which locally generate active, extensile, dipolar forces along their division axes. In this paper we study the competition between these effects to describe the flow and orientation of cells in dense multicellular aggregates.
Our results are based on the continuum theory of three-dimensional active nematic fluids, which has been shown to reproduce the spatio-temporal dynamics in a variety of living systems, from myosin-driven actin-microtubule networks6 to bacterial biofilms7 and confluent cell monolayers.8–11
We start in Section II by presenting the hydrodynamic theory that describes cell flows and cell orientation inside dense cell aggregates and list the equations of motion which we solve analytically and numerically. The main results are presented in Section III, which is divided into four subsections:
In the first part, III A, we show that radial cell flows created by gradients in the isotropic cell growth rate give rise to radial cell elongation profiles inside multicellular spheroids, where cells are aligned either radially or circumferentially (tangentially) throughout the aggregate.
In the second part III B, we investigate how anisotropic active forces produced by cell division and death affect the cell orientation and flows inside spheroids. We highlight that gradients in active stress give rise to an effective cell anchoring at the surface and in the bulk, and the emergence of chaotic cell flows in the aggregate if active stress is sufficiently large.
We then show, in III C, that the interplay between growth driven flow and anisotropic stress can give rise to a variety of cell alignment profiles in proliferating spheroids. We subsequently demonstrate, in III D, that our theory allows us to estimate mechanical and dynamical tissue parameters directly from experimental measurements of the distribution of cell orientations inside freely grown spheroids.
The last section of the paper, IV, summarizes the key results and points out future research directions that it would be interesting to pursue as more sophisticated experimental data becomes available.
II. Theoretical model
We consider a multicellular spheroid embedded in an environment with a fixed concentration m0 of metabolites, such as oxygen, glucose or growth factors, which are necessary for cell proliferation. We assume that metabolites freely diffuse throughout tissue with diffusion constant Dm and are consumed by cells at a rate proportional to α*. In the diffusive limit (Péclet number Pe ≪ 1), the time evolution of metabolite concentration m(x, t) across tissues is governed by the reaction–diffusion equation| ∂tm = Dm∇2m − α*φm, | (1) |
 .
.
We describe the motion of cells inside spheroids in a continuum limit, where tissue is characterised by a cell-velocity field u and a tensorial order parameter Q, which describes the averaged, local magnitude S and direction n of cell alignment
 | (2) |
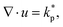 | (3) |
 depends on the local reproduction rate k+ or death rate k− of individual cells. When cells have access to sufficient metabolites, cell division dominates,
depends on the local reproduction rate k+ or death rate k− of individual cells. When cells have access to sufficient metabolites, cell division dominates, 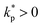 , which acts as a mass source causing diverging local flow. On the other hand, when the metabolite concentration falls below a certain threshold, m < mc, cells die faster than they divide,
, which acts as a mass source causing diverging local flow. On the other hand, when the metabolite concentration falls below a certain threshold, m < mc, cells die faster than they divide, 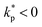 , thus creating a mass sink and locally converging flow. In the vicinity of the homeostatic equilibrium, m = mc, we expand the cell production rate
, thus creating a mass sink and locally converging flow. In the vicinity of the homeostatic equilibrium, m = mc, we expand the cell production rate  rate around the homeostatic metabolite concentration to linear order,
rate around the homeostatic metabolite concentration to linear order, | (4) |
In addition to continuity eqn (3), the cell flow u in tissues must conserve momentum as described by the Navier–Stokes-equations
| ρ(∂t + u·∇)u = ∇·Π | (5) |
| Πact = −ζ*Q | (6) |
| ζ* = ζ(m − mc) | (7) |
Since cells adhere to each other, the shape and orientation of cells in a tissue responds to the cellular flows around them. The time evolution of the nematic tensor Q is thus coupled to the velocity field u and follows the Beris–Edwards equation19
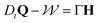 | (8) |
 is the co-rotational term, which describes how cell orientation responds to gradients in flow field u.15,20 The last term is the rotational diffusivity Γ, which controls the relaxation of cell deformations towards the equilibrium cell shape quantified by the molecular field
is the co-rotational term, which describes how cell orientation responds to gradients in flow field u.15,20 The last term is the rotational diffusivity Γ, which controls the relaxation of cell deformations towards the equilibrium cell shape quantified by the molecular field  . The free energy
. The free energy  of tissues encodes the mechanical and geometric properties of cells, such as the aspect ratio at equilibrium and the elastic energy associated with cell deformations (Fig. 1d). Isotropic cells, such as most epithelial cells, are on average isotropic at equilibrium, hence the minimum of the free energy is at Seq = 0. Cells like fibroblasts or rod-shaped bacteria, however, exhibit an elongated morphology and local alignment at equilibrium modelled by choosing Seq > 0. Expressions for the co-rotational term
of tissues encodes the mechanical and geometric properties of cells, such as the aspect ratio at equilibrium and the elastic energy associated with cell deformations (Fig. 1d). Isotropic cells, such as most epithelial cells, are on average isotropic at equilibrium, hence the minimum of the free energy is at Seq = 0. Cells like fibroblasts or rod-shaped bacteria, however, exhibit an elongated morphology and local alignment at equilibrium modelled by choosing Seq > 0. Expressions for the co-rotational term  and the tissue free energy
and the tissue free energy  are presented in the ESI.† It should be noted that in 3D cell shapes do not need to be rotationally symmetric, which implies that Q could, in principle, have a biaxial component. This would modify the ways in which cells mechanically interact which each other, thus adding a correction to the elastic energy and active stresses.
are presented in the ESI.† It should be noted that in 3D cell shapes do not need to be rotationally symmetric, which implies that Q could, in principle, have a biaxial component. This would modify the ways in which cells mechanically interact which each other, thus adding a correction to the elastic energy and active stresses.
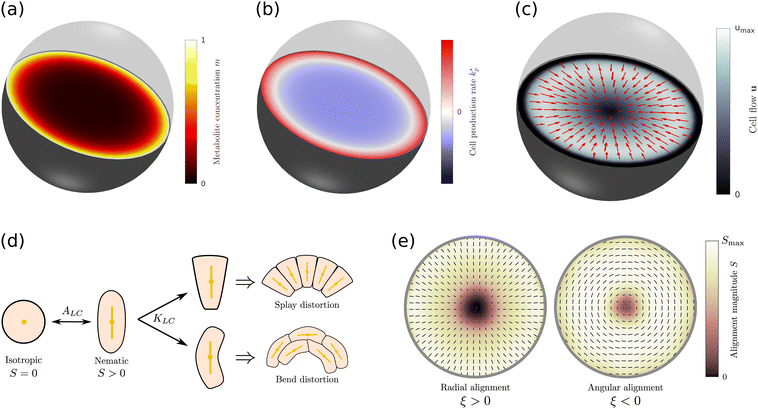 | ||
Fig. 1 (a) Diffusion limited transport of metabolites give rise to radial concentration profiles m(r) which decrease towards the core of spheroids. (b) Assuming the cell proliferation and cell death rates are proportional to the local metabolite concentration, the cell production rate  at steady-state is positive close to the surface and negative in the core, where the transition point at steady-state is positive close to the surface and negative in the core, where the transition point  depends on the critical metabolite concentration mc. (c) In the absence of active dipolar stress spatial variations in the cell production rate create converging flow profiles given by eqn (11). (d) The mechanical and geometric properties of cells give rise to a free energy depends on the critical metabolite concentration mc. (c) In the absence of active dipolar stress spatial variations in the cell production rate create converging flow profiles given by eqn (11). (d) The mechanical and geometric properties of cells give rise to a free energy 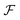 which includes elastic constants associated with cell deformations, where ALC penalizes cell stretching which changes the aspect ratio of cells and KLC penalizes changes in cell shape which results in bend and splay deformations. (e) Isotropic cells inside proliferating spheroids are radially elongated by converging flows for alignment parameter ξ > 0 and align tangential to the surface for ξ < 0. Since the magnitude of flow-induced elongation increases along the radial direction, cells close to the surface are more elongated than cells in the centre. which includes elastic constants associated with cell deformations, where ALC penalizes cell stretching which changes the aspect ratio of cells and KLC penalizes changes in cell shape which results in bend and splay deformations. (e) Isotropic cells inside proliferating spheroids are radially elongated by converging flows for alignment parameter ξ > 0 and align tangential to the surface for ξ < 0. Since the magnitude of flow-induced elongation increases along the radial direction, cells close to the surface are more elongated than cells in the centre. | ||
We simulate growing spheroids by numerically solving the continuum equations of motion eqn (1) for the metabolite concentration and eqn (3), (5) and (8) for the tissue dynamics, on a three-dimensional grid of size 84 × 84 × 84 using a hybrid lattice Boltzmann-finite difference method.20 Numerical details and simulation parameters are stated in the ESI.† Analytical solutions for the flow field u and metabolite concentration m in spherical aggregates are presented in the following Section IIIA.
III. Results
A. Converging flows promote cell alignment
We start by analytically solving the equations of motion (1), (3) and (8) for the metabolite concentration m, cell flow u and nematic tensor Q for spherical aggregates in which active dipolar stress produced by cell division and cell death is negligible, ζ = 0. In this case, the cell flows are caused solely by mass sources and sinks which arise as a consequence of the cell production rate . Solving eqn (1) for the boundary condition m = m0 = 1 at the surface yields a metabolite concentration m(r) which is a function of the radial coordinate only,
. Solving eqn (1) for the boundary condition m = m0 = 1 at the surface yields a metabolite concentration m(r) which is a function of the radial coordinate only,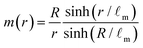 | (9) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m is the characteristic penetration length of metabolites from the surface (Fig. 1a and b). If the initial spheroid size is small, R ⪅
m is the characteristic penetration length of metabolites from the surface (Fig. 1a and b). If the initial spheroid size is small, R ⪅ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m, the total cell production rate is positive and the aggregate grows at a rate
m, the total cell production rate is positive and the aggregate grows at a rate | (10) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) c = Rc/
c = Rc/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m is a function of the critical metabolite concentration only,
m is a function of the critical metabolite concentration only, ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) c = f−1(mc), where f(x) = 3(x
c = f−1(mc), where f(x) = 3(x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) coth
coth![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x − 1)/x2 (ESI† Fig. S1a). Fig. S1b and c (ESI†) shows how mc affects the shape of the metabolite profile m(r) which determines the cell production rate
x − 1)/x2 (ESI† Fig. S1a). Fig. S1b and c (ESI†) shows how mc affects the shape of the metabolite profile m(r) which determines the cell production rate  inside aggregates of size R = Rc.
inside aggregates of size R = Rc.
The cell flow u = ur(r)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) can be obtained by solving the continuity eqn (3) in the domain r ∈ [0, R] using the boundary condition u(R) = Ṙ,
can be obtained by solving the continuity eqn (3) in the domain r ∈ [0, R] using the boundary condition u(R) = Ṙ,
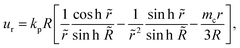 | (11) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = R/
= R/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m and
m and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) = r/
= r/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m. Since Ṙ > 0 in growing spheroids, there is a transition between a diverging cell flow close to the surface, ur > 0, and a converging cell flow ur < 0 in the core of aggregates (ESI† Fig. S2a). At steady-state, cell flows are facing inwards everywhere and vanish at the surface, ur(Rc) = 0 (Fig. 1c), and the shape of flow profiles depends on the critical metabolite concentration mc (Fig. S1d, ESI†). Recently it has been reported that shear stresses created by cell flow ur can create a viscocapillary instability that perturbs the spherical symmetry of aggregates for sufficiently small surface tension.21 In this work, however, we consider the limit in which cell-generated stress is small compared to the surface tension of spheroids and the shape of cell aggregates remains spherical.
m. Since Ṙ > 0 in growing spheroids, there is a transition between a diverging cell flow close to the surface, ur > 0, and a converging cell flow ur < 0 in the core of aggregates (ESI† Fig. S2a). At steady-state, cell flows are facing inwards everywhere and vanish at the surface, ur(Rc) = 0 (Fig. 1c), and the shape of flow profiles depends on the critical metabolite concentration mc (Fig. S1d, ESI†). Recently it has been reported that shear stresses created by cell flow ur can create a viscocapillary instability that perturbs the spherical symmetry of aggregates for sufficiently small surface tension.21 In this work, however, we consider the limit in which cell-generated stress is small compared to the surface tension of spheroids and the shape of cell aggregates remains spherical.
We now describe how the radial flows ur, given by eqn (11), affect the elongation and alignment of cells as quantified by the nematic order parameter Q. To this end, we consider an aggregate of initially isotropic cells, Q(x, t) = 0. As outlined in the ESI,† the stability of the isotropic state is governed by
 | (12) |
In passive liquid crystals the value of ξ is determined by the aspect ratio of the constituents, which predicts ξ > 0 for elongated prolate-shaped cells. In the context of tissue dynamics, an alternative flow-alignment parameter ν is occasionally used,22,23 which quantifies the time-evolution of the cell orientation axis n rather than the nematic tensor Q, where the parameters ν and ξ are related via ν = −ξ(3S + 4)/(9S). To the best of our knowledge, there are only few studies that have attempted to directly extract the flow-alignment parameter of living tissues. The analysis of cell orientations and flows in confluent layers of spindle-shaped cells under confinement revealed, that tissue dynamics follows ν < 0.23 Formalisms have been developed to geometrically decompose large-scale tissue shear into cellular contributions, which include cell shape changes and topological changes in the cellular network. In the absence of topological changes induced by cell divisions, cell deaths or T1 transitions, cell shape dynamics follows ν = −1. Studies of cellular flows in the wing epithelium of Drosophila, however, have revealed that topological T1 transitions greatly contribute to macroscopic tissue shear.24,25 Thus we assume that the flow-alignment parameter ξ is an intrinsic tissue property related to topological changes in the cell network, which may depend on cell type, biochemical signals or the mechanical properties of the environment.
Using spherical coordinates, the initial growth rates of the radial component Qrr and angular components Qϕϕ, Qθθ are (see Section II in the ESI†)
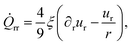 | (13) |
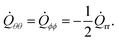 | (14) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) −1
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh
sinh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) + 3
+ 3 ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) −2(
−2(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) −1
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh
sinh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) − cosh
− cosh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ) > 0, thus isotropic cells inside spheroids become radially elongated for ξ > 0 and radially compressed for ξ < 0 (Fig. 1e). Since the strength of the alignment depends on the magnitude of the strain rate, the growth rate of radial alignment scales as
) > 0, thus isotropic cells inside spheroids become radially elongated for ξ > 0 and radially compressed for ξ < 0 (Fig. 1e). Since the strength of the alignment depends on the magnitude of the strain rate, the growth rate of radial alignment scales as ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) rr ∼ ξkp and increases along the radial direction, reaching a maximum at the surface r = R. This is shown in Fig. S1e (ESI†) for different values of mc. Although the magnitude of alignment S initially follows eqn (14), at later times the director field is subject to higher-order effects such as advection, and flow-induced cell elongation through the co-rotational term
rr ∼ ξkp and increases along the radial direction, reaching a maximum at the surface r = R. This is shown in Fig. S1e (ESI†) for different values of mc. Although the magnitude of alignment S initially follows eqn (14), at later times the director field is subject to higher-order effects such as advection, and flow-induced cell elongation through the co-rotational term  is eventually balanced by passive restoring forces arising from the molecular field H (Fig. S1f, ESI†). The cell alignment profile at steady state depends on mechanical cell parameters (Fig. 1d), however, alignment profiles retain the main features seen at early times with cell alignment being maximal near the surface and decreasing towards the core (Fig. S1g and h, ESI†).
is eventually balanced by passive restoring forces arising from the molecular field H (Fig. S1f, ESI†). The cell alignment profile at steady state depends on mechanical cell parameters (Fig. 1d), however, alignment profiles retain the main features seen at early times with cell alignment being maximal near the surface and decreasing towards the core (Fig. S1g and h, ESI†).
B. Active stress gradients induce nematic alignment
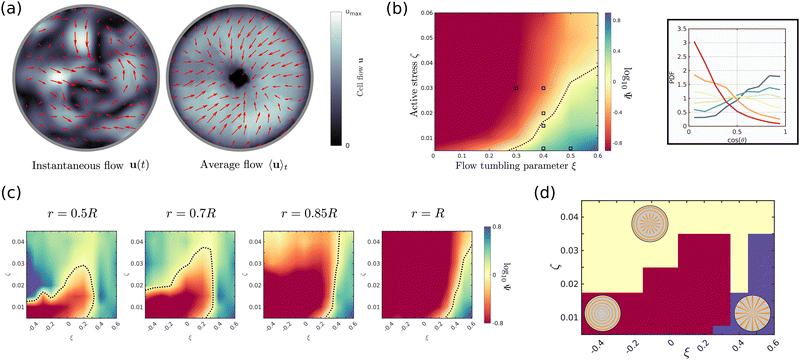
We now consider the limit where cell flows are dominated by dipolar active stress ζ produced by cell division and death and growth-induced radial flows are negligible, ∇·u ≈ 0. Active nematic stress creates a well-known hydrodynamic instability which constantly pushes the system out of equilibrium, leading to a state termed active turbulence. 3D active turbulence is characterised by spatiotemporally chaotic flows (Fig. 2a) and the presence of self-propelled disclination lines (ESI† Fig. S3a and b). In this section we will focus on how activity gradients affect the time-averaged alignment of the director at certain distances from spheroid centre, which is a quantity that can be easily measured in experiments.12,26 | ||
Fig. 2 (a) Two-dimensional cross-section of the velocity field inside an active spheroid showing spatiotemporally chaotic flows caused by self-propelled disclination lines. Arrows and colour bar refer to the in-plane component of the flow field. (b) Histogram (left) and spatial distribution (right) of the angle θ between the director n and the radial vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) at the surface of spheroids shows strong tangential director alignment caused by a hydrodynamic anchoring force termed active anchoring. (c) Two-dimensional cross-section of the in-plane component of the director field (left) and the probability distribution of cos at the surface of spheroids shows strong tangential director alignment caused by a hydrodynamic anchoring force termed active anchoring. (c) Two-dimensional cross-section of the in-plane component of the director field (left) and the probability distribution of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (right) obtained by spatial averages at a given radius [r, r + δr] and over time. The distributions at radii rcore < rtrans < R are shown as blue, grey and red, respectively. (d) ∇2ζ* obtained from simulations of quasi-spherical droplets. Activity gradients set up flows which create radial cell alignment inside the aggregate (∇2ζ* > 0, blue area) and tangential alignment close to the surface (∇2ζ* < 0, red area). The black, dashed line shows the analytical prediction eqn (15) for spherical aggregates with a sharp interface at r = R. (e) Cell alignment parameter Ψ as a function of radial coordinate for different magnitudes of active stress ζ. Simulations were performed using the following parameters, unless stated otherwise in the legend: spheroid radius R = 30, θ (right) obtained by spatial averages at a given radius [r, r + δr] and over time. The distributions at radii rcore < rtrans < R are shown as blue, grey and red, respectively. (d) ∇2ζ* obtained from simulations of quasi-spherical droplets. Activity gradients set up flows which create radial cell alignment inside the aggregate (∇2ζ* > 0, blue area) and tangential alignment close to the surface (∇2ζ* < 0, red area). The black, dashed line shows the analytical prediction eqn (15) for spherical aggregates with a sharp interface at r = R. (e) Cell alignment parameter Ψ as a function of radial coordinate for different magnitudes of active stress ζ. Simulations were performed using the following parameters, unless stated otherwise in the legend: spheroid radius R = 30, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m = 4, mc = 0.3, KLC = 0.04, ζ = 0.025, ξ = 0, kp = 0. m = 4, mc = 0.3, KLC = 0.04, ζ = 0.025, ξ = 0, kp = 0. | ||
To investigate how activity gradients affect cell alignment inside spheroids, we measure the distribution of the angle θ between the director n and the radial vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) at different distances from the centre of aggregates. Since there are more possible configurations for angular alignment (θ = π/2) than for radial alignment (θ = 0), a randomly aligned director field results in a uniform distribution of
at different distances from the centre of aggregates. Since there are more possible configurations for angular alignment (θ = π/2) than for radial alignment (θ = 0), a randomly aligned director field results in a uniform distribution of  . Preferred angular or radial alignment leads to a biased distribution towards 0 or 1, respectively.
. Preferred angular or radial alignment leads to a biased distribution towards 0 or 1, respectively.
Fig. 2c shows a typical alignment profile across the spheroid. In the core cells are preferentially extended radially while close to the surface cells are extended along angular directions. In the transition region r = rtrans between the shell and the core the director field has a random orientation.
Recalling that the active stress is Πact = −ζ*Q, (eqn (6)), we can identify two competing mechanisms that lead to cell alignment. Firstly, radial alignment in the bulk of spheroids is driven by gradients in activity, and hence in active stress, resulting from metabolite gradients. As was shown for bulk active nematic systems,27 hydrodynamic forces set up by activity gradients align the director field parallel to the gradient direction in regions where ∇2ζ* > 0 and perpendicular where ∇2ζ* < 0. Inside spherical aggregates eqn (7) and (9) yield
 | (15) |
Secondly, since the nematic droplet is surrounded by a passive isotropic fluid, the magnitude of active stress ζ* drops rapidly to zero across the surface of the aggregate. The resulting gradient in extensile activity at the surface induces flows which rotate the director field and align it parallel to the surface as indicated by the distribution of the angle θ between the director field n and the surface normal of droplets in Fig. 2b. This hydrodynamic effect, termed active anchoring,28,29 is restricted to the outer shell of spheroids, with a thickness given by the length-scale over which cell density φ drops to zero, which is typically of the order of a single cell size (Fig. 2d).
Thus the cell alignment profile in Fig. 2c results from a competition between radial alignment due to activity gradients in the bulk, tangential alignment resulting from active anchoring at the aggregate surface and elastic forces which tend to smooth out distortions in the director profile. To describe how the average cell alignment varies across aggregates with different magnitudes of active stress ζ, we define the cell alignment parameter
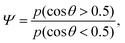 | (16) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 as a function of r, lead to qualitatively similar results (Fig. S3a, ESI†).
θ〉 as a function of r, lead to qualitatively similar results (Fig. S3a, ESI†).
If activity is sufficiently large (ζ ≥ 0.015) the director field shows strong radial alignment close to the core r = rcore and tangential alignment close to the surface r = R, with weak or no alignment in the transition region r = rtrans. Note that, because of symmetry, there is no radial alignment at the centre of aggregates r ≈ 0 since activity driven alignment cannot overcome the increasing elastic energy associated with a nematic hedgehog configuration close to the centre. These values of activity correspond to active turbulence and disclination lines are spontaneously created inside the aggregate (see also Fig. S3c–f, ESI†).
At very low activity (ζ ≤ 0.005) we find that active anchoring creates weak tangential cell alignment close to the surface, with a magnitude that decreases with decreasing activity. The angular alignment decays monotonically towards the core of spheroids without showing any radial alignment at intermediate distances because active stress is not strong enough to overcome elastic forces. Although activity-driven director alignment does not rely on specific shear-alignment ξ ≠ 0, it should be noted that the magnitude of alignment slightly depends on ξ, as shown in Fig. S3b (ESI†).
C. Interplay between proliferation- and activity-induced nematic alignment
We now combine the main findings of Sections IIIA and IIIB and study the interplay between converging flows set up by differential volume growth across spheroids and spatiotemporally chaotic flows created by dipolar stresses Πact = −ζ*Q arising from cell divisions and death. The spatial and temporal variations of flow fields in active turbulence can be characterized by an active length-scale
set up by differential volume growth across spheroids and spatiotemporally chaotic flows created by dipolar stresses Πact = −ζ*Q arising from cell divisions and death. The spatial and temporal variations of flow fields in active turbulence can be characterized by an active length-scale 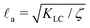 and time-scale τa = η/ζ, where KLC is the elastic constant of the liquid crystal which penalizes distortions in the director field resulting from cell shape deformations, and η is the viscosity of the fluid. While instantaneous flow fields u(x, t) inside spheroids can be indistinguishable from active turbulence if active stress is sufficiently large, ζ/η > kp, chaotic flow patterns average out over time scales T ≫ τa and the time-averaged velocity field 〈u(r)〉t reduces to the converging cell flows given by eqn (11) (Fig. 3a). This behaviour is expected by symmetry since spatio-temporal chaotic flows in bulk active nematics are isotropic, therefore they do not contribute to time-averaged flows.30–32
and time-scale τa = η/ζ, where KLC is the elastic constant of the liquid crystal which penalizes distortions in the director field resulting from cell shape deformations, and η is the viscosity of the fluid. While instantaneous flow fields u(x, t) inside spheroids can be indistinguishable from active turbulence if active stress is sufficiently large, ζ/η > kp, chaotic flow patterns average out over time scales T ≫ τa and the time-averaged velocity field 〈u(r)〉t reduces to the converging cell flows given by eqn (11) (Fig. 3a). This behaviour is expected by symmetry since spatio-temporal chaotic flows in bulk active nematics are isotropic, therefore they do not contribute to time-averaged flows.30–32
We first consider the cell orientation at the surface of a spheroid, where the strain rate of converging flows reaches a maximum. Thus, following eqn (14), the director orientation is most strongly affected by converging flows at the surface. Strains due to the converging component 〈u〉t of the flow field, which is set up by eqn (3), drive radial surface cell orientation for ξ > 0, while active anchoring, driven by active stress Πact in eqn (5), favours cells aligning tangentially to the surface.28,29 The magnitudes of proliferation-driven alignment and active anchoring increase with the flow-alignment parameter |ξ| and active stress ζ, respectively. To investigate the cross-over between these competing effects, we measure the cell alignment parameter Ψ at the surface of steady-state spheroids over a range of parameter values ξ and ζ (Fig. 3b). For ξ = 0 the orientation of cells does not respond to the strain rate of flows, thus active anchoring dominates at any activity level ζ > 0, which creates strong tangential surface alignment. As ξ > 0 increases, however, the cell orientation responds more strongly to the fluid strain rate at the surface and the director field aligns radially due to velocity gradients caused by proliferation as long as active anchoring is sufficiently small, ζ < ζc. Since shear-driven cell alignment scales as ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) ij ∼ ξẼij, the critical activity ζc above which active anchoring dominates increases with the strain rate at the surface Ẽrr ∼ kp and ξ. The function ζc(ξ) is shown by the black, dotted line in Fig. 3b.
ij ∼ ξẼij, the critical activity ζc above which active anchoring dominates increases with the strain rate at the surface Ẽrr ∼ kp and ξ. The function ζc(ξ) is shown by the black, dotted line in Fig. 3b.
In addition to cell orientation at the surface, we can also measure Ψ at a distance 0 < r < R from the centre of spheroids as a function of ζ and ξ (Fig. 3c). For low activity and ξ = 0, the director field in the core (r = 0.5R) shows weak alignment since the orientation at the surface decays very slowly towards the centre due to the dominance of the elastic energy associated with distortions in the director field over active stresses. Thus, in the regime of low activity, cell orientation throughout spheroids is dictated by the cell alignment at the surface. As soon as radial shear-alignment becomes dominant at the surface for ξ > ξc, cells globally switch from angular to radial orientation (see phase diagram Fig. 3d for ζ < 0.02).
In Section IIIB we showed that for sufficiently large activity ζ > ζc, the core of spheroids shows radial alignment while at the surface cells are oriented tangentially because of the balance between activity gradient-induced radial ordering and tangential active anchoring. Surprisingly, the activity threshold ζc above which radial order is created in the core decreases for ξ < 0, even though converging flows favour tangential over radial alignment throughout spheroids for ξ < 0 (see boundary between red and yellow domains in Fig. 3d). This non-trivial behaviour can be explained in terms of the disclination line structure inside aggregates. Active anchoring creates significant surface alignment, but usually it is not strong enough to completely enforce tangential anchoring everywhere on the surface (see Fig. 2b). As ξ < 0 decreases, however, the tangential surface anchoring of the director field eventually becomes sufficiently large that the Gauss-Bonnet theorem can be applied. This states that the total topological charge of a vector field tangentially anchored on a sphere must be +2, the Euler-characteristic χ of the sphere.33
At very low activity and ξ < 0, the director field thus relaxes into a configuration that minimizes its elastic energy while meeting the topological constraint close to the surface. The resulting defect structure is two +1/2 disclination lines which bend towards the centre of the droplet and create four +1/2 defects at the surface. The cross-section of the director field inside droplets is formed by two +1/2 defects located close to the centre and hence resembles that around a two-dimensional +1 defect (ESI† Fig. S4a and d). Due to the large elastic energy associated with a point-like +1 defect, there is a finite repulsion force between the two +1/2 defects which keeps them at a finite distance. On the other hand, contractile active forces on +1/2 defects oppose the elastic forces, thus the distance between the two stationary disclination lines decreases with increasing activity.
If activity reaches a critical threshold ζc(ξ), the two +1/2 defects at the centre slip past each other and subsequently reach a steady-state in which both defects orbit around the centre, thereby creating persistent rotational motion in the core of spheroids (Fig. S4b, ESI†). In 3D this corresponds to a dancing disclination state, where the +1/2 line segments in the core orbit around the centre, while the end-points of disclination lines at the surface move very slowly. This motion makes it inevitable that disclination lines must cross after each full rotation, thereby rewiring some of the line segments in the core (Fig. S4e, ESI†). We note that the rotational motion of disclination lines is reminiscent of persistent clockwise or counter-clockwise rotations in active nematic systems in circular (2D) or spherical (3D) confinement which has been observed in experiments34 and simulations.35–37 The orientation of +1/2 defects in the dancing disclination state creates significant radial alignment of the director field outside the orbiting defects, hence Ψ shows a sharp transition from angular to radial director alignment in the core at ζ = ζc(ξ) (Fig. 3c). As the activity ζ is increased even further, the motion of the disclination lines becomes more chaotic and eventually the oscillations are lost in the active turbulent background (Fig. S4c and f, ESI†).
D. Parameter inference for biological systems
Finally we apply our theoretical active fluid model to experimental data obtained from freely grown proliferating spheroids to make quantitative predictions about dynamical tissue parameters, such as active stress ζ and the flow-alignment parameter ξ. Since it is rarely possible in experiments to simultaneously measure proliferation gradients, active stress, cell flows and cell orientations inside spheroids, we require physical estimates for model parameters![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m, mc and kp.
m, mc and kp.
The characteristic penetration length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m of metabolites can be estimated by measuring proliferation profiles in spheroids. This can be realized either by using immuno-fluorescence staining procedures to mark proliferating cells38 or by using spheroid models expressing Fucci (Fluorescence Ubiquitination Cell Cycle Indicators) tools that allow monitoring the cell cycle position of a cell.39 The metabolite penetration length from the surface can vary upon the cell packing density and the cell type, however, for most types of human tumor cells grown under optimal nutrient and oxygen conditions the penetration length typically varies between
m of metabolites can be estimated by measuring proliferation profiles in spheroids. This can be realized either by using immuno-fluorescence staining procedures to mark proliferating cells38 or by using spheroid models expressing Fucci (Fluorescence Ubiquitination Cell Cycle Indicators) tools that allow monitoring the cell cycle position of a cell.39 The metabolite penetration length from the surface can vary upon the cell packing density and the cell type, however, for most types of human tumor cells grown under optimal nutrient and oxygen conditions the penetration length typically varies between ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m ≈ 100–200 μm.40–42 Assuming spheroids are at steady-state, the critical metabolite concentration mc can then be inferred from the aggregate size Rc using eqn (10), mc = 3(x
m ≈ 100–200 μm.40–42 Assuming spheroids are at steady-state, the critical metabolite concentration mc can then be inferred from the aggregate size Rc using eqn (10), mc = 3(x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) coth
coth![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) x − 1)/x2, where x = Rc/
x − 1)/x2, where x = Rc/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m (Fig. S1a, ESI†).
m (Fig. S1a, ESI†).
The cell division rate k+ is determined by the time interval between cell divisions, the cell-cycle time TC, and the proportion of cells engaged in the cell cycle, the growth fraction f, such that k+ = f/TC. The growth fraction f(x) depends on the local metabolite concentration and varies within spheroids.13,41 Assuming kp = k+ at the surface (no cell death), the growth magnitude kp can be most easily estimated from the growth fraction at the surface of spheroids,
| kp = fs/[Tc(1 − mc)] | (17) |
To validate the proposed parameter estimates, we compare our model to a system of freely grown CT26 spheroids at steady-state with radius Rc = 450 μm, corresponding to mc ≈ 0.7. In the outer layer of the spheroids, 0.8 < r/R < 1, eqn (11) predicts an average radial flow velocity ur ≈ 0.06 fs/Tc ≈ 26 μm day−1, which is in good agreement with the radial flow measured in experiments using fluorescently labeled particles, uexpr = 21 μm day−1.45
Mitotic cells in three-dimensional microenvironments generate substantial protrusive forces which were estimated to be on the order of ζ+ ≈ 1–2 kPa.46 Considering that the mitotic time TM over which strong anisotropic forces are generated is relatively short compared to the cell cycle time, TM/TC ≈ 0.1, the average stress produced by cell divisions over a cell cycle is ζ ≈ 100–200 Pa. Similar magnitudes of cell-generated anisotropic stress were measured within proliferating multicellular spheroids using fluorescently labelled, cell-sized oil droplets or polyacrylamide microspheres to measure stresses in situ.43,47 We now compare our active fluid model to experimental data obtained from freely grown proliferating spheroids (R ≈ 300 μm) consisting of human colon carcinoma cells (HCT116),26 colon adenocarcinoma cell (HT29) and human breast cancer cells (BC52).12 It has been reported that both the orientation and the division axis of cells inside HCT116 spheroids show significant tangential alignment close to the surface (Ψexps < 1, cos〈θ〉 = 0.22) while showing no significant alignment in the core (Ψexpc ≈ 1, cos〈θ〉 = 0.44). On the other hand, the analysis of cell shapes and polarity inside HT29 and BC52 spheroids revealed that cells show only weak surface alignment (Ψexps ≈ 1) while cells are increasingly radially elongated towards the core (Ψexpc > 1).
Assuming ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m = 150 μm, fs = 0.7 and TC = 20 h, we calculated the average cell alignment Ψs at the surface (r = 300 μm) and Ψc in the core of spheroids (r = 180 μm) over a range of values for ζ and ξ (Fig. 4a). The full list of simulation parameters with their mapping from lattice units to physical values are shown in the ESI.† By comparing Ψs and Ψc obtained from simulations with experimental data, we calculate the posterior distributions p(Θ|X) over model parameters Θ = [ζ, ξ] given data X = [Ψexps, Ψexpc]. Given the qualitative nature of the experimental data, we assume that the likelihood function
m = 150 μm, fs = 0.7 and TC = 20 h, we calculated the average cell alignment Ψs at the surface (r = 300 μm) and Ψc in the core of spheroids (r = 180 μm) over a range of values for ζ and ξ (Fig. 4a). The full list of simulation parameters with their mapping from lattice units to physical values are shown in the ESI.† By comparing Ψs and Ψc obtained from simulations with experimental data, we calculate the posterior distributions p(Θ|X) over model parameters Θ = [ζ, ξ] given data X = [Ψexps, Ψexpc]. Given the qualitative nature of the experimental data, we assume that the likelihood function  follows a normal distribution,
follows a normal distribution,  , where σ quantifies the allowed tolerance between data and experimental measurements (see ESI,† Fig. S5). The parameter distributions p(ζ, ξ|X) obtained for HCT116 (green) and HT29/BC52 spheroids (magenta) are presented in Fig. 4b. We find that tissue dynamics within HT29 and BC52 spheroids is governed by a positive flow-alignment parameter (ξ ≈ 0.5) while in HCT116 spheroids shear-alignment of cells is less dominant (ξ < 0.3) and potentially even negative (Fig. 4c). We also gain some additional information about the magnitude of active stress inside aggregates, where cell divisions inside HCT116 spheroids produce on average ζ = 100–200 Pa (Fig. 4c), thus confirming our previous experimental estimate based on ζ = ζ+TM/TC.
, where σ quantifies the allowed tolerance between data and experimental measurements (see ESI,† Fig. S5). The parameter distributions p(ζ, ξ|X) obtained for HCT116 (green) and HT29/BC52 spheroids (magenta) are presented in Fig. 4b. We find that tissue dynamics within HT29 and BC52 spheroids is governed by a positive flow-alignment parameter (ξ ≈ 0.5) while in HCT116 spheroids shear-alignment of cells is less dominant (ξ < 0.3) and potentially even negative (Fig. 4c). We also gain some additional information about the magnitude of active stress inside aggregates, where cell divisions inside HCT116 spheroids produce on average ζ = 100–200 Pa (Fig. 4c), thus confirming our previous experimental estimate based on ζ = ζ+TM/TC.
 | ||
Fig. 4 (a) Cell alignment Ψ in the core and close to the surface of spheroids of size R = 300 μm using simulation parameters estimated from experimental data (see Section III in the ESI†). (b) Posterior distributions p(ζ,ξ|X) of activity ζ and flow-alignment parameter ξ inferred from cell orientations inside HCT116 (green) and HT29/BC52 spheroids (magenta) using σ = 0.2. Based on the available data,12,26 we estimated X = [log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψexpc > 0.1, log Ψexpc > 0.1, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψexps = 0] for HT29/BC52 spheroids and X = [log Ψexps = 0] for HT29/BC52 spheroids and X = [log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψexpc = 0, log Ψexpc = 0, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψexps < −0.4] for HCT116. (c and d) Marginal distributions p(ξ|X) and p(ζ|X). Ψexps < −0.4] for HCT116. (c and d) Marginal distributions p(ξ|X) and p(ζ|X). | ||
IV. Conclusion
We have investigated how radial flows and active stresses affect cell alignment inside proliferating multicellular spheroids using three-dimensional active nematic droplets as a model system. Cell orientation and flows inside aggregates are described by a continuous director n and velocity field u, which follow the hydrodynamic equations of motion of active nematics. Diffusive transport of metabolites creates proliferation gradients across spheroids, where cells close to the surface have sufficient access to metabolites and divide, while metabolites are depleted in the core of spheroids and cells die. Since cell division/death is associated with a mass source/sink and extensile/contractile active stress along the cell orientation axis, proliferation gradients induce radial cell flows and activity gradients inside spheroids.We show that converging cell flows inside steady-state spheroids can promote radial or circumferential cell alignment, depending on the sign of the flow-alignment parameter ξ, a tissue parameter quantifying how cell orientations respond to shear-flows. The magnitude of shear-driven alignment scales with ξ and with the strain rate, the latter reaching a maximum at the surface and decreasing towards the core.
Active stress, on the other hand, creates a well-known hydrodynamic instability which leads to a chaotic steady state termed active turbulence. Activity gradients impact the average director field orientation inside spheroids in two ways: first, smooth variations between contractile stress in the core and extensile stress at the surface of spheroids drive radial cell alignment by creating flows which reorient the director field.27 The second contribution is active anchoring created by the sudden drop of extensile activity across the interface of spheroids, which are embedded in a passive fluid. The resulting sharp activity gradients at the surface induce flows which rotate the director field parallel to the interface, thus creating strong tangential surface alignment. Therefore gradients in active stress are responsible for radial core alignment and tangential surface alignment.
Depending on the relative strength of flow-driven shear-alignment and activity induced alignment, we find three distinct cell orientation regimes inside spheroids: for small activity, cell orientation is either tangential throughout the aggregate for ξ < ξc or radial for ξ > ξc > 0. If active stress becomes sufficiently large, ζ > ζc(ξ), one recovers spheroids with radial core alignment and tangential surface alignment (Fig. 3d).
The cell orientation profile inside aggregates significantly affects the stress distribution and short-time response of spheroids to external pressure jumps.12 It has also been shown that the elongation and orientation of cells within fibrosarcoma spheroids contribute to invasive behaviour by priming cells at the spheroid periphery to exhibit the correct morphology and polarisation for effective invasion into the surrounding matrix.48 The activity level and flow alignment properties of cellular aggregates could thus be used as control parameters to guide the migratory behaviour of spheroids and their mechanical response to changes in their environment.
Furthermore, we apply our model to experimental systems of freely grown HCT116, HT29 and BC52 spheroids to infer distributions of tissue parameters ξ and ζ based on the distribution of cell orientations inside spheroids. We find a significant difference in shear-alignment across different systems, with ξ ≈ 0.5 for HT29/BC52 spheroids, while for HCT116 spheroids shear-alignment ξ < 0.3 is less dominant and potentially even negative. It is of interest to compare these results with previous measurements of cell motion in two-dimensional systems, which indicated that cell orientation and flows in dense monolayers of myoblasts and epithelial cells are governed by a negative flow-alignment parameter ν, which corresponds to ξ > 0.22,23 This suggests that the same biomechanical mechanisms that cause flow-induced realignment of cells in monolayers may play an important role in three-dimensional tissue organisation.
In this paper we have focused on tissue dynamics in the hydrodynamic limit, where cell aggregates are described as a viscous fluid on long time scales. This continuum model could be easily generalized to viscoelastic spheroids by also including an elastic response on time scales smaller than a characteristic relaxation time τ. The viscoelastic relaxation time of cell aggregates, which is typically on the order of τ ≈ 5–40 min,49,50 is much smaller than typical cell-cycle times of TC ≈ 20 h, thus elastic contributions should be negligible on the time scales of freely grown spheroids. However, cell compressibility and the elastic properties of spheroids become important when they are subject to fast environmental changes, such as external pressure jumps.12,14,51 Mechanical confinement or compressive stress also alters proliferation profiles inside spheroids, where k+ decreases with increasing pressure, while k− stays approximately constant.13,52 Our model could also be used to study systems in which the surface tension of spheroids is sufficiently small that active stress can strongly deform spherical aggregates. This would allow avascular spheroids to overcome diffusion-limited, spherical growth by forming protrusions, thereby creating a branched network structure that grows indefinitely in environments with an unlimited supply of nutrients.
We hope that recent developments in experimental techniques and data processing will permit the measurement of 3D cell orientations inside aggregates with high spatial and temporal resolution in the future. This would allow the inference of more complex dynamics, including features like non-linear relationships between proliferation rate  and metabolite concentration m or spatial variations of ξ within aggregates. Furthermore, data with a sufficient temporal resolution would allow the testing of hypotheses relating to the underlying dynamics of cells, such as a possible dependence of intrinsic activity ζ0 or flow-alignment ξ on internal cell states, giving rise to time-dependent parameters ζ*(t) and ξ(t), which could be inferred from the cell alignment profiles. Here we highlight the potential of active fluid theories to model complex biological systems and show that cell orientation profiles in proliferating spheroids can be used to extract dynamical tissue parameters, which are otherwise difficult to measure directly.
and metabolite concentration m or spatial variations of ξ within aggregates. Furthermore, data with a sufficient temporal resolution would allow the testing of hypotheses relating to the underlying dynamics of cells, such as a possible dependence of intrinsic activity ζ0 or flow-alignment ξ on internal cell states, giving rise to time-dependent parameters ζ*(t) and ξ(t), which could be inferred from the cell alignment profiles. Here we highlight the potential of active fluid theories to model complex biological systems and show that cell orientation profiles in proliferating spheroids can be used to extract dynamical tissue parameters, which are otherwise difficult to measure directly.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project was funded by the European Commissions Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 812780.References
- B. Alberts, Molecular Biology of the Cell, Garland Science, 2008 Search PubMed.
- T. D. Pollard and G. G. Borisy, Cellular motility driven by assembly and disassembly of actin flaments, Cell, 2003, 112(4), 453–465 CrossRef CAS.
- M. Dogterom, J. W. Kerssemakers, G. Romet-Lemonne and M. E. Janson, Force generation by dynamic microtubules, Curr. Opin. Cell Biol., 2005, 17(1), 67–74 CrossRef CAS.
- F. Hirschhaeuser, H. Menne, C. Dittfeld, J. West, W. Mueller-Klieser and L. A. Kunz-Schughart, Multicellular tumor spheroids: an underestimated tool is catching up again, J. Biotechnol., 2010, 148(1), 3–15 CrossRef CAS.
- N. Jagiella, B. Müller, M. Müller, I. E. Vignon-Clementel and D. Drasdo, Inferring growth control mechanisms in growing multi-cellular spheroids of NSCLC cells from spatialtemporal image data, PLoS Comput. Biol., 2016, 12(2), e1004412 CrossRef.
- G. Lee, G. Leech, M. J. Rust, M. Das, R. J. McGorty and J. L. Ross, et al., Myosin-driven actin-microtubule networks exhibit self-organized contractile dynamics, Sci. Adv., 2021, 7(6), eabe4334 CrossRef.
- Y. I. Yaman, E. Demir, R. Vetter and A. Kocabas, Emergence of active nematics in chaining bacterial biofilms, Nat. Commun., 2019, 10(1), 1–9 CrossRef.
- T. B. Saw, A. Doostmohammadi, V. Nier, L. Kocgozlu, S. Thampi and Y. Toyama, et al., Topological defects in epithelia govern cell death and extrusion, Nature, 2017, 544(7649), 212–216 CrossRef PubMed.
- R. Mueller, J. M. Yeomans and A. Doostmohammadi, Emergence of active nematic behavior in monolayers of isotropic cells, Phys. Rev. Lett., 2019, 122(4), 048004 CrossRef PubMed.
- G. Duclos, C. Erlenkämper, J. F. Joanny and P. Silberzan, Topological defects in confined populations of spindle-shaped cells, Nat. Phys., 2017, 13(1), 58–62 Search PubMed.
- T. B. Saw, W. Xi, B. Ladoux and C. T. Lim, Biological tissues as active nematic liquid crystals, Adv. Mater., 2018, 30(47), 1802579 CrossRef.
- M. Delarue, J. F. Joanny, F. Jülicher and J. Prost, Stress distributions and cell flows in a growing cell aggregate, Interface Focus, 2014, 4(6), 20140033 CrossRef.
- F. Montel, M. Delarue, J. Elgeti, D. Vignjevic, G. Cappello and J. Prost, Isotropic stress reduces cell proliferation in tumor spheroids, New J. Phys., 2012, 14(5), 055008 CrossRef.
- K. Alessandri, B. R. Sarangi, V. V. Gurchenkov, B. Sinha, T. R. Kieling and L. Fetler, et al., Cellular capsules as a tool for multicellular spheroid production and for investigating the mechanics of tumor progression in vitro, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(37), 14843–14848 CrossRef CAS.
- D. Marenduzzo, E. Orlandini and J. M. Yeomans, Hydrodynamics and rheology of active liquid crystals: a numerical investigation, Phys. Rev. Lett., 2007, 98(11), 118102 CrossRef CAS.
- A. Doostmohammadi, S. P. Thampi, T. B. Saw, C. T. Lim, B. Ladoux and J. M. Yeomans, Celebrating Soft Matter's 10th Anniversary: Cell division: a source of active stress in cellular monolayers, Soft Matter, 2015, 11(37), 7328–7336 RSC.
- R. A. Simha and S. Ramaswamy, Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles, Phys. Rev. Lett., 2002, 89(5), 058101 CrossRef.
- C. Blanch-Mercader, V. Yashunsky, S. Garcia, G. Duclos, L. Giomi and P. Silberzan, Turbulent dynamics of epithelial cell cultures, Phys. Rev. Lett., 2018, 120(20), 208101 CrossRef CAS PubMed.
- A. N. Beris and B. J. Edwards, Thermodynamics of flowing systems with internal microstructure, Oxford University Press, 1994, vol. 36 Search PubMed.
- D. Marenduzzo, E. Orlandini, M. E. Cates and J. M. Yeomans, Steady-state hydrodynamic instabilities of active liquid crystals: Hybrid lattice Boltzmann simulations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76(3), 031921 CrossRef CAS PubMed.
- M. Martin and T. Risler, Viscocapillary instability in cellular spheroids, New J. Phys., 2021, 23(3), 033032 CrossRef.
- B. Aigouy, R. Farhadifar, D. B. Staple, A. Sagner, J. C. Röper and F. Jülicher, et al., Cell flow reorients the axis of planar polarity in the wing epithelium of Drosophila, Cell, 2010, 142(5), 773–786 CrossRef CAS PubMed.
- G. Duclos, C. Blanch-Mercader, V. Yashunsky, G. Salbreux, J. F. Joanny and J. Prost, et al., Spontaneous shear flow in confined cellular nematics, Nat. Phys., 2018, 14(7), 728–732 Search PubMed.
- R. Etournay, M. Popovic, M. Merkel, A. Nandi, C. Blasse and B. Aigouy, et al., Interplay of cell dynamics and epithelial tension during morphogenesis of the Drosophila pupal wing, eLife, 2015, 4, e07090 Search PubMed.
- M. Merkel, R. Etournay, M. Popovic, G. Salbreux, S. Eaton and F. Jülicher, Triangles bridge the scales: Quantifying cellular contributions to tissue deformation, Phys. Rev. E, 2017, 95(3), 032401 CrossRef.
- A. Desmaison, L. Guillaume, S. Triclin, P. Weiss, B. Ducommun and V. Lobjois, Impact of physical confinement on nuclei geometry and cell division dynamics in 3D spheroids, Sci. Rep., 2018, 8(1), 1–8 CAS.
- L. J. Ruske and J. M. Yeomans, Activity gradients in two- and three-dimensional active nematics, Soft Matter, 2022, 18(30), 5654–5661 RSC.
- M. L. Blow, S. P. Thampi and J. M. Yeomans, Biphasic, lyotropic, active nematics, Phys. Rev. Lett., 2014, 113(24), 248303 CrossRef PubMed.
- L. J. Ruske and J. M. Yeomans, Morphology of active deformable 3D droplets, Phys. Rev. X, 2021, 11(2), 021001 CAS.
- L. Giomi, Geometry and topology of turbulence in active nematics, Phys. Rev. X, 2015, 5(3), 031003 Search PubMed.
- R. Alert, J. F. Joanny and J. Casademunt, Universal scaling of active nematic turbulence, Nat. Phys., 2020, 16(6), 682–688 Search PubMed.
- S. P. Thampi and J. M. Yeomans, Active turbulence in active nematics, Eur. Phys. J.: Spec. Top., 2016, 225(4), 651–662 Search PubMed.
- M. Eisenberg and R. Guy, A proof of the hairy ball theorem, Am. Math. Monthly, 1979, 86(7), 571–574 CrossRef.
- A. Opathalage, M. M. Norton, M. P. Juniper, B. Langeslay, S. A. Aghvami and S. Fraden, et al., Self-organized dynamics and the transition to turbulence of confined active nematics, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(11), 4788–4797 CrossRef.
- T. Gao, M. D. Betterton, A. S. Jhang and M. J. Shelley, Analytical structure, dynamics, and coarse graining of a kinetic model of an active fluid, Phys. Rev. Fluids, 2017, 2(9), 093302 CrossRef.
- Y. N. Young, M. J. Shelley and D. B. Stein, The many behaviors of deformable active droplets, Math. Biosci. Eng., 2021, 18(3), 2849–2881 Search PubMed.
- L. N. Carenza, G. Gonnella, D. Marenduzzo and G. Negro, Rotation and propulsion in 3D active chiral droplets, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(44), 22065–22070 CrossRef.
- R. Yerushalmi, R. Woods, P. M. Ravdin, M. M. Hayes and K. A. Gelmon, Ki67 in breast cancer: prognostic and predictive potential, Lancet Oncol., 2010, 11(2), 174–183 CrossRef PubMed.
- A. Sakaue-Sawano, H. Kurokawa, T. Morimura, A. Hanyu, H. Hama and H. Osawa, et al., Visualizing spatiotemporal dynamics of multicellular cell-cycle progression, Cell, 2008, 132(3), 487–498 CrossRef PubMed.
- R. M. Sutherland, Cell and environment interactions in tumor microregions: the multicell spheroid model, Science, 1988, 240(4849), 177–184 CrossRef CAS PubMed.
- J. Laurent, C. Frongia, M. Cazales, O. Mondesert, B. Ducommun and V. Lobjois, Multicellular tumor spheroid models to explore cell cycle checkpoints in 3D, BMC Cancer, 2013, 13(1), 1–12 CrossRef.
- K. E. LaRue, M. Khalil and J. P. Freyer, Microenvironmental regulation of proliferation in multicellular spheroids is mediated through differential expression of cyclin-dependent kinase inhibitors, Cancer Res., 2004, 64(5), 1621–1631 CrossRef CAS.
- W. Lee, N. Kalashnikov, S. Mok, R. Halaoui, E. Kuzmin and A. J. Putnam, et al., Dispersible hydrogel force sensors reveal patterns of solid mechanical stress in multicellular spheroid cultures, Nat. Commun., 2019, 10(1), 1–14 CrossRef PubMed.
- R. Eidukevicius, D. Characiejus, R. Janavicius, N. Kazlauskaite, V. Pasukoniene and M. Mauricas, et al., A method to estimate cell cycle time and growth fraction using bromodeoxyuridine-flow cytometry data from a single sample, BMC Cancer, 2005, 5(1), 1–11 CrossRef PubMed.
- M. Delarue, F. Montel, O. Caen, J. Elgeti, J. M. Siaugue and D. Vignjevic, et al., Mechanical control of cell flow in multicellular spheroids, Phys. Rev. Lett., 2013, 110(13), 138103 CrossRef PubMed.
- S. Nam and O. Chaudhuri, Mitotic cells generate protrusive extracellular forces to divide in three-dimensional microenvironments, Nat. Phys., 2018, 14(6), 621–628 Search PubMed.
- A. A. Lucio, A. Mongera, E. Shelton, R. Chen, A. M. Doyle and O. Campas, Spatiotemporal variation of endogenous cell-generated stresses within 3D multicellular spheroids, Sci. Rep., 2017, 7(1), 1–11 Search PubMed.
- A. M. J. Valencia, P. H. Wu, O. N. Yogurtcu, P. Rao, J. DiGiacomo and I. Godet, et al., Collective cancer cell invasion induced by coordinated contractile stresses, Oncotarget, 2015, 6(41), 43438 Search PubMed.
- K. Guevorkian, M. J. Colbert, M. Durth, S. Dufour and F. Brochard-Wyart, Aspiration of biological viscoelastic drops, Phys. Rev. Lett., 2010, 104(21), 218101 CrossRef.
- P. Marmottant, A. Mgharbel, J. Käfer, B. Audren, J. P. Rieu and J. C. Vial, et al., The role of fluctuations and stress on the effective viscosity of cell aggregates, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(41), 17271–17275 CrossRef CAS.
- M. Delarue, F. Montel, D. Vignjevic, J. Prost, J. F. Joanny and G. Cappello, Compressive stress inhibits proliferation in tumor spheroids through a volume limitation, Biophys. J., 2014, 107(8), 1821–1828 CrossRef CAS PubMed.
- A. Desmaison, C. Frongia, K. Grenier, B. Ducommun and V. Lobjois, Mechanical stress impairs mitosis progression in multi-cellular tumor spheroids, PLoS One, 2013, 8(12), e80447 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01239a |
| This journal is © The Royal Society of Chemistry 2023 |