Multivalent binding proteins can drive collapse and reswelling of chromatin in confinement†
Sougata
Guha
 and
Mithun K.
Mitra
and
Mithun K.
Mitra
 *
*
Department of Physics, Indian Institute of Technology Bombay, Mumbai 400076, India. E-mail: mithun@phy.iitb.ac.in
First published on 9th December 2022
Abstract
Collapsed conformations of chromatin have been long suspected of being mediated by interactions with multivalent binding proteins, which can bring together distant sections of the chromatin fiber. In this study, we use Langevin dynamics simulation of a coarse grained chromatin polymer to show that the role of binding proteins can be more nuanced than previously suspected. In particular, for chromatin polymer in confinement, entropic forces can drive reswelling of collapsed chromatin with increasing binder concentrations, and this reswelling transition happens at physiologically relevant binder concentrations. Both the extent of collapse, and also of reswelling depends on the strength of confinement. We also study the kinetics of collapse and reswelling and show that both processes occur in similar timescales. We characterise this reswelling of chromatin in biologically relevant regimes and discuss the non-trivial role of multivalent binding proteins in mediating the spatial organisation of the genome.
Introduction
The physical principles behind the three-dimensional organisation of the genome remain an interesting question in cell biology. The packaging of the chromatin polymer inside the confined space of a nucleus requires organisation and compaction at multiple hierarchical scales, while respecting topological and functional constraints. The organisation of chromatin inside the eukaryotic nucleus is a complex process, mediated by interactions of the DNA with multiple proteins. The organisation is dynamic,1–3 and changes in response to the environmental signals,4,5 epigenetic state markers,6,7 and cell cycle stages,8,9 among others.One of the important motifs of this structural organisation is the formation of long-range contacts between distant chromatin segments, mediated by DNA–binding proteins. An important characteristic of many of these proteins is multivalency, with the presence of two or more DNA binding domains.10 In general, the phenomenon of multivalency is recognised to be an widespread hallmark of interactions between chromatin and binding proteins.11 For example, HP1 and PRC1 are two proteins which brings together distal chromatin segments through gene specific interactions with chromatin.12–14 While HP1 proteins are known to vary their binding valencies through oligomerization,15 PRC1 proteins are observed to simultaneously localize at least five or more distant target sites.16 The CCCTC-binding factor (CTCF) protein has also been implicated in loop formation.17–20 CTCF contains 11 zinc-finger domains, and is known to bind to multiple DNA motifs through a combinatorial clustering of these domains, with the zinc-finger domains 1–2, 4–7, and 8–11 hypothesised to function as discrete DNA binding subdomains.21 Further, proteins of the Structural Maintenance of Chromosomes (SMC) family, such as cohesin or condensin bring together distant segments of chromatin through loop extrusion.22–25 In addition, many transcription factors are known to contain multiple chromatin binding domains, and can thus aggregate multiple nucleosomes.10 These long chromatin loops, mediated by different families of DNA binding proteins, are known to play an important role in the structural organisation of the genome,26–28 as well as in regulating gene expression.29 Modifications in the structural organisation of chromatin has also been associated with various diseases.5,30
Experiments such as Hi-C and its variants have yielded a wealth of genome-wide data about long-range contacts,31–34 and various polymer models have been proposed to integrate these experimental observations into a fundamental understanding of the physical principles of genome assembly.35–38 Different variants of self-avoiding polymer models have been used to reproduce different aspects of chromosome organisation, such as the emergence of chromosome domains and compartments,39,40 Topologically Associated Domains (TADs),41,42 interactions of chromatin with the nuclear lamina,43,44 and to understand the role of looping proteins in the formation and maintenance of chromatin loops.45
Chromatin folding in presence of diffusible binding proteins have been studied extensively. A widely used class of models for describing chromatin organisation inside nucleus is known as the “Strings and Binders Switch” (SBS) model.39,46 In this model the chromatin is assumed to be a self-avoiding polymer which consists of binding sites for diffusing binder proteins. These binders can generate different stable configurations of chromatin polymer through attachments to the chromatin backbone. The chromatin polymer is found to undergo a coil-globule like transition from an open state to folded state as the binder concentration is increased.39,47,48 The contact probability exponents in these studies are consistent with experimental observations.49 On the other hand, stiffness of chromatin polymer and switching of binders between ‘on’ state and ‘off’ state play an important role in determining the structure of the clusters of chromatin formed by binders, and their kinetics.50–52 Bridging by different multivalent transcription factors has shown separate clusters to form by different transcription factors and hence generates TADs.53 Implicit bridging through direct interactions between monomers depending on their epigenetic states has also been studied.40,41,54–57 Other than forming different chromatin structure like loops, rosettes, TADs etc., distribution of epigenetic patterns on chromatin leads to coexistence or compartmentalization of different polymer domains (polymer–polymer phase separation).
A striking feature of chromatin organisation is the presence of structural and functional compartments within the nucleus.29,58,59 At the largest scales, the nuclear volume confines the space available to chromosomes. However, confinement occurs at multiple smaller scales as well. Hi-C contact maps have shown that chromatin segregates into two types of distinct compartments – A and B – which represent euchromatin and heterochromatin regions respectively.18,31 Each chromosome has also been shown to occupy its own distinct space, known as chromosome territories.49,60 Within a chromosome, as revealed by Hi-C experiments, TADs represent megabasepair long regions enriched in internal contacts which play a key role in gene regulation.40,61,62 The boundaries of these domains have been shown to be associated with CTCF proteins.20 Confinement of chromosomes has been recognised to be a potential regulator of both chromosome structure43,63 and dynamics.64 In recent years, much research has focused on dynamic phase separated condensates in the nucleus, such as transcription factories associated with RNA polymerase II,65 and heterochromatin foci.66
While the role of DNA–binding protein complexes in driving compaction of the chromosome has been studied in detail,39,47,48,50–53 these studies neglect the role of spatial confinement. For polymers in periodic boundary systems, the box size is necessarily larger than the free polymer radius of gyration Rg, to exclude the possibility of unphysical conformations due to binder interactions with spatially distant monomers across the periodic boundary, which can arrest the polymer into a stretched conformation.67 This necessity of large box size imposes computational constraints on the binder concentrations that can be accessed in periodic boundary simulations. On the contrary, for confined polymer systems, in addition to the biological relevance of confined chromatin, one can access higher concentrations of binding proteins to systematically investigate the role of multivalency on polymer conformations. Multivalent counterions are known to drive non-monotonic behaviour of polymer sizes in polyelectrolytes,68–70 and multivalent DNA–binding proteins can play a similar role within the nucleus at higher concentrations. Compartmental organisation of nuclear material enable large fluctuations in concentration of DNA–binding proteins through local accumulation, which can in turn influence chromatin configuration. In this work, we systematically investigate the effect of multivalent DNA binder proteins on conformations of confined chromatin, and show that chromatin–binder interactions can lead to rich and non-trivial behaviour of interphase chromosomes.
Model and methods
In this paper, we implement a variant of the SBS model by modeling chromatin as a self-avoiding flexible polymer chain consisting of 256 monomers. The interaction between the polymer beads can simply be expressed as a combination of finitely extensible nonlinear elastic (FENE) bonds and Weeks–Chandler–Anderson (WCA) potential.71 The FENE potential between nearest neighbour beads is given by,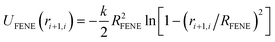 | (1) |
Self-avoidance between monomer beads (and also between two binder beads) is implemented by a WCA interaction72 given by,
 | (2) |
The attractive interaction between binders and monomers is maintained by a truncated and shifted Lennard-Jones potential, consistent with existing binder models, and is given by,
 | (3) |
Different DNA binding proteins have been reported to have an array of binding valencies, ranging from two up to as large a number as ten.10 In line with the original SBS model,39 we choose a binder valency of six for the binder proteins. A binder–monomer bond is considered to have formed instantaneously if they are separated by a distance less than rc and the binder is attached to less than 6 monomers (see ESI† for details).
The chromatin polymer as well as the binders are assumed to be confined within a sphere of radius R (Fig. 1). Confinement is implemented as a soft repulsive wall modeled by the WCA potential, eqn (2). The separation between the wall and the particle (monomer bead or binder) is measured from the closest point of the wall to the particle. We choose confinement radii to conform with the biologically relevant chromatin density inside nucleus, estimated to be in the range 0.01–0.25 (see ESI† for details). We choose confinement radii between R = 6.5σ − 15σ consistent with these estimates.
In our simulations, the energy and length scales are scaled by ε and σ respectively. All length scales – including confinement radii and polymer sizes – are reported in units of σ throughout the manuscript. A choice of σ corresponds to a choice of the coarse graining scale, with polymer based models for chromatin having reported a range of values from nucleosome level resolution (∼200 bp)73,74 to 100 kbp level resolution.47 We choose a coarse graining scale of 40 kbp,41 which implies a bead size of σ = 70 nm (see ESI† for details). The simulated polymer is thus around ∼10 Mb, and hence the confinement can be interpreted as that at the level of chromatin A/B compartments.31,75 For simplicity, we choose the binding protein size to be the same as this coarse-grained chromatin bead size.47,48 For the CTCF protein, recent experiments estimate an abundance in human cells of the order of ∼105 per cell,76 which suggests a physiologically relevant number density in the range ∼0.04–0.3 in our simulation scale (see ESI† for details). In our simulations, we explore binder densities consistent with both this experimentally estimated density range,76 as well as previously reported theoretical studies.39,47,48,51 Unless stated otherwise, we simulated at least 5 independent runs with each run being ∼105τ (∼2 × 108 simulation steps) long where τ denotes our simulation time unit (see ESI† for details). All equilibrium properties are calculated by averaging over 1000 independent configurations.
Results
A reswelling transition of chromatin
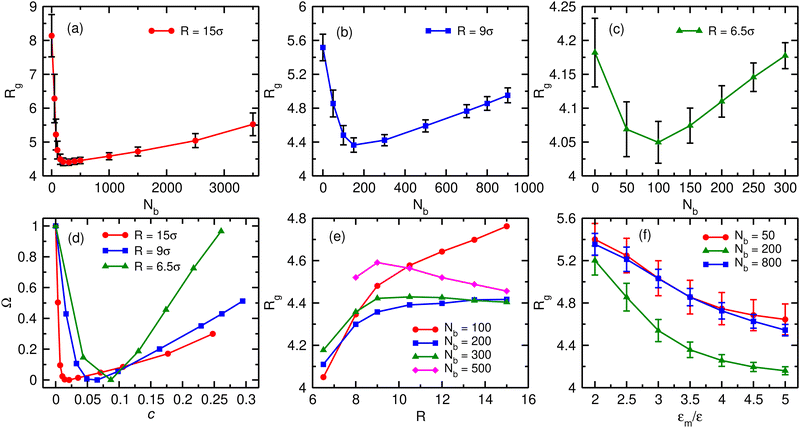
We first characterise the equilibrium properties of the chromatin polymer for different compaction levels and with differing binder numbers. For the largest radius of confinement (R = 15σ, ϕ = 0.01), as shown in Fig. 2a, in the absence of binders the polymer adopts a semi-open conformation (R0g ≃ 8.1σ, R0g/Rfreeg ≃ 0.6, where Rfreeg denotes the radius of gyration for the unconfined polymer). As binders are introduced, the polymer collapses due to binder-mediated long-range interactions between distant polymer segments. For R = 15σ, the minimum radius of gyration, Rcg ≃ 4.4σ is achieved at a critical binder number of Nminb = 300 with number density cmin ≃ 0.02. Contrary to existing models of binder mediated collapse however, on further increasing the number of binders, the polymer does not stay in the maximally collapsed conformation, but starts to reswell with increasing binder numbers. The extent of reswelling depends on the number of binders, but also on the confinement radius. For R = 15σ, where the polymer volume fraction is low, the collapse occurs much faster, followed by a slow reswelling. This generic nature of a collapse from a semi-open state to a compact conformation, followed by a reswelling on further increasing binder concentrations is observed at all values of the confinement (Fig. 2b for R = 9σ, and Fig. 2c for R = 6.5σ). The critical concentration required for the collapse of the polymer increases with increasing confinement. Note that the fully collapsed conformation corresponds to the maximisation of binder mediated long range loops. The number of binders required for this maximisation of loops depends only on the size of the polymer, and not on the confinement radius. Thus, for a given polymer size, this similar number of binders translates to larger concentrations for more confined systems and hence the critical binder density (cmin) increases with stronger confinement. Further, with increasing confinement, the polymer is increasingly compact even in the absence of binders, and hence the relative change in Rg from the zero-binder case to the maximally compact conformation decreases with stronger confinement. Conversely, the relative extent of reswelling with increasing binder concentration is much higher for stronger confinement, with radius of gyration reverting to the zero-binder value for R = 6.5σ. In order to take into account this differential degrees of collapse for different values of the confinement radius, we define a compaction parameter,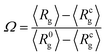 | (4) |
While we choose a polymer of size N = 256 throughout this work, we verified that the generic nature of the reswelling is not an artefact of the finite size of the polymer (Fig. S1, ESI†), nor do the results reported here depend sensitively on the exact binder valency (Fig. S2, ESI†). Further, while we assumed that binder sizes are equal to the monomer size, the qualitative results of our manuscript do not depend on this assumption (Fig. S3, ESI†). Finally, the assumption of a flexible polymer is also not crucial to this reswelling transition, which we verify to be present for a semiflexible polymer model of chromatin as well (Fig. S4, ESI†).
This reswelling transition suggests that the polymer size (Rg) can be controlled by changing the geometric confinement radius, and hence the local binder concentration, while keeping binder numbers the same. This is shown in Fig. 2e for different values of the binder number Nb. For low number of binders, when the chromatin polymer is in the semi-open state, it is expected that the polymer is distributed over the whole available volume, and hence Rg is expected to increase with increasing volume (and equivalently R). Evidently we found this to be true in presence of less number of binders (Nb = 100). As the binder number is increased (Nb ∼ 200–300), Rg tends to saturate with increasing confinement radius. This is due to the fact that the binder number is close to the critical binder number Nminb for larger values of the confinement radii and the polymer collapse into a compact state in these cases. Further increase in binder numbers results in a non-monotonic behaviour of the polymer size (Nb = 500). For strong confinement, Rg initially increases with increasing R. However, beyond a certain confinement radius, Rg starts to reduce with increasing R. This can be explained in terms of reswelling of the chromatin. For strong confinement Nb = 500 is significantly larger than Nminb corresponding to those confinement radii and thus the polymer is in reswollen state. On the other hand for large confinement radii Nb = 500 is close to Nminb for weak confinements and therefore the polymer is still in a moderately compact state resulting in lower Rg values. Thus changing the geometrical confinement radius can result in non-trivial behaviour of the chromatin size, for the same number of binding proteins. We note that while in our model, both the polymer and the binding proteins are confined, in principle, confinement of the chromatin polymer alone is sufficient to observe reswelling at physiological concentrations (Fig. S5, ESI†).
One parameter that may affect the chromatin structure strongly is the binding affinity of binders to chromatin. Fig. 2f shows the variation of Rg for range of interaction strength (εm) between binders and monomers, for three different binder numbers. As is expected, for any fixed binder number, the polymer Rg decreases with increasing εm. This is because higher εm means the bonds are stronger and long-lived and thus collapse the chromatin. However, for all values of the interaction strength, we observe a re-entrant behaviour, with the polymer size being smaller at Nb = 200 compared to the Nb = 50 and Nb = 800 cases. Thus, re-entrant behaviour of polymer size with increasing binder number is robust over all binder–monomer interaction energy scales that we investigated.
Binder mediated reswelling is driven by competition between energy and entropy
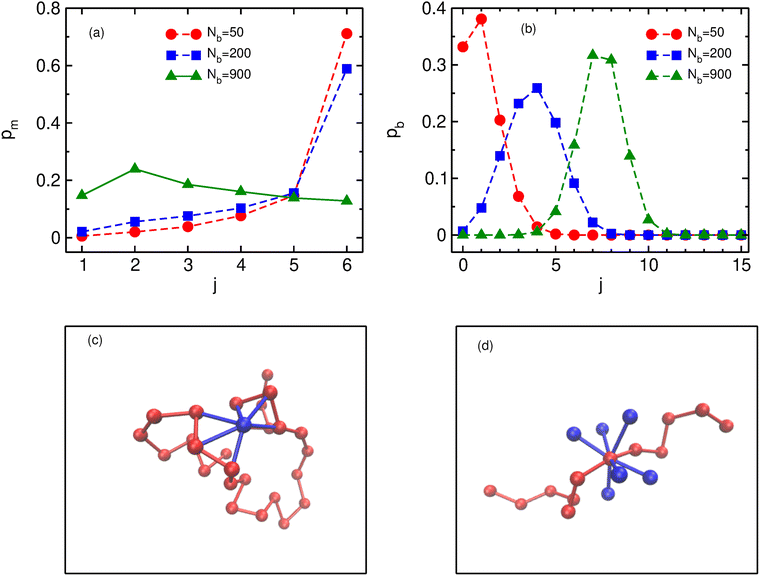
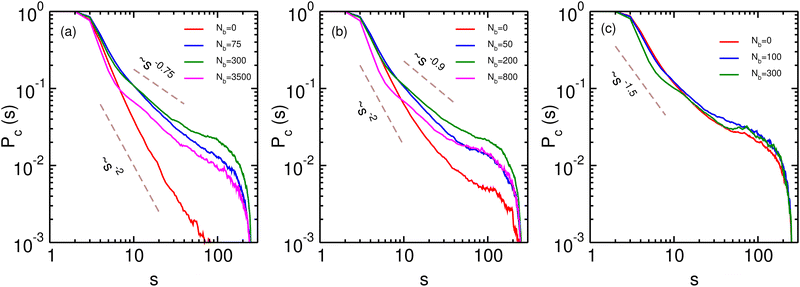
In order to understand the role of binders in the collapse and reswelling of the polymer, we plot the probability pm(j) of having j monomers bound to a single binder protein (Fig. 3a), and the probability pb(j) of having j binders bound to a single monomer (Fig. 3b), for different binder numbers. The plots are shown for the intermediate confinement case, R = 9σ, but the general trend holds true for any strength of confinement. When the number of binders is very low (Nb = 50), the polymer is in a semi-open conformation (Ω = 0.5), and most binders have the maximum possible number of monomers bound to them, resulting in a distribution of pm peaked at 6 monomers. However, because of the low number of binders, most monomers have none or one binder bound to it (Fig. 3b), resulting in very few long-range contacts, as expected for this semi-open conformation. In this conformation state therefore, most binders are surrounded by a cloud of monomers, as shown in Fig. 3c. If we now consider the case of the critical binder number for which we observe the most compact conformation, Nminb = 200, the distribution of the number of monomers bound to a single binder is qualitatively similar to the Nb = 50 case, with most binders saturating their maximum valency of 6 monomers. However, for this compact conformation, the pb distribution undergoes a significant change from the low binder regime, with a distribution peaked at around 4 binders, and very few monomers remain which have at most one binder bound to them. At this critical binder number therefore, the polymer–binder system achieves an optimum for the compact conformation. On increasing binder numbers past this critical value, there is now an excess of binders, which results in a drastic change in the pm distribution, with very few binders now achieving the maximum valency. Conversely, the distribution of pb shifts even further to the right, resulting in each monomer acquiring a cloud of binders surrounding it, as shown in Fig. 3d. Since each monomer is now surrounded by a binder cloud, binders no longer require long-range contacts to minimise their energy, and hence the polymer reswells as it becomes more entropically favorable. Further, the binder cloud surrounding a monomer increases the effective size of a single monomer, and hence excluded volume forces also contribute to the reswelling.We now turn to the contact probability distributions in order to understand the coupled effects of binder concentration and confinement for the (semi-)open, compact and reswollen conformations. Generically, the contact probability scales with genomic distance as, Pc(s) ∼ 1/sα, where the exponent α in this case depends on both the binder concentration as well as confinement. We first consider the case of weak confinement, R = 15σ, shown in Fig. 4a. In the absence of binders, the contact probability exponent goes as α ∼ 2.0, indicating the polymer conformation is similar to the open random SAW polymer.77 Close to the transition point for the collapsed conformation, Nb = Nminb = 300, the contact probability exponent is α ∼ 0.75, which is in the biological range observed in experiments. On increasing the binder concentrations (Nb = 3500), the polymer reswells, which is reflected in a corresponding increase in the exponent, α ∼ 0.9, indicating a decreased probability of contact between distant monomer segments. Note that for this case of weak confinement, biological constraints on the binder concentrations preclude a full reswelling of the polymer. In order to understand the equilibrium properties of the conformations of this partially reswollen conformation, we then compare it to the conformation at a pre-collapse binder concentration, Nb = 75 < Nminb, such that the radius of gyration of these two conformations are roughly similar (Rg(Nb = 3500) ≈ Rg(Nb = 75) ≃ 5.3σ). Firstly we note that for small genomic separations (s/σ < 10), the contact probabilities for the reswollen polymer are lower than the partially collapsed polymer, which can be understood by the presence of the binder cloud surrounding monomers in the reswollen case, as discussed above. At larger separations however, the contact probability exponent in both these cases are roughly similar, indicating that reswollen conformations are statistically similar to the open counterparts. For the case of intermediate confinement, R = 9σ, again in the absence of binders, the contact probability behaves similar to a semi-open conformation (α ∼ 2.0 for Nb = 0). At the collapsed conformation, the contact probability exponent becomes much smaller, α ∼ 0.9, reflecting the increased long-range contacts in this collapsed conformation. As the polymer reswells (Nb = 800), the contact probability itself becomes lower due to the presence of a binder cloud surrounding each monomer, although the exponent α in this case is roughly similar to the compact conformation. Similar features are observed for R = 6.5σ, although the determination of the exponent in this case is complicated due to a strong confinement induced collapse even when binders are absent, and consequently, a weak binder mediated collapse and reswelling.
The kinetics of collapse and reswelling
We now turn to the kinetics of the collapse and the reswelling of the chromatin polymer in order to investigate whether both of these processes can occur within biological timescales. We first look at the distributions of compaction times. At a given value of the confinement radius R, we allow the chromatin polymer to equilibrate in the absence of any binders (Nb = 0). We then instantaneously increase the number of binders to the critical binder number corresponding to maximum compaction (Nminb), and monitor the time evolution of the radius of gyration of the polymer (Rg(t)). The compaction time τc is defined as the minimum time at which Rg(t) reaches the equilibrium value Rcg ± ΔRcg, and the time-averaged 〈Rg〉t remains within this equilibrium range for the next 105(200τ) steps. The distributions as well as averages are done over 1000 independent runs in this case. The distributions (pc) of this τc for three different compaction radii are shown in Fig. 5a–c. The distributions of the compaction times are unimodal, with long tails. In order to reliably estimate the mean compaction times we fit the data with log-normal distributions. The mean compaction times increase with increasing radius of confinement, and are given by| 〈τc(R = 15)〉 ≃ 581τ 〈τc(R = 9)〉 ≃ 98τ 〈τc(R = 6.5)〉 ≃ 3.6τ |
Local binder concentrations in cells can be sensitively controlled by changing the strength of the geometric confinement (radius of the compartment). Here, we study the effect of varying confinement radius on the collapse timescales. We first characterise how mean collapse times τc change with changing confinement. For a given value of the confinement radius (R), the extent of collapse can be identified as the difference between the binder-free radius of gyration R0g and the final compaction value Rcg both of which depends explicitly on R. While R0g depends strongly on R, the variation of Rcg with confinement radius is comparatively smaller indicating a weaker dependence of Rcg on R. Therefore we use R0g − Rcg as a proxy for variation of confinement radius to determine how compaction time depends on confinement. We find that the mean collapse times scales with the extent of compaction as τc ∼ (R0g − Rcg)μ with μ = 1.45 ± 0.06 (Fig. 5d). Previous studies,78 in the absence of confinement, have reported compaction time scaling with polymer size with a similar exponent, τc ∼ N1.5. Confinement has a non-trivial effect on the scaling of polymer Rg with polymer size,64 and hence the extent of confinement R0g − Rcg provides a more robust characterisation of the compaction timescales.
We next ask whether binder mediated reswelling also occurs within comparable timescales. To check this, we initialise our system in the compact conformation, by equilibrating the chromatin polymer with Nminb binders. We then instantaneously increase the binder concentration to c = 0.2 for all values of the confinement radii R. This induces a reswelling of chromatin, and the reswelling time τr is defined similarly to τc by noting the minimum time taken to reach the equilibrium Rg and then fluctuate around this value for 200τ steps. Similar to compaction timescales, the distributions and averages are done over 1000 independent runs. The distributions of the reswelling times are again unimodal, and well-approximated by log-normal distributions (Fig. 5e–g). Note that since the concentration of binders is kept uniform, the extent of reswelling is different for different R (Ω15 = 0.2, Ω9 = 0.3, Ω6.5 = 0.7). For the case of maximal confinement, when c = 0.2 approaches the maximum possible reswelling (Ω ∼ 1), we note that the mean reswelling time 〈τr〉 ≃ 5〈τc〉. Irrespective of the extent of reswelling, we note that the mean reswelling times are comparable to the collapse timescales, suggesting that modulating local binder concentrations can lead to collapse and expansion of polymers within biological timescales.
Similarly to the collapse, we also characterise the scaling of the mean reswelling time with changing confinement radius. For a given confinement radius, we characterise the extent of reswelling by the difference between the reswelled radius of gyration Rrg and the compact radius of gyration Rcg. Therefore, similar to compaction times, in this case we use Rrg − Rcg as the proxy for variation of confinement. The reswelling time scales with the extent of reswelling as τr ∼ (Rrg − Rcg)ν with ν = 1.71 ± 0.07 (Fig. 5h). The reswelling exponent is thus slightly higher than the compaction exponent (ν > μ), and for all biologically relevant values of (R0/rg − Rcg), and equivalently of the confinement radius, the compaction and reswelling times are expected to be similar in magnitude, and hence both processes are expected to be physiologically relevant.
Discussion
We show, that contrary to existing models of binder protein mediated collapse of chromatin conformations, high concentrations of binders can in fact drive reswelling of chromatin. Our simulations show that while at low concentrations binders mediate collapse by forming loops between distant polymer segments which lowers the energy of these compact conformations, at larger concentrations there are enough binders that each monomer is surrounded by a binder cloud, and hence the polymer preferentially maximises entropy through semi-open swollen conformations. Additionally, we show that timescales of collapse are similar to timescales of reswelling, and hence both of these effects are expected to play an important role within cells.The coil-globule transition of chromatin in unconfined space has been well studied in the literature.39,47–52 For unconfined polymers (in periodic boundary conditions), the periodic box is necessarily large enough that accessing large binder concentrations has remained computationally challenging and hence the phenomenon of reswelling in these systems has remained unexplored. Introducing confinement of chromatin, in addition to being biologically relevant, allows us to explore these regions of high volume fractions, where a combination of entropic forces and self-avoidance drives reswelling of chromatin. We show that confinement of the chromatin polymer, and not necessarily binder proteins, allows us to access this previously unexplored region of parameter space. Reswelling of chromatin is observed when binder concentrations are large enough to dress the entire polymer backbone with a binder cloud, which screens interactions with other binders. We also note that binding proteins themselves often act in a cooperative manner,79 and assemblies of many proteins can regulate the strength of this screening by changing the effective strength of excluded volume interactions. Future experiments may provide more clarity on such screening effects on chromatin–binder conformations. Further, we note that the extent of reswelling, in unscaled units, is often quite small, especially for strong confinement. This is concomitant with the relatively small extent of collapse as well in strongly confined systems. Thus binder mediated collapse of chromatin can be weak or strong depending on the extent of confinement. Independent of this, our current work shows that the extent of reswelling is comparable to the extent of compaction, and are both modulated by the strength of confinement. Our study suggests that the reswelling of chromatin depends heavily on the confinement radius as well as presence of multivalent binding proteins, and the onset of reswelling appears at different binder density for different confinement radii even when the binder–chromatin interaction strength is unchanged.
Recent studies has also systematically investigated the collapse of the chromatin polymer via monomer–binder bridging in confinement,67 and the formation of long-lived, phase separated compartments through binder interactions.80 However the binders in these cases are mutually attractive, leading to formation of large cluster of binders and consequently no reswelling was observed. Another recent study involving implicit binders in the absence of excluded volume interactions among binders suggests that over-expression of binders can cause reswelling for the case of bivalent binders on a polymer chain where monomers can bind only a single binder.81 The absence of explicit binders, and consequently volume exclusion among binders, and the imposition of strict limits on the binder and monomer valencies limits the applications of this study to real systems. We believe that the entropic origins of the reswelling remain the same, however, multivalency of binders and volume exclusion represent additional physical forces that non-trivially affect the reswelling transition.
Our simulations show that the chromatin sizes and compaction can be sensitively controlled by changing the confinement radius. This offers a tantalising probability for the control of formation and stability of phase-separated condensates in the nucleus.59 Recent experiments have shown that CTCF is locally concentrated inside transcriptional condensates, and CTCF mediated looping is in fact an essential architectural prerequisite for the formation of such condensates.19 This is consistent with our simulations. We find that multivalent binding proteins are locally enriched within the polymer phase (with an average concentration 10–100 times higher inside the collapsed polymer phase as compared to the surrounding fluid). Fluctuations in the size of the compartment can then push local concentrations above or below the reswelling threshold, with an accompanying change in the structure of the chromatin polymer.
In summary, using a simple self-avoiding polymer model, we show that in the presence of confinement, multivalent binding proteins can either stabilise or destabilise the collapsed polymer conformation by varying the local binder density in the confined compartment. Our model has multiple simplifying assumptions – in particular, it neglects sequence heterogeneity and the partitioning of chromatin into heterochromatin and euchromatin regions, and also the role of crowding due to presence of binder proteins. Additionally, we make simplifying assumptions regarding the monomer valencies, where a monomer can bind to any number of binders, subject only to volume exclusion. Nevertheless, we believe that our coarse-grained model simulations, captures the qualitative physical mechanism underlying collapse and reswelling of the chromatin polymer and suggests a non-trivial role for binding proteins in regulating spatial organisation of chromatin.
Author contributions
M. K. M. designed the research. S. G. developed and carried out all simulations. S. G. and M. K. M. analysed all data, interpreted results, and wrote the article.Conflicts of interest
Authors declare no conflict of interests.Acknowledgements
SG and MKM acknowledge IIT Bombay for research funds and support. MKM acknowldges IIT Bombay Grant No. 14IRCCSG009 for financial support. SG and MKM thank Dibyendu Das and Ranjith Padinhateeri for helpful discussions.References
- H. A. Shaban and A. Seeber, Nucleic Acids Res., 2020, 48, 3423–3434 CrossRef CAS PubMed.
- T. Nozaki, R. Imai, M. Tanbo, R. Nagashima, S. Tamura, T. Tani, Y. Joti, M. Tomita, K. Hibino and M. T. Kanemaki, et al. , Mol. Cell, 2017, 67, 282–293 CrossRef CAS PubMed.
- E. I. Prieto and K. Maeshima, Essays Biochem., 2019, 63, 133–145 CrossRef CAS PubMed.
- A. I. Badeaux and Y. Shi, Nat. Rev. Mol. Cell Biol., 2013, 14, 211–224 CrossRef CAS.
- B. M. Turner, Philos. Trans. R. Soc., B, 2009, 364, 3403–3418 CrossRef CAS.
- M. W. Vermunt, D. Zhang and G. A. Blobel, J. Cell Biol., 2019, 218, 12–26 CrossRef CAS.
- G. J. Filion, J. G. van Bemmel, U. Braunschweig, W. Talhout, J. Kind, L. D. Ward, W. Brugman, I. J. de Castro, R. M. Kerkhoven and H. J. Bussemaker, et al. , Cell, 2010, 143, 212–224 CrossRef CAS PubMed.
- S. W. Criscione, M. De Cecco, B. Siranosian, Y. Zhang, J. A. Kreiling, J. M. Sedivy and N. Neretti, Sci. Adv., 2016, 2, e1500882 CrossRef.
- I. Solovei, K. Thanisch and Y. Feodorova, Curr. Opin. Cell Biol., 2016, 40, 47–59 CrossRef CAS PubMed.
- S. A. Lambert, A. Jolma, L. F. Campitelli, P. K. Das, Y. Yin, M. Albu, X. Chen, J. Taipale, T. R. Hughes and M. T. Weirauch, Cell, 2018, 172, 650–665 CrossRef CAS.
- A. J. Ruthenburg, H. Li, D. J. Patel and C. D. Allis, Nat. Rev. Mol. Cell Biol., 2007, 8, 983–994 CrossRef CAS.
- K. Isono, T. A. Endo, M. Ku, D. Yamada, R. Suzuki, J. Sharif, T. Ishikura, T. Toyoda, B. E. Bernstein and H. Koseki, Dev. Cell, 2013, 26, 565–577 CrossRef CAS.
- S. Schoenfelder, R. Sugar, A. Dimond, B.-M. Javierre, H. Armstrong, B. Mifsud, E. Dimitrova, L. Matheson, F. Tavares-Cadete and M. Furlan-Magaril, et al. , Nat. Genet., 2015, 47, 1179–1186 CrossRef CAS PubMed.
- S. Kundu, F. Ji, H. Sunwoo, G. Jain, J. T. Lee, R. I. Sadreyev, J. Dekker and R. E. Kingston, Mol. Cell, 2017, 65, 432–446 CrossRef CAS PubMed.
- S. Kilic, A. L. Bachmann, L. C. Bryan and B. Fierz, Nat. Commun., 2015, 6, 1–11 Search PubMed.
- S. Boyle, I. M. Flyamer, I. Williamson, D. Sengupta, W. A. Bickmore and R. S. Illingworth, Genes Dev., 2020, 34, 931–949 CrossRef CAS PubMed.
- J. R. Dixon, S. Selvaraj, F. Yue, A. Kim, Y. Li, Y. Shen, M. Hu, J. S. Liu and B. Ren, Nature, 2012, 485, 376–380 CrossRef CAS.
- S. S. Rao, M. H. Huntley, N. C. Durand, E. K. Stamenova, I. D. Bochkov, J. T. Robinson, A. L. Sanborn, I. Machol, A. D. Omer and E. S. Lander, et al. , Cell, 2014, 159, 1665–1680 CrossRef CAS.
- R. Lee, M.-K. Kang, Y.-J. Kim, B. Yang, H. Shim, S. Kim, K. Kim, C. M. Yang, B.-G. Min and W.-J. Jung, et al. , Nucleic Acids Res., 2021, 50, 207–226 CrossRef PubMed.
- J. Dekker and L. Mirny, Cell, 2016, 164, 1110–1121 CrossRef CAS PubMed.
- H. Nakahashi, K.-R. K. Kwon, W. Resch, L. Vian, M. Dose, D. Stavreva, O. Hakim, N. Pruett, S. Nelson and A. Yamane, et al. , Cell Rep., 2013, 3, 1678–1689 CrossRef CAS.
- J. Lee, J. Reprod. Dev., 2013, 59, 431–436 CrossRef CAS.
- F. Uhlmann, Nat. Rev. Mol. Cell Biol., 2016, 17, 399–412 CrossRef CAS.
- K. C. Yuen and J. L. Gerton, PLoS Genet., 2018, 14, e1007118 CrossRef PubMed.
- T. Terakawa, S. Bisht, J. M. Eeftens, C. Dekker, C. H. Haering and E. C. Greene, Science, 2017, 358, 672–676 CrossRef CAS.
- T. Misteli, Cell, 2020, 183, 28–45 CrossRef CAS.
- J. Dekker and T. Misteli, Cold Spring Harbor Perspect. Biol., 2015, 7, a019356 CrossRef.
- L. A. Mirny and I. Solovei, Nat. Rev. Mol. Cell Biol., 2021, 22, 439–440 CrossRef CAS PubMed.
- C. Lanctôt, T. Cheutin, M. Cremer, G. Cavalli and T. Cremer, Nat. Rev. Genet., 2007, 8, 104–115 CrossRef.
- Z. Wang, R. Cao, K. Taylor, A. Briley, C. Caldwell and J. Cheng, PLoS One, 2013, 8, e58793 CrossRef CAS PubMed.
- E. Lieberman-Aiden, N. L. Van Berkum, L. Williams, M. Imakaev, T. Ragoczy, A. Telling, I. Amit, B. R. Lajoie, P. J. Sabo and M. O. Dorschner, et al. , Science, 2009, 326, 289–293 CrossRef CAS PubMed.
- J. Dekker, K. Rippe, M. Dekker and N. Kleckner, Science, 2002, 295, 1306–1311 CrossRef CAS.
- J. Dekker, Nat. Methods, 2006, 3, 17–21 CrossRef CAS PubMed.
- L. Giorgetti and E. Heard, Genome Biol., 2016, 17, 1–9 CrossRef.
- J. Mateos-Langerak, M. Bohn, W. de Leeuw, O. Giromus, E. M. Manders, P. J. Verschure, M. H. Indemans, H. J. Gierman, D. W. Heermann and R. Van Driel, et al. , Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 3812–3817 CrossRef CAS.
- J. F. Marko and E. D. Siggia, Mol. Biol. Cell, 1997, 8, 2217–2231 CrossRef CAS.
- M. Barbieri, A. Scialdone, A. Piccolo, A. M. Chiariello, C. di Lanno, A. Prisco, A. Pombo and M. Nicodemi, Front. Genet., 2013, 4, 113 Search PubMed.
- G. Fudenberg and L. A. Mirny, Curr. Opin. Genet. Dev., 2012, 22, 115–124 CrossRef CAS PubMed.
- M. Barbieri, M. Chotalia, J. Fraser, L.-M. Lavitas, J. Dostie, A. Pombo and M. Nicodemi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16173–16178 CrossRef CAS.
- D. Jost, P. Carrivain, G. Cavalli and C. Vaillant, Nucleic Acids Res., 2014, 42, 9553–9561 CrossRef CAS PubMed.
- M. Falk, Y. Feodorova, N. Naumova, M. Imakaev, B. R. Lajoie, H. Leonhardt, B. Joffe, J. Dekker, G. Fudenberg and I. Solovei, et al. , Nature, 2019, 570, 395–399 CrossRef CAS PubMed.
- S. Bianco, D. G. Lupiáñez, A. M. Chiariello, C. Annunziatella, K. Kraft, R. Schöpflin, L. Wittler, G. Andrey, M. Vingron and A. Pombo, et al. , Nat. Genet., 2018, 50, 662–667 CrossRef CAS.
- A. Maji, J. A. Ahmed, S. Roy, B. Chakrabarti and M. K. Mitra, Biophys. J., 2020, 118, 3041–3050 CrossRef CAS PubMed.
- D. Amiad-Pavlov, D. Lorber, G. Bajpai, A. Reuveny, F. Roncato, R. Alon, S. Safran and T. Volk, Sci. Adv., 2021, 7, eabf6251 CrossRef CAS PubMed.
- A. Goloborodko, J. F. Marko and L. A. Mirny, Biophys. J., 2016, 110, 2162–2168 CrossRef CAS PubMed.
- M. Nicodemi and A. Prisco, Biophys. J., 2009, 96, 2168–2177 CrossRef CAS PubMed.
- A. M. Chiariello, C. Annunziatella, S. Bianco, A. Esposito and M. Nicodemi, Sci. Rep., 2016, 6, 1–8 CrossRef.
- A. Kumar and D. Chaudhuri, J. Phys.: Condens. Matter, 2019, 31, 354001 CrossRef CAS PubMed.
- T. Cremer and C. Cremer, Nat. Rev. Genet., 2001, 2, 292–301 CrossRef CAS.
- C. A. Brackley, S. Taylor, A. Papantonis, P. R. Cook and D. Marenduzzo, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E3605–E3611 CrossRef CAS.
- J. Johnson, C. Brackley, P. Cook and D. Marenduzzo, J. Phys.: Condens. Matter, 2015, 27, 064119 CrossRef CAS PubMed.
- C. A. Brackley, B. Liebchen, D. Michieletto, F. Mouvet, P. R. Cook and D. Marenduzzo, Biophys. J., 2017, 112, 1085–1093 CrossRef CAS PubMed.
- C. A. Brackley, J. Johnson, S. Kelly, P. R. Cook and D. Marenduzzo, Nucleic Acids Res., 2016, 44, 3503–3512 CrossRef CAS.
- D. Michieletto, E. Orlandini and D. Marenduzzo, Phys. Rev. X, 2016, 6, 041047 Search PubMed.
- D. Michieletto, M. Chiang, D. Coli, A. Papantonis, E. Orlandini, P. R. Cook and D. Marenduzzo, Nucleic Acids Res., 2018, 46, 83–93 CrossRef CAS.
- M. Di Pierro, R. R. Cheng, E. Lieberman Aiden, P. G. Wolynes and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12126–12131 CrossRef CAS PubMed.
- Y. Qi and B. Zhang, PLoS Comput. Biol., 2019, 15, e1007024 CrossRef CAS PubMed.
- M. Nicodemi and A. Pombo, Curr. Opin. Cell Biol., 2014, 28, 90–95 CrossRef CAS PubMed.
- F. Erdel and K. Rippe, Biophys. J., 2018, 114, 2262–2270 CrossRef CAS.
- K. J. Meaburn and T. Misteli, Nature, 2007, 445, 379–381 CrossRef CAS.
- R. D. Acemel, I. Maeso and J. L. Gómez-Skarmeta, Dev. Biol., 2017, 6, e265 Search PubMed.
- N. Sauerwald, A. Singhal and C. Kingsford, NAR: Genomics Bioinf., 2020, 2, lqz008 Search PubMed.
- G. Gürsoy, Y. Xu, A. L. Kenter and J. Liang, Nucleic Acids Res., 2014, 42, 8223–8230 CrossRef.
- H. Kang, Y.-G. Yoon, D. Thirumalai and C. Hyeon, Phys. Rev. Lett., 2015, 115, 198102 CrossRef PubMed.
- A. Papantonis and P. R. Cook, Chem. Rev., 2013, 113, 8683–8705 CrossRef CAS PubMed.
- A. V. Probst and G. Almouzni, Differentiation, 2008, 76, 15–23 CrossRef CAS PubMed.
- M. Ancona and C. A. Brackley, Biophys. J., 2022, 121, 2600–2612 CrossRef CAS PubMed.
- M. Muthukumar, J. Chem. Phys., 2004, 120, 9343–9350 CrossRef CAS.
- J. Hua, M. K. Mitra and M. Muthukumar, J. Chem. Phys., 2012, 136, 134901 CrossRef.
- A. Kundagrami and M. Muthukumar, J. Chem. Phys., 2008, 128, 244901 CrossRef.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- O. Wiese, D. Marenduzzo and C. A. Brackley, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17307–17315 CrossRef CAS.
- S. K. Ghosh and D. Jost, PLoS Comput. Biol., 2018, 14, e1006159 CrossRef.
- J.-P. Fortin and K. D. Hansen, Genome Biol., 2015, 16, 1–23 CrossRef CAS.
- C. Cattoglio, I. Pustova, N. Walther, J. J. Ho, M. Hantsche-Grininger, C. J. Inouye, M. J. Hossain, G. M. Dailey, J. Ellenberg and X. Darzacq, et al. , eLife, 2019, 8, e40164 CrossRef PubMed.
- P.-G. De Gennes and P.-G. Gennes, Scaling concepts in polymer physics, Cornell university press, 1979 Search PubMed.
- M. Conte, L. Fiorillo, C. Annunziatella, A. Esposito, F. Musella, A. Abraham, S. Bianco and A. M. Chiariello, Phys. Rev. E, 2021, 104, 054402 CrossRef CAS.
- D. Rieder, Z. Trajanoski and J. G. McNally, Front. Genet., 2012, 3, 221 Search PubMed.
- M. M. Tortora, L. Brennan, G. Karpen and D. Jost, bioRxiv, 2022, preprint, DOI:10.1101/2022.07.11.499635.
- I. Malhotra, B. Oyarzún and B. M. Mognetti, Biophys. J., 2021, 120, 1247–1256 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00612j |
| This journal is © The Royal Society of Chemistry 2023 |