Open Access Article
Open Access ArticleAn equivariant generative framework for molecular graph-structure Co-design†
Zaixi
Zhang
 ab,
Qi
Liu
*ab,
Chee-Kong
Lee
c,
Chang-Yu
Hsieh
ab,
Qi
Liu
*ab,
Chee-Kong
Lee
c,
Chang-Yu
Hsieh
 d and
Enhong
Chen
ab
d and
Enhong
Chen
ab
aAnhui Province Key Lab of Big Data Analysis and Application, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: qiliuql@ustc.edu.cn
bState Key Laboratory of Cognitive Intelligence, Hefei, Anhui 230088, China
cTencent America, Palo Alto, CA 94306, USA
dInnovation Institute for Artificial Intelligence in Medicine of Zhejiang University, College of Pharmaceutical Sciences, Zhejiang University, Hangzhou, Zhejiang 310058, China
First published on 19th July 2023
Abstract
Designing molecules with desirable physiochemical properties and functionalities is a long-standing challenge in chemistry, material science, and drug discovery. Recently, machine learning-based generative models have emerged as promising approaches for de novo molecule design. However, further refinement of methodology is highly desired as most existing methods lack unified modeling of 2D topology and 3D geometry information and fail to effectively learn the structure–property relationship for molecule design. Here we present MolCode, a roto-translation equivariant generative framework for molecular graph-structure Co-design. In MolCode, 3D geometric information empowers the molecular 2D graph generation, which in turn helps guide the prediction of molecular 3D structure. Extensive experimental results show that MolCode outperforms previous methods on a series of challenging tasks including de novo molecule design, targeted molecule discovery, and structure-based drug design. Particularly, MolCode not only consistently generates valid (99.95% validity) and diverse (98.75% uniqueness) molecular graphs/structures with desirable properties, but also generates drug-like molecules with high affinity to target proteins (61.8% high affinity ratio), which demonstrates MolCode's potential applications in material design and drug discovery. Our extensive investigation reveals that the 2D topology and 3D geometry contain intrinsically complementary information in molecule design, and provide new insights into machine learning-based molecule representation and generation.
Introduction
Designing molecules with desirable characteristics is of fundamental importance in many applications, ranging from drug discovery1–3 to catalysis4 and semiconductors.5,6 However, the size of the drug-like chemical space is estimated to be in the order of 1033,7 which precludes an exhaustive computational or experimental search of possible molecular candidates. In recent years, advances in machine learning (ML) methods have greatly accelerated the exploration of chemical compound space.8–18 Many studies propose to generate 2D/3D molecules and optimize molecular properties with deep generative models.19–28Molecules can be naturally represented as 2D graphs where nodes denote atoms, and edges represent covalent bonds. Such concise representation has motivated a series of studies in the tasks of molecule design and optimization. These works either predict the atom type and adjacency matrix of the graph,29–32 or employ autoregressive models to sequentially add nodes and edges.23,33 Furthermore, some methods leverage the chemical priors of molecular fragments/motifs and propose to generate molecular graphs fragment-by-fragment.34,35 However, complete information about a molecule cannot be obtained from these methods since the 3D structures of molecules are still unknown, which limits their practical applications. Due to intramolecular interactions or rotations of structural motifs, the same molecular graph can correspond to various spatial conformations with different quantum properties.36–40 Therefore, molecular generative models considering 3D geometry information are desired to better learn structure–property relationships.
Recently, some studies characterize molecules as 3D point clouds where each point has atom features (e.g., atom types) and 3D coordinates and corresponding generative models have been proposed for 3D molecule design. These methods include estimating pairwise distances between atoms,41 employing diffusion models to predict atom types and coordinates of all atoms,42 and using autoregressive models to place atoms in 3D space step-by-step.24,26,43 Since molecular drugs inhibit or activate particular biological functions by binding to the target proteins, another line of work further proposes generating 3D molecules inside the target protein pocket, which is a complex conditional generation task.44–47 However, most of these methods do not explicitly consider chemical bonds and valency constraints and may generate molecules that are not chemically valid. Moreover, the lack of bonding information also inhibits the generation of realistic substructures (e.g., benzene rings).
In this work, we propose MolCode, a roto-translation equivariant generative model for molecular graph-structure Co-design from scratch or conditioned on the target protein pockets. Different from previous works that focus on a certain modality (e.g., 2D molecular graphs) our method designs 2D molecular graphs or 3D structures simultaneously, i.e., co-design. Our model is motivated by the intuition that the information of the 2D graph and 3D structure is intrinsically complementary to each other in molecule generation: the 3D geometric structure information empowers the generation of chemical bonds, and the bonding information can in turn guide the prediction of 3D coordinates to generate more realistic substructures by constraining the searching space of bond length/angles. We note one concurrent work MiDi48 has a similar idea and proposes a novel diffusion-based generative model for jointly generating molecular 2D graphs and 3D structures. In MolCode, we employ autoregressive flow as the backbone framework to generate atom types, chemical bonds, and 3D coordinates sequentially. To encode intermediate 3D graphs, roto-translation equivariant graph neural networks (GNNs)49,50 are first used to obtain node embeddings. Note that our MolCode is agnostic to the choice of encoding GNNs. Then, a novel attention mechanism with bond encoding enriches embeddings with global context as well as bonding information. In the decoding process, we construct a local coordinate system based on local reference atoms and predict the relative coordinates, ensuring the equivariance of atomic coordinates and the invariance of likelihood. The generated 2D molecular graphs also help check the chemical validity of the generated molecules in each step. In our experiments, we show that MolCode outperforms existing generative models in generating diverse, valid, and realistic molecular graphs and structures from scratch. Further investigations on targeted molecule discovery show that MolCode can generate molecules with desirable properties that are scarce in the training set, demonstrating its strong capability of capturing structure–property relationships for generalization. In the future, the Bayesian optimization methods19,20,22,51–54 can be applied to our MolCode for further improvement. Finally, we extend MolCode to the structure-based drug design task and manage to generate drug-like ligand molecules with high binding affinities. Systematic hyperparameter analysis and ablation studies show that MolCode is robust to hyperparameters and the unified modeling of 2D topology and 3D geometry consistently improves molecular generation performance.
Results
Sequential generation with flow models
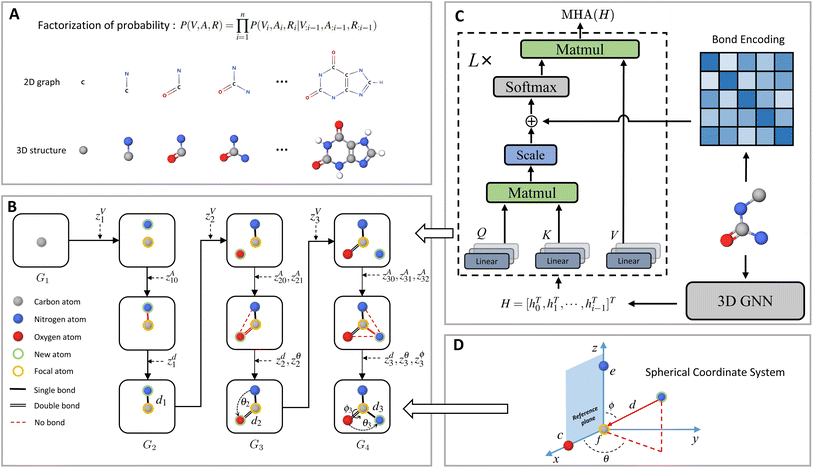
Contrary to previous works that treat molecules solely as 2D graphs or 3D point clouds, a molecule is comprehensively represented as a 3D-dimensional graph G = (V, A, R) in this work. Let a and b denote the number of atom types and bond types. For a molecule with n atoms, V ∈ {0,1}n×a is the atom type matrix, A ∈ {0,1}n×n×(b+1) is an adjacency matrix, and R ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×3 is the 3D atomic coordinate matrix. We add one additional type of edge between two atoms, which corresponds to no edge between two atoms. Following previous works like GraphAF23 and G-SchNet,24 we formalize the problem of molecular graph generation as a sequential decision process (Fig. 1A and B). We can factorize the probability of molecule P(V, A, R) as:
n×3 is the 3D atomic coordinate matrix. We add one additional type of edge between two atoms, which corresponds to no edge between two atoms. Following previous works like GraphAF23 and G-SchNet,24 we formalize the problem of molecular graph generation as a sequential decision process (Fig. 1A and B). We can factorize the probability of molecule P(V, A, R) as: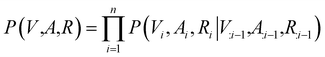 | (1) |
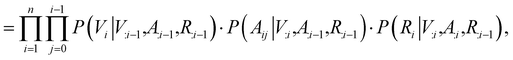 | (2) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d → x ∈
d → x ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d. The latent distribution pZ is a pre-defined probability distribution, e.g., a Gaussian distribution. The data distribution pX is unknown. But given a data point x, its log-likelihood can be computed with the change-of-variable theorem:
d. The latent distribution pZ is a pre-defined probability distribution, e.g., a Gaussian distribution. The data distribution pX is unknown. But given a data point x, its log-likelihood can be computed with the change-of-variable theorem:log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pX(x) = log pX(x) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pZ(fθ−1(x)) + log|detJ|, pZ(fθ−1(x)) + log|detJ|, | (3) |
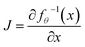 is the Jacobian matrix. To train a flow model on molecule datasets, the log-likelihoods of all data points are computed from eqn (3) and maximized via gradient ascent. In the sampling process, a latent variable z is first sampled from the pre-defined latent distribution pZ. Then the corresponding data point x is obtained by performing the feedforward transformation x = fθ(z). Therefore, fθ needs to be invertible, and the computation of det
is the Jacobian matrix. To train a flow model on molecule datasets, the log-likelihoods of all data points are computed from eqn (3) and maximized via gradient ascent. In the sampling process, a latent variable z is first sampled from the pre-defined latent distribution pZ. Then the corresponding data point x is obtained by performing the feedforward transformation x = fθ(z). Therefore, fθ needs to be invertible, and the computation of det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J should be tractable for the training and sampling efficiency. A common choice is the affine coupling layers23,56,57 where the computation of det
J should be tractable for the training and sampling efficiency. A common choice is the affine coupling layers23,56,57 where the computation of det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J is very efficient because J is an upper triangular matrix.
J is very efficient because J is an upper triangular matrix.
Fig. 1 shows a schematic depiction of the MolCode architecture. At each generation step, we predict the new atom type, bond types, and the 3D coordinates sequentially. We use an equivariant graph neural network for the extraction of conditional information from intermediate molecular graphs. A novel multi-head self-attention network with bond encoding is proposed to further capture the global and bonding information. For the generation of atomic coordinates, MolCode firstly constructs a local spherical coordinate system and generates the relative coordinates i.e. d, θ, ϕ, which ensure the equivariance of coordinates and the invariance of likelihood. In the de novo molecule design and targeted molecule discovery, MolCode generates molecules from scratch. In structure-based drug design, which is a conditional generation task, the target protein pocket represented as a 3D-dimensional graph is first input into MolCode. Then MolCode generates ligand molecules based on the protein pocket.
We train MolCode on a set of molecular structures and the corresponding molecular graphs can be obtained with toolkits in chemistry.58,59 In the generation process, we check whether the generated bonds violate the valency constraints at each step. If the newly added bond breaks the valency constraint, we just reject it, sample a new latent variable and generate another new bond type. More details on the model architecture and training procedure can be found in the Methods section.
De novo molecule design
For virtual screening, the generative model should be able to sample a large quantity of valid and diverse molecules from scratch. In the random molecule generation task, we evaluate MolCode on the QM9 dataset61 consisting of 134k organic molecules with up to nine heavy atoms from carbon, nitrogen, oxygen, and fluorine. We use validity, uniqueness, and novelty to evaluate the quality of the generated molecules: validity calculates the percentage of valid molecules among all the generated molecules; uniqueness is the percentage of unique molecules among all the valid molecules; novelty measures the fraction of novel molecules among all the valid and unique ones. Specifically, the 3D molecular structures are first converted to 2D graphs, and the bond types (single, double, triple, or none) are determined based on the distances between pairs of atoms and the atom types.59 A molecule is considered valid if it obeys the chemical valency rules; it is considered unique or novel if its 2D molecular graph appears only once in the whole sampled molecule set or does not exist in the training set. In Table. S3,† we compare MolCode with four state-of-the-art baselines including E-NFs,60 G-SchNet,24 G-SphereNet43, and EDM42 on 3D molecule generation. We also compare MolCode with its two variants i.e. MolCode without validity check (MolCode w/o check) and MolCode without bond information (MolCode w/o bond) for ablation studies. Note that we still conduct bond prediction and validity check while the bonding information is not used for 3D coordinate prediction in MolCode w/o bond. All metrics are computed from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated molecular structures. We observe that MolCode achieves the best performance in generating valid and diverse molecular structures (99.95% validity, 98.75% uniqueness). With the advantage of the generated bonds, MolCode can rectify the generation process when the valency constraints are violated, and therefore better explore the chemical space with the autoregressive flow framework. Interestingly, even without a validity check, MolCode can still achieve validity as high as 94.60%, which indicates the strong ability of MolCode to capture the underlying chemical rules by modeling the generation of bonds. In MolCode (w/o bond), the bonding information is not provided to the conditional information extraction block. The validity drops from 99.95% to 92.12% and the uniqueness drops from 98.75% to 94.32%, which also verifies the usefulness of bonding information in MolCode. Regarding novelty, as discussed by previous work42 that QM9 is the exhaustive enumeration of molecules that satisfy a predefined set of constraints, the novelty of MolCode is reasonable and acceptable (Table 1).
000 generated molecular structures. We observe that MolCode achieves the best performance in generating valid and diverse molecular structures (99.95% validity, 98.75% uniqueness). With the advantage of the generated bonds, MolCode can rectify the generation process when the valency constraints are violated, and therefore better explore the chemical space with the autoregressive flow framework. Interestingly, even without a validity check, MolCode can still achieve validity as high as 94.60%, which indicates the strong ability of MolCode to capture the underlying chemical rules by modeling the generation of bonds. In MolCode (w/o bond), the bonding information is not provided to the conditional information extraction block. The validity drops from 99.95% to 92.12% and the uniqueness drops from 98.75% to 94.32%, which also verifies the usefulness of bonding information in MolCode. Regarding novelty, as discussed by previous work42 that QM9 is the exhaustive enumeration of molecules that satisfy a predefined set of constraints, the novelty of MolCode is reasonable and acceptable (Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. The best results are bolded
000 molecules. The best results are bolded
| Method | Validity | Uniqueness | Novelty | Time (s) |
|---|---|---|---|---|
| E-NFs60 | 41.30% | 92.96% | 81.12% | 3360 |
| G-SchNet24 | 84.19% | 94.11% | 83.47% | 92 |
| G-SphereNet43 | 87.54% | 95.49% | 81.55% | 450 |
| EDM42 | 92.27% | 98.24% | 72.84% | 4339 |
| MolCode (w/o check) | 94.60% | 96.54% | 74.18% | 563 |
| MolCode (w/o bond) | 92.12% | 94.32% | 75.43% | 655 |
| MolCode (w/o angle) | 86.43% | 87.60% | 72.91% | 653 |
| MolCode | 99.95% | 98.75% | 75.90% | 674 |
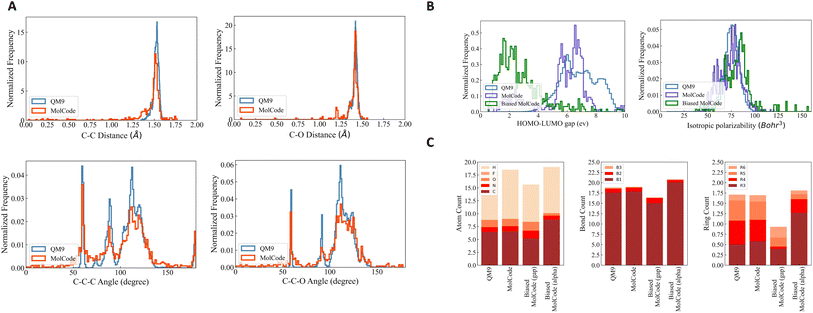
To further investigate how well our model fits the distribution of QM9, we conduct qualitative substructure analysis (Table S1†). Specifically, we first collect the bond length/angle distributions in the generated molecules and the training dataset and then employ Kullback–Leibler (KL) divergence to compute their distribution distances. We show several common bond and bond angle types. We can observe that MolCode obtains much lower KL divergence than the other methods and its variant without bond information, indicating that the molecules generated by MolCode capture more geometric attributes of data. Moreover, we show two sets of bond length distributions (carbon–carbon single bond and carbon–oxygen single bond) and two sets of bond angle distributions (carbon–carbon–carbon and carbon–carbon–oxygen chains) in Fig. 2A. Generally, the distributions of MolCode align well with those of QM9, indicating that the distances and angles between atoms are accurately modeled and reproduced. We illustrate some randomly sampled molecules generated by MolCode in the ESI (Fig. S1†).
Targeted molecule discovery
The ability to generate molecules with desirable properties that are either absent or rare in the training data (e.g., new materials) is quite useful for the target exploration of chemical space. Here we conduct two targeted molecule discovery experiments, namely the HOMO–LUMO gap minimization and the isotropic polarizability maximization. Following previous works,24,43 we finetune the pretrained generative models on the collected biased datasets. Specifically, we collect all molecular structures whose HOMO–LUMO gaps are smaller than 4.5 eV and all molecular structures whose isotropic polarizabilities are larger than 91 bohr3 from the QM9 as the biased datasets. Afterward, we generate 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular structures with the finetuned model and compute the quantum properties (HOMO–LUMO gap and isotropic polarizability) with the PySCF package.62,63 The performance is then evaluated by calculating the mean and optimal value over all property scores (mean and optimal) and the percentage of molecules with good properties (good percentage). Molecules with good properties are those with HOMO–LUMO gaps smaller than 4.5 eV and isotropic polarizabilities larger than 91 bohr3, respectively.
000 molecular structures with the finetuned model and compute the quantum properties (HOMO–LUMO gap and isotropic polarizability) with the PySCF package.62,63 The performance is then evaluated by calculating the mean and optimal value over all property scores (mean and optimal) and the percentage of molecules with good properties (good percentage). Molecules with good properties are those with HOMO–LUMO gaps smaller than 4.5 eV and isotropic polarizabilities larger than 91 bohr3, respectively.
The results of targeted molecule discovery for two quantum properties are shown in Table 2. For the two properties, our MolCode outperforms all the baseline methods and its variants without validity check and bonding information, demonstrating MolCode's strong capability in capturing structure–property relationships and generating molecular structures with desirable properties. For instance, even though the biased datasets are only 3.20% and 2.04% of QM9 respectively, the fine-tuned MolCode achieves good percentages of 87.76% and 38.40%. We also illustrate the property distributions of QM9, MolCode, and biased MolCode in Fig. 2B. Clearly, we can observe that the property distributions of MolCode align well with those of the QM9 dataset while the property distributions of the biased MolCodes shift towards smaller HOMO–LUMO gap and larger isotropic polarizability respectively.
| Method | HOMO–LUMO gap | Isotropic polarizability | ||||
|---|---|---|---|---|---|---|
| Mean | Optimal | Good percentage | Mean | Optimal | Good percentage | |
| QM9 (dataset) | 6.833 | 0.669 | 3.20% | 75.19 | 196.62 | 2.04% |
| G-SchNet24 | 3.332 | 0.671 | 75.50% | 78.20 | 216.06 | 31.39% |
| G-SphereNet43 | 2.967 | 0.315 | 81.58% | 87.21 | 378.63 | 34.72% |
| EDM42 | 3.255 | 0.453 | 76.19% | 89.10 | 381.24 | 33.23% |
| MolCode (w/o check) | 2.905 | 0.284 | 81.80% | 92.20 | 359.48 | 36.15% |
| MolCode (w/o bond) | 2.874 | 0.267 | 83.56% | 90.82 | 372.19 | 35.31% |
| MolCode | 2.809 | 0.178 | 87.76% | 95.36 | 403.57 | 38.40% |
Fig. 2C reveals further insights into the structural statistics of the generated molecules. First, we observe that MolCode captures the atom, bond, and ring counts of the QM9 dataset accurately. Second, for the biased MolCode towards smaller HOMO–LUMO gaps, the generated molecules exhibit an increased number of nitrogen/oxygen atoms and double-bonds in addition to a tendency towards forming six-atom rings. These features indicate the presence of aromatic rings with nitrogen/oxygen atoms and conjugated systems with alternating single and double bonds, which are important motifs in organic semiconductors with small HOMO–LUMO gaps. Finally, for the biased MolCode towards larger isotropic polarizability, the generated molecules contain more atoms, bonds, and rings, which are the prerequisites for large isotropic polarizabilities.
Structure-based drug design
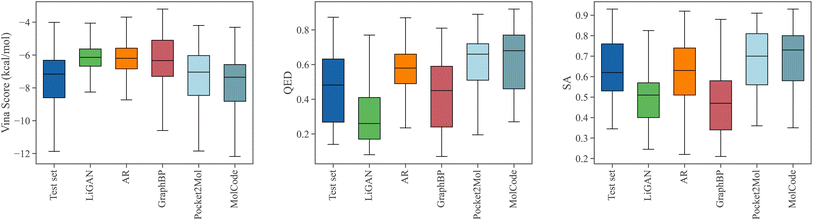
Designing ligand molecules binding with target proteins is a fundamental and challenging task in drug discovery.64 According to the lock and key model,65,66 the molecules that bind tighter to a disease target are more likely to be drug candidates with higher bioactivity against the disease. Therefore, it is beneficial to take the structure of the target proteins into consideration when generating molecules for drug discovery. Here, we train MolCode on the CrossDocked2020 dataset67 which contains 22.5 million protein-molecule complexes for structure-based drug design. Starting with the target protein pocket as the context, MolCode iteratively predicts the ligand atom types, bond types, and atom coordinates. We generate 100 ligand molecules for each target protein pocket in the test set. More details are included in the Methods section.Fig. 3 shows the property distributions of the sampled ligand molecules. Here, we mainly focus on the following metrics following previous works:44,47 Vina score measures the binding affinity between the generated molecules and the protein pockets; QED68 measures how likely a molecule is a potential drug candidate; synthesizability (SA) represents the difficulty of drug synthesis (the score is normalized between 0 and 1 and higher values indicate easier synthesis). In our work, The Vina score is calculated by QVina,69,70 and the chemical properties are calculated by RDKit71,72 over the valid molecules. Before feeding to Vina, all the generated molecular structures are firstly refined by universal force fields.73 Four competitive baselines including LiGAN,74 AR,44 GraphBP,46 and Pocket2Mol47 are compared. We also show the distributions of the test set for reference. MolCode can generate ligand molecules with higher binding affinities (lower Vina scores) than baseline methods. Specifically, MolCode succeeds to generate molecules with higher affinity than corresponding reference molecules for 61.8% protein pockets on average (Table S2†). Moreover, the generated molecules also exhibit more potential to be drug candidates (higher QED and SA). These improvements indicate that MolCode effectively captures the distribution of 3D ligand molecules conditioned on binding sites with the graph-structure co-design scheme. More detailed evaluations are shown in Table S2.†
In Fig. 4, we further show several examples of generated 3D molecules with higher affinities to the target proteins than their corresponding reference molecules in the test set. It can be observed that our generated molecules with higher binding affinity also have diverse structures and are largely different from the reference molecules. It demonstrates that MolCode is capable of generating diverse and novel molecules to bind target proteins, instead of just memorizing and reproducing known molecules in the dataset, which is quite important in exploring novel drug candidates.
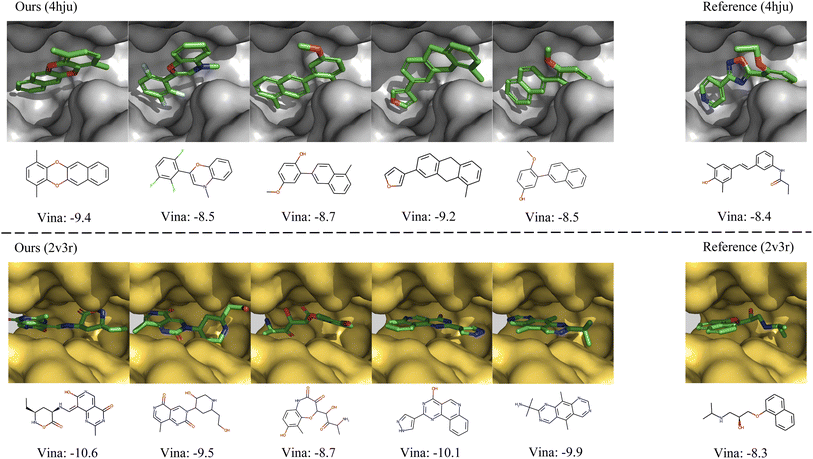 | ||
| Fig. 4 Examples of the generated molecules with higher binding affinities than the references. We report the Vina scores and a lower Vina score indicates higher binding affinity. | ||
Conclusion
In this article, we have reported a roto-translation equivariant generative framework for molecular graph-structure co-design from scratch or conditioned on the target protein pockets. As compared to existing methods that only represent and generate 2D topology graphs or 3D geometric structures, MolCode concurrently designs 2D molecular graphs and 3D structures and can well capture complex molecular relationships. Extensive experiments on de novo molecule design, targeted molecule discovery, and structure-based drug design demonstrate the effectiveness of our model. Our investigation demonstrates that the 2D topology and 3D geometry contain intrinsically complementary information for molecular representation and generation and the unified modeling of them greatly improve the molecular generation performance.There are also several potential extensions of MolCode as future works. First, MolCode may be extended and applied to significantly larger systems with more diverse atom types such as proteins and crystal materials. Although MolCode has been trained on ligand–protein pocket complexes from the Crossdocked2020 dataset, modifications will be necessary to ensure further scalability. Another potential improvement is to incorporate chemical priors such as ring structures into MolCode to generate more valid molecules and realistic 3D structures. For example, the molecules may be generated fragment-by-fragment instead of atom-by-atom, which can also speed up the generation process. Furthermore, wet-lab experiments may be conducted to validate the effectiveness of MolCode. Overall, we anticipate that further developments in deep generative models will greatly accelerate and benefit various applications in material design and drug discovery.
Methods
Dataset
For the task of random molecule generation and targeted molecule discovery, we evaluate MolCode on the QM9 (ref. 61) and the GEOM-Drug75 dataset. The QM9 dataset contains over 134k molecules and their corresponding 3D molecular geometries computed by density functional theory (DFT). In the random molecular geometry generation task, we randomly select 100k 3D molecular geometries as the training set and 10k 3D molecular geometries as the validation set. For the targeted molecule discovery, we collect all molecular geometries whose HOMO–LUMO gaps are smaller than 4.5 eV and all molecular geometries whose isotropic polarizabilities are larger than 91 bohr3 as the finetuning dataset. The GEOM-Drug dataset contains larger drug-like molecules with an average of 44 atoms and up to 181 atoms. We filtered GEOM-Drug following previous work.76 After filtering, we removed the hydrogen atoms and constructed the training, validation, and testing sets with 231![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523, 28
523, 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 941, and 28
941, and 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 molecules, respectively.
940 molecules, respectively.
As for the structure-based drug design, we use the CrossDocked dataset67 which contains 22.5 million protein-molecule structures following ref. 44 and 47. We filter out data points whose binding pose RMSD is greater than 1 Å and molecules that can not be sanitized with RDkit,71,72 leading to a refined subset with around 160k data points. We use mmseqs2 (ref. 77) to cluster data at 30% sequence identity, and randomly draw 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 protein–ligand pairs for training and 100 proteins from remaining clusters for testing. For evaluation, we randomly sample 100 molecules for each protein pocket in the test set.
000 protein–ligand pairs for training and 100 proteins from remaining clusters for testing. For evaluation, we randomly sample 100 molecules for each protein pocket in the test set.
For all the tasks including random/targeted molecule generation and structure-based drug design, MolCode and all the other baseline methods are trained with the same data split for a fair comparison.
Overview of MolCode
Let a be the number of atom types, b be the number of bond types, and n denote the number of atoms in a molecule. We can represent the molecule as a 3D-dimensional graph G = (V, A, R), where V ∈ {0,1}n×a is the atom type matrix, A ∈ {0,1}n×n×(b+1) is an adjacency matrix, and R ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×3 is the 3D atomic coordinate matrix. Note that we add one additional type of edge between two atoms, which corresponds to no edge between two atoms. Here, each element Vi in V and Aij in A are one-hot vectors. Viu = 1 and Aijv = 1 represent that the i-th atom has type u and there is a type v bond between the i-th and j-th atom respectively. The i-th row of the coordinate matrix Ri represents the 3D Cartesian coordinate of the i-th atom.
n×3 is the 3D atomic coordinate matrix. Note that we add one additional type of edge between two atoms, which corresponds to no edge between two atoms. Here, each element Vi in V and Aij in A are one-hot vectors. Viu = 1 and Aijv = 1 represent that the i-th atom has type u and there is a type v bond between the i-th and j-th atom respectively. The i-th row of the coordinate matrix Ri represents the 3D Cartesian coordinate of the i-th atom.
We adopt the autoregressive flow framework55 to generate the atom type Vi of the new atom, the bond types Aij, and the 3D coordinates at each step. Since both the node type Vi and the edge type Aij are discrete, which do not fit into a flow-based model, we adopt the dequantization method21,23 that converts them into continuous numbers via adding noise as follows:
| Ṽi = Vi + u, u ∼ U(0, 1)a; Ãij = Aij + u,u ∼ U(0, 1)b+1, i ≥ 1. | (4) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) a and zAij ∈
a and zAij ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) b+1 from the standard Gaussian distribution
b+1 from the standard Gaussian distribution 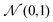 , and then map zVi and zAij to Ṽi and Ãij respectively by the following affine transformation:
, and then map zVi and zAij to Ṽi and Ãij respectively by the following affine transformation:| Ṽi = sVi⊙zVi + tVi; Ãij = sAij⊙zAij + tAij, i ≥ 1, 0 ≤ j ≤ i − 1, | (5) |
However, it is non-trivial to generate coordinates that satisfy the equivariance to rigid transformations and the invariance property of likehood. Inspired by G-SchNet,24 MolGym,78 and G-SphereNet,43 we choose to construct a local spherical coordinate system and generate the distance di ,the angle θi, and the torsion angle ϕi w.r.t. the constructed local SCS. Specifically, we first choose a focal atom from all atoms in Gi, which is employed as the reference point for the new atom. The new atom is expected to be placed in the local area of the selected focal atom. Assume that the focal node is the f-th node in Gi. First, the distance di from the focal atom to the new atom is generated, i.e., di = ‖Ri − Rf‖. Then, if i ≥ 2, the angle θi ∈ [0, π] between the lines (Rf, Ri) and (Rf, Rc) is generated, where c is the closest atom to the focal atom in Gi. Finally, if i ≥ 3, the torsion angle ϕi ∈ [−π, π] formed by planes (Rf, Rc, Ri) and (Rf, Rc, Re) is generated, where e denotes the atom closest to c but different from f in Gi. Similar to Ṽi and Ãij, di, θi, ϕi can be obtained by:
| di = sdi⊙zdi + tdi, i ≥ 1, | (6) |
| θi = sθi⊙zθi + tθi, i ≥ 2, | (7) |
| ϕi = sϕi⊙zϕi + tϕi, i ≥ 3, | (8) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) denote the sampled latent variables from standard Gaussian distributions and the scale factors sdi, sθi, sϕi ∈
denote the sampled latent variables from standard Gaussian distributions and the scale factors sdi, sθi, sϕi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) are the shift factors tdi, tθi, tϕi ∈
are the shift factors tdi, tθi, tϕi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) are the functions of Gi. The coordinate Ri of the new atom is computed based on the relative coordinates di, θi, ϕi and the reference atoms (f, c, e), hence satisfying the roto-translation equivariance property.
are the functions of Gi. The coordinate Ri of the new atom is computed based on the relative coordinates di, θi, ϕi and the reference atoms (f, c, e), hence satisfying the roto-translation equivariance property.
Encoder
Generating the atom type, covalent bonds, and 3D position at each step requires capturing the conditional information of the intermediate graph Gi with an equivariant encoder. In MolCode, we use SphereNet49 for the QM9 dataset and EGNN50 for the CrossDocked2020 dataset to obtain the node embeddings. Note that MolCode is agnostic to the choice of equivariant graph neural networks. SphereNet can capture the complete geometric information inside molecular structures including bond length/angles and dihedral angles but can hardly scale to large molecules due to computational complexity. In contrast, EGNN only encodes pairwise distances between atoms and is more efficient than SphereNet on systems with more atoms e.g., ligand–protein pocket complexes. For the input graph Gi, let the node embedding matrix computed by 3D GNN be H = [hT0,hT1,…,hTi−1,]T ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) i×d, where hj is the embedding of the j-th atom and d is the dimension of embedding.
i×d, where hj is the embedding of the j-th atom and d is the dimension of embedding.
To further encode the information of covalent bonds and capture the global information in the molecule graph, we modify the self-attention mechanism79 and propose a novel bond encoding. The multi-head self-attention (MHA) with bond encoding is calculated as:
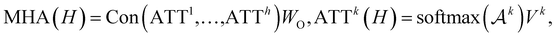 | (9) |
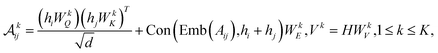 | (10) |
In MolCode, we use the SphereNet49 with 4 layers or EGNN50 with 6 layers to extract features from the intermediate 3D graphs, where the input embedding size is set to 64 and the output embedding size is set to 256. The cutoff is set as 5 Å. The node features are set as the one-hot vectors of atom types and the edge representations are initialized with spherical basis functions. In the multi-head self-attention module with bond encoding, there are 4 attention heads. Besides that, we employ 6 flow layers with a hidden dimension of 128 for the decoder. We use the model configuration for all the experiments.
Decoder
To generate new atoms, the scale factor sVi and shift factor tVi in eqn (5) can be computed as:| sVi,tVi = MLP(Con(hf,MHAV(H)f)), | (11) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) and predict sAij and tAij in eqn (5):
and predict sAij and tAij in eqn (5):![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = [hT0,hT1,…,hTi−1, = [hT0,hT1,…,hTi−1,![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) Ti]T, Ti]T, ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) i = Emb(Vi), i = Emb(Vi), | (12) |
sAij,tAij = MLPA(Con(![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) i,hj,MHA( i,hj,MHA(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) )f)), 0 ≤ j ≤ i − 1, )f)), 0 ≤ j ≤ i − 1, | (13) |
sdi,tdi = MLPd(Con(hf,MHA(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) )i)), i ≥ 1, )i)), i ≥ 1, | (14) |
sθi,tθi = MLPθ(Con(hf,hc,MHA(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) )i)), i ≥ 2, )i)), i ≥ 2, | (15) |
sϕi,tϕi = MLPϕ(Con(hf,hc,he,MHA(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) )i)), i ≥ 3, )i)), i ≥ 3, | (16) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) )i is the node embedding of the newly added atom from the output of the multi-head self-attention network.
)i is the node embedding of the newly added atom from the output of the multi-head self-attention network.
As for the focal atom selection, we employ a multi-layer perceptron (MLP) with the atom embeddings as input. Atoms that are not valence filled are labeled 1, otherwise 0. Particularly, in the structure-based drug design task where there is no ligand atom at the beginning, the focal atoms are defined as protein atoms that have ground-truth ligand atoms within 4 Å at the first step. After the generation of the first ligand atom, MolCode selects focal atoms from the generated ligand atoms. At the inference stage, we randomly choose the focal atom f from atoms whose classification scores are higher than 0.5. The sequential generation process stops if all the classification scores are lower than 0.5 or there is no generated bond between the newly added atom and the previously generated atoms.
Validity filter
The graph-structure codesign scheme in MolCode makes it feasible to check the chemical validity based on the generated 2D graphs at each step. Specifically, we explicitly consider the valency constraints during sampling to check whether current bonds have exceeded the allowed valency. The valency constraint is defined as: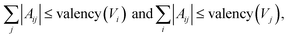 | (17) |
Model training and inference
To make sure the generated atoms are in the local region of their corresponding reference atoms, we propose to use Prim's algorithm to obtain the generation orders of atoms. The weights of the edges are set as the distances between atoms. The first atoms of molecules are randomly sampled in each epoch to encourage the generalization ability of the model. With such obtained trajectories, MolCode is trained by stochastic gradient descent with the following loss function. For a 3D molecular graph G with n atoms (n > 3), we maximize its log-likelihood in eqn (18) and (19) to train the MolCode model. Besides, the atom-wise classifier for focal atom selection is trained with a binary cross entropy loss.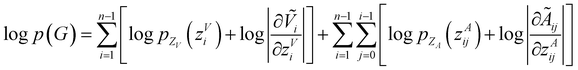 | (18) |
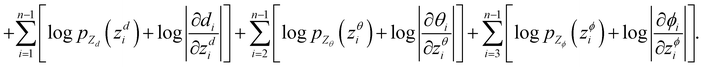 | (19) |
In the random molecule generation task, our MolCode model is trained with Adam80 for 100 epochs. The learning rate is set as 0.0001 and the batch size is set as 64. We report the results from the epoch with the best validation loss. It takes around 36 hours to train a MolCode from scratch on 1 Tesla V100 GPU. In the task of targeted molecule discovery, the model is further fine-tuned with a learning rate of 0.0001 and a batch size of 32. The fine-tuning epochs are set as 40 for the HOMO–LUMO gap and 80 for the isotropic polarizability. In the task of structure-based drug design, we train MolCode with Adam optimizer for 100 epochs with a learning rate of 0.0001 and a batch size of 8. β1 and β2 in Adam is set to 0.9 and 0.999, respectively.
For all the tasks including random/targeted molecule generation and structure-based drug design, MolCode, and all the other baseline methods are trained with the same data split for a fair comparison. We run the code provided by the authors to obtain the results of baseline methods. Due to the randomness of training and molecule sampling, the results are not exactly the same but roughly match the results in the original papers. For example, the validity reported in G-SphereNet is 88.18% and we have 86.43% in Table S3.†
During generation, we use temperature hyperparameters from the prior Gaussian distributions. Specifically, we change the standard deviation of the Gaussian distribution to the temperature hyperparameters. To decide the specific values of temperature hyperparameters, we perform a grid search over {0.3, 0.5, 0.7} based on validity and uniqueness in random molecule generation to encourage generating more valid and diverse molecules. We use 0.5 for sampling zVi, 0.5 for sampling zAi, 0.3 for sampling zdi, 0.3 for sampling zθi, and 0.7 for sampling zϕi as the default setting. We have the following interesting insights for choosing temperature hyperparameters: to generate valid and diverse molecules, the hidden variables for bond lengths/angles (zdi and zθi) are assigned with small temperature hyperparameters (low variance) since the values of a certain type of bond lengths/angles are largely fixed. In contrast, the torsion angles are more flexible in molecules so that the temperature hyperparameter of zϕi is larger. We use the same fixed temperature hyperparameters for the targeted molecule discovery and structure-based drug design experiments. In Fig. S2,† we show the hyperparameter analysis with respect to zVi, zAi, zdi, zθi, and zϕi. The default values with these hyperparameters are set to 0.5. MolCode is generally robust to the choice of hyperparameters and can further benefit from setting appropriate hyperparameter values. In the future, the generation may be further improved with Bayesian optimization over the hyperparameters.81
Algorithm 1 and 2 show the pseudo-codes of the training and generation process of MolCode for random/targeted molecule generation. Note that to scale to large molecules in experiments, the bonds are only generated and predicted between new atoms and the reference atoms. The pseudo-codes of MolCode for structure-based drug design are similar to Algorithm 1 and 2, except that the ligand atoms are generated conditioned on the protein pocket instead of generated from scratch.
Data availability
The data necessary to reproduce our numerical benchmark results are publicly available at https://github.com/divelab/DIG and https://github.com/gnina/models.Code availability
The code used in the study is publicly available from the GitHub repository: https://github.com/zaixizhang/MolCode.Author contributions statement
Z. X. Z., Q. L., C. L., C. H., and E. H. C. designed the research, Z. X. Z. conducted the experiments, Z. X. Z., Q. L., and C. L. analyzed the results. All authors reviewed the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This research was partially supported by grants from the National Natural Science Foundation of China (Grants No. 61922073 and U20A20229).References
- P. J. Hajduk and J. Greer, A decade of fragment-based drug design: strategic advances and lessons learned, Nat. Rev. Drug Discovery, 2007, 6, 211–219 CrossRef CAS PubMed.
- A. D. Lawson, Antibody-enabled small-molecule drug discovery, Nat. Rev. Drug Discovery, 2012, 11, 519–525 CrossRef CAS.
- Y. Wang, J. Wang, Z. Cao and A. Barati Farimani, Molecular contrastive learning of representations via graph neural networks, Nat. Mach. Intell., 2022, 4, 279–287 CrossRef.
- J. G. Freeze, H. R. Kelly and V. S. Batista, Search for catalysts by inverse design: artificial intelligence, mountain climbers, and alchemists, Chem. Rev., 2019, 119, 6595–6612 CrossRef CAS PubMed.
- R. Gómez-Bombarelli, et al., Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- R.-P. Xu, Y.-Q. Li and J.-X. Tang, Recent advances in flexible organic light-emitting diodes, J. Mater. Chem. C, 2016, 4, 9116–9142 RSC.
- P. G. Polishchuk, T. I. Madzhidov and A. Varnek, Estimation of the size of drug-like chemical space based on gdb-17 data, J. Comput.-Aided Mol. Des., 2013, 27, 675–679 CrossRef CAS PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- J. Vamathevan, et al., Applications of machine learning in drug discovery and development, Nat. Rev. Drug Discovery, 2019, 18, 463–477 CrossRef CAS PubMed.
- S. Ekins, et al., Exploiting machine learning for end-to-end drug discovery and development, Nat. Mater., 2019, 18, 435–441 CrossRef CAS PubMed.
- O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Exploring chemical compound space with quantum-based machine learning, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef PubMed.
- J. Westermayr, M. Gastegger, K. T. Schütt and R. J. Maurer, Perspective on integrating machine learning into computational chemistry and materials science, J. Chem. Phys., 2021, 154, 230903 CrossRef CAS PubMed.
- Z. Zhang, Q. Liu, H. Wang, C. Lu and C.-K. Lee, Motif-based graph self-supervised learning for molecular property prediction, Adv. Neural Inf. Process., 2021, 34, 15870–15882 Search PubMed.
- M. Ceriotti, C. Clementi and O. Anatole von Lilienfeld, Machine learning meets chemical physics, 2021 Search PubMed.
- J. A. Keith, et al., Combining machine learning and computational chemistry for predictive insights into chemical systems, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS.
- X. Fang, et al., Geometry-enhanced molecular representation learning for property prediction, Nat. Mach. Intell., 2022, 4, 127–134 CrossRef.
- D. Wang, et al., Efficient sampling of high-dimensional free energy landscapes using adaptive reinforced dynamics, Nat. Comput. Sci., 2022, 2, 20–29 CrossRef CAS.
- A. Madani, et al., Large language models generate functional protein sequences across diverse families, Nat. Biotechnol., 2023, 1–8 Search PubMed.
- M. J. Kusner, B. Paige and J. M. Hernández-Lobato, Grammar variational autoencoder, in International conference on machine learning, PMLR, 2017, pp. 1945–1954 Search PubMed.
- R. Gómez-Bombarelli, et al., Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- J. You, B. Liu, Z. Ying, V. Pande and J. Leskovec, Graph convolutional policy network for goal-directed molecular graph generation, in Advances in neural information processing systems, 2018, pp. 6410–6421 Search PubMed.
- R.-R. Griffiths and J. M. Hernández-Lobato, Constrained Bayesian optimization for automatic chemical design using variational autoencoders, Chem. Sci., 2020, 11, 577–586 RSC.
- C. Shi, et al., Graphaf: a flow-based autoregressive model for molecular graph generation, International Conference on Learning Representations, 2020 Search PubMed.
- N. Gebauer, M. Gastegger and K. Schütt, Symmetry-adapted generation of 3d point sets for the targeted discovery of molecules, in Advances in Neural Information Processing Systems, 2019, pp. 7566–7578 Search PubMed.
- J. Wang, et al., Multi-constraint molecular generation based on conditional transformer, knowledge distillation and reinforcement learning, Nat. Mach. Intell., 2021, 3, 914–922 CrossRef.
- N. W. Gebauer, M. Gastegger, S. S. Hessmann, K.-R. Müller and K. T. Schütt, Inverse design of 3d molecular structures with conditional generative neural networks, Nat. Commun., 2022, 13, 1–11 Search PubMed.
- Z. Zhang, Y. Min, S. Zheng and Q. Liu, Molecule generation for target protein binding with structural motifs, in The Eleventh International Conference on Learning Representations, 2022 Search PubMed.
- Z. Zhang and Q. Liu, Learning subpocket prototypes for generalizable structure-based drug design, ICML, 2023 Search PubMed.
- T. Ma, J. Chen and C. Xiao, Constrained generation of semantically valid graphs via regularizing variational autoencoders, Adv. Neural Inf. Process., 2018, 31 CAS , https://proceedings.neurips.cc/paper/2018/hash/1458e7509aa5f47ecfb92536e7dd1dc7-Abstract.html.
- N. De Cao and T. Kipf, Molgan: An implicit generative model for small molecular graphs. ICML 2018 workshop on Theoretical Foundations and Applications of Deep Generative Models, 2018 Search PubMed.
- C. Zang and F. Wang, Moflow: an invertible flow model for generating molecular graphs, in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020, pp. 617–626 Search PubMed.
- K. Madhawa, K. Ishiguro, K. Nakago and M. Abe, Graphnvp: An invertible flow model for generating molecular graphs, arXiv, 2019, preprint, arXiv:1905.11600, DOI:10.48550/arXiv.1905.11600.
- Y. Luo, K. Yan and S. Ji, Graphdf: A discrete flow model for molecular graph generation, in International Conference on Machine Learning, PMLR, 2021, pp. 7192–7203 Search PubMed.
- W. Jin, R. Barzilay and T. Jaakkola, Junction tree variational autoencoder for molecular graph generation, in International conference on machine learning, PMLR, 2018, pp. 2323–2332 Search PubMed.
- W. Jin, R. Barzilay and T. Jaakkola, Hierarchical generation of molecular graphs using structural motifs, in ICML, PMLR, 2020, pp. 4839–4848 Search PubMed.
- O. Ganea, et al., Geomol: Torsional geometric generation of molecular 3d conformer ensembles, Adv. Neural Inf. Process., 2021, 34, 13757–13769 Search PubMed.
- M. Xu, et al., An end-to-end framework for molecular conformation generation via bilevel programming, in International Conference on Machine Learning, PMLR, 2021, pp. 11537–11547 Search PubMed.
- C. Shi, S. Luo, M. Xu and J. Tang, Learning gradient fields for molecular conformation generation, in International Conference on Machine Learning, PMLR, 2021, pp. 9558–9568 Search PubMed.
- S. Liu, et al., Pre-training molecular graph representation with 3d geometry, International Conference on Learning Representations, 2022 Search PubMed.
- O. Mahmood, E. Mansimov, R. Bonneau and K. Cho, Masked graph modeling for molecule generation, Nat. Commun., 2021, 12, 1–12 Search PubMed.
- M. Hoffmann and F. Noé, Generating valid euclidean distance matrices, arXiv, 2019, preprint, arXiv:1910.03131, DOI:10.48550/arXiv.1910.03131.
- E. Hoogeboom, V. G. Satorras, C. Vignac and M. Welling, Equivariant diffusion for molecule generation in 3d, International Conference on Machine Learning, 2022 Search PubMed.
- Y. Luo and S. Ji, An autoregressive flow model for 3d molecular geometry generation from scratch, in International Conference on Learning Representations, 2021 Search PubMed.
- S. Luo, J. Guan, J. Ma and J. Peng, A 3d generative model for structure-based drug design, Adv. Neural Inf. Process., 2021, 34, 6229–6239 Search PubMed.
- O. Méndez-Lucio, M. Ahmad, E. A. del Rio-Chanona and J. K. Wegner, A geometric deep learning approach to predict binding conformations of bioactive molecules, Nat. Mach. Intell., 2021, 3, 1033–1039 CrossRef.
- M. Liu, Y. Luo, K. Uchino, K. Maruhashi and S. Ji, Generating 3d molecules for target protein binding, International Conference on Machine Learning, 2022 Search PubMed.
- X. Peng, et al., Pocket2mol: Efficient molecular sampling based on 3d protein pockets, International Conference on Machine Learning, 2022 Search PubMed.
- C. Vignac, N. Osman, L. Toni and P. Frossard, Midi: Mixed graph and 3d denoising diffusion for molecule generation, arXiv, 2023 preprint, arXiv:2302.09048, DOI:10.48550/arXiv.2302.09048.
- Y. Liu, et al., Spherical message passing for 3d graph networks, in International Conference on Learning Representations, 2022 Search PubMed.
- V. G. Satorras, E. Hoogeboom, F. B. Fuchs, I. Posner and M. E. Welling, (n) equivariant normalizing flows, NeurIPS, 2021 Search PubMed.
- A. Grosnit, et al., High-dimensional Bayesian optimisation with variational autoencoders and deep metric learning, arXiv, 2021, preprint, arXiv:2106.03609, DOI:10.48550/arXiv.2106.03609.
- P. Notin, J. M. Hernández-Lobato and Y. Gal, Improving black-box optimization in vae latent space using decoder uncertainty, Adv. Neural Inf. Process., 2021, 34, 802–814 Search PubMed.
- N. Maus, et al., Local latent space Bayesian optimization over structured inputs, Adv. Neural Inf. Process., 2022, 35, 34505–34518 Search PubMed.
- N. Maus, K. Wu, D. Eriksson and J. Gardner, Discovering many diverse solutions with Bayesian optimization, Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, ed. F. Ruiz, J. Dy and J.-W. van de Meent, PMLR, 2023, vol. 206, pp. 1779–1798 Search PubMed.
- G. Papamakarios, E. Nalisnick, D. J. Rezende, S. Mohamed and B. Lakshminarayanan, Normalizing flows for probabilistic modeling and inference, J. Mach. Learn Res., 2021, 22, 1–64 Search PubMed.
- L. Dinh, D. Krueger and Y. Bengio, Nice: Non-linear independent components estimatio, arXiv, 2014, preprint, arXiv:1410.8516, DOI:10.48550/arXiv.1410.8516.
- L. Dinh, J. Sohl-Dickstein and S. Bengio, Density estimation using real nvp, International Conference on Learning Representations, 2017 Search PubMed.
- N. M. O'Boyle, et al., Open babel: An open chemical toolbox, J. Cheminformatics, 2011, 3, 1–14 CrossRef PubMed.
- Y. Kim and W. Y. Kim, Universal structure conversion method for organic molecules: from atomic connectivity to three-dimensional geometry, Bull. Korean Chem. Soc., 2015, 36, 1769–1777 CrossRef CAS.
- V. Garcia Satorras, E. Hoogeboom, F. Fuchs, I. Posner, M. E. Welling, E(n) Equivariant Normalizing Flows, Advances in Neural Information Processing Systems, ed. M. Ranzato, A. Beygelzimer, Y. Dauphin, P.S. Liang and J. Wortman Vaughan, Curran Associates, Inc., 2021, vol. 34, pp. 4181–4192 Search PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1, 1–7 Search PubMed.
- Q. Sun, et al., Pyscf: the python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- Q. Sun, et al., Recent developments in the pyscf program package, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- A. C. Anderson, The process of structure-based drug design, Chem. Biol., 2003, 10, 787–797 CrossRef CAS PubMed.
- A. Tripathi and V. A. Bankaitis, Molecular docking: from lock and key to combination lock, J. Mol. Med. Clin. Appl., 2017, 2 DOI:10.16966/2575-0305.106.
- A. Alon, et al., Structures of the σ2 receptor enable docking for bioactive ligand discovery, Nature, 2021, 600, 759–764 CrossRef CAS PubMed.
- P. G. Francoeur, et al., Three-dimensional convolutional neural networks and a cross-docked data set for structure-based drug design, J. Chem. Inf. Model., 2020, 60, 4200–4215 CrossRef CAS PubMed.
- G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Quantifying the chemical beauty of drugs, Nat. Chem., 2012, 4, 90–98 CrossRef CAS PubMed.
- O. Trott and A. J. Olson, Autodock vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading, J. Comput. Chem., 2010, 31, 455–461 CAS.
- A. Alhossary, S. D. Handoko, Y. Mu and C.-K. Kwoh, Fast, accurate, and reliable molecular docking with quickvina 2, Bioinformatics, 2015, 31, 2214–2216 CrossRef CAS PubMed.
- G. Landrum, et al., Rdkit: A software suite for cheminformatics, computational chemistry, and predictive modeling, Greg. Landrum, 2013, 8, 31 Search PubMed.
- A. P. Bento, et al., An open source chemical structure curation pipeline using rdkit, J. Cheminf., 2020, 12, 1–16 Search PubMed.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, Uff, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- M. Ragoza, T. Masuda and D. R. Koes, Generating 3d molecules conditional on receptor binding sites with deep generative models, Chem. Sci., 2022, 13, 2701–2713 RSC.
- S. Axelrod and R. Gomez-Bombarelli, Geom, energy-annotated molecular conformations for property prediction and molecular generation, Sci. Data, 2022, 9, 1–14 CrossRef PubMed.
- X. Peng, J. Guan, Q. Liu and J. Ma, Moldiff: Addressing the atom-bond inconsistency problem in 3d molecule diffusion generation, Proceedings of the 40th International Conference on Machine Learning, ed. A. Krause, E. Brunskill, K. Cho, B. Engelhardt, S. Sabato and J. Scarlett, PMLR, 2023, vol. 202, pp. 27611–27629 Search PubMed.
- M. Steinegger and J. Söding, Mmseqs2 enables sensitive protein sequence searching for the analysis of massive data sets, Nat. Biotechnol., 2017, 35, 1026–1028 CrossRef CAS PubMed.
- G. Simm, R. Pinsler and J. M. Hernández-Lobato, Reinforcement learning for molecular design guided by quantum mechanics, in International Conference on Machine Learning, PMLR, 2020, pp. 8959–8969 Search PubMed.
- A. Vaswani, et al., Attention is all you need, Adv. Neural Inf. Process., 2017, 30, 5998 Search PubMed.
- D. P. Kingma and J. Ba, Adam: A method for stochastic optimization, arXiv, 2014, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- A. I. Cowen-Rivers, et al., Hebo: pushing the limits of sample-efficient hyper-parameter optimisation, J. Artif. Intell. Res., 2022, 74, 1269–1349 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02538a |
| This journal is © The Royal Society of Chemistry 2023 |