Open Access Article
Open Access ArticleAcetate exchange mechanism on a Zr12 oxo hydroxo cluster: relevance for reshaping Zr–carboxylate coordination adaptable networks†
Meenu
Murali
a,
Christian
Bijani
a,
Jean-Claude
Daran
a,
Eric
Manoury
a and
Rinaldo
Poli
 *ab
*ab
aCNRS, LCC (Laboratoire de Chimie de Coordination), Université de Toulouse, UPS, INPT, 205 Route de Narbonne, BP 44099, F-31077, Toulouse Cedex 4, France. E-mail: rinaldo.poli@lcc-toulouse.fr
bInstitut Universitaire de France, 1, rue Descartes, 75231 Paris Cedex 05, France
First published on 4th July 2023
Abstract
The kinetics and mechanism of the acetate ligand exchange with free acetic acid in [Zr6O4(OH)4(O2CCH3)12]2, used as a molecular model of crosslink migration in [Zr6O4(OH)4(carboxylate)12−n(OH)n]-based coordination adaptable networks with vitrimer-like properties, has been thoroughly investigated by dynamic 1H NMR and DFT calculations. The compound maintains its C2h-symmetric Zr12 structure in CD2Cl2 and C6D6, while it splits into its Zr6 subunits in CD3OD and D2O. In the Zr12 structure, the topologically different acetates (3 chelating, 6 belt-bridging, 2 intercluster-bridging and 1 inner-face-bridging) of the Zr6 subunits behave differently in the presence of free CH3COOH: very fast exchange for the chelating (coalesced resonance at room temperature), slower exchange for the belt-bridging (line broadening upon warming), no observable exchange up to 65 °C (by EXSY NMR) for the intercluster- and inner-face-bridging. The rates of the first two exchange processes have zero-order dependence on [CH3COOH]. Variable-temperature line broadening studies yielded ΔH‡ = 15.0 ± 0.4 kcal mol−1, ΔS‡ = 8 ± 1 cal mol−1 K−1 (−30 to +25 °C range in CD2Cl2) for the chelating acetates and ΔH‡ = 22.7 ± 1.6, 22.9 ± 2.1 and 20.6 ± 1.0 kcal mol−1 and ΔS‡ = 13 ± 5, 14 ± 6 and 9 ± 3 cal mol−1 K−1, respectively (+25 to +70 °C range in C6D6), for three distinct resonances of magnetically inequivalent belt-bridging acetates. With support of DFT calculations, these results point to an operationally associative mechanism involving a rate-determining partial dissociation to monodentate acetate, followed by rapid acid coordination and proton transfer. The cluster μ3-OH ligands accelerate the exchange processes through H-bonding stabilization of the coordinatively unsaturated intermediate. The lower exchange barrier for the chelated vs. bridging acetates is associated to the release of ring strain. The results presented in this investigation may help the interpretation of carboxylate exchange phenomena in other systems and the design of new carboxylate-based materials.
Introduction
The introduction of dynamic covalent crosslinks has a massive impact on the properties of three-dimensional polymeric materials, including reshaping, recyclability, stress relaxation and self-healing.1–4 These materials are known as Covalent Adaptable Networks (CANs). They have the same topology and properties of thermosets at low temperatures, but a dynamic and reversible crosslink migration (e.g. by transesterification, Diels–Alder, disulphide metathesis, etc.) can be activated at higher temperature, causing the materials to flow like thermoplastics. Light or the presence of additives (e.g. catalysts) may also activate crosslink exchange reactions. The mechanism of the exchange reactions leading to crosslink migration may be either dissociative (i.e. a crosslink is broken before being formed again at a different network position) or associative. The latter type of exchange maintains a constant crosslink density at elevated temperatures, and associative CANs have also been named “vitrimers”, because their high-temperature rheological behaviour is analogous to that of vitreous silica.5–7 Conversely, there is a rapid decrease of crosslink density in dissociative CANs at elevated temperatures.Coordination adaptable networks (CooANs) are a new subclass of the CAN family, in which metal complexes are used as crosslinks and the migration is due to a thermally activated exchange of coordinative bonds.8,9 Recently, we have reported CooANs based on the [Zr6O4(OH)4]12+ unit (Scheme 1A) as crosslink and on carboxylate ligand exchange with a polymer matrix that is functionalized with an excess of carboxylic acid functions (Scheme 1B and C).10 It is important to underline that the structure shown in Scheme 1A for the Zr6 crosslinker unit is ideal. Zirconium clusters with the [Zr6O4(OH)4(O2CR)12] stoichiometry have been shown to adopt at least three different types of structures. The fully symmetric (Oh) geometry shown in Scheme 1A, where each of the twelve octahedral edges of the Zr6 core is spanned by a bridging carboxylate, is featured by the acetate when crystallized from water.11 This basic architecture is also the most commonly observed one for the [Zr6O4(OH)4(O2CR)12] “secondary building units” (SBU) in a large variety of metal–organic frameworks (MOFs).12–23 Other clusters adopt a C3v-symmetrical structure with both chelating and bridging carboxylates around the [Zr6O4(OH)4]12+ core.24,25 Finally, the compounds may also adopt a C2h-symmetric structure consisting of two octahedral Zr6 clusters linked by four bridging carboxylates, [Zr6O4(OH)4(O2CR)10]2(μ-O2CR)4.24,26,27 The precise structure of this Zr12 scaffold, which also contains both chelating and edge-bridging carboxylates and is the subject of our investigation, will be detailed below.
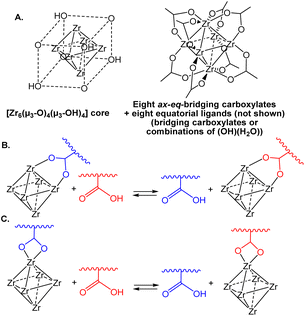 | ||
| Scheme 1 (A) Ideal structure of the [Zr6O4(OH)4(O2CR)12] crosslink in the Zr–CooAN-x materials. Exchange process for bridging (B) and chelating (C) carboxylate ligands. | ||
The observed structure of the [Zr6O4(OH)4(O2CR)12] compounds delicately depends not only on the carboxylate nature (for instance, the acrylate shows the Zr12C2h structure24 while the similar methacrylate adopts the Zr6C3v structure28), but also on the crystallization conditions: the acetate was obtained as either a Zr6 (Oh)11 or a Zr12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 compound from dichloromethane or water, respectively. The Zr6 (C3v) and Zr12 structures were shown not to interconvert under mild conditions,26 but a more recent study has demonstrated that the Zr12 molecule can be broken up into the Zr6 fragments under more forcing conditions (70 °C in the presence of free acid).29 Therefore, the harsher conditions used for the synthesis of our Zr6O4(OH)4-based 3D networks (exchange between the Zr12 acetate compound and a –COOH-functionalized acrylate–methacrylate copolymer, followed by curing at 120 °C)10 may produce all possible structures for the crosslinks and the reshaping may involve an exchange of both chelating and bridging carboxylate ligands (Scheme 1B and C, respectively). In addition, other stoichiometries may also occur by replacement of equatorial bridging acetates with the combination of monodentate OH and H2O ligands, [{Zr6O4(OH)4}(O2CR)12−n(OH)n(H2O)n], as found when n = 4 for the SBUs of certain other MOFs.21,30,31 Our CooAN materials, named Zr–CooAN-x (x = percent of polymer carboxylic functions bonded to the [Zr6O4(OH)4]12+ core), display the characteristic mechanical and rheological properties of vitrimers and could be easily reshaped at temperatures as low as 50 °C without modification of the properties for x up to 50.
26 compound from dichloromethane or water, respectively. The Zr6 (C3v) and Zr12 structures were shown not to interconvert under mild conditions,26 but a more recent study has demonstrated that the Zr12 molecule can be broken up into the Zr6 fragments under more forcing conditions (70 °C in the presence of free acid).29 Therefore, the harsher conditions used for the synthesis of our Zr6O4(OH)4-based 3D networks (exchange between the Zr12 acetate compound and a –COOH-functionalized acrylate–methacrylate copolymer, followed by curing at 120 °C)10 may produce all possible structures for the crosslinks and the reshaping may involve an exchange of both chelating and bridging carboxylate ligands (Scheme 1B and C, respectively). In addition, other stoichiometries may also occur by replacement of equatorial bridging acetates with the combination of monodentate OH and H2O ligands, [{Zr6O4(OH)4}(O2CR)12−n(OH)n(H2O)n], as found when n = 4 for the SBUs of certain other MOFs.21,30,31 Our CooAN materials, named Zr–CooAN-x (x = percent of polymer carboxylic functions bonded to the [Zr6O4(OH)4]12+ core), display the characteristic mechanical and rheological properties of vitrimers and could be easily reshaped at temperatures as low as 50 °C without modification of the properties for x up to 50.
The hypothesis of an associative ligand exchange process for these CooANs appears obvious, because a dissociative exchange would necessitate not only a preliminary ligand rearrangement from bridging or chelating to monodentate, but also heterolytic cleavage with charge separation, which is rather difficult in a low-permittivity polymer matrix. However, the associative nature of the carboxylate exchange was not demonstrated.
The carboxylate exchange reaction for this family of [Zr6O4(OH)4] clusters32,33 is also a key step in the synthesis13,34 and post-modification35,36 of Zr-based metal–organic frameworks (MOFs), cluster-reinforced organic polymers37,38 and other materials,39 as well as in the catalysed oleic acid esterification29 and carboxylic acid amidation.40,41 Detailed mechanistic studies, however, are lacking. Indeed, such studies are rare for any metal. An example is the degenerative exchange between the mononuclear cadmium complex [(TmtBu)Cd(O2CC6H4-4-F)] (TmtBu = tris(2-mercapto-1-tert-butylimidazolyl)hydroborato) and free 4-F-C6H4COOH, for which the non-zero order in free acid suggested an associative mechanism, but activation parameters were not reported.42
For a few [Zr6O4(OH)4]-based carboxylates, the reaction has been studied by one- and two-dimensional NMR spectroscopy.26,37,43 Notably, for the C2h-symmetric Zr12 propionate cluster, it was shown that only 9 out of 12 propionate ligands are exchanged by acetic acid.26 An associative mechanism, with an intermediate containing the incoming carboxylic acid hydrogen bonded to a monocoordinated carboxylate was proposed.32,37 A kinetic investigation was carried out for the exchange of benzene dicarboxylate with 2,5-pyridinedicarboxylic acid in the UiO-66 MOF in DMF, which features a [Zr6O4(OH)4]12+ SBU, yielding the activation parameters ΔH‡ = 86.6 kJ mol−1 and ΔS‡ = −72 J K−1 mol−1.36 A subsequent DFT investigation on a model Zr6O4(OH)4(O2CR)12 cluster (R = –CMe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, Oh symmetry) pointed out the role of acid catalysis for the exchange process, which occurs via an associative substitution mechanism.44
CH2, Oh symmetry) pointed out the role of acid catalysis for the exchange process, which occurs via an associative substitution mechanism.44
In the present contribution, we address the exchange processes of Scheme 1B and C by a detailed variable temperature NMR investigation on [Zr6O4(OH)4(O2CMe)12]2 as a model cluster of our [Zr6O4(OH)4]-based vitrimers, with backup by DFT calculations on yet simpler models.
Results and discussion
Structure of the [Zr6O4(OH)4(O2CMe)12]2 compound
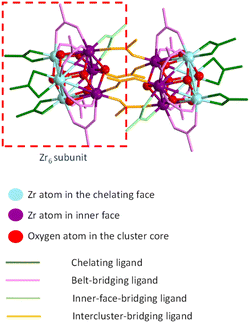
The [Zr6O4(OH)4(O2CMe)12]2 cluster compound used in the present investigation was synthesized on the basis of the previously reported method.26 Thus, it contains co-crystallized acetic acid and dichloromethane molecules as revealed by the previous structural determination by X-ray diffraction on a crystal directly obtained from the synthesis. However, a new crystal has also been obtained by the addition of excess acetic acid to a methanolic solution. Its molecular structure, determined by X-ray diffraction (crystal data in Table S1†), is identical to that reported in the previous paper, but the crystal habit is different, with a different content of co-crystallized interstitial molecules (four molecules of CH3COOH and two of water as well-behaved interstitial molecules). Additional disordered molecules are certainly present, because diffused electron density that could not be properly modelled remained in the final refinement (see Experimental section for further details). A comparison between the most relevant metric parameters of the two [Zr6O4(OH)4(O2CMe)12]2 structures, given in the ESI (Table S2†), shows generally good agreement.The structure can be described as a dimer of two Zr6 octahedra, in which the triangular faces are alternatively capped by μ3-O and μ3-OH groups. The ideal C2h molecular symmetry is reduced to an inversion centre (Ci) in the crystal, thus a full Zr6 subunits constitutes the crystallographic asymmetric unit. Like in previous structures of compounds having the same stoichiometry with various carboxylates, the μ3-O and μ3-OH ligand can be easily distinguished by the Zr–O distances, which are significantly shorter for Zr-(μ3-O) (average 2.07 ± 0.02 Å) than for Zr-(μ3-OH) (average 2.26 ± 0.06 Å). It is useful to classify the Zr atoms in each octahedron in two separate sets (see colour coding in the schematic diagram of Fig. 1): three atoms in the outer triangular face (light blue) and three in the opposite inner triangular face (purple), which faces the equivalent purple atoms in the other Zr6 subunit. There is distinct difference between the three different types of Zr⋯Zr distances: longer between inner-face atoms (3.56 ± 0.03 Å), intermediate between outer-face atoms (3.52 ± 0.01 Å) and shorter for distances connecting one inner-face and one outer-face Zr atom (belt distances, 3.49 ± 0.02 Å). Four different types of carboxylate ligands can be distinguished: chelating (green colour in Fig. 1, all bonded to the Zr atoms in the outer triangular faces) and three topologically different bridging ligands (pink, light green and orange). The belt-bridging ligands (6 per Zr6 subunit, pink) connect one atom of the outer triangular face with one atom of the opposite inner face. The inner-face-bridging ligands (light green, only one per Zr6 subunit) connect two atoms of the inner triangular face. Finally, the inter-cluster-bridging ligands (four overall, orange) link together the two Zr6 subunits. Views of the molecule with the atomic numbering scheme are available in the ESI (Fig. S1†). The Zr–O distances to the bridging acetate ligands, whether they are belt-, inner-face or intercluster-bridging, are a bit shorter (average 2.21 ± 0.02 Å) than the Zr–O distances to the chelating acetate ligands (average 2.28 ± 0.01 Å), reflecting the increased ring tension of the latter. This ring tension also results in a greater exchange rate (vide infra). One μ3-OH ligand (linking the three Zr atoms of the inner face) establishes an H-bond with an O atom of one intercluster-bridging acetate ligands (see Fig. S1†) and the other three μ3-OH ligands are proton donors in H-bonding with the interstitial molecules: two with the acetic acid molecules and one with the water molecule (see Fig. S2†). In addition, the two interstitial acetic acid molecules are proton donors in H-bonding with two of the three chelating acetate ligands.
1H NMR properties in various solvents
1H NMR gives useful information on the structure of the compound in solution. For the C2h-symmetric Zr12 structure, in addition to the topological difference described above (Fig. 1), the C2h symmetry further splits the chelating ligands of each Zr6 subunit into two inequivalent sets (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and the belt-bridging ligands into three sets (2
1) and the belt-bridging ligands into three sets (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2). As a result, seven distinct resonances should be observed in a 2
2). As a result, seven distinct resonances should be observed in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The C3v Zr6 geometry, on the other hand, should yield only three resonances in a 3
1 ratio. The C3v Zr6 geometry, on the other hand, should yield only three resonances in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio, whereas all acetate ligands are equivalent in the Oh Zr6 structure, yielding only one resonance.
3 ratio, whereas all acetate ligands are equivalent in the Oh Zr6 structure, yielding only one resonance.
A previously reported 1H NMR spectrum recorded in the temperature range −40 to +20 °C in CD2Cl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 was described as having seven methyl resonances at −40 °C (integrals given as 2
26 was described as having seven methyl resonances at −40 °C (integrals given as 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in accordance with the expected C2h symmetry) and only five remained visible at 20 °C. Tentative assignments were made on the basis of a 1H/13C HMBC spectrum, but the presence of free acetic acid, which indeed was co-crystallized with the Zr12 cluster, was not considered. A more recent investigation by room-temperature 1H NMR-DOSY in CDCl3 has shown that the highest-frequency resonance in the acetate Me region has a greater diffusion coefficient and was suggested to correspond to free acetic acid.29 Our new investigations (vide infra) have allowed the complete assignment of all these resonances.
1 in accordance with the expected C2h symmetry) and only five remained visible at 20 °C. Tentative assignments were made on the basis of a 1H/13C HMBC spectrum, but the presence of free acetic acid, which indeed was co-crystallized with the Zr12 cluster, was not considered. A more recent investigation by room-temperature 1H NMR-DOSY in CDCl3 has shown that the highest-frequency resonance in the acetate Me region has a greater diffusion coefficient and was suggested to correspond to free acetic acid.29 Our new investigations (vide infra) have allowed the complete assignment of all these resonances.
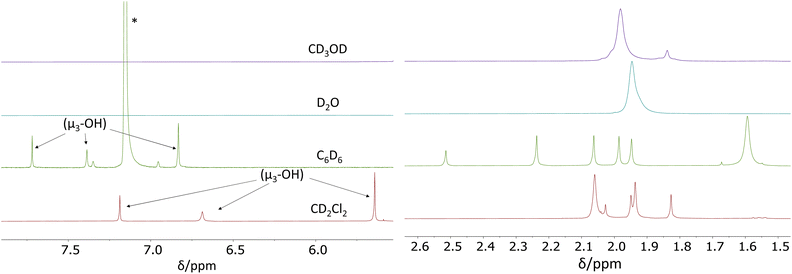
We have now carried out more detailed investigations of the 1H NMR properties of this compound in various solvents, using the material synthesized according to the literature method (i.e. containing co-crystallized acetic acid and dichloromethane molecules).26Fig. 2 shows the acetate CH3 and OH regions of the 1H NMR spectra recorded at room temperature in CD2Cl2, C6D6, D2O and CD3OD. The full individual spectra are provided in the ESI (Fig. S3–S6†). In CD2Cl2, the acetate Me region matches the spectra reported in the above-cited earlier studies.26,29 Setting the resonance at δ 1.83 as 6H (two acetates), the sum of the two overlapping resonances at δ 1.94 and 1.95 (which were shown in one of the previous studies26 to split into three equivalent resonances at −40 °C) integrate as 18H (six acetates) and the smaller δ 2.03 resonance as 3H (1 acetate). These four bands account for nine acetate ligands in total. The expected pattern for the C2h Zr12 structure requires three additional acetate per Zr6 subunit, which must therefore be part of the remaining more intense and broader δ 2.06 resonance, the integrated intensity of which corresponds to ca. 22 protons. Considering also the greater diffusion coefficient measured for this band at room temperature,29 we assign this more intense resonance to the sum of three chelating acetate ligands (9H) and free acetic acid (13H) in rapid exchange. Further investigations, detailed in the next section, confirm this proposition. Thus, the amount of free acid is estimated as ca. 4.3 molecules per Zr6 subunit. Three additional resonances (apparently not previously reported for this compound) are visible at δ 7.18, 6.69 and 5.64 and are assigned to the μ3-OH ligand in the cluster core. They have relative intensities of 1H, 1H and 2H, respectively, as expected for the stoichiometry and C2h symmetry of this compound (see Fig. S3†). It is to be noted that an OH resonance for the co-crystallized acetic acid could not be detected.
The 1H NMR spectrum in C6D6 exhibits a similar pattern as in CD2Cl2: three different μ3-OH resonances in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio (at δ 7.72, 7.39 and 6.83, respectively), six different methyl resonance peaks at δ 2.51 (3H), 2.24 (6H), 2.06 (6H), 1.88 (6H), 1.94 (6H), and a last more intense and broader resonance at δ 1.59, integrating for ca. 24H (9H of the three chelating acetates plus 15H for free acetic acid, in rapid exchange), from which we deduce five free CH3COOH molecules per Zr6 subunit (see Fig. S4†). An OH resonance for the free acetic acid molecules is again undetected.
2 ratio (at δ 7.72, 7.39 and 6.83, respectively), six different methyl resonance peaks at δ 2.51 (3H), 2.24 (6H), 2.06 (6H), 1.88 (6H), 1.94 (6H), and a last more intense and broader resonance at δ 1.59, integrating for ca. 24H (9H of the three chelating acetates plus 15H for free acetic acid, in rapid exchange), from which we deduce five free CH3COOH molecules per Zr6 subunit (see Fig. S4†). An OH resonance for the free acetic acid molecules is again undetected.
The 1H NMR spectra in D2O and CD3OH are different and much simpler, consistent with the Oh Zr6 structure. No resonance is visible for the μ3-OH protons, probably because of rapid exchange with the solvent, whereas the acetate Me resonance is observed as a broad single peak at δ 1.95 with a shoulder on the high-field side in D2O. In CD3OD, the acetate Me resonance is also visible as a broad main peak at δ 1.98, but additional small peaks are present at higher fields. The shoulder in D2O and the additional peaks in CD3OD are too small to be consistent with the Me protons of free CH3COOH, given the established amount of ca. five molecules per Zr6 cluster unit (12 coordinated acetates), from which it can be deduced that there is rapid exchange between free acetic acid and all coordinated acetates. This is also confirmed by the different chemical shifts measured for solutions of acetic acid, in the absence of the Zr12 cluster, in D2O (δ 1.85) and in CD3OD (δ 2.01), in close correspondence to the values reported in the literature45 (see insets in Fig. S5 and S6†). The origin of the observed additional small resonances is not clear, but a hypothesis is the presence of stoichiometrically different compounds in small amounts, generated by acetate dissociation equilibria. It is relevant to note that a similarly complex spectrum in the acetate Me region was described for a solution generated from ZrOCl2 and excess acetic acid in a low-pH H2O/D2O mixture, presumably yielding the Oh-symmetric Zr6 species (which indeed was crystallized under closely related conditions).11 Note that the simpler spectra observed in D2O and CD3OD may also result from an accelerated dynamic exchange between free acetic acid and all the coordinated acetate ligands in the C2h-symmetric Zr12 structure.
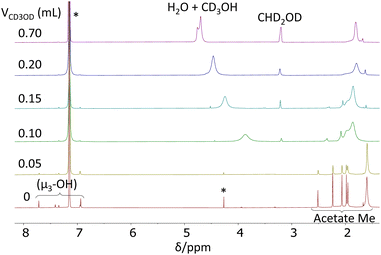
In order to learn more about the possible Zr6(Oh)/Zr12(C2h) rearrangement, an additional 1H NMR investigation was carried out at room temperature in C6D6/CD3OD mixture of different compositions. The results are shown in Fig. 3. Relative to the spectrum in neat C6D6 (Fig. 3a), the addition of the first 0.05 mL of CD3OD to the NMR tube resulted in the broadening of all resonances in an approximately equivalent fashion (average increase of 167 ± 27% inclusive of the μ3-OH and acetate Me resonances), except for the broader resonance at δ 1.60, which becomes 18% sharper (Fig. 3b). This result demonstrates that deuterated methanol accelerates the Oh–C2h structural rearrangement and not just the selective acetate ligand exchange, otherwise there would be no broadening effect on the μ3-OH resonances. By the same token, a selective H/D exchange at the μ3-OH positions, without converting the C2h structure into a more symmetric one, would not broaden the acetate resonances. The sharpening of the δ 1.60 resonance is due to the fact that this is already a coalesced average of the free acetic acid and chelating acetate ligand resonances, thus the sharpening effect of this accelerated exchange predominates over the broadening effect of the accelerated exchange between the free acetic acid and the other acetate ligands. The continued addition of 0.05 mL aliquots of CD3OD results in the disappearance of the resonances characteristic of the C2h structure and convergence of the spectrum towards that observed in neat CD3OD (Fig. S6†). Note also that the μ3-OH resonances disappear rather soon, after addition of the second aliquot of CD3OD (Fig. 3c).
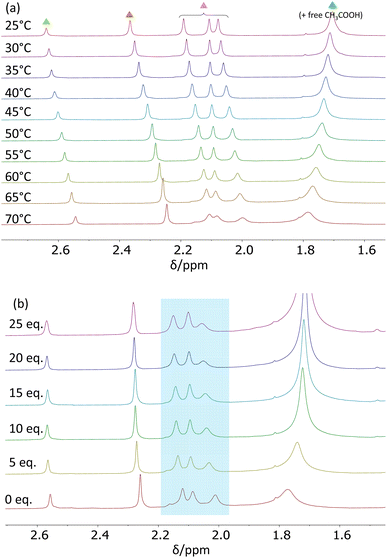
Kinetic investigations in CD2Cl2
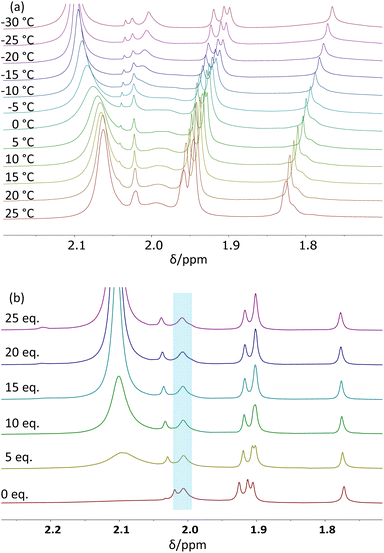
A variable temperature 1H NMR investigation was carried out for the Zr12 cluster in CD2Cl2 at 5 °C intervals between 25 and −30 °C. The observed behaviour in the acetate Me resonance region (see Fig. 4a) matches that reported in the previous study.26 The two partially overlapping resonances in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio observed at δ 1.96 and 1.94 at 25 °C slightly shift to lower frequencies upon cooling, while resonance splitting occurs to yield an overall 1
2 ratio observed at δ 1.96 and 1.94 at 25 °C slightly shift to lower frequencies upon cooling, while resonance splitting occurs to yield an overall 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 pattern. This behaviour is not a result of decoalescence, but rather of the removal of accidental degeneracy, as indirectly suggested by the corresponding behaviour in C6D6 (vide infra). On the other hand, the strong resonance observed at δ 2.06 at 25 °C broadens upon cooling and decoalesces below −10 °C to generate three separate resonances, which then sharpen again upon further cooling. The more intense of these resonances converges to δ 2.10 at −30 °C and is assigned to free CH3COOH, while the other two (larger band with shoulder on the high-field side) converge to δ 2.00. The assignment of the δ 2.10 resonance to free CH3COOH, which was already suggested by the previous DOSY investigation (though only for the coalesced band at room temperature), has been confirmed by measurements carried out in the presence of variable free acetic acid amounts, as well as by a DOSY spectrum at low temperature (vide infra). The assignment of the other two decoalesced bands (2
1 pattern. This behaviour is not a result of decoalescence, but rather of the removal of accidental degeneracy, as indirectly suggested by the corresponding behaviour in C6D6 (vide infra). On the other hand, the strong resonance observed at δ 2.06 at 25 °C broadens upon cooling and decoalesces below −10 °C to generate three separate resonances, which then sharpen again upon further cooling. The more intense of these resonances converges to δ 2.10 at −30 °C and is assigned to free CH3COOH, while the other two (larger band with shoulder on the high-field side) converge to δ 2.00. The assignment of the δ 2.10 resonance to free CH3COOH, which was already suggested by the previous DOSY investigation (though only for the coalesced band at room temperature), has been confirmed by measurements carried out in the presence of variable free acetic acid amounts, as well as by a DOSY spectrum at low temperature (vide infra). The assignment of the other two decoalesced bands (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to the three chelating acetate ligands is based on the reasonable assumption that chelating ligands are more labile than bridging ones, as further supported by the DFT calculations (also described below).
1) to the three chelating acetate ligands is based on the reasonable assumption that chelating ligands are more labile than bridging ones, as further supported by the DFT calculations (also described below).
The temperature-dependent spectra in the μ3-OH region are shown in Fig. S7.† The three resonances shift with temperature but their line shape and relative intensity do not change. The upper-frequency resonance (relative intensity 1) shifts only slightly upon cooling in the lower frequency direction, whereas the other two resonances (relative intensities of 1 and 2) are strongly shifted to higher frequencies, consistent with their greater exposure to intermolecular H-bonding with the acetic acid molecules, which becomes entropically less disfavoured at lower temperatures. This leads to the clear assignment of the upper-frequency resonance (at δ 7.20 at 25 °C) to the μ3-OH ligand that caps the inner face (O135 in Fig. S1†), which is H-bonded to one of the four intercluster-bridging acetate ligands and is sterically protected by these bridging ligands from additional intermolecular H-bonds.
Line-shape simulations of the acetate Me resonances between −25 and 15 °C (Fig. S8†) afforded temperature-dependent pseudo-first-order rate coefficients related to the average lifetime of the chelating acetate sites (Table S3†). In order to establish the true rate coefficient of the exchange process, it was necessary to verify the reaction order in acetic acid. For this purpose, additional experiments were conducted at −20 °C with variable amounts of added acetic acid (0–5 μL, corresponding to 0–25 equivalents with respect to the Zr12 unit). The corresponding spectra are shown in Fig. 4b. At this temperature, the chelating acetate resonances (highlighted by the blue box) are decoalesced from the free acid resonance and sufficiently sharp for their linewidth to be measured. The amount of added free acid has essentially no effect on the linewidth of these resonance (see Fig. S9†), thus establishing a zero-order dependence of the lifetime of these ligand sites on the acid concentration. Hence, the pseudo-first-order rate coefficient derived from the average lifetime of the chelating ligand sites also corresponds to the true site exchange rate coefficient, establishing the non-involvement of free acetic acid in the rate-determining step of the process, which therefore must have a dissociative character. In addition, the Eyring analysis of the site exchange rate coefficient as a function of temperature (Fig. S10†) furnished the activation data ΔH‡ = 15.0 ± 0.4 kcal mol−1 and ΔS‡ = 8 ± 1 cal mol−1 K−1. The slightly positive activation entropy is consistent with the dissociative nature of the rate-determining transition state, in agreement with the zero order in free acid.
Further analysis of the spectra recorded at −20 °C with variable amounts of added free CH3COOH in the μ3-OH region (Fig. S11†) confirms the assignment of the three resonances made on the basis of the temperature-dependent behaviour: the highest-frequency resonance (δ 7.10 in the absence of added acetic acid, intensity 1) is unaltered by the added acid, consistent with its assignment to the inner-face-capping ligand, whereas the other two resonances (δ 6.91, intensity 1, and 5.86, intensity 2, in the absence of added acid) are considerably and progressively shifted to higher frequencies as increasing amounts of free acid are added.
Additional 1H experiments were carried out using EXSY and DOSY pulse sequences. An EXSY spectrum was first recorded at −80 °C (Fig. S12a†) to verify that the free acid/chelating acetate exchange is completely frozen under these conditions (absence of cross-peaks). At this temperature, the DOSY spectrum (Fig. S13†) shows that the highest-frequency resonance in the Me region (which is at δ 2.09 at this temperature) corresponds to a much greater diffusion coefficient (D = 1.55 × 10−10 m2 s−1) than the other resonances, consistent with its assignment to free CH3COOH. Interestingly, this spectrum also reveals a small resonance at δ 2.03 that does not belong to the C2h Zr12 molecule and that has a slightly higher associated diffusion coefficient (D = 4.90 × 10−11 m2 s−1) than the average one of the Zr12 cluster acetate Me resonances, (4.06 ± 0.16) × 10−11 m2 s−1. This δ 2.03 resonance is also clearly visible in some of the other spectra recorded at different temperatures (e.g. Fig. S7† between +10 and −30 °C) and its chemical shift is essentially temperature-independent. Given the diffusion coefficient, it seems logical to assign this resonance to a small equilibrium amount of the Zr6Oh structure, since its chemical shift closely corresponds to those observed in D2O (Fig. S5†) and CD3OD (Fig. S6†), where the compound exists in this symmetric geometry.
Finally, the EXSY spectrum recorded at 25 °C (Fig. S12b†), where the free acetic acid and chelating acetate resonances are coalesced, reveals additional dynamic behaviour, which involves the already coalesced resonance and those in the δ 1.94–1.96 range, but not that at δ 1.82. For the last Zr12 acetate Me resonance (one acetate per Zr6 subunit) at δ 2.04, the presence of exchange is unclear from this spectrum because of overlap of the other stronger cross-resonances. It seems reasonable to deduce that the three resonances in the δ 1.94–1.96 range (integrating for 6H each) correspond to the belt-bridging acetates and that at δ 1.82 (intensity 6H) is due to the intercluster-bridging acetates, because of their different chemical shift ranges and higher propensity of the former to exchange with free acetic acid. This leaves, by exclusion, the assignment of the δ 2.04 (intensity 3H) resonance to the inner-face-bridging acetate ligand. Further investigations of the higher-temperature ligand exchange are prevented by the low boiling point of dichloromethane. Therefore, this phenomenon has been further investigated in C6D6 (next section).
To summarize this section, the collective acquired data have allowed full assignment of all resonances of the C2h Zr2 molecule as shown in Fig. 5, using the representative spectrum recorded at −20 °C without added acetic acid (Fig. 4b and S9†).
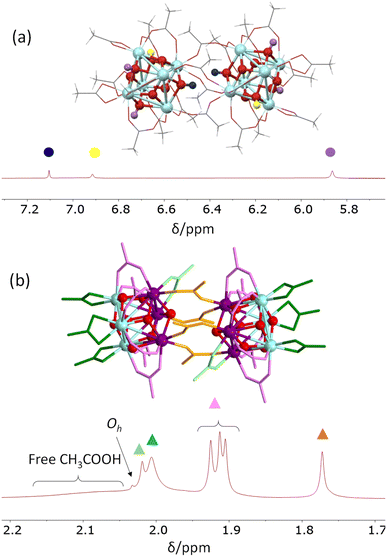 | ||
| Fig. 5 Assignment of all proton resonances observed in CD2Cl2 at −20 °C for dissolved crystals of [Zr6O4(OH)4(O2CMe)12]2 (5.3 mg in 0.8 mL). (a) μ3-OH resonance region; (b) acetate resonance region. | ||
Kinetic investigations in C6D6
The decoalescence of the more intense resonance at δ 1.59, which is assigned to the rapidly exchanging free acetic acid and chelating acetate Me protons, could not be investigated in this solvent because of the freezing point limitation (5.5 °C). Spectra were recorded in the 25–70 °C range. The acetate Me region (Fig. 6a) shows, in addition to a slight temperature dependence of the chemical shifts, progressive broadening of the three (integrating for 6H each) resonances in the δ 2.2–2.0 range and of the coalesced (free acid – chelating acetates) resonance, whereas the linewidths of the other two resonances (integrating for 6H and 3H) remain essentially unchanged. By comparison with the room-temperature EXSY spectrum in CD2Cl2, the three resonances in the δ 2.2–2.0 range can therefore be assigned to the belt-bridging ligands. The relative integrated intensities allow all other assignments: the δ 2.64 resonance (3H) to the inner-face-bridging acetate and the δ 2.37 resonance (6H) to the intercluster-bridging acetates. The temperature dependence of all linewidths, obtained by spectral simulation (Fig. S15†), is illustrated in Fig. S16† and yields the pseudo-first-order exchange rate coefficients collected in Table S4.† This variable-temperature line-broadening study thus confirms that the intercluster-bridging acetates do not rapidly exchange with free acid and the same is clearly shown for the inner-face-bridging acetate ligand. The possible occurrence of exchange processes for these two sites at a higher temperature was further probed by EXSY, which can access dynamic phenomena occurring on longer timescales, at 65 °C. However, no cross-resonances involving the intercluster- and inner-face-bridging acetate resonances are visible in the resulting spectrum (Fig. S17†).The effect of temperature on the μ3-OH region in C6D6 (Fig. S14†) is similar to that observed in CD2Cl2 (Fig. S7†): the resonance of the inner-face-capping OH ligand (at δ 7.84, intensity 1H) remains largely unaffected, whereas the other two (at δ 7.54, intensity 1H and at δ 7.07, intensity 2H) shift to lower frequencies at higher temperatures, due to the weakening of the intermolecular H-bonding interactions. However, a new phenomenon is also revealed by this high-temperature investigation. The intermediate-field resonance broadens and is no longer visible at T ≥ 50 °C, but probably only because it is overshadowed by the stronger solvent resonance (at least at intermediate temperatures) and further broadened. More interestingly, the upper-field resonance, which exhibits a very strong temperature shift, splits into two unequal intensity bands at T ≥ 50 °C. The sum of the two band intensities remains equal to 2H but the relative intensities change: the upper field one is more prominent at lower temperatures and vice versa. This behaviour is triggered at the same temperature as the exchange of the six belt-bridging ligands, thus the two phenomena may be correlated, but we have no solid evidence of the second species identity. A possibility, suggested by the DFT investigation presented below, is an intermediate of the exchange process, i.e.A (Scheme 2). Whatever this species is, however, the structural change affects the chemical shifts of all resonances in a very minor way (visible only for the μ3-OH resonance of intensity 2H, undetectable for all the others).
The rate law for the acetate site exchange processes involving the belt-bridging ligands was established, like for the above-described site exchange of the chelating acetates in CD2Cl2, by examining the effect of variable amounts of added acetic acid on the resonance linewidths. The spectra, measured at 65 °C, are collected in Fig. 6b. Like for the chelating acetate exchange process, the amount of excess acid has essentially no effect on the linewidth of the three belt-bridging acetate resonances involved in the exchange (highlighted in Fig. 6b by the blue box, see analysis in Fig. S19†), establishing a zero-order dependence on the free acid. The Eyring plots of the rate coefficients (Fig. S20†), limited to the 313–343 K range, yields activation parameters of ΔH‡ = 22.7 ± 1.6 kcal mol−1 and ΔS‡ = 13 ± 5 cal mol−1 K−1 for the highest-frequency resonance (δ 2.19 at 25 °C), ΔH‡ = 22.9 ± 2.1 kcal mol−1 and ΔS‡ = 14 ± 6 cal mol−1 K−1 for the intermediate resonance (δ 2.11 at 25 °C) and ΔH‡ = 20.6 ± 1.0 kcal mol−1 and ΔS‡ = 9 ± 3 cal mol−1 K−1 for the lowest-frequency resonance (δ 2.08 at 25 °C). The activation data are essentially the same, within experimental error, for the three site exchange processes. The activation entropies are again significantly positive and similar to those measured for the chelating acetate exchange, suggesting again a dissociative nature of the rate-determining transition state in agreement with the zero-order dependence on free acid. The activation enthalpies for the belt-bridging acetate exchange are slightly higher than those measured for the chelating acetate exchange. Therefore, the exchange rate at the different sites is enthalpically controlled.
DFT calculations
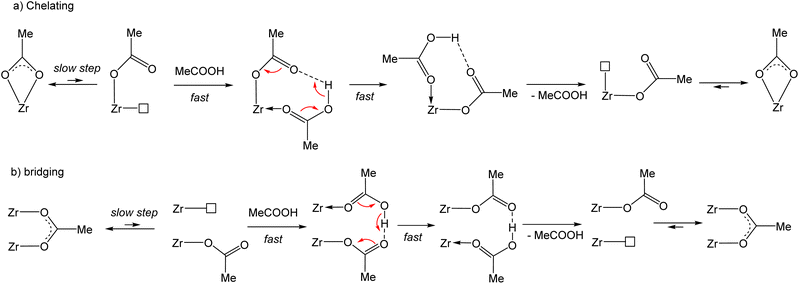
The full molecular structure of [Zr6O4(OH)4(O2CMe)12]2 constitutes a formidable challenge for DFT calculations at a decent computational level with the current computational power (details of our method are presented in the Experimental section). Consequently, simpler models have been considered. To model the chemical exchange of a chelating acetate ligand, a mononuclear model may be sufficient, but at least a dinuclear one is needed to understand the different rates of the chelating and belt-bridging exchange processes. In addition, the kinetic results indicate a similar mechanism for both coordination modes, with a dissociative character and the non-involvement of the free acid at the level of the rate-determining transition state. This leads to the working hypothesis of a rate-determining rearrangement of the outgoing acetate ligand from bidentate (chelating or bridging) to monodentate, followed by fast addition of the incoming acid molecule, proton transfer, reverse acid dissociation and back-rearrangement to the bidentate coordination mode (Scheme 3). Hence, the exchange mechanism is operationally associative, even though it entails a partial dissociation as the rate-determining step. In this respect, the previously published DFT study of the carboxylate ligand exchange in [Zr6O4(OH)4(OMc)12] (OMc = methacrylate) by Tsai et al.44 is unsatisfactory, not only because it was limited to the bridging carboxylate exchange, but also because the proposed pathway involves the participation of an external acid molecule in an associative rate-determining transition state, contrasting with the above-presented kinetic evidence of a dissociative rate-determining step.Exploratory studies were carried out for the chelated acetate exchange on mononuclear models. As shown in Fig. 7, in addition to the chelating acetate ligand, the coordination geometry of each Zr atom in the cluster outer face is completed by two μ3-OH, one μ3-O, and two belt-bridging acetate ligands. The simplest molecule to be used as a model is the homoleptic tetraacetate, [Zr(O2CMe)4]. However, the presence of oxo and hydroxo ligands in the coordination sphere of the Zr atom suggests that better models might be built by replacement of one or more acetate ligands in [Zr(O2CMe)4] with an (OH)(H2O) combination. We have therefore considered three additional model systems: a triacetate, [Zr(H2O)(OH)(O2CMe)3], a diacetate, [Zr(H2O)2(OH)2(O2CMe)2] and a monoacetate, [Zr(H2O)3(OH)3(O2CMe)]. The homoleptic tetraacetate, [Zr(O2CMe)4], is apparently unknown, but a closely related molecule, [Zr(O2CtBu)4(tBuCOOH)2], has been reported and structurally characterized.46 It features two bidentate and two monodentate pivalate ligands, plus two coordinated pivalic acid molecules, each of which is coordinated via the carbonyl O atom and interacts with one monodentate pivalate ligand via by H-bonding (O–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). This molecule is therefore a good model of the proposed associative exchange intermediate (Scheme 3a). Another known tetracarboxylate of ZrIV, Zr(XDK)2 [XDK = constrained carboxylate ligand m-xylylenediamine bis(Kemp's triacid imide)],47 features four chelating carboxylates like our chosen [Zr(O2CMe)4] model. In that compound, the tether between two carboxylate donors in the XDK ligand protects the ZrIV centre from the coordination of additional donor ligands with chelate ring opening.
C). This molecule is therefore a good model of the proposed associative exchange intermediate (Scheme 3a). Another known tetracarboxylate of ZrIV, Zr(XDK)2 [XDK = constrained carboxylate ligand m-xylylenediamine bis(Kemp's triacid imide)],47 features four chelating carboxylates like our chosen [Zr(O2CMe)4] model. In that compound, the tether between two carboxylate donors in the XDK ligand protects the ZrIV centre from the coordination of additional donor ligands with chelate ring opening.
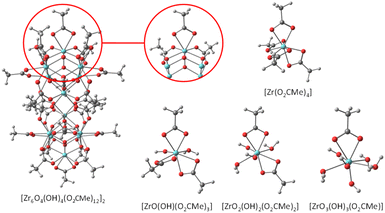 | ||
| Fig. 7 Geometries of the [Zr6O4(OH)4(O2CMe)12]2 molecule and of the mononuclear models used for the DFT calculation of the chelating acetate exchange. | ||
The partial acetate ligand dissociation from [Zr(O2CMe)4] occurs through a barrier of 10.2 kcal mol−1 to generate a [Zr(κ2-O2CMe)3(κ1-OCOMe)] intermediate, which is located at 8.5 kcal mol−1 from the starting complex (Fig. 8). Full dissociation of the acetate anion, leaving the 6-coordinate [Zr(O2CMe)3]+ complex, leads to a Gibbs energy increase of 65.5 kcal mol−1, ruling out the option of an operationally dissociative ligand exchange. Acetic acid addition to this unsaturated intermediate generates a [Zr(κ2-O2CMe)3(κ1-OCOMe)(MeCOOH)] adduct, which features an H-bonding interaction between the acetic acid ligand and the monodentate acetate, exactly as proposed in Scheme 3a and as experimentally observed for the ZrIV pivalate – pivalic acid adduct.46 The O–H and H⋯O distances in this intermediate are respectively 1.038 and 1.495 Å. Note that this adduct has a quite close Gibbs energy to that of the starting complex (see Fig. 8), giving credence to the hypothesis that the second product observed by NMR for [Zr6O4(OH)4(O2CMe)12]2 (Fig. S14b†) may indeed correspond to a [{Zr6O4(OH)4}2(O2CMe)24(MeCOOH)] complex with a partially dissociated ligand. The proton transfer from the acetic acid ligand to the monodentate acetate, resulting in a swap of the ligand nature, is extremely facile. The transition state was located as a stationary point with only one imaginary frequency along the expected O⋯H⋯O motion, with essentially equivalent O⋯H distances (1.172 and 1.248 Å). This transition state has a barely higher (0.17 kcal mol−1) electronic energy relative to the starting acetic acid adduct, but the application of the thermal correction actually places it at a lower Gibbs energy than both start and end points of the proton transfer process. The end point is essentially equivalent to the start point, with 1.495 and 1.042 Å distances in the final O⋯H–O moiety. An alternative pathway, where the acetic acid molecule assists the acetate rearrangement from chelating to monodentate via the establishment of an H-bond with the dissociating carbonyl group in [Zr(O2CMe)4], has a slightly greater barrier (see Fig. S21†). The activation cost from the [Zr(O2CMe)4]⋯MeCOOH adduct is in fact significantly reduced (to 4.6 kcal mol−1), thanks to the labilization of the Zr–O bond by the H-bond. However, this H-bonded adduct is located at 7.2 kcal mol−1 from the sum of [Zr(O2CMe)4] and ½(MeCOOH)2, which is mostly related to the cost of breaking the strong H-bond in the acetic acid dimer. Besides, this pathway would not be consistent with the observed zero-order dependence of the exchange rate on the acetic acid concentration.
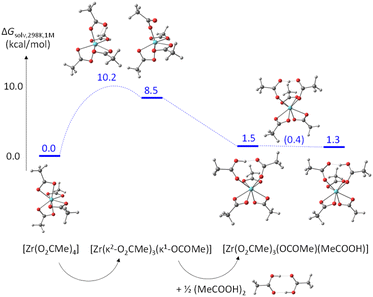 | ||
| Fig. 8 Gibbs energy profile (25 °C in dichloromethane, 1 M standard state) of the chelating acetate exchange in [Zr(O2CMe)4]. | ||
The acetate rearrangement from chelating to monodentate was also investigated for the other three mononuclear model systems shown in Fig. 7 (triacetate, diacetate and monoacetate complexes). Their corresponding Gibbs energy profiles are illustrated in Fig. 9. The chelate ring opening barrier progressively decreases as the number of acetate groups replaced by an (OH)(H2O) combination is increased. The initial drop from 10.2 kcal mol−1 for the tetraacetate to 8.2 kcal mol−1 for the triacetate can easily be understood on the basis of the assistance of the equatorial OH ligand via an H-bond with the liberated carbonyl function of the monodentate acetate ligand. This interaction provides a thermodynamic stabilization for the monodentate intermediate (only 5.1 kcal mol−1 up from the starting complex, vs. 8.5 kcal mol−1 for the tetraacetate system), but the same interaction is already present at the transition state level (OH⋯O = 2.306 Å, vs. 1.741 Å in the generated monodentate acetate complex). For the diacetate system, the additional transition state stabilization may be attributed to the presence of two stabilizing OH⋯O interactions with equatorial OH ligands, one of which is even stronger (2.278 Å) than in triacetate system (the second one has a longer distance of 2.462 Å). The closer OH⋯O approach is probably related to the release of geometrical constraints following the replacement of one small-bite acetate ligand with the monodentate OH and aqua ligands. The same principle may also rationalize the further decrease of activation barrier for the monoacetate system (OH⋯O = 2.107 Å). Electronically, the closest model to the real [Zr6O4(OH)4(O2CMe)12]2 system is probably the diacetate complex, because of the presence and orientation of two OH groups in the coordination sphere.
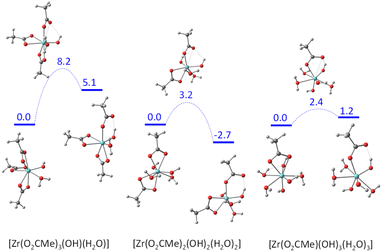 | ||
| Fig. 9 Gibbs energy profile (25 °C in dichloromethane, 1 M standard state) of the chelating acetate partial dissociation in [Zr(OH)(H2O)(O2CMe)3], [Zr(OH)2(H2O)2(O2CMe)2] and [Zr(OH)3(H2O)3(O2CMe)]. | ||
Thus, this DFT investigation suggests that the presence of the μ3-OH ligands adjacent to the chelating acetates of the [Zr6O4(OH)4(O2CMe)12]2 cluster plays a determining role in the acceleration of the ligand exchange via stabilization of the coordinatively unsaturated monodentate acetate complex by H-bonding. Additional calculations on these models were not carried out, because the tetraacetate system already shows that the follow-up steps (acetic acid coordination and proton transfer) are very facile and because we know from the line broadening kinetics investigation that the partial acetate dissociation is the rate-determining step of the exchange process.
The next step of the computational investigation was a comparison of the activation barriers for the partial dissociation of a chelating and a bridging acetate ligand in the same system, which requires the use of a system with at least two Zr atoms. The literature offers a suitable example, namely the structurally characterized dinuclear ZrIVtert-butylacetate46 (Fig. 10), which features both chelating and bridging carboxylate ligands. For the purpose of the computational investigation, the tert-butyl groups were simplified to methyl groups and, since the above-presented investigations of mononuclear systems have demonstrated a stabilizing effect of OH ligands, one bridging carboxylate ligand per Zr subunit was replaced with the (OH)(H2O) monodentate ligand combination.
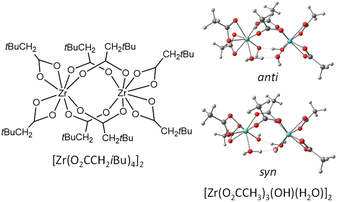 | ||
| Fig. 10 Geometries of the [Zr(O2CH2tBu)4]2 molecule and of the [Zr(O2CMe)3(OH)(H2O)] models used for the DFT calculation of the comparative chelating and bridging acetate exchange. | ||
Two different OH conformations were needed to explore the partial dissociation of both chelating and bridging ligands, as shown in Fig. 10. In the anti conformation, the O–H bonds point away from the bridging acetate ligand O atoms, thus making them unsuitable to assist the partial dissociation of the bridging acetates, but suitable to assist the partial dissociation of the chelating acetates. Conversely, the O–H bonds in the syn conformation can assist the partial dissociation of the bridging acetates but not that of the chelating ones. In both conformations, an OH⋯O interaction is established between each OH ligand as a proton acceptor and a water ligand on the other Zr center as proton donor. According to the calculations, the anti conformation is slightly more stable, 2.6 kcal mol−1 below the syn. The energy profiles of the partial acetate dissociation for the two acetates are shown in Fig. 11. The partial dissociation of the chelating acetate (left) is clearly easier than that of the bridging acetate (right), notwithstanding the ground state difference (10.4 kcal mol−1 for the bridging ligand vs. 6.7 for the chelating one). This difference is easily rationalized on the basis of the strain release associated to the opening of the 4-membered chelate ring, which is attested by the different Zr–O distances of the two bonds undergoing the dissociation process (2.306 Å for the chelating, 2.230 Å for the bridging). The release of ring strain is also reflected in the greater stabilization of the intermediate unsaturated structure (2.6 kcal mol−1 for the dissociated chelating ligand vs. 8.5 kcal mol−1 for the dissociated bridging ligand), as also signaled by the greater Zr–O bond shortening for the resulting monodentate acetate ligand (chelating: from 2.224 to 2.102 Å – shortening by 0.102 Å; bridging: from 2.144 to 2.066 Å – shortening by 0.078 Å). The greater thermodynamic stabilization of the unsaturated intermediate for the chelating acetate partial dissociation is thus reflected, in line with the Hammond principle, in a greater stabilization of the transition state. Inspection of the bonding parameters at the transition state level shows that the chelating acetate partial dissociation is characterized by an earlier transition state (shorter Zr⋯O distance, 3.084 Å, and longer O⋯H distance, 2.056 Å) than the bridging acetate partial dissociation (3.213 and 1.918 Å, respectively).
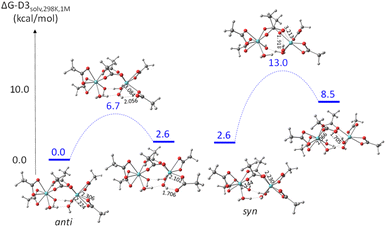 | ||
| Fig. 11 Gibbs energy profile (25 °C in dichloromethane, 1 M standard state) of the partial dissociation of chelating (left) and bridging (right) acetate in [Zr(O2CMe)3(OH)(H2O)]2. | ||
The acceleration of the acetate exchange by assistance of the cis-OH ligand, clearly demonstrated for the mononuclear models (Fig. 9) and also hinted for the dinuclear model by the H-bond stabilization of the monodentate acetate in the intermediate, provides a rationalization for the lack of observed exchange at the inner-face- and intercluster-bridging sites. Indeed, the inner-face-bridging acetate binds to Zr atoms that have only the inner-face capping μ3-OH in a cis position, suitably placed to stabilize the monodentate acetate produced by partial dissociation. However, this μ3-OH ligand is already engaged in an intramolecular H-bond with an intercluster-bridging acetate (see the structure in Fig. S1†) and is therefore not readily available to stabilize an additional proton acceptor in H-bonding. Indeed, the 1H NMR investigations of the μ3-OH resonances at variable temperature and variable free CH3COOH concentrations, both in CD2Cl2 (Fig. S9 and S10†) and in C6D6 (Fig. S12 and S13†), reveal the insensitivity of this specific μ3-OH ligand to H-bonding with external molecules, whereas the other three μ3-OH ligands are highly affected by the external environment. For the exchange of the intercluster-bridging acetates, the same considerations hold. We suggest that these ligands can be easily exchanged only after liberating the inner-face capping μ3-OH ligand from the H-bond with the intercluster-bridging acetate, which may occur upon transferring the molecule into a more strongly H-bonding solvent such as methanol or water. As we have demonstrated by the 1H NMR investigation in a mixed C6D6–CD3OD solvent with variable composition (Fig. 3), the increased H-bonding power as the CD3OD fraction is increased entails a rearrangement of the C2h Zr12 structure to produce the Oh Zr6 structure, which features rapid exchange of all equivalent bridging acetates with acetic acid.
In conclusion, the DFT calculations fully support the kinetic evidence of a rate-determining dissociative process (slightly positive activation entropy) without participation of external acid molecules (zero-order rate in the acid concentration), although the exchange is operationally associative, as previously suggested for related systems.32,37,44 In addition, they highlight the key role of the μ3-OH ligand in the stabilization of the coordinatively unsaturated intermediate by H-bonding, thus rationalizing the non-observed exchange of the inner-face- and intercluster-bridging acetates. Finally, they also rationalize the faster exchange of the chelating acetate ligands with respect to the belt-bridging ones.
Conclusions
The present contribution advances our understanding of carboxylate ligand exchange with external acid, a process that has generally been employed in the synthesis by transcarboxylation of new coordination compounds, of metal–organic frameworks, and (by us)10 of coordination adaptable networks (CooANs), as well as in the post-synthesis modification and/or reshaping of these materials. Carboxylate ligands can adopt a variety of coordination modes, including monodentate and bidentate (chelating, intra- or inter-cluster bridging). Thus, this exchange reaction has a more complex mechanistic landscape than the exchange of monodentate ligands and a limited number of fundamental studies have previously been published, as highlighted in the introduction. Using the specific C2h-symmetric [Zr6O4(OH)4(O2CMe)12]2 compound, which contains chelating, intracluster-bridging and intercluster-bridging acetates, as a model system of our Zr–CooANs, we have highlighted an operationally associative mechanism for both chelating and intracluster-bridging, which involves the dissociative acetate rearrangement from bidentate to monodentate without involvement of external free acid (zero-order rate, positive activation entropy). In addition, the investigation has pinpointed the key assistance by an OH ligand cis to the dissociating acetate donor in the stabilization of the intermediate monodentate carboxylate, rationalizing the non-observation of an exchange process for the inner-face bridging and intercluster-bridging acetate ligands. The much faster exchange of the chelating relative to the bridging acetates, both having an equally available cis OH ligand, is related to an enthalpic gain associated to the release of ring strain for the chelating ligand. Finally, the investigation has also highlighted the role of the solvent H-bonding ability for the structural rearrangement of this specific C2h-symmetric Zr12 cluster into its Zr6 subunits. The results presented in this investigation may help the interpretation of carboxylate exchange phenomena in other systems and the design of new carboxylate-based materials.Data availability
The source data related to this paper can be downloaded from https://hal.science/hal-04155107.Author contributions
MM; investigation, formal analysis, writing – original draft. CB; investigation (NMR). JCD; investigation (X-ray diffraction). EM; supervision; writing – review and editing. RP; conceptualisation, funding acquisition; investigation (DFT), writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The French National Research Agency (ANR) is gratefully acknowledged for funding this research (AFCAN program, ANR-19-CE06-0014). RP is grateful to the CALMIP mesocenter of the University of Toulouse for the allocation of computational resources.Notes and references
- C. J. Kloxin, T. F. Scott, B. J. Adzima and C. N. Bowman, Macromolecules, 2010, 43, 2643–2653 CrossRef CAS PubMed.
- C. J. Kloxin and C. N. Bowman, Chem. Soc. Rev., 2013, 42, 7161–7173 RSC.
- N. Van Herck, D. Maes, K. Unal, M. Guerre, J. M. Winne and F. E. Du Prez, Angew. Chem., Int. Ed., 2020, 59, 3609–3617 CrossRef CAS.
- M. Podgorski, B. D. Fairbanks, B. E. Kirkpatrick, M. McBride, A. Martinez, A. Dobson, N. J. Bongiardina and C. N. Bowman, Adv. Mater., 2020, 32, 1906876 CrossRef CAS PubMed.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS.
- M. Guerre, C. Taplan, J. M. Winne and F. E. Du Prez, Chem. Sci., 2020, 11, 4855–4870 RSC.
- B. Krishnakumar, R. Sanka, W. H. Binder, V. Parthasarthy, S. Rana and N. Karak, Chem. Eng. J., 2020, 385, 12382 CrossRef.
- M. Zhang, H. Yu, Q. Zou, Z.-A. Li, Y. Lai, L. Cai and P. Yin, CCS Chem., 2022, 4, 3563–3572 CrossRef CAS.
- W. Li, H.-Q. Wang, W.-T. Gao, Z. Wang, P. Xu, H. Ma and C.-H. Li, CCS Chem., 2022, 4, 3781–3797 CrossRef CAS.
- M. Murali, D. Berne, C. Joly-Duhamel, S. Caillol, E. Leclerc, E. Manoury, V. Ladmiral and R. Poli, Chem.–Eur. J., 2022, 28, e202202058 CrossRef CAS.
- C. Hennig, S. Weiss, W. Kraus, J. Kretzschmar and A. C. Scheinost, Inorg. Chem., 2017, 56, 2473–2480 CrossRef CAS PubMed.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851 CrossRef PubMed.
- V. Guillerm, S. Gross, C. Serre, T. Devic, M. Bauer and G. Ferey, Chem. Commun., 2010, 46, 767–769 RSC.
- M. Kandiah, M. H. Nilsen, S. Usseglio, S. Jakobsen, U. Olsbye, M. Tilset, C. Larabi, E. A. Quadrelli, F. Bonino and K. P. Lillerud, Chem. Mater., 2010, 22, 6632–6640 CrossRef CAS.
- S. J. Garibay and S. M. Cohen, Chem. Commun., 2010, 46, 7700–7702 RSC.
- F. Vermoortele, R. Ameloot, A. Vimont, C. Serre and D. De Vos, Chem. Commun., 2011, 47, 1521–1523 RSC.
- M. L. Foo, S. Horike, T. Fukushima, Y. Hijikata, Y. Kubota, M. Takata and S. Kitagawa, Dalton Trans., 2012, 41, 13791–13794 RSC.
- M. J. Katz, Z. J. Brown, Y. J. Colon, P. W. Siu, K. A. Scheidt, R. Q. Snurr, J. T. Hupp and O. K. Farha, Chem. Commun., 2013, 49, 9449–9451 RSC.
- S. Biswas, J. Zhang, Z. B. Li, Y. Y. Liu, M. Grzywa, L. X. Sun, D. Volkmer and P. Van der Voort, Dalton Trans., 2013, 42, 4730–4737 RSC.
- K. K. Yee, N. Reimer, J. Liu, S. Y. Cheng, S. M. Yiu, J. Weber, N. Stock and Z. T. Xu, J. Am. Chem. Soc., 2013, 135, 7795–7798 CrossRef CAS PubMed.
- M. Lammert, H. Reinsch, C. A. Murray, M. T. Wharmby, H. Terraschke and N. Stock, Dalton Trans., 2016, 45, 18822–18826 RSC.
- S. Waitschat, D. Frohlich, H. Reinsch, H. Terraschke, K. A. Lomachenko, C. Lamberti, H. Kummer, T. Helling, M. Baumgartner, S. Henningerb and N. Stock, Dalton Trans., 2018, 47, 1062–1070 RSC.
- T. Ntep, H. Reinsch, B. Moll, E. Hasturk, S. Goekpinar, H. Breitzke, C. Schlusener, L. Schmolke, G. Buntkowsky and C. Janiak, Chem.–Eur. J., 2018, 24, 14048–14053 CrossRef.
- G. Kickelbick, P. Wiede and U. Schubert, Inorg. Chim. Acta, 1999, 284, 1–7 CrossRef CAS.
- Y. Gao, F. R. Kogler, H. Peterlik and U. Schubert, J. Mater. Chem., 2006, 16, 3268–3276 RSC.
- M. Puchberger, F. R. Kogler, M. Jupa, S. Gross, H. Fric, G. Kickelbick and U. Schubert, Eur. J. Inorg. Chem., 2006, 3283–3293, DOI:10.1002/ejic.200600348.
- F. Faccini, H. Fric, U. Schubert, E. Wendel, O. Tsetsgee, K. Mueller, H. Bertagnolli, A. Venzo and S. Gross, J. Mater. Chem., 2007, 17, 3297–3307 RSC.
- G. Kickelbick and U. Schubert, Chem. Ber., 1997, 130, 473–477 CrossRef CAS.
- D. Van den Eynden, R. Pokratath, J. P. Mathew, E. Goossens, K. De Buysser and J. De Roo, Chem. Sci., 2023, 14, 573–585 RSC.
- W. Morris, B. Volosskiy, S. Demir, F. Gandara, P. L. McGrier, H. Furukawa, D. Cascio, J. F. Stoddart and O. M. Yaghi, Inorg. Chem., 2012, 51, 6443–6445 CrossRef CAS PubMed.
- J. E. Mondloch, W. Bury, D. Fairen-Jimenez, S. Kwon, E. J. DeMarco, M. H. Weston, A. A. Sarjeant, S. T. Nguyen, P. C. Stair, R. Q. Snurr, O. K. Farha and J. T. Hupp, J. Am. Chem. Soc., 2013, 135, 10294–10297 CrossRef CAS.
- U. Schubert, Coord. Chem. Rev., 2017, 350, 61–67 CrossRef CAS.
- U. Schubert, Coord. Chem. Rev., 2022, 469, 214686 CrossRef CAS.
- A. A. Bezrukov, K. W. Tornroos, E. Le Roux and P. D. C. Dietzel, Chem. Commun., 2018, 54, 2735–2738 RSC.
- M. Kim, J. F. Cahill, Y. X. Su, K. A. Prather and S. M. Cohen, Chem. Sci., 2012, 3, 126–130 RSC.
- M. Taddei, R. J. Wakeham, A. Koutsianos, E. Andreoli and A. R. Barron, Angew. Chem., Int. Ed., 2018, 57, 11706–11710 CrossRef CAS PubMed.
- F. R. Kogler, M. Jupa, M. Puchberger and U. Schubert, J. Mater. Chem., 2004, 14, 3133–3138 RSC.
- S. Gross, J. Mater. Chem., 2011, 21, 15853–15861 RSC.
- D. Turetsky, D. M. Alzate-Sánchez, M. C. Wasson, A. Yang, H. Noh, A. Atilgan, T. Islamoglu, O. K. Farha and W. R. Dichtel, ACS Mater. Lett., 2022, 4, 1511–1515 CrossRef CAS.
- Y. J. Zhang, F. de Azambuja and T. N. Parac-Vogt, Catal. Sci. Technol., 2022, 12, 3190–3201 RSC.
- Y. J. Zhang, I. Y. Kokculer, F. de Azambuja and T. N. Parac-Vogt, Catal. Sci. Technol., 2023, 13, 100–110 RSC.
- A. Kreider-Mueller, P. J. Quinlivan, J. S. Owen and G. Parkin, Inorg. Chem., 2015, 54, 3835–3850 CrossRef CAS PubMed.
- J. Kreutzer, M. Puchberger, C. Artner and U. Schubert, Eur. J. Inorg. Chem., 2015, 2145–2151, DOI:10.1002/ejic.201403209.
- C.-C. Chiu, F.-K. Shieh and H.-H. G. Tsai, Inorg. Chem., 2019, 58, 14457–14466 CrossRef CAS PubMed.
- G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw and K. I. Goldberg, Organometallics, 2010, 29, 2176–2179 CrossRef CAS.
- T. J. Boyle, D. T. Yonemoto, T. Q. Doan and T. M. Alam, Inorg. Chem., 2014, 53, 12449–12458 CrossRef CAS PubMed.
- D. P. Steinhuebel, P. Fuhrmann and S. J. Lippard, Inorg. Chim. Acta, 1998, 270, 527–536 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, tables and views of the X-ray structure, experimental and simulated NMR spectra, tables of rate coefficient data, table of the Cartesian coordinates and energies of the DFT-optimized geometries. CCDC 2253409. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc02204h |
| This journal is © The Royal Society of Chemistry 2023 |