Open Access Article
Open Access ArticleDynamic-dependent selectivity in a bisphosphine iron spin crossover C–H insertion/π-coordination reaction†
Michael T.
Davenport
 ,
Justin K.
Kirkland
and
Daniel H.
Ess
,
Justin K.
Kirkland
and
Daniel H.
Ess
 *
*
Department of Chemistry and Biochemistry, Brigham Young University, Provo, Utah, USA 84604. E-mail: dhe@chem.byu.edu
First published on 21st August 2023
Abstract
Reaction pathway selectivity is generally controlled by competitive transition states. Organometallic reactions are complicated by the possibility that electronic spin state changes rather than transition states can control the relative rates of pathways, which can be modeled as minimum energy crossing points (MECPs). Here we show that in the reaction between bisphosphine Fe and ethylene involving spin state crossover (singlet and triplet spin states) that neither transition states nor MECPs model pathway selectivity consistent with experiment. Instead, single spin state and mixed spin state quasiclassical trajectories demonstrate nonstatistical intermediates and that C–H insertion versus π-coordination pathway selectivity is determined by the dynamic motion during reactive collisions. This example of dynamic-dependent product outcome provides a new selectivity model for organometallic reactions with spin crossover.
Introduction
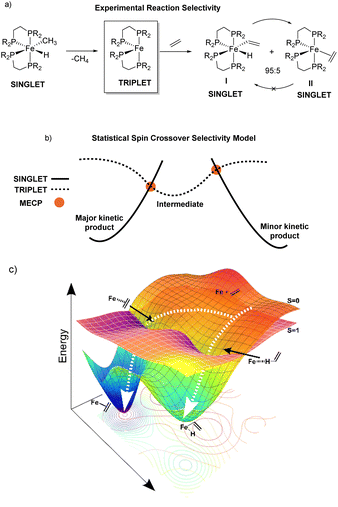
Reaction pathway selectivity is generally evaluated using density functional theory (DFT) calculated potential energy surfaces combined with transition-state theory or related statistical theories.1–3 For many organometallic systems, an additional complication to evaluating pathway selectivity arises for reactions with spin state crossover (e.g. singlet spin state to triplet spin state).4,5 In these pathways, in addition to calculating transition states and intermediates it is common to locate so-called minimum energy crossing point (MECP) structures where two spin states have identical structures and energies.6 While not a stationary point, a MECP represents a portion of the potential energy surface where there is high probability of spin crossover and, like a transition state, MECPs have the potential to be a reaction pathway bottleneck and control selectivity.An example of a reaction where spin crossover potentially impacts pathway selectivity was reported by Field where singlet spin (DEPE)2Fe(CH3)(H) (DEPE = 1,2-bis(diethylphosphino)ethane) undergoes reductive elimination of methane to generate the triplet spin (DEPE)2Fe intermediate followed by reaction with ethylene to give a kinetic 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ratio of the singlet vinyl C–H insertion (DEPE)2Fe(H)(C2H3) complex I and the singlet π-coordination (DEPE)2Fe(η2-C2H4) complex II (Fig. 1a).7,8 This reaction is a unique example where the π-coordination structure II is thermodynamically more stable and does not convert to the Fe-vinyl hydride I.9 We initially assumed that the location of singlet and triplet spin transition-state structures and MECPs would provide a qualitative (and quantitative) model for (DEPE)2Fe–ethylene vinyl C–H insertion versus π-coordination selectivity.10 In this type of statistical-based selectivity model, like transition-state theory, the (DEPE)2Fe intermediate would have separate transition states or MECPs that each provide a competitive kinetic bottleneck for forming I and II where the energy difference between these bottlenecks would translate to the product ratio. This type of general selectivity model with MECPs is outlined in Fig. 1b. Surprisingly, however, using transition states and MECPs for the statistical evaluation of reaction pathway selectivity gives selectivity opposite to experiment. This prompted us to perform single spin state and mixed spin state quasiclassical direct dynamics trajectories for reactive collisions between the bisphosphine Fe complex and ethylene, which provides a nonstatistical evaluation of reaction selectivity.11,12 The DFT direct dynamics trajectories revealed that dynamic motion during the collision between the reactive bisphosphine Fe complex and ethylene controls C–H insertion versus π-coordination selectivity. Fig. 1c outlines this dynamic motion model with qualitative trajectories leading I and II and overlaid singlet and triplet energy surfaces. The discovery of nonstatistical dynamic selectivity12–16 provides a new framework for modeling product outcomes in organometallic spin crossover reactions.
5 ratio of the singlet vinyl C–H insertion (DEPE)2Fe(H)(C2H3) complex I and the singlet π-coordination (DEPE)2Fe(η2-C2H4) complex II (Fig. 1a).7,8 This reaction is a unique example where the π-coordination structure II is thermodynamically more stable and does not convert to the Fe-vinyl hydride I.9 We initially assumed that the location of singlet and triplet spin transition-state structures and MECPs would provide a qualitative (and quantitative) model for (DEPE)2Fe–ethylene vinyl C–H insertion versus π-coordination selectivity.10 In this type of statistical-based selectivity model, like transition-state theory, the (DEPE)2Fe intermediate would have separate transition states or MECPs that each provide a competitive kinetic bottleneck for forming I and II where the energy difference between these bottlenecks would translate to the product ratio. This type of general selectivity model with MECPs is outlined in Fig. 1b. Surprisingly, however, using transition states and MECPs for the statistical evaluation of reaction pathway selectivity gives selectivity opposite to experiment. This prompted us to perform single spin state and mixed spin state quasiclassical direct dynamics trajectories for reactive collisions between the bisphosphine Fe complex and ethylene, which provides a nonstatistical evaluation of reaction selectivity.11,12 The DFT direct dynamics trajectories revealed that dynamic motion during the collision between the reactive bisphosphine Fe complex and ethylene controls C–H insertion versus π-coordination selectivity. Fig. 1c outlines this dynamic motion model with qualitative trajectories leading I and II and overlaid singlet and triplet energy surfaces. The discovery of nonstatistical dynamic selectivity12–16 provides a new framework for modeling product outcomes in organometallic spin crossover reactions.
Results and discussion
Energy surfaces and statistical theory based analysis
Field reported that the reaction between (DEPE)2Fe(CH3)(H) and ethylene after ∼6 hours at −28 °C results in a 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 kinetic mixture of the C–H insertion product (DEPE)2Fe(H)(C2H3) I to the π-coordination product Fe(DMPE)2(η2-ethylene) II. When the temperature was increased to 25 °C I isomerized to II and it remained the only product. This indicates that the vinyl insertion product I is the kinetic product and the η2-ethylene complex II is the thermodynamic product. As mentioned in the Introduction, this is a unique example where the π-coordination structure II is thermodynamically more stable and does not convert to the Fe-vinyl hydride I. This implies that in this reaction, and perhaps in other related reactions, π-coordination is not required to activate/cleave sp2 C–H bonds.
5 kinetic mixture of the C–H insertion product (DEPE)2Fe(H)(C2H3) I to the π-coordination product Fe(DMPE)2(η2-ethylene) II. When the temperature was increased to 25 °C I isomerized to II and it remained the only product. This indicates that the vinyl insertion product I is the kinetic product and the η2-ethylene complex II is the thermodynamic product. As mentioned in the Introduction, this is a unique example where the π-coordination structure II is thermodynamically more stable and does not convert to the Fe-vinyl hydride I. This implies that in this reaction, and perhaps in other related reactions, π-coordination is not required to activate/cleave sp2 C–H bonds.
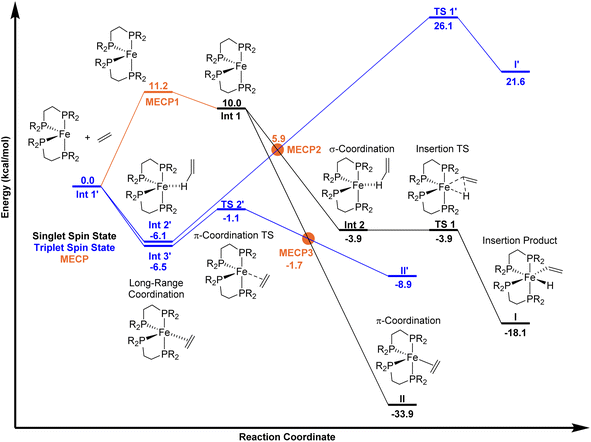
Using unrestricted M06-L/Def2-TZVP//M06-L/6-31G**[LANL2DZ for Fe] (Gaussian 16)17–20 we extensively explored the singlet and triplet spin state potential-energy surfaces with the ligand only slightly modified to be DMPE (1,2-bis(dimethylphosphino)ethane). The M06-L functional was selected because it provides accurate geometries and relative energies of spin states for first-row transition metals, especially Fe.21,22 Calculations included the implicit solvent model for mesitylene.23 As anticipated, (DMPE)2Fe has a ground triplet spin state with the unrestricted, open-shell singlet 10.0 kcal mol−1 higher in energy (singlet has 〈S2〉 = 1.0) on the electronic energy surface. Using our MECPro program,24 we located the singlet-triplet MECP for (DMPE)2Fe (MECP1), which has an energy of 11.2 kcal mol−1 relative to the triplet structure. Importantly, the Fe-solvent structure (DMPE)2Fe(mesitylene) is endergonic by 1.7 kcal mol−1 relative to separated (DMPE)2Fe and mesitylene (see ESI†) and therefore, if the transient Fe-solvent intermediate is formed, it would be in equilibrium with the coordinatively unsaturated intermediate (DMPE)2Fe and unlikely to significantly affect the reaction with ethylene.
On the singlet spin state surface (Fig. 2, black surface), there is a σ-CH coordination structure INT 2 that is stabilized by −3.9 kcal mol−1 relative to separated triplet (DMPE)2Fe and ethylene. This weak coordination intermediate leads to the C–H insertion transition state TS 1 that results in the cis Fe-vinyl hydride product (DMPE)2Fe(H)(C2H3) I. Manual displacement of the TS 1 negative vibrational mode followed by optimization provided assignment of TS 1 to connect intermediate INT 2 and product I. The C–H activation/hydrogen atom transfer transition state for reaction with trans-(DMPE)2Fe and ethylene is nearly 30 kcal mol−1 and not viable (see ESI†). This means that the equilibrium between cis and transI occurs after kinetic formation of cisI. Consistent with experiment, the energy difference between cis and transI is only 0.5 kcal mol−1 (see ESI†). No potential energy barrier was found for forming (DMPE)2Fe(η2-C2H4) II starting from the cis-bisphosphine Fe complex (see ESI† for potential-energy scans). No stable π-coordination structure was found between the trans-bisphosphine Fe complex and ethylene. The π-coordination energy of ethylene is −33.9 kcal mol−1 relative to triplet (DMPE)2Fe and ethylene. Our calculations confirm that II is thermodynamically 15.8 kcal mol−1 more stable than I.
On the triplet surface (Fig. 2, blue surface) we located corresponding structures to those shown on the singlet surface. As expected, the triplet spin structures are much less stabilized and exhibit less coordination between the Fe metal center and the bisphosphine ligand to weaken the ligand field. For example, the triplet I′ and II′ complexes show elongated Fe–P bonds, and the triplet π-complex INT 3′ has significantly longer coordination lengths. Fig. 3 displays 3D structures of the key stationary points and MECPs. Location of the π-coordination transition state, TS 2′, on the triplet surface indicates that this transition-state structure does not exist on the singlet surface due to the much more reactive singlet (DMPE)2Fe structure. The barrier for C–H bond cleavage on the triplet surface is >30 kcal mol−1 and is not competitive with the barrier for singlet spin C–H insertion.
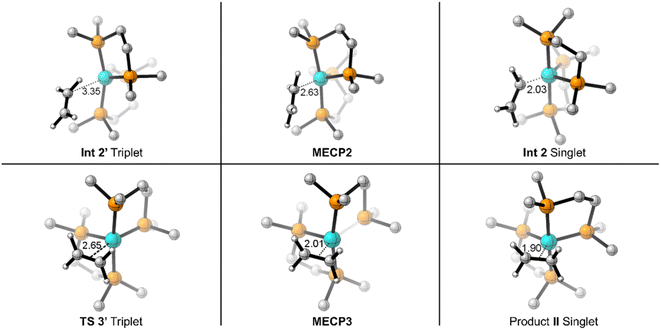 | ||
| Fig. 3 3D depiction of M06-L optimized geometries for reaction between (DMPE)2Fe and ethylene with key bond/coordination distances (in Å). | ||
Because the coordinatively unsaturated cis-(DMPE)2Fe complex has a triplet spin state and the insertion and π-coordination products have singlet spin states, there is the possibility of spin crossover resulting from collision with ethylene. Therefore, we extensively examined possible MECPs with ethylene in or near the coordination sphere of the Fe center. Fig. 2 shows the locations of MECP2 and MECP3. MECP2 with an energy of 5.9 kcal mol−1 connects the singlet and triplet energy surfaces for the σ-CH coordination structure INT 2′ and would precede TS 1 for C–H bond cleavage. MECP3 has a structure that likely provides singlet-triplet surface crossover for π-coordination to II.
The compilation of the singlet surface, the triplet surface, and the MECPs provides the possibility to estimate vinyl C–H insertion versus π-coordination selectivity using a statistical transition-state theory type approach. As described in the Introduction, the slow step in the C–H insertion and/or π-coordination pathways can either be potential energy surface transition-state structures or MECP structures. Fig. 2 indicates that the lowest energy route to the C–H insertion product I involves first formation of the triplet π-complex INT 3′ that is in equilibrium with the triplet σ-complex INT 2′. From INT 2′, spin crossover occurs through MECP2 to generate the singlet σ-complex INT 2 and then TS 1 results in C–H insertion and the Fe-vinyl hydride product I. In this series of reaction steps, MECP2 with an effective bottleneck barrier of 12.0 kcal mol−1 relative to triplet INT 2′ would govern the rate of C–H insertion. For formation of the π-complex product II, the lowest energy route involves triplet intermediate INT 3′ followed by triplet TS 2′ and then MECP3. In this series of reaction steps the triplet TS 2′ structure governs the rate of forming the π-complex product II and has an energy of only 5.4 kcal mol−1 relative to triplet Int 3′. From a statistical point of view, assuming Curtin–Hammett-type equilibrium of weak coordination structures triplet INT 2′ and triplet Int 3′, the energy difference that controls pathway selectivity is the energy to achieve MECP2 for C–H insertion and the energy to achieve the triplet TS 2′ for π-coordination. This energy difference is 7.0 kcal mol−1, and importantly, massively favors forming the π-complex II, which is opposite to the experimental 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ratio favoring vinyl C–H bond insertion.
5 ratio favoring vinyl C–H bond insertion.
Quantitative disagreement with experiment could perhaps be expected given that MECPs only represent an estimate for crossover between singlet and triplet surfaces. Therefore, we estimated the spin–orbit coupling value for MECP2 using CASPT2(18,11)/ANO-RCC-MB (see ESI†) coupling the lowest energy singlet and triplet states. The energy gap between the singlet and triplet spin states using CASPT2 was calculated to be 2.5 kcal mol−1. Estimation of the spin–orbit coupling value indicates that the energy of MECP2 would be lowered less than 0.5 kcal mol−1 compared to the energy without inclusion of spin–orbit coupling and this does not change the general interpretation of the energy landscapes shown in Fig. 3. Additionally, we also used variational transition state theory (with Polyrate)25 to re-optimize TS 2′. This variational triplet structure has bond distances that are slightly different than TS 2′, but the energy is nearly identical. Therefore, this statistical selectivity-based analysis using the singlet and triplet energy surfaces neither provides quantitative nor qualitative agreement with the experimental selectivity.
Dynamics trajectory analysis of reaction pathway selectivity
Because of the disagreement between the energy landscape/statistical analysis and the experimental product ratio, we speculated that the weak σ-coordination and π-coordination intermediates (INT 2, INT 2′, and Int 3′) are likely nonstatistical intermediates, which means there is a lack of significant intermolecular vibrational energy redistribution (IVR) and that these intermediates would either have a very short lifetime or be completely skipped. Moreover, we also speculated that the shapes of the combined singlet and triplet energy surfaces, especially the relatively flat surfaces in the vicinity of the reactive unsaturated triplet and singlet (DMPE)2Fe complex, would provide wandering non-IRC motion during reactive collisions. To test these hypotheses, we performed direct dynamics simulations that can directly account for atomic motion during reactions and identify nonstatistical effects, such as the lack of IVR and non-IRC motion.Nonstatistical intermediates and non-IRC26 reaction pathways are now relatively established for some organic reactions.27–36 However, these types of scenarios are now emerging in organometallic reactions.37 Most germane, we recently showed that dynamics trajectories were necessary to model the selectivity for the reaction between Cp(PMe3)2Re and ethylene that results in a mixture of Re-vinyl hydride and Cp(PMe3)2Re(η2-ethylene) products.38 In this case, trajectories showed that the σ-CH-coordination structure is likely a nonstatistical intermediate and that there are direct pathways for forming the Re-vinyl hydride without σ-coordination or π-coordination. Importantly, the Cp(PMe3)2Re structure and all other structures have a low-spin singlet energy surface. Therefore, a major challenge to address for trajectories involving reactive collision of (DMPE)2Fe with ethylene is the possibility of spin crossover between singlet and triplet spin states.
There are multiple approaches for performing dynamics trajectories that incorporate multiple electronic spin states. Perhaps the most well-known approach is Tully's fewest switches algorithm that provides diabatic surface hopping.39,40 However, this approach is generally available for hopping between singlet and triplet spin states for photodynamic frameworks. Alternatively, there is the possibility to use an approach based on an adiabatic type of energy surface created through a mixture of spins. Truhlar recently showed that a mixed spin model that incorporates surface coupling provides an approach to obtain energies, forces, and force constants of structures. Therefore, we implemented this mixed spin model into our quasiclassical direct dynamics program Milo.41,42 This enabled us to execute dynamics trajectories on only singlet and only triplet energy surfaces as well as dynamics trajectories using a mixed spin state surface. Quasiclassical trajectories were initialized by creating a vibrationally-averaged velocity distribution based on normal mode sampling at the experimental temperature of −28 °C, which includes zero-point energy. For transition-state structures, the imaginary frequency was assigned a specific direction to progress and sampled as a positive 10 cm−1 normal mode. Each trajectory was propagated using a Verlet integration algorithm with a 0.75 femtosecond (fs) time step. At each step, energies and forces were calculated using UM06-L/6-31G**[LANL2DZ for Fe]. Trajectories were propagated for ∼500–1000 fs.
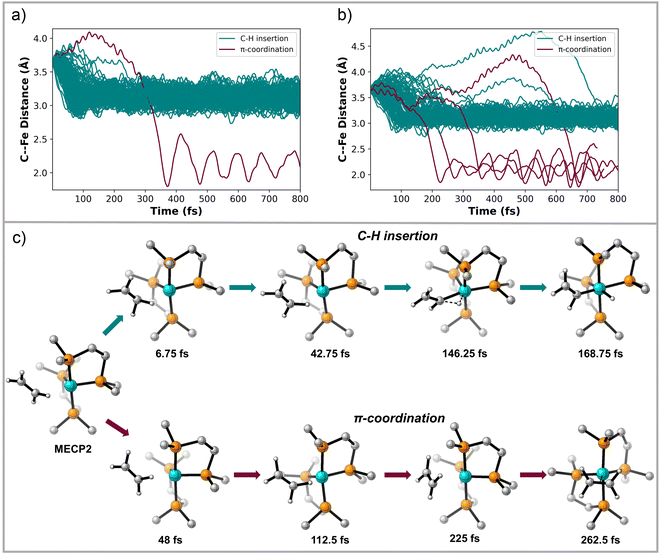
Starting 50 quasiclassical trajectories from TS 1 with motion in the forwards direction (towards products) on the singlet surface showed only the formation of (DMPE)2Fe(H)(C2H3) I. Formation of this product occurred in less than 50 fs. Trajectories starting from TS 1 in the reverse (away from products) direction showed initial motion towards the singlet σ-coordination structure INT 2 but then quickly reverted to the forwards direction in a paddle ball type motion43 and like the forward direction trajectories only resulted in formation of I (see ESI†).
Importantly, these reverse trajectories indicate that the σ-coordination structure INT 2 is likely a nonstatistical intermediate without a significant lifetime, despite being a fully optimized potential-energy structure. This nonstatistical description is also consistent with INT 2 having a very shallow potential-energy well and energy almost identical to TS 1. This implies that reactive collision trajectories started before the σ-coordination structure will likely breeze through this structure with direct formation of (DMPE)2Fe(H)(C2H3) I. Additionally, this also indicates that the pathway selectivity for C–H insertion versus π-coordination likely occurs before C–H bond σ-coordination with the Fe metal center. This prompted us to examine trajectories starting at MECP2, which occurs before the σ-coordination structure INT 2 (see Fig. 2).
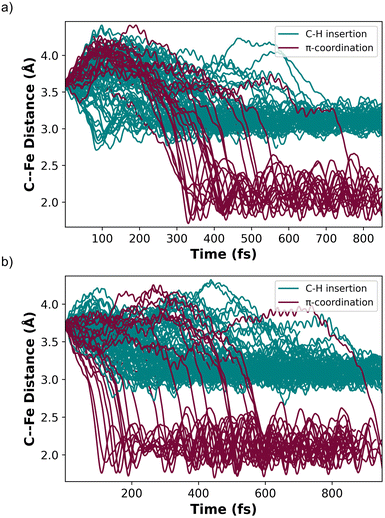
MECP2 has ∼0.6 Å longer distance between the ethylene and the Fe metal center compared to structure INT 2. We propagated 130 trajectories on the singlet spin state surface in the forward direction starting from MECP2. Fig. 4a plots these 130 trajectories as the breaking C–H bond length (in the forward direction) in Å versus time. When the distance between the distal carbon on ethylene to the Fe center was less than 2.5 Å the trajectory was classified as ending at product II. When the distance was close to 3.3 Å then the trajectory was classified as product I. This plot shows that within 50 fs nearly all trajectories have fully broken the C–H bond and generated I. One of the trajectories recrossed and ended forming II. Fig. 4b maps the motion of the 113 reverse direction trajectories by plotting the distance from the distal carbon on ethylene to the Fe center versus time. Again, these trajectories propagated on the singlet surface in the reverse direction resulted in initial dissociation of ethylene followed by rebounding back to collide with the Fe metal center, which is similar motion that occurred in the reverse trajectories starting from TS 1. However, unlike the trajectories started from TS 1, there was formation of both (DMPE)2Fe(H)(C2H3) I and (DMPE)2Fe(η2-C2H4) II structures in this case. The teal-colored trajectories in Fig. 4b end at product I and the burgundy-colored trajectories end at II. Surprisingly, and likely quantitatively fortuitous, the ratio of I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II trajectories (108
II trajectories (108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) is close to the experimental ratio measured by Field. We also initiated and propagated 20 singlet-triplet mixed spin state trajectories starting at MECP2. During these trajectories energies and forces are calculated by mixing unrestricted singlet and unrestricted triplet spin states. This provides effective spin crossover if the system changes from a configuration dominated by the triplet spin state to a configuration dominated by the singlet spin state. See the ESI† for further details. The dynamic motion of these mixed spin trajectories was nearly identical to the singlet spin trajectories. However, whenever the triplet spin state dominated the electronic configuration, there was only repulsion between ethylene and Fe center. This triplet surface repulsion was confirmed with 20 trajectories started from MECP2 and propagated only on the triplet surface.
5) is close to the experimental ratio measured by Field. We also initiated and propagated 20 singlet-triplet mixed spin state trajectories starting at MECP2. During these trajectories energies and forces are calculated by mixing unrestricted singlet and unrestricted triplet spin states. This provides effective spin crossover if the system changes from a configuration dominated by the triplet spin state to a configuration dominated by the singlet spin state. See the ESI† for further details. The dynamic motion of these mixed spin trajectories was nearly identical to the singlet spin trajectories. However, whenever the triplet spin state dominated the electronic configuration, there was only repulsion between ethylene and Fe center. This triplet surface repulsion was confirmed with 20 trajectories started from MECP2 and propagated only on the triplet surface.
We also examined 20 trajectories starting from MECP3, and as expected, all singlet spin state trajectories in the forward direction led to the (DMPE)2Fe(η2-C2H4) II structure in about 10 fs. Reverse trajectories resulted in a loosely coordinated structure for only about 5–10 fs followed by return to the metal center to exclusively form structure II. No C–H insertion was found from these trajectories. Mixed spin state trajectories starting at MECP3 resulted in the formation of II for both propagation in the forwards and backwards directions because this crossing point occurs after transition state on the triplet surface (see Fig. 2).
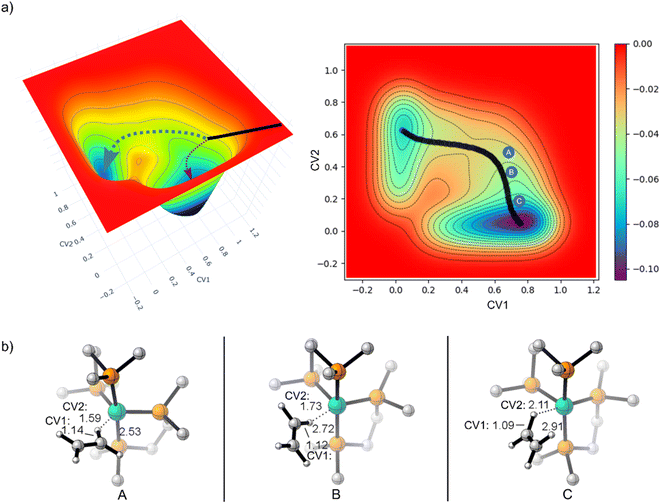
Because of the reaction pathway branching that occurred in the reverse and rebound trajectories starting at MECP2 we decided to sample the reaction landscape using metadynamics simulations, which provided alternative starting points for reactive collision trajectories. Specifically, the metadynamics simulations provided a straightforward way of identifying starting structures before MECP2. Metadynamics simulations were performed using GTH-PBE44/DZVP-MOLOPT-SR-GTH45 in CP2K 7.1.46Fig. 5a shows the singlet spin state metadynamics simulation energy surface that connects structures I to II using collective variables (CVs) that describe both C–H bond formation/cleavage and ethylene coordination/dissociation (see ESI† for CV descriptions). Fig. 5b shows structures A, B, and C that correspond to metadynamics structures with Fe–C distances of 2.5, 2.7, and 2.9 Å. Because the metadynamics simulations served only to identify general structures before MECP2, structures A, B, and C were then constrained with their CV values and then reoptimized with UM06-L/6-31G**[LANL2DZ] in preparation for trajectories. Structures A and B have a slightly lower singlet energy while structure C has a slightly lower triplet energy.
Because structure C has a lower energy triplet spin state, we launched mixed spin state trajectories with the expectation that reactive collisions would occur with crossover from a triplet spin dominated structure to a singlet spin dominated structure. However, the mixed spin state trajectories resulted in repulsive collision between ethylene and the Fe metal center and no formation of either I or II. Additionally, none of these mixed spin state trajectories showed a significant increase in singlet spin-state character. The trajectories remained dominated by the triplet spin configuration, and after the collision, there was repulsion between ethylene and (DMPE)2Fe, which would be anticipated by inspection of the triplet surface that is overall repulsive. In retrospect the results of the trajectories starting from structure C are perhaps not surprising since the MECPs are several kcal mol−1 higher in energy. This scenario is akin to trajectories starting at reactant-like structures with reactant energy, which has low probability of overcoming a barrier. To test this theory, we started trajectories from C with up to 20 kcal mol−1 of additional center of mass translational velocity for ethylene, which would provide enough energy to overcome the MECP bottleneck. Indeed, in these 10 mixed spin state trajectories (see ESI†) with extra translational energy there was crossover from a triplet spin dominated structure to a singlet spin dominated structure, but surprisingly there was only formation of the π-coordination structure II. This suggests that in these trajectories C–H insertion did not occur because the additionally translational energy induced ultrafast collision between ethylene and the Fe center before the added energy could redistribute to the C–H vibrational modes, which is required for C–H bond cleavage.
In contrast to starting at structure C, the mixed spin state trajectories started from structures A and B showed formation of I and II, but only from trajectories that were generally had a singlet ground state. This provided the impetus to perform adiabatic singlet spin state surface dynamics for the remainder of the trajectories. Fig. 6a plots 91 singlet spin state reactive collision trajectories sampled and propagated starting from structure A. The teal lines represent trajectories that ended in product I and the burgundy lines represent trajectories that ended at product II. In this set of trajectories, there was a nearly 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 ratio of I
22 ratio of I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II (Fig. 6a). Fig. 6b plots 100 singlet spin state reactive collision trajectories sampled and propagated starting from structure B. Again, the teal lines represent trajectories that ended in product I and the burgundy lines represent trajectories that ended at product II. For the B set of trajectories there was a nearly 77
II (Fig. 6a). Fig. 6b plots 100 singlet spin state reactive collision trajectories sampled and propagated starting from structure B. Again, the teal lines represent trajectories that ended in product I and the burgundy lines represent trajectories that ended at product II. For the B set of trajectories there was a nearly 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 ratio for forming I
23 ratio for forming I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II.
II.
Inspection of the plotted trajectories in Fig. 6 reveals that I and II are generally formed in 100–200 fs from the start of the trajectory, although there are few trajectories that lag up to about 400 fs to form a product. This relatively short time between the start of the trajectory and product formation confirms that the weak σ-complex INT 2 should probably best be viewed as a nonstatistical intermediate with a very shallow energy well that is likely skipped or bypassed in most trajectories. This viewpoint is consistent with the metadynamics generated energy landscape that shows a relatively flat energy surface when ethylene only weakly interacts with the Fe metal center and suggests that the initial collisional orientation between ethylene and (DMPE)2Fe determines the reaction pathway. On the singlet energy surface (and the mixed spin surface) the pathway towards the insertion product I is probably best viewed as the dynamically direct pathway while the π-coordination product is the off-pathway (non-IRC type) product, which is illustrated by the dotted trajectory arrows in Fig. 5a. This preference occurs regardless of the starting ethylene position and is surprising because the Fe-vinyl hydride product is thermodynamically less stable than the π-coordination product. However, it is important to realize that entry into the π-coordination pathway is more restricted since it is only favorable when the Fe d-orbitals (occupied and vacant) are properly aligned with the ethylene π and π* orbitals.47 This restriction will naturally provide kinetic selectivity in a reaction where dynamic nonstatistical motion controls selectivity.
Conclusions
DFT optimized singlet and triplet spin state energy landscapes with transition-state structures and MECP structures provides an incorrect interpretation of pathway selectivity for the spin crossover reaction between ethylene and (DMPE)2Fe. Using both single spin state and mixed singlet/triplet spin state quasiclassical DFT-based direct dynamics trajectories we showed that there are direct dynamic pathways leading to both the vinyl insertion product (DMPE)2Fe(H)(C2H3) I and II with an inherent preference for I. The trajectory results are qualitatively and quantitatively consistent with the experimental kinetic ratio of products. Overall, this work demonstrates the need to consider evaluating dynamics trajectories in spin crossover reactions to determine the origin of reaction pathway selectivity, especially for highly reactive, coordinatively unsaturated metal complexes.Data availability
Computational details to replicate the data in this work can be found in the ESI†. The Milo direct dynamics program that can be used to replicate trajectories can be found on GitHub at: https://github.com/DanielEss-lab/milo.Author contributions
D. Ess designed calculations. M. Davenport carried out calculations. M. Davenport, J. Kirkland, and D. Ess analyzed results and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Office of Research Computing at BYU for computational resources. We acknowledge and the United States National Science Foundation Chemical Structure, Dynamics, and Mechanisms B (CSDM-B) Program for support under award CHE-2244799.Notes and references
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- K. J. Laidler and M. C. King, J. Phys. Chem., 1983, 87, 2657–2664 CrossRef CAS.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- R. Poli, Chem. Rev., 1996, 96, 2135–2204 CrossRef CAS PubMed.
- D. Schröder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145 CrossRef PubMed.
- J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99 Search PubMed.
- M. V. Baker and L. D. Field, J. Am. Chem. Soc., 1986, 108, 7436–7438 CrossRef CAS.
- M. V. Baker and L. D. Field, J. Am. Chem. Soc., 1986, 108, 7433–7434 CrossRef CAS.
- P. O. Stoutland and R. G. Bergman, J. Am. Chem. Soc., 1985, 107, 4581–4582 CrossRef CAS.
- K. M. Smith, R. Poli and J. N. Harvey, Chem.–Eur. J., 2001, 7, 1679–1690 CrossRef CAS PubMed.
- D. H. Ess, Acc. Chem. Res., 2021, 54, 4410–4422 CrossRef CAS PubMed.
- M. Paranjothy, R. Sun, Y. Zhuang and W. L. Hase, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 296–316 CAS.
- B. K. Carpenter, Annu. Rev. Phys. Chem., 2005, 56, 57–89 CrossRef CAS PubMed.
- B. K. Carpenter, Chem. Rev., 2013, 113, 7265–7286 CrossRef CAS PubMed.
- U. Lourderaj, K. Park and W. L. Hase, Int. Rev. Phys. Chem., 2008, 27, 361–403 Search PubMed.
- X. Ma and W. L. Hase, Philos. Trans. R. Soc., A, 2017, 375, 20160204 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- D.-H. Kwon, B. L. Small, O. L. Sydora, S. M. Bischof and D. H. Ess, J. Phys. Chem. C, 2019, 123, 3727–3739 CrossRef CAS.
- W. Lee, J. Zhou and O. Gutierrez, J. Am. Chem. Soc., 2017, 139, 16126–16133 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- L.-A. H. J. D. Snyder, K. E. Faleumu, A. R. Schultz and D. H. Ess, MECPro Version 1.0.6, Minimum Energy Crossing Program, 2020 Search PubMed.
- J. Zheng, J. L. Bao, R. Meana-Pañeda, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, A. Ratkiewicz, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, Polyrate-version 2017-C, University of Minnesota, Minneapolis, MN, 2017 Search PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- T. Bekele, C. F. Christian, M. A. Lipton and D. A. Singleton, J. Am. Chem. Soc., 2005, 127, 9216–9223 CrossRef CAS PubMed.
- B. Biswas and D. A. Singleton, J. Am. Chem. Soc., 2015, 137, 14244–14247 CrossRef CAS PubMed.
- B. K. Carpenter, J. Am. Chem. Soc., 1995, 117, 6336–6344 CrossRef CAS.
- Z. Chen, Y. Nieves-Quinones, J. R. Waas and D. A. Singleton, J. Am. Chem. Soc., 2014, 136, 13122–13125 CrossRef CAS PubMed.
- C. Doubleday, G. Li and W. L. Hase, Phys. Chem. Chem. Phys., 2002, 4, 304–312 RSC.
- C. Doubleday, C. P. Suhrada and K. N. Houk, J. Am. Chem. Soc., 2006, 128, 90–94 CrossRef CAS PubMed.
- S. R. Hare, A. Li and D. J. Tantillo, Chem. Sci., 2018, 9, 8937–8945 RSC.
- S. R. Hare and D. J. Tantillo, Pure Appl. Chem., 2017, 89, 679–698 CrossRef CAS.
- J. G. López, G. Vayner, U. Lourderaj, S. V. Addepalli, S. Kato, W. A. deJong, T. L. Windus and W. L. Hase, J. Am. Chem. Soc., 2007, 129, 9976–9985 CrossRef PubMed.
- B. R. Ussing, C. Hang and D. A. Singleton, J. Am. Chem. Soc., 2006, 128, 7594–7607 CrossRef CAS PubMed.
- S. R. Hare and D. J. Tantillo, Chem. Sci., 2017, 8, 1442–1449 RSC.
- B. Yang, A. Schouten and D. H. Ess, J. Am. Chem. Soc., 2021, 143, 8367–8374 CrossRef CAS PubMed.
- J. E. Subotnik, J. Phys. Chem. A, 2011, 115, 12083–12096 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- M. S. Teynor, N. Wohlgemuth, L. Carlson, J. Huang, S. L. Pugh, B. O. Grant, R. S. Hamilton, R. Carlsen and D. H. Ess, Milo, Revision 1.0.1, Brigham Young University, Provo UT, 2022 Search PubMed.
- B. Yang, L. Gagliardi and D. G. Truhlar, Phys. Chem. Chem. Phys., 2018, 20, 4129–4136 RSC.
- R. Carlsen, J. R. Jenkins, T.-C. J. Huang, S. L. Pugh and D. H. Ess, Organometallics, 2019, 38, 2280–2287 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- T. D. Kühne, M. Iannuzzi, M. D. Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- J. Silvestre, M. J. Calhorda, R. Hoffmann, P. O. Stoutland and R. G. Bergman, Organometallics, 1986, 5, 1841–1851 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02078a |
| This journal is © The Royal Society of Chemistry 2023 |