Open Access Article
Open Access ArticleDo metastable polymorphs always grow faster? Measuring and comparing growth kinetics of three polymorphs of tolfenamic acid†
Pietro
Sacchi
 *ab,
Petros
Neoptolemou
b,
Roger J.
Davey
*ab,
Petros
Neoptolemou
b,
Roger J.
Davey
 b,
Susan M.
Reutzel-Edens
b,
Susan M.
Reutzel-Edens
 a and
Aurora J.
Cruz-Cabeza
a and
Aurora J.
Cruz-Cabeza
 *bc
*bc
aThe Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK. E-mail: psacchi@ccdc.cam.ac.uk
bDepartment of Chemical Engineering, University of Manchester, Manchester, UK
cDepartment of Chemistry, Durham University, Durham, UK. E-mail: aurora.j.cruz-cabeza@durham.ac.uk
First published on 6th October 2023
Abstract
The phenomenon of molecular crystal polymorphism is of central importance for all those industries that rely on crystallisation for the manufacturing of their products. Computational methods for the evaluation of thermodynamic properties of polymorphs have become incredibly accurate and a priori prediction of crystal structures is becoming routine. The computational study and prediction of the kinetics of crystallisation impacting polymorphism, however, have received considerably less attention despite their crucial role in directing crystallisation outcomes. This is mainly due to the lack of available experimental data, as nucleation and growth kinetics of polymorphs are generally difficult to measure. On the one hand, the determination of overall nucleation and growth kinetics through batch experiments suffers from unwanted polymorphic transformations or the absence of experimental conditions under which several polymorphs can be nucleated. On the other hand, growth rates of polymorphs obtained from measurements of single crystals are often only recorded along a few specific crystal dimensions, thus lacking information about overall growth and rendering an incomplete picture of the problem. In this work, we measure the crystal growth kinetics of three polymorphs (I, II and IX) of tolfenamic acid (TFA) in isopropanol solutions, with the intention of providing a meaningful comparison of their growth rates. First, we analyse the relation between the measured growth rates and the crystal structures of the TFA polymorphs. We then explore ways to compare their relative growth rates and discuss their significance when trying to determine which polymorph grows faster. Using approximations for describing the volume of TFA crystals, we show that while crystals of the metastable TFA-II grow the fastest at all solution concentrations, crystals of the metastable TFA-IX become kinetically competitive as the driving force for crystallisation increases. Overall, both metastable forms TFA-II and TFA-IX grow faster than the stable TFA-I.
1. Introduction
Crystal polymorphism is a common phenomenon1 of fundamental significance for a number of chemical industries that rely on crystallisation for the purification, development, manufacturing and assurance of storage stability of their products. The ability of a compound to form different polymorphs, with different close-packing arrangements and different physicochemical properties, can impact many steps of a product's research and development pipeline: from production through formulation to product registration and lifecycle management.2 Our inability to predict and control crystal polymorphism is strictly related to our lack of understanding of the balance between thermodynamic and kinetic aspects of crystallisation in polymorphic systems.3The thermodynamics of crystal polymorphism, as reflected in various phase equilibria, are well established.2 Modern crystal structure prediction (CSP) methods applied to a given molecule allow for the computational prediction of an array of plausible crystal structures. Their corresponding lattice energies then provide, with increasing accuracy and reliability, a prediction of the thermodynamically most stable polymorph.4,5 However, predicting which polymorph will appear under various experimental crystallisation conditions is a much more difficult exercise. This is because crystallisation kinetics (i.e., relative rates of nucleation and growth of various forms) rely on a delicate balance between not only thermodynamic factors but also kinetic ones. It is the latter that have so far evaded our attempts at robust prediction. Often the so-called Ostwald's Rule of Stages6–8 is used to justify the expectation that metastable forms will appear first during crystallisation. Only very recently have the inherent flaws in this rule been exposed.9,10 Here Cardew and Davey10 used the previously measured kinetic data for the polymorphs of gestodene to predict the conditions under which either or both polymorphs might crystallise. This approach demonstrates the potential of being able to predict not only thermodynamic stabilities but also relative kinetics of polymorphic forms. Such predictive capability does not yet generally exist, however, and collection, analysis, and dissemination of good quality experimental data on the kinetics of nucleation and growth of polymorphs is a prerequisite if a predictive link between CSP landscapes and crystallisation conditions is to be established.11
Such kinetic data are unfortunately rare, existing in only a handful of studies including cimetidine,12L-histidine,13 piracetam,14,15 glycine,16,17 stearic acid,18,19o-amino benzoic acid,20 paracetamol,21 gestodene22 and aripiprazole (see ESI†).23 Of these, only in the case of gestodene have both nucleation and growth rates been reported. Otherwise, only growth rate data is available. Even in the case of growth rates, comparison of kinetics across polymorphs is not straightforward and the choice between overall bulk measurements and individual face growth rates depends very much on the ultimate purpose the data will serve.24,25 Single crystal growth measurements are potentially attractive, but are normally measured only for a few selected directions. With rate data on few crystal dimensions alone, the interpretation of growth kinetics to explain the appearance or to aid the prediction of polymorphs can be difficult, especially if there exist evident differences between the polymorphs' morphologies or arrangements of intermolecular interactions in their crystal structures. Overall, there is no clear consensus on how to compare growth rate data across polymorphs.
Here, we study the growth kinetics of three polymorphs of tolfenamic acid (TFA), a model compound with nine polymorphs known to date.26–29 The stable form I (TFA-I) and the metastable form II (TFA-II, computed to be +0.9 kJ mol−1 less stable than TFA-I at 300 K)29 can be crystallised from a variety of organic solvents and can often be found concomitantly.30,31 Recently, a new metastable polymorph of TFA, form IX (TFA-IX, computed to be +2.3 kJ mol−1 less stable than TFA-I at 300 K),29 was obtained from highly supersaturated isopropanol (IPA) solutions kept at low temperature (also crystallised concomitantly with both TFA-I and TFA-II).29 The concomitant crystallisation of these three polymorphs suggests that their nucleation and growth kinetics can be competitive.32 The system, thus, can serve as an excellent model for the measurement and comparison of growth kinetics across three distinct polymorphs which, to the best of our knowledge, has never been done before. The aim of this study was to develop links between growth rates of polymorphs and their crystal structures, in order to aid CSP in the quest of predicting which of the potential polymorphs will actually appear experimentally. The first important challenge in the development of such links concerned how the kinetics of crystal growth of polymorphs should be compared. Here, we explore and discuss different approaches to this problem. In doing this, we rationalise the late-appearance of TFA-IX and we set some important methodological recommendations for comparing and predicting crystal growth rates of polymorphs.
2. Methods
2.1 Materials
Tolfenamic acid was purchased from Fluorochem Ltd; isopropanol (IPA) from either Fischer Scientific UK Ltd or from Honeywell Research Chemicals, in both cases with a purity > 98%.2.2 Crystal seeds
All crystal seeds were grown from IPA. Crystal seeds of TFA-I and TFA-II were grown by slow evaporation while seeds of TFA-IX were grown by cooling as described previously.29 Between 23 and 35 crystal seeds were used for the growth measurements for each of the polymorphs.2.3 Cutting of needle crystal seeds
Because of their high aspect ratios, the seed crystals of TFA-I and TFA-II used for our single-crystal growth measurements were cut with a blade to ensure that they would not grow out of the microscope camera's field of view: this ensured that measurements could be carried out for a sufficient time. Crystals of TFA-I and TFA-II are brittle and can be damaged quite easily as a result of cutting. Crystals that showed evident defects after cutting were discarded, and all crystal seeds were partially dissolved prior to each measurement to reduce superficial defects.2.4 Face indexing of TFA crystals
Crystals of TFA-I and TFA-IX were indexed using X-ray diffraction data collected on an Agilent Supernova diffractometer using Mo-Kα monochromated radiation (0.71073 Å). The data analysis and crystal shape determination were performed with the CrysalisPro software.33 Experimental face indexing of the needle-crystals of TFA-II was not possible, due to the very small size of the crystals tested. Instead, crystal morphologies of TFA-II were indexed by comparison with TFA-I and with predictive morphological models (see ESI†).2.5 Solubilities and supersaturation
The relative supersaturation of each TFA polymorph, σi, was calculated using eqn (1), where x is the concentration of TFA in IPA and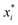 is the equilibrium solubility of each polymorph in IPA at 25 °C, obtained from previously reported experiments.29,30 The molar fraction solubilities of TFA-I, TFA-II and TFA-IX in IPA at 25 °C are 0.0039, 0.0043 and 0.0048, respectively. Using these solubilities and the relationship ΔG = RT
is the equilibrium solubility of each polymorph in IPA at 25 °C, obtained from previously reported experiments.29,30 The molar fraction solubilities of TFA-I, TFA-II and TFA-IX in IPA at 25 °C are 0.0039, 0.0043 and 0.0048, respectively. Using these solubilities and the relationship ΔG = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(xi/xj), the free energy difference of TFA-II and TFA-IX with respect to the stable TFA-I were calculated to be +0.2 kJ mol−1 and +0.5 kJ mol−1, respectively.
ln(xi/xj), the free energy difference of TFA-II and TFA-IX with respect to the stable TFA-I were calculated to be +0.2 kJ mol−1 and +0.5 kJ mol−1, respectively.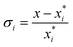 | (1) |
2.6 Single crystal growth experiments
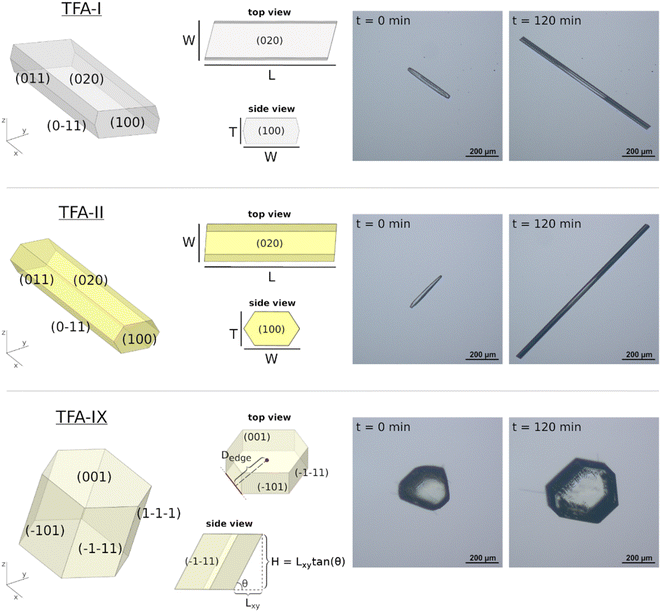
The growth of single crystal seeds of TFA polymorphs at 25 °C in IPA solutions of various concentrations above saturation was monitored in situ using a temperature-controlled growth cell and an inverted microscope.9,34 For each solution concentration, a crystal seed was manually selected and placed in a 0.4 ml glass cuvette, which was then completely filled with a warm, filtered solution of the required concentration. The sealed cuvette was placed in the temperature-controlled cell (Huber Ministat 230 circulator with a temperature probe) and the crystal seed was partially dissolved by circulating hot water (around 40 °C for this work) to eliminate any superficial defects. After dissolution, the temperature was lowered and held constant at 25 °C. Images of the growing seed crystals were collected at intervals of about 10 seconds using an Olympus CKX41 inverted microscope equipped with an Olympus UC30 camera and pre-processed using the Olympus StreamEssentials software. The growth of each crystal seed was monitored for about two hours, during which the solution supersaturation was assumed to remain constant. The growth rates of 35, 26 and 23 seed crystals were measured for TFA-I, TFA-II and TFA-IX, respectively. Experiments were carried out using IPA solutions with TFA molar fraction concentrations in the range of 0.0043 to 0.0063, which were carefully prepared so that growth rates of at least four single crystal seeds could be measured for selected supersaturations. Six different supersaturations were considered for TFA-I (σI: 0.1–0.6), and five for TFA-II and TFA-IX (σII: 0.12–0.45; σIX: 0.05–0.30).2.7 Crystal dimensions of TFA needles as a function of time
Images of growing needle crystals of TFA-I and TFA-II as a function of time were processed by computing the minimum-area bounding box35 in each of the images. This resulted in the derivation of two box dimensions, the length (L) and the width (W), as a function of time to describe the growth of needle morphologies. Although identification of specific facets in the growing needles was not possible, the L and W box dimensions are aligned with the [100] and the [001] crystallographic directions in both polymorphs.2.8 Crystal dimensions of TFA-IX blocks as a function of time
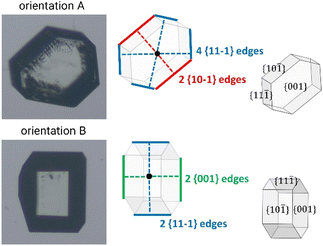
Derivation of growing dimensions of TFA-IX crystals as a function of time was significantly more complex. Since all dimensions of a blocky crystal are significant, growth measurements had to be carried out by orienting the crystals in two perpendicular orientations as shown in Fig. 1 (denoted as orientations A and B). In orientation A, the crystallographic a and b axes were parallel to the image xy plane, and the distance between the crystals' centroids and the edges formed by the {10−1} facets and by the {11−1} facets with the {001} facets were measured. In orientation B, the distances from the centroid to the edges formed by the {001} facets with the {10−1} facets and the edges formed by the {11−1} facets were measured. These distances were measured as a function of time from the sequence of crystal images using a methodology recently developed by Offiler et al.25 Unfortunately, positioning the crystals in orientation B was difficult, and only 5 crystals in this orientation were measured. As an alternative, information about the growth in the direction perpendicular to the image plane was obtained by measuring the projection of the slanted facets on the image plane (the Lxy dimension, as denoted in Fig. 2) and considering the corresponding interfacial angle. The height of the TFA-IX crystals obtained this way was also used to calculate perpendicular facet distances by applying a geometrical correction to the experimentally measured centroid-edge distances, as discussed in the ESI.†2.9 Linear growth rates (G)
Growth rates for various linear crystal dimensions (G) were obtained from the line of best fit of the measured crystal dimensions data against time. In all cases, the dimensions were expressed relative to the centroid of the crystal. Crystal linear growth rates have units of velocity, length per unit of time (μm min−1). For TFA-I and TFA-II, growth rates for the length and width dimensions were derived and denoted as G[100] (dL/2dt) and G[001] (dW/2dt) due to the dimensions aligning with those crystallographic directions in both polymorphs. For TFA-IX, G{10−1} and G{11−1} were derived from orientation A and G{001} and G{11−1}from orientation B. All rates are derived relative to the centroid of the crystal (or bounding box).2.10 Computation of crystal volumes for the different forms
For TFA-I and TFA-II, the shape of the needle crystals was approximated with a cylinder of dimensions L and W, having volume V = (π/4) × L × W2. For TFA-IX, the centroid-edge distances were converted to centroid-facet distances as described in the ESI.† The latter were then used for the generation of a convex hull according to the Wulff's construction method, whose volume was calculated using an in-house Python code described in the ESI† and named the Particle Property Calculator (PPC).2.11 Volume growth rates (Gvol)
The computed experimental crystal volumes as a function of time were used to derive volume growth rates (Gvol = dV/dt) for all polymorphs. Volume growth rates are intrinsically dependent on the crystal size and shape (and thus the overall area of the growing crystal), as discussed later. These rates have units of volume per unit of time (μm3 min−1).2.12 Volume-equivalent diameter growth rates (GD)
The calculated experimental (non-spherical) crystal volumes were equated to sphere volumes for which the corresponding diameters were derived. Those were then used to derive the volume-equivalent diameter growth rates (GD). GD rates have units of velocity, length per unit of time (μm min−1). Further details are provided in the ESI.†2.13 Calculation of crystal growth volumes after a specific time (Vgrowth)
The change of crystal volume after a fixed time t can be calculated to evaluate the influence of linear growth rates on the overall crystal volume change. Crystal growth volumes for the TFA polymorphs were calculated using the relevant crystal linear growth rates making some assumptions on the size of crystal seeds at growth time 0. In all cases, the initial crystal volume was fixed to an average volume of about 8 × 106 μm3, typical of the average seeds used in our experiments. Different seed volumes were also tested as explained later and in the ESI.†For TFA-I and TFA-II, the volume at time t and solution concentration x was calculated using eqn (2), where L0, W0 and T0 are the initial crystal dimensions and GL(x), GW(x) are the derived average experimental linear growth rates which are concentration-dependent.
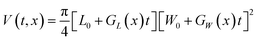 | (2) |
For TFA-IX, the volume at time t and concentration x was calculated from facet distances and their experimental growth rates using the PPC algorithm described above and using eqn (3) where the initial distances d{hkl},0 were proportional to the average distances of the seeds measured for our experiments and were scaled to achieve the desired initial volume.
| V(t, x) = f(d{hkl},0 + G{hkl}(x)t) | (3) |
2.14 Isothermal seeded batch de-supersaturation experiments for TFA-I and TFA-II
Crystal seeds of TFA-I and TFA-II for batch desupersaturation experiments were prepared by crash cooling supersaturated solutions of TFA in IPA. The fraction of fines in the products was reduced by temperature cycling and washing with water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IPA (50
IPA (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) mixtures. The population size distributions (PSDs) of the seeds and of the products of the experiments were characterised with the method developed by Neoptolemou et al.36 All experiments were conducted in IPA at 25 °C (298 K) in a 75 ml reactor using a 4-blade PTFE impeller at a stirring rate of 130 rpm. Temperature was controlled using a Huber Ministat 230 circulator. Suspensions of TFA (commercial form I) in IPA were dissolved and kept at the dissolution temperature for 1 hour. The temperature was then decreased to 25 °C and kept constant. Seeds were added as soon as the temperature inside the reactor was constant within 0.1 °C. The change in concentration over time was monitored using an ATR-UV Hellma 661.872 immersion probe connected to a Zeiss MCS621-CLD600 spectrometer, collecting data every 5 seconds. Absorbance data from solutions of known concentration were used to build a calibration model using Partial Least Squares (PLS) regression. Experimental data were analysed using a simple Population Balance Model (PBM) where only growth was considered (see ESI† for details).
50) mixtures. The population size distributions (PSDs) of the seeds and of the products of the experiments were characterised with the method developed by Neoptolemou et al.36 All experiments were conducted in IPA at 25 °C (298 K) in a 75 ml reactor using a 4-blade PTFE impeller at a stirring rate of 130 rpm. Temperature was controlled using a Huber Ministat 230 circulator. Suspensions of TFA (commercial form I) in IPA were dissolved and kept at the dissolution temperature for 1 hour. The temperature was then decreased to 25 °C and kept constant. Seeds were added as soon as the temperature inside the reactor was constant within 0.1 °C. The change in concentration over time was monitored using an ATR-UV Hellma 661.872 immersion probe connected to a Zeiss MCS621-CLD600 spectrometer, collecting data every 5 seconds. Absorbance data from solutions of known concentration were used to build a calibration model using Partial Least Squares (PLS) regression. Experimental data were analysed using a simple Population Balance Model (PBM) where only growth was considered (see ESI† for details).
2.15 DFT calculation of attachment energies
Attachment energies for the TFA polymorphs were calculated using dispersion-corrected DFT. The crystal structures with CSD37 refcodes KAXXAI01 (TFA-I), KAXXAI (TFA-II) and KAXXAI11 (TFA-IX) were used for the calculations. All calculations were performed using VASP 5.4.4 (ref. 38–41) with the PBE functional42 and PAW43,44 pseudopotentials as described in detail the ESI.† The effect of IPA on calculated attachment energies was estimated with an implicit solvent model using the VASPsol module.45,463. Results
3.1 Crystal morphologies of TFA polymorphs
Prior to the measurement of any linear growth rates, a full morphological and face indexing characterisation of the three polymorphs of TFA was carried out. Fig. 2 shows the crystal morphologies of TFA-I, TFA-II and TFA-IX, together with a depiction of the crystal dimensions measured during our single-crystal growth experiments and the approximations used to calculate the crystal thickness or height. The sizes of the measured crystal seeds differed considerably between the needle crystals of TFA-I and TFA-II and the blocky crystals of TFA-IX, with the volumes of the latter calculated to be at least one order of magnitude larger than those of the former. Although the size of the crystal seeds has a profound effect on the volume growth rates, the measured linear growth rates were assumed size-independent, within the expected experimental variabilities, which is a reasonable assumption for the crystal sizes considered here (100–1000 μm).47,483.2 Unusual growth of TFA needle crystals
During the single crystal growth experiment of TFA needles, darkened edges of the extremities of the TFA needle crystals were observed (Fig. 3), revealing that the growth along the needle direction was the result of the simultaneous advancement of several aligned smaller needle fronts to give the appearance of lamellae. This mode of growth has been previously observed for irbersartan and other organic compounds49,50 including urea,51 and has also recently been reported for plates of benzamide form I.52 In most of our single crystal growth experiments, the growth of each of these individual fronts along the needle axis proceeded independently until a common growth front was established (Fig. 3a and b). The only exception observed was that of TFA-II crystals at high supersaturation, where individual constituent micro-needles kept growing independently with exceptionally fast growth rates (Fig. 3c).We cannot exclude that the observed growth behaviour may have been caused by defects introduced by our need to cut the needle crystals for our measurements. We note, however, that the experimental deviations found for the growth rates along the needle direction between different samples were small, with coefficients of variation (ratio of standard deviation to mean value) between 10% and 30%, which are comparable to values reported for other single-crystal growth kinetics experiments.15 Parallel micro-needles were observed also for crystals of TFA that were not cut, suggesting the possibility that this growth behaviour is peculiar to TFA grown from IPA. We highlight the case of a very large crystal of TFA-I (about 1.5 cm long and 2 mm wide) which was left in an IPA solution for six months. Although this crystal appeared as single to the naked-eye (or with a conventional microscope), analysis under a polarising microscope showed that it was composed of different parallel fragments all with the same pleochroic response (Fig. S13†).
3.3 Linear growth rates of TFA polymorphs
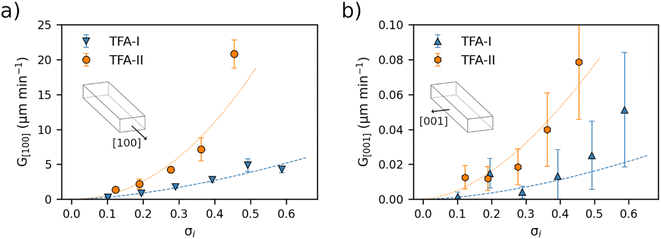
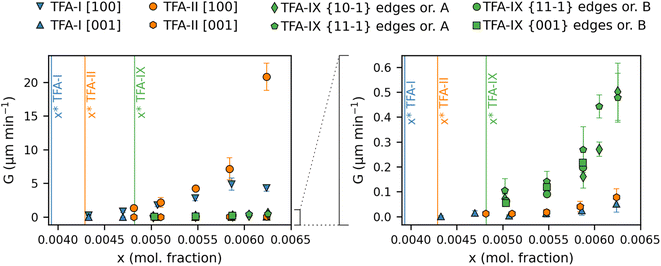
Average linear growth rates for crystal dimensions of TFA-I, TFA-II and TFA-IX in IPA at 25 °C are presented in Fig. 4 and 5 and reported in Tables S4 and S5 in the ESI.†Fig. 4 shows the growth rates along the length and width dimensions of the TFA-I and TFA-II needles. For both polymorphs, growth along the length direction (G[100], Fig. 4a) is about two orders of magnitude faster than the along the width direction (G[001], Fig. 4b). At identical relative supersaturation conditions, crystals of the metastable TFA-II polymorph grow faster than crystals of TFA-I along both needle dimensions, although differences are more evident for the length direction.
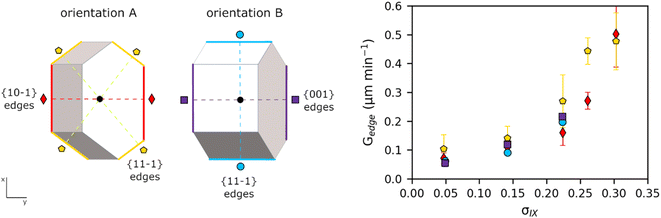
Fig. 5 shows the average growth rates of the visible edges of crystals of TFA-IX as measured in our experiments. The growth rates of TFA-IX along different directions have comparable magnitude, consistent with the growth of this form as blocky crystals. Both the measured edge rates and the geometrically corrected facet growth rates in TFA-IX (Table S5†) range from about 0.04 μm min−1 at low supersaturation to about 0.5 μm min−1 at the highest supersaturation considered here, and they are one order of magnitude faster than the width and one order of magnitude slower than the length of TFA-I and TFA-II.
Fitting of crystal growth models (screw dislocation mechanism, birth and spread mechanism and rough growth mechanism) to experimental data of linear growth rates for all three polymorphs was attempted but found to lead to inconclusive results (see ESI†). For TFA-I and II, as a result of the unconventional needle growth mechanism observed, fits using conventional growth models53 had little significance. For TFA-IX, instead, no evident unconventional growth mechanism was directly observed for TFA-IX, and growth models were fitted to the corrected perpendicular facet growth rates. Only the growth rates of the {001} facets of TFA-IX were found to be fitted reasonably well with a birth and spread mechanism model (R2 = 0.982), but no good fits were found for the {10−1} and the {11−1} facets.
3.4 Linear growth rates and energetics at the molecular level
Attachment energies54 of the three TFA polymorphs, calculated using an implicit solvent model for IPA, are reported in Table 1. The calculated energies were found to show a good qualitative agreement with the observed crystal morphologies and the measured growth rates. For TFA-I and TFA-II, the attachment energies of facets along the length dimension are significantly more stabilising (with values around −80 kJ mol−1) than for the facets defining the width and thickness (around −30 kJ mol−1 and −19 kJ mol−1, respectively), reflecting the observed needle anisotropy for these two polymorphs. We note that, although the attachment energies of TFA-II along the length dimension are more stabilising than those of TFA-I, the calculated values do not reflect the significant difference of experimental growth rates along this direction found from our experiments. This observation is in accordance with known limitations of the attachment energy model, especially when calculations are performed for needle-forming systems.55 For TFA-IX, the calculated attachment energies along different directions (between −34 and −60 kJ mol−1) have smaller differences, and their relative order correlates well with the corrected growth rates of the corresponding facets (Fig. S24†). Also, in accordance with experimental growth rates, the attachment energies of TFA-IX have intermediate values compared to those found for both TFA-I and TFA-II in either the length or the width direction.| Form | Planes | M | d hkl /Å | Growth dimension | E att,{hkl}/kJ mol−1 M. I.b | Relative Eatt morphology volume | |
|---|---|---|---|---|---|---|---|
| a Facet multiplicity. b Morphological importance. | |||||||
| TFA-I | {020} | 2 | 16.09 | T | −19.1 | 0.57 | 1.5 |
| {011} | 4 | 7.57 | W | −42.0 | 0.28 | ||
| {100} | 2 | 4.55 | L | −76.2 | 0.13 | ||
| TFA-II | {020} | 2 | 10.95 | T | −19.3 | 0.40 | 1.0 |
| {011} | 4 | 11.94 | W | −26.9 | 0.47 | ||
| {10−1} | 2 | 3.68 | L | −81.9 | 0.11 | ||
| TFA-IX | {10−1} | 2 | 9.14 | — | −34.4 | 0.33 | 2.5 |
| {001} | 2 | 14.54 | — | −41.5 | 0.36 | ||
| {11−1} | 4 | 5.92 | — | −59.8 | 0.31 | ||
The computed relative volumes of crystal morphologies predicted using the attachment energy model have been previously used as an indication of possible kinetic advantage when comparing polymorphs.56,57 In our case, the relative volumes calculated for the attachment energies morphologies of TFA-I, TFA-II and TFA-IX were 1.5, 1.0 and 2.5, respectively. Therefore, growth rates predicted with the attachment energy model find TFA-II to be the slowest growing polymorph, followed by TFA-I and finally TFA-IX. We will discuss later how these relative volumes compared with the volumetric growth data obtained from our experiments.
As for the continuous intermolecular interactions controlling the growth of these polymorphs (chains), the growth along the needle axis of TFA-I and TFA-II is entirely dominated by aromatic stacking (∼−44 kJ mol−1 in strength).29 For TFA-IX, chains are also present but involve alternating hydrogen bonds between carboxylic groups and stacking of chlorine-substituted rings which form pseudo-continuous chains along the [101] direction, as well as chains of translation-related molecules interacting through t-type contacts between their aromatic rings. Intermolecular interactions in TFA-IX also have an intermediate strength (∼−23 kJ mol−1) compared to the interactions found in TFA-I and TFA-II along their length (∼−44 kJ mol−1) and along their width (∼−13 kJ mol−1), as calculated in ref. 29 using DFT-d.
In summary, all energetic considerations point towards TFA-I and TFA-II having anisotropic growth behaviour with length growth directed by strong aromatic interactions and width and thickness growth directed by very weak interactions. TFA-IX, by contrast, is significantly more isotropic in its growth behaviour, with a mixture of interactions of intermediate strength along all significant crystal directions. The nature and strength of the interactions in the TFA polymorphs correlate well with the measured linear growth rates.
3.5 Growth rates comparisons
To embark in further comparisons of growth kinetics of the TFA polymorphs, it is important to consider that different polymorphic forms have different solubilities, and thus a solution of a given concentration will be more supersaturated with respect to the stable polymorph, while the supersaturation of metastable polymorphs will be lower. As a result, the conclusions drawn from comparing growth rates can vary depending on whether the comparison has been carried out against solution concentration or relative supersaturation of each form. For example, in the case of piracetam,14,15 the metastable form II was reported to have faster growth rates than the stable form III based on a comparison against supersaturation of each form; if the same data are plotted against solution concentration, however, the stable form III is found to actually grow faster than the metastable one.
In the case of the linear growth rates of TFA polymorphs presented here, a comparison against relative supersaturation (Fig. 4 and 5) or against solution concentration, as shown in Fig. 6, leads to the same conclusion despite the difference in solubility between the stable TFA-I and the metastable TFA-II (+0.2 kJ mol−1 relative free energy) and TFA-IX (+0.5 kJ mol−1 relative free energy). Again, TFA-IX is found to grow at an intermediate rate (in all its dimensions) between the length and width of the TFA-I and TFA-II needles. Although linear growth rates suggest that the growth kinetics of the TFA polymorphs follow the order TFA-II > TFA-IX > TFA-I, additional attention needs to be paid if the crystal morphologies of the forms are considerably different, like in the present case. For example, since both TFA-I and TFA-II have comparable needle morphologies, it is intuitive to state that at solution concentrations above the solubility of TFA-II, TFA-II grows faster than TFA-I since both the length and the width growth rates of TFA-II are slightly higher than the length and width growth rates of TFA-I. Such comparison is not straight forward when comparing the kinetics of growth of the TFA-I or TFA-II needles with the blocky crystals of TFA-IX. This difficulty was also found in a previous study which compared the growth kinetics of two polymorphs of paracetamol.55
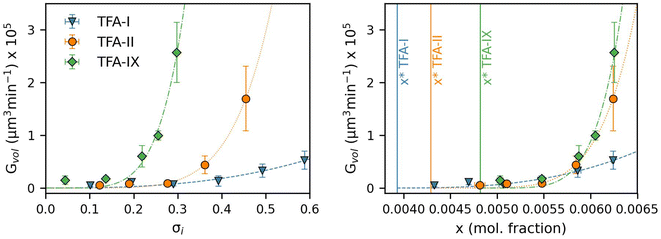
To compare overall kinetics of growth across polymorphs, therefore, one ought to either compare overall mass growth rates or volumetric growth rates (the two can be related by considering crystal densities), rather than just growth rates along specific crystal dimensions. It must be stressed, however, that while growth rates measured along linear dimensions can be size-independent and thus amenable to a straight comparison without crystal size assumptions (this was the case for our system, however other systems may show significant size-dependent growth or growth rate dispersion), volumetric growth rates are intrinsically size dependent. For example, for an idealised spherical crystal growing isotropically with a constant radius growth rate expressed as 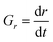 , the change of volume
, the change of volume 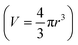 as a function of time
as a function of time 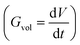 will be proportional to its surface area, since
will be proportional to its surface area, since 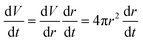 .
.
Given this, in the following sections, we present different ways of comparing the kinetics of growth of the TFA polymorphs through calculation of crystal volumes, either directly from images collected during our growth experiments, or by simulations of the effect of linear growth rates on the change of crystal volume over time. We also discuss the great significance in the assumptions made, approximations and limitations of our approach and show that the question “which polymorph grows faster?” does not have a simple answer even when crystal volumes are considered.
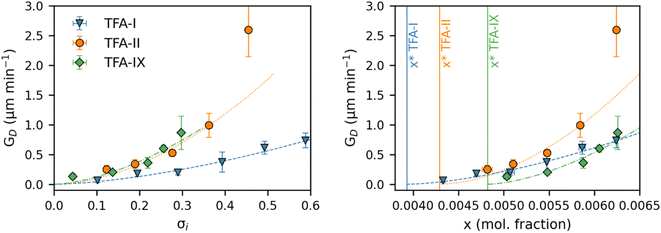
Fig. 8 shows the equivalent diameter growth rates of the TFA polymorphs as obtained from our growth experiments as a function of relative supersaturation and solution concentration. Compared to the volume growth rates presented in the previous section, the resulting picture here is notably different. GD data show that TFA-II grows the fastest at all solution concentrations, followed by TFA-I at lower solution concentrations and by TFA-IX at higher solution concentrations (above x = 0.0063). If the same data are presented as a function of relative supersaturation, however, TFA-IX is found to grow as fast as TFA-II.
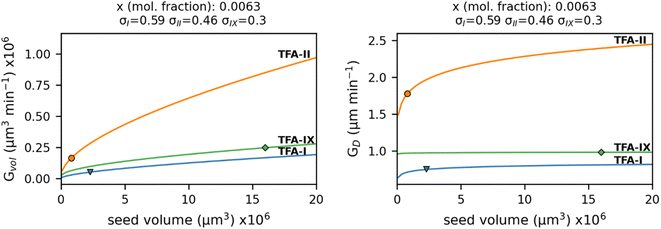
Our simulations show a very strong dependence of Gvol on the volume of the crystal seed. As expected from its intrinsic relationship, crystal seeds with larger volumes (thus larger surface areas) result in larger volume growth rates. Such dependence is considerably minimised when considering the simulated growth rates of equivalent diameters, GD, especially for TFA-IX. The blocky crystal morphology and the near-isotropic linear growth rates of this polymorph mean that choosing a sphere to describe the change of volume over time of its crystals is more appropriate than in the case of TFA-I and TFA-II, which in contrast have needle morphologies and very anisotropic growth rates.
The evident dependence of both Gvol and GD on crystal seed size is a consequence of the relations used to couple the crystal linear dimensions to the resulting crystal volumes, which assume the use of a constant shape factor. For small crystal sizes, however, the relative change of crystal dimensions over time (i.e., the linear growth rates) with respect to the seed size is non-negligible, and a constant shape factor cannot be assumed.59,60
Therefore, the nature of the crystal seeds used for experiments must be taken into consideration when utilising equivalent diameter growth rates to compare growth kinetics of polymorphs.
Nevertheless, because the seed crystals of TFA-I and TFA-II used in our experiments had similar dimension and shape, and because the diameter growth rates of TFA-IX are expected to show little variation for different seed volumes, the comparison of its GD with those of TFA-I and TFA-II is indeed possible in this case.
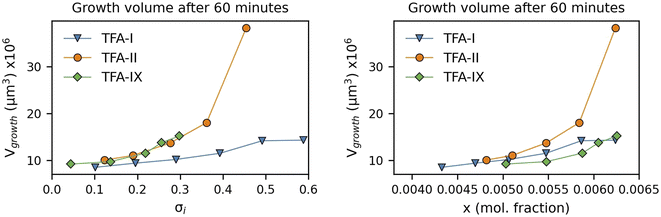
Here we have calculated the growth volume (Vgrowth) of all three polymorphs in IPA at 25 °C after 60 minutes, making the assumption of identical seed volumes for all three forms (8 × 106 μm3, typical volume of seeds used in our experiments). The calculated Vgrowth(60 min) at different relative supersaturations and solution concentrations is shown in Fig. 10.
The calculated Vgrowth(60 min) show that after 60 minutes of growth, crystals of the metastable TFA-II have the largest volume at any given solution concentration. While the volumes of TFA-IX are the smallest at low solution concentrations, they become larger than TFA-I as the driving force for crystal growth increases (x > 0.0063). The dependence of Vgrowth on relative supersaturation, instead, is similar for TFA-II and TFA-IX. We note that the trends observed here for Vgrowth are very similar to the trends obtained for the GD data presented previously.
Fig. 11 shows a comparison of the GD rates from SC experiments with those from the SID experiments. We note that the experimental conditions of SC and SID experiments are very different (i.e., differences in solution volume, stirring conditions, single vs. multiple seeds, etc.), and thus comparisons between growth rates obtained with the two techniques should be performed with care.
In our case, considering that crystal seeds of TFA-I and TFA-II used in our SC and SID experiments had comparable size (see ESI†), and that experiments were conducted at the same temperature, the most significant difference was perhaps the fact that SID experiments were carried out with controlled stirring, whereas SC growth rates were measured in stagnant IPA solutions.
We found GD rates derived from SC and SID experiments to have a similar order of magnitude and to follow surprisingly similar trends and dependence on solution concentration. This is very encouraging since our results show that GD rates derived from SC experiments could be a viable approach to estimate kinetic growth parameters for polymorphs for which SID experiments are not possible (i.e., TFA-IX).
4. Discussion
In the context of the results and data presented above, we come to the realisation that to try and answer the question “which polymorph grows faster” is extremely difficult, and that the question is perhaps best formulated as “which polymorph grows faster under a well-defined set of conditions”.First, differences in solubilities across polymorphs mean that for a defined solution concentration the system will have different supersaturation levels with regard to each of the polymorphs. Thus, specifying whether the comparison of kinetics refers to identical conditions of relative supersaturation or overall solution concentration is important. For example, if one wishes to compare crystal growth rates predicted starting from crystal structure and strength of intermolecular interactions (i.e., attachment energies), a comparison at the same level of relative supersaturation is appropriate. If, by contrast, one wishes to understand which dimension grows faster at a specific solution concentration, then the solubility differences need to be considered. We presented our results both at relative identical supersaturations and at different values of solution concentration. Since the original aim of this work was to rationalise the difficult discovery of TFA-IX, we will further discuss our results by comparing growth rates in terms of identical solution concentrations.
Second, provided that the linear rates are size independent (which is the case for TFA but may not always be a reasonable assumption), the growth rates of various measurable dimensions across polymorphs can be directly compared but might not tell the whole tale. We have found here that GIIL > GIL > GIX{hkl} > GIIW > GIW. However, linear growth rates alone cannot provide an answer to the question “which polymorph grows faster” and thus considerations of volume or mass growth rates is a necessity.
Third, assuming a solution concentration above the solubility of the least stable polymorph (TFA-IX), the answer to the question “which polymorph grows faster” is, it depends on the solution concentration and on the relative size and shape of the polymorphic crystals used for the experiment. Thus, because the blocky crystal seeds of TFA-IX used for our stagnant cell growth experiments had a significantly larger volume than those of the TFA-I and TFA-II needles, TFA-IX crystals grew faster (faster volume growth rates). The volume growth rates here give the overall answer, but this answer is strongly dependent on the crystal size and thus our choice of seeds in the experiments.
If we wish to compare growth kinetics for the hypothetical case of all polymorphs starting from seeds of identical volume, the answer to the question “which polymorph grows faster” can be inferred by either calculating growth volumes after a given growth time t from identical size seeds or sphere equivalent diameter growth rates. We have shown that both these approaches provide similar outcomes. They show that at molar fraction concentrations above 0.0048 (the solubility of TFA-IX) and below 0.0063 the growth kinetic ordering is TFA-II > TFA-I > TFA-IX and above 0.0063 TFA-II > TFA-IX > TFA-I. Most importantly, all three growth rates are comparable and competitive thus, provided that the forms can be nucleated concomitantly, they can also grow at similar rates and appear together macroscopically. These conditions seem to occur, for this system, at low temperature, which allowed for the discovery of TFA-IX.29
Finally, perhaps an important observation from this data is that conditions exist (molar fraction solution concentrations above 0.0063) for which both metastable TFA-II and TFA-IX grow faster than the stable form TFA-I. This may be an important observation, since provided all polymorphs can be nucleated in the solution, the seeds of the metastable forms will consume supersaturation faster than the seeds of the stable form which will allow for sufficient time for them to be observed macroscopically (and thus the forms discovered) before the supersaturation is consumed and they start dissolving in favour of the growth of the stable form.
5. Conclusions
We have measured, presented and compared the growth kinetics of three polymorphs of TFA in IPA solutions at 25 °C. To the best of our knowledge, this is the first time such data has been presented for three different polymorphs of a molecular system. The growth kinetics of TFA-I and TFA-II were determined by direct measurements on single crystals as well as by SID experiments. For TFA-IX, growth rates were determined by single-crystal measurements only since SID experiments failed due to the rapid solvent-mediated conversion of TFA-IX into the stable TFA-I.From growth measurements carried out on single crystals, we were able to derive and compare linear growth rates (Glinear) for all three TFA polymorphs. Comparison of Glinear for TFA-I and TFA-II polymorphs was straightforward since both forms crystallise as needles and the data showed that both the length and width dimensions of the metastable TFA-II grow faster than the stable TFA-I, and thus TFA-II grows faster overall. TFA-IX, however, crystallises as blocky crystals. Direct comparison of the measured Glinear of TFA-IX with those of TFA-I and TFA-II shows that rates for the growth of TFA-IX lie between those along the length and the width dimensions of both TFA-I and TFA-II needles. Using linear growth rates alone, answering the question “which polymorph grows faster” becomes tricky. If linear growth rates are used to compare polymorphs with different shapes results can be misleading, and so volume growth rates, calculated crystal volumes after a specific growth time or equivalent diameter growth rates need to be derived in order to answer this question. This means that the question can only be answered if the conditions of growth of the various polymorphs can be established with clarity. Since volume growth rates of large crystals tend to be greater than volume growth rates of smaller crystals, a polymorph having larger seeds is likely to grow faster than a polymorph having small seeds.
Establishing the boundary condition that the growth occurs from seeds of identical initial volume, we were able to use calculated growth volumes or equivalent diameter growth rates to establish that at molar fraction concentrations above 0.0048 and below 0.0063 the growth kinetic ordering is TFA-II > TFA-I > TFA-IX and above 0.0063 it becomes TFA-II > TFA-IX > TFA-I. For TFA, there is therefore a range of solution concentration were both metastable forms grow faster than the stable TFA-I from seeds of original identical volume. Interestingly, we have only observed TFA-IX at conditions of high supersaturations and low temperature which presumably are needed for all three forms to nucleate, grow at a similar rate and be observed concomitantly. The effect of temperature on the growth rates of different polymorphs could also result in different relative growth rates than those considered here. Although we have not investigated this effect here, this remains an interesting topic for future investigations.
Ultimately, the answer to the question “will I be able to observe a specific predicted polymorph” needs to come from a combined prediction of nucleation and growth kinetics. Several scenarios exist:
A. If the metastable polymorph can be nucleated faster than the stable form, then its observation will be possible.
B. If the metastable polymorph is nucleated concomitantly with the stable form, two possibilities arise: (i) the metastable polymorph grows faster than the stable form so it will be able to grow to a detectable size before supersaturation is consumed and it dissolves in favour of the growth of the stable form and (ii) the metastable polymorph grows slower than the stable form thus it will be difficult to observe and it will be an elusive form.
C. If the metastable polymorph is slower at nucleating than the stable form, it will be difficult to discover.
These scenarios have been modelled mathematically for hypothetical systems using the concept of the Ostwald ratio.10,61
Ultimately, to be able to use CSP landscapes to predict which polymorphs will crystallise, we ought to be able to predict both nucleation and growth kinetics56 from crystal structure alone and under different crystallisation conditions including solvent, supersaturation levels and temperature. Disappointingly, the predicted relative volumes of morphologies calculated from solvent corrected attachment energies (TFA-IX > TFA-I > TFA-II) were in total discordance with our experimental results. This was somewhat expected, considering the known limitations of the attachment energy model in considering the effect of the growth environment (solvent, supersaturation) on the crystal growth rates.
When it comes to the prediction of growth kinetics, part of the problem lies in the fact that growth mechanisms can vary amongst different crystal facets. In addition, growth mechanisms along some crystal directions can be very different than well-established mechanisms commonly used in crystal growth predictions, as we have shown here for the length growth of the TFA needles. Predicting kinetics of nucleation for hundreds of predicted polymorphs is also extremely challenging, and although simulations of nucleation using molecular dynamics have been attempted,62–66 this task remains computationally expensive. As an alternative, some qualitative correlations using structural rugosity have been proposed.67 In conclusion, it is clear that further good quality experimental data on kinetics of nucleation and growth of polymorphs is needed for theoretical model validation. Even comparing experimental growth rates is challenging in itself, as we have shown here. Whilst we have come a long way, we still have a very long way to go.
Data availability
Processed data are available in the ESI.† Additional data can be obtained by the authors upon request.Author contributions
A. J. C. C., R. J. D. and S. M. R. E. conceived the project. P. S. collected experimental data, performed data analysis, performed computer simulations and wrote the initial manuscript. P. N. contributed to the data analysis and to the design of computer simulations. All authors discussed the results and contributed to the final manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Pietro Sacchi would like to thank Eli Lilly and Company for funding, and Dr Thomas Vetter and Dr Alexandru Moldovan for helpful discussions.References
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Facts and Fictions about Polymorphism, Chem. Soc. Rev., 2015, 44(23), 8619–8635, 10.1039/C5CS00227C.
- J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, Oxford, 2nd edn, 2020 Search PubMed.
- A. J. Cruz-Cabeza, N. Feeder and R. J. Davey, Open Questions in Organic Crystal Polymorphism, Commun. Chem., 2020, 3(1), 142, DOI:10.1038/s42004-020-00388-9.
- D. H. Bowskill, I. J. Sugden, S. Konstantinopoulos, C. S. Adjiman and C. C. Pantelides, Crystal Structure Prediction Methods for Organic Molecules: State of the Art, Annu. Rev. Chem. Biomol. Eng., 2021, 12(1), 593–623, DOI:10.1146/annurev-chembioeng-060718-030256.
- G. J. O. Beran, I. J. Sugden, C. Greenwell, D. H. Bowskill, C. C. Pantelides and C. S. Adjiman, How Many More Polymorphs of ROY Remain Undiscovered, Chem. Sci., 2022, 13(5), 1288–1297, 10.1039/D1SC06074K.
- W. Ostwald, Studien Über Die Bildung Und Umwandlung Fester Körper. 1. Abhandlung: Übersättigung und Überkaltung, Z. Phys. Chem., 1897, 22U(1), 289–330, DOI:10.1515/zpch-1897-2233.
- J. Nývlt, The Ostwald Rule of Stages, Cryst. Res. Technol., 1995, 30, 443–449 CrossRef.
- T. Threlfall, Structural and Thermodynamic Explanations of Ostwald's Rule, Org. Process Res. Dev., 2003, 7(6), 1017–1027, DOI:10.1021/op030026l.
- J. F. B. Black, P. T. Cardew, A. J. Cruz-Cabeza, R. J. Davey, S. E. Gilks and R. A. Sullivan, Crystal Nucleation and Growth in a Polymorphic System: Ostwald's Rule, p-Aminobenzoic Acid and Nucleation Transition States, CrystEngComm, 2018, 20(6), 768–776, 10.1039/C7CE01960B.
- P. T. Cardew and R. J. Davey, The Ostwald Ratio, Kinetic Phase Diagrams, and Polymorph Maps, Cryst. Growth Des., 2019, 19(10), 5798–5810, DOI:10.1021/acs.cgd.9b00815.
- S. L. Price, Progress in Understanding Crystallisation: A Personal Perspective, Faraday Discuss., 2022, 235, 569–581, 10.1039/D2FD00077F.
- S. Sudo, K. Sato and Y. Harano, Growth and Solvent-Mediated Phase Transition of Cimetidine Polymorphic Forms A and B, J. Chem. Eng. Jpn., 1991, 24(5), 628–632, DOI:10.1252/jcej.24.628.
- M. Kitamura, H. Furukawa and M. Asaeda, Solvent Effect of Ethanol on Crystallization and Growth Process of L-Histidine Polymorphs, J. Cryst. Growth, 1994, 141(1–2), 193–199, DOI:10.1016/0022-0248(94)90112-0.
- R. Soto and Å. C. Rasmuson, Crystal Growth Kinetics of Piracetam Polymorphs in Ethanol and Isopropanol, Cryst. Growth Des., 2019, 19(8), 4273–4286, DOI:10.1021/acs.cgd.8b01733.
- A. Lynch, R. Soto and Å. Rasmuson, Single Crystal Growth Kinetics of Two Polymorphs of Piracetam, Cryst. Growth Des., 2021, 21(10), 5631–5640, DOI:10.1021/acs.cgd.1c00455.
- R. Dowling, R. J. Davey, R. A. Curtis, G. Han, S. K. Poornachary, P. S. Chow and R. B. H. Tan, Acceleration of Crystal Growth Rates: An Unexpected Effect of Tailor-Made Additives, Chem. Commun., 2010, 46(32), 5924, 10.1039/c0cc00336k.
- G. Han, P. S. Chow and R. B. H. Tan, Direct Comparison of α- and γ-Glycine Growth Rates in Acidic and Basic Solutions: New Insights into Glycine Polymorphism, Cryst. Growth Des., 2012, 12(5), 2213–2220, DOI:10.1021/cg201321f.
- W. Beckmann and R. Boistelle, Growth Kinetics of the (110) Face of Stearic Acid Growing from Butanone Solutions - Pure Solutions and in the Presence of an Emulsifier, J. Cryst. Growth, 1985, 72(3), 621–630, DOI:10.1016/0022-0248(85)90213-1.
- W. Beckmann, S. Kämmer, J. Meier and R. Boistelle, Growth Kinetics of the (110) Face of the B and C Polymorphs of Stearic Acid Growing from Octanone-2 Solutions, J. Cryst. Growth, 1986, 74(2), 326–330, DOI:10.1016/0022-0248(86)90121-1.
- S. Jiang, J. H. ter Horst and P. J. Jansens, Concomitant Polymorphism of O-Aminobenzoic Acid in Antisolvent Crystallization, Cryst. Growth Des., 2008, 8(1), 37–43, DOI:10.1021/cg070517n.
- Y. Liu, B. Gabriele, R. J. Davey and A. J. Cruz-Cabeza, Concerning Elusive Crystal Forms: The Case of Paracetamol, J. Am. Chem. Soc., 2020, 142(14), 6682–6689, DOI:10.1021/jacs.0c00321.
- L. Zhu, L. Wang, Z. Sha, Y. Wang, L. Yang, X. Zhao and W. Du, Interplay between Thermodynamics and Kinetics on Polymorphic Appearance in the Solution Crystallization of an Enantiotropic System, Gestodene, Cryst. Growth Des., 2017, 17(9), 4582–4595, DOI:10.1021/acs.cgd.7b00335.
- Z. Gao, Z. Cen, J. Lin, Z. Li, L. Fang, Z. Gao, D. Han and J. Gong, Synergistic Control of Nonlinear Growth Kinetics and Nucleation Kinetics in the Concomitant Crystallization of Aripiprazole as Reflected by the Ostwald Ratio, Ind. Eng. Chem. Res., 2022, 61(46), 17183–17195, DOI:10.1021/acs.iecr.2c03731.
- J. Davey and A. Rutti, Single versus Suspension Growth, J. Cryst. Growth, 1974, 26, 149–150 CrossRef.
- C. A. Offiler, A. J. Cruz-Cabeza, R. J. Davey and T. Vetter, Crystal Growth Cell Incorporating Automated Image Analysis Enabling Measurement of Facet Specific Crystal Growth Rates, Cryst. Growth Des., 2022, 22(5), 2837–2848, DOI:10.1021/acs.cgd.1c01019.
- K. V. Andersen, S. Larsen, B. Alhede, N. Gelting and O. Buchardt, Characterization of Two Polymorphic Forms of Tolfenamic Acid, N-(2-Methyl-3-Chlorophenyl)Anthranilic Acid: Their Crystal Structures and Relative Stabilities, J. Chem. Soc., Perkin Trans. 2, 1989,(10), 1443–1447, 10.1039/P29890001443.
- V. López-Mejías, J. W. Kampf and A. J. Matzger, Polymer-Induced Heteronucleation of Tolfenamic Acid: Structural Investigation of a Pentamorph, J. Am. Chem. Soc., 2009, 131(13), 4554–4555, DOI:10.1021/ja806289a.
- D. H. Case, V. K. Srirambhatla, R. Guo, R. E. Watson, L. S. Price, H. Polyzois, J. K. Cockcroft, A. J. Florence, D. A. Tocher and S. L. Price, Successful Computationally Directed Templating of Metastable Pharmaceutical Polymorphs, Cryst. Growth Des., 2018, 18(9), 5322–5331, DOI:10.1021/acs.cgd.8b00765.
- P. Sacchi, S. M. Reutzel-Edens and A. J. Cruz-Cabeza, The Unexpected Discovery of the Ninth Polymorph of Tolfenamic Acid, CrystEngComm, 2021, 23(20), 3636–3647, 10.1039/D1CE00343G.
- W. Du, A. J. Cruz-Cabeza, S. Woutersen, R. J. Davey and Q. Yin, Can the Study of Self-Assembly in Solution Lead to a Good Model for the Nucleation Pathway? The Case of Tolfenamic Acid, Chem. Sci., 2015, 6(6), 3515–3524, 10.1039/C5SC00522A.
- W. Tang, Y. Quan, J. Gong, J. Wang, Q. Yin and T. Li, Form Selection of Concomitant Polymorphs: A Case Study Informed by Crystallization Kinetics Modeling, AIChE J., 2021, 67(4), e17129, DOI:10.1002/aic.17129.
- J. Bernstein, R. J. Davey and J.-O. Henck, Concomitant Polymorphs, Angew. Chem., Int. Ed., 1999, 38(23), 3440–3461 CrossRef PubMed.
- Agilent, Crysalis PRO, 2014 Search PubMed.
- T. D. Turner, T. T. H. Nguyen, P. Nicholson, G. Brown, R. B. Hammond, K. J. Roberts and I. Marziano, A Temperature-Controlled Single-Crystal Growth Cell for the in Situ Measurement and Analysis of Face-Specific Growth Rates, J. Appl. Crystallogr., 2019, 52(2), 463–467, DOI:10.1107/S1600576719002048.
- H. Freeman and R. Shapira, Determining the Minimum-Area Encasing Rectangle for an Arbitrary Closed Curve, Commun. ACM, 1975, 18(7), 409–413, DOI:10.1145/360881.360919.
- P. Neoptolemou, N. Goyal, A. J. Cruz-Cabeza, A. A. Kiss, D. J. Milne and T. Vetter, A Novel Image Analysis Technique for 2D Characterization of Overlapping Needle-like Crystals, Powder Technol., 2022, 399, 116827, DOI:10.1016/j.powtec.2021.09.017.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72(2), 171–179, DOI:10.1107/S2052520616003954.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Open-Shell Transition Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(17), 13115–13118, DOI:10.1103/PhysRevB.48.13115.
- G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269, DOI:10.1103/PhysRevB.49.14251.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit Solvation Model for Density-Functional Study of Nanocrystal Surfaces and Reaction Pathways, J. Chem. Phys., 2014, 140(8), 084106, DOI:10.1063/1.4865107.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit Self-Consistent Electrolyte Model in Plane-Wave Density-Functional Theory, J. Chem. Phys., 2019, 151(23), 234101, DOI:10.1063/1.5132354.
- J. W. Mullin, Crystallisation, Butterworth Heinemann, Oxford, UK, 4th edn, 2002, vol. 6 Search PubMed.
- S. Srisanga, A. E. Flood, S. C. Galbraith, S. Rugmai, S. Soontaranon and J. Ulrich, Crystal Growth Rate Dispersion versus Size-Dependent Crystal Growth: Appropriate Modeling for Crystallization Processes, Cryst. Growth Des., 2015, 15(5), 2330–2336, DOI:10.1021/acs.cgd.5b00126.
- P. Taulelle, J. P. Astier, C. Hoff, G. Pèpe and S. Veesler, Pharmaceutical Compound Crystallization: Growth Mechanism of Needle-Like Crystals, Chem. Eng. Technol., 2006, 29(2), 239–246, DOI:10.1002/ceat.200500361.
- F. Puel, E. Verdurand, P. Taulelle, C. Bebon, D. Colson, J.-P. Klein and S. Veesler, Crystallization Mechanisms of Acicular Crystals, J. Cryst. Growth, 2008, 310(1), 110–115, DOI:10.1016/j.jcrysgro.2007.10.006.
- R. Davey, W. Fila and J. Garside, The Influence of Biuret on the Growth Kinetics of Urea Crystals from Aqueous Solutions, J. Cryst. Growth, 1986, 79(1, Part 2), 607–613, DOI:10.1016/0022-0248(86)90527-0.
- C. A. Offiler, C. P. Fonte, W. Kras, P. Neoptolemou, R. J. Davey, T. Vetter and A. Cruz-Cabeza, J. Complex Growth of Benzamide Form I: Effect of Additives, Solution Flow, and Surface Rugosity, Cryst. Growth Des., 2022, 22(10), 6248–6261, DOI:10.1021/acs.cgd.2c00842.
- J. R. Bourne and R. J. Davey, The Role of Solvent-Solute Interactions in Determining Crystal Growth Mechanisms from Solution: I. The Surface Entropy Factor, J. Cryst. Growth, 1976, 36(2), 278–286, DOI:10.1016/0022-0248(76)90290-6.
- P. Hartman and P. Bennema, The Attachment Energy as a Habit Controlling Factor: I. Theoretical Considerations, J. Cryst. Growth, 1980, 49(1), 145–156, DOI:10.1016/0022-0248(80)90075-5.
- H. Meekes, S. X. M. Boerrigter, F. F. A. Hollander and P. Bennema, Needle Crystal Morphology Explained, Chem. Eng. Technol., 2003, 26(3), 256–261, DOI:10.1002/ceat.200390037.
- D. S. Coombes, C. R. A. Catlow, J. D. Gale, A. L. Rohl and S. L. Price, Calculation of Attachment Energies and Relative Volume Growth Rates As an Aid to Polymorph Prediction, Cryst. Growth Des., 2005, 5(3), 879–885, DOI:10.1021/cg049707d.
- Y. A. Abramov, P. Zhang, Q. Zeng, M. Yang, Y. Liu and S. Sekharan, Computational Insights into Kinetic Hindrance Affecting Crystallization of Stable Forms of Active Pharmaceutical Ingredients, Cryst. Growth Des., 2020, 20(3), 1512–1525, DOI:10.1021/acs.cgd.9b01153.
- A. Ruf, J. Worlitschek and M. Mazzotti, Modeling and Experimental Analysis of PSD Measurements through FBRM, Part. Part. Syst. Charact., 2000, 17(4), 167–179, DOI:10.1002/1521-4117(200012)17:4<167::AID-PPSC167>3.0.CO;2-T.
- M. Matuchová and J. Nývlt, Determination of Linear Growth Rates of Crystals (I). Calculation of Linear Growth Rates of Individual Crystal Faces from Overall Rates, Krist. Tech., 1976, 11(2), 149–161, DOI:10.1002/crat.19760110206.
- J. Nývlt and M. Matuchová, Determination of Linear Growth Rates of Crystals (II). The Shape Factors Method, Krist. Tech., 1976, 11(3), 245–253, DOI:10.1002/crat.19760110306.
- R. J. Davey, General Discussion, Faraday Discuss., 1993, 95, 160–161, 10.1039/FD9939500145.
- N. Duff, Y. R. Dahal, J. D. Schmit and B. Peters, Salting out the Polar Polymorph: Analysis by Alchemical Solvent Transformation, J. Chem. Phys., 2014, 140(1), 014501, DOI:10.1063/1.4853775.
- M. Salvalaglio, C. Perego, F. Giberti, M. Mazzotti and M. Parrinello, Molecular-Dynamics Simulations of Urea Nucleation from Aqueous Solution, Proc. Natl. Acad. Sci., 2015, 112(1), E6–E14, DOI:10.1073/pnas.1421192111.
- C. Liu, F. Cao, S. A. Kulkarni, G. P. F. Wood and E. E. Santiso, Understanding Polymorph Selection of Sulfamerazine in Solution, Cryst. Growth Des., 2019, 19(12), 6925–6934, DOI:10.1021/acs.cgd.9b00576.
- L. Lo Presti, S. Rizzato and A. Gavezzotti, Kinetic-Bias Model for the Dynamic Simulation of Molecular Aggregation. The Liquid, Solute, Solvated-Nanodrop, and Solvated-Nanocrystal States of Benzoic Acid, Cryst. Growth Des., 2022, 22(3), 1857–1866, DOI:10.1021/acs.cgd.1c01410.
- Y. Iida, T. Hiratsuka, M. T. Miyahara and S. Watanabe, Mechanism of Nucleation Pathway Selection in Binary Lennard-Jones Solution: A Combined Study of Molecular Dynamics Simulation and Free Energy Analysis, J. Phys. Chem. B, 2023, 127(15), 3524–3533, DOI:10.1021/acs.jpcb.2c08893.
- R. Montis, R. J. Davey, S. E. Wright, G. R. Woollam and A. J. Cruz-Cabeza, Transforming Computed Energy Landscapes into Experimental Realities: The Role of Structural Rugosity, Angew. Chem., 2020, 132(46), 20537–20540, DOI:10.1002/ange.202006939.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02040a |
| This journal is © The Royal Society of Chemistry 2023 |