Open Access Article
Open Access ArticleComputational molecular refinement to enhance enantioselectivity by reinforcing hydrogen bonding interactions in major reaction pathway†
Taishi
Nakanishi
and
Masahiro
Terada
 *
*
Department of Chemistry, Graduate School of Science, Tohoku University, 6-3 Aramaki Aza Aoba, Aoba-ku, Sendai, Miyagi 980-8578, Japan. E-mail: mterada@tohoku.ac.jp
First published on 2nd May 2023
Abstract
Computational analyses have revealed that the distortion of a catalyst and the substrates and their interactions are key to determining the stability of the transition state. Hence, two strategies “distortion strategy” and “interaction strategy” can be proposed for improving enantiomeric excess in enantioselective reactions. The “distortion strategy” is used as a conventional approach that destabilizes the TS (transition state) of the minor pathway. On the other hand, the “interaction strategy” focuses on the stabilization of the TS of the major pathway in which an enhancement of the reaction rate is expected. To realize this strategy, we envisioned the TS stabilization of the major reaction pathway by reinforcing hydrogen bonding and adopted the chiral phosphoric acid-catalysed enantioselective Diels–Alder reaction of 2-vinylquinolines with dienylcarbamates. The intended “interaction strategy” led to remarkable improvements in the enantioselectivity and reaction rate.
Introduction
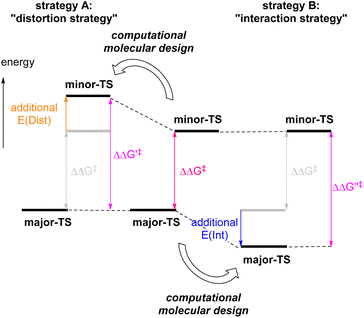
The development of enantioselective catalysis using a chiral catalyst has evolved into an active area of research over the past half-century. In current organic synthesis, catalytic enantioselective reactions are considered one of the indispensable methodologies for affording enantioenriched compounds in an efficient fashion. However, the development of catalytic enantioselective reactions requires enormous effort and costs to optimize not only the catalyst structure but also other reaction conditions. Moreover, in some cases, even substrate modifications are necessary to achieve high performance in terms of catalytic efficiency and stereochemical control. As a way to overcome these inherent difficulties, computational studies have been widely applied to the design of catalyst molecules and reaction systems to achieve highly efficient enantioselective catalysis in recent years.1 Indeed, clarifying the structural features of transition states (TSs) that afford enantiomeric products by means of DFT calculations are helpful to improve the stereochemical outcome through rational refinement of the catalyst molecule and the reaction system.2Among computational approaches reported thus far, the distortion/interaction analysis has been recognized as an intriguing method to characterize TSs.3 On the basis of this analytical method, two strategies can be proposed, which are aimed at improving enantioselectivity. One approach is the “distortion strategy” (Fig. 1, strategy A), and the other is the “interaction strategy” (Fig. 1, strategy B). The former strategy is commonly used as a conventional approach mainly to destabilize minor-TS (the transition state of the minor reaction pathway) by the repulsive steric effect. This strategy offers the advantage of simplicity of designing catalyst molecules and reaction systems, because the steric effect is readily predictable from the TS structures. In addition, a relatively large difference in free energy is anticipated between major-TS (the transition state of the major reaction pathway) and minor-TS.2c,d,f,g However, in some cases, the approach results in unpredictable conformational changes, which often generate diverse TS variants. This increases computational complexity in evaluating whether the structural modification of a catalyst and/or substrate is suitable or not.4
In contrast to the “distortion strategy”, the “interaction strategy” is aimed at stabilizing major-TS (Fig. 1, strategy B). The advantages of this strategy are that significant conformational changes in the TSs are unlikely to occur and, more importantly, that the stabilization of major-TS is expected to improve the reaction rate when the stereo-determining step is also the rate-determining step. However, the stabilization factors in major-TS are often difficult to predict visually because TS stability in enantioselective catalysis is determined by a delicate balance between the strain in the catalyst–substrate complex and the sum of weak interactions including hydrogen bonding, π-stacking, and dispersion interactions, as even relatively weak interactions can have a significant impact on the enantioselectivity.1a,5 Another issue to consider is whether a slight change in interaction energy could be precisely estimated by computational chemistry.6 Recently, Anderson et al.2b and Hartwig et al.2e have independently overcome this critical issue by computational design to reinforce metal–π interaction and dispersion interaction, respectively, to improve the enantioselectivity as well as the reaction rate.
Hydrogen bonding is a ubiquitous interaction that is universally used in the formation of organized molecular structures. It has also played an important role in the development of enantioselective reactions using not only organocatalysts7 but also transition metal catalysts.8,9 Because hydrogen bonding interaction, as broadly defined, is highly directional and electrostatic, it can be readily recognized visually; this allows the strength of the interaction to be controlled at the intended location by changing the electronic property around the bond. We envisioned the selective stabilization of major-TS by strengthening its hydrogen bonding interactions; it was anticipated that the enantioselectivity and the reaction rate would be improved efficiently without causing significant conformational changes in the TSs. This new methodology based on the “interaction strategy” using hydrogen bonding as the key interaction is expected to offer a versatile approach that will contribute to the development of a variety of catalytic enantioselective reactions.
Enantioselective catalysis using a chiral Brønsted acid has been a useful tool in organic synthesis.7,10 Since the introduction of 1,1′-bi-2-naphthol (BINOL)-derived chiral phosphoric acids (CPAs) as privileged chiral Brønsted acid catalysts,11 continuous efforts have been devoted to achieving a broad range of unprecedented catalytic enantioselective reactions by improving the acidity and the chiral environment.12–14 Such catalytic enantioselective reactions have been achieved because the acid/base dual function of the monofunctional phosphate moiety of CPAs is able to strictly define substrate location through hydrogen bonding and other interactions. In addition, the pseudo-C2 symmetry of CPAs has rendered the design of CPA derivatives using computational and machine learning approaches possible.2d,g,15
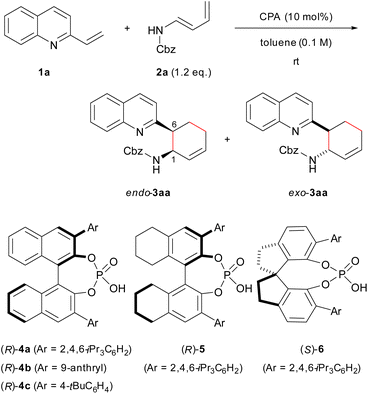
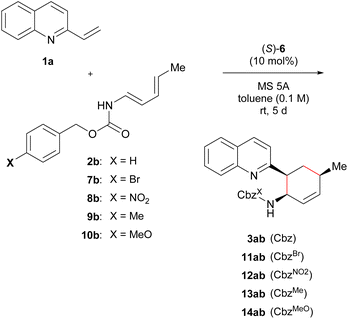
Previous studies have shown that the stereochemical outcome of CPA-catalysed reactions is markedly affected by hydrogen bonds.11d,14d,16 We hypothesized that the selective enhancement of hydrogen bonding interactions in major-TS would improve the stereochemical outcome. To demonstrate the viability of this hypothesis, we adopted the CPA-catalysed Diels–Alder reaction of 2-vinylquinolines 1 with dienylcarbamates as a model reaction (Scheme 1).17,18 In the present reaction system, it is anticipated that both vinylquinolines 1 and dienylcarbamates are captured by CPA through hydrogen bonding interactions, and hence, the reaction would proceed under the chiral environment created by CPA.14c,19 In addition, the Diels–Alder reaction generally proceeds through a concerted fashion. This reaction profile limits the conformational flexibility of the corresponding TSs, and the rate enhancement is also expected by the intended strategy because the rate-determining step coincides with the stereo-determining step. Therefore, the proposed Diels–Alder reaction is an ideal system for verifying the “interaction strategy”.
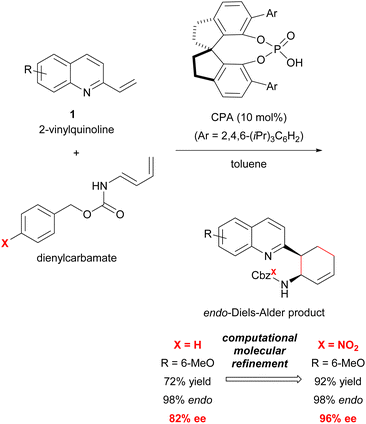 | ||
| Scheme 1 Model reaction for the “interaction strategy”: enantioselective Diels–Alder reaction of 2-vinylquinolines with dienylcarbamates catalysed by CPA. | ||
Here we report the realization of the “interaction strategy,” which resulted in a marked improvement of the enantioselectivity and the reaction rate, by computational molecular refinement of dienylcarbamates. As the representative result shown in Scheme 1, a slight modification (i.e., the introduction of an electron-withdrawing nitro group) to the benzene ring of the Cbz protecting group markedly enhanced the enantioselectivity. The molecular refinement was accomplished by a thorough analysis of the TS structures followed by adjustment of the strength of hydrogen bonds to enhance the interaction energy in the TS of the major reaction pathway. The present approach provides a practical in silico molecular refinement strategy for enantioselective catalysis as well as a synthetic route to potentially useful quinoline derivatives in a highly endo- and enantioselective manner.20
Results and discussion
At the outset of our study, we conducted a brief screening of CPAs that could be used to realize the “interaction strategy”. The model reaction was performed using 2-vinylquinoline 1a and dienylcarbamate 2a under the influence of 10 mol% CPA catalyst in toluene at room temperature (Table 1). The use of typical BINOL-derived CPA catalysts (R)-4a and (R)-4b having 2,4,6-triisopropylphenyl and 9-anthryl groups, respectively, at the 3,3′-positions resulted in the complete consumption of 1a, and desired product 3aa was obtained in high yield (entries 1 and 2). On the other hand, (R)-4c having a 4-tBu group was less effective (entry 3), affording 3aa in moderate yield presumably because of catalyst deactivation. The endo-selectivity (80–90%) was not markedly influenced by the substituent introduced at the 3,3′-positions of BINOL, whereas the enantioselectivity was highly dependent on the structural property of the introduced substituent (entries 1–3). Among typical substituents tested, the 2,4,6-triisopropylphenyl group displayed the highest enantioselectivity (entry 1: 71% ee for endo-3aa). To enhance the enantioselectivity, the catalyst chiral backbone was further investigated using 2,4,6-triisopropylphenyl substituted catalysts (entries 4 and 5); endo-3aa was obtained exclusively with high enantioselectivity, albeit in moderate yield, when SPINOL-derived (S)-6 was used (entry 5). Because of the partial hydrolysis of dienylcarbamate 2a during the course of the reaction, MS 5A was added (entry 6), affording (1R,6S)-endo-3aa as the major enantiomer in high yield with slightly improved enantioselectivity (92% ee) (see Table S1† for details). The relative and absolute stereochemistry of 3aa was determined by the derivatization of 3aa into a stereochemically known compound (see ESI† for details).| Entry | CPA | Time (h) | Yield of 3aab (%) | endo/exoc | eec (%) |
|---|---|---|---|---|---|
| a Unless otherwise noted, all reactions were carried out using 0.1 mmol of 1a, 0.12 mmol of 2a, and 0.010 mmol of CPA catalyst (10 mol%) in toluene (1 mL). b Isolated yield. c Diastereomeric and enantiomeric excess were determined by chiral stationary phase HPLC analysis. d ND: not determined. e MS 5A (50 mg) was used as an additive. | |||||
| 1 | (R)-4a | 12 | 95 | 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 19 |
71/88 |
| 2 | (R)-4b | 36 | 95 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12 |
5/−12 |
| 3 | (R)-4c | 36 | 67 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
5/−3 |
| 4 | (R)-5 | 20 | 95 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 |
71/NDd |
| 5 | (S)-6 | 74 | 62 | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
88/NDd |
| 6e | (S)-6 | 5 d | 91 | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
92/NDd |
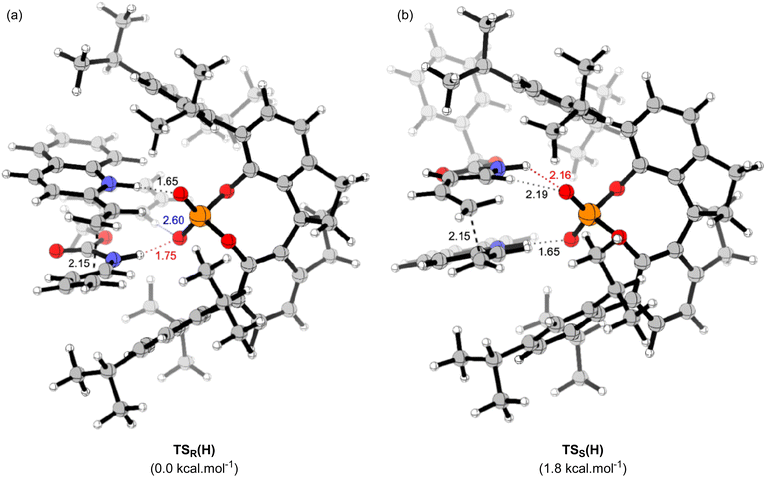
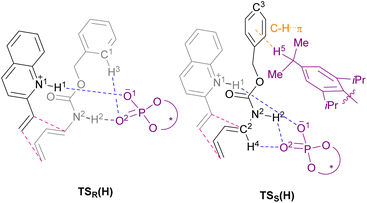
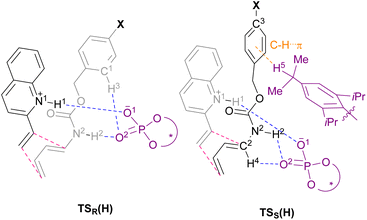
The main goal of this study was to realize the intended “interaction strategy” based on the initial reaction system identified by the brief screening of CPAs. To investigate the interaction mode between catalyst (S)-6 and substrates (1a and 2a) in the TSs, we thoroughly explored the favourable TSs for each enantiomer of endo-3aa. Structure searches were manually performed by primarily changing the conformation of the Cbz group: the orientation of the benzyl moiety and the geometry of the carbamate unit, i.e., s-cis and s-trans, because, in general, the Diels–Alder reaction proceeds through a concerted fashion and hence the simultaneous formation of the two carbon–carbon bonds restricts the flexibility of the relative location between dienophile 1a and diene 2a. As shown in Fig. 2 and schematic models in Table 2, TSR(H) and TSS(H) for the formation of major enantiomer (1R,6S)-endo-3aa and the minor one, respectively, were optimized by DFT calculations at the M06-2X/6-31g(d) level of theory in gas phase (Tables S2 and S3† for details).21 As expected, both dienophile 1a and diene 2a were fixed in the appropriate positions by the phosphoric acid unit of catalyst (S)-6 primarily through hydrogen bonding (N1⋯H1⋯O1 and N2⋯H2⋯O2) in stable TSR(H) and TSS(H) (see schematic models shown in Table 2). TSR(H), which led to (1R,6S)-endo-3aa, was energetically more favorable than TSS(H) at 1.8 kcal mol−1 (calcd: 91% ee); this was in good agreement with the experimental value (observed: 92% ee) and the absolute stereochemistry obtained. In addition, the results of IRC calculations suggested that the present Diels–Alder reaction proceeds through an asynchronous concerted pathway rather than a stepwise mechanism.22
| Hydrogen bond | L: length (Å), A: angle (°), E: energy (kcal mol−1) | TSR(H) | TSS(H) |
|---|---|---|---|
| N1⋯H1⋯O1 | L (H1–O1) | 1.65 | 1.65 |
| A (N1–H1–O1) | 169 | 171 | |
| E (H1–O1) | 13.3 | 12.8 | |
| N2⋯H2⋯O2 | L (H2–O2) | 1.75 | 2.16 |
| A (N2–H2–O2) | 167 | 123 | |
| E (H2–O2) | 10.4 | 1.3 | |
| C1–H3⋯O2 | L (H3–O2) | 2.60 | — |
| A (C1–H3–O2) | 167 | — | |
| E (H3–O2) | 0.8 | — | |
| C2–H4⋯O2 | L (H4–O2) | — | 2.19 |
| A (C2–H4–O2) | — | 123 | |
| E (H4–O2) | — | 2.4 | |
| C–H5⋯C3 | L (H5–C3) | — | 2.82 |
We conducted the distortion/interaction analysis of TSR(H) and TSS(H) (see Table S4† for details),3,16f,23 followed by a detailed analysis of characteristic interactions, in particular, hydrogen bonding interactions and their energies. As shown in Fig. 2, the conformation of the Cbz protecting group of dienylcarbamate 2a is completely different. In TSR(H), the benzyl moiety of the Cbz group and the carbamate unit are coplanar, whereas in TSS(H), the benzyl moiety is oriented outside the plane formed by the carbamate unit. As summarized in Table 2, the detailed comparison between the respective TSs revealed marked differences in some of the interactions in terms of not only the energy but also the site of hydrogen bonds. The strength of the hydrogen bonds was estimated using NBO calculations.24 The interaction energy of the hydrogen bond (H1⋯O1) formed between dienophile 1a (N1–H1) and CPA (O1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P) was comparable between the two states [TSR(H): 13.3 kcal mol−1vs.TSS(H): 12.8 kcal mol−1] presumably because it is the key interaction to activate dienophile 1a (i.e., through protonation) [L (H1–O1) = 1.65 Å for both TSR(H) and TSS(H)]. In contrast, the hydrogen bond (H2⋯O2) formed between dienylcarbamate (N2–H2) and CPA (O2
P) was comparable between the two states [TSR(H): 13.3 kcal mol−1vs.TSS(H): 12.8 kcal mol−1] presumably because it is the key interaction to activate dienophile 1a (i.e., through protonation) [L (H1–O1) = 1.65 Å for both TSR(H) and TSS(H)]. In contrast, the hydrogen bond (H2⋯O2) formed between dienylcarbamate (N2–H2) and CPA (O2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P) was significantly shorter in TSR(H) than in TSS(H) [L (H2–O2) = 1.75 Å vs. 2.16 Å]. In addition, the three atoms (N2, H2, and O2) involved in hydrogen bonding formed an almost straight line in TSR(H) [A (N2–H2–O2) = 167°], whereas in TSS(H), the corresponding bond formed a bent structure [A (N2–H2–O2) = 123°]. Reflecting these differences in bond length and angle, the interaction energy of the hydrogen bond (H2⋯O2) in TSR(H) (10.4 kcal mol−1) was markedly higher than that in TSS(H) (1.3 kcal mol−1). The significant difference in interaction energy appeared to contribute to the high enantioselectivity. More interestingly, in TSR(H), ortho C1–H3 of the phenyl ring in the Cbz group formed a hydrogen bond with the phosphoryl oxygen of CPA (O2
P) was significantly shorter in TSR(H) than in TSS(H) [L (H2–O2) = 1.75 Å vs. 2.16 Å]. In addition, the three atoms (N2, H2, and O2) involved in hydrogen bonding formed an almost straight line in TSR(H) [A (N2–H2–O2) = 167°], whereas in TSS(H), the corresponding bond formed a bent structure [A (N2–H2–O2) = 123°]. Reflecting these differences in bond length and angle, the interaction energy of the hydrogen bond (H2⋯O2) in TSR(H) (10.4 kcal mol−1) was markedly higher than that in TSS(H) (1.3 kcal mol−1). The significant difference in interaction energy appeared to contribute to the high enantioselectivity. More interestingly, in TSR(H), ortho C1–H3 of the phenyl ring in the Cbz group formed a hydrogen bond with the phosphoryl oxygen of CPA (O2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P), although its interaction energy was small [E (H3–O2) = 0.8 kcal mol−1]. In contrast, in TSS(H), other bonds were formed between dienylcarbamate (C2–H4) and CPA (O2
P), although its interaction energy was small [E (H3–O2) = 0.8 kcal mol−1]. In contrast, in TSS(H), other bonds were formed between dienylcarbamate (C2–H4) and CPA (O2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P) [E (H4–O2) = 2.4 kcal mol−1], as well as between the catalyst substituent (C–H5) and the π orbital of the phenyl ring in the Cbz group (Fig. S2†).
P) [E (H4–O2) = 2.4 kcal mol−1], as well as between the catalyst substituent (C–H5) and the π orbital of the phenyl ring in the Cbz group (Fig. S2†).
We then moved on to redesign the substrates to further enhance the enantioselectivity, which is the core of the present study. The detailed analysis of the TSs revealed that, in TSR(H) and TSS(H), different hydrogen bonds were formed between the Cbz protecting group of dienylcarbamate 2a and CPA (S)-6: in TSR(H), C–H⋯O interaction occurred between ortho C1–H3 of the Cbz phenyl ring and CPA (O2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P), whereas in TSS(H), C–H⋯π interaction occurred between the isopropyl group of the CPA substituent (C–H5) and the Cbz phenyl ring (Table 2 and Fig. 2). These findings led us to hypothesize that the intended “interaction strategy” might be accomplished through the modification of the phenyl ring of the Cbz moiety, i.e., the protective group of the nitrogen atom of 2a. When the electron density of the Cbz phenyl ring is reduced by the introduction of an electron-withdrawing group (EWG), an increase in the hydrogen bonding interaction (C1–H3⋯O2) owing to the enhancement of the acidity of C1–H3 is anticipated only in TSR(H). Consequently, the hydrogen bond (H3⋯O2) stabilizes TSR(H), i.e., the TS of the major reaction pathway, but not TSS(H). The modification of the Cbz phenyl ring by the introduction of an EWG is thus predicted to result in increased enantioselectivity.25
P), whereas in TSS(H), C–H⋯π interaction occurred between the isopropyl group of the CPA substituent (C–H5) and the Cbz phenyl ring (Table 2 and Fig. 2). These findings led us to hypothesize that the intended “interaction strategy” might be accomplished through the modification of the phenyl ring of the Cbz moiety, i.e., the protective group of the nitrogen atom of 2a. When the electron density of the Cbz phenyl ring is reduced by the introduction of an electron-withdrawing group (EWG), an increase in the hydrogen bonding interaction (C1–H3⋯O2) owing to the enhancement of the acidity of C1–H3 is anticipated only in TSR(H). Consequently, the hydrogen bond (H3⋯O2) stabilizes TSR(H), i.e., the TS of the major reaction pathway, but not TSS(H). The modification of the Cbz phenyl ring by the introduction of an EWG is thus predicted to result in increased enantioselectivity.25
In order to confirm the above hypothesis, we calculated the TSs of the Diels–Alder reaction between dienophile 1a and dienylcarbamates having a bromo group (7a: X = Br) or a nitro group (8a: X = NO2) as an EWG at the para-position of the Cbz phenyl ring. Characteristic hydrogen bonds in these TSs are summarized in Table 3 [the structures of TSR(Br)/TSS(Br) for the reaction of 1a with 7a and TSR(NO2)/TSS(NO2) for the reaction of 1a with 8a are shown in Fig. S3 and S4,† respectively]. As expected, neither 7a nor 8a displayed significant changes in the TS structures compared with those of parent dienylcarbamate 2a (X = H) (Table 3 and Fig. 2vs. Fig. S3 and S4†). Specifically, almost no differences in hydrogen bond length and angle were observed in TSS(X) (X = H, Br, or NO2). In contrast, the detailed analysis of TSR(X) structure revealed that the length of the hydrogen bond formed between the Cbz phenyl ring of dienylcarbamate (C1–H3) and CPA (O2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P) tended to become shorter [L (H3–O2) (Å), X = H: 2.60 → Br: 2.37 → NO2: 2.31] with increasing electron-withdrawing nature of the substituent (Hammett σm constants, X = H: 0.0 → Br: +0.393 → NO2: +0.710).26
P) tended to become shorter [L (H3–O2) (Å), X = H: 2.60 → Br: 2.37 → NO2: 2.31] with increasing electron-withdrawing nature of the substituent (Hammett σm constants, X = H: 0.0 → Br: +0.393 → NO2: +0.710).26
| L: length (Å), A: angle (°) | TSR(H) | TSR(Br) | TSR(NO2) | TSS(H) | TSS(Br) | TSS(NO2) |
|---|---|---|---|---|---|---|
| L (H1–O1) | 1.65 | 1.65 | 1.64 | 1.65 | 1.65 | 1.64 |
| A (N1–H1–O1) | 169 | 170 | 170 | 171 | 171 | 171 |
| E (H1–O1) | 13.3 | 13.7 | 13.9 | 12.8 | 12.5 | 12.8 |
| L (H2–O2) | 1.75 | 1.76 | 1.76 | 2.16 | 2.17 | 2.14 |
| A (N2–H2–O2) | 167 | 165 | 165 | 123 | 123 | 124 |
| E (H2–O2) | 10.4 | 9.9 | 10.0 | 1.3 | 1.2 | 1.4 |
| L (H 3 –O 2 ) | 2.60 | 2.37 | 2.31 | — | — | — |
| A (C1–H3–O2) | 167 | 168 | 172 | — | — | — |
| E (H 3 –O 2 ) | 0.8 | 1.8 | 2.3 | — | — | — |
| L (H4–O2) | — | — | — | 2.19 | 2.17 | 2.19 |
| A (C2–H4–O2) | — | — | — | 123 | 124 | 122 |
| E (H4–O2) | — | — | — | 2.4 | 2.6 | 2.4 |
| L (H5–C3) | — | — | — | 2.82 | 2.81 | 2.76 |
The introduction of an EWG to the Cbz phenyl ring decreases the electron density of the proton H3, making the hydrogen bonding interaction stronger and the bond length shorter. Indeed, as shown in Table 4, the electron density around H3 decreased [P (H3), X = H: 0.7188 → Br: 0.7073 → NO2: 0.7016] with an increase in the electron-withdrawing nature of the substituent. NBO calculations revealed that the interaction energy of the hydrogen bond (H3⋯O2) in TSR(X) was enhanced gradually [E (H3–O2) (kcal mol−1), X = H: 0.8 → Br: 1.8 → NO2: 2.3] and more importantly, ΔΔG‡ markedly improved [ΔΔG‡ (kcal mol−1), X = H: 1.8 → Br: 2.0 → NO2: 3.0]. On the basis of these calculation results, we predicted that the introduction of an EWG at the para-position of the Cbz phenyl ring would result in increased enantioselectivity, and hence, the intended “interaction strategy” could improve the enantioselectivity of the present Diels–Alder reaction.
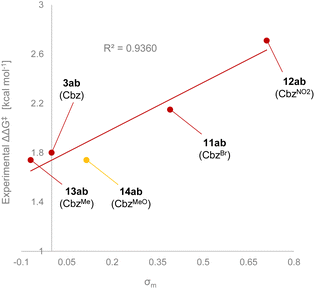
To verify our calculation results, a series of dienylcarbamates 2b and 7b–10b having electronically different substituents X were tested in the reaction of 1a catalysed by (S)-6a. As shown in Table 5, the intended “interaction strategy” was achieved: the enantioselectivity improved with the introduction of stronger electron-withdrawing substituents [X = H (2b): 91% ee → Br (7b): 95% ee → NO2 (8b): 98% ee], as predicted by the calculations. When dienylcarbamate 8b having a nitro group27 was applied to the reaction, a large improvement in enantioselectivity (98% ee) was observed compared with when parent dienylcarbamate 2b (91% ee) was used. Since this modification site is far from the reaction site i.e., the diene moiety, these improvements in enantioselectivities could only be achieved by computational predictions, otherwise it is extremely difficult to find an appropriate modification method and site of the substrate through experimental exploration.
| Entry | X | Product | Yieldb (%) | endo/exoc | eec (%) |
|---|---|---|---|---|---|
| a General conditions: 1a (0.1 mmol), dienylcarbamate (0.3 mmol), and (S)-6 (0.01 mmol) in toluene (1 mL) with MS 5A (50 mg) at room temperature for 5 days. b Isolated yield. c Diastereomeric and enantiomeric excess were determined by chiral stationary phase HPLC analysis. | |||||
| 1 | H (2b) | 3ab (Cbz) | 86 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
91 |
| 2 | Br (7b) | 11ab (CbzBr) | 98 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
95 |
| 3 | NO2 (8b) | 12ab (CbzNO2) | 98 | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
98 |
| 4 | Me (9b) | 13ab (CbzMe) | 85 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
90 |
| 5 | MeO (10b) | 14ab (CbzMeO) | 95 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
90 |
On the other hand, no significant difference in enantioselectivity (90% ee) was observed when electron-donating substituents such as methyl (9b) and methoxy (10b) groups were introduced at the para-position of the Cbz phenyl ring. Fig. 3 shows the Hammett plot of σm constants vs. ΔΔG‡, which were calculated from enantioselectivities obtained experimentally. Generally, a nearly linear correlation was observed with only the methoxy substituent slightly deviating from this relationship. This discrepancy is likely attributed to the electron-donating methoxy substituent enhancing the C–H⋯π interaction in TSS(MeO),28i.e., the TS of the minor reaction pathway. Consequently, TSS(MeO) was stabilized, and hence, the reduction of enantioselectivity was estimated. However, the inductive effect of the methoxy group at the meta-position (Hammett σm constants, X = MeO: +0.115)26 could stabilize TSR(MeO), i.e., the TS of the major reaction pathway, through the hydrogen bond (H3⋯O2). It is thus presumed that the stabilization of TSS(MeO) by the C–H⋯π interaction counterbalanced the stabilization of TSR(MeO) by the hydrogen bond (H3⋯O2), making the enantioselectivity of 14ab (X = MeO) comparable to that of 3ab (X = H).
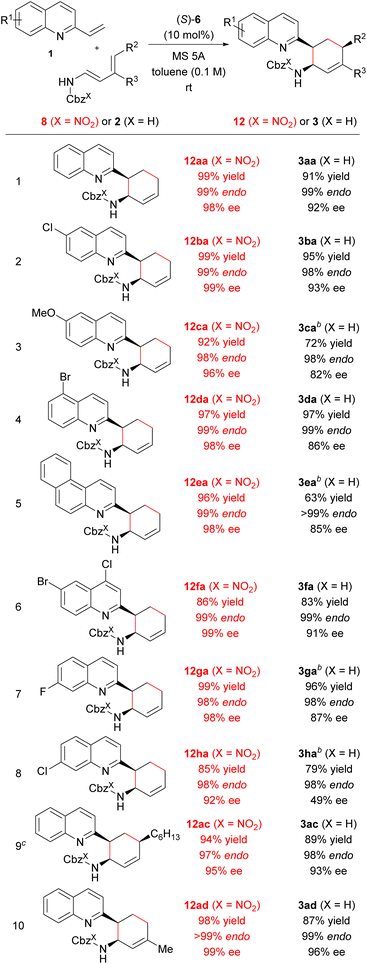
Next, we investigated the generality of the “interaction strategy” in the reactions of a series of vinylquinolines 1 with redesigned dienylcarbamates 8 (X = NO2) having a nitro group on the Cbz phenyl ring. As shown in Table 6, all substrates tested underwent the reactions smoothly, affording corresponding products endo-12 (X = NO2) exclusively in high chemical yields with improved enantioselectivities compared with when parent dienylcarbamates 2 (X = H) having the normal Cbz group were used. In fact, investigation of the substituent effect of a variety of vinylquinolines 1 revealed that the use of redesigned dienylcarbamate 8a facilitated the reactions (entries 1–8). Corresponding products 12 were obtained in high yields with extremely high enantioselectivities, regardless of the electronic nature or position of the substituent introduced to the quinoline ring. In particular, the enantioselectivity in the reaction of vinylquinoline 1h having a chloride substituent at the 7-position with redesigned dienylcarbamate 8a was markedly improved (92% ee) compared with the enantioselectivity in the reaction of 1h with parent dienylcarbamate 2a (49% ee) (entry 8). Furthermore, the use of dienylcarbamates 8c (R2 = nBu, R3 = H) and 8d (R2 = H, R3 = Me), whose substituents and substitution pattern differ from those of 8b (R2 = Me, R3 = H), respectively, also resulted in increases in both yield and enantioselectivity (entries 9 and 10).
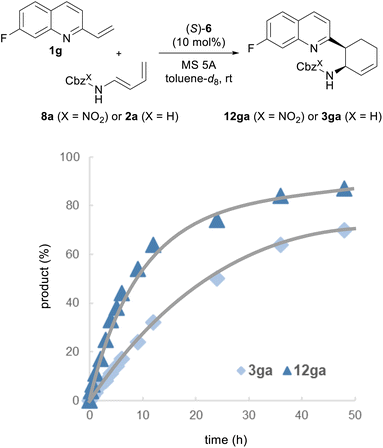
Finally, we performed a kinetic analysis to determine whether a marked improvement in the enantioselectivities of 12 could be achieved by the intended “interaction strategy” (Fig. 4). If the improvement of enantioselectivity stems from the stabilization of the TS of the major reaction pathway, the use of redesigned dienylcarbamates 8 is expected to enhance the rate of the present reaction, i.e., a normal electron demand Diels–Alder reaction, despite the introduction of the electron-withdrawing nitro substituent to the diene subunit.2b,e,29 This prediction is also supported by the calculated activation free energy (ΔG‡): ΔG‡ of TSR(NO2) in the reaction of 8a with 1a [TSR(NO2): 9.4 kcal mol−1] is lower than that of TSR(H) in the reaction of 2a with 1a [TSR(H): 10.1 kcal mol−1] (Fig. S1†). Moreover, because TSR(NO2) and TSR(H) have the highest energy barrier, the pathway involving these TSs is the rate-determining step, and consequently, the stereo-determining step is also the rate-determining step. With these considerations in mind, we conducted kinetic studies on the reaction of 1g with redesigned 8a catalyzed by (S)-6 and compared the results with those of the reaction of 1g with parent 2a. The progress of the reaction was monitored by 1H NMR and 19F NMR measurements. As predicted, the reaction rate was clearly higher with redesigned 8a than with parent 2a. These results prove that the intended “interaction strategy” is successful and confirm the validity of our molecular design.
Conclusions
We have demonstrated the enantioselective Diels–Alder reaction of 2-vinylquinolines with dienylcarbamates as a model reaction under the influence of CPA catalyst in accordance with the “interaction strategy”. In the development of enantioselective catalysis, computational studies have aided in the design of catalyst molecules and reaction systems in recent years. Among computational approaches reported thus far, the “interaction strategy”, which focuses on the stabilization of the TS of the major reaction pathway to improve enantioselectivity, has largely been unexplored despite the marked advantages of the intended strategy. In order to realize the “interaction strategy”, we envisaged the effective use of hydrogen bonding interactions. Indeed, the hydrogen bonding interactions made a significant impact on not only the enantioselectivity but also the reaction rate and are useful in refining reaction systems. Particularly, in the present molecular refinement aided by the computational studies, these achievements could only be realized by computational predictions, otherwise it is difficult to find out the modification site through experimental explorations because the modified site of the Cbz group is located far from the reaction site. More importantly, the improvement of enantioselectivity is anticipated by applying the present strategy not only to the most stable TS, but also to the second or third most stable TS. This is because the reinforced hydrogen bonding interaction may also reverse the order of stability between these TSs. This new methodology based on the “interaction strategy” using hydrogen bonding as the key interaction is a versatile “in silico” approach that will contribute to the refinement of a variety of catalytic enantioselective reactions. Further application of the “interaction strategy” is in progress to develop efficient and distinctive enantioselective reactions using not only CPA catalysts but also organocatalysts and transition metal catalysts.Data availability
The exploratory investigation, experimental procedures, computational data, and characterization data are available.Author contributions
T. N. contributed conceptualization, design of the work, data curation, formal analysis, investigation (experimental and theoretical studies), and writing – original draft. M. T. contributed conceptualization, project administration, writing – review & editing, supervision, and funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computation was performed using Research Center for Computational Science, Okazaki, Japan (Project: 22-IMS-C127). This work was supported by a Grant-in-Aid for Scientific Research on Innovative Areas “Hybrid Catalysis for Enabling Molecular Synthesis on Demand” (JP17H06447) from MEXT, Japan (M. T.), a Grant-in-Aid for Challenging Research (Exploratory) (JP22K19018) from JSPS (M. T.), and a Grant-in-Aid for Young Scientists (JP21J14551) from JSPS, Japan (T. N.).Notes and references
- For selected reviews, see: (a) S. E. Wheeler, T. J. Seguin, Y. Guan and A. C. Doney, Acc. Chem. Res., 2016, 49, 1061–1069 CrossRef CAS PubMed; (b) Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093–6107 RSC; (c) J. P. Reid and M. S. Sigman, Nat. Rev. Chem., 2018, 2, 290–305 CrossRef CAS; (d) D. Ess, L. Gagliardi and S. Hammes-Schiffer, Chem. Rev., 2019, 119, 6507–6508 CrossRef CAS PubMed; (e) S. Ahn, M. Hong, M. Sundararajan, D. H. Ess and M.-H. Baik, Chem. Rev., 2019, 119, 6509–6560 CrossRef CAS PubMed; (f) P. Nakliang, S. Yoon and S. Choi, Org. Chem. Front., 2021, 8, 5165–5181 RSC.
- (a) G. Jindal and R. B. Sunoj, Org. Biomol. Chem., 2014, 12, 2745–2753 RSC; (b) R. N. Straker, Q. Peng, A. Mekareeya, R. S. Paton and E. A. Anderson, Nat. Commun., 2016, 7, 10109 CrossRef CAS PubMed; (c) H. Iwamoto, T. Imamoto and H. Ito, Nat. Commun., 2018, 9, 2290 CrossRef PubMed; (d) S.-S. Meng, P. Yu, Y.-Z. Yu, Y. Liang, K. N. Houk and W.-H. Zheng, J. Am. Chem. Soc., 2020, 142, 8506–8513 CrossRef CAS PubMed; (e) Y. Xi, B. Su, X. Qi, S. Pedram, P. Liu and J. F. Hartwig, J. Am. Chem. Soc., 2020, 142, 18213–18222 CrossRef CAS PubMed; (f) A. Hamza, K. Sorochkina, B. Kótai, K. Chernichenko, D. Berta, M. Bolte, M. Nieger, T. Repo and I. Pápai, ACS Catal., 2020, 10, 14290–14301 CrossRef CAS; (g) M. Duan, C. D. Díaz-Oviedo, Y. Zhou, X. Chen, P. Yu, B. List, K. N. Houk and Y. Lan, Angew. Chem., Int. Ed., 2022, 61, e202113204 CAS.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- (a) A. C. Doney, B. J. Rooks, T. Lu and S. E. Wheeler, ACS Catal., 2016, 6, 7948–7955 CrossRef CAS; (b) L. C. Burrows, L. T. Jesikiewicz, G. Lu, S. J. Geib, P. Liu and K. M. Brummond, J. Am. Chem. Soc., 2017, 139, 15022–15032 CrossRef CAS PubMed.
- (a) R. R. Knowles and E. N. Jacobsen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20678–20685 CrossRef CAS PubMed; (b) R. J. Phipps, Synlett, 2016, 27, 1024–1026 CrossRef CAS; (c) C. R. Kennedy, S. Lin and E. N. Jacobsen, Angew. Chem., Int. Ed., 2016, 55, 12596–12624 CrossRef CAS PubMed; (d) W. Yan, M. Zheng, C. Xu and F.-E. Chen, Green Synthesis and Catalysis, 2021, 2, 329–336 CrossRef.
- R. Huber, A. Passera, E. Gubler and A. Mezzetti, Adv. Synth. Catal., 2018, 360, 2900–2913 CrossRef CAS.
- For reviews, see: (a) M. S. Taylor and E. N. Jacobsen, Angew. Chem., Int. Ed., 2006, 45, 1520–1543 CrossRef CAS PubMed; (b) A. G. Doyle and E. N. Jacobsen, Chem. Rev., 2007, 107, 5713–5743 CrossRef CAS PubMed; (c) X. Yu and W. Wang, Chem.–Asian J., 2008, 3, 516–532 CrossRef CAS PubMed; (d) M. J. Ajitha and K.-W. Huang, Synthesis, 2016, 48, 3449–3458 CrossRef CAS.
- (a) K. T. Mahmudov, A. V. Gurbanov, F. I. Guseinov and M. F. C. Guedes da Silva, Coord. Chem. Rev., 2019, 387, 32–46 CrossRef CAS; (b) A. Fanourakis, P. J. Docherty, P. Chuentragool and R. J. Phipps, ACS Catal., 2020, 10, 10672–10714 CrossRef CAS PubMed.
- (a) P. Fackler, C. Berthold, F. Voss and T. Bach, J. Am. Chem. Soc., 2010, 132, 15911–15913 CrossRef CAS PubMed; (b) M. C. Schwarzer, A. Fujioka, T. Ishii, H. Ohmiya, S. Mori and M. Sawamura, Chem. Sci., 2018, 9, 3484–3493 RSC; (c) K. Imai, Y. Takayama, H. Murayama, H. Ohmiya, Y. Shimizu and M. Sawamura, Org. Lett., 2019, 21, 1717–1721 CrossRef CAS PubMed; (d) H. Murayama, Y. Heike, K. Higashida, Y. Shimizu, N. Yodsin, Y. Wongnongwa, S. Jungsuttiwong, S. Mori and M. Sawamura, Adv. Synth. Catal., 2020, 362, 4655–4661 CrossRef CAS; (e) C.-T. Chen, Y.-C. Su, C.-H. Lu, C.-I. Lien, S.-F. Hung, C.-W. Hsu, R. Agarwal, R. Modala, H.-M. Tseng, P.-X. Tseng, R. Fujii, K. Kawashima and S. Mori, ACS Catal., 2021, 11, 7160–7175 CrossRef CAS; (f) S. Sakai, A. Fujioka, K. Imai, K. Uchiyama, Y. Shimizu, K. Higashida and M. Sawamura, Adv. Synth. Catal., 2022, 364, 2333–2339 CrossRef CAS.
- For reviews on chiral Brøsnted acid catalysis, see: (a) T. Akiyama, Chem. Rev., 2007, 107, 5744–5758 CrossRef CAS PubMed; (b) D. Kampen, C. M. Reisinger and B. List, Top. Curr. Chem., 2010, 291, 395–456 CrossRef CAS PubMed; (c) T. Akiyama and K. Mori, Chem. Rev., 2015, 115, 9277–9306 CrossRef CAS PubMed; (d) T. James, M. van Gemmeren and B. List, Chem. Rev., 2015, 115, 9388–9409 CrossRef CAS PubMed.
- For reviews on BINOL-derived phosphoric acids and derivatives, see: (a) M. Terada, Chem. Commun., 2008, 4097–4112 RSC; (b) M. Terada, Synthesis, 2010, 1929–1982 CrossRef CAS; (c) D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2014, 114, 9047–9153 CrossRef CAS PubMed; (d) R. Maji, S. C. Mallonjjala and S. E. Wheeler, Chem. Soc. Rev., 2018, 47, 1142–1158 RSC; (e) B.-C. Da, S.-H. Xiang and B. Tan, Chin. J. Chem., 2021, 39, 1787–1796 CrossRef CAS; For seminal studies of chiral phosphoric acid catalysts, see: (f) T. Akiyama, J. Itoh, K. Yokota and K. Fuchibe, Angew. Chem., Int. Ed., 2004, 43, 1566–1568 CrossRef CAS PubMed; (g) D. Uraguchi and M. Terada, J. Am. Chem. Soc., 2004, 126, 5356–5357 CrossRef CAS PubMed.
- For selected examples on chiral phosphoric acids and phosphate in photoredox reactions, see: (a) L. J. Rono, H. G. Yayla, D. Y. Wang, M. F. Armstrong and R. R. Knowles, J. Am. Chem. Soc., 2013, 135, 17735–17738 CrossRef CAS PubMed; (b) E. C. Gentry, L. J. Rono, M. E. Hale, R. Matsuura and R. R. Knowles, J. Am. Chem. Soc., 2018, 140, 3394–3402 CrossRef CAS PubMed; (c) R. S. J. Proctor, H. J. Davis and R. J. Phipps, Science, 2018, 360, 419–422 CrossRef CAS PubMed; (d) N. Y. Shin, J. M. Ryss, X. Zhang, S. J. Miller and R. R. Knowles, Science, 2019, 366, 364–369 CrossRef CAS PubMed; (e) C. B. Roos, J. Demaerel, D. E. Graff and R. R. Knowles, J. Am. Chem. Soc., 2020, 142, 5974–5979 CrossRef CAS PubMed; (f) A. S. K. Lahdenperä, P. D. Bacos and R. J. Phipps, J. Am. Chem. Soc., 2022, 144, 22451–22457 CrossRef PubMed.
- L. Schreyer, R. Properzi and B. List, Angew. Chem., Int. Ed., 2019, 58, 12761–12777 CrossRef CAS PubMed.
- (a) D. Nakashima and H. Yamamoto, J. Am. Chem. Soc., 2006, 128, 9626–9627 CrossRef CAS PubMed; (b) P. García-García, F. Lay, P. García-García, C. Rabalakos and B. List, Angew. Chem., Int. Ed., 2009, 48, 4363–4366 CrossRef PubMed; (c) N. Momiyama, T. Konno, Y. Furiya, T. Iwamoto and M. Terada, J. Am. Chem. Soc., 2011, 133, 19294–19297 CrossRef CAS PubMed; (d) N. Momiyama, K. Funayama, H. Noda, M. Yamanaka, N. Akasaka, S. Ishida, T. Iwamoto and M. Terada, ACS Catal., 2016, 6, 949–956 CrossRef CAS; (e) J. Kikuchi, H. Aramaki, H. Okamoto and M. Terada, Chem. Sci., 2019, 10, 1426–1433 RSC; (f) J. Kikuchi and M. Terada, Angew. Chem., Int. Ed., 2019, 58, 8458–8462 CrossRef CAS PubMed; (g) S. A. Schwengers, C. K. De, O. Grossmann, J. A. A. Grimm, N. R. Sadlowski, G. G. Gerosa and B. List, J. Am. Chem. Soc., 2021, 143, 14835–14844 CrossRef CAS PubMed.
- (a) A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, eaau5631 CrossRef CAS PubMed; (b) J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343–348 CrossRef CAS PubMed.
- (a) K. Kanomata, Y. Toda, Y. Shibata, M. Yamanaka, S. Tsuzuki, I. D. Gridnev and M. Terada, Chem. Sci., 2014, 5, 3515–3523 RSC; (b) J. P. Reid and J. M. Goodman, J. Am. Chem. Soc., 2016, 138, 7910–7917 CrossRef CAS; (c) P. A. Champagne and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 12356–12359 CrossRef CAS PubMed; (d) C. Liu, M. Besora and F. Maseras, Chem.–Asian J., 2016, 11, 411–416 CrossRef CAS PubMed; (e) F. Li, T. Korenaga, T. Nakanishi, J. Kikuchi and M. Terada, J. Am. Chem. Soc., 2018, 140, 2629–2642 CrossRef CAS PubMed; (f) K. Kanomata, Y. Nagasawa, M. Yamanaka, Y. Shibata, F. Egawa, J. Kikuchi and M. Terada, Chem.–Eur. J., 2020, 26, 3364–3372 CrossRef CAS PubMed.
- (a) A. E. Davis, J. M. Lowe and M. K. Hilinski, Chem. Sci., 2021, 12, 15947–15952 RSC; (b) S. Portela and I. Fernández, J. Org. Chem., 2022, 87, 9307–9315 CrossRef CAS PubMed.
- J. Chen, Y. Fu, Y. Yu, J.-R. Wang, Y.-W. Guo, H. Li and W. Wang, Org. Lett., 2020, 22, 6061–6066 CrossRef CAS PubMed.
- (a) J. Pous, T. Courant, G. Bernadat, B. I. Iorga, F. Blanchard and G. Masson, J. Am. Chem. Soc., 2015, 137, 11950–11953 CrossRef CAS PubMed; (b) N. Momiyama, H. Tabuse, H. Noda, M. Yamanaka, T. Fujinami, K. Yamanishi, A. Izumiseki, K. Funayama, F. Egawa, S. Okada, H. Adachi and M. Terada, J. Am. Chem. Soc., 2016, 138, 11353–11359 CrossRef CAS PubMed; (c) T. Varlet, C. Gelis, P. Retailleau, G. Bernadat, L. Neuville and G. Masson, Angew. Chem., Int. Ed., 2020, 59, 8491–8496 CrossRef CAS PubMed.
- (a) J. J. Li, Heterocyclic Chemistry in Drug Discovery, John Wiley & Sons, Hoboken, NJ, 2013 Search PubMed; (b) V. Dhayalan, R. Dandela, K. V. Devi and R. Dhanusuraman, SynOpen, 2022, 6, 31–57 CrossRef CAS.
- For M06-2X, see: Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- (a) B. R. Beno, K. N. Houk and D. A. Singleton, J. Am. Chem. Soc., 1996, 118, 9984–9985 CrossRef CAS; (b) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2021, 23, 20095–20106 RSC.
- For selected examples on distortion/interaction analysis in catalytic asymmetric reactions, see: (a) M. Odagi, K. Furukori, Y. Yamamoto, M. Sato, K. Iida, M. Yamanaka and K. Nagasawa, J. Am. Chem. Soc., 2015, 137, 1909–1915 CrossRef CAS PubMed; (b) J. Quyang, R. Maji, M. Leutzsch, B. Mitschke and B. List, J. Am. Chem. Soc., 2022, 144, 8460–8466 CrossRef; (c) K. Ogura, I. Isozumi, T. Takehara, T. Suzuki and S. Nakamura, Org. Lett., 2022, 24, 8088–8092 CrossRef CAS PubMed.
- For natural bond orbital (NBO) analysis, see: A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- (a) S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and A. Fujii, J. Phys. Chem. A, 2006, 110, 10163–10168 CrossRef CAS PubMed; (b) S. Karthikeyan, V. Ramanathan and B. K. Mishra, J. Phys. Chem. A, 2013, 117, 6687–6694 CrossRef CAS.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- (a) T. Kumagai, T. Abe, Y. Fujimoto, T. Hayashi, Y. Inoue and Y. Nagao, Heterocycles, 1993, 36, 1729–1734 CrossRef CAS; (b) Y. Blériot, A. T. Tran, G. Prencipe, Y. Jagadeesh, N. Auberger, S. Zhu, C. Gauthier, Y. Zhang, J. Désiré, I. Adachi, A. Kato and M. Sollogoub, Org. Lett., 2014, 16, 5516–5519 CrossRef PubMed.
- The higher the electron density of the aromatic ring, the stronger the C–H⋯π interaction; if the electron density of the aromatic ring is low, the strength of the C–H⋯π interaction is not markedly affected by the electron density of the aromatic ring. Therefore, the introduction of the electron-donating methoxy substituent leads to the enhancement of the C–H⋯π interaction. In contrast, the strength of the C–H⋯π interaction does not change markedly when an electron-withdrawing substituent is introduced to the aromatic ring, irrespective of the electron density of the aromatic ring. See: ref. 25b.
- C. Eschmann, L. Song and P. R. Schreiner, Angew. Chem., Int. Ed., 2021, 60, 4823–4832 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc01637d |
| This journal is © The Royal Society of Chemistry 2023 |