Concentration–modulated global organizational chirality at the liquid/solid interface

Abstract

Understanding the origin of homochirality in macroscopic assemblies and manipulating organizational chirality still remain a challenge. Herein, homochirality is achieved by combination of the majority-rules principle and concentration-dependent molecular assembly at the liquid/solid interface. A lower molecular concentration in solution facilitates more efficient amplification of chirality, which is formulated by a cooperative equilibrium model based on the Langmuir adsorption isotherm. Our results contribute to gain a new insight into chiral amplification in supramolecular assemblies. Particularly, a homochiral monolayer can be obtained just through modulating the molecular concentration in mixed enantiomer systems.

---

Introduction

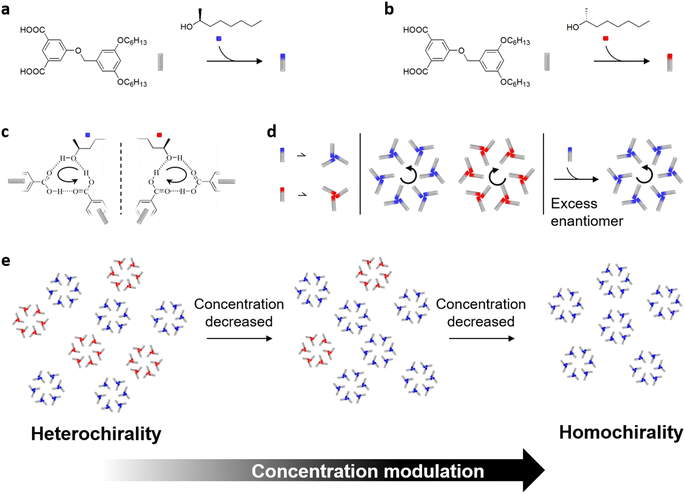
Chiral symmetry breaking of living matter during formation of life on earth has remained a puzzle for years since L. Pasteur first separated mirror-imaged enantiomers. Understanding how the enantiomerically pure structures emerged has attracted considerable attention.^1–5 Several theories such as the parity non-conservation of weak interaction and Salam's hypothesis have been proposed to elucidate how initial enantiomeric excess could have arisen from a probably racemic prebiotic world. However, their effects are very small, just acting as a trigger. Spontaneous chiral amplification of the small enantiomeric excess is necessary to generate macroscopic homochiral assemblies.^6,7 Pioneering studies performed by Green et al. on the amplification of chirality in polyisocyanates have demonstrated that chiral amplification in helical polymeric systems can occur via two approaches.⁸ The ability of a few chiral units (sergeants) to flip the chirality of large numbers of achiral building blocks (soldiers) to the same handedness is termed as sergeants-and-soldiers principle.^9,10 As for mixed enantiomeric monomers, the organizational chirality of the assembly shows a nonlinear dependence on the enantiomeric excess (ee) of the chiral monomers, which is referred to as the majority-rules effect.¹¹ Molecular-level insights into the mechanism of chiral amplification may be conducive to understand the origin of homochirality in life on earth.

Exploring self-assembly of organic building blocks at surfaces is one of the convenient ways to understand chiral amplification phenomena. In analogy to supramolecular copolymerization systems in solution, chiral amplification principles have been successfully applied to construct homochiral surfaces. Symmetry breaking may occur when achiral molecules are confined to the substrate. Globally homochiral two-dimensional (2D) assemblies can be achieved via addition of chiral coadsorbed species.^12,13 When enantiomers are applied to the surface simultaneously, the presence of a small imbalance in the enantiomeric ratio can alter the adsorption system in favour of a single handedness.^14,15 As is known, the outcome of the self-assembling process relies on a series of factors,^16,17 including temperature,^18,19 electric field,²⁰ magnetic field²¹ and the nature of the solvent.²² Notably, the concentration of the assembled molecules has a striking influence on the formation of self-assembled architectures as well.^23,24 Depending on the solute concentration, the handedness of chiral seeds can either be amplified or reversed in the monolayer composed of achiral molecules.²⁵ The concentration of natural amino acids and sugars in oceans must have been low, since the current water content of the earth's oceans is in the order of 1.4 × 10²¹ kg. The low concentration in oceans could presumably be a contributing factor to the origin of homochirality in life on earth. However, there is little information available about the effect of molecular concentration on chiral amplification following the majority-rules principle. The mechanism underlying concentration-modulated chiral amplification behavior is unclear.

Homologous chiral networks can be fabricated by applying 5-(benzyloxy)-isophthalic acid derivatives (BIC) at the interface between 2-octanol and highly oriented pyrolytic graphite (HOPG) under the control of the majority-rules principle.²⁶ The chirality of chiral inducer 2-octanol defines the handedness of the hexagonal porous networks (Scheme 1a and b), where stereochemical information in 2-octanol is transferred to the achiral BIC building block over noncovalent hydrogen bonding interactions (Scheme 1c). As for the mixed enantiomer system, a slight excess of one enantiomer is sufficient to generate a homochiral monolayer preferred by the majority enantiomers (Scheme 1d).

Scheme 1 (a) Enantiomeric unit formed by achiral BIC-C6 (gray column) and chiral (S)-2-octanol (blue dot). (b) Enantiomeric unit constituted by BIC-C6 and (R)-2-octanol (red dot). (c) Mirror-imaged hydrogen bonding circles preferred by (S)-2-octanol (left) and (R)-2-octanol (right), respectively. (d) Symmetry breaking in mixed enantiomers under control of the majority-rules principle. (e) Chiral amplification modulated by the molecular concentration.

Herein, in terms of the classic majority-rules principle used in cooperative assembly of BIC-C6, we unveil that the efficiency of chiral amplification at the interface shows a monotonic increase on decreasing the molecular concentration in solution. As the molecular concentration decreased, the surface organizational chirality changes from heterochirality to homochirality (Scheme 1e). The enantiomeric excess of chiral 2-octanol co-adsorbed on the surface is further biased. To unravel the chiral amplification mechanism, we have developed a cooperative nucleation-elongation model based on the Langmuir adsorption type.²⁷ A good description of the concentration-dependent amplification of chirality in 2D supramolecular organization is obtained. This work provides insights into how chiral amplification is affected by the molecular concentration at the nanoscale, which contributes to a further understanding of the emergence of homochirality in supramolecular assemblies.

Results

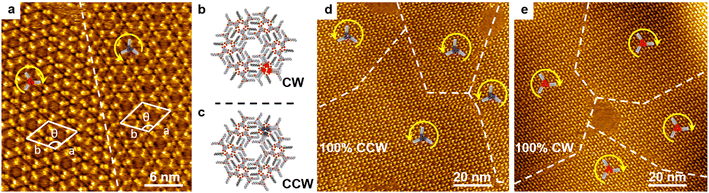
The scanning tunneling microscopy (STM) image of the well-defined hexagonal porous networks co-assembled by BIC-C6 and chiral 2-octanol on HOPG is shown in Fig. 1a. Two enantiomeric domains labeled as the counterclockwise (CCW) trimer and clockwise (CW) trimer, respectively, emerge equally at the liquid/solid interface, when (R)-2-octanol (R-OA) and (S)-2-octanol (S-OA) are mixed in a 1 : 1 ratio. Unit cell parameters are measured to be a = b = 4.6 nm, and θ = 120°. Every three BIC-C6 molecules constitute a chiral trimer serving as a structural unit in the porous network. According to the molecular models proposed in Fig. 1b and c, 2-octanol molecules are filled between the alkane chains of BIC and dominate the handedness in the monolayer through hydrogen bonding interactions. When enantiopure S-OA is applied, domains observed by STM reveal that the CCW pattern is exclusively formed on the whole HOPG surface, as depicted in Fig. 1d. On the other hand, the self-assembly of enantiopure R-OA triggers a preferential formation of the 100% CW motif (Fig. 1e). The maximum area of one homochiral domain can reach 100 × 100 nm².

Fig. 1 (a) Representative STM image of self-assemblies of BIC-C6 at the racemic 2-octanol/HOPG interface. Backbones in BIC molecules are indicated by columns to identify chirality. Yellow arrows indicate the rotation direction of the trimers (I_set = 1.2 nA andV_bias = 900 mV). (b) and (c) display the molecular models of CW and CCW networks, respectively. A red-gray column corresponds to a BIC molecule linked with R-OA, while a blue-gray column reflects a BIC molecule co-deposited with S-OA. (d) Large-scale STM image showing the homochiral CW pattern formed at the enantiopure R-OA/HOPG interface (I_set = 0.9 nA and V_bias = 900 mV). (e) Large-scale STM image showing a homochiral CCW motif formed at the enantiopure S-OA/HOPG interface (I_set = 0.9 nA and V_bias = 900 mV).

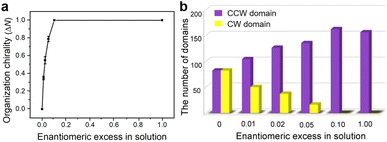
Then chiral amplification experiments under control of the majority-rules principle are performed at various ee values. The ee of mixtures represents the excess of one enantiomer relative to the other and is quantified from the number (N) of each chiral monomer, which is defined as:

ee = (N_S-OA − N_R-OA)/(N_S-OA + N_R-OA) (1)

The global organizational chirality (ΔN) in the monolayer investigated by STM is calculated from the quantitative difference between the two mirror-imaged domains as a function of ee in solution, expressed as

ΔN = (N_CCW − N_CW)/(N_CCW + N_CW) (2)

where N_CCW and N_CW are defined as the number of CCW and CW domains on the substrate, respectively. Outcomes presented in Fig. 2 reveal that a slight excess of S-OA is sufficient to bias the handedness of the supramolecular assembly. Although the ee in the solution is only 0.1, the organization chirality ΔN in the assembly reaches a value of 1, implying an efficient amplification of molecular chirality. A homochiral monolayer containing CCW patterns exclusively is generated.

Fig. 2 (a) Statistics for chiral amplification in the monolayer under control of majority-rules. (b) Bar graph denoting the correlation between the relative number of the enantiomeric domains on the surface and the ee value in solution. The concentration of BIC-C6 is 7.1 × 10⁻⁴ M.

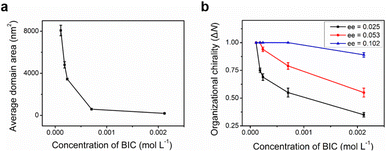
Concentration-dependent STM measurements are carried out in a mixed enantiomer system keeping the ee of chiral 2-octanol in the solution constant. As the molecular concentration in the solution decreases, the average domain area becomes larger accordingly (Fig. 3a). Statistics from sets of STM experiments indicates that the lower the concentration of BIC-C6, the larger the fraction of CCW domains formed on the surface at a fixed ee of 2-octanol (Fig. 3b). By modulating the solute concentration in the solution, the organizational chirality can be altered from heterochirality to homochirality. That is, a lower molecular concentration facilitates a more efficient amplification of chirality from the molecular to supramolecular level, contributing to a homochiral assembly. For example, when ee of S-OA in solution is fixed at 0.025, with the reduction of molecular concentration from 2.1 × 10⁻³ M to 1.0 × 10⁻⁴ M, the excess of CCW domains preferred by S-OA increases from 0.35 to 1.00 (Fig. 4). An enantiomerically pure surface is finally fabricated just by reducing the molecular concentration in solution.

Fig. 3 (a) Average domain area as a function of molecular concentration of BIC-C6. (b) Global organizational chirality (ΔN) in BIC-C6 networks at the surface versus molecular concentration at fixed ee value of chiral solvents. Statistic deviations for the average domain size and organizational chirality excess in the assembly are defined by using the average values in more than three sessions. For each sample, typically more than 20 large-scale STM images were captured at different locations.

Fig. 4 A selection of analyzed STM images displaying the controllable chiral amplification modulated by the molecular concentration. The concentration of BIC-C6 is (a) 2.1 × 10⁻³ M; (b) 7.1 × 10⁻⁴ M; (c) 2.4 × 10⁻⁴ M; (d) 1.8 × 10⁻⁴ M; (e) 1.0 × 10⁻⁴ M. ee of S-OA in solution is fixed at 0.025. CW domains are colored in yellow and CCW domains are painted purple. The bar graph in the upper right corner denotes the statistical relative proportion of the CW and CCW domain regions. Gray lines separate adjacent domains. The image size is 100 × 100 nm². Imaging conditions: I_set = 1 nA and V_bias = 900 mV. (f) Statistical graph representing the relative number of CW and CCW domain regions as a function of molecular concentration in solution.

Discussion

Considering the molecular origin of chiral amplification, we set out to investigate how the changes in concentration would affect chiral amplification behavior by an cooperative equilibrium modeling based on Langmuir type adsorption. Note that BIC-C6 co-assembles with 2-octanol into a chiral trimer in an equal proportion. Within a trimer, a BIC molecule interacts with 2-octanol through hydrogen bonding interactions while adjacent trimers interdigitate with each other via van der Waals interactions between alkyl chains. To simplify the modeling process, BIC trimer linked with three 2-octanol molecules is considered as a group when we simulate the supramolecular organization on the surface. Moreover, the chirality of co-adsorbed 2-octanol determines the handedness of the composite trimer unit. In the following discussion, R refers to the entity composed of BIC-C6 and R-OA while S denotes the BIC-C6/S-OA complex. Since there is no mismatched structure observed in the BIC-C6 monolayer, we only consider the situation in which R aggregates into the CW domain and S constitutes the CCW domain.

To describe the chiral amplification in the BIC-C6 monolayer at the liquid/solid interface, a 2D cooperative equilibrium model based on Langmuir adsorption^28–30 is proposed. We first describe the formation of CW motifs in more detail. For the formation of a CW domain (CW_n), n building units aggregate on the solid surface and constitute a chiral oligomer that determines the domain chirality. A sequence of equilibriums at the liquid/solid interface is described as

Although in the case of Langmuir theory, each adsorption step is independent of the other, the model proposed here considers the interactions between adjacent molecules. The first step in eqn (3) depicts the nucleation step described by using the nucleation constant K_n, which is equal to σ·K_e. K_e is the elongation constant which describes subsequent stepwise elongation processes and parameter σ is the cooperativity factor defined as the ratio of K_n/K_e. The following steps denote monomer assembling and disassembling to/from the existing oligomers. Unlike the two-sided growth of 1D helical polymers in solution, 2D molecular ordering is n-sided growth. The total probability is n times the product of the probabilities of individual events. Hence, the equilibrium concentration of CW oligomers [CW_n] containing n building units on the surface is given by using

[CW_n] = σ·[substrate]·K_eⁿ·[R]ⁿ (4)

where the square bracket notation is used to denote the equilibrium concentration of a species, that is, [substrate] relates to the molar concentration of active sites on the substrate and [R] is the free monomer concentration of R-enantiomer in solution. When the whole HOPG surface is covered by BIC-C6 assembly, the reduction of the solute concentration is estimated to be 3.4 × 10⁻⁶ M. As the concentration of molecules adsorbed on surface is negligible relative to that in supernatant solution, the equilibrium concentration is supposed to be the same as the initial concentration of the enantiomers in solution. From eqn (4), we can find that the lower the monomer concentration in solution, the lower the concentration of chiral oligomers at the surface. Similarly, the equilibrium concentration of CCW oligomers [CCW_n] assembled by S-enantiomers in the monolayer is found to be

[CCW_n] = σ·[substrate]·K_eⁿ·[S]ⁿ (5)

where [S] is the free monomer concentration of S-enantiomer in solution. The equilibrium constants for assembling the regime are equal in CW and CCW domains.

Combined with eqn (2), (4) and (5), the organizational chirality of adlayers could be expressed as:

ΔN = ([S]ⁿ − [R]ⁿ)/([S]ⁿ + [R]ⁿ) (6)

If δ = [S]/[R] (δ > 1) is defined, then it leads to

ΔN = (δⁿ − 1)/(δⁿ + 1) (7)

The ee of enantiomers is given by using

ee = (δ − 1)/(δ + 1) (8)

Eqn (7) reveals that the organizational chirality at the surface grows logarithmically on increasing the proportion difference between the two enantiomers (δ) in solution. That is, only a small perturbation in ee is sufficient to induce a profound change in supramolecular chirality on the surface, resulting in the generation of chiral amplification.

Then it comes to the concentration-dependent chiral amplification in the monolayer. If the ee of enantiomers is not changed, δ is invariant. Consequently, there is a positive correlation between the number of molecules n in chiral oligomers and organizational chirality ΔN (eqn (7)). n is subject to the molecular concentration in solution. As the molecular concentration in solution is reduced, the number of molecules n in chiral oligomers increases accordingly, as depicted in Fig. 3a. As a result, based on eqn (7), the organizational chirality ΔN would increase sharply when the molecular concentration in solution decreases. A strong amplification of chirality is generated.

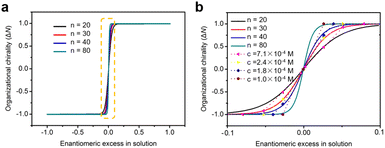
On the basis of eqn (7) and (8), simulated chiral amplification curves showing the monolayer organizational chirality as a function of ee in solution with different n values are obtained and shown in Fig. 5. When n = 20, 30, 40, and 80, the modelling curves are in good agreement with the experimental data. It reveals that the degree of chiral amplification in the majority-rules principle depends not only on the ee values of enantiomers but also on the number of building units in chiral oligomers, which can be modulated by the molecular concentration in solution. Global organizational chirality ΔN has an obvious growth with the decrease in the molecular concentration at a fixed ee. As the molecular concentration decreases, the molecular number n in chiral oligomers increases and the excess of the CCW pattern relative to the CW pattern in the monolayer at a specified ee grows accordingly. In other words, to achieve a globally homochiral surface, the absolute value of critical ee is reduced with the decrease in the molecular concentration in solution. Although the variation trend of chiral amplification on modulating the molecular concentration is consistent between the simulation and experiment, there is still some difference. The major contribution to the discrepancy between simulated and experimental results may be that even though the average domain area at a specified concentration tends to a definite value, the domains on the surface can be a variety of sizes. To simplify the model, the simulations assume identical size of domains formed on surface, and the number of molecules n in the chiral oligomer that determines the domain chirality remains constant when the molecular concentration is fixed.

Fig. 5 Modeling results for the chiral amplification controlled by the majority-rules principle. (a) Nonlinear amplification of chirality as a function of ee in solution. n is the number of building units in the chiral oligomer. (b) is a magnification of the area indicated with an orange frame in (a). To present the correlation between the experimental and simulated data, the experimental data are described by dashed lines and superimposed on the graph.

Conclusions

Overall, concentration modulation is explored as a powerful tool to manipulate chiral features of supramolecular assembly. When chiral 2-octanol was employed as the solvent, a chiral hexagonal lattice of BIC-C6 can be fabricated at the liquid/solid interface. STM results demonstrate that the ee of co-adsorbed chiral 2-octanol is amplified by lowering the molecular concentration of BIC-C6, which is reproduced by a 2D cooperative equilibrium model derived from Langmuir-type adsorption. This modeling approach reveals the inherent quantitative relationship between the enantiomeric monomers in solution and the resulting organizational chirality on the surface in the majority-rules principle controlled chiral amplification process. A minute difference in the concentration of enantiomers results in a dramatic change in the expression of chirality at the supramolecular level.

Data availability

Molecular models, supplementary STM images for the chiral amplification in the monolayer under control of majority-rules, STM images for the concentration-modulated chiral amplification, correlation among molecular concentration, domain area and the number of trimers in one domain, and additional experimental methods are available in the ESI.†

Author contributions

S. L. performed all of the experiments with help from all authors. S. L., D. W. and G. Z. wrote the manuscript. T. C. and D. W. helped to analyze the data. D. W. and G. Z. conceived the project. All authors approved the final version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Natural Science Foundation of Jilin Province (YDZJ202201ZYTS328), the National Natural Science Foundation of China (Grant No. 22131004, U21A20330, 22022203), the “111” project (B18012), the Science and Technology Research Foundation of the Education Department of Jilin Province (JJKH20231301KJ), and the Fundamental Research Funds for the Central Universities.

Notes and references

1. K. K. Konstantinov and A. F. Konstantinova, Orig. Life Evol. Biosph., 2018, 48, 93–122.
2. X. Song, L. Liu, Y. Chen, H. Yang, Z. Huang, B. Hou, Y. Hou, X. Han, H. Yang, Q. Zhang, T. Zhang, J. Zhou, Y. Huang, Y. Zhang, H.-J. Gao and Y. Wang, Nat. Commun., 2022, 13, 1843.
3. J. Labella, G. Lavarda, L. Hernández-López, F. Aguilar-Galindo, S. Díaz-Tendero, J. Lobo-Checa and T. Torres, J. Am. Chem. Soc., 2022, 144, 16579–16587.
4. C. Li, R. Li, Z. Xu, J. Li, X. Zhang, N. Li, Y. Zhang, Z. Shen, H. Tang and Y. Wang, J. Am. Chem. Soc., 2021, 143, 14417–14421.
5. H. Song, H. Zhu, Z. Huang, Y. Zhang, W. Zhao, J. Liu, Q. Chen, C. Yin, L. Xing, Z. Peng, P. Liao, Y. Wang, Y. Wang and K. Wu, ACS Nano, 2019, 13, 7202–7208.
6. S. C. Karunakaran, B. J. Cafferty, A. Weigert-Muñoz, G. B. Schuster and N. V. Hud, Angew. Chem., Int. Ed., 2019, 58, 1453–1457.
7. Y. Yun and A. J. Gellman, Nat. Chem., 2015, 7, 520–525.
8. M. M. Green, B. A. Garetz, B. Munoz, H. Chang, S. Hoke and R. G. Cooks, J. Am. Chem. Soc., 1995, 117, 4181–4182.
9. T. Chen, S. Y. Li, D. Wang, M. Yao and L. J. Wan, Angew. Chem., Int. Ed., 2015, 54, 4309–4314.
10. Y. Li, A. Hammoud, L. Bouteiller and M. Raynal, J. Am. Chem. Soc., 2020, 142, 5676–5688.
11. H. Cao and S. De Feyter, Nat. Commun., 2018, 9, 3416.
12. A. Nuermaimaiti, C. Bombis, M. M. Knudsen, J. R. Cramer, E. Lægsgaard, F. Besenbacher, K. V. Gothelf and T. R. Linderoth, ACS Nano, 2014, 8, 8074–8081.
13. I. Destoop, H. Xu, C. Oliveras Gonzalez, E. Ghijsens, D. B. Amabilino and S. De Feyter, Chem. Commun., 2013, 49, 7477–7479.
14. S. Haq, N. Liu, V. Humblot, A. P. J. Jansen and R. Raval, Nat. Chem., 2009, 1, 409–414.
15. R. Fasel, M. Parschau and K. H. Ernst, Nature, 2006, 439, 449–452.
16. L. Xie, Y. Ding, D. Li, C. Zhang, Y. Wu, L. Sun, M. Liu, X. Qiu and W. Xu, J. Am. Chem. Soc., 2022, 144, 5023–5028.
17. D. Li, L. Sun, Y. Ding, M. Liu, L. Xie, Y. Liu, L. Shang, Y. Wu, H.-J. Jiang, L. Chi, X. Qiu and W. Xu, ACS Nano, 2021, 15, 16896–16903.
18. S. Li, S. Duan, Z. Zha, J. Pan, L. Sun, M. Liu, K. Deng, X. Xu and X. Qiu, ACS Nano, 2020, 14, 6331–6338.
19. F. De Marchi, G. Galeotti, M. Simenas, M. C. Gallagher, E. Hamzehpoor, O. MacLean, R. M. Rao, Y. Chen, D. Dettmann, G. Contini, E. E. Tornau, M. Ebrahimi, D. F. Perepichka and F. Rosei, Nanoscale, 2019, 11, 19468–19476.
20. M.-X. Shi, J. Xu, K. Sun, M.-L. Tao, J.-Y. Yang, D.-X. Yang, Z.-L. Wang, Z. Li, J.-Z. Wang, Q.-K. Xue and S. Meng, Nano Res., 2022, 15, 5316–5321.
21. A. M. Berg and D. L. Patrick, Angew. Chem., Int. Ed., 2005, 117, 1855–1857.
22. M. Ke, X. Tan, Y. Wang, B. Li, X. Zeng, X. Miao, X. Cheng and W. Deng, J. Phys. Chem. C, 2021, 125, 19325–19332.
23. G. Velpula, C. Martin, B. Daelemans, G. Hennrich, M. Van der Auweraer, K. S. Mali and S. De Feyter, Chem. Sci., 2021, 12, 13167–13176.
24. Y. Xiao, J. Tao, X. Peng, Y. Song, P. Lei, H. Xu, X. Xiao, B. Tu and Q. Zeng, ACS Appl. Mater. Interfaces, 2021, 13, 17129–17138.
25. Y. Fang, E. Ghijsens, O. Ivasenko, H. Cao, A. Noguchi, K. S. Mali, K. Tahara, Y. Tobe and S. De Feyter, Nat. Chem., 2016, 8, 711–717.
26. T. Chen, W. H. Yang, D. Wang and L. J. Wan, Nat. Commun., 2013, 4, 1389.
27. F. Zerbetto, Adv. Mater., 2013, 25, 449–455.
28. A. J. Markvoort, H. M. ten Eikelder, P. A. Hilbers, T. F. de Greef and E. W. Meijer, Nat. Commun., 2011, 2, 509.
29. S. Yokoyama, T. Hirose and K. Matsuda, Chem. Commun., 2014, 50, 5964–5966.
30. H. M. isodesmicten Eikelder, A. J. Markvoort, T. F. de Greef and P. A. Hilbers, J. Phys. Chem. B, 2012, 116, 5291–5301.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06746c

---