Open Access Article
Open Access ArticleElectric fields drive bond homolysis †
Boyuan
Zhang‡
 a,
Cedric
Schaack‡
a,
Cedric
Schaack‡
 b,
Claudia R.
Prindle
b,
Ethan A.
Vo
b,
Miriam
Aziz
b,
Claudia R.
Prindle
b,
Ethan A.
Vo
b,
Miriam
Aziz
 b,
Michael L.
Steigerwald
b,
Timothy C.
Berkelbach
*bc,
Colin
Nuckolls
b,
Michael L.
Steigerwald
b,
Timothy C.
Berkelbach
*bc,
Colin
Nuckolls
 *b and
Latha
Venkataraman
*b and
Latha
Venkataraman
 *ab
*ab
aDepartment of Applied Physics and Applied Mathematics, Columbia University, New York 10027, New York, US. E-mail: lv2117@columbia.edu
bDepartment of Chemistry, Columbia University, New York 10027, New York, USA. E-mail: cn37@columbia.edu
cCenter for Computational Quantum Physics, Flatiron Institute, New York, New York 10010, USA. E-mail: tcb2112@columbia.edu
First published on 16th January 2023
Abstract
Electric fields have been used to control and direct chemical reactions in biochemistry and enzymatic catalysis, yet directly applying external electric fields to activate reactions in bulk solution and to characterize them ex situ remains a challenge. Here we utilize the scanning tunneling microscope-based break-junction technique to investigate the electric field driven homolytic cleavage of the radical initiator 4-(methylthio)benzoic peroxyanhydride at ambient temperatures in bulk solution, without the use of co-initiators or photochemical activators. Through time-dependent ex situ quantification by high performance liquid chromatography using a UV-vis detector, we find that the electric field catalyzes the reaction. Importantly, we demonstrate that the reaction rate in a field increases linearly with the solvent dielectric constant. Using density functional theory calculations, we show that the applied electric field decreases the dissociation energy of the O–O bond and stabilizes the product relative to the reactant due to their different dipole moments.
Introduction
Electromagnetic forces form the basis of chemical bonds, while electrostatic effects direct most chemical reactivity.1 However, using applied external electric fields (EEFs) to catalyze reactions represents an emerging area of biomimetic control for organic reactions that has been primarily confined to biochemistry and bioenzymatic reactions.2–9 Theoretical investigations have suggested that EEFs can be used to catalyze chemical reactions.10–17 Researchers have only recently begun applying EEFs to chemical reactions.18–25 For example, EEFs that are generated with a scanning tunneling microscope-based break-junction technique (STM-BJ) have been shown to successfully catalyze chemical reactions.26–28 However, despite this progress, it is not understood how to develop and optimize reactions that are EEF-catalyzed. Here, we study the homolytic O–O bond cleavage reaction of a benzoyl peroxide derivative, substrates that are used to initiate radical polymerization reactions,29 through the catalytic effect of an EEF.We monitor the homolysis of the O–O bond in 4-(methylthio)benzoic peroxyanhydride (1) at room temperature, in the absence of light, with an applied electric field using the STM-BJ technique (Fig. 1a). We show that the homolysis in an electric field generated between the tip and substrate of an STM can be initiated at applied voltages as low as 10 mV. Ex situ characterization by high performance liquid chromatography (HPLC) with UV-vis analysis as a function of time reveals that the electric field catalyzes the reaction. The chemoselectivity of the product formed depends on the solvent environment. In polar solvents, the reaction yields 4-(methylthio)benzoic acid 2 (Fig. 1b) at a rate that depends on the applied bias and the solvent dielectric constant. In non-polar solvents, the reaction yields 4,4′-bis(methylthio)biphenyl as evidenced by single-molecule conductance measurements. Density functional theory (DFT) is used to calculate the peroxide bond dissociation energy and the reactant and product dipole moments in different solvents, the results of which are used to estimate the impact of the EEF. This study is the first systematic quantification of chemical rate enhancement by an electric field and establishes EEFs as a methodology for catalysis without chemical reagents.
Results
Synthesis
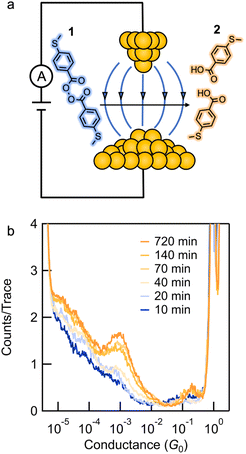
We synthesized compound 1 along with its potential homolysis products. Synthetic procedures and characterization can be found in the ESI.† The thiomethyl groups in 1 allow binding to the gold tip and substrate. We employed the STM-BJ technique to expose molecular solutions of 1 to a strong electric field produced by the bias voltage applied between a gold tip and a gold substrate.26,30STM-BJ conductance measurements
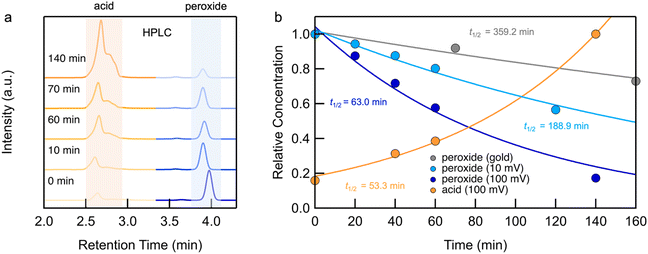
We first present the results from STM-BJ measurements of a 1 mM solution of 1 measured in propylene carbonate (PC) while applying a 100 mV bias in the dark and at room temperature. The solution was deposited onto an Au-coated steel puck and conductance versus displacement traces were collected over a period of 12 h. We compiled these traces into one-dimensional (1D) conductance histograms, revealing a clear peak, which grows with time, at a conductance of ∼7 × 10−4G0 (Fig. 1b). This peak can be attributed to the conductance of molecular junctions formed with 4-(methylthio)benzoic acid 2, as can be seen in the conductance histograms of the ex situ synthesized reference compound (Fig. S1†). Note that there is no peak for 1 as its conductance is below the STM-BJ instrument noise floor as also confirmed through DFT calculations (Fig. S2†). We periodically removed an aliquot of the solution from the STM-BJ substrate and determined the concentrations of starting material 1 and the only product formed, 2, through HPLC analysis (Fig. 2a). Formation of 2 was also confirmed by high resolution mass spectroscopy (HR-MS, Fig. S3†). Although we cannot confirm the source of the electrons and protons needed to yield 2, it is likely that the Au electrodes supply the electrons and the protons comes from the non-anhydrous environment, in accordance with other literature reports.31 To test this hypothesis, we repeat the STM-BJ measurements in a non-polar solvent tetradecane (TD). We observe a clear conductance peak for 4,4′-bis(methylthio)biphenyl in situ (Fig. S4†) but no peak was observed for 2 which is to be expected since there are no protons in this solvent. Upon adding acetic acid to the solution of 1 in tetradecane (TD), we observed a clear conductance peak for 2 (Fig. S4†) confirming that in PC, the acid is formed with protons in solution. After 4 h, when acetic acid evaporates, we no longer have a proton source and the product reverts to biphenyl. We note here that we did not detect formation of 2 or 4,4′-bis(methylthio)biphenyl in TD from ex situ HPLC analysis even upon prolonged EEF exposure (up to 24 h) which indicates that the conversion is likely very low in TD.Reaction investigation using HPLC
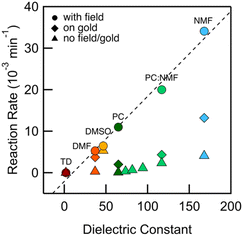
We integrate the area under the peaks corresponding to 1 and 2 in the HPLC data obtained from PC-based measurements shown in Fig. 2a to determine concentrations as a function of time which we plot in Fig. 2b. We apply a first-order kinetic rate law to calculate the rate of consumption of 1 and the rate of formation of 2. At a 100 mV applied bias, we find a half-life of t1/2 ∼ 1 hour for the consumption of 1 (Fig. 2b). This matches the rate of formation of 2, demonstrating the chemoselective conversion of 1 to 2 over time with no other detectable side products. In Fig. 2b, we additionally include the rate of consumption of 1 when STM-BJ measurements are repeated at a smaller 10 mV bias and when a solution is simply placed on the Au substrate and no field is applied. At a 10 mV bias, the half-life increases by a factor of 3 compared to that at 100 mV indicating a clear bias dependence and thus confirming that the reaction is field-driven. Without a field, the half-life increases by almost a factor of 6 compared to that with a 100 mV bias suggesting that gold also catalyzes the reaction, but only to a minor extent. We did not find quantifiable rates even after 3 days in the dark and in the absence of gold in PC.We next repeated the same measurements in different solvents of varying polarities and quantifies the reaction rate with and without an applied electric field using HPLC characterization by monitoring the consumption of 1 over time. We considered solvents with dielectric constant, ε from 2 (TD) to 168 (N-methylformamide, NMF) as well as mixtures of PC and NMF of varying ratios to achieve a range of ε. We show in Fig. 3 the observed rates determined as a function of the solvent dielectric. Conductance histograms from STM-BJ measurements are provided in Fig. S5.† We see that the rate of the reaction in an electric field with a bias of 100 mV correlates linearly with the dielectric of the solvent (Fig. 3) with a coefficient of determination, R2, of 0.99. The rates in solution (i.e. without a field or exposure to Au) do not show such a strong correlation with the solvent dielectric (R2 = 0.82 excluding DMSO data), although overall an increased background reactivity in more polar solvents is observed, in line with published reports.32,33 The background rate is the highest in dimethylsulfoxide (DMSO), and NMR analysis shows that 1 converts rapidly to 2via an intermediate, possibly a peracid, sulfone, or both. We observe some background reactivity in dimethylformamide (DMF) and NMF, while none is observed in TD or PC.
These data show that the EEF clearly drives the reaction even in highly polar solvents where one would expect the fields to be substantially screened based on simple dielectric continuum theories. In an external field, the solvent molecules can polarize and reorient to screen the field; however, this does not preclude having large local fields at the reaction site (O–O bond), which likely catalyze this reaction. For example, in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of PC:NMF with an ε of 117, we get a reaction rate of 0.02 min−1 at a 100 mV bias compared with a rate of 0.002 min−1 in solvent alone. This constitutes a substantial increase in reactivity. This is further confirmed by measurements in the same solvent mixture but with an added electrolyte (0.1 M tetrabutylammonium hexafluorophosphate, TBAPF6). This creates a strong double layer at the tip and substrate that screens the field seen by the solution bulk. This also increases the concentration of mobile ions and the conductivity of the solution, and thus the voltage drop within the solution bulk is decreased, decreasing the field in the solution. We find that the reaction rate is reduced by a factor of 6 compared to the measurement without TBAPF6 (Fig. S6†), yielding rates similar to those of the background reactivity on gold. Repeating this measurement while keeping the tip-surface separation over 1 μm, and thus decreasing the field also results in a reaction rate comparable to the background reactivity on gold. Both these results confirm that the electric field strength is the major factor in the observed catalysis of the bond cleavage.
50 mixture of PC:NMF with an ε of 117, we get a reaction rate of 0.02 min−1 at a 100 mV bias compared with a rate of 0.002 min−1 in solvent alone. This constitutes a substantial increase in reactivity. This is further confirmed by measurements in the same solvent mixture but with an added electrolyte (0.1 M tetrabutylammonium hexafluorophosphate, TBAPF6). This creates a strong double layer at the tip and substrate that screens the field seen by the solution bulk. This also increases the concentration of mobile ions and the conductivity of the solution, and thus the voltage drop within the solution bulk is decreased, decreasing the field in the solution. We find that the reaction rate is reduced by a factor of 6 compared to the measurement without TBAPF6 (Fig. S6†), yielding rates similar to those of the background reactivity on gold. Repeating this measurement while keeping the tip-surface separation over 1 μm, and thus decreasing the field also results in a reaction rate comparable to the background reactivity on gold. Both these results confirm that the electric field strength is the major factor in the observed catalysis of the bond cleavage.
Theoretical analysis
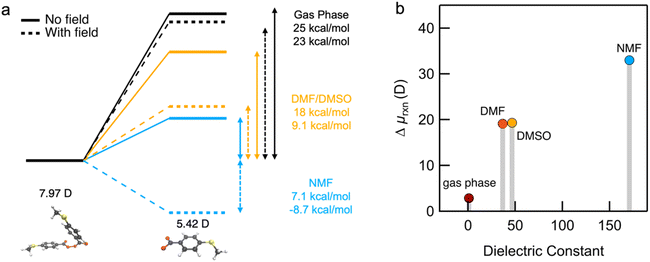
To help understand our findings, we performed DFT calculations using the PBE0 functional with geometry optimization (see the ESI† for computational details). We first consider the homolysis of the O–O bond of 1 to yield two aroyloxy radicals in the gas phase. The O–O bond dissociation energy (BDE) is calculated to be 25 kcal mol−1 (1.1 eV), which could be an underestimate as DFT has been shown to predict peroxide BDEs that are ∼10 kcal mol−1 lower than those obtained using higher levels of theory.34 Nonetheless, this range of values is consistent with the fact that we do not observe any decomposition of 1 at room temperature over a period of a few days. We next compute the molecular dipole moments for 1 to be 8.0 D and of the single aroyloxy radical to be 5.4 D (Fig. 4a) in the gas phase. The change in the dipole moment following dissociation,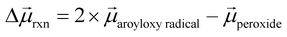 , is positive (+2.8 D), indicating that in an EEF, the BDE will decrease, as the molecules rotate and align with the field.
, is positive (+2.8 D), indicating that in an EEF, the BDE will decrease, as the molecules rotate and align with the field.
We repeated the calculations in DMF, DMSO and NMF using the continuum universal solvation model (SMD)35 to determine BDE and the change in the dipole moment Δμrxn. The BDE decreases as the solvent dielectric increases due to the increased polarizability of the aroyloxy radical and concomitant larger solvation energy (Fig. 4a). This trend is in qualitative agreement with the experimental results shown in Fig. 3, although quantitatively correlating the reaction rate to the BDE is nontrivial. We also find that Δμrxn increases with solvent dielectric (Fig. 4b) for the same reason as that for the decreased BDE. This suggests that when an EEF is applied, the energy difference will increase more dramatically in solvents with a higher dielectric constant in agreement with experiments. To further support our findings, we approximate the application of an external field of 1 V nm−1 and compute the BDE in the three solvents. The applied field stabilizes the aroyloxy radicals while also decreasing the dissociation energy (Fig. 4a).
The BDE calculations only indirectly address the mechanism of homolytic cleavage. To provide more direct insight, we studied the effect of an EEF on the electronic structure of 1 without reoptimizing the geometry. We express the DFT density matrix calculated in the presence of a field on the basis of the molecular orbitals calculated in the absence of a field. We find that the EEF causes an increased occupation of the O–O antibonding orbital, the lowest unoccupied molecular orbital (LUMO) and a decreased occupation of the O–O bonding orbital, the second highest occupied orbital (HOMO-1). The EEF induces a population transfer that weakens the O–O bond and facilitates cleavage (Fig. S7† and ESI). Our calculations indicate that the EEF weakens the O–O bond and thermodynamically favors the aroyloxy radical. Taken together, these theoretical predictions are in agreement with our experimental observations.
Conclusions
In summary, we have demonstrated that the STM-BJ technique can induce the electric field-driven homolytic cleavage of a benzoyl peroxide in a bulk solution. The electric field catalyzes the reaction, and the environment dictates chemoselectivity. Importantly, we determine reaction kinetics as a function of time ex situ by HPLC. The reaction is accelerated by the field and its rate is linearly correlated with solvent dielectric constants. We rationalize the findings by DFT calculations and reveal the important role of the peroxide and radical dipole moments in decreasing the dissociation energy in different solvents and under an applied field.Methods
General methods
All reactions were performed in oven-dried round bottom flasks, with a Teflon magnetic stir bar and rubber septa, and reactions were conducted under a positive pressure of nitrogen. Anhydrous and anaerobic solvents were obtained from Sigma-Aldrich, and all commercially available reagents were used without further purification. Compound 1 was prepared according to a known procedure.31
1H NMR and 13C NMR spectra in deuterated solvents were recorded on a Bruker DMX500 (500 MHz) spectrometer. High-resolution mass spectrometry (HRMS) spectra were recorded on a Waters XEVO G2-XS QTOF spectrometer in dichloromethane solutions. HPLC separation was performed on an Agilent LC1220 HPLC instrument, using an Agilent Zobrax Eclipse Plus C18 column (5 μm × 21.2 mm × 250 mm) stationary phase and a 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 acetonitrile:water mobile phase. UV-vis absorption spectra were recorded in situ on the HPLC instrument.
5 acetonitrile:water mobile phase. UV-vis absorption spectra were recorded in situ on the HPLC instrument.
STM-BJ measurement
STM-BJ measurements were made using a custom-built scanning tunnelling microscope.30 The electric field is applied between a 0.25 mm gold wire (99.998%, Alfa Aesar) as a gold STM-tip and a gold-coated (99.999%, Alfa Aesar) steel puck (Ted Pella) as a gold substrate, while the strength of the field was modulated either by changing the bias applied or the distance between the tip and substrate.36 Conductance measurements were performed in dilute solutions (1 mM) of reaction mixtures in different solvents as indicated in the main text. In polar solvents, the insulated tips were created by driving a mechanically cut gold tip through Apiezon wax. A commercially available z-axis piezoelectric positioner (P-840.10, PI) was used to drive the tip in and out of contact with the substrate at a speed of 20 nm s−1 in a dilute solution of the target molecule in an ambient environment at room temperature. The junction current (I) was recorded as a function of tip-substrate displacement at a fixed applied bias voltage (with a 100 kΩ resistor in series). The current, voltage across the junction and electrode position data are all collected at a 40 kHz acquisition rate using a custom Igor Pro (Wavemetric, Inc). Conductance (G = I/V) was determined as a function of displacement and analyzed further using one-dimensional (1D) conductance and two-dimensional (2D) conductance-displacement histograms. A gold point-contact is first formed with a conductance close to 1G0 (= 2 × 102 h, conductance quantum) and then followed by a molecular conductance plateau below 1G0. The measured conductance traces were then collected and compiled into logarithmically binned 1D histograms (100/decade), and 2D histograms along the conductance axis (100 decade−1) and linear bins (1000 nm−1) along the displacement axis without data selection. All the measurements are performed using fresh solutions, without any exposure to light, and in a dark acoustic box.DFT calculations
DFT calculations for transmission functions (including geometry optimization) were carried out using the closed-shell Kohn–Sham formulation of density functional theory with FHI-aims software.37 A non-empirical generalized gradient-corrected approximation (PBE) for the exchange-correlation functional38 was used. Scalar relativistic corrections to the kinetic energy were incorporated in the first-principles calculations at the atomic zeroth-order regular approximation (ZORA) level.39 The Kohn–Sham states were represented in an optimized all-electron numeric atom-centered basis set with “light” computational settings. The energy-dependent transmission functions were calculated using the non-equilibrium Green's function formalism with the transport package AITRANSS.40–42 The junction electrodes were modelled using tetrahedral clusters of 22 atoms each with an interatomic distance of 2.88 Å.DFT calculations of the O–O bond dissociation energy (BDE) were performed with the PBE0 hybrid functional43 and the def2-TZVP44 basis set using the ORCA quantum chemistry package.45 Atom-pairwise dispersion corrections with Becke-Johnson damping46 were included in the O–O BDE calculations. Solvent influences on the BDE and dipole moment were estimated using the continuum universal solvation model (SMD) and the default parameters of DMF, DMSO and NMF included in the ORCA package. Orbital occupations were determined in the PySCF quantum chemistry package47 by calculating the 1-particle reduced density matrix with and without an EEF. The changes in orbital occupations were calculated by expressing the density matrix in the presence of an EEF on the basis of the molecular orbitals without an EEF.
Data availability
The data that support the findings of this study are available only on request from the corresponding authors.Author contributions
B. Z., C. S., C. N., and L. V. designed and conceived the experiments. B. Z., C. S., and C. P. performed experiments. E. A. V., M. A. and T. C. B. performed calculations. All authors co-wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported primarily by the NSF CHE-2023568 CCI Phase I: Center for Chemistry with Electric Fields. C. R. P. was supported by a National Defense Science and Engineering Graduate Fellowship. High resolution mass spectra (HR-MS) were obtained from the Columbia University Chemistry Department Mass Spectrometry Facility. E. A. V. and T. C. B. thank Dr Xiao Wang (Flatiron Institute) for helpful discussions.Notes and references
- A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106(8), 3210–3235 CrossRef CAS PubMed.
- J.-Y. Cho, M. K. Tse, D. Holmes, R. E. Maleczka and M. R. Smith, Science, 2002, 295(5553), 305–308 CrossRef CAS PubMed.
- M. A. Dasari, P.-P. Kiatsimkul, W. R. Sutterlin and G. J. Suppes, Appl. Catal., A, 2005, 281(1), 225–231 CrossRef CAS.
- C.-W. Chiu, M. A. Dasari, G. J. Suppes and W. R. Sutterlin, AIChE J., 2006, 52(10), 3543–3548 CrossRef CAS.
- E. Skucas, M.-Y. Ngai, V. Komanduri and M. J. Krische, Acc. Chem. Res., 2007, 40(12), 1394–1401 CrossRef CAS PubMed.
- R. A. Sheldon, Chem. Commun., 2008, 29, 3352–3365 RSC.
- E. S. Beach, Z. Cui and P. T. Anastas, Energy Environ. Sci., 2009, 2(10), 1038–1049 RSC.
- W. Leitner, Acc. Chem. Res., 2002, 35(9), 746–756 CrossRef CAS PubMed.
- M. P. Eng, T. Ljungdahl, J. Mårtensson and B. Albinsson, J. Phys. Chem. B, 2006, 110(13), 6483–6491 CrossRef CAS PubMed.
- S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8(12), 1091–1098 CrossRef CAS PubMed.
- K. D. Dubey, T. Stuyver, S. Kalita and S. Shaik, J. Am. Chem. Soc., 2020, 142(22), 9955–9965 CrossRef PubMed.
- Z. F. Wang, D. Danovich, R. Ramanan and S. Shaik, J. Am. Chem. Soc., 2018, 140(41), 13350–13359 CrossRef CAS PubMed.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47(14), 5125–5145 RSC.
- S. Shaik, S. P. de Visser and D. Kumar, J. Am. Chem. Soc., 2004, 126(37), 11746–11749 CrossRef CAS PubMed.
- S. D. Fried, S. Bagchi and S. G. Boxer, Science, 2014, 346(6216), 1510–1514 CrossRef CAS PubMed.
- S. Shaik, D. Danovich, J. Joy, Z. F. Wang and T. Stuyver, J. Am. Chem. Soc., 2020, 142(29), 12551–12562 CrossRef CAS PubMed.
- S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55(1), 117–129 CrossRef CAS.
- S. A. Sorenson, J. G. Patrow and J. M. Dawlaty, J. Am. Chem. Soc., 2017, 139(6), 2369–2378 CrossRef CAS PubMed.
- C. F. Gorin, E. S. Beh, Q. M. Bui, G. R. Dick and M. W. Kanan, J. Am. Chem. Soc., 2013, 135(30), 11257–11265 CrossRef CAS PubMed.
- C. F. Gorin, E. S. Beh and M. W. Kanan, J. Am. Chem. Soc., 2012, 134(1), 186–189 CrossRef CAS PubMed.
- J. T. Wang, X. Jin, Z. B. Liu, G. Yu, Q. Q. Ji, H. M. Wei, J. Zhang, K. Zhang, D. Q. Li, Z. Yuan, J. C. Li, P. Liu, Y. Wu, Y. Wei, J. P. Wang, Q. Q. Li, L. Zhang, J. Kong, S. S. Fan and K. L. Jiang, Nat. Catal., 2018, 1(5), 326–331 CrossRef CAS.
- L. Zhang, E. Laborda, N. Darwish, B. B. Noble, J. H. Tyrell, S. Pluczyk, A. P. Le Brun, G. G. Wallace, J. Gonzalez, M. L. Coote and S. Ciampi, J. Am. Chem. Soc., 2018, 140(2), 766–774 CrossRef CAS PubMed.
- L. Yue, J. L. Li, S. D. Zhou, X. Y. Sun, M. Schlangen, S. Shaik and H. Schwarz, Angew. Chem., Int. Ed., 2017, 56(34), 10219–10223 CrossRef CAS PubMed.
- M. Lindner, M. Valasek, M. Mayor, T. Frauhammer, W. Wulfhekel and L. Gerhard, Angew. Chem., Int. Ed., 2017, 56(28), 8290–8294 CrossRef CAS PubMed.
- M. Liu, Y. J. Pang, B. Zhang, P. De Luna, O. Voznyy, J. X. Xu, X. L. Zheng, C. T. Dinh, F. J. Fan, C. H. Cao, F. P. G. de Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537(7620), 382–386 CrossRef CAS PubMed.
- Y. P. Zang, Q. Zou, T. R. Fu, F. Ng, B. Fowler, J. J. Yang, H. X. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nat. Commun., 2019, 10, 4482 CrossRef PubMed.
- H. X. Li, T. A. Su, V. V. Zhang, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, J. Am. Chem. Soc., 2015, 137(15), 5028–5033 CrossRef CAS PubMed.
- X. Y. Huang, C. Tang, J. Q. Li, L. C. Chen, J. T. Zheng, P. Zhang, J. B. Le, R. H. Li, X. H. Li, J. Y. Liu, Y. Yang, J. Shi, Z. B. Chen, M. D. Bai, H. L. Zhang, H. P. Xia, J. Cheng, Z. Q. Tian and W. J. Hong, Sci. Adv., 2019, 5(6), eaaw3072 CrossRef CAS PubMed.
- J. C. Bevington and J. Toole, J. Polym. Sci., 1958, 28(117), 413–420 CrossRef CAS.
- L. Venkataraman, J. E. Klare, I. W. Tam, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nano Lett., 2006, 6(3), 458–462 CrossRef CAS PubMed.
- J.-i. Hashimoto, K. Segawa and H. Sakuragi, Chem. Phys. Lett., 1999, 314(3), 261–266 CrossRef CAS.
- E. M. Chellquist and W. G. Gorman, Pharm. Res., 1992, 9(10), 1341–1346 CrossRef CAS PubMed.
- F. Nielloud, J. P. Mestres and G. Marti-Mestres, Drug Dev. Ind. Pharm., 2002, 28(7), 863–870 CrossRef CAS PubMed.
- R. D. Bach and H. B. Schlegel, J. Phys. Chem. A, 2020, 124(23), 4742–4751 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS.
- M. Kamenetska, M. Koentopp, A. C. Whalley, Y. S. Park, M. L. Steigerwald, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Phys. Rev. Lett., 2009, 102(12), 126803 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180(11), 2175–2196 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- E. V. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99(6), 4597–4610 CrossRef.
- J. Wilhelm, M. Walz, M. Stendel, A. Bagrets and F. Evers, Phys. Chem. Chem. Phys., 2013, 15(18), 6684–6690 RSC.
- A. Bagrets, J. Chem. Theory Comput., 2013, 9(6), 2801–2815 CrossRef CAS PubMed.
- A. Arnold, F. Weigend and F. Evers, J. Chem. Phys., 2007, 126(17), 174101 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110(13), 6158–6170 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152(22), 224108 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS.
- Q. M. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. D. Li, J. Z. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K. L. Chan, Wires Comput. Mol. Sci., 2018, 8(1), e1340 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis details, HPLC analysis and additional figures. See DOI: https://doi.org/10.1039/d2sc06411a |
| ‡ B. Z. and C. S. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |