Open Access Article
Open Access ArticleQuantum chemistry simulation of ground- and excited-state properties of the sulfonium cation on a superconducting quantum processor
Mario
Motta
 *a,
Gavin O.
Jones
*a,
Gavin O.
Jones
 a,
Julia E.
Rice
a,
Tanvi P.
Gujarati
a,
Rei
Sakuma
b,
Ieva
Liepuoniute
a,
Jeannette M.
Garcia
a and
Yu-ya
Ohnishi
a,
Julia E.
Rice
a,
Tanvi P.
Gujarati
a,
Rei
Sakuma
b,
Ieva
Liepuoniute
a,
Jeannette M.
Garcia
a and
Yu-ya
Ohnishi
 b
b
aIBM Quantum, IBM Research – Almaden, 650 Harry Road, San Jose 95120, CA, USA. E-mail: mario.motta@ibm.com; gojones@us.ibm.com; jmgarcia@us.ibm.com
bMaterials Informatics Initiative, RD Technology & Digital Transformation Center, JSR Corporation, 3-103-9, Tonomachi, Kawasaki-ku, Kawasaki, 210-0821, Kanagawa, Japan. E-mail: yuuya_oonishi@jsr.co.jp
First published on 15th February 2023
Abstract
The computational description of correlated electronic structure, and particularly of excited states of many-electron systems, is an anticipated application for quantum devices. An important ramification is to determine the dominant molecular fragmentation pathways in photo-dissociation experiments of light-sensitive compounds, like sulfonium-based photo-acid generators used in photolithography. Here we simulate the static and dynamical electronic structure of the H3S+ molecule, taken as a minimal model of a triply-bonded sulfur cation, on a superconducting quantum processor of the IBM Falcon architecture. To this end, we generalize a qubit reduction technique termed entanglement forging or EF [A. Eddins et al., Phys. Rev. X Quantum, 2022, 3, 010309], currently restricted to the evaluation of ground-state energies, to the treatment of molecular properties. While in a conventional quantum simulation a qubit represents a spin-orbital, within EF a qubit represents a spatial orbital, reducing the number of required qubits by half. We combine the generalized EF with quantum subspace expansion [W. Colless et al., Phys. Rev. X, 2018, 8, 011021], a technique used to project the time-independent Schrodinger equation for ground- and excited-states in a subspace. To enable experimental demonstration of this algorithmic workflow, we deploy a sequence of error-mitigation techniques. We compute dipole structure factors and partial atomic charges along ground- and excited-state potential energy curves, revealing the occurrence of homo- and heterolytic fragmentation. This study is an important step towards the computational description of photo-dissociation on near-term quantum devices, as it can be generalized to other photodissociation processes and naturally extended in different ways to achieve more realistic simulations.
1 Introduction
Solving the Schrödinger equation for ground- and excited-states of many-electron quantum systems is one of the grand challenges of contemporary science.1,2 In particular, the accurate computation of excited-state properties by numerical simulations stands to impact many problems in pure and applied quantum chemistry, exemplified by photochemical processes that result from absorption of photons and promotion of electrons to excited states.The semiconductor industry has employed these processes to use photolithographic materials in solid-state chip fabrication.3,4 Fundamentally, fabrication involves coating a silicon wafer with a thin film of a precisely engineered block co-polymer with different functional side chains on blocks that self-assemble into lamellae when processed. In this example, blocks have distinct reaction profiles, and some engineered systems include acid-sensitive side chains that, when reacted, change the block solubility coefficient. A photo-acid generator (PAG) can be embedded in the polymer film and photochemically reacts at specific wavelengths of light to release a free proton in the solid-state that can subsequently react with acid-sensitive side chains.5–8 Patterns form with the use of a mask that blocks or exposes different parts of the film to ultraviolet (UV) light, modifying the solubility of the polymer such that it can be selectively washed away from the wafer in aqueous solvents. One such effective industrial PAG contains the triphenylsulfonium (Ph3S+) cation.9–14
The computational description of these photochemical processes poses a number of challenges, for example: characterizing the light–matter interaction to determine transitions to electronic (and, in general, vibronic) excited states; and, in photo-dissociation reactions, assessing the electronic structure of excited states to determine the nature of the dissociation path (e.g. homolytic15–17 or heterolytic18). In addition, qualitatively correct and quantitatively accurate calculations require incorporating solvation and thermal effects, and reliably assessing the electronic structure of the studied species by accounting for static and dynamical correlations in realistic basis sets. Capturing such effects accurately is essential for understanding molecular properties, for predictive computations, and ultimately for introducing new PAGs, because the current semiconductor process requires molecular-size order controlling.
Over the last decades, research in computational many-electron quantum mechanics has generated algorithms for conventional classical computers that yield approximate, though often very accurate, estimates of ground- and excited-state molecular properties at polynomial cost.19–22
Digital quantum computers are an alternative and complementary framework to simulate many-body quantum systems.23–26 Assuming high-quality qubits in a sufficiently large number, they allow simulation of the time-dependent Schrödinger equation at polynomial cost introducing controllable approximations only,27,28 thus being capable of accessing a vast class of excited-state properties. Recent advances in hardware manufacturing has produced quantum computers that can carry out computations on a limited scale. Despite the rapid development of quantum hardware, modern quantum computation platforms are immature. As a consequence, simulations of excited states on near-term devices are typically restricted to heuristic quantum subspace algorithms,29–35 that yield approximations to excited-state wavefunctions and properties within the budget of these devices by projecting the Schrödinger equation onto a suitably constructed subspace. It is therefore a real possibility, and of central importance at this time, to assess the potential usefulness of near-term quantum devices on problems of conceptual and practical interest, e.g. the computation of molecular excited states.
Here, we report the development of a heuristic methodology that leverages structured entanglement in many-electron wavefunctions to calculate ground- and excited-state molecular properties, and its experimental demonstration on a superconducting quantum processor. More specifically, we generalize a qubit reduction technique called entanglement forging (EF),36 initially proposed for variational simulations of ground-state energies, to the computation of generic many-body observables. While in a conventional quantum simulation a qubit represents a spin-orbital, within EF a qubit represents a spatial orbital, reducing the number of required qubits by half.
To improve the accuracy of this technique, and to approximate excited-state energies and properties, we combine EF with quantum subspace expansion (QSE), an example of a heuristic quantum subspace algorithm29,35,37 which, in its simplest form, projects the Schrödinger equation onto a subspace spanned by single and double excitations on top of a reference wavefunction. The proposed methodology extends the applicability of EF, allowing the computation of a significant set of observables, and that of QSE, facilitating its demonstration on contemporary quantum hardware due to the qubit reduction operated by EF.
We apply the proposed technique, in combination with multiple error mitigation methods, to investigate the gas-phase photo-dissociation of H3S+, taken as the simplest molecular model for Ph3S+. Common to both compounds is the presence of a triply-bonded sulfur cation. The most accurate description of the computational model for Ph3S+ requires the inclusion of the π-conjugated phenyl groups, which determines the energy and character of its excited states, but this feature corresponds to a higher computational cost which makes H3S+ a more suitable target for simulations on contemporary quantum hardware.
We assess the interaction between H3S+ and UV light within the electric dipole approximation in response theory, and characterize dissociation paths as homo- or heterolytic by computing partial atomic charges and other properties of the excited-states. Our study contains approximations and limitations, that we endeavor to document. Notwithstanding these limitations, it illustrates that near-term quantum hardware can be effectively used to explore ground- and excited-states of molecules by means of active-space calculations. While active spaces treated in our study are still small, the underlying methodology naturally extends to larger active spaces. Furthermore, our algorithm is amenable to multiple algorithmic improvements and extensions (for example to treat dynamical correlation, solvation effects, and larger chemical systems), that draw a path towards larger and more realistic simulations.
2 Methods
Several authors have shown that the absorption cross-section of electromagnetic radiation by a molecular system can very generally be represented as a Fourier integral.38–41Let Ĥ be the unperturbed time-independent molecular Hamiltonian, with eigenstates Ĥ|ΦA〉 = εA|ΦA〉. If the system, initially at equilibrium at zero temperature, interacts weakly with an external electric field of frequency ω, transitions from the ground state into other quantum states |ΦA〉 occur if the frequency of the radiation is close to ΔεA0 = εA − ε0. Assuming a field with wavelength much larger than molecular dimensions, the perturbation can be written as ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t) = −
(t) = −![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ·Ê(t), where
·Ê(t), where ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) is the dipole moment operator. According to time-dependent quantum-mechanical perturbation theory, to first order in the perturbation, the rate of transition from the ground state to any excited state is given by Fermi's golden rule42–48 and is proportional to the dipole dynamical structure factor (DSF),
is the dipole moment operator. According to time-dependent quantum-mechanical perturbation theory, to first order in the perturbation, the rate of transition from the ground state to any excited state is given by Fermi's golden rule42–48 and is proportional to the dipole dynamical structure factor (DSF),
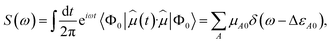 | (1) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Φ0〉|2 is the transition dipole between Hamiltonian eigenstates Φ0 and ΦA. Combined with the excitation energy ΔεA0, it permits evaluation of the oscillator strength μA0ΔεA0, which in turn specifies the absorption cross section of electromagnetic radiation.45–48 It should be noted that the scalar character of the DSF is due to the assumption of an isotropic system, for which any response is independent from the polarization vector of the incident radiation. Furthermore, while an appropriate description of photo-dissociation requires a joint quantum mechanical treatment of electrons and nuclei,42,43 particularly near conical intersections, here, concerned with valence-electron UV/vis spectroscopy, we focus on vertical electronic transitions.
|Φ0〉|2 is the transition dipole between Hamiltonian eigenstates Φ0 and ΦA. Combined with the excitation energy ΔεA0, it permits evaluation of the oscillator strength μA0ΔεA0, which in turn specifies the absorption cross section of electromagnetic radiation.45–48 It should be noted that the scalar character of the DSF is due to the assumption of an isotropic system, for which any response is independent from the polarization vector of the incident radiation. Furthermore, while an appropriate description of photo-dissociation requires a joint quantum mechanical treatment of electrons and nuclei,42,43 particularly near conical intersections, here, concerned with valence-electron UV/vis spectroscopy, we focus on vertical electronic transitions.
DSFs of the form shown in eqn (1) are natural targets for quantum computers, where the time-dependent dipole correlation function f(t) = 〈Φ0|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (t)·
(t)·![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Φ0〉 can be computed by simulating Hamiltonian time evolution.26 Note that f(t) needs to be computed over a sufficiently long time interval to allow for accurate reconstruction of its Fourier transform, time evolution needs to be controllably approximated e.g. with product formulae, and computation of correlation functions involves deep quantum circuits comprising the Hadamard test or mid-circuit measurements.49 Approximate ground- and excited states can also be computed by means of quantum diagonalization algorithms. These heuristic methods may require shallower quantum circuits, making them compatible with near-term quantum computers. Furthermore, they enable evaluation of eqn (1) directly in the frequency domain; for example, they allow to evaluate the right member of eqn (1) by summing over the set of computed excited states without computing time-dependent correlation functions. Access to excited-state wavefunctions also allows computing densities
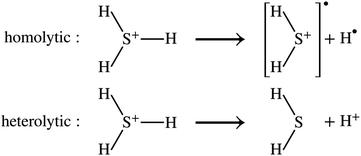
|Φ0〉 can be computed by simulating Hamiltonian time evolution.26 Note that f(t) needs to be computed over a sufficiently long time interval to allow for accurate reconstruction of its Fourier transform, time evolution needs to be controllably approximated e.g. with product formulae, and computation of correlation functions involves deep quantum circuits comprising the Hadamard test or mid-circuit measurements.49 Approximate ground- and excited states can also be computed by means of quantum diagonalization algorithms. These heuristic methods may require shallower quantum circuits, making them compatible with near-term quantum computers. Furthermore, they enable evaluation of eqn (1) directly in the frequency domain; for example, they allow to evaluate the right member of eqn (1) by summing over the set of computed excited states without computing time-dependent correlation functions. Access to excited-state wavefunctions also allows computing densities 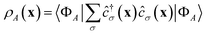 , where the operator ĉ†σ(x)/ĉσ(x) creates or destroys an electron with spin σ at position x. From these, one can extract partial atomic charges, which in turn allow characterization of the dissociation of a single SH bond as a homolytic (H3S+ → H2S+ + H) or heterolytic (H3S+ → H2S + H+) process, as illustrated in Fig. 1.
, where the operator ĉ†σ(x)/ĉσ(x) creates or destroys an electron with spin σ at position x. From these, one can extract partial atomic charges, which in turn allow characterization of the dissociation of a single SH bond as a homolytic (H3S+ → H2S+ + H) or heterolytic (H3S+ → H2S + H+) process, as illustrated in Fig. 1.
2.1 Algorithm
In this Section, we describe the algorithms used in the present work. Additional methodological details are provided in Appendix A–C.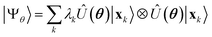 , where Û(θ) is a parameterized unitary, λk are a set of coefficients, and |xk〉 are a set of computational basis states. Observables are written as linear combinations of tensor products
, where Û(θ) is a parameterized unitary, λk are a set of coefficients, and |xk〉 are a set of computational basis states. Observables are written as linear combinations of tensor products 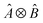 , and their expectation values are expressed (see Appendix B for a derivation) as
, and their expectation values are expressed (see Appendix B for a derivation) as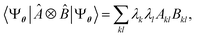 | (2) |
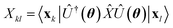 is evaluated as
is evaluated as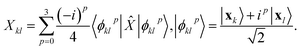 | (3) |
Within EF, one prepares the states |ϕpkl〉 on a quantum processor, measures the matrix elements Xkl for ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) = Â,
= Â,![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) and the expectation values in eqn (2). In this formalism, a qubit represents a spatial orbital rather than a spin-orbital, and thus the number of qubits required for a simulation is reduced by half.
and the expectation values in eqn (2). In this formalism, a qubit represents a spatial orbital rather than a spin-orbital, and thus the number of qubits required for a simulation is reduced by half.
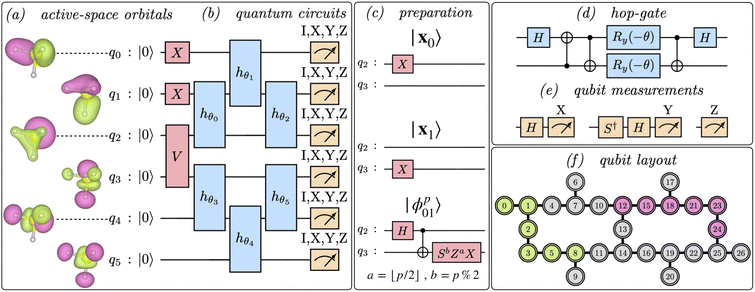
The unitary Û(θ) and states |xk〉 are Ansätze, and parameters θ are optimized variationally along with coefficients λk. Here, we choose xk ∈ {|111000〉, |110100〉} to highlight entanglement across frontier active-space orbitals, and Û(θ) as a product of 6 “hop-gates” (i.e. number-conserving functionally complete 2-qubit gates). The circuits executed in this work are shown in Fig. 2a–e, and additional details are in Appendix B.
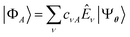 , where the columns of c are solutions of the eigenvalue equation HcA = McAεA. Here, we employ as excitation operators single- and double-electronic excitations, as this choice is natural for electronic systems and compatible with the representation of QSE matrices by eqn (3).
, where the columns of c are solutions of the eigenvalue equation HcA = McAεA. Here, we employ as excitation operators single- and double-electronic excitations, as this choice is natural for electronic systems and compatible with the representation of QSE matrices by eqn (3).
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) and Ŝ2, two important constants of motion used to label excited states and classify transitions, and the density matrices (RDMs)
and Ŝ2, two important constants of motion used to label excited states and classify transitions, and the density matrices (RDMs) 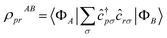 . Transition RDMs ρA0 provide access to the dipole DSF eqn (1), whereas ground- and excited-state RDMs (respectively ρ00 and ρAA) provide access to partial atomic charges.
. Transition RDMs ρA0 provide access to the dipole DSF eqn (1), whereas ground- and excited-state RDMs (respectively ρ00 and ρAA) provide access to partial atomic charges.
2.2 Hardware experiments
Simulations were run on IBM's 27-qubit processor ibm_kolkata based on the Falcon architecture, as shown in Fig. 2f. Segments of best-performing qubits were selected monitoring average readout and cX errors, and IBM's Qiskit and runtime libraries were used to interface with quantum hardware.52 Along with hardware simulations, we performed noiseless and noisy simulations of quantum circuits using the statevector and qasm simulators of Qiskit, and exact diagonalization (full configuration interaction of FCI) calculations using PySCF.53,54 To reduce decoherence effects and systematic errors occurring on quantum hardware, we resorted to a combination of error mitigation techniques, detailed below and further discussed in Appendix C.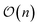 calibration circuits.56 This result holds when: A can be approximated as a tensor product of n matrices of shape 2 × 2 (tensored Ansatz); A is diagonally-dominated, allowing efficient matrix-free solution of the linear system; pnoisy is well-approximated by a vector with sparsity at most
calibration circuits.56 This result holds when: A can be approximated as a tensor product of n matrices of shape 2 × 2 (tensored Ansatz); A is diagonally-dominated, allowing efficient matrix-free solution of the linear system; pnoisy is well-approximated by a vector with sparsity at most 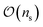 , where ns is the number of accumulated statistical samples (or shots).
, where ns is the number of accumulated statistical samples (or shots).
| Xideal(θ) ≃ Xhw(θ) + Xideal(θ*) − Xhw(θ*). | (4) |
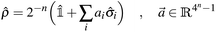 | (5) |
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) is defined so that
is defined so that ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) =
= ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) † and Tr[
† and Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ] = 1, and must be compatible with the condition
] = 1, and must be compatible with the condition ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ≥ 0. In particular, since the purity Tr[
≥ 0. In particular, since the purity Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 2] of a density operator lies60 in the interval [2−n, 1], and Tr[
2] of a density operator lies60 in the interval [2−n, 1], and Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 2] = 2−n(1 + ‖
2] = 2−n(1 + ‖![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ‖2), then ‖
‖2), then ‖![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ‖2 must lie in the interval [0, 2n − 1]. Due to decoherence and artifacts of error mitigation, we may observe Tr[
‖2 must lie in the interval [0, 2n − 1]. Due to decoherence and artifacts of error mitigation, we may observe Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 2] ∉ [2−n,1] despite the target state being pure. When that happens, we scale the Bloch vector so that Tr[
2] ∉ [2−n,1] despite the target state being pure. When that happens, we scale the Bloch vector so that Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 2] = 1. In the remainder of this work raw, readout-error mitigated (only technique a), and fully error-mitigated results (all of the four mitigation techniques in subsections 2.2.1 to 2.2.4) will be labeled raw, roem, and em respectively.
2] = 1. In the remainder of this work raw, readout-error mitigated (only technique a), and fully error-mitigated results (all of the four mitigation techniques in subsections 2.2.1 to 2.2.4) will be labeled raw, roem, and em respectively.
3 Results
3.1 Ground-state simulations
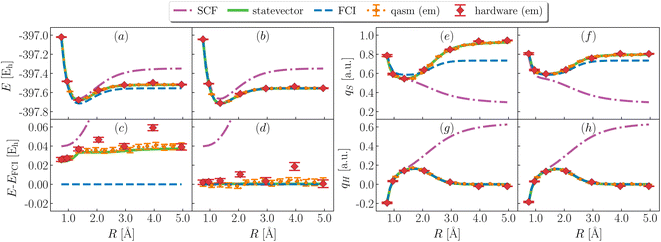
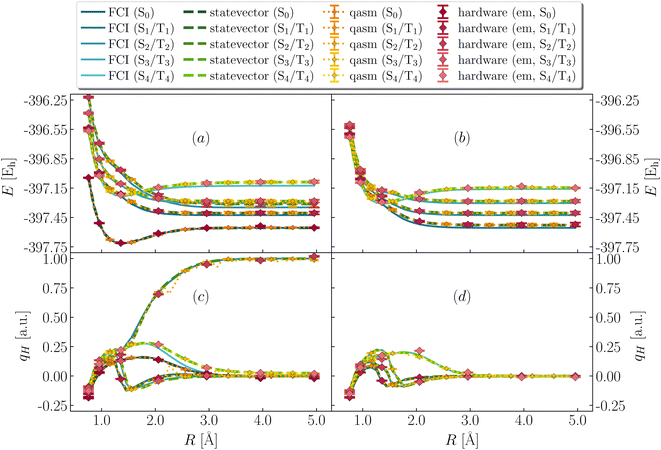
Fig. 3 shows simulation results for the ground state of H3S+. Variational EF simulations (panels a and c) are on average ∼40 mEh above FCI, with a non-parallelity error (defined as npe = maxR|ΔE(R) − 〈ΔE(R)〉| with ΔE(R) = E(R) − EFCI(R)) of 10.2, 11 ± 3, 20 ± 3 mEh and a binding energy (defined as E(Rmax) − minRE(R) of 163, 164 ± 4, 162 ± 4 mEh for statevector, qasm and ibm_kolkata respectively. It should be noted that binding energies are challenging to evaluate on quantum hardware, due to a non-smooth potential energy curve for large R. The combined use of EF and QSE (panels b and d) significantly improves the agreement between variational and FCI energies, and decreases non-parallelity errors to 0.4, 2 ± 6, 6 ± 13 mEh for statevector, qasm and ibm_kolkata respectively. Binding energies decrease slightly, respectively to 159.0, 163 ± 4, 156 ± 5 mEh.Fig. 3 also shows ground-state partial atomic charges. Hartree-Fock (SCF) incorrectly predicts (panels g and h) the charge qH on the departing hydrogen to remain finite as R diverges, i.e. a heterolytic ground-state dissociation path. All other methods predict qH to vanish as R diverges, i.e. a homolytic ground-state dissociation path. These observations are in line with the difference between experimental61 gas-phase ionization potentials of H2S and H being (10.5–13.6) eV = −3.1 eV†.
EF inaccurately approximates the electronic structure of the H2S+ moiety, leading to discrepancies between computed and exact values of qS (panel e). QSE improves agreement of qS with FCI, but quantitatively significant differences remain (∼0.1 a.u., panel f). The qualitative agreement between computed and exact charges is primarily due to methodological approximations, with decoherence on quantum hardware introducing additional deviations in the amount of ∼0.01 a.u. on average.
3.2 Excited-state simulations
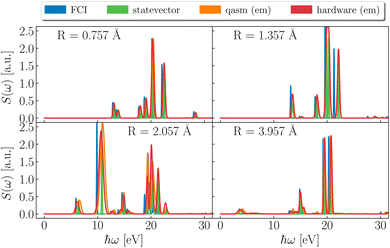
Dipole DSFs are shown in Fig. 4. While positions and strengths of dominant peaks are in qualitative agreement between exact and simulated results, noisy simulations show uncertainties on excitation energies, which translate into broadening and overlapping of peaks. Notwithstanding such limited precision, simulations consistently indicate the absorption of ultraviolet (UV) radiation by H3S+. For all geometries, pronounced peaks are present at ℏω ≃ 20 eV (0.73 Eh or 0.9 nm), in the high-energy end of UV. At R = 0.757, 1.357 Å the spectrum is supported above 13 eV (0.48 Eh or 95 nm). As R further increases, structures appear at lower energies, specifically ℏω ≃ 4–10 eV (0.15–0.37 Eh).To interpret the vertical electronic excitations highlighted by dipole DSFs, in Fig. 5 we show low-lying singlet and triplet excited states (respectively S0, S1⋯S4 and T1⋯T4 in ascending order of energy at large bond-length). Simulations on classical and quantum devices predict qualitatively correct curves, with T1, S0 degenerate for large R and T2, S1 more than 100 mEh above S0 across dissociation, albeit with statistical uncertainties of ∼5 mEh for noisy simulations.
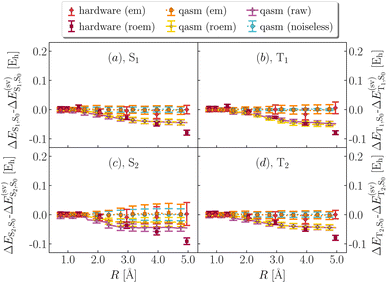
Vertical singlet–singlet and singlet–triplet gaps computed from Fig. 5 are listed in Table 1. Noiseless simulations tend to overestimate gaps by 10 and 20 mEh respectively. Noisy classical and hardware simulations are in line with such trends, but feature statistical uncertainties of 5 mEh respectively. Note also that FCI predicts S1, S2 and T1, T2 to be degenerate, but these degeneracies are lifted in QSE, even with the statevector simulation, because the excitation operators are not symmetry-adapted.
| Gap | FCI | s.v. | qasm | ibm_kolkata |
|---|---|---|---|---|
| a Vertical singlet–singlet and singlet–triplet gaps from FCI, and from QSE with singles and doubles on top of the EF wavefunction using statevector (abbreviated s.v.), qasm, and ibm_kolkata. Gaps are computed at the equilibrium geometry R = 1.357 Å and listed in Hartree units. | ||||
| S1–S0 | 0.484 | 0.493 | 0.494 ± 5 | 0.492 ± 5 |
| S2–S0 | 0.484 | 0.501 | 0.502 ± 6 | 0.499 ± 6 |
| T1–S0 | 0.405 | 0.417 | 0.417 ± 5 | 0.416 ± 5 |
| T2–S0 | 0.405 | 0.428 | 0.429 ± 5 | 0.426 ± 6 |
Fig. 5 also shows partial atomic charges on the departing H as a function of R. Charges exhibit discontinuous behavior around equilibrium geometry. While FCI and noiseless curves are in agreement with each other, noisy and hardware simulations significantly deviate from FCI and noiseless values, indicating the sensitivity of excited-state partial atomic charges to finite measurement error and decoherence. Nevertheless, for large R, all simulations agree that S1, T1 and T2 lead to homolytic dissociation, whereas S2 leads to heterolytic dissociation.
Comparison between Fig. 4 and 5 indicates that absorption of UV light at the equilibrium geometry (1.357 Å) causes transitions to low-lying singlet states S1 and S2 (indeed, the lowest-energy peaks of S(ω) are located at ℏω = ΔES1,S0 and ΔES2,S0), in turn suggesting coexistence of both homolytic and heterolytic pathways in the gas-phase dissociation of H3S+, described within an active space.
4 Conclusions
In this work, we took a step towards delivering physically relevant simulations on near-term quantum devices. By integrating the EF technique for qubit reduction with quantum diagonalization algorithms exemplified by QSE, we computed ground- and excited-state wavefunctions and properties of H3S+. Combining these algorithmic developments with a sequence of state-of-the-art error mitigation techniques, we experimentally realized the proposed algorithmic workflow on a superconducting quantum computer. Note that this is not a direct extension of previous work, but a careful combination and generalization of independent algorithms.By computing dipole spectral functions and excited-state energies and partial atomic charges, we were able to elucidate the mechanism of dissociation of H3S+ upon absorption of UV light.
Our study is among the earliest simulations of excited-state molecular spectra on a quantum processor.35,62–64 Comparison against exact diagonalization indicates that the proposed methodology is capable to deliver accurate results, at least for the active space sizes currently accessible. Notwithstanding this encouraging result, a number of challenges need to be addressed to provide chemically meaningful results, particularly in connection with the photo-acid generating properties of Ph3S+. This goal can be achieved by integrating additional functionalities in the algorithmic workflow considered here.
This study simulates electrons in an active space derived from a minimal basis. While simulations of this kind provide benchmarks and occasions to illustrate algorithmic workflows, useful quantum simulations require accounting for static and dynamical electron correlation in realistic basis sets; on near-term devices, this can be achieved using N-electron valence perturbation theory or otherwise approximate techniques.65–67 Industrially relevant photodissociation processes require describing realistic functional groups such as phenyl, which on near-term devices can be done integrating the algorithms presented here with quasi-complete active space68,69 or fragmentation techniques.70,71 Simulations are carried out in the gas phase, whereas photo-dissociation reactions may occur in a solvent. Solvation effects can be accounted for using implicit or explicit solvation models.72,73 Research into these algorithmic extensions and improvements is underway.
Encouragingly, the algorithmic workflow considered in this work appears useful, in conjunction with near-term quantum architectures and in combination with other algorithms, and serves to demonstrate the usefulness of hybrid quantum-classical simulation techniques in the continuing search for physically relevant simulations.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
G. O. J. and Y.-y. O. conceived, initiated, and supervised the project. M. M. developed the quantum simulation codebase, ran experiments on emulators and quantum hardware, and wrote the initial version of the manuscript. All the authors analyzed computational and experiment results and participated in the composition of the manuscript.Conflicts of interest
There are no conflicts to declare.Appendices
A Additional methodological details
For brevity, the Einstein summation convention is used in most of the equations, while vector expansions, linear combinations of tensor products, and summation over nuclei are explicitly described with the summation symbol.For each geometry, we carried out a restricted closed-shell Hartree-Fock (RHF or SCF) calculation with the quantum chemistry software PySCF at STO-6G level, yielding a set of orthonormal molecular orbitals (MOs) 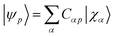 , where |χα〉 are atomic orbitals AOs, and a second-quantization Born–Oppenheimer Hamiltonian of the form
, where |χα〉 are atomic orbitals AOs, and a second-quantization Born–Oppenheimer Hamiltonian of the form
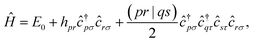 | (6) |
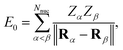 | (7) |
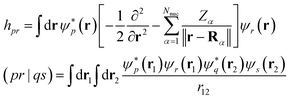 | (8) |
The Born–Oppenheimer Hamiltonian is restricted to an active space spanned by the 6 higher-energy MOs, corresponding to linear combinations of S[3p] and H[1s] orbitals. To this end, we froze the 7 lower-energy MOs with a standard frozen-core procedure,
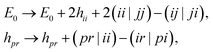 | (9) |
While larger active spaces are necessary for applications of practical interest, we elected to focus on a 6-orbital active space because S is valence-isoelectronic with O, and S is not playing a hypervalent role as, for example, in SO2−4. In Table 2 we show the binding energy, vertical singlet–singlet, and vertical singlet–triplet gaps of H3S+ using CASCI(6e,6o) and CASCI(8e,7o). As seen, results are quantitatively but not qualitatively affected by the extension of the active space. Similarly, both CASCI calculations predict homolytic dissociation along the ground-state potential energy curve.
| Quantity | CASCI(6e,6o) | CASCI(8e,7o) |
|---|---|---|
| a Binding energies (BE) and vertical singlet–singlet, singlet–triplet gaps from CASCI(6e,6o) and CASCI(8e,7o). Gaps are computed at the equilibrium geometry R = 1.357 Å and listed in Hartree units. | ||
| S1–S0 | 0.484 | 0.474 |
| S2–S0 | 0.484 | 0.474 |
| T1–S0 | 0.405 | 0.403 |
| T2–S0 | 0.405 | 0.403 |
| BE | 0.164 | 0.157 |
Another limitation of the present study is the use of a minimal STO-6G basis set. In Table 3 we show the binding energy, vertical singlet–singlet, and vertical singlet–triplet gaps of H3S+ using classical coupled-cluster with singles and doubles (CCSD) and equation-of-motion CCSD (EOM-CCSD) for ground- and excited-state calculations respectively, in a minimal STO-6G and a correlation-consistent cc-pVTZ basis. Gaps and binding energies are significantly affected by dynamical correlation, but qualitative features (ordering and degeneracy of the excited states) are preserved.
| Quantity | STO-6G | cc-pVTZ |
|---|---|---|
| a Binding energies (BE) and vertical singlet–singlet, singlet–triplet gaps from CCSD and EOM-CCSD respectively, in a STO-6G and a cc-pVTZ basis set, with 5 frozen orbitals. Gaps are computed at the equilibrium geometry R = 1.357 Å and listed in Hartree units. | ||
| S1–S0 | 0.475 | 0.359 |
| S2–S0 | 0.475 | 0.359 |
| T1–S0 | 0.403 | 0.302 |
| T2–S0 | 0.403 | 0.302 |
| BE | 0.156 | 0.178 |
A.2.1 The Hamiltonian. In this work, we chose to partition molecular spin-orbitals into spin-up and spin-down. A Cholesky decomposition74–77 of the electron-repulsion integral, (pr|qs) = LγprLγqs, and a reordering of the creation and destruction operators,
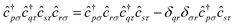 | (10) |
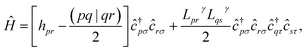 | (11) |
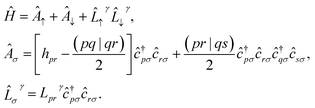 | (12) |
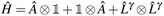 | (13) |
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) γ are the qubit representations of Â↑/Â↓ and
γ are the qubit representations of Â↑/Â↓ and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) γ↑/
γ↑/![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) γ↓ restricted to the first/last m qubits respectively.
γ↓ restricted to the first/last m qubits respectively.
A.2.2 Spin-summed one-body operators. A simpler formula holds for generic one-body operators,
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) = xprĉ†pσĉrσ = = xprĉ†pσĉrσ = ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) ↑ + ↑ + ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) ↓. ↓. | (14) |
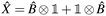 | (15) |
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) is the qubit representation of
is the qubit representation of ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) ↑/
↑/![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) ↓ restricted to the first/last m qubits. eqn (15) holds for particle number xpr = δpr, the spin-summed one-body density matrix, xpr = δpp0δrr0 for element (p0, r0), and the charge-gauge electronic dipole operator,
↓ restricted to the first/last m qubits. eqn (15) holds for particle number xpr = δpr, the spin-summed one-body density matrix, xpr = δpp0δrr0 for element (p0, r0), and the charge-gauge electronic dipole operator,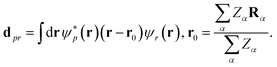 | (16) |
A.2.3 Total spin. The total spin operator is
| Ŝ2 = Ŝ−Ŝ+ + Ŝz(Ŝz + 1) | (17) |
Ŝ2 = c†p↓ĉp↑ĉ†q↑ĉq↓ = ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ↓ − ĉ†p↑ĉq↑ĉ†p↓ĉq↓ ↓ − ĉ†p↑ĉq↑ĉ†p↓ĉq↓ | (18) |
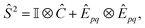 | (19) |
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ↓ restricted to the last m qubits, and Êpq is the qubit representation of ĉ†p↑ĉq↑/ĉ†p↓ĉq↓ restricted to the first/last m qubits.
↓ restricted to the last m qubits, and Êpq is the qubit representation of ĉ†p↑ĉq↑/ĉ†p↓ĉq↓ restricted to the first/last m qubits.
A.2.4 QSE operators. In this work, we chose the QSE excitation operators to be single- and double-electron excitations, respectively
| Êai,σ = ĉ†aσĉiσ,Êaibj,στ = ĉ†aσĉ†bτĉjτĉiσ. | (20) |
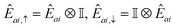 | (21) |
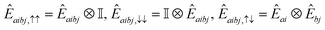 | (22) |
Given two or more operators ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) , Ŷ of the form
, Ŷ of the form 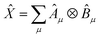 and
and 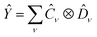 , i.e. compatible with eqn (2), their product can be written as
, i.e. compatible with eqn (2), their product can be written as
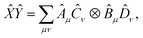 | (23) |
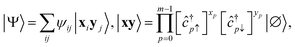 | (24) |
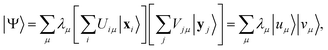 | (25) |
Thus, the EF Ansatz can reproduce any fermionic wavefunction, provided that (i) all the singular values λμ are retained in the representation eqn (25) and (ii) quantum circuits Û and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) such that |uμ〉 = Û|xμ〉, |vμ〉 =
such that |uμ〉 = Û|xμ〉, |vμ〉 = ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) |yμ〉 are available.
|yμ〉 are available.
In practice, however, the non-zero singular values may be up to 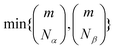 , which increases combinatorially with active space size, requiring a truncation. Furthermore, while Û and
, which increases combinatorially with active space size, requiring a truncation. Furthermore, while Û and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) can be represented as a product of hop-gates with all-to-all connectivity,36 implementing such circuits on near-term devices is technically challenging, requiring to use a heuristic Ansatz.
can be represented as a product of hop-gates with all-to-all connectivity,36 implementing such circuits on near-term devices is technically challenging, requiring to use a heuristic Ansatz.
Determining the expressive power of the EF Ansatz in the presence of a singular-value truncation and of a heuristic Ansatz for the quantum circuits Û and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is an open problem. However, an insightful limiting case can be immediately identified: when the circuits
is an open problem. However, an insightful limiting case can be immediately identified: when the circuits
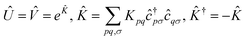 | (26) |
B Details of simulations
The variational optimization of coefficients λk is performed as follows: it is observed that the energy is a second-degree polynomial in the variables λ,
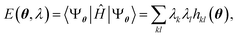 | (27) |
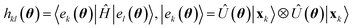 | (28) |
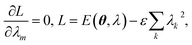 | (29) |
B.1.1 Ansatz design. The Ansatz in Fig. 2 was chosen to attain a balance between chemical realism and adequacy for contemporary quantum hardware. The computational basis states xk are chosen to highlight entanglement between frontier molecular orbitals, and to ensure that preparation unitaries require linear qubit connectivity only, as per Fig. 2c. Similar considerations are made for the subsequent product of hop-gates. The hop-gate portion of the circuit consists of two blocks of gates, each acting on a sub-group of 3 qubits. Such a condition ensures that one of the reference states is preserved by the action of the EF circuit, Û(θ)|x0〉 = |x0〉, so that h00(θ) in eqn (28) takes the form
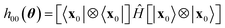 | (30) |
B.1.2 HOMO–LUMO orbital optimization. In this study, MOs were not used as active-space basis functions. Instead, we carried out an orbital optimization81,82 limited to the HOMO–LUMO subspace, i.e.
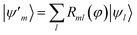 where Rml(φ) acts as a SU(2) rotation on the HOMO and LUMO orbitals. The angle φ was optimized along with other variational parameters in a preliminary set of ground-state EF calculations (see Section B.1), then the unitary R was used to transform the integrals in the Born–Oppenheimer Hamiltonian with a standard transformation.
where Rml(φ) acts as a SU(2) rotation on the HOMO and LUMO orbitals. The angle φ was optimized along with other variational parameters in a preliminary set of ground-state EF calculations (see Section B.1), then the unitary R was used to transform the integrals in the Born–Oppenheimer Hamiltonian with a standard transformation.
B.1.3 Evaluation of observables. Once the optimal hop-gate angles and orbital-optimization angles were computed, quantum state tomography was executed on the EF circuits in Fig. 2, for the purpose of characterizing decoherence effects, enabling purification error mitigation, and avoiding repeated measurements. More specifically, n = 6 qubits were measured in the 3n eigenbases of X, Y, and Z Pauli operators using the circuit-runner program from the runtime library of Qiskit, and the 4n entries of the Bloch vector were computed, along with their statistical uncertainties for noisy simulators, by standard post-processing. Post-selection was conducted on the probability distributions of the Pauli measurements. Readout error mitigation and Clifford error mitigation were conducted on the individual entries of the Bloch vector, and purification on the resulting Bloch vector.
Expectation values of quantities like the energy were computed from the entries of the Bloch vector through standard error propagation. For example, given an operator
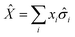 | (31) |
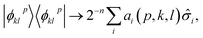 | (32) |
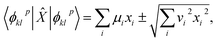 | (33) |
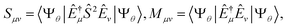 | (34) |
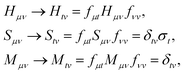 | (35) |
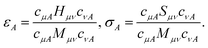 | (36) |
B.2.1 Statistical uncertainties. Determining eigenvalues and eigenvectors of noisy matrices is a notoriously delicate procedure.83,84 Since eigenvalues of a matrix where elements are normally distributed are not normally distributed, statistical uncertainties are difficult to estimate and are not simply associated with variances of Gaussian distributions.
In this work, we resorted to a simple numerical protocol to assign indicative statistical uncertainties to measured quantities: (i) we solve the eigenvalue equation Sf = Mfσ and Hg = Mgε using the mean values of the matrices S and M, without assigning statistical uncertainties to solutions c = fg. In this work, we obtained non-singular metric matrices, det(M) ≫ 0, so that no eigenvalue truncation was necessary. (ii) we propagate statistical uncertainties from the matrix elements Hμν, Sμν, Mμν to the numerators and denominators of eqn (36), and to the ratio between these quantities, using standard error propagation. (iii) An identical procedure was used to assign statistical uncertainties to particle numbers, RDMs, and derived quantities. Ground- and excited-state RDMs were rescaled so that their trace was statistically compatible with total particle number.
B.2.2 Evaluation of partial atomic charges. Upon computing a ground- or excited-state RDM (the former with EF, the latter with either EF or QSE), the RDM was transformed from the active-space to the MO basis with a simple unitary transformation ρ → R(φ)ρR†(φ), then an extended RDM was generated, by padding the MO-basis RDM with contributions from frozen MOs,
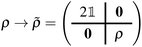 | (37) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) → C
→ C![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) C−1. Partial charges were then computed with a Mulliken population analysis based on meta-Lowdin atomic orbitals as implemented in the PySCF package. Statistical uncertainties were assigned to partial atomic charges by drawing n = 100 samples of the RDM
C−1. Partial charges were then computed with a Mulliken population analysis based on meta-Lowdin atomic orbitals as implemented in the PySCF package. Statistical uncertainties were assigned to partial atomic charges by drawing n = 100 samples of the RDM ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) in the AO basis, computing partial atomic charges for each sample, and averaging results with standard statistical operations.
in the AO basis, computing partial atomic charges for each sample, and averaging results with standard statistical operations.
C Details of hardware simulations
Hardware simulations were carried out on ibm_kolkata. Jobs submitted on the hardware consisted of 150 circuits and ns = 100, 000 shots each. We adapted the circuit-runner program from the runtime library of Qiskit. One of the unique options for the circuit-runner program is the ability to correct for measurement errors (i.e. the roem technique) automatically in the cloud.C.1 Effect of error mitigation
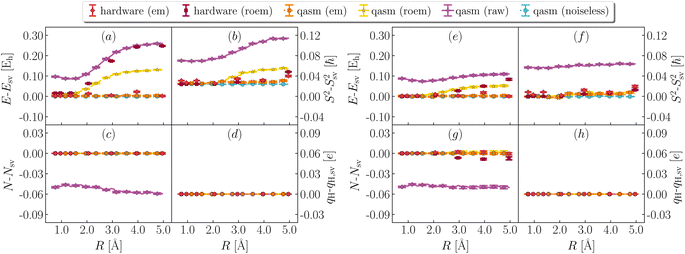
In Fig. 6 and 7, we illustrate the impact of various error mitigation techniques on the result of this work. In Fig. 6a and e we focus on ground-state energies, also shown in Fig. 3 of the main text. Raw/roem noisy simulations on qasm and roem hardware simulations differ by hundreds of mEh from noiseless results. Comparison between qasm (roem) and ibm_kolkata (roem) results indicates that noise models underestimate the impact of decoherence on observable properties, and comparison between panels (a) and (e) shows that QSE errors are less pronounced than EF errors, on average.In Fig. 6b and f we focus on total spins, and observe that decoherence causes a form of singlet–triplet spin contamination, greatly reduced by error mitigation. In Fig. 6c and g we focus on particle number. Owing to post-selection, this quantity is essentially noise-free even at the level of roem data. In Fig. 6d and h we show instead partial charges on the departing H. Results indicate that partial charges. While this level of accuracy is satisfactory for qualitative applications (e.g. determining the distribution of electric charge along dissociation), higher accuracy is needed for quantitative tasks, such as determination of electrostatic properties. Fig. 7 shows the effect of error mitigation technique on excited-state energies. Decoherence tends to underestimate singlet–singlet and singlet–triplet gaps, especially for large R. Error mitigation restores agreement with noiseless results, but excited-state energies and derived gaps feature large statistical uncertainties, as documented in Table 1 of the main text. The reduction of such statistical uncertainties is an important direction of future research.
Acknowledgements
We thank Agata M. Brańczyk and Iskandar Sitdikov for generous help and guidance in understanding and using a computational package implementing the entanglement forging method. We acknowledge Riddhi Gupta for valuable interactions regarding the runtime library. We thank Joseph Latone for access to the Clifford cluster at IBM Almaden Research Center, where classical computations were carried out. We thank Andrew Eddins, Hajime Nakamura, Yukio Kawashima, Paul Nation, Zhendong Li, and Barbara Jones for helpful feedback about the manuscript.Notes and references
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristensen, J. Olsen and K. Ruud, Chem. Rev., 2012, 112, 543–631 CrossRef CAS PubMed.
- R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6648–6653 CrossRef CAS PubMed.
- B. D. Gates, Q. Xu, M. Stewart, D. Ryan, C. G. Willson and G. M. Whitesides, Chem. Rev., 2005, 105, 1171–1196 CrossRef CAS PubMed.
- A. S. Gangnaik, Y. M. Georgiev and J. D. Holmes, Chem. Mat., 2017, 29, 1898–1917 CrossRef CAS.
- O. Nalamasu, M. Cheng, J. M. Kometani, S. Vaidya, E. Reichmanis and L. F. Thompson, Advances in Resist Technology and Processing VII, 1990, pp. 32–48 Search PubMed.
- R. Fallica and Y. Ekinci, J. Mat. Chem. C, 2018, 6, 7267–7273 RSC.
- C. J. Martin, G. Rapenne, T. Nakashima and T. Kawai, J. Photochem. Photobiol., C, 2018, 34, 41–51 CrossRef CAS.
- K. Sambath, Z. Wan, Q. Wang, H. Chen and Y. Zhang, Org. Lett., 2020, 22, 1208–1212 CrossRef CAS PubMed.
- N. Ohmori, Y. Nakazono, M. Hata, T. Hoshino and M. Tsuda, J. Phys. Chem. B, 1998, 102, 927–930 CrossRef CAS.
- J. L. Dektar and N. P. Hacker, J. Org. Chem., 1988, 53, 1833–1835 CrossRef CAS.
- J. L. Dektar and N. P. Hacker, J. Am. Chem. Soc., 1990, 112, 6004–6015 CrossRef CAS.
- N. Klikovits, P. Knaack, D. Bomze, I. Krossing and R. Liska, Polym. Chem., 2017, 8, 4414–4421 RSC.
- M. Jin, H. Hong, J. Xie, J.-P. Malval, A. Spangenberg, O. Soppera, D. Wan, H. Pu, D.-L. Versace and T. Leclerc, et al. , Polym. Chem., 2014, 5, 4747–4755 RSC.
- W. Zhou, S. M. Kuebler, D. Carrig, J. W. Perry and S. R. Marder, J. Am. Chem. Soc., 2002, 124, 1897–1901 CrossRef CAS PubMed.
- J. W. Knapczyk and W. E. McEwen, J. Am. Chem. Soc., 1969, 91, 145–150 CrossRef CAS.
- J. Crivello and J. Lam, J. Polym. Sci., Polym. Chem. Ed., 1979, 17, 1059–1065 CrossRef CAS.
- S. P. Pappas, B. C. Pappas, L. R. Gatechair, J. H. Jilek and W. Schnabel, Polym. Photochem., 1984, 5, 1–22 CrossRef CAS.
- R. Davidson and J. Goodin, Eur. Polym. J., 1982, 18, 589–595 CrossRef CAS.
- J. P. F. LeBlanc, et al. , Phys. Rev. X, 2015, 5, 041041 Search PubMed.
- B.-X. Zheng, C.-M. Chung, P. Corboz, G. Ehlers, M.-P. Qin, R. M. Noack, H. Shi, S. R. White, S. Zhang and G. K.-L. Chan, Science, 2017, 358, 1155–1160 CrossRef CAS PubMed.
- M. Motta, D. M. Ceperley, G. K.-L. Chan, J. A. Gomez, E. Gull, S. Guo, C. A. Jiménez-Hoyos, T. N. Lan, J. Li, F. Ma, A. J. Millis, N. V. Prokof'ev, U. Ray, G. E. Scuseria, S. Sorella, E. M. Stoudenmire, Q. Sun, I. S. Tupitsyn, S. R. White, D. Zgid and S. Zhang, Phys. Rev. X, 2017, 7, 031059 Search PubMed.
- K. T. Williams, Y. Yao, J. Li, L. Chen, H. Shi, M. Motta, C. Niu, U. Ray, S. Guo and R. J. Anderson, et al. , Phys. Rev. X, 2020, 10, 011041 CAS.
- I. M. Georgescu, S. Ashhab and F. Nori, Rev. Mod. Phys., 2014, 86, 153 CrossRef.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre and N. P. Sawaya, et al. , Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed.
- B. Bauer, S. Bravyi, M. Motta and G. Kin-Lic Chan, Chem. Rev., 2020, 120, 12685–12717 CrossRef CAS PubMed.
- M. Motta and J. E. Rice, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2021, e1580 Search PubMed.
- S. Lloyd, Science, 1996, 273, 1073–1078 CrossRef CAS PubMed.
- J. M. Martyn, Z. M. Rossi, A. K. Tan and I. L. Chuang, PRX Quantum, 2021, 2, 040203 CrossRef.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. de Jong, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Phys. Rev. X, 2020, 10, 011004 CAS.
- J. Cohn, M. Motta and R. M. Parrish, PRX Quantum, 2021, 2, 040352 CrossRef.
- N. Yoshioka, H. Hakoshima, Y. Matsuzaki, Y. Tokunaga, Y. Suzuki and S. Endo, Phys. Rev. Lett., 2022, 129, 020502 CrossRef CAS PubMed.
- E. N. Epperly, L. Lin and Y. Nakatsukasa, A theory of quantum subspace diagonalization, arXiv, 2021, preprint, arXiv:2110.07492, DOI:10.48550/arXiv.2110.07492.
- U. Baek, D. Hait, J. Shee, O. Leimkuhler, W. J. Huggins, T. F. Stetina, M. Head-Gordon and K. B. WhaleySay NO to optimization: a non-orthogonal quantum eigensolver, arXiv, 2022, preprint, arXiv:2205.09039, DOI:10.48550/arXiv.2205.09039.
- J. I. Colless, V. V. Ramasesh, D. Dahlen, M. S. Blok, M. E. Kimchi-Schwartz, J. R. McClean, J. Carter, W. A. de Jong and I. Siddiqi, Phys. Rev. X, 2018, 8, 011021 CAS.
- A. Eddins, M. Motta, T. P. Gujarati, S. Bravyi, A. Mezzacapo, C. Hadfield and S. Sheldon, PRX Quantum, 2022, 3, 010309 CrossRef.
- S. E. Smart and D. A. Mazziotti, Phys. Rev. Lett., 2021, 126, 070504 CrossRef CAS PubMed.
- M. Lax, J. Chem. Phys., 1952, 20, 1752–1760 CrossRef CAS.
- E. J. Heller, J. Chem. Phys., 1978, 68, 3891–3896 CrossRef CAS.
- K. C. Kulander and E. J. Heller, J. Chem. Phys., 1978, 69, 2439–2449 CrossRef CAS.
- B. R. Johnson and J. L. Kinsey, J. Chem. Phys., 1989, 91, 7638–7653 CrossRef CAS.
- R. Gordon, J. Chem. Phys., 1965, 43, 1307–1312 CrossRef CAS.
- C. Boulet and D. Robert, J. Chem. Phys., 1982, 77, 4288–4299 CrossRef CAS.
- A. A. Clerk, M. H. Devoret, S. M. Girvin, F. Marquardt and R. J. Schoelkopf, Rev. Mod. Phys., 2010, 82, 1155 CrossRef.
- V. Vitale, J. Dziedzic, S. M.-M. Dubois, H. Fangohr and C.-K. Skylaris, J. Chem. Theory Comput., 2015, 11, 3321–3332 CrossRef CAS PubMed.
- D. R. Nascimento and A. E. DePrince III, J. Chem. Theory Comput., 2016, 12, 5834–5840 CrossRef CAS PubMed.
- J. J. Goings, P. J. Lestrange and X. Li, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, e1341 Search PubMed.
- X. Li, N. Govind, C. Isborn, A. E. DePrince III and K. Lopata, Chem. Rev., 2020, 120, 9951–9993 CrossRef CAS PubMed.
- S. Endo, I. Kurata and Y. O. Nakagawa, Phys. Rev. Res., 2020, 2, 033281 CrossRef CAS.
- S. Bravyi, G. Smith and J. A. Smolin, Phys. Rev. X, 2016, 6, 021043 Search PubMed.
- P. Huembeli, G. Carleo and A. Mezzacapo, Entanglement forging with generative neural network models, arXiv, 2022, preprint, arXiv:2205.00933, DOI:10.48550/arXiv.2205.00933.
- G. Aleksandrowicz, T. Alexander, P. Barkoutsos, L. Bello, Y. Ben-Haim, D. Bucher, F. Cabrera-Hernández, J. Carballo-Franquis, A. Chen, C. Chen, et al., Qiskit: An open-source framework for quantum computing, 2019, https://zenodo.org/record/2562111#.XhA8qi2ZPyI Search PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova and S. Sharma, et al. , Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- Q. Sun, et al. , J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- F. B. Maciejewski, Z. Zimborás and M. Oszmaniec, Quantum, 2020, 4, 257 CrossRef.
- P. D. Nation, H. Kang, N. Sundaresan and J. M. Gambetta, PRX Quantum, 2021, 2, 040326 CrossRef.
- W. J. Huggins, J. R. McClean, N. C. Rubin, Z. Jiang, N. Wiebe, K. B. Whaley and R. Babbush, Npj Quantum Inf., 2021, 7, 1–9 CrossRef.
- D. Gottesman, The Heisenberg representation of quantum computers, arXiv, 1998, preprint, arXiv:quant-ph/9807006, DOI:10.48550/arXiv.quant-ph/9807006.
- P. Czarnik, A. Arrasmith, P. J. Coles and L. Cincio, Quantum, 2021, 5, 592 CrossRef.
- M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information, Cambridge University Press, 2010 Search PubMed.
- R. D. Johnson III, et al., NIST 101. Computational chemistry comparison and benchmark database, 1999, https://cccbdb.nist.gov Search PubMed.
- Q. Gao, G. O. Jones, M. Motta, M. Sugawara, H. C. Watanabe, T. Kobayashi, E. Watanabe, Y.-y. Ohnishi, H. Nakamura and N. Yamamoto, npj Comput. Mater., 2021, 7, 1–9 CrossRef.
- K. Huang, X. Cai, H. Li, Z.-Y. Ge, R. Hou, H. Li, T. Liu, Y. Shi, C. Chen and D. Zheng, et al. , J. Phys. Chem. Lett., 2022, 13, 9114–9121 CrossRef CAS PubMed.
- I. Khan, M. Tudorovskaya, J. Kirsopp, D. M. Ramo, P. Warrier, D. Papanastasiou and R. Singh, Chemically aware unitary coupled cluster with ab initio calculations on system model H1: a refrigerant chemicals application, arXiv, 2022, preprint, arXiv:2210.14834, DOI:10.48550/arXiv.2210.14834.
- A. Tammaro, D. E. Galli, J. E. Rice and M. Motta, J. Phys. Chem. A, 2023, 127, 817–827 CrossRef CAS PubMed.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Phys. Rev. X, 2020, 10, 011004 CAS.
- J.-N. Boyn, A. O. Lykhin, S. E. Smart, L. Gagliardi and D. A. Mazziotti, J. Chem. Phys., 2021, 155, 244106 CrossRef CAS PubMed.
- H. Nakano and K. Hirao, Chem. Phys. Lett., 2000, 317, 90–96 CrossRef CAS.
- H. Nakano, J. Nakatani and K. Hirao, J. Chem. Phys., 2001, 114, 1133–1141 CrossRef CAS.
- Y. Kawashima, E. Lloyd, M. P. Coons, Y. Nam, S. Matsuura, A. J. Garza, S. Johri, L. Huntington, V. Senicourt and A. O. Maksymov, et al. , Commun. Phys., 2021, 4, 1–9 CrossRef.
- H. Ma, M. Govoni and G. Galli, npj Comput. Mater., 2020, 6, 1–8 CrossRef.
- H.-P. Cheng, E. Deumens, J. K. Freericks, C. Li and B. A. Sanders, Front. Chem., 2020, 8, 587143 CrossRef CAS PubMed.
- D. Castaldo, S. Jahangiri, A. Delgado and S. Corni, Quantum simulation of molecules in solution, arXiv, 2021, preprint, arXiv:2111.13458, DOI:10.48550/arXiv.2111.13458.
- N. H. F. Beebe and J. Linderberg, Int. J. Quantum Chem., 1977, 12, 683–705 CrossRef CAS.
- F. Aquilante, T. B. Pedersen and R. Lindh, J. Chem. Phys., 2007, 126, 194106 CrossRef PubMed.
- M. Motta and S. Zhang, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, e1364 Search PubMed.
- M. Motta, J. Shee, S. Zhang and G. K.-L. Chan, J. Chem. Theory Comput., 2019, 15, 3510–3521 CrossRef CAS PubMed.
- L. Bello, A. M. Brańczyk, S. Bravyi, A. Eddins, J. Gacon, T. P. Gujarati, I. Hamamura, T. Imamichi, C. Johnson, I. Liepuoniute, M. Motta, M. Rossmannek, T. L. Scholten, I. Sitdikov and S. Woerner, Entanglement forging module, https://github.com/qiskit-community/prototype-entanglement-forging, 2021 Search PubMed.
- C. Zhu, R. H. Byrd, P. Lu and J. Nocedal, ACM Trans. Math. Softw., 1997, 23, 550–560 CrossRef.
- J. L. Morales and J. Nocedal, ACM Trans. Math. Softw., 2011, 38, 1–4 CrossRef.
- W. Mizukami, K. Mitarai, Y. O. Nakagawa, T. Yamamoto, T. Yan and Y.-y. Ohnishi, Phys. Rev. Res., 2020, 2, 033421 CrossRef CAS.
- I. O. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, J. Chem. Phys., 2020, 152, 124107 CrossRef CAS PubMed.
- J. Lee, F. D. Malone, M. A. Morales and D. R. Reichman, J. Chem. Theory Comput., 2021, 17, 3372–3387 CrossRef CAS PubMed.
- N. S. Blunt, A. Alavi and G. H. Booth, Phys. Rev. B, 2018, 98, 085118 CrossRef CAS.
Footnote |
| † Since E(H2S+ + H) − E(H2S + H+) = [E(H2S+) − E(H2S)] + [E(H) − E(H+)] = IP(H2S) – IP(H), the inequality IP(H2S) − IP(H) < 0 implies E(H2S+ + H) < E(H2S + H+). |
| This journal is © The Royal Society of Chemistry 2023 |