Open Access Article
Open Access ArticleExperimental assignment of long-range magnetic communication through Pd & Pt metallophilic contacts†
Emil M. H.
Larsen‡
 a,
Niels A.
Bonde‡
ab,
Høgni
Weihe
a,
Jacques
Ollivier
b,
Tom
Vosch
a,
Niels A.
Bonde‡
ab,
Høgni
Weihe
a,
Jacques
Ollivier
b,
Tom
Vosch
 a,
Thomas
Lohmiller
a,
Thomas
Lohmiller
 cd,
Karsten
Holldack
f,
Alexander
Schnegg
de,
Mauro
Perfetti
cd,
Karsten
Holldack
f,
Alexander
Schnegg
de,
Mauro
Perfetti
 g and
Jesper
Bendix
g and
Jesper
Bendix
 *a
*a
aDepartment of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark. E-mail: Jesper.bendix@chem.ku.dk
bInstitut Laue-Langevin, 71 avenue des Martyrs, CS 20156, 38042 Grenoble Cedex 9, France
cHumboldt-Universität zu Berlin, Institut für Chemie, Brook-Taylor-Str. 2, 12489 Berlin, Germany
dEPR4 Energy Joint Lab, Department Spins in Energy Conversion and Quantum Information Science, Helmholtz Zentrum Berlin für Materialien und Energie GmbH, Albert-Einstein-Straße 15, 12489 Berlin, Germany
eMax Planck Institute for Chemical Energy Conversion, Stiftstrasse 34-36, D-45470 Mülheim an der Ruhr, Germany
fDepartment of Optics and Beamlines, Helmholtz Zentrum Berlin für Materialien und Energie GmbH, Albert-Einstein-Straße 15, 12489 Berlin, Germany
gDepartment of Chemistry “U. Schiff”, University of Florence, Via della Lastruccia 3-13, Sesto Fiorentino, 50019, Italy
First published on 22nd November 2022
Abstract
Record-breaking magnetic exchange interactions have previously been reported for 3d-metal dimers of the form [M(Pt(SAc)4)(pyNO2)]2 (M = Ni or Co) that are linked in the solid state via metallophilic Pt⋯Pt bridges. This contrasts the terminally capped monomers [M(Pt(SAc)4)(py)2], for which neither metallophilic bridges nor magnetic exchange interactions are found. Computational modeling has shown that the magnetic exchange interaction is facilitated by the pseudo-closed shell d8⋯d8 metallophilic interaction between the filled Pt2+ 5dz2 orbitals. We present here inelastic neutron scattering experiments on these complexes, wherein the dimers present an oscillatory momentum-transfer-dependence of the magnetic transitions. This allows for the unequivocal experimental assignment of the distance between the coupled ions, which matches exactly the coupling pathway via the metallophilic bridges. Furthermore, we have synthesized and magnetically characterized the isostructural palladium-analogues. The magnetic coupling across the Pd⋯Pd bridge is found through SQUID-magnetometry and FD-FT THz-EPR spectroscopy to be much weaker than via the Pt⋯Pt bridge. The weaker coupling is traced to the larger radial extent of the 5dz2 orbitals compared to that of the 4dz2 orbitals. The existence of a palladium metallophilic interaction is evaluated computationally from potential surface cuts along the metal stretching direction. Similar behavior is found for the Pd⋯Pd and Pt⋯Pt-systems with clear minima along this coordinate and provide estimates for the force constant for this distortion. The estimated M⋯M stretching frequencies are found to match experimental observed, polarized bands in single-crystal Raman spectra close to 45 cm−1. This substantiates the existence of energetically relevant Pd⋯Pd metallophilic interactions. The unique properties of both Pt2+ and Pd2+ constitutes an orthogonal reactivity, which can be utilized for steering both the direction and strength of magnetic interactions.
1 Introduction
Structure–property relations are the cornerstone of the development of molecule-based magnetic systems. This is true for both fundamental science as well as for application-directed research towards quantum computing and spintronics.1–5 However, controlling the molecular structure and the solid state packing of coordination compounds remains a difficult and yet unsolved challenge.6–10 This can be considered a result of the much narrower range of orthogonal reaction pathways in coordination chemistry compared to the vast range of selective, orthogonal reactions in the toolbox of organic synthetic chemistry. The Pearson HSAB principle is by far the most well-established example of orthogonal reactivities in coordination chemistry, but also very specific metallophilic interactions may be considered orthogonal to competing reactivities and hence a way of tailoring products. The ideal ligand in molecular magnetism provides not only structural control but also opportunities for strong and tunable magnetic exchange coupling pathways and ideally a second coordination sphere amenable for modular buildup of polynuclear assemblies or for deposition on surfaces. A recently introduced class of metalloligands [M′(SOCR)4]2− (M′ = Pt2+/Pd2+, SOCR = thiocarboxylate) has been found to meet these criteria in a way no other ligand has. In these metalloligands, the soft sulfur of the thiocarboxylate group coordinates to the soft Pt2+/Pd2+ ion, leaving the hard oxygen open for coordination towards another ion. They have been shown to act as tetradentate chelating ligands toward a range of hard metal ions (see scheme in Fig. 1). For nearly a decade, the Doerrer group has been working on developing the science of heterobimetalic lantern complexes incorporating the Pt-metalloligands and a variable hard metal ion of group two and first-row transition metals.11–19 In parallel, the coordination chemistry of both the Pt- and Pd-metalloligands with the lanthanide elements has been developed by us20–24 and the group of Yamashita.25–29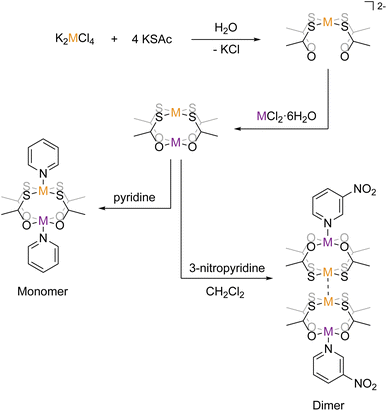 | ||
| Fig. 1 Schematization of the synthetic pathways to the monomeric and dimeric structures. Orange metal = Pd or Pt and purple metal = Co or Ni. | ||
In the transition metal chemistry of the Pt-ligands, the complexes are formed by the bridging action of the four thiocarboxylate linking the soft Pt2+ ion with the hard metal ion. An apical ligand may coordinate either metal termini, thereby completing the coordination environment (see scheme in Fig. 1). Mono-dentate apical ligands may be chosen such that they bind to either the Pt2+ ion, the hard metal ion, or both. In the cases where the apical ligand binds only to the hard metal ion, the complexes often form dimeric structures in the crystalline phase. The dimerisation is caused by a metallophilic interaction, where the Pt2+ ions of two lantern complexes interact with one another, forming a weak “bond”. It was found by the Doerrer group for complexes of Co2+ and Ni2+ that pyridine (py) coordinates both the hard and soft metal ions, thereby forming monomeric [M(Pt(SAc)4)(py)2] structures, but 3-nitropyridine (pyNO2) coordinates only the hard metal ion, thereby forming dimeric [M(Pt(SAc)4)(pyNO2)]2 structures. The monomeric complexes of Co2+ and Ni2+ (abbr. {CoPt} and {NiPt}) and their dimeric congeners (abbr. {CoPt}2 and {NiPt}2) provide an unique opportunity to investigate the ability of the metallophilic bond to direct the formation of dinuclear assemblies and to mediate a magnetic exchange interaction between the paramagnetic ions. In order to probe the magnetic exchange via metallophilic bridges we synthesize and determine the properties of both monomeric and dimeric palladium analogues of the above-mentioned platinum systems.
For {CoPt}2 and {NiPt}2, a surprisingly strong magnetic exchange interaction has been reported to occur over distances of more than 8.5 Å. In the early days of molecular magnetism, Coffman and Buettner30 proposed an upper limit function for an antiferromagnetic exchange interaction (J > 0, ĤHDvV = JŜ1·Ŝ2 formalism), which would limit interactions over 8.5 Å to a maximum of 2.5 cm−1. {NiPt}2 breaks this limit by one order of magnitude. To verify the strength of the exchange interaction and that the coupling pathway is indeed via metallophilic Pt⋯Pt bridges, inelastic neutron scattering (INS) was employed. It is well-known that INS is capable of investigating both the strength and pathway of magnetic exchange interactions. This is most commonly used for extended systems, but it also holds for molecular magnetic materials. This was first illustrated by Furrer and Güdel for exchange-coupled dimers using powder-averaged INS. They observed that the magnetic transitions show a momentum-transfer-dependence that decays with the magnetic formfactors of the coupled ions, but does so in an oscillatory manner. The rate of oscillation was shown to be directly determined by the distance between the coupled ions. This has been coined an ‘interference effect’, because of its connection with the interference of scattered waves from e.g. a double slit. The momentum-transfer-dependence of magnetic transitions thus gives a fingerprint of the exchange pathway, which can be used to unravel complex molecular magnetic materials.31,32 A similar oscillatory momentum-transfer-dependence is observed for {CoPt}2 and {NiPt}2, fully consistent with the distance between paramagnetic ions across the metallophilic bond and corroborated by our simulations of the INS. We analyze the strength of the magnetic coupling in Pd⋯Pd versus Pt⋯Pt dimerized systems by magnetometry and THz spectroscopy and demonstrate a drastic difference. Therefrom, we go on to establish that this difference does not imply that the Pd⋯Pd metallophilic interactions are correspondingly weaker than those in the platinum-bridged systems. Rather, they are energetically similar and addressable by vibrational spectroscopy.
2 Experimental
2.1 Synthesis
All chemicals were purchased commercially and were used without further purification. Elemental analysis was performed using a FlashEA 1112 instrument. For simplicity, the complexes will be abbreviated with the metals and denoted as either a monomeric or dimeric structure. So, [Ni(Pt(SAc)4)(pyNO2)]2 will be {NiPt}2 and the corresponding monomer {NiPt}. The complexes {CoPt}2, {CoPt} and {NiPt} were synthesized with modified published procedures. Detailed synthetic work for the remaining complexes can be found in ESI.†2.2 Magnetic measurements
Magnetic measurements were performed on a Quantum Design MPMS-XL SQUID magnetometer equipped with a 5 T magnet. All samples were ground to a fine powder and congregated with hexadecane before loaded into a polycarbonate capsule. The dc susceptibility measurement was carried out with a field at 0.1 T and in the temperature range 2 to 300 K. The data work-up were done by a locally-written program based on the EasySpin33 package input to the MATLAB software, and the experimental data were fitted incorporating a g-factor, an axial (D) and rhombic (E) zero-field splitting (ZFS), a TIP parameter, and a coupling (J) expressed with the Hamiltonian: ĤHDvV = JŜ1·Ŝ2. Diamagnetic corrections were done using tabulated data for Pascal's constants.34 The dimeric platinum compounds were fitted incorporating a magnetic impurity which was assumed to be a the monomeric phase without an inter-molecular metallophilic interaction.2.3 Single crystal and powder X-ray diffraction
Single crystal X-ray diffraction data were collected on a Bruker D8 VENTURE diffractometer equipped with a Mo Kα X-ray (λ = 0.71073 Å), and a PHOTON 100 CMOS detector. For low temperature measurements at either 100 or 120 K the diffractometer is equipped with an Oxford Cryosystem. All crystals were mounted on capton loops with a small amount of silicone grease. The data reductions were performed in the APEX3 software, and the absorption correction was carried out with the multi-scan method SADABS. The structures were solved in the Olex2 (ver. 1.3) software with the ShelXT software package included. Powder X-ray diffraction data were collected on a Bruker D8 ADVANCE powder diffractometer equipped with a Cu Kα X-ray source (λ = 1.5418 Å).2.4 Computational
DFT calculations were done on both {NiPt}2 and {NiPd}2. By varying the distance between the two either Pt or Pd metal centers, final stage energies were calculated for a geometry optimized structure in both cases. The calculations were done in ORCA with the PBE0 functional and the def2-TZVP basis set. A ZORA formalism was used for the Pt and Pd elements to invoke relativistic effects together with Grimmes dispersion correction to reasonably handle the soft character of the metallophilic interactions.2.5 Inelastic neutron scattering
Inelastic Neutron Scattering (INS) was performed on the samples {CoPt}, {CoPt}2, {NiPt}, and {NiPt}2 at the time-of-flight cold neutron spectrometer IN5 at Institut Laue-Langevin, Grenoble, France.35 Samples of approximately 1 g were wrapped in aluminium foil and packed in aluminium canisters. Using a standard ILL Orange Cryostat, the samples were measured at select temperatures in the range of 1.5 to 100 K and with varying incident neutron wavelength in the range 2 to 3 Å. All measurements were normalized to a standard Vanadium sample. Data was reduced using the program Large Array Manipulation Program (LAMP)36 and cuts in S(Q, ω) were exported for plotting. Here Q is the momentum-transfer, which is also known as the scattering factor, and ℏω is the neutron energy loss. All observed magnetic scattering and the corresponding spin Hamiltonian parameters derived therefrom were corroborated by simulating the magnetic scattering. The magnetic scattering by localized spins is given by eqn (1).37,38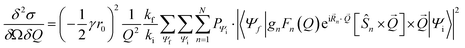 | (1) |
Here, the scattering 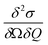 is expressed as a sum of all possible magnetic transitions. For N = 1 it describes the scattering from paramagnetic monomers, i.e. Ψ is the single-ion eigenfunction. Equally, N = 2 describes the scattering from the dimers, where Ψ is the coupled eigenfunction. Here, γ = −1.913 μN is the neutron magnetic moment, r0 = 2.818 × 10−15 m is the classical radius of the electron.
is expressed as a sum of all possible magnetic transitions. For N = 1 it describes the scattering from paramagnetic monomers, i.e. Ψ is the single-ion eigenfunction. Equally, N = 2 describes the scattering from the dimers, where Ψ is the coupled eigenfunction. Here, γ = −1.913 μN is the neutron magnetic moment, r0 = 2.818 × 10−15 m is the classical radius of the electron. ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) =
= ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i −
i − ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) f is the neutron momentum transfer, with Q, ki, and kf being the length of the corresponding vectors. gn, Fn(Q), Rn, and Ŝn is the g-factor, magnetic form factor, position, and spin of the n'th ion, respectively. Simulation of magnetic INS spectra were performed with a locally written program, which solves eqn (1) for the given spin system. All simulations are powder-averaged and expressed as S(Q, ω). Constant-Q or constant-ℏω cuts are scaled ex post facto.
f is the neutron momentum transfer, with Q, ki, and kf being the length of the corresponding vectors. gn, Fn(Q), Rn, and Ŝn is the g-factor, magnetic form factor, position, and spin of the n'th ion, respectively. Simulation of magnetic INS spectra were performed with a locally written program, which solves eqn (1) for the given spin system. All simulations are powder-averaged and expressed as S(Q, ω). Constant-Q or constant-ℏω cuts are scaled ex post facto.
2.6 Frequency-domain THz-EPR spectroscopy
Frequency Domain-Fourier Transform THz-EPR (FD-FT THz-EPR) samples of the {NiPd}2, {NiPd}, {NiPt}2 and {NiPt} were prepared by blending 83–103 mg of the respective polycrystalline sample with 50–62 mg polyethylene powder and pressing it into a pellet. FD-FT THz-EPR spectra were recorded using low-α mode coherent synchrotron radiation39,40 in Voigt geometry with its magnetic field component B1 perpendicular to the static magnetic field B0. The experimental resolution was 0.5 cm−1. To remove the incident background transmission from the spectrum, referencing was done between spectra recorded at different fields. Magnetic-field division spectra (MDS) at two magnetic fields Bi and Bj are presented as relative transmittance T, experimentally obtained from the measured spectral intensities I as Texp = IBi/IBj, and calculated from the simulated absorbance spectra A as Tsim = 10ABj − ABi. A 1st-order polynomial baseline correction was applied to the experimental MDS. Simulations were performed using the EasySpin toolbox.332.7 Raman spectroscopy
Raman measurements were performed using a micro-Raman setup in back-scattering geometry. The 632.8 nm line of a HeNe laser (Melles-Griot 25-LHR-991-230) was used (85 μW on top of the objective). The beam was focused in an inverted confocal microscope (Olympus IX71) by an Olympus 100X, 1.4-NA oil immersion objective into a diffraction-limited spot. A LL01-633 filter (Semrock) and a BP-633 filter (Optigrate) were used to clean and spectrally narrow the laser light in the excitation path. The polarization of the light was controlled using a polarizing beam splitter (Thorlabs). Raman spectra were recorded using a Princeton Instruments SPEC 10:100 B/LN-eXcelon CCD detector and a SP 2356 spectrometer with a 600 grooves per millimetre grating. A 30:70 beam splitter (XF122 Omega Optical) was used instead of a dichroic mirror in the microscope. Three RFS-633-OD3-11M filters (Optigrate) were used to block the laser light in the detection path. X-Axis calibration was performed with a Neon spectral calibration lamp (6032 Newport). No Y-axis corrections or background removal procedures were performed.3 Results and discussion
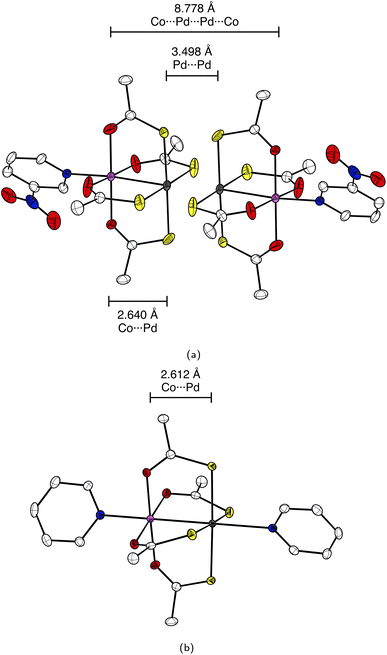
The fundamental design of the lantern complexes was developed in the Doerrer group,11 here, we expand the series of lantern complexes with the Pd analogs of the complexes [Ni(Pt(SAc)4)(pyNO2)]2, [Co(Pt(SAc)4)(pyNO2)]2, [Co(Pt(SAc)4)(py)2] and [Ni(Pt(SAc)4)(py)2]. The synthesis of the Pd complexes proved more challenging compared to the Pt complexes. The combination of a more labile metal center and the insolubility of the binary sulfides restricts reaction conditions and care must be taken to obtain phase-pure products. Simultaneously, the Pd⋯Pd metallophilic interaction is weaker than the Pt⋯Pt interaction to the extent that formation of the dimerized products is contingent on exact reaction conditions and solvent purity. Thus, the Pd complexes with apical 3-nitropyridine ligands were observed to crystallize both in a monomeric phase without the metallophilic interaction as well as a dimeric phase with the desired metallophilic interaction. The two phases with identical stoichiometry and comparable stability resulted in a mixture of the two crystalline phases for bulk samples if the described synthetic procedures were not carefully followed. To overcome a monomeric impurity in bulk samples of {NiPd}2, it was found that evaporation to dryness from solvent mixtures yielded phase-pure products. While constituting a synthetic complicating factor, the existence of the compounds as monomers and dimers of identical stoichiometry provides for the most direct comparison between monomer and dimer systems. Conversely, a bulk sample with a pure monomeric crystalline phase of the platinum systems, [M(Pt(SAc)4)(pyNO2)] was never obtained. However, small levels of monomeric impurities could be detected in powder diffractograms for bulk sample preparations of the dimer phases of [M(Pt(SAc)4)(pyNO2)]2. To circumvent that higher propensity of platinum for metallophilic interactions, we have chosen to include monomeric systems with apical ligators on both metals, namely the [M(Pt(SAc)4)(py)2] (M = Co, Ni). To make a direct comparison of Pt versus Pd complexes the bis-pyrdine Pd based monomers have been synthesized as well.The structure of all new compounds were characterized crystallographically, and the data are summarized in Tables S1 and S2 in the ESI.† The solid-state structure of {CoPd}2 and {NiPd}2 showed a metallophilic interaction between the two Pd metals linking two lantern complexes, similar to the interaction observed in the dimeric Pt complexes previously reported. In the dimerization of the two lantern units, the rotational barrier of the M′⋯M′ bond (M′ = Pd, Pt) is expected to be small and the ensuing conformational freedom to be governed by crystal packing interactions. The conformation is quantified with an averaged dihedral twist angle (τ) across the two MS4 entities. Not all M⋯M′⋯M′⋯M cores of the dimeric complexes are observed to be linear. Accordingly, a parameter, the displacement angle ϕ: (M⋯M′⋯M′), expresses the divergence from the ideal linear metallophilic geometry (ϕ = 180 deg). The four dimeric complexes {CoPd}2, {NiPd}2, {CoPt}2 and {NiPt}2 presented in this work are all in an eclipsed conformation. Compared to the previously reported [Ni(Pt(SAc)4)(pyNO2)]2 complex in the staggered conformer the series of four complexes in the same conformer makes for a better direct comparison. Hence, without the conformal change the {NiPt}2 in the eclipsed conformer exhibits a longer metallophilic interaction (3.421 vs. 3.058 Å)13 and a smaller displacement angle (158.8 vs. 177.8 deg) making the structural parameters significantly more comparable to the remaining three dimers. The dimerization of the two lantern units and the eclipsed conformer for {CoPd}2 is seen in Fig. 2.
The four dimeric complexes are iso-structural. However, the {NiPd}2 stands out due to its slightly longer metallophilic interaction. Some key structural parameters are summarized in Table 1.
| Compound | |||||
|---|---|---|---|---|---|
| Distance/Å | Distance/Å | Distance/Å | Average displacement angle ϕ/deg | Average dihedral angle τ/deg | |
| {CoPd}2 | 2.640 | 3.498 | 8.778 | 155.8 | 0.87 |
| {CoPt}2 | 2.627 | 3.437 | 8.691 | 160.5 | 0.63 |
| {NiPd}2 | 2.595 | 3.500 | 8.690 | 152.9 | 0.60 |
| {NiPt}2 | 2.587 | 3.421 | 8.595 | 158.8 | 0.50 |
| {CoPd} | 2.612 | — | — | — | — |
| {CoPt} | 2.582 | — | — | — | — |
| {NiPd} | 2.574 | — | — | — | — |
| {NiPt} | 2.551 | — | — | — | — |
In these structures the Pd2+ centers are arguably 6-coordinated, which, is a rare situation for Pd(II) and as it is mostly observed in the higher oxidation III and IV. An experimental argument for considering the 3d metals as ligands towards the 4d and 5d centers is the trans-influence weakening of the Pd⋯Pd interaction going from d7 (Co2+) to d8 (Ni2+). The length of the metallophilic interaction in the dimeric Pd complexes is similar to the one in the Pt complexes. Examples of complexes which exhibit non-ligand-supported Pd⋯Pd metallophilic interactions are quite sparse, but the complex catena-[Pd2(dithiopropionato)4]41 has an intermolecular metallophilic interaction at 3.439 Å, similar to the distances observed for the complexes {CoPd}2 and {NiPd}2, at 3.438 Å and 3.500 Å, respectively.
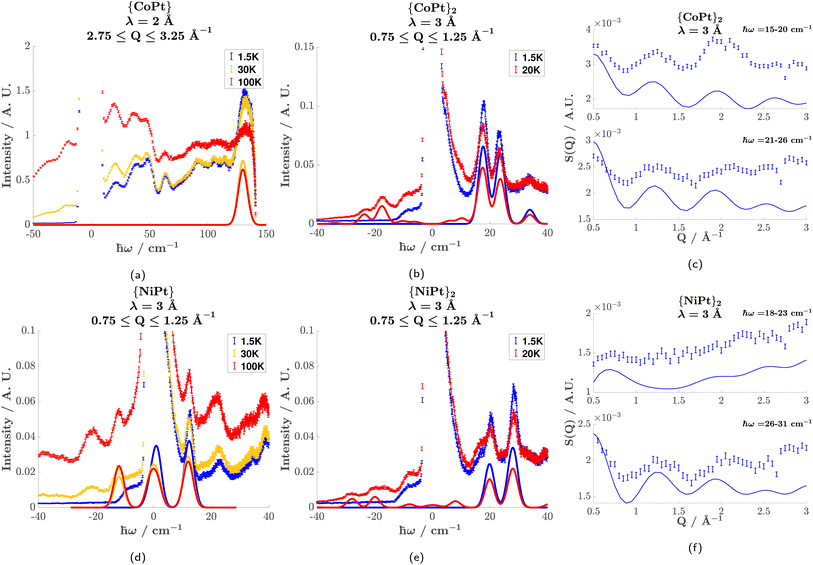
INS was performed on the Pt-analogues of both the monomer and dimer compounds. Fig. 3 illustrates the observed INS spectra (see Fig. S8† for S(Q, ω) plots) and simulations of the magnetic scattering. From the spectra of the monomers, the zero-field splitting of the Co2+S = 3/2 and the Ni2+S = 1 is given by the observed magnetic transitions.
{CoPt} (Fig. 3(a)) showed one magnetic transition at ℏω = 130 cm−1 corresponding to the 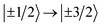 transition. The large positive axial zero-field splitting D = 65 cm−1 is corroborated by SQUID (cf. the global fitting in Table 2).
transition. The large positive axial zero-field splitting D = 65 cm−1 is corroborated by SQUID (cf. the global fitting in Table 2).
| {CoPt} | {CoPt}2 | {NiPt} | {NiPt}2 | {CoPd} | {CoPd}2 | {NiPd} | {NiPd}2 | |
|---|---|---|---|---|---|---|---|---|
| D/cm−1 | 65 | 65 | −12 | −8 | 70 | 65 | −12 | −12 |
| |E|/cm−1 | — | — | 0.6 | 0.6 | — | — | 0.6 | 0.6 |
| g | 2.53 | 2.65 | 2.21 | 2.29 | 2.59 | 2.48 | 2.17 | 2.17 |
| J/cm−1 | — | [10, 7, 13] | — | 24.5 | — | 1.3 | — | 1.65 |
| TIP/emu mol−1 | — | 5.9 × 10−3 | — | 5 × 10−4 | 5 × 10−4 | — | 1 × 10−3 | — |
{NiPt} (Fig. 3(d)) showed one magnetic transition at ℏω = 12 cm−1 which shifts slightly to lower energy with increasing temperature. This is explained by a negative axial zero-field (D = −12 cm−1) and a small rhombic term (E = 0.6 cm−1).
For the dimers, the spectra contain more information, as the energy of the magnetic transitions is defined by the zero-field splitting and the exchange-interaction. Furthermore, the Q-dependence of the transitions is dependent on the distance between the coupled ions (vide infra).
{CoPt}2 (Fig. 3(b)) showed three magnetic transitions in the range 10–40 cm−1. Assuming an identical zero-field splitting as in {CoPt}, SQUID magnetometry indicates an anti-ferromagnetic exchange interaction. This identifies these transitions as stemming from the S = 0 (coupled basis) to an S = 1 first exited state. Reproducing the energy, relative intensity, and momentum-transfer-dependence (vide infra) of these three transitions is only possible by implementing an anisotropic exchange interaction [Jxx, Jyy, Jzz] = [10, 7, 13] cm−1, which splits the S = 1 multiplet. This is the first experimental evidence of anisotropic exchange in these dimeric compounds, which shows that the mechanism of magnetic exchange across the metallophillic Pt⋯Pt bond is far more complicated than hitherto assumed. The assignment of the anisotropic exchange parameters is corroborated by SQUID-magnetometry, as they perfectly reproduce the observed susceptibility.
{NiPt}2 (Fig. 3(e)) shows two magnetic transitions. Interestingly, there is no evidence of anisotropy in the exchange-interaction. However, the value J = 24.5 cm−1 is much higher than is to be expected of ions coupled across more than 8 Å.30 The axial zero-field splitting (D = −8 cm−1) is significantly reduced relative to {NiPt} (D = −12 cm−1). The difference in coordination strength of pyNO2 (dimer axial ligand) and py (monomer axial ligand) is not great enough to cause such a drastic decrease in D. It is therefore believed that the decrease partially results from the delocalization of electrons from the filled Pt2+ dz2 orbital into bonding (metallophillic) molecular orbitals,42 thereby reducing its coordination strength towards Ni2+.
For {CoPt}2 and {NiPt}2, the momentum-transfer (Q) dependence of the magnetic transitions shows an interference effect, that results from the geometry of the coupled ions. This interference effect manifests as an oscillation in the Q-dependence superimposed on the magnetic form factor. The rate of oscillation is a direct result of the distance between the coupled ions and can therefore serve as an indicator for the nature of the coupling.
For {CoPt}2 (Fig. 3(c)) and {NiPt}2 (Fig. 3(f)), the Q-dependence of the two highest-intensity magnetic transitions is shown. Superimposed on the measured Q-dependence (errorbars) is a simulation of the magnetic excitations. It is noted that the transitions do not decay with increasing Q, following the magnetic form factors. This is due to a monotonically increasing incoherent phonon background, which is approximated in the simulations as an added term of Q2. The simulations accurately reproduce the energy and relative intensity of these transitions, giving merit to the spin-Hamiltonian parametrization. The simulation of the Q-dependence has been done based on the full anisotropic spin-Hamiltonian description contrary to earlier approaches, which for dimers have only dealt with coupled isotropic paramagnetic centers. The rate of oscillation is consistent with two ions separated by 8.5 Å, which is the distance between the two paramagnetic ions across the Pt⋯Pt bridge. This proves that the exchange-interaction is mediated by a metallophilic Pt⋯Pt bond, and not a through-space coupling to the nearest neighbor, which is only 7 Å away (see Fig. S5 in the ESI†). A Q-dependence corresponding to 7 Å cannot reproduce the experimental result.
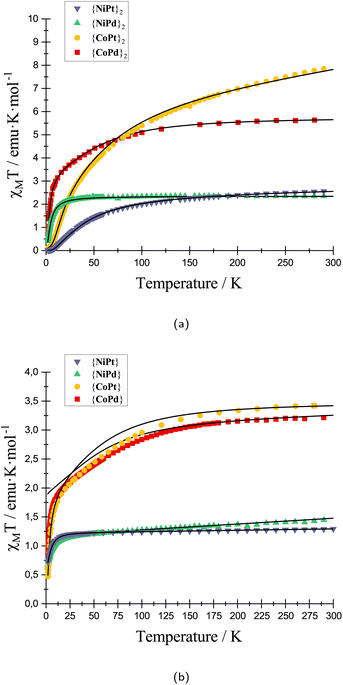
To support the INS study, SQUID magnetometry was measured on all eight compounds. The solid-state molar magnetic susceptibility data for all eight species and their modeling are shown in Fig. 4.
At 300 K the χMT product for {CoPd}2, {CoPt}2, {NiPd}2 and {NiPt}2 are 5.55, 6.06, 2.35 and 2.38 emu K mol−1 respectively. The experimental values are higher than expected for two uncoupled S = 3/2 for Co2+ and S = 1 for Ni2+, consistent with a coupling of the two spins and an unquenched orbital contribution to the total angular momentum. The monomeric complexes were synthesized and magnetically characterized in respect to correlate the parameters between the monomeric and dimeric complexes and provide a consistent model for magnetometry and INS data. The χMT curve for all four dimeric complexes shows a drastic drop at low temperature concurring with an anti-ferromagnetic coupling of two paramagnetic metals. The coupling was fitted to an isotropic exchange model for all dimeric complexes, except the {CoPt}2 for which, the INS data mandates modeling with an anisotropic coupling. The modeling of the low temperature regime of the {CoPd} data is not perfect. It could be improved by including weak (0.5 cm−1 > J) anti-ferromagnetic couplings within a tetrameric unit of Co2+ centers. However, this ad hoc improvement has not been included as we consider it beyond the scope of unfolding the present story. From the parameters extracted from the model of the magnetic susceptibility and INS data two primary trends emerge. First, the coupling constants in the {CoPd}2 and {NiPd}2 complexes are significantly smaller than their respective Pt complexes. The Pd and Pt complexes are iso-structural with a minimal derivation in the molecular distances and angles in the solid-state structure. Therefore, the influence on the magnetic coupling must be found in the change from Pd to Pt and the communication between the two lantern units. The metallophilic interaction originates from an overlap of the dz2 orbitals of either Pt or Pd. The larger radial extent of the Pt 5dz2 orbitals compared to the Pd 4dz2 orbitals make for a larger overlap and a concomitantly stronger interaction. This argument is valid if the inter- and intra-molecular distances between the metals are similar as is true for the complexes presented here. Second, for {NiPd}2 to {NiPt}2 the relative increase in the coupling is remarkably larger than the change going from {CoPd}2 to {CoPt}2. The {NiPd}2 stood out from the remaining dimeric complexes with a slightly longer metallophilic interaction. This elongation of the metallophilic bond contributes to the more drastic change, and hence a larger span of the coupling constants.
To obtain further insight into the spin coupling parameters and correlate them to the metallophilic interaction of either Pt⋯Pt or Pd⋯Pd, the Ni dimers ({NiPt}2, {NiPd}2) and monomers ({NiPt}, {NiPd}) were investigated by FD-FT THz-EPR in the temperature range from 5 to 23 K at the BESSY II storage ring. All of them showed field-dependent signals from magnetic transitions in the magnetic-field division spectra (MDS), which were simulated using the same spin-Hamiltonian as for the magnetometry data.
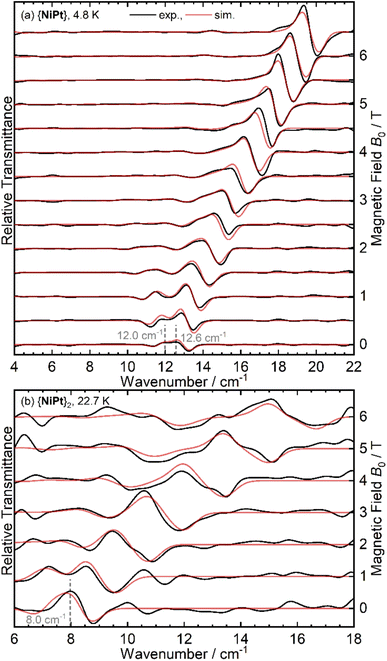
Resulting magnetic-field division spectra are shown for {NiPt} and {NiPt}2 in Fig. 5 A detailed discussion on the analysis of the THz data as well as the spectra of {NiPd} and {NiPd} can be found in ESI:6.†
{NiPt} exhibits a doublet signal centered at 12.3 cm−1, the zero-field peaks of which appear at 12.0 and 12.6 cm−1 in the MDS (Fig. 5(a)). This readily determines the ZFS parameters to be D = − 12.3 cm−1 and |E| = 0.6 cm−1, consistent with the parameters derived from the INS and SQUID modeling. For {NiPt}2, no transitions are discernible at the lowest temperature of 5 K, while starting from 9 K, a transition with a zero-field transition energy of 8.0 cm−1 gains intensity, reaching its maximum at 23 K (see Fig. 5(b) and S10†). This is assigned as an internal transition within the excited triplet state, consistent with the difference between the observed INS transitions at 20 and 28 cm−1 and also corroborating the strong antiferromagnetic coupling in the platinum bridged dimer.
For the {NiPd}2 (see Fig. S9b†), in contrast, signals are observed already at T = 5 K which are not present in the {NiPd} spectrum (Fig. S9a†). Thus, the coupling in the {NiPd}2 must be significantly smaller than for {NiPt}2 and the significant population of the excited triplet state at T = 5 K is consistent with this. THz spectroscopy delivers more detail on the ZFS and indicates smaller values for D in the nickel palladium systems (cf. ESI†).
The dramatically lower magnetic coupling via the Pd⋯Pd bridge as compared to that occurring via the Pt⋯Pt bridge may spur suspicion concerning the existence of an actual Pd⋯Pd metallophilic interaction. This hesitation may be further fueled by the preparative challenges associated with obtaining the monomeric platinum systems and the dimeric palladium systems, respectively. In order to address this question we decided to computationally investigate the potential surface along the M′⋯M′ stretching coordinate for both the platinum and palladium dimers. We chose a similar level of theory and methodology as that employed in a recent study of the exchange coupling in related dinuclear platinum systems.42 DFT calculations were performed for both {NiPt}2 and {NiPd}2. Geometry scans of the Pt⋯Pt and Pd⋯Pd distances were done on geometry optimized rigid structures for the remaining internal coordinates using the ORCA software and including dispersion correction to account for the soft M′⋯M′ interaction.
The energy curves in Fig. 6 are referenced to the practically dissociated system with a separation of 6 Å. The variation of the total energy of the system along the M′⋯M′ stretching coordinate shows a clear energy minimum valley validating the presence of an actual interaction between the Pd centers as well as between the Pt centers. The calculated minima lie at shorter distances than the experimental structures, which has been observed, previously, and which is not unexpected for computational modeling of a low-energy interaction disregarding crystal packing effects. Notably, though, the minima occur at very similar distances for the two metals as observed in the experimental crystal structures. 3.421 Å for {NiPt}2 and 3.500 Å for {NiPd}2, with the computed minimum for the Pd⋯Pd interaction occurring at similar M′⋯M′ separation as for the platinum system. Most significantly is the very similar energy stabilization of ca. 0.5 eV for both metals upon formation of the dimers, and almost identical curvature of the potential surfaces near the energy minimum. This points to similar strength and force constants for both “bonds”. The computed potential energy surfaces demonstrating reasonable stabilization and concomitant curvature around the minima raises the question of whether the M′⋯M′ stretching may actually be experimentally observable. Very recently43 the vibrational signature of the Au–Pt metallophilic interaction in [Pt(terpy)Cl][Au(CN)2] was observed experimentally at 57 cm−1. This system is well selected for this specific purpose due to the rigidity and the scarcity of obvious low-energy modes. In contrast, the present systems are far from trivial in this context with several potential soft local and phononic modes conceivable. However, The simultaneous existence of isostructural Pd⋯Pd and Pt⋯Pt dimers facilitates the task. Furthermore, although the dimers do not crystallize with high crystallographic local symmetry, the packing is fortunate enough to align the individual dimers relatively well as illustrated in the top panel of Fig. 7. The dimers crystallize in nice single crystals with dimensions easily reaching 4-500 μm.
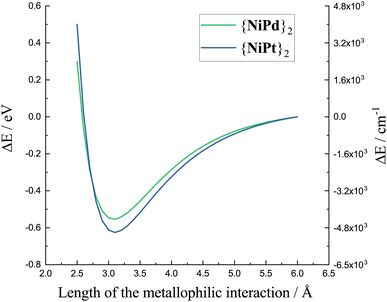 | ||
| Fig. 6 Final stage energy calculations obtained while making a geometrical scan of the Pt⋯Pt distance in {NiPt}2 and the Pd⋯Pd distance in {NiPd}2. | ||
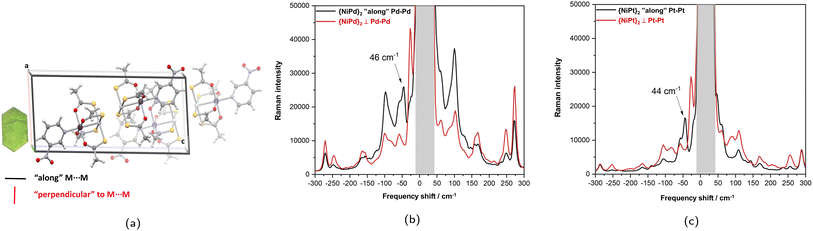
Raman spectra collected on a crystallographically indexed single crystal with the electric field component polarized approximately parallel and perpendicular to the M′⋯M′ directions reveals strongly polarized transitions at 46 cm−1 for {NiPd}2 and 44 cm−1 for {NiPt}2.
Considering as a reference system for these vibrations the dimeric Hg(I) cation, Hg22+, gas phase computation was performed with the identical level of theory as the Pd and Pt dimers and no counter ions present. The curvatures of the potential surfaces were fitted to a harmonic potential near the minimum distance and the relative curvatures were determined to be {NiPd}2: 0.036(4); {NiPt}2: 0.046(5); Hg⋯Hg: 0.128(17), which translates into relative vibrational frequencies of 0.53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.58
0.58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.00 assuming identical reduced masses. With the low range of [Hg⋯Hg]2+ stretching frequencies reported around 110 cm−1,44 the assignment of the M′⋯M′ stretch to the distinctly polarized bands just below 50 cm−1 appears consistent and suggests that the metallophilic interactions might indeed be prone to direct spectroscopic observation.
1.00 assuming identical reduced masses. With the low range of [Hg⋯Hg]2+ stretching frequencies reported around 110 cm−1,44 the assignment of the M′⋯M′ stretch to the distinctly polarized bands just below 50 cm−1 appears consistent and suggests that the metallophilic interactions might indeed be prone to direct spectroscopic observation.
4 Conclusions
We have further developed metallophilic interactions as an orthogonal reactivity allowing control of molecular structure and solid-state packing for molecule-based magnetic systems. This was done by augmenting a set of mono- and dimeric systems featuring Pt⋯Pt bridging12,13 with their palladium counterparts. Synthetically, it was found to be significantly more challenging to obtain the dimerized palladium systems. Four of these complexes, [M(M′(SAc)4)(pyNO2)]2, (M = Co, Ni; M′ = Pt, Pd) dimerize in the solid-state through a metallophilic interaction which facilitates an anti-ferromagnetic exchange coupling. It was demonstrated that the Pt⋯Pt metallophilic interaction is capable of facilitating an exchange coupling, which can be either large, as was found for {NiPt}2, or anisotropic, as was found for {CoPt}2. An inelastic neutron scattering study on the platinum systems yielded detailed spectroscopic information on both the zero-field splitting and the exchange interaction parameters. For the dimers, INS showed a distinct oscillation in the Q-dependence, which complies perfectly with two coupled paramagnetic ions being separated by a distance of 8.5 Å. This matches the crystallographically determined intra dimer separation of the paramagnetic centers and hence proves the intramolecular pathway for strong exchange. To give a consistent parametrization of the series of anti-ferromagnetically coupled dimers the INS was supported by magnetometry on all systems and THz spectroscopy on the Ni members of the series. While the palladium-bridged systems had very comparable ZFS compared to the platinum systems, the magnetic interaction via the Pd⋯Pd metallophilic interaction was found to be much reduced compared to the platinum-bridged dimers which correlates with longer M′⋯M′ distances in the solid state for the smaller Pd(II) and most notably with significantly smaller radial extent of the 4dz2 orbitals of Pd(II) as compared to the 5dz2 orbital on Pt(II). A similar difference in the interaction of Pd(II) and Pt(II) with trivalent lanthanides was previously reported.23 Concerns regarding the actual existence of an energetically relevant Pd⋯Pd interaction were addressed computationally and found that the energetic stabilization is quite similar to that of the Pt⋯Pt linked dimer and no more than 10% reduced for the Pd⋯Pd dimer. A single crystal Raman investigation comparing {NiPd}2 and {NiPt}2 demonstrated polarized vibrational bands at frequencies consistent with estimates from the potential energy curves and provides support for similar interaction strengths in the metallophilic interactions. This makes Pd(II) a credible structure-directing motif for assembly of polynuclear, molecular magnetic systems and allows for significantly different magnetic interaction strength compared to the established Pt–Pt metallophilic interactions.Author contributions
E. M. H. L. and N. A. B. contributed equally to this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Helmholtz-Zentrum Berlin for the allocation of synchrotron radiation beamtime at BESSY II (201-09107, 202-09859). We are grateful to Dirk Ponwitz for assistance with the FD-FT THz-EPR experiments. TL is indebted to the Deutsche Forschungsgemeinschaft (DFG, Project No. LO 2898/1-1). We also also thank Institut Laue-Langevin for providing the facilities for the INS experiments and analysis thereof. JB acknowledges support from Independent Research Fund Denmark in grant 8021-00410B. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Project ELECTRA, Grant agreement No. 101039890).Notes and references
- M. M. Hänninen, A. J. Mota, R. Sillanpää, S. Dey, G. Velmurugan, G. Rajaraman and E. Colacio, Inorg. Chem., 2018, 57, 3683–3698 CrossRef PubMed.
- M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875 CrossRef CAS PubMed.
- J. P. S. Walsh, S. Sproules, N. F. Chilton, A.-L. Barra, G. A. Timco, D. Collison, E. J. L. McInnes and R. E. P. Winpenny, Inorg. Chem., 2014, 53, 8464–8472 CrossRef CAS PubMed.
- S. Giménez-Santamarina, S. Cardona-Serra, J. M. Clemente-Juan, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2020, 11, 10718–10728 RSC.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- C. Rovira and J. Veciana, CrystEngComm, 2009, 11, 2031 CAS.
- M.-X. Xu, Z. Liu, B.-W. Dong, H.-H. Cui, Y.-X. Wang, J. Su, Z. Wang, Y. Song, X.-T. Chen, S.-D. Jiang and S. Gao, Inorg. Chem., 2019, 58, 2330–2335 CrossRef CAS PubMed.
- E. Garlatti, L. Tesi, A. Lunghi, M. Atzori, D. J. Voneshen, P. Santini, S. Sanvito, T. Guidi, R. Sessoli and S. Carretta, Nat. Commun., 2020, 11, 1751 CrossRef CAS.
- A. Lunghi and S. Sanvito, Sci. Adv., 2019, 5, eaax7163 CrossRef CAS.
- D. Reta, J. G. C. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143, 5943–5950 CrossRef CAS PubMed.
- E. W. Dahl, F. G. Baddour, S. R. Fiedler, W. A. Hoffert, M. P. Shores, G. T. Yee, J. P. Djukic, J. W. Bacon, A. L. Rheingold and L. H. Doerrer, Chem. Sci., 2012, 3, 602–609 RSC.
- F. G. Baddour, S. R. Fiedler, M. P. Shores, J. W. Bacon, J. A. Golen, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2013, 52, 13562–13575 CrossRef CAS PubMed.
- F. G. Baddour, S. R. Fiedler, M. P. Shores, J. A. Golen, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2013, 52, 4926–4933 CrossRef CAS PubMed.
- J. L. Guillet, I. Bhowmick, M. P. Shores, C. J. Daley, M. Gembicky, J. A. Golen, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2016, 55, 8099–8109 CrossRef CAS PubMed.
- A. Nimthong-Roldán, J. L. Guillet, J. McNeely, T. J. Ozumerzifon, M. P. Shores, J. A. Golen, A. L. Rheingold and L. H. Doerrer, Dalton Trans., 2017, 46, 5546–5557 RSC.
- F. G. Baddour, A. S. Hyre, J. L. Guillet, D. Pascual, J. M. Lopez-De-Luzuriaga, T. M. Alam, J. W. Bacon and L. H. Doerrer, Inorg. Chem., 2017, 56, 452–469 CrossRef CAS.
- S. A. Beach and L. H. Doerrer, Acc. Chem. Res., 2018, 51, 1063–1072 CrossRef CAS.
- H. Skipper, C. May, A. Rheingold, L. Doerrer and M. Kamenetska, J. Am. Chem. Soc., 2021, 143, 16439–16447 CrossRef CAS PubMed.
- S. A. Beach, A. L. Rheingold and L. H. Doerrer, Polyhedron, 2021, 208, 115403 CrossRef CAS.
- M. A. Sørensen, H. Weihe, M. G. Vinum, J. S. Mortensen, L. H. Doerrer and J. Bendix, Chem. Sci., 2017, 8, 3566–3575 RSC.
- M. A. Sørensen, U. B. Hansen, M. Perfetti, K. S. Pedersen, E. Bartolomé, G. G. Simeoni, H. Mutka, S. Rols, M. Jeong, I. Zivkovic, M. Retuerto, A. Arauzo, J. Bartolomé, S. Piligkos, H. Weihe, L. H. Doerrer, J. Van Slageren, H. M. Rønnow, K. Lefmann and J. Bendix, Nat. Commun., 2018, 9, 1–9 Search PubMed.
- M. Perfetti, M. A. Sørensen, U. B. Hansen, H. Bamberger, S. Lenz, P. P. Hallmen, T. Fennell, G. G. Simeoni, A. Arauzo, J. Bartolomé, E. Bartolomé, K. Lefmann, H. Weihe, J. van Slageren and J. Bendix, Adv. Funct. Mater., 2018, 28, 1–8 CrossRef.
- N. A. Bonde, J. B. Petersen, M. A. Sørensen, U. G. Nielsen, B. Fåk, S. Rols, J. Ollivier, H. Weihe, J. Bendix and M. Perfetti, Inorg. Chem., 2020, 59, 235–243 CrossRef CAS.
- N. A. Bonde, M. Appel, J. Ollivier, H. Weihe and J. Bendix, Chem. Commun., 2022, 58, 7431–7434 RSC.
- T. Yoshida, D. C. Izougu, D. Iwasawa, S. Ogata, M. Hasegawa, B. K. Breedlove, G. Cosquer, W. Wernsdorfer and M. Yamashita, Chem.–Eur. J., 2017, 23, 10527–10531 CrossRef CAS PubMed.
- T. Yoshida, G. Cosquer, D. C. Izuogu, H. Ohtsu, M. Kawano, Y. Lan, W. Wernsdorfer, H. Nojiri, B. K. Breedlove and M. Yamashita, Chem.–Eur. J., 2017, 23, 4551–4556 CrossRef CAS.
- D. C. Izuogu, T. Yoshida, H. Zhang, G. Cosquer, K. Katoh, S. Ogata, M. Hasegawa, H. Nojiri, M. Damjanović, W. Wernsdorfer, T. Uruga, T. Ina, B. K. Breedlove and M. Yamashita, Chem.–Eur. J., 2018, 24, 9285–9294 CrossRef CAS.
- T. Yoshida, D. C. Izuogu, H. T. Zhang, G. Cosquer, H. Abe, W. Wernsdorfer, B. K. Breedlove and M. Yamashita, Dalton Trans., 2019, 48, 7144–7149 RSC.
- D. C. Izuogu, T. Yoshida, G. Cosquer, J. N. Asegbeloyin, H. Zhang, A. J. Thom and M. Yamashita, Chem.–Eur. J., 2020, 26, 6036–6049 CrossRef CAS PubMed.
- R. E. Coffman and G. R. Buettner, J. Phys. Chem., 1979, 83, 2387–2392 CrossRef CAS.
- M. L. Baker, T. Guidi, S. Carretta, J. Ollivier, H. Mutka, H. U. Güdel, G. A. Timco, E. J. Mcinnes, G. Amoretti, R. E. Winpenny and P. Santini, Nat. Phys., 2012, 8, 906–911 Search PubMed.
- A. Chiesa, F. Tacchino, M. Grossi, P. Santini, I. Tavernelli, D. Gerace and S. Carretta, Nat. Phys., 2019, 15, 455 Search PubMed.
- EasySpin, http://www.easyspin.org.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
- M. A. Sørensen, J. Bendix, N. A. Bonde, J. O. Christensen, J. Ollivier, M. Perfetti and H. Weihe, Quantifying antiferromagnetic exchange interactions mediated by metallophilic contacts, 2018, doi: DOI:10.5291/ILL-DATA.4-06-7.
- D. Richard, M. Ferrand and G. J. Kearley, J. Neutron Res., 1996, 4, 33–39 CrossRef.
- M. A. Dunstan, R. A. Mole and C. Boskovic, Eur. J. Inorg. Chem., 2019, 2019, 1090–1105 CrossRef CAS.
- S.-H. Lee and I. A. Zaliznyak, Magnetic Neutron Scattering, 2004 Search PubMed.
- J. Nehrkorn, K. Holldack, R. Bittl and A. Schnegg, J. Magn. Reson., 2017, 280, 10–19 CrossRef CAS PubMed.
- A. Schnegg, J. Behrends, K. Lips, R. Bittl and K. Holldack, Phys. Chem. Chem. Phys., 2009, 11, 6820–6825 RSC.
- A. Kobayashi, T. Kojima, R. Ikeda and H. Kitagawa, Inorg. Chem., 2006, 45, 322–327 CrossRef CAS.
- Z. Sandoval-Olivares, E. Solis-Céspedes and D. Páez-Hernández, Inorg. Chem., 2022, 61, 1401–1417 CrossRef CAS PubMed.
- K. J. Trerayapiwat, H. Kitadai, V. Pazmany, S. P. Lagueux, H. E. Skipper, L. H. Doerrer, X. Ling and S. Sharifzadeh, J. Phys. Chem. C, 2021, 125, 22188–22194 CrossRef CAS.
- P. A. W. Dean and D. G. Ibbott, Can. J. Chem., 1976, 54, 177–187 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental, crystallographic details, computational data, INS data, FD-FT THz-EPR data. CCDC 2207828–2207833. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc05201f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |