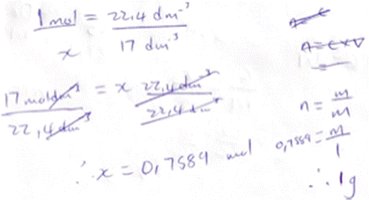The efficacy of instruction in application of mole ratios and submicro- and macro-scopic equivalent forms of the mole within the unit factor method

Abstract

The unit factor method, a generic strategy for solving any proportion-related problem, is known to be effective at reducing cognitive load through unit-cancellation providing step-by-step guidance. However, concerns have been raised that it can be applied mindlessly. This primarily quantitative prepost study investigates the efficacy of instruction aimed at addressing such concerns. This was done by making submicro- and macro-scopic equivalent forms of the mole concept, and the meanings of mole ratios, explicit, and emphasising the application of these within the unit factor method to solve stoichiometry calculations. Data were collected from 161 South African Physical Sciences teachers’ answers to four calculation, and 14 conceptual, questions in each of a pre- and a post-test written at the start and end, respectively, of a two-day workshop at which such instruction was implemented. These data were analysed for changes in strategy type and calculation and conceptual knowledge, i.e., heuristic power. A small (n = 7) group retained deficient calculation strategies in which they failed to recognise the need to apply proportion to the mole ratio. For the remainder, a weak but significant correlation was found between their conceptual and calculation improvements. There was high uptake of the unit factor method in the posttest, although a group (n = 33) which began with relatively good calculation knowledge largely rejected this method. Statistically significant improvements in both conceptual and calculation knowledge were found regardless of the extent of uptake of the unit factor method, however the calculation improvement measured was significantly lower for the group which showed moderate uptake of the unit factor method, suggesting they may have needed a longer intervention. Based on the findings, speculations are made regarding the nature of knowledge and the mechanism of development of heuristic power. Long-term effects of such an intervention would, however, still need to be determined.

---

Introduction

Algorithms may be seen as necessary evils in that they are required to reduce cognitive load (Hartman and Nelson, 2021), yet they may be applied incorrectly due to rote, rather than meaningful, usage (Nyachwaya et al., 2014), and may detract from conceptual development (Skemp, 1987). Ideally, an algorithm should provide metacognitive support (Vo et al., 2022), e.g. by directing the user from one step to the next (Gulacar et al., 2021), while also directing attention to the integration of relevant concepts at the macroscopic, submicroscopic, and symbolic levels of representation (Johnstone, 2000). This is an investigation into the efficacy of an instructional sequence designed with the intention of guiding deployment of an algorithm, the unit factor method, in this desired manner through explicit application of the meaning of the mole ratio and the mole concept's role in connecting these levels of representation, and so propelling participants along Niaz's (1995) algorithmic-conceptual continuum of developing heuristic power. Each of these concepts is explained below. Since this study focuses on the efficacy of this instructional sequence within a series of 2 day in-service workshops for South African physical sciences teachers, the difficulties they are known to experience with stoichiometry calculations are discussed first.

Literature review and conceptual framework

South African physical sciences teachers’ difficulties with stoichiometry calculations

Mathematics competence, particularly regarding use of proportion, largely determines the extent of challenge experienced in performing stoichiometry calculations (Ralph and Lewis, 2018). It is therefore not surprising that South African physical sciences (SA PS) teachers, who are known to have difficulty with mathematics in general (Taylor, 2019), and proportion in particular (Selvaratnam, 2011), largely fail to obtain the correct answer to basic stoichiometry calculation exercises (Stott, 2021). These teachers’ failure to recognise the need to use proportion was found to be a considerable contributor to their limited success with stoichiometry calculations (Stott, 2021). This failure is consistent with Gulacar et al.'s (2021) finding that not knowing what to do in subproblems within the calculation process is a critical contributor to difficulties experienced during stoichiometry calculations.

Cognitive load theory and the necessity of algorithms

These difficulties are unsurprising, given the mathematical and conceptual complexity of stoichiometry (Ramful and Narod, 2014) and the limitations to working memory experienced by novices, described by cognitive load theory (Sweller, 2011). Central to cognitive load theory in the context of chemistry education (see, for example, Hartman and Nelson, 2021), is the view that algorithms are crucial for novices to engage fluently in well-defined calculations. The terms relevant to this premise, as well as the way each is operationalised in this study, are explained in Table 1. The term algorithm is used, here, to refer to a wide range of procedures which include both narrowly applicable formulae and more generic methods, such as the unit factor method.

Table 1 Some terms relevant to the application of cognitive load theory in chemistry learning

Term	Explanation	Ref.	Operationalisation in this study
Algorithm	“Procedures with sequential steps to achieve a goal”	(Hartman and Nelson, 2015, p. 8)	E.g., the unit factor method
Fluency	The ability to attain the correct answer to well-defined calculations, such as asked in chemistry examinations	(Hartman and Nelson, 2015)	Calculation success, indicated by score/16
Novices within a particular domain	People who do not possesses an extensive and highly structured knowledge system about that domain in their long-term memory	(Hartman and Nelson, 2015)	Most of the teachers included in this study, as suggested by their low pretest scores
Well-defined calculations	Calculation questions for which experts in the field agree that specific rules and procedures could be used to obtain correct answers	(Spiro and Deschryver, 2009)	Typical grade 10 and 11 end-of-chapter stoichiometry calculation exercises, used in the pre- and post-tests

---

The reason why algorithms are necessary for novices to attain fluency is that their knowledge, stored in long term memory, is of limited extent and degree of structure (Hartman and Nelson, 2015). This reduces their ability to chunk information, resulting in high levels of cognitive load which prohibits effective engagement in all types of problems (Sweller, 2011; Tsaparlis, 2021). For well-defined calculations this prohibition can be overcome by repeated use of an algorithm until automaticity has been achieved (Hartman and Nelson, 2015). Algorithm automaticity can be attained by scaffolding practice such that initially a high degree of structure is provided, and this is faded as automaticity is reached (Graulich et al., 2021). This necessary use of algorithms comes, however, at a potential cost: an overreliance on memorised procedures at the expense of development of conceptual understanding, with associated inappropriate application of these algorithms, particularly to novel contexts (Skemp, 1987).

Conceptual understanding and levels of representation in chemistry

In the context of chemistry education, development of conceptual understanding is believed to be closely related to development of an understanding of interrelations between the various levels of representation: submicroscopic, macroscopic and symbolic (Johnstone, 2000). Indeed, the mole concept, central to stoichiometry, serves as a connection between these levels of representation and can therefore only be understood if attention is paid to interrelations between these levels (Fang et al., 2014). This belief in the conceptual value of such interrelations has, for example, led to recent calls for greater use and interconnection of these forms of representation in Chemistry textbooks (Ramnarain and Chanetsa, 2016) and their modelling and explicit instruction in teacher education programmes (Mweshi et al., 2020). From the perspective of cognitive load theory, it is, however, unsurprising that teachers find it difficult to pay attention to each of these forms of representation, as well as their interconnection, in the classroom (Koopman, 2017), and therefore unsurprising that the mole concept specifically (Malcolm et al., 2019), and stoichiometry more broadly (Stott, 2020), tend to be poorly understood.

The unit factor method

The instructional sequence investigated was designed to introduce participants to use of the unit factor method as both an algorithm and a way to direct attention towards the meaning of the mole reacting ratio given in a balanced equation and the interconnections between the submicroscopic, macroscopic and symbolic forms of representation. To explain the rationale behind this sequence, the unit factor method is explained, and exemplified, below, and potential strengths are discussed, as well as threats to its effective use as an agent for reducing cognitive load while also directing attention towards conceptual understanding.

The unit factor method (Herron and Wheatley, 1978), also called the factor label method (Poole, 1989), is an application of dimensional analysis (DeMeo, 2008), i.e., the conversion of units of measurement through use of unit equivalence. As illustrated in Fig. 1, in the unit factor method, the value given in a proportion-related question is multiplied by a conversion factor which is, in effect, unity, due to its numerator and denominator being equivalent to one another. The conversion factor's denominator has the unit of the given variable, and its numerator the unit of the required variable. In this way the given unit cancels out and the required unit remains in the answer. These units can therefore be used to guide the student towards a productive sequence of steps. In this way the common difficulty identified by Gulacar et al. (2021), of students not knowing what to do next when solving stoichiometry calculations, may be mitigated. It is therefore unsurprising that the unit factor method is generally considered effective at helping students of a wide range of mathematical competencies to obtain the correct answers to well-defined stoichiometry problems (Herron and Wheatley, 1978; Gabel and Sherwood, 1983), even with limited conceptual knowledge (Robinson, 2003; Cook and Cook, 2005). It is also unsurprising that DeMeo (2008) found this to be the most popular method for teaching stoichiometry calculations in his sample, drawn largely from chemistry teachers from the United States of America. An additional potential benefit of the unit factor method in contexts, such as South Africa, where failure to recognise the need to apply proportion to the mole ratio is a common error (Stott, 2021), is that it is a generic proportion method, and so is well suited to drawing attention to the need to use proportion.

Fig. 1 An example of a well-defined stoichiometry calculation problem and its solution using the unit factor method.

Viewed from another angle, the unit factor method may be seen as potentially providing metacognitive support, at least within the analysis and solution phases of problem solving (Vo et al., 2022). This is because identification of the given and required information and their units, i.e., analysis of the problem, is central to this method, as is the relationship between the given and required quantities, required for the solution of the problem. It is hoped that the solver's attention will be directed towards the relationship between given and required quantities by the need to cancel the given, and introduce the required, unit. However, this very feature, powerful for reducing cognitive load as it provides metacognitive support, has invited criticism for this method through: (1) its ability to allow users to calculate the correct answer despite possessing little conceptual knowledge of stoichiometry (Robinson, 2003); (2) the finding that users may focus so much on the units that they fail to think about the associated concepts (Tang et al., 2014); (3) the speculation that the method might stunt conceptual development through reliance on unit cancelling at the expense of attention to the relevant concepts (DeToma, 1994; Robinson, 2003; Cook and Cook, 2005; DeMeo, 2008; Page et al., 2018).

In potential rebuttal of these criticisms, it is argued that these problems are not inherent to the unit factor method. Instead, the conversion factor(s) can be used as vehicles for drawing attention to the mole ratio and connections within and between submicro- and macro-scopic quantities of chemicals, expressed symbolically. This is because these conversion factors express mole reaction ratios or equivalent forms of the mole concept, as discussed below.

The mole concept's role in connecting the macro- and submicro-scopic levels

The purpose of the mole concept is to bridge the submicro–macro-scopic gap in chemistry. This gap exists because people conceptualise chemical reactions on the submicroscopic level, e.g., regarding molecules reacting with one another, for which particle counts – how many – is the best measure of quantity. However, people work, practically, with chemicals on the macroscopic level where macroscopic quantities, such as mass – how heavy – and volume – how large – are needed. The mole concept bridges this submicro–macro-scopic gap in two ways: (1) it allows elements’ mass numbers to be reusable on both the submicroscopic level (as the mass, in amu, of a single atom or molecule) and the macroscopic level (as the mass, in grams, of a mole of atoms or molecules) and (2) it enables use of the particle count quantity – how many – at the macroscopic level too. In order to help learners to understand this, it is necessary to help them to appreciate: (1) the enormity of Avagadro's number (6.02 × 10²³); (2) the concept of using group words, such as pair, dozen, or Avagadro's number, interchangeably with certain numbers; and (3) why 6.02 × 10²³ was deemed sufficiently valuable to be assigned group-word status, namely that 1 amu, the fundamental unit of mass since it is the mass of a nucleon, the category of submicroscopic particles which have significant mass, equals .

This discussion has stated what the mole concept's purpose is and how it achieves this purpose, but not what the mole is. A common explanation given to learners is to equate the mole to Avagadro's number, i.e., that the mole is a group word meaning 6.02 × 10²³ (Fang et al., 2014). However, this is ontologically incorrect, since the mole is the amount of substance which has Avagadro's number of particles in it, rather than being Avagadro's number itself, hence the phrase amount of substance in both the latest IUPAC definition, and the older definition still in use in the South African Curriculum. According to the latest IUPAC definition, “The mole, symbol mol, is the SI unit of amount of substance. One mole contains exactly 6.02214076 × 10²³ elementary entities. This number is the fixed numerical value of the Avogadro constant, N_A, when expressed in the unit mol⁻¹ and is called the Avogadro number. The amount of substance, symbol n, of a system is a measure of the number of specified elementary entities. An elementary entity may be an atom, a molecule, an ion, an electron, any other particle or specified group of particles” (BIMP, 2019, p. 134). The older definition, even more opaque to a learner is: “a mole is the amount of substance having the same number of particles as there are atoms in 12 g carbon-12” (DBE, 2011, p. 24).

Heuristic power

Niaz (1995) described development of competence in stoichiometry as progressing from algorithmic dependence to conceptual competence through stages of increasing heuristic power, with this progression being led by evolving conceptual knowledge. Based on this framework, it seems unreasonable to expect a 2 day workshop to propel all its participants to conceptual competence, particularly those who started the workshop at a stage of heavy algorithmic dependence. However, it does seem reasonable to expect an intervention to propel a large proportion of participants along the conceptual – algorithmic continuum, for it to be considered at all efficacious and to view the extent of this propulsion as an indication of the extent of the instructional sequence's efficacy. Increase in heuristic power, operationalised as an increase in both the ability to solve calculation and to answer conceptual, questions, correctly, can therefore be viewed as an indicator of intervention efficacy.

Problem statement

The issue at the heart of this study is whether explicit instruction into a focus on the meaning of the mole reaction ratio and the submicro–macro-scopic connections which the mole concept provides, and an application of these within the unit factor method, can result in uptake of this method in a manner which increases heuristic power. This would suggest that the benefits of an algorithm (calculation success through reduced cognitive load) had been attained without the curses of an algorithm (inflexible application without conceptual understanding).

Research questions

Considering the discussion above, this paper reports on an investigation into the efficacy of instruction aimed at developing an understanding of the mole reaction ratio and submicro- and macro-scopic equivalent forms of the mole concept and applying this to compile appropriate conversion factors within the unit factor method, and so to improve Stoichiometry heuristic power. This was operationalised within a series of two-day professional development workshops for South African physical sciences teachers. In reference to these, this investigation was guided by the research questions: (1) To what extent did the teachers’ stoichiometry strategy use, and heuristic power, change during this intervention? (2) How was uptake of the unit factor method related to changes in heuristic power?

Method

This is a pragmatically conducted, primarily quantitative, survey study, informed by the framework for integrated methodologies (FraIM) (Plowright, 2011). According to FraIM, warrantability, characterised by logic and coherence, serves as a proxy for validity. Besides this constraint, research choices are made pragmatically in manners best suited to answering the research questions. Consistent with this framework, attention is paid to transparent reporting of the methods used to answer the research questions, so that the reader can judge the warrantability of the claims made, and although a quantitative focus is used, a qualitative illustrative example is also drawn on.

Instructional sequence

The instructional sequence under investigation had three foci: (1) the mole concept's central role in connecting the various levels of representation in stoichiometry; (2) the meaning of the mole reacting ratio given in balanced equations; (3) application of these connections and meanings within the unit factor method. This was done by incrementally answering, and guiding learners to understand and apply the answers to the following questions:

• What are submicro- and macro-scopic levels of representation of chemicals, and how does use of these necessitate use of the mole concept?

• What is the mole and how does it connect the submicro- and macro-scopic levels of representation? What is Avagadro's number, how large is it, and why was it chosen to represent the number of particles in a mole?

• What are equivalent ways of describing a mole of various types of particles?

• What is the unit factor method? Why is it valid to multiply a value by a fraction in which the numerator and denominator are equivalent? How can such fractions be arranged to perform a unit conversion, in general, and use equivalent ways of describing a mole, in particular?

• What is proportion? How do ratios and actual amounts differ from one another?

• What is the meaning of a balanced chemical equation? How can the mole reacting ratio given by the balanced equation be expressed in equivalent ways using a variety of units?

• How can proportion, e.g., by means of the unit factor method, be applied to the mole reacting ratio and its equivalent ratios to convert between ratios and actual amounts, and so solve a reaction-based stoichiometry question?

The way this instructional sequence was operationalised in the intervention under investigation is described in the section about the intervention, and an example of partial uptake of the methods promoted is given in the findings section. This instructional sequence is also exemplified in an online program which can be found at https://www.learnscience.co.za/challenge-page/mole-concept.

Intervention

This study refers to a series of eight 2 day (16 hour) in-service stoichiometry professional development interventions conducted across the Free State (FS) province of South Africa (SA) from November 2017 to March 2018 and to which FS physical sciences teachers across the province were invited, by their subject advisors. The intervention was prefaced by a pretest and followed by a posttest and biographical survey. The intervention was guided by the instructional sequence referred to above. This was done through a series of four sessions, each of which consisted of roughly one-hour-long periods of interactive teaching followed by roughly two-hour-long periods in which the participants applied what they had learnt to answer corresponding questions in a fill-in workbook. The participants were also expected to work through sections of the workbook as homework on the evening of the first day. This workbook had been designed with the same foci on concepts, proportion, and the unit factor method, as adopted in the intervention. See a two-page extract of the 42-page workbook in Appendix A. This workbook provides multiple opportunities to practice each type of stoichiometry calculation question relevant to the South African grades 10 and 11 physical sciences curriculum. Each section in the book begins with relevant conceptual questions, followed by a calculation example, using the unit factor method. A consistent colour-coding system is used throughout the book to indicate given and required information and units. These colours are used in the examples provided at the start of a section as well as for fill-in lines given for the first few questions of that section. Annotations are also given regarding the equivalent values required in conversion factors. This colour coding and the provided annotations may be classified as instructional prompts since they are embedded in the task design and are content-dependent (Graulich et al., 2021). These supports are reduced, and eventually removed, in later questions in each section, and at the end of each related group of sections unguided questions are provided about all these sections. This approach matches Graulich et al.'s (2021) description of use of scaffolding prompts.

Sample

The sample used in this research is a subgroup of the 220 teachers who attended these interventions. It consists of the same teachers as included in Stott (2021) on the basis of their completion of the pretest, biographical survey and provision of written informed consent to the anonymous use of their data, minus the 10 of that sample who did not also answer the posttest. Some characteristics of the sample are given in Table 2 to enable judgement of the likelihood that findings from this study may be generalisable to other contexts. There are two routes to qualify to teach physical sciences in South Africa: the BSc (38.5% of this sample), or BEd routes. In either of these, it is not necessary to major in chemistry. Almost half (46%) of this sample did major in chemistry, while most of the remainder (39%) studied only one year of chemistry at the tertiary level. Only 7 (4%) had not studied any chemistry at tertiary level and only 14 (8%) had not taught stoichiometry at school level for at least one year. Before data collection commenced, the ethics committee for educational research at the University of the Free State evaluated the research proposal for compliance with relevant laws and institutional guidelines for ethical research and awarded ethical clearance for the study (UFS-HSD2017/1520).

Table 2 Some characteristics of the sample (n = 161)

Socioeconomic status of the learners taught	Possess a BSc degree	Stoichiometry teaching experience category	N
a 3 years or less. b 3–10 years. c 10 years or more.
High (teach at a quintile 5 school)	No (n = 9)	Inexperienced^a	6
n = 19 (12%)		Moderately experienced^b	3
		Experienced^c	0
	Yes (n = 10)	Inexperienced	4
		Moderately experienced	1
		Experienced	5
Low (teach at quintile 1–4 schools)	No (n = 90)	Inexperienced	46
n = 142 (88%)		Moderately experienced	20
		Experienced	24
	Yes (n = 52)	Inexperienced	26
		Moderately experienced	16
		Experienced	10

---

Data collection

The pre- and post-tests each contained sixteen multiple choice questions which were identical between the tests, and four calculation questions which differed slightly between the tests, although the difficulty (Horvat et al., 2016) and complexity (Knaus et al., 2011) levels of corresponding questions are considered comparable, as indicated in Appendix B. The multiple choice questions have been given, justified and analysed, in Stott (2020). Two of these questions measured algorithmic manipulation rather than conceptual understanding, and so have been excluded from this study. The remaining 14 questions fall into the following categories: (1) minimal conceptual interpretation (2 questions); (2) knowledge of foundational facts (4 questions); common conceptual errors (2 questions); understanding of equivalent submicroscopic and macroscopic values and ratio-amount distinctions (6 questions). The scores extracted from these questions in the manners described below comprise the study's quantitative data, and descriptions of selected calculations comprise the study's qualitative data, as explained in the section on qualitative analysis. All test questions and answers were collected at the end of the test sessions and after this the teachers were not given access to either these questions or their answers. The presenter also took care to avoid any discussion of these questions during or after the intervention, to decrease the limitation arising from prior exposure to the questions from pre- to post-tests, or by teachers from later implementations of the intervention receiving questions from their peers.

Analysis

Scoring for the calculation questions. The researcher engaged with each teacher's calculation questions at least twice: (1) immediately after the test had been written, using the marking guide given in Appendix B; (2) in preparation for this article, using both the marking guide and a checklist of presence of (a) formula provision and (b) substitution into formulae for each of the five relevant formulae given in Appendix B; (c) use of proportion in relation to the mole ratio, regardless of method used; (d) use of the unit factor method. During the second, more thorough, engagement, the initial marking was also checked, and the few marking errors found were then checked across the entire data set to ensure consistency. Each participant's pre- and post-test calculation scores (/16), rather than the numbers of questions for which they obtained the correct answer (/4) in each test, were used to indicate calculation success since these scores give greater precision to the data and they were found to be strongly correlated (r = 0.8 and 0.9 for the pre- and post-tests respectively) to the number of questions for which the correct answer was obtained.

Constructs determined per participant. As illustrated in Fig. 2, and in correspondence to the research questions, the following constructs were determined per participant for each of the pre- and post-tests: strategy use, and conceptual and calculation knowledge (i.e., heuristic power). Strategy use was operationalised by using each participant's four written calculation questions, per test, to categorise them within one of the four strategy groups given in Table 3 and described below, for each of the pre- and post-tests. Conceptual and calculation knowledge were operationalised by the pre- and post-test conceptual (/14) and calculation (/16) scores, respectively, obtained per participant. Conceptual and calculation knowledge changes from pre- to post-tests were also calculated per participant. In correspondence to the second research question, uptake of the unit factor method was measured, operationalised through counting the number of questions (/4) for which the unit factor method was used in the posttest, and consequently assigning them to a posttest unit factor method usage group, as explained below.

Fig. 2 An overview of the constructs determined per participant in preparation for the statistical analysis performed.

Table 3 The strategy classification system used in this article, derived from Stott (2021)

Strategy	Recognition of the need to use of proportion	Explicit statement of, and substitution into, formulae	Example of algorithm which would result in this classification if used to a high degree	Remarks
a Recognised the need to apply proportion to the mole ratio for more than half of the questions. b 7/10 or higher for statement of, and substitution into, formulae.
Proportion reliant	High^a	Low	Unit factor method	Non-deficient
Formula and proportion	High	High^b	Use of formulae and proportion
Formula reliant	Low	High	Use of formulae	Deficient since they do not account for the mole ratio
Minimal	Low	Low	None

---

Strategy groups. The strategy classification system used (see Table 3), was taken from Stott (2021). Relevant to this system, for each of the pre- and post-tests each participant was assigned a Statement of formulae and substitution steps score (/10) and a Proportion usage score (/4). The score out of 10 was obtained by assigning one mark to each of the explicit statement and substitution of values into, each of the five relevant formulae listed in the last column of the table in Appendix B. The score out of 4 was obtained by assigning one mark to each of the four questions for which proportion was applied to the equation's mole reacting ratio, whether this was done correctly or not. Arbitrary threshold points (7/10 and 3/4) were used to define each of the four strategies. Choice of these points was such that approximately equal numbers of participants fell into the deficient and non-deficient strategies in the pretest data. This is discussed in greater detail, together with examples of each strategy group, in Stott (2021).

Posttest unit factor method usage category. Each participant was assigned to a posttest unit factor method usage category. Usage of this method in all four questions was considered particularly meaningful. This group was defined as high usage (n = 70). The other extents of method usage were considered to be more arbitrary, therefore each possible way of grouping the remaining participants into two groups was used and various statistical analyses were performed to determine the most meaningful delineation of these groups (i.e., such that participants of more similar outcomes were grouped together). The first conclusion of this process was that seven of the participants who retained a minimal or formula-reliant strategy in the posttest should be excluded from this analysis to enable comparison of the efficacy of the unit factor method with other non-deficient methods. This is illustrated by means of the dashed block in Fig. 2. Once this was done, it was found that those participants who chose not to use the unit factor method at all, or to use it in only one of the four posttest questions, displayed more similar starting and ending calculation knowledge to one another than those who chose to use this method in two or three of these questions. The former group is referred to as the little to no (n = 33), and the latter as the moderate (n = 58) usage categories.

Statistical analysis. Descriptive and inferential statistics were used. To answer the first research question, regarding changes in strategy use and heuristic power (related to conceptual and calculation knowledge), paired t-tests were used to determine prepost conceptual and calculation improvement, per teacher per grouping. Correlation was also sought between the changes in conceptual and calculation knowledge across the duration of the intervention. To answer the second research question, regarding the relationship between uptake of the unit factor method and changes in conceptual and calculation knowledge (i.e., heuristic power), Anova, followed by Tukey–Kramer, tests were performed for each of these dependent variables, between the three posttest unit factor method usage categories of participants. In all cases values of p < 0.05 were taken as indicating statistical significance. For the Tukey–Kramer tests, the relevant critical q values were determined from statistical tables which are readily available.

Qualitative analysis. Consistent with the pragmatic paradigm adopted in this study (Plowright, 2011), qualitative data were also drawn on to answer the research questions. Guided by the classification systems used, participants were identified who showed changes from deficient (minimal or formula reliant) strategies to high use of the unit factor method within nondeficient strategies. This is consistent with the focus of this study on the value of the unit factor method in improving heuristic power. The identified participants’ written calculation answers to the pre- and post-tests were scrutinised and descriptions were written regarding what was done, together with suggestions of why this may have been done. The pre- and post-test answers, and associated descriptions, for one participant's prepost answers to one question type, is given in the findings section. This example was chosen since it exemplifies and provides nuance to the quantitative findings, as will be argued below.

Findings

Changes in strategy use and heuristic power

Shift towards proportion reliance. As shown in Fig. 3, there was a considerable shift, from pre- to post-tests, towards the proportion reliant strategy, with 80% of the sample displaying this strategy in the posttest, compared to 16% in the pretest. Of particular value is the observed shift of 71 (44%) of the teachers from the deficient minimal or formula reliant strategies to either of the non-deficient (formula and proportion or proportion reliant) strategies. Most (63) of these 71 teachers made this shift towards the proportion reliant strategy, which is unsurprising since the intervention had favoured the unit factor method, which is a proportion reliant strategy, as is explained below.

Fig. 3 Pre–post-test changes in numbers of teachers (/161) and mean calculation scores (/16) for each of the four strategy groups. Tick sizes indicate the magnitude of the mean scores.

High uptake of the unit factor method. Consistent use, or a high degree of use, of the unit factor method, is likely to result in a person being classified as showing a proportion reliant strategy since the unit factor method: (1) is inherently proportional, potentially drawing attention to the need to apply proportion across the mole reaction ratio; (2) makes it unnecessary to provide, and substitute values into, formulae such as those listed in the final column of the table in Appendix B. However, classification in this group does not necessarily imply use of the unit factor method. For example, of the 26 members of the sample classified as showing a proportion reliant strategy in the pretest, only one used the unit factor method. The rest were classified in this group based on their tendency to apparently perform some steps within what could be called symbolic algebra (DeToma, 1994), in their minds. Therefore, their written solutions showed skipped steps of either explicit statement of formulae or substitution into these. In contrast, all 129 of the participants who were classified as showing a proportion reliant strategy in the posttest, made use of the unit factor method for at least one question. Table 4 gives more details about the teachers’ use of the unit factor method in the posttest, with 128 (89% of the sample) using it to a moderate n = 58) or high (n = 70) degree in the posttest.

Table 4 Posttest unit factor method usage

Posttest unit factor method usage category	Number of posttest questions for which the unit factor method was used (/4)	Number of teachers (/161)	Fraction of sample (%)
Little to none	0 & 1	33	20.5
Moderate	2 & 3	58	36
High	4	70	43.5

---

Significantly lower performance for the few who retained a deficient strategy. As shown, unsurprisingly, in Table 5, the few (n = 7) who ended with a deficient strategy started and ended with significantly lower calculation and conceptual knowledge and calculation improvement. A less expected finding is that these groups did not show significantly different conceptual improvement.

Table 5 Initial, final and change in calculation and conceptual scores, for those ending with deficient vs. non-deficient strategies

Ending strategy use category	N (/161)	%	Mean (SD) pre-calculation score (/16)	Mean (SD) post-calculation score (/16)	Mean (SD) pre–post calculation improvement (/16)	Mean (SD) pre- conceptual score (/14)	Mean (SD) post- conceptual score (/14)	Mean (SD) pre–post conceptual improvement (/14)
Deficient	7	4	3.6 (1.9)	4.7 (2.2)	1.1 (3.8)	3.1 (0.8)	5.7 (2.0)	2.1 (2.2)
Non-deficient	154	96	7.1 (4.4)	11.5 (3.3)	4.4 (4.0)	5.1 (2.6)	8.44 (2.7)	3.0 (2.4)
T-test			t(9) = −4.1, p < 0.05	t(7) = −7.3, p < 0.05	t(159) = −2.1, p < 0.05	t(12) = −4.95, p < 0.05	t(7) = −3.25, p < 0.05	t(159) = −0.89, p = 0.37

---

Weak significant correlation between calculation and conceptual improvement. As shown in Table 6, for teachers who ended using a non-deficient strategy, improvements in conceptual and calculation knowledge showed a weak significant correlation (r = 0.2, p < 0.05). The correlation found for the small group who ended with a deficient strategy was not found to be statistically significant. It is acknowledged that the small size (n = 7) of this group reduces the value of this, and other, statistics related to this group.

Table 6 Correlation between conceptual and calculation prepost improvement for each of the deficient and nondeficient ending strategy categories

Ending strategy use category	n	Correlation between conceptual and calculation improvement (r)	p
Deficient	7	−0.5	0.26
Nondeficient	154	0.21 (weak)	<0.05

---

Significant average improvement in heuristic power for those who ended with a non-deficient strategy. As shown in Table 7, paired t-tests for those teachers who ended with a non-deficient strategy showed significant improvement, on average, in both calculation and conceptual scores. This is interpreted as evidence of these teachers’ movement, on average, along Niaz's (1995) algorithmic-conceptual continuum, i.e. gain of heuristic power. In contrast, those who ended with a deficient strategy showed significant improvement in their conceptual, but not calculation, scores.

Table 7 Pre- and post-conceptual and calculation score comparisons for each of the deficient and non-deficient ending strategy use categories of teachers

Ending strategy use category	N (/161)	%	Mean (SD) pre-calculation score (/16)	Mean (SD) post-calculation score (/16)	T-test for pre- and post-calculation scores	Mean (SD) pre-conceptual score (/14)	Mean (SD) post-conceptual score (/14)	T-test for pre- and post-conceptual scores
Deficient	7	4	3.6 (1.9)	4.7 (2.2)	t(6) = −0.74, p = 0.48	3.1 (0.8)	5.7 (2.0)	t(6) = 2.58, p < 0.05
Non-deficient	154	96	7.1 (4.4)	11.5 (3.3)	t(153) = −13.56, p < 0.05	5.1 (2.6)	8.44 (2.7)	t(153) = −13.75, p < 0.05

---

Unit factor method uptake and changes in heuristic power

Except for several higher, and a few very low, achievers, there was a high uptake of the unit factor method. The seven participants who retained deficient strategies in the posttest both started and ended with low calculation knowledge. Three of these seven did not use the unit factor method at all in the posttest, one used it for one question, and three for two questions. For the remainder of the findings these seven have been removed from the analysis. Amongst the remaining teachers (n = 154), those teachers (n = 33, i.e., 20%) who showed little to no uptake of the unit factor method started with significantly higher calculation knowledge. Table 8 shows this, as well as the finding that uptake of the unit factor method was unrelated to starting conceptual knowledge. As has already been pointed out, most of the teachers showed moderate or high use of the unit factor method in the posttest, with these groups not differing significantly from one another in average starting conceptual and calculation scores.

Table 8 Pretest calculation and conceptual averages for each of the posttest unit factor method usage categories, for the 154 teachers who ended with a non-deficient strategy

Posttest unit factor method usage category	N (/161)	%	Mean (SD) pretest calculation score (/16)	Anova	Tukey–Kramer: ^a		Mean (SD) pretest conceptual score (/14)	Anova
a Critical q value: 3.31 for alpha = 0.05.
Little to none	33	20.5	9.8 (4.2)	F(2, 151) = 8.56, p < 0.05			5.6 (2.4)	F(2, 151) = 2.75, p = 0.07
Moderate	58	36	5.8 (4.3)				4.5 (2.9)
High	70	43.5	7.1 (4.1)				5.4 (2.4)

---

Teachers who used the unit factor method to a moderate degree ended with lower calculation scores, on average. Table 9 shows that teachers displaying a moderate uptake of the unit factor method ended with significantly lower calculation scores than each of the other non-deficient groups. However, all these groups’ posttest conceptual scores differed insignificantly to one another.

Table 9 Posttest calculation and conceptual averages for each of the posttest unit factor method usage categories, for the 154 teachers who ended with a non-deficient strategy

Posttest unit factor method usage category	N (/161)	%	Mean (SD) posttest calculation score (/16)	Anova	Tukey–Kramer: ^a		Mean (SD) posttest conceptual score (/14)	Anova
a Critical q value: 3.31 for alpha = 0.05.
Little to none	29	18.8	13.0 (2.5)	F(2, 151) = 12.88, p < 0.05			9.2 (2.8)	F(2, 151) = 1.79, p = 0.17
Moderate	55	35.7	9.9 (3.7)				7.9 (2.9)
High	70	43.5	12.2 (2.7)				8.6 (2.5)

---

Changes in heuristic power were independent of uptake of the unit factor method for non-deficient strategies. Regardless of the difference in starting and ending scores, discussed above, as shown in Table 10, no statistically significant difference was found between the average improvement in calculation or conceptual knowledge for the three non-deficient posttest unit factor usage categories.

Table 10 Pre–post calculation and conceptual improvement averages for each of the posttest unit factor method usage categories, for the 154 teachers who ended with a non-deficient strategy

Posttest unit factor method usage category	N (/161)	%	Mean (SD) pre–post calculation improvement (/16)	Anova	Mean (SD) pre–post conceptual improvement (/14)	Anova
Little to none	29	18.8	3.2 (3.5)	F(2, 151) = 2.59, p = 0.08	3.6 (2.4)	F(2, 151) = 2.47, p = 0.09
Moderate	55	35.7	4.1 (4.0)		2.4 (2.3)
High	70	43.5	5.2 (4.0)		3.1 (2.3)

---

Qualitative example suggests that uptake of the unit factor method can mediate enhanced heuristic power. See Table 11 for the pre- and post-test answers to question 2 (see Appendix B) for one of the 45 teachers who shifted from the minimal to the proportion reliant strategy, using the unit factor method to a high degree in the posttest. A comparison between these answers and the marking and checklist guidelines given in Appendix B, for this question, shows that for both the pre- and post-tests this teacher: (a) did not use any formulae relevant to answering the question and (b) made use of proportion. Despite these similarities, their calculation success differed greatly between pretest (1 mark out of 5) and posttest (5/5) for this question. This difference in success corresponds to an apparent difference in focus. In the pretest the teacher seemingly aimlessly gave two irrelevant formulae, crossed one out and used the other inappropriately, and did not apply proportion to the mole ratio. This is even though this teacher had a BSc degree with first year Chemistry. They were, however, inexperienced, being in their first year of teaching.

Table 11 A single teacher's solution to two similar questions without and with use of the unit factor method in pre- and post-tests, respectively

Question 2: number of atoms	Answer and commentary
Pretest:
How many atoms of hydrogen are needed to fully react with 17 dm^3 of nitrogen gas at STP according to the reaction equation: 2N2 + 3H2 → 2NH3?	Avogadro's law is applied, via the cross-product method, converting dm^3 to mole, but proportion has not been applied to the mole ratio. Two irrelevant equations are provided, one crossed out and one used inappropriately.
Posttest:
How many atoms of hydrogen are needed to fully react with nitrogen to form 13 dm^3 of NH3 at STP according to the reaction equation: 2N2 + 3H2 → 2NH3?	Equivalent information is tabulated for the balanced equation, after which the unit factor method is used to obtain the correct answer. The alterations suggest later considerations of the diatomic nature of H2 molecules, which is applied pragmatically although not entirely correctly. Note H2 atoms and the inappropriate tabulated information regarding molecule ratios. The cancelled and overwritten work suggests that they initially provided molecule ratios in the table and solved for the number of H2 molecules required. They then realized that the question referred to atoms rather than molecules, and so they inflated the two diatomic elements’ coefficients in the molecule line of the table, but left NH3's information as it was, in so doing making the entire ratio incorrect, but enabling correct answering of the question about H atoms.

---

In contrast to this aimless approach in the pretest, the unit factor method was clearly used to focus the teacher's thinking productively in the posttest. They began by tabulating equivalent reacting values relevant to the question (molar, molecular and volume) for each substance, after which they used these values to compile conversion factors within the unit factor method. This suggests development of understanding of the relationship between measurements on the macro- and submicro-scopic levels, although this view is somewhat undermined by their incorrect reference to H₂ atoms, as well as the error present in the tabulated row referring to molecules, which likely arose pragmatically as speculated in the table.

Consistent with the remarks made above, this teacher showed considerable pre- to post-test conceptual (4 to 8/14) and calculation (2 to 14/16) improvements. However, they showed little conceptual improvement regarding equivalent values (0 to 1/6) despite their ability to use these correctly in the calculations in the posttest, as shown in this example.

Discussion

Changes in strategy use and heuristic power

Shift to non-deficient strategies coupled with increased heuristic power. The large shift to non-deficient strategies, the statistically significant improvements in both conceptual and calculation knowledge, and the correlation found between these improvements, suggest that the instructional sequence used can be effective in increasing heuristic power. There is the possibility that this may have occurred via the mechanism of conceptual understanding having been developed through direct instruction in the meanings of the mole ratio and the macro- and submicro-scopic relationships within the mole concept and application of these within the unit factor method, and this conceptual understanding then improving the participants’ calculation skill. This would be consistent with Niaz's (1995) thesis that development of heuristic power is led by development of conceptual understanding. However, possibly inconsistent with this, the qualitative example given shows the teacher's ability to seemingly implement conceptual knowledge within an algorithm without that conceptual knowledge being detected by the conceptual test. Also, once the seven outliers were removed from the analysis, no significant difference was found between the various groups’ conceptual knowledge, regardless of presence of significant differences between these groups’ abilities to perform calculations correctly. This apparent mismatch is discussed further, below.

Mismatch between successful application of mole-related equivalence within calculation and conceptual questions. The findings given in Stott (2020) are related to those discussed in this article, since they refer to the same data set resulting from the same series of interventions. These showed that improvement for various categories of conceptual knowledge across the intervention was context dependent. The category of conceptual knowledge which fewest teachers managed to develop across the duration of the 2 day intervention was the category most relevant to application of conceptual knowledge to the unit factor method, focused on in this article: equivalent submicro- and macro-scopic values and ratio-amount distinctions. Only the small group (n = 19) of teachers teaching at schools serving richer communities, displayed considerable average improvement in this conceptual area. This seems not to correspond to this study's finding of high levels of calculation success, largely through use of the unit factor method, and therefore largely correct compilation of conversion factors using sets of equivalent values, as illustrated by the qualitative example included above.

Attempts to explain this mismatch. There are several possible explanations for this mismatch in terms of limitations of the study: perhaps the conceptual test was not sensitive enough to detect presence of the conceptual knowledge evidenced in the calculation; perhaps the suggestion that conceptual knowledge was present, based on the observed calculation success, is an illusion, as described by Niaz and Robinson (1993). Other possibilities also exist, for example that the context of use of the unit factor method primed, and provided metacognitive support for, activation of conceptual knowledge within the written calculation, whereas this failed to occur in the absence of this method within the conceptual questions. Alternatively, or additionally, superficial features of the conceptual questions may have primed an intuitive response which masked the presence of the relevant conceptual knowledge (Talanquer, 2006). These explanations are consistent with a Knowledge in Pieces (KiP) view of knowledge (diSessa, 2018) and may have parallels to Hartman and Nelson's (2021) distinction between implicit and explicit conceptual understanding. If so, then perhaps Hartman and Nelson's (2021) call for satisfaction with implicit conceptual understanding in school-level learners and university students who do not major in Chemistry, may be understood as follows. Implicit conceptual understanding may improve heuristic power sufficiently to empower correct calculation solution with sufficient meaningfulness to reduce the problems associated with rote application of algorithms (Nyachwaya et al., 2014) to an acceptable level, given contextual constraints. This raises several issues, such as how empirical evidence could be gathered in future research to examine these speculations, and whether implicit conceptual knowledge is sufficient for chemistry teachers. It would certainly be preferable for a teacher to be able to verbalise their understanding to communicate this to their learners (Skemp, 1987). Indeed, they would be unable to replicate the instructional sequence under investigation without this ability, reducing its value and sustainability.

Unit factor method uptake and changes in heuristic power

Regarding uptake of the unit factor method and enhanced heuristic power in Stoichiometry, the findings suggests that: (1) increase in heuristic power across the duration of the intervention was dependent on participants developing awareness of the need to use proportion in Stoichiometry, but this awareness did not necessarily have to be developed through uptake of the unit factor method; (2) participants who started with good calculation knowledge were particularly likely to reject uptake of the unit factor method; (3) moderate uptake of the unit factor method, possibly resulting from the intervention period being too short for development of confidence in the method, was characterised by more modest gains in calculation skill during the intervention.

These assertions are unsurprising, given that (1) multiple valid methods exist in Stoichiometry, including the collection of methods referred to here as formula and proportion strategies, (2) which most of the teachers who rejected the unit factor method were competent in at the start of the intervention (see Fig. 3), and which is favoured in South African chemistry marking guidelines at the school level (Stott, 2021); (3) teacher development tends to be a slow process (Luft and Hewson, 2014), and learning a new algorithm can be time-consuming, as discussed in the limitations section below.

Limitations

The findings of this study are limited to the duration of these 2 day workshops. The requirement for continued use of an algorithm until automaticity has been obtained, for a person to attain fluency (Hartman and Nelson, 2015), may undermine the long-term efficacy of such an intervention. This would certainly be the case for teachers whose use of the method would end at the end of the workshop. Providing the teachers with enough write-and-wipe scaffolded fill-in workbooks for use in their classes likely reduced the extent to which the uptake ended at the end of the investigated intervention. However, the current failure to recognise the unit factor method within the South African physical sciences examination marking guidelines (Stott, 2021), increases the likelihood that uptake ended at the end of the workshop. Additional limitations have been discussed within the text above.

The argument could be made that the measured learning gains resulted from time on task, rather than from the efficacy of the instructional sequence used. Improvement related to time on task is, however, not by any means assured (Rudduck, 1986; Luft and Hewson, 2014), particularly in the developing world (Rogan, 2004; Stott, 2020). This view is supported by the low initial mean scores these teachers attained for these basic school-level calculations in the pretest, despite all but 7 having studied chemistry at tertiary level, and all but 14 having taught at least one year of stoichiometry at the high school level.

Conclusion

The objective of this study was to contribute to understanding the efficacy of providing explicit instruction into the meaning of the mole reaction ratio and the mole concept's connection between the macro- and submicro-scopic levels of representation in Chemistry and application of this knowledge to compile conversion factors within the unit factor method when solving Stoichiometry calculations. Such instruction is aimed at enhancing the participants’ heuristic power and so enhancing their ability to apply both algorithms and conceptual knowledge correctly (Niaz, 1995), for example to attain the correct answer to calculation and conceptual questions. The findings suggest that such instruction can effectively enhance heuristic power, although it appears that: (1) a two-day workshop is too short for optimal efficacy for approximately a third of teachers in this context; (2) the efficacy of the instructional sequence is dependent on development of an understanding of the importance of proportion in Stoichiometry, although this does not need to be coupled with uptake of the unit factor method; (3) the implicit understanding of how to apply mole-related equivalent values within the unit factor method in calculations may develop without development of explicit understanding of this equivalence.

Conflicts of interest

There are no conflicts to declare.

Appendix A: a part of the workbook used in the intervention

Appendix B: the questions used

Question	Topic	Pretest	Posttest	Difficulty level (according to Horvat et al., 2016)	Concepts	Interactivity value (according to Horvat et al., 2016)	Complexity rating (applying Knaus et al.'s (2011) rubric)	Marks and mark allocation	Formulae relevant to formula-accessible calculations
1	Yield determined by limiting reagent	A reaction mixture contains 17 g N2 and 0.5 mol H2. One of these is limiting. They react according to the given equation. What is the maximum number of moles of NH3 produced?	A reaction mixture contains 3.5 mol N2 and 18 g H2. One of these is limiting. They react according to the given equation. What is the maximum number of moles of NH3 that can be produced?	Medium, since given and required units differ, with one being moles	Limiting reagent, stoichiometric calculation	0, since only 2 concepts are applied	3	(1) Application of mole ratio	(not included in the checklist since the pretest could be answered without its use)
								(2) To the correctly chosen limiting reagent
								(3) Correct answer
								(3 Marks)
2	Number of H atoms needed to react with a given volume of N2	How many atoms of hydrogen are needed to fully react with 17 dm^3 of nitrogen gas at STP?	How many atoms of hydrogen are needed to fully react with nitrogen to form 13 dm^3 NH3 at STP?	Difficult, since given and required units differ, with neither being moles	Avogadro's law, stoichiometric calculation, submicroscopic particles	1, since 3 concepts are applied	6 + 1 = 7	(1) Volume to molar conversion
								(2) Application of mole ratio	N = nNA
								(3) Conversion to molecules
								(4) Conversion to atoms
								(5) Correct answer
								(5 Marks)
3	Percentage yield	7 g H2 reacts completely with N2 to form 28 g NH3. What is the percentage yield?	7 g N2 react completely with H2 to form 8 g NH3. What is the percentage yield?	Difficult, since given and required units differ, with neither being moles	Stoichiometric calculation, percent yield	0, since only 2 concepts are applied	5	(1) Application of mole ratio
								(2) To find theoretical yield
								(3) % yield formula
								(4) Correct answer
								(4 Marks)
4	Yield without limiting reagent	Calculate the maximum mass of SO3 that could be produced from 1.9 mol of oxygen and excess sulphur.	Calculate the maximum mass of SO3 that could be produced from 6 mol of oxygen and excess sulphur.	Medium, since given and required units differ, with one being moles	Chemical equation, stoichiometric calculation	0, since only 2 concepts are applied	3	(1) Balanced equation
								(2) MSO3 = 80 g mol^−1
								(3) Application of mole ratio
								(4) Correct answer
								(4 Marks)

References

1. BIMP, (2019), in Inglis B., Ullrich J. and Milton M. J. T. (ed.), The international system of units, SI Brochure, 9th edn, International Bureau of Weights and Measures, https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf.
2. Cook E. and Cook R. L., (2005), Cross-proportions: A conceptual method for developing quantitative problem-solving skills, J. Chem. Educ., 82(8), 1187 DOI:10.1021/ed082p1187.
3. DBE, (2011), Physical sciences curriculum and assessment policy statement, Pretoria: Department of Basic Education.
4. DeMeo S., (2008), Multiple solution methods for teaching science in the classroom: Improving quantitative problem solving using dimensional analysis and proportional reasoning, Universal-Publishers.
5. DeToma R. P., (1994), Symbolic algebra and stoichiometry, J. Chem. Educ., 71(7), 568 DOI:10.1021/ed071p568.
6. diSessa A. A., (2018), A friendly introduction to “knowledge in pieces”: Modeling types of knowledge and their roles in learning, Invited Lectures from the 13th International Congress on Mathematical Education, pp. 65–84 DOI:10.1007/978-3-319-72170-5_5.
7. Fang S.-C., Hart C. and Clarke D., (2014), Unpacking the meaning of the mole concept for secondary school teachers and students, J. Chem. Educ., 91(3), 351–356.
8. Gabel D. L. and Sherwood R. D., (1983), Facilitating problem solving in high school chemistry, J. Res. Sci. Teach., 20(2), 163–177 DOI:10.1002/tea.3660200207.
9. Graulich N., Langner A., Vo K. and Yuriev E., (2021), Scaffolding Metacognition and Resource Activation During Problem Solving: A Continuum Perspective, in Tsaparlis G. (ed.), Problems and Problem Solving in Chemistry Education: Analysing Data, Looking for Patterns and Making Deductions, The Royal Society of Chemistry, pp. 38–67 10.1039/9781839163586-00038.
10. Gulacar O., Cox C. and Fynewever H., (2021), Deconstructing the Problem-solving Process: Beneath Assigned Points and Beyond Traditional Assessment, in Tsaparlis G. (ed.), Problems and Problem Solving in Chemistry Education: Analysing Data, Looking for Patterns and Making Deductions, The Royal Society of Chemistry, pp. 68–92 10.1039/9781839163586-00068.
11. Hartman J. R. and Nelson E. A., (2015), “Do we need to memorize that?” or cognitive science for chemists, Found. Chem., 17(3), 263–274 DOI:10.1007/s10698-015-9226-z.
12. Hartman J. R. and Nelson E. A., (2021), A paradigm shift: The implications of working memory limits for physics and chemistry instruction, arXiv, preprint, arXiv:2102.00454 DOI:10.48550/arXiv.2102.00454.
13. Herron J. D. and Wheatley G. H., (1978), A unit factor method for solving proportion problems, Math. Teach., 71(1), 18–21 DOI:10.5951/MT.71.1.0018.
14. Horvat S., Segedinac M. D., Milenković D. D. and Hrin T. N., (2016), Development of procedure for the assessment of cognitive complexity of stoichiometric tasks, Macedonian J. Chem. Chem. Eng., 35(2), 275–284.
15. Johnstone A. H., (2000), Teaching of chemistry-logical or psychological? Chem. Educ. Res. Pract., 1(1), 9–15 10.1039/A9RP90001B.
16. Knaus K., Murphy K., Blecking A. and Holme T., (2011), A Valid and Reliable Instrument for Cognitive Complexity Rating Assignment of Chemistry Exam Items, J. Chem. Educ., 88(5), 554–560 DOI:10.1021/ed900070y.
17. Koopman O., (2017), Investigating how science teachers in South Africa engage with all three levels of representation in selected chemistry topics, Afr. J. Res. Math., Sci. Technol. Educ., 21(1), 15–25.
18. Luft J. A. and Hewson P. W., (2014), Research on teacher professional development programs in science, Handbook of Research on Science Education, Volume II, Routledge, pp. 903–924.
19. Malcolm S. A., Mavhunga E. and Rollnick M., (2019), The Validity and Reliability of an Instrument to Measure Physical Science Teachers’ Topic Specific Pedagogical Content Knowledge in Stoichiometry, Afr. J. Res. Math., Sci. Technol. Educ., 22(2), 181–194.
20. Mweshi E., Munyati O. and Nachiyunde K., (2020), Teachers’ Understanding of the Link between the Atomic Theory and the Mole Concept, Afr. J. Res. Math., Sci. Technol. Educ., 24(3), 411–422.
21. Niaz M., (1995), Progressive transitions from algorithmic to conceptual understanding in student ability to solve chemistry problems: A Lakatosian interpretation, Sci. Educ., 79(1), 19–36.
22. Niaz M. and Robinson W. R., (1993), Teaching algorithmic problem solving or conceptual understanding: Role of developmental level, mental capacity, and cognitive style, J. Sci. Educ. Technol., 2(2), 407–416.
23. Nyachwaya J. M., Warfa A.-R. M., Roehrig G. H. and Schneider J. L., (2014), College chemistry students’ use of memorized algorithms in chemical reactions, Chem. Educ. Res. Pract., 15(1), 81–93.
24. Page M. F. Z., Escott P., Silva M. and Barding G. A., (2018), The effect of teaching the entire academic year of high school chemistry utilizing abstract reasoning, Chem. Educ. Res. Pract., 19(2), 500–507 10.1039/c7rp00252a.
25. Plowright D., (2011), Using mixed methods: Frameworks for an integrated methodology, SAGE Publications.
26. Poole R. L., (1989), Teaching stoichiometry: A two cycle approach, J. Chem. Educ., 66(1), 57 DOI:10.1021/ed066p57.
27. Ralph V. R. and Lewis S. E., (2018), Chemistry topics posing incommensurate difficulty to students with low math aptitude scores, Chem. Educ. Res. Pract., 19(3), 867–884.
28. Ramful A. and Narod F. B., (2014), Proportional reasoning in the learning of chemistry: levels of complexity, Math. Educ. Res. J., 26(1), 25–46.
29. Ramnarain U. and Chanetsa T., (2016), An analysis of South African Grade 9 natural sciences textbooks for their representation of nature of science, Int. J. Sci. Educ., 38(6), 922–933.
30. Robinson W. R., (2003), Chemistry problem-solving: Symbol, macro, micro, and process aspects, ACS Publications DOI:10.1021/ed080p978.
31. Rogan J., (2004), Professional Development: Implications for developing countries, in O-Saki K., Hosea K. and Ottevanger W. (ed.), Reforming Science and Mathematics Education in Sub-Saharan Africa: Obstacles and Opportunities, University of Dar es Salaam, pp. 155–170.
32. Rudduck J., (1986), Making the most of the short inservice course, in Hopkins D. (ed.), Inservice Training and Educational Development: An International Survey, Croom Helm, pp. 302–311.
33. Selvaratnam M., (2011), High school Physical Sciences teachers’ competence in some basic cognitive skills, S. Afr. J. Chem., 64, 231–236.
34. Skemp R. R., (1987), Relational understanding and instrumental understanding, in Skemp R. R. (ed.), The Psychology of Learning Mathematics, Routledge, pp. 232–244 DOI:10.4324/9780203396391.
35. Spiro R. J. and Deschryver M., (2009), Constructivism: When it's the wrong idea and when it's the only idea, in Tobias S. and Duffy T. M. (ed.), Constructivist Instruction: Success or Failure? Routledge, pp. 106–124.
36. Stott A. E., (2020), Influence of Context on Stoichiometry Conceptual and Algorithmic Subject Matter Knowledge among South African Physical Sciences Teachers, J. Chem. Educ., 97(5), 1239–1246 DOI:10.1021/acs.jchemed.9b01056.
37. Stott A. E., (2021), South African physical sciences teachers’ use of formulae and proportion when answering reaction-based stoichiometry calculation questions, Chem. Educ. Res. Pract., 22(2), 443–456 10.1039/D0RP00291G.
38. Sweller J., (2011), Cognitive load theory, Psychology of learning and motivation, Elsevier, vol. 55, pp. 37–76.
39. Talanquer V., (2006), Commonsense chemistry: A model for understanding students’ alternative conceptions, J. Chem. Educ., 83(5), 811.
40. Tang H., Kirk J. and Pienta N. J., (2014), Investigating the effect of complexity factors in stoichiometry problems using logistic regression and eye tracking, J. Chem. Educ., 91(7), 969–975 DOI:10.1021/ed4004113.
41. Taylor N., (2019), Inequalities in teacher knowledge in South Africa, in Spaull N. and Jansen J. (ed.), South African schooling: The enigma of inequality, Springer, pp. 263–282 DOI:10.1007/978-3-030-18811-5.
42. Tsaparlis G., (2021), It Depends on the Problem and on the Solver: An Overview of the Working Memory Overload Hypothesis, Its Applicability and Its Limitations, in Tsaparlis G. (ed.), Problems and Problem Solving in Chemistry Education, The Royal Society of Chemistry, pp. 93–126 10.1039/9781839163586-00093.
43. Vo K., Sarkar M., White P. J. and Yuriev E., (2022), Problem solving in chemistry supported by metacognitive scaffolding: teaching associates’ perspectives and practices, Chem. Educ. Res. Pract., 23(2), 436–451 10.1039/D1RP00242B.

---