Predictions of success in organic chemistry based on a mathematics skills test and academic achievement

Abstract

Organic Chemistry I presents challenges to many students pursuing diverse fields of study, oftentimes curtailing further progress in those fields. The ability to identify students at risk of unsuccessful course outcomes may lead to improved success rates by offering tailored resources to those students. Previously identified predictors include college entrance exam scores, grade point averages (GPA), General Chemistry II course grades, first exam scores, and results from a logical thinking assessment. This work explores the use of the 20-item Math-Up Skills Test (MUST) in a first-semester organic chemistry course over two years at a small private university. Analysis of scores on the MUST, which is taken during the first week of the semester, indicates a statistically significant difference between successful and unsuccessful first-time students (n = 74 and 49, respectively) as the MUST has good internal consistency (Cronbach's alpha = 0.861) and a large effect size (Cohen's d = 1.29). Taken alone, the MUST predicts students at risk of not passing the course with 64% accuracy; addition of start-of-term science GPA data improves predictions to 82% accuracy. Predictions are further improved with incorporation of scores from the first exam of the semester. Observations to date indicate that the MUST is an easily administered assessment that can be utilized alone or as part of a trio of measures to predict success in first-semester Organic Chemistry. Implications of a mathematics assessment as a predictor for Organic Chemistry are addressed.

---

Introduction

Organic Chemistry maintains a long-held reputation among science majors as a course to fear because of the high rate of students who withdraw or fail each year. Indeed, attrition rates vary from 30–50% each year for the two-semester sequence (Grove et al., 2008). Such reduction impacts the number of students prepared to obtain advanced degrees in the sciences as well as in medicine (Hall et al., 2014; Harris et al., 2020; Zhang et al., 2020). Improvements to student retention and success in organic chemistry courses would therefore help to repair one leak in the STEM pipeline resulting in a larger number of graduates entering professional careers as scientists and health-care providers.

Efforts to compare levels of student success fall into two categories: those that examine common characteristics of successful students and those that employ assessments or measures to predict success from the outset of the course. Characteristics common amongst students who successfully complete organic chemistry include a positive perception of the field and attitude toward chemistry (Steiner and Sullivan, 1984; Turner and Lindsay, 2003), self-efficacy (Lynch and Trujillo, 2011; Villafañe et al., 2016), increasing levels of autonomous motivation (Black and Deci, 2000), more frequent studying early in the semester (Szu et al., 2011), and engaging in help-seeking behaviors (Horowitz et al., 2013). Grove and Bretz (2010) indicate that the study of organic chemistry requires learners to function at the multiplistic or relativistic levels of epistemological development. Furthermore, students classified as abstraction learners outperform exemplar learners in Organic Chemistry II (Frey et al., 2017).

While decisions relating to classroom practices and the development of resources may be informed by characteristics of successful students, these characteristics do little to identify which individuals will likely struggle through the class. Assessments and measures that can serve as an early warning system offer valuable information to instructors who can offer tailored resources to students at risk of not passing Organic Chemistry before any damage to grades occurs. Previously identified warning signals include several measures of general achievement, briefly described here in the order a student would encounter the assessment.

Standardized tests, taken prior to a student's entering college, show a moderate correlation with organic chemistry grades (Rixse and Pickering, 1985; Turner and Lindsay, 2003; Pursell, 2007; Hall et al., 2014). Rixse and Pickering found the mathematics and verbal sections of the SAT to correlate equally well with organic grades (n = 117, r² = 0.16 and 0.14, respectively), while Turner and Lindsay found organic scores correlated slightly better with the ACT-mathematics section than with they did with the English, reading, or science reasoning sections of the ACT (n = 221). Other groups have reported conflicting results concerning standardized test scores and organic grades. The Cadet Entrance Evaluation Report, a score comprised of 48% SAT-mathematics, 22% SAT-verbal, and 30% high school rank, showed widely varying correlations (r² = 0.001–0.59) with organic scores in four sections of the course (n = 18–20) at the United States Military Academy at West Point (Pursell, 2007). Steiner and Sullivan (1984) also reported better performance on the ACT-mathematics amongst the organic students earning a C or lower compared with those earning C+ or better (n = 64). Taken together, standardized test scores may not serve as the most reliable predictor of success.

Students typically enroll in organic chemistry during their second or third year of college, approximately two or three years after taking the standardized tests. Thus, students enrolling in organic courses have grade point averages (GPA) from coursework done during their first year or two of college. Students’ incoming GPA showed moderate to high correlations with organic grades (r² = 0.18–0.67) (Pursell, 2007; Szu et al., 2011). In addition to indicating a level of general knowledge, part of this measure may include affective traits such as study skills and habits. Lopez and colleagues (2014) limited the incoming GPA to that of a prior science GPA, which included any science courses completed prior to organic, and found the refined measure accounted for 19% of the variability in students’ problem-solving performance.

Among the courses that would comprise a science GPA are those in the general chemistry sequence, which typically serves as a prerequisite for enrollment in first-semester organic. Indeed, general chemistry courses address several concepts (e.g., electronegativity, bonding, molecular geometry, hybridization, etc.) that are foundational to a solid understanding of the structure and reactivity of organic compounds, so it is unsurprising that general chemistry scores have been positively related to organic chemistry (Pursell, 2007; Austin et al., 2015). General Chemistry II courses, which tend toward quantitative analyses, show a range of correlations with Organic Chemistry I outcomes (r² = 0.32–0.52) (Rixse and Pickering, 1985; Turner and Lindsay, 2003; Horowitz et al., 2013). A comparison of course grades revealed that more than 50% of students in organic chemistry earn within one-third of a grade step of their general chemistry grade (such as B to B–), with most changes in the downward direction (Rixse and Pickering, 1985).

Less is known of the relationship between General Chemistry I scores and Organic Chemistry I grades despite the fact that General Chemistry I houses the aforementioned relevant topics. Rixse and Pickering (1985) report sophomores’ fall organic chemistry grades more weakly correlate with fall freshman chemistry than with spring freshman chemistry (r² = 0.30 and 0.38, respectively), but the reverse holds true for juniors (r² = 0.50 and 0.37, respectively). Jasien (2003) compared students having either one or two semesters of general chemistry and found no statistically significant difference between their organic course outcomes, which might indicate that only General Chemistry I was important for success in organic courses. However, he also reported that the groups were statistically significantly different in age (with older students having two semesters of general chemistry) and in the amount of time since their most recent chemistry course. Both studies may indicate that organic course performance depends on the student's total amount of college experience (Robinson et al., 2007).

When multiple predictors were measured within a single study, general chemistry scores outperformed help-seeking behaviors (Horowitz et al., 2013), standardized test scores (Rixse and Pickering, 1985), and noncognitive variables (Turner and Lindsay, 2003) but fell behind incoming GPA (Pursell, 2007).

The first exam of the semester has been shown to indicate which students might not pass first semester organic at the University of North Georgia (Hollabaugh et al., 2019). Nearly two-thirds of students earned course averages within 10 points of their first exam score. As these first exam scores accounted for only 15% of the overall course grade, researchers discounted “arithmetic determinism” as the sole cause of the relationship between the two scores. Rather, they postulated that the first exam assesses students’ knowledge of review topics (e.g., Lewis structures and molecular geometries) and new concepts (e.g., structure representations, resonance, and acid-base chemistry) that are essential due to the cumulative nature of the course; inability to master these topics leads to shaky understanding of later concepts (Hollabaugh et al., 2019). Exam scores were also found to have a small but positive reciprocal effect with self-efficacy on performance (Villafañe et al., 2016).

Cognitive ability

Piaget's cognitive development theory posits that children and adults progress through four stages of development, with each stage relating to certain thought processes and abilities and constructed on earlier stages (Piaget, 1964; Bodner, 1986; Ojose, 2008). As children transition into adolescence and then adulthood, they also transition from concrete operational to formal operational. This last stage is marked by abstract thought and an ability to reason hypothetically, without physical objects or models. Piagetian tasks associated with formal thought include combinatorial reasoning, control of variables, probabilistic reasoning, and proportional reasoning (Lawson, 1979; Jiang et al., 2010).

Herron (1975), Goodstein and Howe (1978), and Bird (2010) indicate that the study of college chemistry requires students to be at the formal operational level but that many still are pre-formal thinkers. Indeed, formal thought assessment scores correlate with outcomes in general chemistry courses (Bender and Milakofsky, 1982; Bunce and Hutchinson, 1993; Lewis and Lewis, 2007; Bird, 2010). While similar comparisons between cognitive development and organic chemistry course outcomes do not seem to have been explored, Bunce and Hutchinson found a moderate correlation (r² = 0.22) between the Group Assessment of Logical Thinking (Roadrangka et al., 1983) and outcomes in an organic and biochemistry course for nursing majors (1993). Certainly, a one-semester organic chemistry course for nonmajors would entail a different level of rigor than a two-semester sequence for science majors, though there would be noteworthy similarities in the course materials. While the developmental level required by organic chemistry students is nebulous, select factors may provide an indication of the students’ general level of reasoning ability.

Spatial ability, including mental visualization and rotation of objects, has long been recognized as having strong ties to chemistry (Harle and Towns, 2011) and has been shown to have a small correlation with organic chemistry course outcomes (Turner and Lindsay, 2003). The correlation most likely manifests in the ability's significant main effects on tasks involving: (1) conversion between names and structural formulas, (2) three-dimensional features of molecules, (3) completion of a reaction equation with either a missing reagent or product, (4) outline of a multi-step synthesis, (5) identification of a wrong or incomplete structure or formula, and (6) answering higher-order multiple choice questions (Pribyl and Bodner, 1987). Furthermore, spatial ability has been shown to have a significant relationship to mathematical ability (Guay and McDaniel, 1977; Battista et al., 1982; Jones et al., 2011; Cheng and Mix, 2014; Mix et al., 2016; Resnick et al., 2020). A meta-analysis examining the intricacies of the relationship revealed spatial ability is more strongly correlated with logical ability than with numerical or arithmetical ability (Xie et al., 2020).

Mathematical ability enjoys further ties to logical ability. The two require cognitively demanding mental operations such as the ability to process symbolic and abstract representations, to apply rules and draw conclusions, and to reason abstractly (Morsanyi and Szücs, 2014). In exploring the long-held idea that mathematics training develops general thinking ability, Inglis and Simpson (2009) determined that undergraduate students of mathematics outperform intelligence-matched non-mathematics students in conditional inference tasks. Further exploration of 16- to 18-year-olds revealed that students studying mathematics show greater improvement in their logical reasoning on the same conditional inference tasks than their non-mathematics peers (Attridge and Inglis, 2013). Use of a larger battery of rational and logical reasoning tasks provided similar results: more extensive mathematics training correlated with increased success on reasoning tasks amongst participants ranging from first-year undergraduates through research academic mathematicians (Cresswell and Speelman, 2020). The relationship between mathematic ability and logical reasoning may even be observed as early the age of six. Nunes et al. (2007) reported that logical competence at the start of primary school is causally related to mathematics achievement over the first 16 months and that training in logical competence has a large effect size on mathematics ability even after 13 months.

Mathematics assessments and chemistry courses

Chemistry and mathematics are connected more directly than just their mutual relationships with logical ability as mathematics is the language of sciences. As such, chemistry education research has extensively reported on the use of mathematics assessments to predict success in general chemistry courses. Many of these include the mathematics portion of the SAT or ACT (Craney and Armstrong, 1985; Rixse and Pickering, 1985; Spencer, 1996; Lewis and Lewis, 2007; Ralph and Lewis, 2018; Kreiser et al., 2022), while others are more institution-based and cover common topics. Logarithms, scientific notation, graphs, algebra, and arithmetic without the use of a calculator frequently appear on these assessments of quantitative literacy and quantitative reasoning (Bohning, 1982; Leopold and Edgar, 2008; Kennepohl et al., 2010; Shelton et al., 2021).

Tai et al. (2006) identified multiple significant mathematics-related predictor variables in a regression model for success in first-semester college chemistry; these included enrollment in calculus in high school, SAT-math score, last grade in a high school mathematics course, and experience with stoichiometry in high school chemistry. They propose that calculus experience denotes a level of mathematics fluency essential for comprehension of chemistry lectures and texts that assume an understanding of symbols and equations. Furthermore, Kennepohl et al. (2010) found scores on mathematics and critical thinking questions more closely correlated with chemistry course performance than scores on conceptual basics, problem solving, or previous schoolwork.

Recently, researchers from six Texas universities reported the use of a 20-item Math-Up Skills Test (MUST) and a demographics survey to predict success in General Chemistry I (Williamson et al., 2020) and in General Chemistry II (Powell et al., 2020). Advantages of the MUST include the ability to assess student strength from the first day of class, a minimal time commitment for the assessment, and the availability of results for every student. With the established relationships between organic chemistry performance and logical reasoning and between mathematics ability and logical reasoning, we were curious to see if the MUST could predict course outcomes for first-semester organic chemistry, the next course in the typical college chemistry sequence.

Research questions

(1) To what extent does an assessment of arithmetic skills (the MUST) predict which students will have successful course outcomes (scores of 69.5% or higher)?

(2) Will the predictability of the MUST improve with incorporation of other academic measures, such as grade point average and first exam scores, which have been previously shown to correlate with OChem success?

Methods

Participants and setting

This study took place at a private, four-year liberal arts university in Texas with an M1 Carnegie classification and an undergraduate enrollment of approximately 4700 students. The student body is 39% racially and ethnically diverse and is designated as a Hispanic-emerging institution. At this study's institution, Organic Chemistry I (OChem) has a typical annual enrollment of 80–95 students divided between two sections. Each section is taught three times per week in 50-minute sessions by two different instructors working from the same textbook and online homework platform. Although the instructors’ notes, delivery, and homework assignments differ, the sections are coordinated in pace and level of difficulty. All students enrolled in OChem take identical exams on the same date, which are graded with common keys and designated partial credit point values for open response questions. Researchers applied for and received Internal Review Board (IRB) approval for exempt research. All students enrolled in OChem during the fall semesters of 2019 and 2020 were invited to participate in the study without any offer of compensation or reward. Consent forms, in which students permitted the sharing of their de-identified data, remained in a sealed envelope until after the release of final semester grades by the Registrar's Office and are secured for the required subsequent five years.

Curriculum for OChem taken by the study population aligns with the American Chemical Society Examination Institute's Organic Chemistry—First-Term exam and includes a review of relevant concepts from general chemistry, structure and stereochemistry, nomenclature, reaction mechanisms, reactivity of alkenes, and nucleophilic substitution and elimination reactions. Students earn three credit hours for successful completion of the semester-long course and must earn a C or better to enroll in the next course in the sequence, Organic Chemistry II. The study's institution requires concurrent enrollment in the associated laboratory course for an additional one credit hour.

Assessment instrument

The MUST is the same mathematics skills assessment employed in the General Chemistry I and II studies (Williamson et al., 2020; Powell et al., 2020, respectively). The MUST evaluates a student's ability to perform the following tasks: multiplication of two-digit numbers, multiplication and division of numbers in scientific notation, zeroth power application, changing fraction to decimal notation, division of a fraction by a fraction, rearranging algebraic equation (combined gas law), determining base-10 logarithms, square and square root of a number in scientific notation, recognition that division by zero is undefined, fraction simplification, recognition of fraction-decimal equivalents, and balancing simple chemical equations. Students were given 12 minutes during class to complete the 20-item test without the use of a calculator. Prior to the assessment, students were informed that the MUST would be used for information purposes only and have no bearing on student grades.

Two different versions of the MUST were distributed to the students so that no neighboring students would have the same version of the test. The two versions present items in the same order but employ different numbers within items. For example, item 1 asks for the product of 87 × 96 on one version and the product of 78 × 96 on the second version. Both versions of the MUST may be found in the ESI† of the General Chemistry I study (Williamson et al., 2020). Instructors hand-graded the assessments, marking each response as correct or incorrect for a possible range of scores from 0 to 20. Partially correct responses and incorrectly reported answers received no credit. All of the MUST questions were free response so students could not arrive at the correct answer by guessing or by working backwards.

The MUST was administered during the first week of the semester. For every student, instructors recorded a score for each item and the total MUST score. A two-tailed t-test of participant scores on the two versions of the MUST indicates no significant difference between the versions (p = 0.084). The MUST showed good internal consistency with Cronbach's alpha = 0.861 for the 150 participating students.

Statistical modeling

Comparisons of the successful and unsuccessful participant groups were made using two-tailed t-tests assuming equal variances. Effect sizes between successful and unsuccessful groups were determined using Cohen's d.

The data from the 2019 and 2020 study participants were used to develop two regression models in which the MUST score served as the numerical predictor variable. Overall semester grades were the numeric response in the linear regression, while the logistic regression utilized OChem success as a categorical, binary response. For the purpose of this study, success is defined as earning an A, B, or C. Grades of C or better (minimum of 69.5%) were chosen as the cutoff for successful completion as that is the minimum grade required for students to enroll in second-semester organic chemistry at the study institution. Students who earned a D or F or withdrew (W) before the end of the semester have been classified as unsuccessful in OChem for data processing. Success was assigned a value of 1 in the regression model while all other outcomes (D, F, or W) were assigned a value of 0.

Subsequent logistic regressions utilized categorical predictor variables to predict success in OChem. MUST scores were divided into three categories such that the middle category ranged from one-half standard deviation below to one-half standard deviation above the mean. Additional categorical predictor variables worked into the hierarchical logistic regressions included participants’ science GPA and score on the first exam of the semester. Coefficients for the resulting models are included in Appendix Table 5.

Results

A total of 150 students out of a total population of 182 students signed the IRB consent form to participate in the study during the Fall 2019 and 2020 semesters. Of those, 123 were first-time enrollees in OChem. The remaining 27 students were repeating the course because of an unsatisfactory previous attempt, either due to a withdrawal (W) or an insufficient grade (D or F). The MUST average, standard deviation (SD), and standard error (SE) for all students was 11.19 (4.94) (0.40) and first-time enrollees earned an average of 11.84 (4.80) (0.43). Those who were repeating the course averaged 8.22 (4.50) (0.87).

At the completion of the semester, MUST scores were compared to overall semester grades. Table 1 shows the average (SD) (SE) for various groups, based on whether students successfully or unsuccessfully completed the course. The average MUST score for successful students was approximately 5 points higher than that of their unsuccessful counterparts and is statistically significantly different when comparing all successful and unsuccessful participants (p = 2.1 × 10⁻¹⁰ and Cohen's d = 1.07) as well as the successful and unsuccessful participants who were enrolled in OChem for the first time (p = 1.8 × 10⁻¹⁰ and Cohen's d = 1.29). The group of students retaking the course after a previous withdrawal or unsuccessful attempt is much smaller (n = 27), but we see a similar pattern with the average MUST score 2 points higher for successful participants (p = 0.250). The bulk of the analysis for the remainder of the study focuses on the first-time enrollees to eliminate any bias of prior organic chemistry knowledge in those retaking the course.

Table 1 MUST scores of successful and unsuccessful participants

Participant group		MUST (SD) (SE)
a MUST scores for successful students statistically significantly higher at p < 0.05 level.
All students	n = 150 (%)
Successful (A, B, or C)	90 (60.0%)	13.07 (4.74) (0.50)^a
Unsuccessful (D, F, or W)	60 (40.0%)	8.37 (3.78) (0.49)
First-time enrollees	n = 123 (%)
Successful (A, B, or C)	74 (60.2%)	13.93 (4.21) (0.49)^a
Unsuccessful (D, F, or W)	49 (39.8%)	8.67 (3.85) (0.55)
Repeating enrollees	n = 27 (%)
Successful (A, B, or C)	16 (59.3%)	9.06 (5.13) (1.28)
Unsuccessful (D, F, or W)	11 (40.7%)	7.00 (3.23) (0.97)

---

Correlation of MUST score and course outcome

A scatter plot of the semester grades and MUST scores for the first-time students reveals an approximately linear relationship (Fig. 1) with higher semester grades corresponding with higher MUST scores. The average MUST score for successful first-time enrollees in the study, 13.93, marks an interesting division between successful participants and unsuccessful participants. Forty-four of the 47 (94%) students who scored a 14 or better on the MUST earned an A, B, or C in the class. Course grades showed greater dispersion for students scoring less than 14. Participants who earned an A (≥89.5) in the course all had a MUST score of 11 or higher. Students who earned a B (79.5–89.4) had a range of MUST scores from 6–20, while those who earned a C (69.5–79.4) also earned a range (9–14) of scores on the MUST. Fig. 1 includes semester grades for all first-time enrollee partcicpants, regardless of when the student's enrollment ended. For students who withdrew from the course, we used the grade they were earning at the time of their withdrawal. Thus, their grades exclude some portion of the assignments, and the number of assignments varies within the set of withdrawn students. We acknowledge that students withdraw from courses for a wide variety of reasons, some unrelated to course performance. However, only one of the participants in this study was passing the course with a C or better at the time of the withdrawal.

Fig. 1 Scatter plot of course grade versus MUST score for first-time enrollees in the study (n = 123). Course grades were taken at completion of semester or at time of withdrawal from the course.

To achieve a uniform measure of grades, we calculated the average of the first three exam scores and plotted them against the MUST (Appendix Fig. 9). At the study institution, the third exam is taken during the ninth week of the semester, before students typically begin to withdraw. All but four of the 123 participants took the first three exams; these four students withdrew prior to the third exam. The r² value for the linear regression increased slightly from 0.410 for semester grades vs MUST to 0.486 for three-exam averages vs MUST (Appendix Fig. 9), indicating a slightly stronger correlation between the measures. Both plots exhibit less variation in grades for the higher MUST scores and greater ranges in grades for the lower end.

The alluvial diagram in Fig. 2 compares MUST scores to course letter grades. The three MUST ranges illustrated were based on one standard deviation around the mean to establish “below average” as 0–8, “average” as 9–14, and “above average” as 15–20. The “above average” scores almost completely translated to a successful course outcome, and 72% of students in the “below average” category finished with an unsuccessful grade or withdrew. The “average” range is distributed throughout the three successful letter grades and represents the second largest source of DFW scores.

Fig. 2 Alluvial diagram of MUST range compared to course score (A, B, C, or DFW) for first-time participants. (Prepared using: https://app.rawgraphs.io) Ranges are statistically significantly different at the p < 0.05 level: upper outperformed middle, middle outperformed lower.

Fig. 3 illustrates the results of the MUST questions by success for all study participants, first-time enrollees, and repeaters. Each group follows the same general pattern although the percent answering correctly varies between the groups. For example, over 50% of test-takers in each category answered questions 1, 5, 10, 17, 19, and 20 correctly but questions 7 and 13 were answered incorrectly by at least 50% of the participants in each group. These question success patterns for our study cohort match those reported for a large population of students (n = 1073 and n = 1599) from different universities in the General Chemistry I and II studies (Williamson et al., 2020; Powell et al., 2020, respectively). Furthermore, the percentage correct on each question for successful groups is higher than for the corresponding unsuccessful groups with the exception of question 1, which tests 2-digit multiplication. The percentage correct for students repeating the class was not divided into “successful” and “unsuccessful” due to the small number represented therein (among repeaters: n = 16 successful and 11 unsuccessful). The results for all repeaters closely resemble those of the unsuccessful groups. Any repeater would have at one time been included in an “unsuccessful first-time” group, so similar scores are unsurprising.

Fig. 3 MUST scores by question for successful or unsuccessful students.

With the MUST scores in hand, we sought to determine the ability of the MUST to predict organic chemistry course outcomes using a logistic regression. The resulting curve, which allows for the prediction of probability of success, may be seen in Fig. 4. Based on the curve, a student taking OChem for the first time has even odds of passing with a score of 9 on the MUST. This model predicts successful course outcomes with 80.3% accuracy and unsuccessful outcomes with 63.8% accuracy.

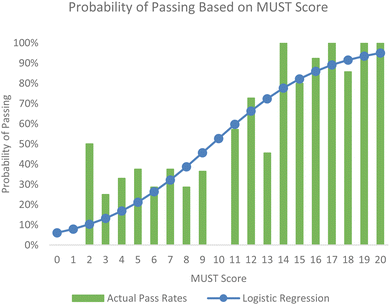Fig. 4 Comparison of actual passing rates and logistic regression curve for the probability of success based on MUST scores for first-time enrollee participants.

The receiver operating characteristic curve offers another indicator of the quality of a classifier such as a logistic regression by plotting sensitivity (or the true positive rates) versus 1 – specificity (or the false positive rates) at varying cutoffs for the classifier (Fawcett, 2006; García-Valcárcel and Tejedor, 2012; Han, 2022). The area under the curve (AUC) indicates the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance; values range from 0 to 1, with a value of 0.5 corresponding to random guessing (Fawcett, 2006). The AUC for the logistic regression based on the MUST is 0.840. An AUC is considered acceptable between 0.7 and 0.8, excellent between 0.8 and 0.9, and outstanding between 0.9 and 1.0 (Han, 2022).

Using the MUST and science GPA to predict success

After examining the relationship between our study population outcomes and GPA (Appendix 3), our next objective was to evaluate the course outcomes based on a combination of the MUST score and the science GPA. Science GPA was defined as the GPA based on two semesters of general chemistry and associated labs (8 total semester hours) coupled with two semesters of general biology and associated labs (8 semester hours). If the students did not take general biology, only the general chemistry scores were used. The majority of the participants (>85%) in this study were preparing for health professions and therefore had all four courses with their respective laboratory sections. The scores from transferred credits or from other natural science courses were not included in order to maintain consistency. In the event that a student repeated a course, both earned grades were averaged to provide a better representation.

By using both the MUST and science GPA, the intent was to provide a more robust risk assessment for a student's performance in the course. For example, if a student had a high MUST score, but a lower science GPA, they may be perceived as being successful where they may have predicted to have a DFW result based on their science GPA alone. Likewise, students with a higher science GPA and low MUST score may be predicted to need some type of intervention at the outset of the course, based on the MUST score alone, when it may not be necessary. An initial cross tabulation examined the distribution of MUST scores within three ranges of science GPA (Fig. 5).

As expected, those participants in the lowest science GPA range had the highest percentage (>50%) of low MUST scores in the 0–8 range. Those in the uppermost GPA range had the highest percentage (>55%) of top MUST scores. In comparison, those participants who scored in the 9–14 range for the MUST were fairly evenly distributed throughout the science GPA ranges, with the highest percentage being found, interestingly, for those with the lowest GPA ranking. It was curious that for those participants in the midrange science GPA field, the MUST scores were equally distributed (Fig. 5).

Fig. 5 Distribution of MUST scores between lower, middle, and upper science GPA ranges.

Two new logistic regressions were created, using either the MUST ranges or science GPA ranges as the categorical input variable; coefficients for the predictor variables may be found in Appendix 5. Table 2 shows the overall success rates for the study participants, compared separately based on the range of MUST score and on the range of their science GPA, along with the probability of success predicted by the logistic regression.

Table 2 Success rates of study participants for specified science GPA and MUST score ranges. Predicted success rates are based on logistic regressions with a single categorical input variable

Measure	Range	OChem success rate (%)
		Observed	Predicted
Science GPA	3.3–4.0 (n = 62)	95.2	95.2
	2.7–3.29 (n = 18)	55.6	55.6
	<2.7 (n = 40)	15.0	15.0
MUST score	15–20 (n = 44)	90.9	99.1
	9–14 (n = 43)	58.1	57.8
	0–8 (n = 33)	30.3	29.4

---

Both sets of data show that the highest performers in each category have a high chance of success, while those with the lowest science GPA or the lowest MUST score have a much lower likelihood of success. Participants were then cross tabulated by science GPA range and MUST range, and the course success rates were calculated for the groups. These results are shown in Fig. 6.

Fig. 6 Success rates for participants earning scores in specified MUST and science GPA ranges. All n values for each group are listed above bars in chart.

Fig. 7 Observed success rates in OChem when first exam score is (a) passing or (b) not passing. The population values for n are shown above each bar.

The study's participants in the highest science GPA range had the highest success rates irrespective of their MUST score. Even the participants in this range with the lowest MUST scores (n = 6) had a 100% success rate in this study. For the midrange science GPA, the success rates were similarly independent of the MUST scores. These participants were not as successful overall as those with a higher GPA, but they still maintained a 56% success rate. The effect of the MUST score was most evident for those participants that fell in the lowest science GPA range. These participants had a >65% chance of success if they scored high on the MUST, with this success rate dropping dramatically for lower MUST scores. Indeed, of the twenty-one participants who had a low science GPA and a low MUST score only one was able to achieve success in the course. It should be noted that the overall success rate for this group is 15%, due in part to the fact that there were very few participants (n = 3) who attained the high MUST score while having a low science GPA.

The next step was to incorporate both sets of ranges into the hierarchical logistic regression to see the impact of the MUST score and science GPA on the success rate. The predicted probabilities of passing were calculated using the regression's coefficients for all possible combinations and are shown in parentheses in Table 3 alongside the actual success rates. Any population calculated to have a passing rate of 50% or higher was predicted to be successful; they are represented by unshaded cells. Populations calculated to have success rates below 50% were predicted to be unsuccessful and are represented by the red shading. A classification table of predicted versus observed outcomes identified 8 students who were incorrectly predicted to succeed and 9 students incorrectly predicted to not succeed. As shown on the right side of Table 3, nearly half of the incorrectly predicted participants belong to the midrange science GPA, with slightly more incorrectly predicted to be successful (n = 5) than unsuccessful (n = 3). Overall, the model's prediction rate for successful students is 88.0%, while those who are unsuccessful may be predicted at an 82.2% accuracy rate.

Table 3 Observed OChem success rates and prediction outcomes for participants earning scores in specified MUST and science GPA ranges. Predicted probabilities of passing based on the logistic regression are indicated in parentheses

---

Incorporation of the first exam score

The final element incorporated into the logistic regression prediction model was that of the first exam score. As previously described, the first exam score has been shown to correlate with overall semester grades in organic chemistry courses (Villafañe et al., 2016; Hollabaugh et al., 2019). Similar analyses exist in other courses, including first-semester general chemistry (Mills et al., 2009), introductory biology for nonmajors, sophomore-level genetics, and upper division biology courses (Jensen and Barron, 2014).

The first exam in OChem at the study institution is approximately 10% multiple choice and 90% free response. It covers some review material from general chemistry that is adapted to OChem (acid/base theory, formal charges, valence electrons, and lone pairs) and an introduction to the fundamental concepts of OChem including resonance in organic compounds, organic line-bond structures, orbital hybridization, alkane naming, and constitutional isomers. The exam is the same for both sections of the course and is taken by the students during the third week of the semester. Each exam during the semester accounts for 15% of the overall semester grade, with the lowest exam score discounted to 10% of the semester grade. Only seven of the 123 first-time enrollee participants earned their lowest score on this first exam, thus the exam counted for 15% for the vast majority of the first-time enrollee participants. Homework (5%), participation (5%), and the ACS first-term standardized final (20%) comprise the remainder of the grade. A linear regression of course grade on the first exam score revealed a marked correlation between the two measures (r² = 0.854, Appendix Fig. 12a). When semester grades were adjusted to exclude the first exam score, the r² decreased only slightly to 0.804 (Appendix Fig. 12b).

Fig. 7 shows the actual passing rates for student groups based on the MUST, the science GPA, and the score of the first exam (grouped as D or F < 69.5% ≤ ABC). Compared to Fig. 6, there is a clearer picture of those participants who fall in the midrange science GPA as these students had a much higher success rate in the course if they attained a passing grade on the first exam and were uniformly unsuccessful if they scored a D or F on the first exam. Similarly, 50% of participants in the low science GPA range were successful in OChem if they passed the first exam, but only 6% of participants in the low GPA range passed the course with an unsuccessful first exam score. Among the participants with a low science GPA, higher MUST score ranges appeared to correspond with increased success rates regardless of the first exam outcome. In the study population, two groups contained zero participants: those with a high GPA, low MUST, and unsuccessful first exam and those with a low GPA, high MUST, and scored a D or F. It should be noted that the inclusion of a third variable reduced the population for some of these subgroups to low n values. Despite the low n values, the general trend holds that students who are in the middle or lower GPA range and do not make a C or higher on the first exam have a greatly reduced probability of passing the course.

The first exam was added to the hierarchical logistic regression as the third and final categorical input variable. Grades of 69.5 or better were assigned a 1 while scores below 69.5 were marked 0 for the analysis. Coefficients from the resulting model were used to calculate predicted probabilities of passing for the various combinations of science GPA, MUST range, and first exam outcome. Populations with >50% chance of passing were predicted to be successful (unshaded cells in Table 4), and all others were predicted to be unsuccessful (cells shaded in red in Table 4).

Table 4 Observed OChem success rates and number of incorrect predictions where participants were grouped based on science GPA, MUST score, and first exam score. Predicted probabilities of passing based on the logistic regression are indicated in parentheses

---

Analysis of the model's classification is shown on the right side of Table 4. As in the previous logistic regression, eight participants were incorrectly be predicted to be successful for an accuracy rate of 82.2%. Where half of these incorrectly predicted outcomes fell in the midrange science GPA from the previous model, the new model only incorrectly placed one participant in this range. Instead, half of the new model's incorrectly predicted students (n = 4) fell in the low science GPA and successful first exam category. Only two students, both in the low GPA and unsuccessful first exam category, were incorrectly predicted to be unsuccessful so that the prediction rate for successful students increased to 97.3%. The AUC for this final model is an outstanding 0.950.

Discussion

The Math-Up Skills Test provides an early estimation of student performance in OChem, despite the fact that the course does not directly depend on mathematical calculations. Based on the available data, students have a 50% chance of passing the course if they attain a score of 9 on the MUST (Fig. 4). As a single measure, the MUST predicts successful course outcomes with 80% accuracy and unsuccessful outcomes with 64% accuracy. This level of accuracy is similar to that observed for predicted outcomes in General Chemistry I using a combination of MUST score and demographic data (Williamson et al., 2020). In the current study, the MUST combined with science GPA predicts successful course outcomes with 88% accuracy and unsuccessful ones with 82% accuracy (Table 3).

The MUST is primarily a product-oriented test with free-response numerical answers and would therefore be expected to be more applicable to general chemistry since organic chemistry has been described as being more process-oriented than product-oriented (Graulich, 2015). However, the correlation between the MUST and success in OChem may indicate that there are elements in the MUST that also incorporate process-oriented reasoning. Donovan and Wheland (2009) suggest that the mathematics-chemistry connection is based on the development of higher-order cognitive skills required by both disciplines that takes place during the mastery of mathematics. Ralph and Lewis (2018) describe the ability of students at risk of not passing (those who scored in the bottom quartile of mathematics component scores on the SAT) to perform comparably to their peers in a first-semester general chemistry course when they achieved proficiency in mole concept and stoichiometry assessments. Both concepts rely heavily on proportional reasoning skills, one of the Piagetian tasks associated with formal thought.

Alternatively, the relationship between the MUST and OChem outcomes may depend on students’ cognitive load as the MUST is a calculator-free assessment. Students more familiar with the symbols and mathematical manipulations on the MUST and better able to retrieve math facts would experience a lighter load, allowing them to perform better than students with heavier cognitive loads (Royer et al., 1999). Furthermore, an analysis of problem types in organic chemistry revealed that types associated with higher cognitive load (i.e. those involving hybridization, resonance, Lewis structures (Tiettmeyer et al., 2017), isomerism, or multi-step, curved arrow formalisms) were more highly correlated with course success than those with lighter cognitive demands (Austin et al., 2015).

One factor to consider in the administration of the MUST is the students’ motivation to perform well on it. Prior to beginning the test, students are encouraged to perform well even though they are aware that the score they receive on the MUST does not impact their grade. Highly motivated students are probably more likely to strive to do their best, even if the assignment has no grade impact, and these students could reasonably be expected to maintain this motivation throughout the semester. Students that are not self-motivated to perform well on the MUST may or may not have an internal drive to do well in the course. As there is no true incentive to attain a high score on the MUST, the correlation between MUST scores and motivation may merit further investigation.

Both mathematics and organic chemistry have long been known to induce anxiety in students due to students’ anticipated ability (or inability) to succeed in the rigorous courses (Betz, 1978; Steiner and Sullivan, 1984). This anxiety inhibits student enjoyment of the subjects and impacts subsequent performance, negatively influencing motivation to persist in the course (Black and Deci, 2000). Thus, administrators of the test should consider the effects of stereotype threat. According to Spencer, Steele, and Quinn (1999), these effects can be minimized when the instructions for an assessment indicate that no effect has been observed for the assessment in the past. Thus, students taking the MUST should be instructed in such a way as to relieve stereotype threat. For example, the instructor may inform students that they are all equally qualified to take the test because of their experience with similar math problems in their general chemistry coursework. The potential for stereotype threat may be further reduced by separation of any demographics questionnaire from delivery of the MUST. Previously, Lynch and Trujillo (2011) questioned the extent to which factors underlying self-regulated learning, i.e. motivational, cognitive, metacognitive, behavioral, emotional factors (Panadero, 2017), extend across academic domains. Because OChem grades correlate with MUST scores despite a lack of mathematics calculations in OChem, the MUST may provide evidence for a lack of domain specificity in self-regulated learning.

Indeed, a closer examination of the success rates for the various combinations of science GPA and MUST score may provide further insight regarding abilities being measured by the MUST (Fig. 6). The data suggest that students entering OChem with a top-tier science GPA will find success even if their MUST score is low. Similarly, those with a midrange science GPA were more likely than not to find success, irrespective of MUST score, though this was the smallest cohort in the dataset. Certainly, many variables factor into academic performance leading to grade point averages. Students beginning OChem with mid- or high-range GPA may have the attitudes, study habits, and autonomous motivation for success to override differences in developmental level (Steiner and Sullivan, 1984; Black and Deci, 2000; Grove and Bretz, 2010; Szu et al., 2011). For students who fall in the bottom-tier GPA category, success rates are strongly differentiated by scores on the mathematics assessment. Only 5% of students with MUST scores <9 passed the course, while 19% of students with MUST scores of 9–14 obtained successful outcomes. For these students, the MUST implies some level of cognitive ability not reflected in their prior science coursework.

By collecting science GPA data and the MUST scores within the first week of the semester, it is feasible to provide suggestions to students with low or borderline scores and encourage them to seek out resources to ensure that they will improve their chances at finding success. Students with midrange science GPA and a midrange or low MUST score may benefit most from instructions on how to study most effectively. Students with both a low science GPA and a low MUST score may require resources and training to develop their cognitive ability. Early intervention could be critical in helping students at risk of not passing before the first semester exam is given or damage to grades occurs.

There are many types of interventions that can help organic chemistry students, with numerous examples in the literature that describe specific learning tools that can be employed, often in relation to a particular topic. However, in focusing on early intervention for students who are identified as less likely to pass the course at the onset of the semester, the focus should be on approaches that help them get up to speed quickly. Perhaps one of the most important tools is the encouragement of help-seeking behavior. As described in Horowitz et al. (2013), low-performing students often feel shame and are therefore reluctant to engage in help-seeking behaviors. Positive encouragement and assurance that tutoring and office hours would be beneficial may foster an environment that inspires students to take preemptive action to increase their chances for success. At the study institution, organic chemistry students have assigned online homework and access to optional practice problems within the textbook. Instructors also promote and encourage students to take advantage of additional online practice problem resources. The benefits of practice problems have also been described in Szu et al. (2011), where a student with a lower prior GPA outperformed another with higher prior GPA and reported a higher usage of practice problems in Month 1 (front-loading) of an organic chemistry course.

Promotion of peer-led team learning (PLTL) sessions is another method that could be employed to improve performance in organic chemistry. Implementation of PLTL has been shown to improve exam scores (Tien et al., 2002) and lead to higher success rates (Wamser, 2006) in organic chemistry. Online preparatory courses (Fischer et al., 2019; Pulukuri et al., 2021) delivered via a learning management system have also been found to result in higher performance and success rates in organic chemistry. There are also various examples of utilizing social-psychological interventions (SPIs) in order to increase performance and persistence in STEM courses. In a particular, utility value interventions (UVIs), which connect course concepts to the daily lives and/or personal values of the students through assigned research on a topic, showed improved exam scores in general chemistry (Wang et al., 2021). A similar strategy engaged organic chemistry students by assigning them the task of presenting on arrow-pushing, which led to improved perceptions (a goal of SPIs) and, consequently, higher exam scores (Green and Rollnick, 2006). Zavala et al. (2019) describes the use of student role-playing journal exercises to connect abstract course content to their career ambitions, which increased personal connections to organic chemistry and improved scores.

The additional data point of the first semester exam, which has been previously described as being a reliable predictive measure (Mills et al., 2009; Jensen and Barron, 2014; Hollabaugh et al., 2019), provides further strengthening of the predictive model. Participants who scored an A, B, or C on the first exam were overwhelmingly successful unless they were in the lowest-tier science GPA and had a low MUST score. Participants who had a D or F on the first exam were only successful if they had a high science GPA and a high MUST score. Even without considering any other factors, less than 10% of the students in this study who scored below 69.5 on this exam were able to obtain a passing grade in the course (n = 4). Though it is given later in the semester (during the third week for the course in this study), it is early enough to still suggest potentially critical intervention prior to the more rigorous portion of the course. By working these scores into our model, successful course outcomes were predicted with 97% accuracy and unsuccessful outcomes were predicted with 82% accuracy.

Limitations

The current study was conducted at a single institution over two fall semesters. The scores demarcating high and low values for the MUST and for science GPA may change over time as additional data are obtained, particularly with input from other institutions. Transfer and first-year students, for whom prior science GPA may not be known, were limited in number. These students were included in the MUST analysis, but exempted from evaluations which incorporated the science GPA and first exam score.

In the analysis of MUST scores subdivided by science GPA, various groupings had small population sizes. Additional data collection may further clarify the trends that are seen in the data. There was also an insufficient number of participants who were repeating the course to make an adequate evaluation of this subgroup. The limited data suggested that their MUST scores do not significantly increase when participants retake the course (Fig. 3). However, previous exposure to the course material and additional physical science coursework may offset this and aid in success prediction.

Due to the fact that the score on the MUST has no grade impact, students may not be putting in their best effort to maximize their score. This could potentially skew the results for some students, as the MUST may not be an accurate representation of their automaticity skills. Neither prior mathematics coursework, nor elapsed time since such coursework, was taken into consideration for this study.

The definition of science GPA is specific for the institution at which the study took place, and may not be applicable to other institutions. Nonetheless, adaptations to this definition could be tailored for other institutions or programs of study. Course exams (in using the first exam score) were developed in-house and are institution-specific, though previous work has indicated that the use of the first exam, regardless of institution, may be applicable for predicting success (Hollabaugh et al., 2019).

Conclusions

The ease of use of the MUST as a predictor for a first-semester organic chemistry course makes it an attractive option for identifying students at risk of not passing at the course onset compared to other less readily available metrics (e.g. SAT/ACT scores). If accessible, using select grade point average data (science GPA) in conjunction with the MUST provides a higher degree of predictability for identifying these students. Both the science GPA and the MUST speak to prior knowledge that the participants had when they began OChem. Aside from measuring academic achievement, a student's grade point average may also contain components of work ethic and autonomous motivation. Students with lesser innate academic abilities may be able to compensate with a higher work ethic and thus achieve a higher GPA, while students with strong academic skills may lack the motivation to perform their best. The MUST, though a measure of mathematical skills, may contain elements of cognitive ability and logical reasoning assessment, which may overlap with skills necessary for success in OChem.

Consideration of the first OChem exam score further enhances the prediction when coupled with the MUST score and the science GPA. Of these three elements, the MUST is the most practical as it is simple to administer at the beginning of the semester. Incorporation of the science GPA is beneficial, though it requires additional effort by the instructor to obtain. While recommending interventional measures to identified students during the first week of the semester is preferable, instructors could better ascertain individuals’ chances of passing by evaluating the first exam scores. Though each of these methods has a varying level of predictive power, one or more was found to be a useful tool in determining which students were likely to pass or to not pass first-semester Organic Chemistry.

Conflicts of interest

There are no conflicts to declare.

Appendix 1. Comparison of grades to MUST scores for all study participants

Fig. 8 reveals a linear relationship between overall semester grades and MUST scores for all study participants, including both first-time enrollees and repeat enrollees. The r² values for the full population are smallar than the r² values for the first-time enrollees alone (Fig. 1).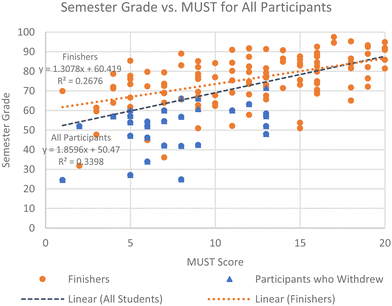

Fig. 8 Comparison of overall semester grades with the MUST score for students participating in the study; n = 120 for “Finishers” and n = 150 for “All Participants”.

Fig. 9 Comparison of average of first three mid-semester exams with MUST scores for first-time enrollees (n = 119).

Appendix 2. Comparison of mid-course exam grade averages to MUST scores

Most withdrawals from OChem at the study institution occur after the fourth of five exams. As such, we identified the first three exams as a potential measure for comparing course success with MUST scores. A scatter plot of the three-exam average compared with the MUST score is shown in Fig. 9.

Appendix 3. Alignment of study population with established predictors of success

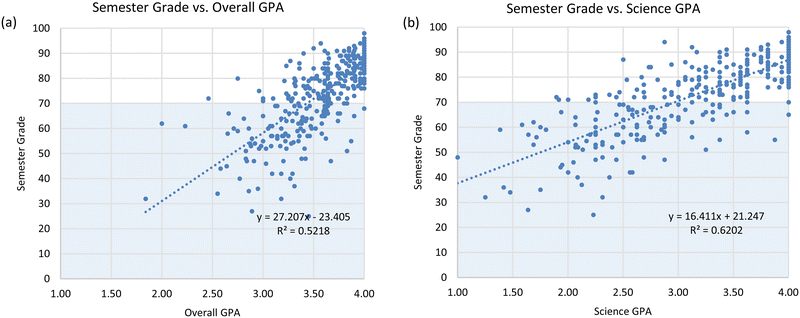
Linear regressions were performed looking at both incoming overall GPA and incoming science GPA relative to the students’ ultimate scores in OChem. Incoming overall GPA was the GPA that the student held prior to the start of the semester in which they were enrolled in OChem. It is recognized that obtaining GPA information for each student, particularly science GPA, can be time-consuming, and such data may not be readily available. While the cohort for the MUST study consisted of 123 participants, grade point average data was available for 422 students, which included students in prior years that did not take the MUST.

Fig. 10a shows the relationship between attained grade in OChem and overall GPA; Fig. 10b shows attained grade versus the science GPA. Science GPA was determined to be a better predictor (r² = 0.620) of overall performance compared to the overall GPA (r² = 0.522) and was therefore used in the following analyses. Not surprisingly, there is also a wider distribution for the science GPA as the overall GPA is more heavily weighted toward the high end as first-year students normally enroll in many lower level core curriculum courses that tend to boost grade point averages. The data points that fall in the shaded area represent students that were not successful in OChem (score <69.5%).

Fig. 10 Scatter plots (n = 422) of (a) OChem semester grade vs students' overall GPA and of (b) OChem semester grade vs students’ science GPA. Overall GPA and science GPA were taken at the start of the student's OChem semester.

For those participants (n = 120) who took the MUST and had previously completed science coursework at the study institution, this trend continues to hold. The correlation between OChem outcome and overall GPA was found to be r² = 0.552, and that with science GPA was r² = 0.676, as illustrated in Fig. 11. Thus, the participants of the current study were judged to be representative of the broader population of students.

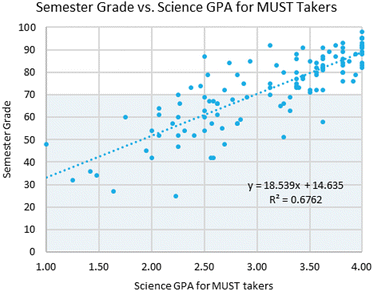Fig. 11 Scatter plot of OChem semester grade vs. science GPA for participants who completed the MUST (n = 120).

Fig. 12 Scatter plots of (a) OChem semester grade vs. first exam score and of (b) adjusted OChem semester grade vs. first exam score for first time enrollees (n = 123).

Appendix 4. Comparison of first exam scores with semester grades

Scatter plots of participants’ semester grades vs. first exam scores revealed a linear relationship (Fig. 12a). A similar analysis was performed using an adjusted semester grade that omitted the first exam score (Fig. 12b).

Appendix 5. Logistic regressions

Logistic regressions utilized OChem success as the categorical, binary response. Successful outcomes (≥69.5) were assigned a value of 1, while all other outcomes were assigned a value of 0. Participant scores for the MUST, Science GPA, and Exam 1 were sorted into categories, which served as the independent variable(s). The reported pseudo-r² value is Nagelkerke's r², which ranges from 0 to 1. AUC indicates the area under the receiver operating characteristic curve, a measure of the regression's specificity and sensitivity (Table 5).

Table 5 Logistic regression coefficients for models with different input variables

Variable	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
*p < 0.05.
Intercept	2.303*	2.979*	3.753*	2.747*	3.674*	3.557*
MUST range
15–20	Reference*		Reference	Reference	Reference
9–14	−1.989*		−1.219	−0.828	−0.272
0–8	−3.178*		−1.652*	−1.371	−0.299
Science GPA range
3.3–4.0		Reference*	Reference*		Reference*	Reference*
2.7–3.29		−2.756*	−2.532*		−1.983*	−2.026*
0–2.69		−4.714*	−4.201*		−3.191*	−3.260*
Exam 1 score
≥69.5				Reference*	Reference*	Reference*
<69.5				−3.766*	−3.288*	−3.376*
Pseudo-r^2	0.331	0.641	0.667	0.669	0.778	0.777
χ ^2	34.320	76.204	80.677	83.294	101.462	101.341
AUC	0.781	0.903	0.926	0.882	0.950	0.948

---

Acknowledgements

The authors gratefully acknowledge the advice and editorial work of Dr Diana Mason and Dr Cynthia Powell.

References

1. Attridge N. and Inglis M., (2013), Advanced Mathematical Study and the Development of Conditional Reasoning Skills, PLoS One, 8(7), e69399.
2. Austin A. C., Ben-Daat H., Zhu M., Atkinson R., Barrows N. and Gould I. R., (2015), Measuring student performance in general organic chemistry, Chem. Educ. Res. Pract., 16(1), 168–178.
3. Battista M. T., Wheatley G. H. and Talsm G., (1982), The Importance of Spatial Visualization and Cognitive Development for Geometry Learning in Preservice Elementary Teachers, J. Res. Math. Educ., 13(5), 332–340.
4. Bender D. S. and Milakofsky L., (1982), College chemistry and Piaget: The relationship of aptitude and achievement measures, J. Res. Sci. Teach., 19(3), 205–216.
5. Betz N. E., (1978), Prevalence, distribution, and correlates of math anxiety in college students, J. Couns. Psychol., 25(5), 441–448.
6. Bird L., (2010), Logical Reasoning Ability and Student Performance in General Chemistry, J. Chem. Educ., 87(5), 541–546.
7. Black A. E. and Deci E. L., (2000), The effects of instructors’ autonomy support and students’ autonomous motivation on learning organic chemistry: A self-determination theory perspective, Sci. Educ., 84(lo), 740–756.
8. Bodner G. M., (1986), Constructivism: A theory of knowledge, J. Chem. Educ., 63(10), 873.
9. Bohning J. J., (1982), Remedial mathematics for the introductory chemistry course: The “CHEM. 99” concept, J. Chem. Educ., 59(3), 207.
10. Bunce D. M. and Hutchinson K. D., (1993), The use of the GALT (Group Assessment of Logical Thinking) as a predictor of academic success in college chemistry, J. Chem. Educ., 70(3), 183.
11. Cheng Y.-L. and Mix K. S., (2014), Spatial Training Improves Children's Mathematics Ability, J. Cogn. Dev., 15(1), 2–11.
12. Craney C. L. and Armstrong R. W., (1985), Predictors of grades in general chemistry for allied health students, J. Chem. Educ., 62(2), 127.
13. Cresswell C. and Speelman C. P., (2020), Does mathematics training lead to better logical thinking and reasoning? A cross-sectional assessment from students to professors, PLoS One, 15(7), e0236153.
14. Donovan W. J. and Wheland E. R., (2009), Comparisons of Success and Retention in a General Chemistry Course Before and After the Adoption of a Mathematics Prerequisite, Sch. Sci. Math., 109(7), 371–382.
15. Fawcett T., (2006), An introduction to ROC analysis, Pattern Recognit. Lett., 27(8), 861–874.
16. Fischer C., Zhou N., Rodriguez F., Warschauer M. and King S., (2019), Improving College Student Success in Organic Chemistry: Impact of an Online Preparatory Course, J. Chem. Educ., 96(5), 857–864.
17. Frey R. F., Cahill M. J. and McDaniel M. A., (2017), Students’ Concept-Building Approaches: A Novel Predictor of Success in Chemistry Courses, J. Chem. Educ., 94(9), 1185–1194.
18. García-Valcárcel A. and Tejedor F. J., (2012), The incorporation of ICT in higher education, The contribution of ROC curves in the graphic visualization of differences in the analysis of the variables, Br. J. Educ. Technol., 43(6), 901–919.
19. Goodstein M. P. and Howe A. C., (1978), Application of Piagetian theory to introductory chemistry instruction, J. Chem. Educ., 55(3), 171.
20. Graulich N., (2015), The tip of the iceberg in organic chemistry classes: how do students deal with the invisible? Chem. Educ. Res. Pract., 16(1), 9–21.
21. Green G. and Rollnick M., (2006), The Role of Structure of the Discipline in Improving Student Understanding: The Case of Organic Chemistry, J. Chem. Educ., 83(9), 1376.
22. Grove N. P. and Bretz S. L., (2010), Perry's Scheme of Intellectual and Epistemological Development as a framework for describing student difficulties in learning organic chemistry, Chem. Educ. Res. Pract., 11(3), 207–211.
23. Grove N. P., Hershberger J. W. and Bretz S. L., (2008), Impact of a spiral organic curriculum on student attrition and learning, Chem. Educ. Res. Pract., 9(2), 157–162.
24. Guay R. B. and McDaniel E. D., (1977), The Relationship between Mathematics Achievement and Spatial Abilities among Elementary School Children, J. Res. Math. Educ., 8(3), 211–215.
25. Hall D. M., Curtin-Soydan A. J. and Canelas D. A., (2014), The Science Advancement through Group Engagement Program: Leveling the Playing Field and Increasing Retention in Science, J. Chem. Educ., 91(1), 37–47.
26. Han H., (2022), The Utility of Receiver Operating Characteristic Curve in Educational Assessment: Performance Prediction, Mathematics, 10(9), 1493.
27. Harle M. and Towns M., (2011), A Review of Spatial Ability Literature, Its Connection to Chemistry, and Implications for Instruction, J. Chem. Educ., 88(3), 351–360.
28. Harris R. B., Mack M. R., Bryant J., Theobald E. J. and Freeman S., (2020), Reducing achievement gaps in undergraduate general chemistry could lift underrepresented students into a “hyperpersistent zone”, Sci. Adv., 6(24), eaaz5687.
29. Herron J. D., (1975), Piaget for chemists. Explaining what “good” students cannot understand, J. Chem. Educ., 52(3), 146.
30. Hollabaugh N., Nolibos P. and Thomas A., (2019), Getting Off to a Good Start in Organic Chemistry: First-Exam Scores Predict Final Grades, Chem. Educ., 24, 6–10.
31. Horowitz G., Rabin L. A. and Brodale D. L., (2013), Improving student performance in organic chemistry: Help seeking behaviors and prior chemistry aptitude, J. Scholarsh. Teach. Learn., 13(3), 120–133.
32. Inglis M. and Simpson A., (2009), Conditional inference and advanced mathematical study: further evidence, Educ. Stud. Math., 72(2), 185–198.
33. Jasien P. G., (2003), Factors Influencing Passing Rates for First-Semester Organic Chemistry Students, Chem. Educ., 8, 155–161.
34. Jensen P. and Barron J., (2014), Research and Teaching: Midterm and First-Exam Grades Predict Final Grades in Biology Courses, J. Coll. Sci. Teach., 44(2), 82–89.
35. Jiang B., Xu X., Garcia A. and Lewis J. E., (2010), Comparing Two Tests of Formal Reasoning in a College Chemistry Context, J. Chem. Educ., 87(12), 1430–1437.
36. Jones M. G., Gardner G., Taylor A. R., Wiebe E. and Forrester J., (2011), Conceptualizing Magnification and Scale: The Roles of Spatial Visualization and Logical Thinking, Res. Sci. Educ., 41(3), 357–368.
37. Kennepohl D., Guay M. and Thomas V., (2010), Using an Online, Self-Diagnostic Test for Introductory General Chemistry at an Open University, J. Chem. Educ., 87(11), 1273–1277.
38. Kreiser R. P., Wright A. K., McKenzie T. L., Albright J. A., Mowles E. D., Hollows J. E., et al., (2022), Utilization of Standardized College Entrance Metrics to Predict Undergraduate Student Success in Chemistry, J. Chem. Educ., 99(4), 1725–1733.
39. Lawson A. E., (1979), The developmental learning paradigm, J. Res. Sci. Teach., 16(6), 501–515.
40. Leopold D. G. and Edgar B., (2008), Degree of Mathematics Fluency and Success in Second-Semester Introductory Chemistry, J. Chem. Educ., 85(5), 724.
41. Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
42. Lopez E. J., Shavelson R. J., Nandagopal K., Szu E. and Penn J., (2014), Factors Contributing to Problem-Solving Performance in First-Semester Organic Chemistry, J. Chem. Educ., 91(7), 976–981.
43. Lynch D. J. and Trujillo H., (2011), Motivational Beliefs and Learning Strategies in Organic Chemistry, Int. J. Sci. Math. Educ., 9(6), 1351–1365.
44. Mills P., Sweeney W. and Bonner S. M., (2009), Using the First Exam for Student Placement in Beginning Chemistry Courses, J. Chem. Educ., 86(6), 738.
45. Mix K. S., Levine S. C., Cheng Y.-L., Young C., Hambrick D. Z., Ping R. and Konstantopoulos S., (2016), Separate but correlated: The latent structure of space and mathematics across development, J. Exp. Psychol. Gen., 145(9), 1206–1227.
46. Morsanyi K. and Szücs D., (2014), The link between mathematics and logical reasoning: implications for research and education, in Chinn S. (ed.), The Routledge International Handbook of Dyscalculia and Mathematical Learning Difficulties, Routledge, pp. 101–114.
47. Nunes T., Bryant P., Evans D., Bell D., Gardner S., Gardner A. and Carraher J., (2007), The contribution of logical reasoning to the learning of mathematics in primary school, Br. J. Dev. Psychol., 25(1), 147–166.
48. Ojose B., (2008), Applying Piaget's Theory of Cognitive Development to Mathematics Instruction, Math. Educ., 18(1), 26–30.
49. Panadero E., (2017), A Review of Self-regulated Learning: Six Models and Four Directions for Research, Front. Psychol., 8, 422.
50. Piaget J., (1964), Part I: Cognitive development in children: Piaget development and learning, J. Res. Sci. Teach., 2(3), 176–186.
51. Powell C. B., Simpson J., Williamson V. M., Dubrovskiy A., Walker D. R., Jang B., et al., (2020), Impact of arithmetic automaticity on students’ success in second-semester general chemistry, Chem. Educ. Res. Pract., 21(4), 1028–1041.
52. Pribyl J. R. and Bodner G. M., (1987), Spatial ability and its role in organic chemistry: A study of four organic courses, J. Res. Sci. Teach., 24(3), 229–240.
53. Pulukuri S., Torres D. and Abrams B., (2021), OrgoPrep: A Remote Peer-Led Summer Program Preparing Students for Organic Chemistry, J. Chem. Educ., 98(10), 3073–3083.
54. Pursell D. P., (2007), Predicted versus Actual Performance in Undergraduate Organic Chemistry and Implications for Student Advising, J. Chem. Educ., 84(9), 1448.
55. Ralph V. R. and Lewis S. E., (2018), Chemistry topics posing incommensurate difficulty to students with low math aptitude scores, Chem. Educ. Res. Pract., 19(3), 867–884.
56. Resnick I., Harris D., Logan T. and Lowrie T., (2020), The relation between mathematics achievement and spatial reasoning, Math. Educ. Res. J., 32(2), 171–174.
57. Rixse J. S. and Pickering M., (1985), Freshman chemistry as a predictor of future academic success, J. Chem. Educ., 62(4), 313.
58. Roadrangka V., Yeany R. H. and Padilla M. J., (1983), The construction and validation of Group Assessment of Logical Thinking (GALT).
59. Robinson J., Reck K. and Oakley M. G., (2007), “Less is More:” The 1:2:1 Curriculum at Indiana University, International Conference on FirstYear College Chemistry, American Chemical Society DivCHED.
60. Royer J. M., Tronsky L. N., Chan Y., Jackson S. J. and Marchant H., (1999), Math-Fact Retrieval as the Cognitive Mechanism Underlying Gender Differences in Math Test Performance, Contemp. Educ. Psychol., 24(3), 181–266.
61. Shelton G. R., Mamiya B., Weber R., Rush Walker D., Powell C. B., Jang B., et al., (2021), Early Warning Signals from Automaticity Diagnostic Instruments for First- and Second-Semester General Chemistry, J. Chem. Educ., 98(10), 3061–3072.
62. Spencer H. E., (1996), Mathematical SAT Test Scores and College Chemistry Grades, J. Chem. Educ., 73(12), 1150.
63. Spencer S. J., Steele, C. M. and Quinn, D. M., (1999), Stereotype Threat and Women's Performance, J. Exp. Soc. Psychol.35, 4–28.
64. Steiner R. and Sullivan J., (1984), Variables correlating with student success in organic chemistry, J. Chem. Educ., 61(12), 1072.
65. Szu E., Nandagopal K., Shavelson R. J., Lopez E. J., Penn J. H., Scharberg M. and Hill G. W., (2011), Understanding Academic Performance in Organic Chemistry, J. Chem. Educ., 88(9), 1238–1242.
66. Tai R. H., Ward R. B. and Sadler P. M., (2006), High School Chemistry Content Background of Introductory College Chemistry Students and Its Association with College Chemistry Grades, J. Chem. Educ., 83(11), 1703.
67. Tien L. T., Roth V. and Kampmeier J. A., (2002), Implementation of a Peer-Led Team Learning Instructional Approach in an Undergraduate Organic Chemistry Course, J. Res. Sci. Teach., 39(7), 606–632.
68. Tiettmeyer J. M., Coleman A. F., Balok R. S., Gampp T. W., Duffy P. L., Mazzarone K. M. and Grove N. P., (2017), Unraveling the Complexities: An Investigation of the Factors That Induce Load in Chemistry Students Constructing Lewis Structures, J. Chem. Educ., 94(3), 282–288.
69. Turner R. C. and Lindsay H. A., (2003), Gender Differences in Cognitive and Noncognitive Factors Related to Achievement in Organic Chemistry, J. Chem. Educ., 80(5), 563.
70. Villafañe S. M., Xu X. and Raker J. R., (2016), Self-efficacy and academic performance in first-semester organic chemistry: testing a model of reciprocal causation, Chem. Educ. Res. Pract., 17(4), 973–984.
71. Wamser C. C., (2006), Peer-Led Team Learning in Organic Chemistry: Effects on Student Performance, Success, and Persistence in the Course, J. Chem. Educ., 83(10), 1562.
72. Wang Y., Rocabado G. A., Lewis J. E. and Lewis S. E., (2021), Prompts to Promote Success: Evaluating Utility Value and Growth Mindset Interventions on General Chemistry Students’ Attitude and Academic Performance, J. Chem. Educ., 98(5), 1476–1488.
73. Williamson V. M., Walker D. R., Chuu E., Broadway S., Mamiya B., Powell C. B., et al., (2020), Impact of basic arithmetic skills on success in first-semester general chemistry, Chem. Educ. Res. Pract., 21(1), 51–61.
74. Xie F., Zhang L., Chen X. and Xin Z., (2020), Is Spatial Ability Related to Mathematical Ability: a Meta-analysis, Educ. Psychol. Rev., 32(1), 113–155.
75. Zavala J. A., Chadha R., Steele D. M., Ray C. and Moore J. S., (2019), Molecular Sciences Made Personal: Developing Curiosity in General and Organic Chemistry with a Multi-Semester Utility Value Intervention, in Kradtap Hartwell S. and Gupta T. (ed.), ACS Symposium Series, American Chemical Society, pp. 105–118.
76. Zhang C., Kuncel N. R. and Sackett P. R., (2020), The process of attrition in pre-medical studies: A large-scale analysis across 102 schools, PLoS One, 15(12), e0243546.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2rp00140c

---