 Open Access Article
Open Access ArticleEffects of transport limitations on rates of acid-catalyzed alkene oligomerization†
Nibras
Hijazi
and
Jorge
Gascon
 *
*
KAUST Catalysis Center, King Abdullah University of Science and Technology, Thuwal 23955-6900, Kingdom of Saudi Arabia. E-mail: jorge.gascon@kaust.edu.sa
First published on 26th July 2023
Abstract
Acid-catalyzed alkene oligomerization is often masked by artifacts of transport limitations. Implications of these limitations on turnover rates and selectivity have been assessed on zeolites with diverse frameworks (MFI, MTW, TON) and crystal sizes over a wide range of temperatures (423–573 K). Measured kinetic data, together with Weisz–Prater estimates, show that reactant diffusion limitations can prevail at high oligomerization temperatures (523–573 K). These data also suggest, through transition state theory treatments, that the zeolite structure has no significant effect on the intrinsic activation energy of oligomerization but does affect profoundly the activation entropy. Isomer speciation of oligomers reveals that the degree of branching increases with the pore diameter and decreases with diffusion limitations. The observed selectivity trends were found to be consistent with sorption transients of structurally relevant hydrocarbons.
1. Introduction
Transport fuels derived from crude oil comprise thousands of hydrocarbons of which a significant portion forms soot pollutants upon combustion in spark-ignition engines. Incomplete combustion of unsaturated hydrocarbons releases photochemically reactive substances to the atmosphere, increases particulate matter and ozone formation potentials, and produces polynuclear aromatics of carcinogenic tendency.1,2 Regulatory organizations such as the U.S. Environmental Protection Agency have made efforts to reduce olefin and aromatic content in gasoline.3 Nonetheless, fossil fuels and their combustion products remain a major source of air pollution.Synthetic fuels, on the other hand, are a key element of the next energy transition.4,5 Synthetic fuels will not only help decentralize energy resources, but also contribute to net-zero emissions when derived from CO2. The key to produce synthetic fuels is converting small molecules to larger ones through catalytic processes. Methanol-to-Gasoline (MTG)6 and Mobil Olefin to Gasoline and Distillate (MOGD)7,8 are prominent examples of processes that underpin such conversions. MOGD offers the advantage of producing fuels free of aromatics. Ideal, paraffinic fuels can be attained by hydrogenation of MOGD products.
MOGD is catalyzed by microporous aluminosilicate materials with strong Brønsted acid character, commonly known as zeolites. Distinguishing them from other classes of porous materials, zeolites tend to discriminate molecules based on shape.9 Weisz and Csicsery10,11 were the first to observe that reactants, transition states, and products are subject to shape selectivity in zeolites. Product shape selectivity, which manifests mass transfer limitations, has been widely accepted in the literature to regulate the rates of oligomer formation in MOGD catalysis. In other words, hindered diffusion of bulky oligomerization products creates intracrystalline gradients in zeolites, thus affecting oligomerization rates and selectivities. Product diffusion limitations were proposed to explain the low activation barrier observed in butene oligomerization over zeolite beta.12 Corma et al.13 observed that catalytic activity decreases with crystallite size of ZSM-5 and attributed that to diffusion limitations of oligomerization products. The authors also stated that product diffusion limitations influence deactivation rates and the chain length of oligomers. Similar observations were made by Van Grieken et al.14 and O'connor et al.15 when studying alkene oligomerization over ZSM-5. Recently, products accumulating within zeolite micropores were found to impose diffusion limitations on reactants during propene oligomerization.16 Prior to this study, the role of reactant diffusion limitations in alkene oligomerization had been understated.
Shape selectivity has also been reported to affect the degree of branching in oligomers. Quann et al.8 attributed the deviation from equilibrium in hexene isomers formed on ZSM-5 to shape selectivity effects. Wilshier et al.17 observed that shape selective oligomerization takes place inside ZSM-5 channels, favoring the formation of linear oligomers over branched ones. Chen and Bridger18 studied the backbone structure of oligomers formed on ZSM-5 and made similar conclusions. However, to the best of our knowledge, a clear-cut discrimination between transition state and product shape selectivity has not been made.
Here, we systematically study how changes in intracrystalline diffusion lengths of microporous solid acids (MFI, MTW, TON) influence alkene oligomerization turnover rates and selectivity. Particularly, we examine the effects of reactant diffusion limitations at a wide range of temperatures (423–573 K). This aspect has not been investigated extensively in the existing literature on alkene oligomerization. Throughout our examination, we observed that intrinsic rates differ considerably among zeolites but proceed at similar activation energies. We interpret this result in terms of transition state theory to discern the role of entropy in determining the reactivity of zeolites. Furthermore, we examine how different classes of shape selectivity influence branching during oligomerization. Our results, supported by transient sorption measurements, demonstrate that transition state and product shape selectivity can limit the formation of highly branched oligomers (e.g., dimethylbutenes).
2. Experimental
2.1 Materials synthesis
Tetraethyl orthosilicate (TEOS, Sigma-Aldrich), colloidal silica (LUDOX® AS-40), aluminum nitrate nonahydrate (Sigma-Aldrich), sodium aluminate (Sigma-Aldrich), aluminum sulfate octadecahydrate (Acros Organics), tetrapropylammonium hydroxide (40% TPAOH, Alfa Aesar), tetraethylammonium hydroxide (35% TEAOH, Sigma-Aldrich), tetraethylammonium bromide (TEABr, Sigma-Aldrich), 1,6-hexanediamine (Thermo Scientific), sodium hydroxide (Sigma-Aldrich), potassium hydroxide (Sigma-Aldrich), and ammonium nitrate (Sigma-Aldrich) were used as received. Deionized water was filtered by means of a Thermo Scientific GenPure Pro™ purification system.ZSM-5, ZSM-12, and ZSM-22 samples with MFI, MTW, and TON topologies, respectively, were prepared following reported procedures in the literature.19–23 The gel composition and crystallization time were varied to achieve crystals of different sizes. Table 1 summarizes the conditions used in zeolite synthesis (see Section S1 of the ESI† for further details).
| Sample | Zeolite | Gel composition | Temperature, K | Time, h | Rotation speed, rpm |
|---|---|---|---|---|---|
| 1 | ZSM-5 | SiO2:0.01Al2O3:0.25TPAOH:0.05Na2O:10H2O | 443 | 24 | 60 |
| 2 | ZSM-5 | SiO2:0.01Al2O3:0.25TPAOH:0.05Na2O:100H2O | 443 | 24 | 60 |
| 3 | ZSM-12 | 80SiO2:Al2O3:12.7TEAOH:Na2O:770H2O | 433 | 132 | — |
| 4 | ZSM-12 | 80SiO2:Al2O3:10TEABr:3.6Na2O:770H2O | 433 | 120 | — |
| 5 | ZSM-22 | 91SiO2:Al2O3:27NH2(CH2)6NH2:13K2O:3640H2O | 453 | 48 | 50 |
| 6 | ZSM-22 | 91SiO2:Al2O3:27NH2(CH2)6NH2:13K2O:4440H2O | 453 | 48 | 50 |
2.2 Structural and chemical characterization
X-ray diffraction (XRD) patterns were collected using a Bruker D8 Advance diffractometer equipped with a Cu Kα radiation source. Measurements were conducted in the 2θ range of 5–60° at a rate of 0.03° s−1 and compared against reference patterns from the International Zeolite Association.24 Nitrogen physisorption measurements at 77 K were performed on a Micromeritics ASAP 2420 system. Total and micropore surface areas were calculated using the Brunauer–Emmett–Teller (BET) and t-plot methods, respectively. Scanning Electron Microscopy (SEM) images were acquired using an FEI Teneo microscope equipped with a Nicole field emission gun. The samples were placed on carbon tape and coated with platinum nanoparticles as needed. 29Si and 27Al MAS NMR spectra were collected on a Bruker Avance 400 MHz spectrometer equipped with a 4 mm probe. The flip angle was π/2 and the spinning frequency was 14 kHz for both analyses. Chemical shifts in 29Si and 27Al were referenced to [(CH3)2SiO]3 and AlCl3·6H2O, respectively. Temperature-programmed desorption (TPD) of ammonia was performed on a Micromeritics AutoChem 2950 system. NH4+-exchanged samples were pretreated in flowing helium at 423 K for 4 h and then heated to 1123 K at 10 K min−1. Desorbed ammonia was quantified by a Hiden Analytical mass spectrometer.2.3 Transient sorption measurements
Transient sorption of 2,3-dimethylbutane (Sigma-Aldrich) and 2,2-dimethylbutane (TCI America) on samples was studied using a Micromeritics ASAP 2020 system. The samples (150–250 μm, 10–50 mg) were evacuated (<1 Pa) at 673 K for 4 h and then cooled to the sorption temperature. The manifold was dosed with 5.0 cm3 (STP) g−1 of sorbate and transient sorption was recorded as the sample is exposed to the manifold. Sorption isotherms were collected at 303 K up to 5 kPa of sorbate pressure.2.4 Catalytic testing
Alkene oligomerization was performed in fixed beds comprised of zeolite samples (150–250 μm, 1–100 mg) supported by quartz wool. Tubular, quartz reactors (2 mm ID) were utilized for catalyst screening in an Avantium Flowrence XD high-throughput system. The catalysts were activated under nitrogen (Air Liquide, Grade 5) at 823 K for 1 h prior to reaction and then cooled to the reaction temperature. Oligomerization reactions were carried out at 423–573 K and atmospheric pressure. Liquified propylene (AHG, 99.95%) was passed to the reactors at 1–8 g h−1 and diluted with helium (Air Liquide, Grade 5) to reach the desired alkene pressure (50 kPa). The alkene residence time was short enough that differential conversion is achieved. The reactor effluent was analyzed by an Agilent 8890 gas chromatograph equipped with GS-GasPro (60 m × 0.32 mm) and HP-InnoWax (30 m × 0.32 mm × 0.5 μm) columns. Detailed analysis of product distribution was performed using a polydimethylsiloxane column (DB-Petro, 100 m × 0.25 mm × 0.5 μm) connected to a PID Eng & Tech reactor (further details in Section S2†). The elution order and retention times of C5–C8 hydrocarbons were determined from GC/MS (Agilent, 7890A/5975C) analyses and known retention indices on similar columns.25–273. Results and discussion
3.1 Structural and chemical characterization
Table 2 lists the structural and chemical characterization results for zeolite samples. XRD patterns (Fig. S1–S3†) confirm crystallization of desired phases with high purity. SEM images (Fig. 1) show cubic, spherical, and needle-like morphologies for MFI, MTW, and TON samples, respectively. 29Si MAS NMR spectra (Fig. S4†) of all samples exhibit chemical shifts between −103 and −115 ppm which correspond to Si(0Al) and Si(1Al) silicon environments.2827Al MAS NMR spectra (Fig. S5†) reflect resonances at ca. 0 and 56 ppm attributed to octahedrally and tetrahedrally coordinated aluminum species, respectively, in the zeolite framework.| Sample | Framework | Crystallite size,a μm | (Si/Al)Fb | AlF,c % | S BET,d m2 g−1 | S micropore,d m2 g−1 | C H+,e mmol cm−3 |
|---|---|---|---|---|---|---|---|
| a Estimated from SEM images. b Framework silicon-to-aluminum ratio determined from 29Si MAS NMR spectra using Löwnstein's rule.28 c Framework aluminum content determined from 27Al MAS NMR spectra. d Surface area calculated from nitrogen physisorption measurements. e Brønsted acid site concentration quantified by TPD and multiplied with molecular weight per unit cell volume using chemical formulae for each framework.29 | |||||||
| 1 | MFI | 0.15 | 41.5 | 92.9 | 500 | 370 | 0.37 |
| 2 | MFI | 1.5 | 43.4 | 92.2 | 465 | 383 | 0.48 |
| 3 | MTW | 0.5 | 38.0 | 97.2 | 509 | 395 | 2.5 |
| 4 | MTW | 2.5 | 44.2 | 98.4 | 375 | 260 | 1.9 |
| 5 | TON | 0.5 | 45.0 | 99.0 | 80 | 58 | 0.57 |
| 6 | TON | 5.0 | 47.5 | 98.0 | 121 | 66 | 0.76 |
3.2 Effects of crystallite size on alkene oligomerization turnover rates
The activation energy is a useful measure to ascertain whether transport limitations disguise kinetics. For an irreversible, nth-order reaction, the apparent activation energy approaches half the intrinsic value under severe diffusion limitations.9 This approximation is applicable in alkene oligomerization given the low diffusional activation barriers of respective alkanes.30 Experimental studies on alkene oligomerization report an intrinsic activation energy of 53 kJ mol−1 and attribute values lower than that to transport limitations.12,31 These studies suggest that alkene oligomerization proceeds through an Eley–Rideal mechanism whose rate takes the form: | (1) |
eqn (1) translates to first-order kinetics under surface coverage of reactants. IR studies conducted by Sarazen and Iglesia,32 in which spectra were collected upon contact of propene and isobutene with TON at 503 K, showed that saturation coverage is reached at 10 kPa of alkene pressure, suggesting first-order dependence of oligomerization rates. Similar dependence was observed for MTW and TON samples when varying propene pressure between 50–80 kPa at 523 K (see Fig. S6†). Hence, catalytic activity can be expressed in terms of first-order rate constants. By contrast, a negative-order dependence was measured on MFI, in consistency with observations by Bickel and Gounder.16 The observed product distribution on MFI (Fig. S7†) reflects a complex series–parallel reaction system in which propene undergoes secondary reactions with oligomerization and β-scission products. This phenomenon makes it difficult to estimate kinetic parameters of relevance from propene consumption rates. Therefore, catalytic activity in MFI samples will be expressed in terms of initial rates.
Fig. 2 shows first-order rate constants calculated for propene oligomerization on MTW and TON samples at 423–573 K. These parameters were estimated from initial rates considering an exponential decay model of catalyst activity (see Section S2†). Rate constants (per H+) were found to be independent of crystallite size in TON (0.5–5.0 μm) at 423–523 K. Such invariance with crystallite size reflects that rates are under kinetic control. As temperature increased above 523 K, rate constants began to vary with crystallite size, which signifies the prevalence of transport limitations under these conditions. In agreement with theory, the activation energy observed for 5.0 μm crystals of TON at 523–573 K (i.e., 19 kJ mol−1) approaches one half the intrinsic value reported by Ngandjui and Thyrion.31 In fact, the observed activation energy closely matches the value reported by Peratello et al.33 (18 kJ mol−1) when describing diffusion limitations in propene oligomerization over mesoporous silica–alumina. Rate constants were found to be invariant with crystallite size in MTW (0.5–2.5 μm) over the entire range of temperatures studied. The insignificant transport effects can be attributed to the lower reactivity and higher propene diffusivity34 in MTW than in TON. These findings, overall, demonstrate that reactant diffusion limitations can be promoted at high temperatures.
 | ||
| Fig. 2 Temperature dependence of propene oligomerization on MTW and TON samples. [PC3H6 = 50 kPa, XC3H6 < 0.1]. | ||
Weisz–Prater criteria corroborate the presence of reactant diffusion limitations. The Weisz–Prater parameter is given by
 | (2) |
A similar effect to that of TON was observed for MFI, where initial rates (estimated considering exponential decay of catalyst activity) varied significantly with crystallite size at 573 K (see Fig. 3). Weisz–Prater estimates for 1.5 μm crystals of MFI (adopting effective propane diffusivity from ref. 37) denote that such effects of crystallite size arise as consequences of reactant diffusion limitations (CWP = 6). Remarkably, initial rates varied, but less significantly, with crystallite size at considerably lower temperatures (473–523 K), which conflicts with Weisz–Prater criteria (CWP ≪ 1). Bickel et al.16 made similar observations and proposed that products accumulating within MFI pores obstruct the transport of reacting species, causing diffusion limitations even at low temperatures. The authors further demonstrated that the composition of accumulating products becomes lighter as temperature increases, suggesting that diffusion limitations caused by this phenomenon are particularly prevalent at low temperatures.
 | ||
| Fig. 3 Initial rates of propene consumption on MFI samples as a function of temperature. [PC3H6 = 50 kPa, XC3H6 < 0.3]. | ||
3.3 Effects of pore diameter on alkene oligomerization turnover rates
Confinement in zeolites results in an enhanced reactivity towards alkene oligomerization. Sarazen et al.36 rationalized this by the ability of confining voids to stabilize transition states through van der Waals interactions. The influence of confinement on propene oligomerization rates is apparent from rate constants which increased with decreasing pore diameter (see Table 3). We interpret this result in terms of transition state theory to determine how enthalpy and entropy changes reflect confinement effects on oligomerization rates. Table 3 shows activation energies and entropies calculated for propene oligomerization on MTW and TON at 523 K using transition state theory formalisms (see derivations in Section S3†). Measured activation energies were nearly invariant on MTW and TON (73–76 kJ mol−1), reflecting similar stabilization of transition states and their precursors by these zeolites. Their values are in agreement with activation enthalpies reported in microkinetic modeling studies of propene oligomerization.38,39 Measured activation entropies, on the other hand, varied by 21 J mol−1 K−1 between MTW and TON, reflecting differences in their ability to confine transition states and their precursors. These findings demonstrate that confinement effects on oligomerization rates arise predominantly from entropy changes.3.4 Transient sorption measurements
Transport limitations in zeolite crystals were studied by monitoring the transient uptake of 2,3-dimethylbutane (5.8 Å) and 2,2-dimethylbutane (6.2 Å) on MFI, MTW, and TON samples. MFI has straight (5.4 × 5.6 Å) and sinusoidal channels (5.1 × 5.6 Å) which form a three-dimensional pore network, while MTW (5.7 × 6.1 Å) and TON (4.6 × 5.7 Å) have unidirectional pore systems. If sorption of probe molecules is slow, transport is likely to be controlled by micropore diffusion and the uptake rate can be used to estimate micropore diffusional time constants (R2/D).30 Fast sorption of probe molecules is indicative of intrusion from surface or macropore resistances. If the size of the probe molecule is significantly larger than that of the zeolite pores, sorption will take place only on the external surface of crystals, which was the case for 2,3-dimethylbutane and 2,2-dimethylbutane sorption on TON samples (see Fig. S8†).Fig. 4 depicts the uptake profiles of 2,3-dimethylbutane and 2,2-dimethylbutane on MFI and MTW samples. The uptake of 2,3-dimethylbutane by 1.5 μm crystals of MFI was found to be controlled by micropore diffusion. The fractional uptake can be formulated by the solution of the transient diffusion equation for spherical particles with a time-dependent boundary condition:30,40–42
 | (3) |
 | (4) |
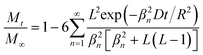 | (5) |
βn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βn + L − 1 = 0 βn + L − 1 = 0 | (6) |
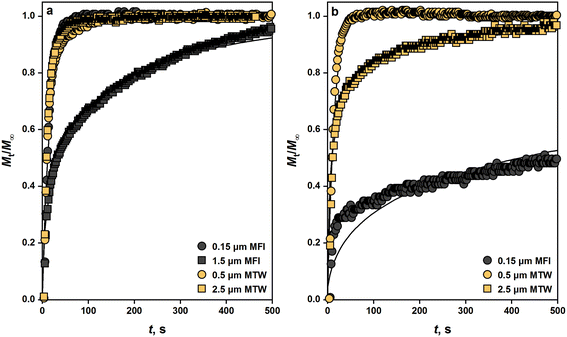 | ||
| Fig. 4 Transient sorption of (a) 2,3-dimethylbutane and (b) 2,2-dimethylbutane on MFI and MTW samples. [T = 303 K, P ≤ 0.05 kPa]. Solid lines represent fits from nonlinear regression. | ||
The uptake of 2,2-dimethylbutane by 0.15 μm crystals of MFI was found to be controlled by micropore diffusion. At 303 K, the intracrystalline diffusivity of 2,2-dimethylbutane in MFI was measured as 1.6 × 10−20 m2 s−1, which matches closely the value reported by Yu et al.43 Micropore resistance was also significant in 2,2-dimethylbutane sorption in 2.5 μm crystals of MTW. The intracrystalline diffusivity of 2,2-dimethylbutane in MTW at 303 K was calculated as 1.3 × 10−16 m2 s−1. The uptake of 2,2-dimethylbutane by 0.5 μm crystals of MTW was found to be controlled by surface or macropore resistance (L > 2).
3.5 Effects of crystallite size on alkene oligomerization selectivity
Propene was reacted over zeolite samples at 523 K to study the effects of crystallite size on alkene oligomerization selectivity. The residence time was varied between 1–40 molH+ s mol−1 to measure selectivity under iso-conversion (5–10%). Table S1† lists the product selectivity (on a carbon basis) for propene reactions on Samples 1–6. Fig. 5 shows the skeletal arrangement of propene dimers formed.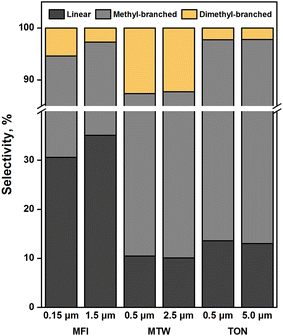 | ||
| Fig. 5 Skeletal arrangement of propene dimers as a function of crystallite size. [T = 523 K, PC3H6 = 20 kPa, XC3H6 = 0.05–0.1, TOS = 1 h]. | ||
Olefin isomers undergo rapid hydride and methyl shifts during oligomerization so that thermodynamic equilibrium is established among isomers of a given size.44 Deviation from equilibrium can be caused by shape selectivity effects, restricting the formation of certain isomers. We examine these effects by studying how the distribution of hexene isomers is affected by crystallite size. The conversion levels were high enough to establish equilibrium, as hexene isomers approach their equilibrium concentrations on MTW (further discussion in Section 3.6). The isomer distribution was not affected by catalyst deactivation in the initial hours of time-on-stream (TOS).
As shown in Fig. 5, dimethylbutene selectivity decreased from 5.4 to 2.7% as the crystallite size of MFI increased from 0.15 to 1.5 μm. This suggests that dimethylbutenes, which are slow diffusing species, suffer from product shape selectivity in MFI crystals. This observation is in line with transient sorption measurements which show that dimethylbutanes diffuse slowly in MFI (Fig. 4). Such analogies can be made given the similar diffusivities of dimethylbutanes and dimethylbutenes.45 Methylpentene selectivity decreased from 64.0 to 62.1% as the crystallite size of MFI increased, suggesting that methylpentenes also undergo product shape selectivity. Dimethylbutene selectivity decreased insignificantly from 12.6 to 12.3% as the crystallite size of MTW increased from 0.5 to 2.5 μm, reflecting the absence of product shape selectivity towards dimethylbutenes. This observation is consistent with the fast sorption of 2,3-dimethylbutane in differently sized MTW crystals (Fig. 4a). The significant differences in shape selectivity exhibited by MTW and MFI towards dimethylbutenes can be ascribed to the higher diffusivity of 2,2-dimethylbutane in MTW than in MFI (i.e., varies by a factor of 104 at 303 K). A low selectivity towards dimethylbutenes (2.2%) was observed with 5.0 μm crystals of TON. Decreasing crystallite size from 5.0 to 0.5 μm resulted in no considerable change to this selectivity. This suggests, together with the weak sorption of dimethylbutanes on TON samples (Fig. S8†), that transition state shape selectivity restricts the formation of dimethylbutenes.
3.6 Effects of pore diameter on alkene oligomerization selectivity
Measurement of intrinsic selectivity in alkene oligomerization is a challenging task owing to diffusion limitations of oligomerization products. Therefore, probing the effects of pore diameter on selectivity under influences of mass transfer can be misleading. In cases where mass transfer limitations govern selectivity, Weitkamp and Ernst46 recommend comparing zeolites of the same intracrystalline diffusion length. We accordingly compare the hexene isomer distribution on zeolites of similar crystallite size (0.15–0.5 μm) with an aim to correlate the degree of branching with the topology of these zeolites. Descriptors developed by First et al.47 such as the pore limiting diameter (PLD) are employed to make such correlations.Fig. 6 compares the hexene isomer distribution on MFI, MTW, and TON at fixed conversion levels (5–10%). The inset shows the equilibrium distribution of hexene isomers at 523 K adopted from ref. 48. The twelve-membered ring zeolite, MTW, showed enhanced selectivity towards dimethylbutenes (12.6%), close to that dictated by thermodynamics (13.9%). This demonstrates that large pore openings can accommodate highly branched dimers of propene. TON showed low selectivity towards dimethylbutenes (2.3%), suggesting that transition states required to form these species are too bulky to fit inside the ten-membered ring channels of TON. This observation is consistent with the results reported by Smit and Maesen,49 who found that TON contributes positively to the Gibbs free energy of formation of double-branched alkanes. Pore-mouth catalysis, as evidenced in alkane isomerization over Pt/ZSM-22,50,51 offers a plausible explanation for the observed selectivity. Another plausible explanation would be reactions on the external surface of TON crystals. MFI showed moderate selectivity towards dimethylbutenes (5.4%), reflecting an ability for these species to be formed within the MFI structure. Such bulky molecules are likely to be formed at the intersections of MFI channels, but ultimately, they experience diffusion limitations in the ten-membered ring channels of MFI. As shown in Fig. 7, a strong correlation is found between the selectivity to dimethyl-branched dimers (relative to linear dimers) and the number of n-membered rings in zeolite channels.
 | ||
| Fig. 6 Hexene isomer distribution on MFI, MTW, and TON. [T = 523 K, PC3H6 = 20 kPa, XC3H6 = 0.05–0.1, TOS = 1 h, crystallite size = 0.15–0.5 μm]. The trans forms are shown for simplicity. The inset represents the equilibrium distribution of hexene isomers at 523 K adopted from ref. 48. Isomers in the inset follow the same order in the figure. | ||
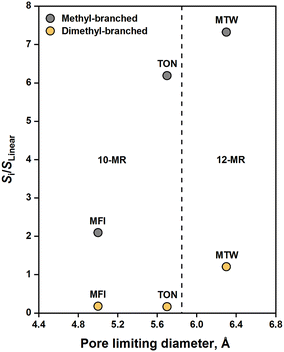 | ||
| Fig. 7 Branched to linear dimer selectivity with respect to the pore limiting diameter. [T = 523 K, PC3H6 = 20 kPa, XC3H6 = 0.05–0.1, TOS = 1 h, crystallite size = 0.15–0.5 μm]. | ||
MFI showed a methylpentene selectivity of 64.0%, which is lower than the equilibrium concentration of methylpentenes (75.4%). Such deviation can be ascribed to diffusion limitations imposed on methylpentenes in MFI channels, as demonstrated in Section 3.5. TON exhibited a methylpentene selectivity of 84.1%, which far exceeds equilibrium. This is likely a result of the spatial limitations imposed on dimethylbutenes that lead to preferential formation of methylpentenes. The fact that methylpentanes diffuse faster in TON than in MFI52 explains the significant differences in methylpentene selectivity shown by TON and MFI. MTW exhibited a methylpentene selectivity of 76.9%, which is close to equilibrium. The absence of spatial or diffusion limitations led to such equilibration. The best correlation for the selectivity to methyl-branched dimers (relative to linear dimers) is found in terms of the PLD of zeolites (see Fig. 7).
4. Conclusions
The effects of crystallite size and pore diameter on alkene oligomerization rates have been studied on MFI, MTW, and TON zeolites at a wide range of temperatures (423–573 K). Turnover rates varied significantly with crystallite size in medium-pore zeolites (MFI, TON), a strong indication of the presence of reactant diffusion limitations. These limitations were found to be prevalent mostly at high oligomerization temperatures (523–573 K). In the absence of diffusion limitations, turnover rates varied considerably among zeolites which differ in their unidirectional channel size (MTW, TON). Interpretation of this result in terms of transition state theory suggests that structural effects on oligomerization rates arise solely from entropy changes.Branching in alkene oligomerization depends on the void environment in which oligomers form and egress. The MTW framework featuring twelve-membered ring channels allows the formation of highly branched oligomers such as dimethylbutenes without constraints of shape selectivity. Intracrystalline diffusion of dimethylbutenes is so rapid in MTW channels that their selectivity is unaffected by changes in crystallite size. The MFI framework featuring intersecting ten-membered ring channels imposes shape selectivity constraints on dimethylbutenes. These constraints are diffusional in origin and increase with increasing crystallite size of MFI. The TON framework featuring non-intersecting ten-membered ring channels restricts by transition state shape selectivity the formation of dimethylbutenes. Consequently, methylpentenes are formed at fractions beyond thermodynamic equilibrium of hexene isomers. Understanding how branching is affected by topology, taking into consideration influences of crystallite size, is key to design more selective materials for applications in olefins-to-gasoline catalysis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge Natalia Morlanes, Adrian Ramirez, Jose Cerrillo, Youssef Saih, Selvedin Telalovic, Daria Poloneeva, Maya Ayach, Gerard Clancy, Jose Primera, Omar El Tall, and Abdelhamid Emwas for assistance with catalytic testing and structural and chemical characterization. The authors also thank Sandra Ramirez for designing the graphical abstract of this work.References
- M. Berlin, J. Gage and E. Jonnson, Work, Environ., Health, 1974, 11, 1–20 CAS.
- M. Hajbabaei, G. Karavalakis, J. W. Miller, M. Villela, K. H. Xu and T. D. Durbin, Fuel, 2013, 107, 671–679 CrossRef CAS.
- U.S. Environmental Protection Agency, Control of Air Pollution from Motor Vehicles: Tier 3 Motor Vehicle Emission and Fuel Standards, 2014 Search PubMed.
- A. Schriesheim and I. Kirshenbaum, Am. Sci., 1981, 69, 536–542 CAS.
- G. A. Olah, A. Goeppert and G. K. S. Prakash, Beyond Oil and Gas: The Methanol Economy, John Wiley, 2nd edn, 2006 Search PubMed.
- C. D. Chang and A. J. Silvestri, J. Catal., 1977, 47, 249–259 CrossRef CAS.
- S. A. Tabak, F. J. Krambeck and W. E. Garwood, AIChE J., 1986, 32, 1526–1531 CrossRef CAS.
- R. J. Quann, L. A. Green, S. A. Tabak and F. J. Krambeck, Ind. Eng. Chem. Res., 1988, 27, 565–570 CrossRef CAS.
- M. E. Davis and R. J. Davis, Fundamentals of Chemical Reaction Engineering, McGraw-Hill, 2003 Search PubMed.
- P. B. Weisz, Stud. Surf. Sci. Catal., 1981, 7, 3–20 CrossRef CAS.
- S. M. Csicsery, Zeolites, 1984, 4, 202–213 CrossRef CAS.
- M. J. Wulfers and R. F. Lobo, Appl. Catal., A, 2015, 505, 394–401 CrossRef CAS.
- A. Corma, C. Martínez and E. Doskocil, J. Catal., 2013, 300, 183–196 CrossRef CAS.
- R. Van Grieken, J. M. Escola, J. Moreno and R. Rodríguez, Appl. Catal., A, 2006, 305, 176–188 CrossRef CAS.
- C. T. O'connor, S. Schwarz and M. Kojima, in Catalysis and Adsorption by Zeolites, ed. G. Öhlmann, H. Pfeifer and R. Fricke, Elsevier, 1991, vol. 65, pp. 491–500 Search PubMed.
- E. E. Bickel and R. Gounder, JACS Au, 2022, 2, 2585–2595 CrossRef CAS PubMed.
- K. G. Wilshier, P. Smart, R. Western, T. Mole and T. Behrsing, Appl. Catal., 1987, 31, 339–359 CrossRef CAS.
- C. S. H. Chen and R. F. Bridger, J. Catal., 1996, 161, 687–693 CrossRef CAS.
- H. Mochizuki, T. Yokoi, H. Imai, R. Watanabe, S. Namba, J. N. Kondo and T. Tatsumi, Microporous Mesoporous Mater., 2011, 145, 165–171 CrossRef CAS.
- S. Ernst, J. Weitkamp, J. A. Martens and P. A. Jacobs, Appl. Catal., 1989, 48, 137–148 CrossRef CAS.
- A. K. Jamil and O. Muraza, Microporous Mesoporous Mater., 2016, 227, 16–22 CrossRef CAS.
- S. Gopal, K. Yoo and P. G. Smirniotis, Microporous Mesoporous Mater., 2001, 49, 149–156 CrossRef CAS.
- K. Yoo, R. Kashfi, S. Gopal, P. G. Smirniotis, M. Gangoda and R. N. Bose, Microporous Mesoporous Mater., 2003, 60, 57–68 CrossRef CAS.
- Collection of Simulated XRD Powder Patterns for Zeolites, ed. M. M. J. Treacy and J. B. Higgins, Elsevier, 4th edn, 2001 Search PubMed.
- C. M. White, J. Hackett, R. R. Anderson, S. Kail and P. S. Spock, J. High Resolut. Chromatogr., 1992, 15, 105–120 CrossRef CAS.
- L. Soják, G. Addová, R. Kubinec, A. Kraus and G. Hu, J. Chromatogr. A, 2002, 947, 101–117 CrossRef PubMed.
- L. Soják, G. Addová, R. Kubinec, A. Kraus and A. Boháč, J. Chromatogr. A, 2004, 1025, 237–253 CrossRef PubMed.
- G. Engelhardt, in Studies in Surface Science and Catalysis, ed. H. van Bekkum, E. M. Flanigen, P. A. Jacobs and J. C. Jansen, Elsevier, 2001, vol. 137, pp. 387–418 Search PubMed.
- C. Baerlocher, L. B. Mccusker and D. H. Olson, Atlas of Zeolite Framework Types, Elsevier, 6th edn, 2007 Search PubMed.
- J. Kärger, D. M. Ruthven and D. N. Theodorou, Diffusion in Nanoporous Materials, Wiley, 2010 Search PubMed.
- L. M. T. Ngandjui and F. C. Thyrion, Ind. Eng. Chem. Res., 1996, 35, 1269–1274 CrossRef CAS.
- M. L. Sarazen and E. Iglesia, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3900–E3908 CrossRef CAS.
- S. Peratello, M. Molinari, G. Bellussi and C. Perego, Catal. Today, 1999, 52, 271–277 CrossRef CAS.
- Z. Liu, Y. Chu, X. Tang, L. Huang, G. Li, X. Yi and A. Zheng, J. Phys. Chem. C, 2017, 121, 22872–22882 CrossRef CAS.
- P. B. Weisz and C. D. Prater, Adv. Catal., 1954, 6, 143–196 CAS.
- M. L. Sarazen, E. Doskocil and E. Iglesia, J. Catal., 2016, 344, 553–569 CrossRef CAS.
- T. Masuda, Y. Okubo, S. R. Mukai, M. Kawase, K. Hashimoto, A. Shichi, A. Satsuma, T. Hattori and Y. Kiyozumi, Chem. Eng. Sci., 2001, 56, 889–896 CrossRef CAS.
- S. Vernuccio, E. E. Bickel, R. Gounder and L. J. Broadbelt, ACS Catal., 2019, 9, 8996–9008 CrossRef CAS.
- S. Vernuccio, E. E. Bickel, R. Gounder and L. J. Broadbelt, J. Catal., 2021, 395, 302–314 CrossRef CAS.
- Adsorption and Diffusion, ed. J. B. Higgins and J. Weitkamp, Springer, 2008 Search PubMed.
- D. M. Ruthven, Principles of Adsorption and Adsorption Processes, John Wiley & Sons, 1984 Search PubMed.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, 2nd edn, 1975 Search PubMed.
- M. Yu, J. C. Wyss, R. D. Noble and J. L. Falconer, Microporous Mesoporous Mater., 2008, 111, 24–31 CrossRef CAS.
- M. L. Sarazen, E. Doskocil and E. Iglesia, ACS Catal., 2016, 6, 7059–7070 CrossRef CAS.
- W. O. Haag, R. M. Lago and P. B. Weisz, Faraday Discuss. Chem. Soc., 1981, 72, 317–330 RSC.
- J. Weitkamp and S. Ernst, Catal. Today, 1994, 19, 107–150 CrossRef CAS.
- E. L. First, C. E. Gounaris, J. Wei and C. A. Floudas, Phys. Chem. Chem. Phys., 2011, 13, 17339–17358 RSC.
- J. E. Kilpatrick, E. J. Prosen, K. S. Pitzer and F. D. Rossini, J. Res. Natl. Bur. Stand., 1946, 36, 559–612 CrossRef CAS.
- B. Smit and T. L. M. Maesen, Nature, 2008, 451, 671–678 CrossRef CAS PubMed.
- J. A. Martens, G. Vanbutsele, P. A. Jacobs, J. Denayer, R. Ocakoglu, G. Baron, J. A. M. Arroyo, J. Thybaut and G. B. Marin, Catal. Today, 2001, 65, 111–116 CrossRef CAS.
- T. L. M. Maesen, M. Schenk, T. J. H. Vlugt, J. P. De Jonge and B. Smit, J. Catal., 1999, 188, 403–412 CrossRef CAS.
- E. B. Webb, G. S. Grest and M. Mondello, J. Phys. Chem. B, 1999, 103, 4949–4959 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00285c |
| This journal is © The Royal Society of Chemistry 2023 |

