Chemometric tools for kinetic investigations of a homogeneously catalysed Sonogashira cross-coupling reaction in flow

Abstract

In chemical research automated reaction screening and analysis are getting more and more important. In this work a chemometrics-based approach for optimizing a chemical reaction and performing kinetic investigations in a continuous-flow microreactor is described. The procedure is exemplified by a Sonogashira cross-coupling reaction. A principal component analysis assisted solvent selection was performed to identify solvents with best performance for flow conditions with minimal experimental effort. Kinetic studies were performed in a continuous-flow microreactor setup under transient conditions. Multivariate curve resolution was applied as chemometrics-based (nearly) calibration free approach for developing a kinetic model. This approach was further expanded by the introduction of the re-parameterized Arrhenius equation to obtain apparent activation energies and reaction rate coefficients.

---

Introduction

Chemometrics is defined as the chemical discipline that uses mathematical and statistical methods, to design or select optimal experiments and to provide maximum chemical information by analysing chemical data.¹ Chemometric tools, such as principal component analysis (PCA), partial least square regression (PLSR) and multivariate curve resolution (MCR), provide a good opportunity for obtaining useful chemical information from the original data and they play a major role in analytical chemistry.^2,3

In this contribution we aim to show the capability of chemometric tools for exemplarily optimizing and investigating a Sonogashira cross-coupling reaction. By performing a PCA assisted solvent screening in batch we were able to identify the best solvents for flow conditions, in order to perform kinetic investigations in a continuous-flow microreactor using an MCR approach.

The selection of the right solvent is a key factor for reaction performance, not only when it comes to homogeneously catalysed reactions.⁴ Solvents can affect catalyst activity, reaction rate and corresponding yields.⁵ Therefore, several solvent selection guides and tools have been developed.^6–10 Most of them consist of rather large spreadsheets with rankings regarding safety, health and environmental impacts and recommendations for substitution of hazardous solvents. The disadvantage of this rather simple approach is that due to the large number of parameters it can be hard to consult the solvent selection guide effectively. The American Chemical Society Green Chemistry Institute Pharmaceutical Roundtable (ACS GCIPR) has provided a more holistic framework for solvent selection based upon the PCA of 30 physicochemical properties of 272 solvents.¹¹ To our knowledge, the solvent selection capacity has not yet been fully utilized by the chemical society, although this tool has been published as an interactive, open-access online tool.¹²

Sonogashira reactions are currently one of the most commonly used methods for alkyne cross-coupling due to their rather simple protocol and mild coupling conditions. A large number of modifications of the protocols and conditions have been reported to improve yields, to create even milder coupling conditions, and to overcome various limitations including the formation of homo-coupled byproducts.^13–16 For a long time, cross-coupling reactions and the corresponding kinetic investigations have mainly been performed in batch processes.^17–19 Since the last decade, several microfluidic/flow or microreactor approaches have been reported for Suzuki, Heck, Stille, Buchwald–Hartwig, Sonogashira and other palladium-catalysed cross-coupling reactions.^20–23 Additionally, microreactors have recently been widely used for precise kinetic studies of various other reactions.^24–26 Performing cross-coupling reactions in flow offers several advantages including nearly isothermal reaction conditions, rapid mixing and enhanced heat and mass transfer. Furthermore, reaction control is improved regarding temperature, pressure and residence time. These advantages can result in higher reaction rates, yields, and selectivities.²⁷ In general, continuous processing results in consistent product quality with lower reaction volumes required, while eliminating the need for set-up times.

The Sonogashira cross-coupling reaction can be conducted as heterogeneous or homogeneous catalysis, depending on the palladium and copper catalyst species. Regarding microreactor systems, metal (coated) tubular reactors have already been successfully applied for heterogeneous catalysis,^28–30 as well as packed-bed reactors with immobilized palladium catalysts.³¹ Heterogeneous catalysis bears the advantage that the reaction accelerates due to the large amount of catalyst present in the reactor and at least in theory the product should be catalyst free. However, palladium species tend to leach from the reactors and contaminate the product. Depending on the application, homogeneous catalysis can be superior to heterogeneous catalysis. Recently, works have been published focusing on homogeneous catalysis.^32–35 Znidar et al. developed a continuous-flow Sonogashira cross-coupling protocol using propyne gas for the synthesis of a key intermediate in the manufacturing of a β-amyloid precursor protein cleaving enzyme 1 (BACE1) inhibitor.³⁶ Placzek et al. synthesized a homolog of the Alzheimer's disease imaging agent Fallypride® using optimized copper-free conditions for Sonogashira type couplings.³⁷ In comparison with the amount of applied studies, the exact mechanism of the homogeneous Sonogashira cross-coupling reaction is still not being fully understood.³⁸

In this work we demonstrate a universally applicable chemometrics-based protocol for kinetic investigations exemplified by a Sonogashira cross-coupling reaction. We performed a principal component analysis (PCA) assisted solvent screening in batch, focusing on best solubility and reactivity performance. Kinetic investigations were performed in a continuous-flow microreactor using a multivariate curve resolution (MCR) approach. The obtained kinetic model is the basis for a model-based scale-up prediction. To our knowledge this is the first time kinetic investigations for process understanding of a Sonogashira cross-coupling reaction have been performed in a continuous-flow microreactor setup.

Methods

Solvent selection

As mentioned before, the American Chemical Society Green Chemistry Institute Pharmaceutical Roundtable (ACS GCIPR) has provided a more holistic framework for solvent selection based upon the PCA of 30 physicochemical properties of 272 solvents, which is accessible online but not yet fully implemented by chemists and engineers.¹² A table of the 30 physicochemical properties can be found in the ESI.† The PCA data reduction resulted in a description of the data variance by six principal components (PC). Principal component 1 and 2 (PC1 and PC2) together describe around 60% of the data variance of the 272 solvents. Therefore, PC1 and PC2 are chosen as axis for the PCA score plot as solvent selection map (Fig. 1). Additionally, the representation of the solvents by PC1 and PC2 allowed the detection of a reactivity trend of the Sonogashira reaction correlated to the chosen solvent (vide infra).

Fig. 1 PCA score plot (PC2 vs. PC1) of all 272 solvents, represented by dots. PC1 and PC2 together describe around 60% of the data variance.^11,12 Figure is adapted from Diorazio et al., (2016).¹¹ Link: https://pubs.acs.org/doi/10.1021/acs.oprd.6b00015. Notice to readers: further permission related to the material excerpted should be directed to the ACS.

Further details on PCA and score plots can be found in the literature.^39,40 Each solvent is represented by a dot. Solvents close to each other on the map have similar physical and chemical properties, while distant solvents are significantly different.¹¹

Multivariate curve resolution

For kinetic investigations, reactions can be monitored inline by several spectroscopic techniques including Raman, MIR, NIR, NMR and UV/Vis spectroscopy. In the classic approach, univariate calibration curves have to be obtained beforehand, which are limited to baseline separated, distinct bands. Multivariate analysis methods bear the advantage that data analysis is not limited to distinct or individual bands. However, obtaining multivariate calibration curves can be quite time consuming. Multivariate curve resolution offers a (nearly) calibration free approach for obtaining kinetic data.‡ MCR is a methodology for the analysis of process data in many different application fields, which has been successfully applied by our group and others for process monitoring and kinetic modeling.^41,42 It provides a bilinear description of the observed data variation which is given a chemical meaning through implementing adequate constraints. The main requirement for MCR is that the linear correlation between concentration and spectral information is valid for the investigated system.⁴³ The spectroscopic data matrix D can then be decomposed into concentration profiles C and spectra of the involved components S^T (eqn (1)). The error matrix E should be close to the spectroscopic noise. A more detailed description of the MCR procedure can be found elsewhere in literature.^44,45

D = C·S^T + E (1)

MCR methods can be divided into soft and hard modeling depending on the chosen constraints.⁴⁶ In soft modeling, C and S^T are computed by an alternating least squares calculation to minimize the error in the reproduction of the original data set D. Constraints such as unimodality, non-negativity and mass balance closure are used to decrease rotational ambiguity, which is related to the uncertainty of the obtained result and to give the result a chemical meaning.^47,48 During hard modeling a kinetic model is used, whose parameters are fitted to reconstruct the data D matrix as well as possible.⁴⁹ This fitting consists of finding a set of kinetic parameters for which the error matrix E is minimal. The choice and weighting of the constraints and kinetic model can have a tremendous impact on the calculated solutions.⁵⁰

Experimental

Reaction

The Sonogashira cross-coupling reaction of iodobenzene 1 (for synthesis, >99%, Sigma-Aldrich) and phenylacetylene 2 (≥98%, Alfa Aesar) in dimethylformamide (technical, 98%, VWR chemicals) leads to diphenylacetylene 3 (Scheme 1). Pd(PPh₃)₄ (>99%, Apollo Scientific) and CuI (for synthesis, ≥98%, Alfa Aesar) were used as homogeneous catalysts. Triethylamine (for synthesis, ≥99%, Sigma-Aldrich) was used as base. Since the catalysts are air sensitive, dimethylformamide was degassed with a HPLC degasser prior to use. The mentioned concentrations (vide infra) refer to the values in the microreactor during the reaction.

Scheme 1 Sonogashira reaction: 1, iodobenzene; 2, phenylacetylene, 3, diphenylacetylene.

Solvent screening

The solvent screenings were performed in a 100 mL round bottom flask under argon atmosphere at room temperature. Pd(PPh₃)₄ (0.289 g, 0.25 mmol, 1 mol%) and CuI (0.095 g, 0.50 mmol, 2 mol%), were dissolved in 32 mL of the desired solvent. Triethylamine (12 mL, 0.088 mol) and iodobenzene 1 (2.8 mL, 0.025 mol) were added. The reaction was started by adding phenylacetylene 2 (3 mL, 0.0275 mol) and followed by offline gas chromatography (GC) analysis. Samples (0.5 mL) were taken after 5, 15 and 60 minutes, quenched with HCl (1 M) and diluted with ethylacetate (4.5 mL). See ESI† for the detailed GC protocol.

Continuous-flow experiments

The continuous-flow experiments were conducted in a microreactor setup, as shown in Scheme 2, consisting of a coiled 1/16 in. stainless steel capillary, which was placed in a temperature-controlled bath thermostat. A detailed picture of the setup can be found in the ESI.† In order to realize a wide range of residence times and reactor geometries, three different microreactors (MR 1, MR 2 and MR L) with different inner diameters and lengths were used. High mixing efficiency, narrow residence time distribution (Bodenstein number >100) and nearly isothermal reaction conditions are crucial for determining reliable kinetic data.⁵¹ Therefore, we have carefully selected the microreactors according to previous studies and investigated the influence of mixing and reactor geometries (vide infra).⁵² The exact properties and calculated Bodenstein numbers can be found in the ESI.† Dosage of the starting materials within 1 mL glass syringes was accomplished by continuously working syringe pumps (SyrDos2, HiTec Zang GmbH, Germany). Temperature, flow rates and pressure were controlled by a laboratory automation system (HiTec Zang GmbH, Germany). A solution of iodobenzene 1, phenyl-acetylene 2 and triethylamine in dimethylformamide was mixed in a T mixer (1.25 mm bore hole) with a solution of CuI and Pd(PPh₃)₄ in dimethylformamide. The flow rate ratio amounted to 1. The synthesis was investigated at temperatures between 80 °C and 100 °C. After the reaction, the reaction medium was quenched by cooling down to room temperature in a water bath before measuring with Raman inline spectroscopy (MultiSpec Raman system, Tec5, 785 nm excitation, output power <500 mW). A detailed description of the custom build Raman flow cell and corresponding details on Raman measurements can be found in the ESI.† A back-pressure regulator (2.76 bar) was installed, in order to prevent the evolution of gas due to the high temperatures. A bypass was introduced in order to measure spectra of the reaction mixture at the starting point of the reaction (τ = 0 s). In order to enhance the time efficiency of data collection, the continuous-flow experiments were conducted under transient conditions, meaning that the residence time was increased at a constant rate α while Raman spectra were collected continuously. Narrow residence time distribution is crucial for this transient approach (see ESI† for more details).⁵³

Scheme 2 Microreactor setup for kinetic investigations of the Sonogashira reaction.

Data evaluation methods

The Raman spectra were processed as follows: the spectra were baseline corrected by designing and minimising a cost function (asymmetric truncated quadratic cost function, 4th polynomial order, threshold 0.01)⁵⁴ and experimental data matrices (Raman spectra over time) were constructed. The baseline correction is exemplarily shown in the ESI.† In order to investigate the kinetic model, concentration profiles were obtained by an MCR soft modeling approach. The MCR-ALS GUI 2.0 working under MATLAB® environment was applied for the soft modeling approach.⁵⁵ The following constraints relating to the row mode (concentration profiles) were defined: non-negativity, horizontal unimodality and mass balance closure. At low catalyst concentrations an initial estimation for the final spectra of the involved components was added. During MCR only two components could be identified. An increasing component, correlated to the product formation and a decreasing component correlated to the educt concentration during the reaction. The formation of the homo-coupled side product 1,4-diphenylbutadiyne was not detected spectroscopically, since the characteristic Raman active band was found to be below the detection limit (confirmed by GC vide infra). Therefore, mass balance and error estimation based on the two identified components was possible.

The resulting concentration profiles were fitted to a kinetic model using DynoChem® (Scale-up Systems Ltd., Ireland) to obtain the kinetic model as well as kinetic parameters. After developing the kinetic model, the hard modeling approach was applied using the FACPACK⁴⁹ software working under MATLAB® environment. The constraints for hard modeling are defined by the kinetic model. The re-parameterized Arrhenius equation was implemented into the kinetic model to fit the rate constants k_ref and the activation energy E_A, simultaneously, as shown in Scheme 3. Additionally, different initial (catalyst) concentrations can now be applied in the kinetic model in the hard modeling approach. A similar approach has already been demonstrated for the estimation of batch process yields at different batch conditions. However, the chemical reactions in batch were investigated at non-isothermal conditions.⁵⁰

Scheme 3 Schematic MCR representation contrasting soft and hard modeling regarding the procedure to estimate the activation energy.

Results and discussion

Solvent screening

Based on the solvent selection guide mentioned above we selected 12 out of 272 solvents for an initial batch screening, which covered most of the solvent space and thereby most of the variance of all 272 solvents (see Fig. 2).

Fig. 2 Solvents selected for initial screening: 1 triethyleneglycol, 2 n-propylpropionate, 3 dimethylformamide, 4 n-methylformamide, 5 diisopropylethylamine, 6 ethanolamine, 7 isopropylamine, 8 triethylamine, 9 anisole, 10 propan-2-ol, 11 toluene, 12 methanol.^11,12 Figure is adapted from Diorazio et al., (2016).¹¹ Link: https://pubs.acs.org/doi/10.1021/acs.oprd.6b00015. Notice to readers: further permission related to the material excerpted should be directed to the ACS.

The selection was based on literature reviews and the intuition and know-how of the chemist. Environmental and health impact and availability for industry and academia were taken into account. Dimethylformamide was included as a typical solvent for Sonogashira cross-coupling reaction.⁵⁶ At this point it should be noted that solvent screenings have already been performed for Sonogashira cross-coupling reactions.^34,57,58 These screenings however neglected the solubility of catalyst and reagents. However, for kinetic investigations of a homogeneous catalysis in a continuous-flow reactor it is crucial that all components are dissolved throughout the reaction. Therefore, our solvent selection focused on the solubility of the reagents (especially product) and catalysts as criteria for the solvent selection. Additionally, we investigated the influence on reactivity and selectivity. As mentioned above, the 12 solvents represented most of the data variance of all 272 solvents. This is visualized by their relative orientation on the solvent map. The results are visualized in Fig. 3. A strong correlation between negative PC1 score values and solubility of product and catalyst was observed. Solvents with negative PC1 values around −5 and slightly positive PC2 values were able to dissolve both catalyst and product. Additionally, a trend in reactivity related to a negative PC2 value was noticed. Reactivity increased with decreasing PC2 value. Side product formation was identified when applying triethyleneglycol as solvent. A more detailed overview of the results of the initial solvent screening can be found in the ESI.† Two solvents, dimethylformamide and isopropylamine, met our requirements regarding the solubility. Based on this result we expanded the solvent selection in the region around these two solvents as shown in Fig. 3 (region is shown as blue box on the solvent selection map), selecting 12 more solvents for screening. Again, the detailed results can be found in the ESI.† In the further investigation, we identified 2 more possible solvents, n-hexylamine and γ-valerolactone, respectively. γ-Valerolactone should especially be highlighted, since it is a biomass derived, environment friendly solvent. A heterogeneously catalysed Sonogashira cross-coupling protocol in γ-valerolactone has already been reported in literature.⁵⁹ By using the solvent selection tool, we were able to identify 4 possible solvents for a homogeneously catalysed Sonogashira cross-coupling reaction by a fast and cost efficient solvent screening of only 24 solvents out of 272. Due to the five times higher purchasing costs of γ-valerolactone and n-hexylamine (see ESI† for more details), we have decided to perform the kinetic investigations in dimethylformamide. However, it should be noted that we recommend using γ-valerolactone as green solvent and consider the investigation of this solvent for the Sonogashira cross-coupling reaction as further work. Isopropylamine was not preferred as solvent due to its low boiling point (32 °C) and high vapour pressure (633 hPa).⁶⁰

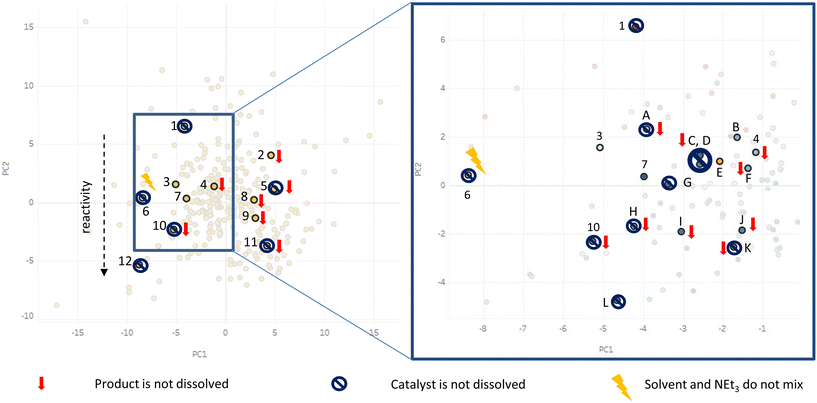Fig. 3 Results of the initial (left) and further (right) solvent screening visualized in the solvent map. 1 triethyleneglycol, 2 n-propylpropionate, 3 dimethylformamide, 4 n-methylformamide, 5 diisopropylethylamine, 6 ethanolamine, 7 isopropylamine, 8 triethylamine, 9 anisole, 10 propan-2-ol, 11 toluene, 12 methanol, A morpholine, B n-hexylamine, C tert-butylamine, D isobutylamine, E γ-valerolactone, F piperidine, G n-propylamine, H butanol, I acetone, J tetrahydrofuran, K methylacetate, L acetonitrile.^11,12 Figure is adapted from Diorazio et al., (2016).¹¹ Link: https://pubs.acs.org/doi/10.1021/acs.oprd.6b00015. Notice to readers: further permission related to the material excerpted should be directed to the ACS.

Continuous-flow experiments

Investigation of mixing performance. To obtain reliable kinetic data, the mixing performance needs to be highly efficient not to influence the reaction progress. Therefore, we have investigated the mixing performance of four different micromixers prior to kinetic investigations. The following micromixers were compared: Caterpillar mixer (CPMM R150, Institute for Microengineering and Microsystems IMM, Germany), X-mixer (HTM-X, Little Things Factory, Germany), T mixer (1.25 mm bore, Upchurch, United States) and static mixing tee (Arrowhead, Upchurch, United States). A more detailed study on the mixing efficiency has already been performed by our group and can be found elsewhere.⁶¹ Additionally, the influence of the microreactor geometry was investigated by performing the reaction in a longer microreactor (MR L) at higher flowrates. Fig. 4 shows the product concentration profiles obtained by using different mixers and different microreactor geometries. During the first six minutes of the reaction, the concentration profiles nearly coincide, meaning that the effect of micromixer selection and reactor geometry can be neglected. This goes in line with the fact that the reaction is rather slow (reaction time about 12 minutes at 90 °C), while mixing-limited reactions are most often very fast in comparison with the mixing time. The small deviations in the product concentration at higher residence times can be explained by small deviations in catalyst activity during the course of reaction. The T mixer (1.25 mm bore hole) was applied in all further investigations.

Fig. 4 Product concentration profiles for different micromixers and microreactors. Reaction conditions: Pd(PPh₃)₄ (0.00125 M), CuI (0.0025 M), iodobenzene (0.45 M), phenylacetylene (0.5 M), NEt₃ (1.5 M), 90 °C.

Influence of preheating. Furthermore, the influence of preheating was investigated. In general, preheating of the educt streams before mixing is to be preferred for exact kinetic investigations, since no induction period is needed to reach the reaction temperature after mixing. However, we observed a decomposition of the catalyst during preheating. Fig. 5a) shows the product concentration profiles with and without preheating. In the preheated case, the reaction slows down after four minutes and stops almost completely. In Fig. 5b) the catalyst decomposition gets visible by the formation of black particles, assumable palladium black, in the catalyst solution after preheating. The decomposition of Pd(PPh₃)₄ in dimethylformamide has already been described in literature.⁶² During further investigations, the educt streams were not preheated and heating time after mixing was regarded as negligible. Detailed information on the calculated heating times after mixing can be found in the ESI.†

Fig. 5 a) Kinetic profiles comparing experiments with and without preheating of the educt streams. Reaction conditions: Pd(PPh₃)₄ (0.00125 M), CuI (0.0025 M), iodobenzene (0.45 M), phenylacetylene (0.5 M), NEt₃ (1.5 M), 90 °C. b) Picture of the catalyst solution in capillaries before and after preheating.

Comparison of steady-state and transient experiments. During kinetic investigations, steady-state and transient experiments were conducted and evaluated. Steady-state experiments were analysed with inline Raman spectroscopy and offline gas chromatography. Concentrations were obtained directly from the Raman spectra by the MCR soft modeling approach. Additionally, GC samples were taken after the experiment time reached three times the corresponding residence time and no significant changes could be detected in the Raman spectrum. Transient flow experiments were conducted as proposed by Jensen and Moore⁵³ (see Experimental section and ESI†) and monitored by inline Raman spectroscopy. Fig. 6 shows the by steady-state and transient obtained and nearly coinciding concentration profiles. However, it should be noted that the number of data points and experimental time differ drastically when comparing the steady-state with the transient flow approach. As long as plug flow behaviour is feasible, the transient approach should be preferred, due to the enormous time efficiency. A more detailed evaluation can be found in the ESI.† All further kinetic investigations were performed using the transient flow approach.

Fig. 6 Kinetic profiles comparing steady-state and transient experiments. Reaction conditions: Pd(PPh₃)₄ (0.00125 M), CuI (0.0025 M), iodobenzene (0.45 M), phenylacetylene (0.5 M), NEt₃ (1.5 M), 90 °C.

Kinetic investigations. For detailed kinetic investigations of the Sonogashira cross-coupling reaction, we first investigated the dependence of the reaction rate on the phenylacetylene and iodobenzene concentration, respectively. In Fig. 7a) the product concentration profiles at varying initial concentration of phenylacetylene at constant initial concentration of iodobenzene (0.5 mol L⁻¹) are shown. The product concentration profile can be modelled using a kinetic model with first order dependence on phenylacetylene. Fig. 7b) shows the product concentration profiles at varying initial concentration of iodobenzene at constant initial concentration of phenylacetylene (0.5 mol L⁻¹). The nearly identical profiles indicate that the reaction is zero-order dependent on the iodobenzene concentration.

Fig. 7 Product concentration profiles at varying initial concentrations of a) phenylacetylene with constant initial concentration of iodobenzene (0.5 mol L⁻¹) and b) iodobenzene with constant initial concentration of phenylacetylene (0.5 mol L⁻¹). Reaction conditions: Pd(PPh₃)₄ (0.0025 M), CuI (0.005 M), NEt₃ (1.5 M), 90 °C.

Furthermore, kinetic measurements with different initial catalyst concentrations were performed. The stoichiometric ratio between the palladium catalyst species and the copper co-catalyst species was held constant and set to 1 : 2. Fig. 8 shows the initial rate of reaction plotted against the square root of the palladium concentration. The linear dependence between the initial rate of reaction and the square root of the palladium concentration results in a fractional order dependence. Additionally, it can be seen that no initial catalyst poisoning or degradation takes place, since the linear fit can be extrapolated through zero. At this point it should be noted that since we held the ratio between catalyst and co-catalyst constant, we describe both catalyst and co-catalyst under the term catalyst in the kinetic model (eqn (2)). This approach is similar to a recent publication.⁶³ The product concentration profiles at varying catalyst concentration can be found in the ESI.† This half-order dependence on the catalyst concentration has already been described in literature for palladium complexes in Heck reactions, which are related to the Sonogashira cross-coupling reactions.^64,65 The oxidative addition of the aryl halide to the active palladium catalyst species results in the formation of a catalytic active monomer species. This is in a fast equilibrium with its catalytic inactive dimeric species, which is one possible explanation for the half-order dependence on the catalyst. Our proposed explanation for the formal kinetic description can be found in the ESI.† However, it should be noted that for our basic kinetic investigation for process understanding and scale-up prediction the following first-principle kinetic model is sufficient:

Fig. 8 Square root of Pd(PPh₃)₄ concentration vs. initial concentration. Reaction conditions: iodobenzene (0.45 M), phenylacetylene (0.5 M), catalyst ratio 2 : 1, Pd(PPh₃)₄ (0.0025/0.00125/0.00063/0.0002 M), CuI (0.005/0.0025/0.00125/0.004 M), NEt₃ (1.5 M), 90 °C.

The general catalytic cycle of the Sonogashira cross-coupling reaction consists of three main steps: oxidative addition of the aryl halide, transmetalation and reductive elimination. In our kinetic investigations, the zero-order dependence on iodobenzene rules out the oxidative addition of iodobenzene with the palladium catalyst as the rate-limiting step. However, the first-order dependence on phenylacetylene and the half-order dependence on the catalyst allow to consider the transmetalation or reductive elimination as rate-limiting step. Usually, the transmetalation is considered as rate-determining step in the catalytic cycle.^18,66 Further investigations are needed for exact determination of the rate-determining step. As mentioned before, for the purpose of process understanding and scale-up prediction the performed basic kinetic investigations are sufficient.

Influence of temperature. Since the basic kinetic model was resolved by the soft modeling approach, we were able to apply this kinetic model in a hard modeling approach, in order to estimate the activation energy. Therefore, we can expand the kinetic model with the re-parameterized Arrhenius equation, in order to fit multiple experiments at different temperatures at the same time (see Scheme 3). Additionally, we included two different catalyst concentrations. Fig. 9 shows different product concentration profiles at varying temperatures and catalyst concentrations contrasting soft and hard modeling. It should be noted that the concentration profiles obtained by soft modeling (Fig. 9a) were afterwards fitted to the above mentioned kinetic model, while the concentration profiles obtained by hard modeling are already forced to follow the kinetic model, in order to reconstruct the data matrix D. The quality parameters (explained variance, lack of fit) are provided in the ESI.† The resulting product concentration profiles are displayed in Fig. 9. The resulting kinetic parameters and the corresponding correlation matrix are summarized in Tables 1 and 2, respectively. While the error limits are both rather narrow, the values for reaction rate coefficients k_ref and activation energy E_A differ noticeably. This can be explained by the fact that soft and hard modeling are based on two different approaches of applying the MCR method: during soft modeling, concentration profiles are obtained for each single experiment at each temperature and catalyst concentration and afterwards all together fit to a kinetic model in order to obtain kinetic parameters. Thus, instead of performing a curve fit to already existing concentration profiles, during hard modeling concentration profiles are directly forced to follow the specified kinetic model. This difference gets particularly evident by taking a look at the concentration profiles at 80 °C and the higher catalyst concentration. There is a strong deviation between the fitted kinetic model concentration profile and the concentration profile obtained by soft modeling, while there is almost no deviation in the profiles obtained by hard modeling. However, it should be noted that the confidence intervals (CI) were calculated from transient experiment data points that are not statistically independent during each experiment. Therefore, the CI values are overestimated and expected to be higher in reality. Additionally, it should be noted that the CI values are not the only criterion to evaluate the quality of the kinetic parameters obtained by soft and hard modeling. Due to the difference between the two approaches, as discussed vide supra, it can be concluded that the k_ref and E_A values regressed by hard modeling should be more reliable, because they were obtained according to the underlying kinetic model.

Fig. 9 Data evaluation using soft and hard modeling. Panel a) displays the soft modeling approach, whereas panel b) displays the hard modeling approach. Legend: points refer to experimental data; lines refer to the underlying kinetic model.

Table 1 Calculated kinetic data obtained by soft and hard modeling

Kinetic parameters	Soft modeling	Hard modeling
Reaction rate coefficient kref	0.002963	0.003500
(CI 95%, at Tref 90 °C)	(±1.69 × 10^−5)	(±1.62 × 10^−5)
[L mol^−0.5 s^−0.5]
Activation energy EA	69.87	80.40
(CI 95%, at Tref 90 °C)	(±0.56)	(±0.84)
[kJ mol^−1]

---

Table 2 Correlation matrix for the obtained kinetic parameters contrasting soft and hard modeling

	Soft modeling		Hard modeling
	k ref	E A	k ref	E A
k ref	1	−0.215	1	0.047
E A	−0.215	1	0.047	1

---

The homo-coupled side product 1,4-diphenylbutadiyne was observed at negligible low concentrations (<1%). Corresponding gas chromatography analysis can be found in the ESI.† Additionally, NMR spectra of the reaction mixture were taken in order to confirm the product formation (see ESI†).

With the obtained kinetic model and the corresponding kinetic parameters, we have now predicted optimal reaction conditions for a continuous process of this Sonogashira reaction. We recommend using the lower catalyst concentration (CuI = 0.0025 M, Pd(PPh₃)₄ = 0.00125 M), due to the high purchasing costs especially of the palladium catalyst, and an initial concentration of iodobenzene, phenylacetylene and triethylamine amounting to 0.45 M, 0.5 M and 1.5 M, respectively. At 100 °C we obtain 99% yield with a residence time of 11 minutes. Due to the possible decomposition of the catalyst at high temperatures we do not recommend increasing the temperature any further for production purposes.

Conclusion

In this work, a chemometrics-based approach for fast kinetic investigations of a homogeneously catalysed reaction in flow was presented. The PCA assisted solvent selection provides a fast and cost-effective methodology for solvent screening to identify solvents for best performance in flow. It should be highlighted that we were able to identify four possible solvents by screening only 24 solvents out of 272. An automated microreactor setup with real-time reaction monitoring through inline Raman spectroscopy enabled precise kinetic investigations under transient conditions. Our studies showed that our carefully chosen experimental setup including micromixer and microreactor geometries satisfied all requirements for assuming an ideal, nearly isothermal plug flow reactor behaviour. Moreover, by repeating the reaction under steady-state conditions using offline GC analysis, the precision and time effectiveness of the transient approach was demonstrated. Multivariate curve resolution offered a (nearly) calibration free method for kinetic modeling. The soft modeling approach was first applied to identify the basic kinetic model. After a suitable kinetic model was identified we applied this kinetic model for the hard modeling approach. By extending the kinetic model using the re-parameterized Arrhenius equation, it is now possible to resolve multiple experiments at different temperatures and different initial concentrations at one time. The results were compared with the results of soft modeling. The similar results show the capability of this faster hard modeling approach for kinetic modeling, which in our opinion should be preferred if the kinetic model or at least a first reasonable guess for the kinetic model is available.

Abbreviations and symbols

C	Concentration profiles
CI	Confidence interval
D	Experimental data matrix
E	Noise matrix
E A	Activation energy
GC	Gas chromatography
k	Reaction rate coefficient
k ref	Reaction rate coefficient at reference temperature
MCR	Multivariate curve resolution
NEt3	Triethylamine
PCA	Principal component analysis
R	Ideal gas constant
ESI	Electronic supplementary information
S ^T	Spectra of the involved components
τ	Residence time
T	Temperature
T ref	Reference temperature

Author contributions

Lisa Schulz: investigation, writing – original draft. Mathias Sawall: software, writing – reviewing and editing. Norbert Kockmann: supervision, writing – reviewing and editing. Thorsten Röder: funding acquisition, supervision, writing – reviewing and Editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr. Christian Holtze, Dr. Philipp Stähle and Dr. Benjamin Frank from BASF SE for the lively exchange and fruitful discussions. This work was funded by the German Federal Ministry of Research (BMBF) and BASF SE as part of the Innovation Partnership M2Aind Project 13FH8I04IA within the framework “Starke Fachhochschulen-Impuls für die Region” (FH-Impuls).

References

1. Handbook of Chemometrics and Qualimetrics: Part A, ed. D. L. Massart, B. G. M. Vandeginste, L. M. C. Buydens, S. De Jong, P. J. Lewi and J. Smeyers-Verbeke, Elsevier, 1998.
2. A. Bansal, V. Chhabra, R. K. Rawal and S. Sharma, J. Pharm. Anal., 2014, 4, 223–233.
3. N. Kumar, A. Bansal, G. S. Sarma and R. K. Rawal, Talanta, 2014, 123, 186–199.
4. P. J. Dyson and P. G. Jessop, Catal. Sci. Technol., 2016, 6, 3302–3316.
5. F. Huxoll, F. Jameel, J. Bianga, T. Seidensticker, M. Stein, G. Sadowski and D. Vogt, ACS Catal., 2021, 11, 590–594.
6. K. Alfonsi, J. Colberg, P. J. Dunn, T. Fevig, S. Jennings, T. A. Johnson, H. P. Kleine, C. Knight, M. A. Nagy, D. A. Perry and M. Stefaniak, Green Chem., 2008, 10, 31–36.
7. D. Prat, J. Hayler and A. Wells, Green Chem., 2014, 16, 4546–4551.
8. D. Prat, O. Pardigon, H.-W. Flemming, S. Letestu, V. Ducandas, P. Isnard, E. Guntrum, T. Senac, S. Ruisseau, P. Cruciani and P. Hosek, Org. Process Res. Dev., 2013, 17, 1517–1525.
9. D. Prat, A. Wells, J. Hayler, H. Sneddon, C. R. McElroy, S. Abou-Shehada and P. J. Dunn, Green Chem., 2016, 18, 288–296.
10. C. M. Alder, J. D. Hayler, R. K. Henderson, A. M. Redman, L. Shukla, L. E. Shuster and H. F. Sneddon, Green Chem., 2016, 18, 3879–3890.
11. L. J. Diorazio, D. R. J. Hose and N. K. Adlington, Org. Process Res. Dev., 2016, 20, 760–773.
12. ACS GCI Pharmaceutical Roundtable, Solvent Selection Tool, (accessed February 2023), https://www.acs.org/greenchemistry/research-innovation/tools-for-green-chemistry/solvent-tool.html.
13. Metal-catalyzed cross-coupling reactions, ed. A. de Meijere and F. Diederich, Wiley-VCH, Weinheim, 2004.
14. K. V. Arundhathi, P. Vaishnavi, T. Aneeja and G. Anilkumar, RSC Adv., 2023, 13, 4823–4834.
15. M. Gazvoda, M. Virant, B. Pinter and J. Košmrlj, Nat. Commun., 2018, 9, 4814.
16. R. Chinchilla and C. Nájera, Chem. Soc. Rev., 2011, 40, 5084–5121.
17. M. R. an der Heiden, H. Plenio, S. Immel, E. Burello, G. Rothenberg and H. C. J. Hoefsloot, Chemistry, 2008, 14, 2857–2866.
18. C. He, J. Ke, H. Xu and A. Lei, Angew. Chem., Int. Ed., 2013, 52, 1527–1530.
19. L.-H. Zou, A. J. Johansson, E. Zuidema and C. Bolm, Chemistry, 2013, 19, 8144–8152.
20. L. M. Baumgartner, J. M. Dennis, N. A. White, S. L. Buchwald and K. F. Jensen, Org. Process Res. Dev., 2019, 23, 1594–1601.
21. P. Filipponi, C. Ostacolo, E. Novellino, R. Pellicciari and A. Gioiello, Org. Process Res. Dev., 2014, 18, 1345–1353.
22. C. Len, in Sustainable Catalysis, ed. R. Luque and F. Leung-Yuk Lam, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2018, pp. 183–206.
23. P. Yaseneva, P. Hodgson, J. Zakrzewski, S. Falß, R. E. Meadows and A. A. Lapkin, React. Chem. Eng., 2016, 1, 229–238.
24. Z. Yan, J. Tian, C. Du, J. Deng and G. Luo, Chin. J. Chem. Eng., 2022, 41, 49–72.
25. X. Xue, R. Jiang, C. Xie, G. Qian, M. Shang, W. Zhu and Y. Su, AIChE J., 2022, 68, year.
26. S. Liu, M. Pasha, M. Shang, Y. Wang, G. Qian, Z.-H. Luo and Y. Su, Chem. Eng. Sci., 2023, 266, 118273.
27. T. Noël and S. L. Buchwald, Chem. Soc. Rev., 2011, 40, 5010–5029.
28. R. Javaid, H. Kawanami, M. Chatterjee, T. Ishizaka, A. Suzuki and T. M. Suzuki, Chem. Eng. J., 2011, 167, 431–435.
29. B. Borcsek, G. Bene, G. Szirbik, G. Dormán, R. Jones, L. Ürge and F. Darvas, ARKIVOC, 2012, 2012, 186–195.
30. L.-M. Tan, Z.-Y. Sem, W.-Y. Chong, X. Liu, Hendra, W. L. Kwan and C.-L. K. Lee, Org. Lett., 2013, 15, 65–67.
31. Y. Ashikari, K. Maekawa, M. Ishibashi, C. Fujita, K. Shiosaki, H. Bai, K. Matsuyama and A. Nagaki, Green Processes Synth., 2021, 10, 722–728.
32. A. D. Clayton, A. M. Schweidtmann, G. Clemens, J. A. Manson, C. J. Taylor, C. G. Niño, T. W. Chamberlain, N. Kapur, A. J. Blacker, A. A. Lapkin and R. A. Bourne, Chem. Eng. J., 2020, 384, 123340.
33. T. Fukuyama and I. Ryu, Green Processes Synth., 2012, 1, year.
34. A. Sugimoto, T. Fukuyama, M. T. Rahman and I. Ryu, Tetrahedron Lett., 2009, 50, 6364–6367.
35. L.-C. Campeau and N. Hazari, Organometallics, 2019, 38, 3–35.
36. D. Znidar, C. A. Hone, P. Inglesby, A. Boyd and C. O. Kappe, Org. Process Res. Dev., 2017, 21, 878–884.
37. M. S. Placzek, J. M. Chmielecki, C. Houghton, A. Calder, C. Wiles and G. B. Jones, J. Flow Chem., 2013, 3, 46–50.
38. X. Wang, Y. Song, J. Qu and Y. Luo, Organometallics, 2017, 36, 1042–1048.
39. S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37–52.
40. G. H. Dunteman, Principal components analysis, Sage Publ, Newbury Park, Calif., [Nachdr.] edn, 2006, vol. 69.
41. V. Fath, P. Lau, C. Greve, N. Kockmann and T. Röder, Org. Process Res. Dev., 2020, 24, 1955–1968.
42. J. Ma, J. Qi, X. Gao, C. Yan, T. Zhang, H. Tang and H. Li, J. Anal. Methods Chem., 2017, 2017, 4595267.
43. S. C. Rutan, A. de Juan and R. Tauler, in Comprehensive Chemometrics, Elsevier, 2009, pp. 249–259.
44. C. Ruckebusch and L. Blanchet, Anal. Chim. Acta, 2013, 765, 28–36.
45. A. de Juan and R. Tauler, Anal. Chim. Acta, 2021, 1145, 59–78.
46. A. de Juan, M. Maeder, M. Martinez and R. Tauler, Chemom. Intell. Lab. Syst., 2000, 54, 123–141.
47. A. C. Olivieri, Anal. Chim. Acta, 2021, 1156, 338206.
48. M. Sawall, H. Schröder, D. Meinhardt and K. Neymeyr, in Comprehensive Chemometrics, Elsevier, 2020, pp. 199–231.
49. H. Schröder, M. Sawall, C. Kubis, D. Selent, D. Hess, R. Franke, A. Börner and K. Neymeyr, Anal. Chim. Acta, 2016, 927, 21–34.
50. P. Gemperline, G. Puxty, M. Maeder, D. Walker, F. Tarczynski and M. Bosserman, Anal. Chem., 2004, 76, 2575–2582.
51. O. Levenspiel, Chemical reaction engineering, Wiley, New York, 2nd edn, 1972.
52. V. Fath, N. Kockmann and T. Röder, Chem. Eng. Technol., 2019, 42, 2095–2104.
53. J. S. Moore and K. F. Jensen, Angew. Chem., 2014, 126, 480–483.
54. V. Mazet, C. Carteret, D. Brie, J. Idier and B. Humbert, Chemom. Intell. Lab. Syst., 2005, 76, 121–133.
55. J. Jaumot, A. de Juan and R. Tauler, Chemom. Intell. Lab. Syst., 2015, 140, 1–12.
56. K. L. Wilson, A. R. Kennedy, J. Murray, B. Greatrex, C. Jamieson and A. J. B. Watson, Beilstein J. Org. Chem., 2016, 12, 2005–2011.
57. L. Ferrazzano, G. Martelli, T. Fantoni, A. Daka, D. Corbisiero, A. Viola, A. Ricci, W. Cabri and A. Tolomelli, Org. Lett., 2020, 22, 3969–3973.
58. J. Sherwood, J. H. Clark, I. J. S. Fairlamb and J. M. Slattery, Green Chem., 2019, 21, 2164–2213.
59. G. Strappaveccia, L. Luciani, E. Bartollini, A. Marrocchi, F. Pizzo and L. Vaccaro, Green Chem., 2015, 17, 1071–1076.
60. GESTIS-Stoffdatenbank, 07.02.2023, https://gestis.dguv.de/data?name=023480.
61. S. Schwolow, J. Hollmann, B. Schenkel and T. Röder, Org. Process Res. Dev., 2012, 16, 1513–1522.
62. F. Wang, J. Mielby, F. H. Richter, G. Wang, G. Prieto, T. Kasama, C. Weidenthaler, H.-J. Bongard, S. Kegnæs, A. Fürstner and F. Schüth, Angew. Chem., Int. Ed., 2014, 53, 8645–8648.
63. A. Lumbreras-Teijeiro, M. Bacic, J. Oliver-Meseguer and A. Leyva-Pérez, Chemistry, 2022, 28, e202202421.
64. T. Rosner, J. Le Bars, A. Pfaltz and D. G. Blackmond, J. Am. Chem. Soc., 2001, 123, 1848–1855.
65. G. P. F. van Strijdonck, M. D. K. Boele, P. C. J. Kamer, J. G. de Vries and P. W. N. M. van Leeuwen, Eur. J. Inorg. Chem., 1999, 1999, 1073–1076.
66. R. Chinchilla and C. Najera, Chem. Rev., 2007, 107, 874–922.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00173c

‡ MCR is regarded as nearly calibration free approach because only relative concentration profiles are obtained and knowledge about the starting concentration is needed.

---