Open Access Article
Open Access ArticleMass transfer enhancement in electrochemical flow cells through 3D-printed biomimetic channels
Inmaculada
García-López
 *a,
Luis Fernando
Arenas
*a,
Luis Fernando
Arenas
 bc,
Thomas
Turek
bc,
Vicente Ismael
Águeda
a and
Amalio
Garrido-Escudero
a
bc,
Thomas
Turek
bc,
Vicente Ismael
Águeda
a and
Amalio
Garrido-Escudero
a
aResearch Group Catalysis & Separation Processes (CYPS), Department of Chemical Engineering, Universidad Complutense de Madrid, 28040, Madrid, Spain. E-mail: inmgarci@ucm.es
bInstitute of Chemical and Electrochemical Process Engineering (ICVT), Clausthal University of Technology, 38678, Clausthal-Zellerfeld, Germany
cResearch Center for Energy Storage Technologies (EST), Clausthal University of Technology, 38640, Goslar, Germany
First published on 13th April 2023
Abstract
Mass transfer is frequently the rate-limiting step in electrochemical processes. In addition to increasing electrolyte flow rate, transfer limitations in electrochemical flow cells can be mitigated by inducing turbulence in the flow fields. This can be achieved by substituting the conventional rectangular channel cell design for flow fields that promote chaotic movement in the electrolyte. In this work, a novel biomimetic channel concept based on space-filling curves created by differential growth, such as those present in rippled surfaces of plants and river meanders, is proposed. The overall performance was analyzed in an undivided flow cell by the limiting current technique as a function of electrolyte flow rate. The performance of the biomimetic flow field is enhanced on average by a factor of 1.9 and 1.1 with respect to the rectangular and serpentine flow fields, respectively. The designed flow field increased pressure drop in comparison to the other flow fields but at levels similar to the typical FM01-LC flow reactor with porous electrodes. Differential growth flow fields open a window to further application in inorganic and organic flow electrosynthesis at various scales, as this parametric design allows for channel adaption to the reaction requirements.
Introduction
Electrolysis is gaining popularity for carrying out a great number of redox reactions. In contrast to traditional processes, which frequently need high temperatures or pressures, electrochemical reactions are typically carried out under milder conditions and shorter reaction times.1,2 In addition, the reaction rate can be speeded up by increasing the operating current.3,4 The filter-press electrochemical reactor with parallel-plane electrodes is often used in the laboratory and in the industry due to its versatility. An example of this type of electrolyzer is the broadly studied ‘FM01-LC’ filter-press flow cell.5–7 Relevant applications of these cells are found in the chlor-alkali industry, organic and inorganic electrosynthesis, redox flow batteries, fuel cells, electrowinning, and water treatment.8 In many cases, the reaction of interest is controlled by mass transfer, for example, when concentrations of reactants are relatively low.9 Because electron transfer can only occur within molecular dimensions of the surface, chemical change cannot occur faster than the reactant reaches the electrode surface.10,11 Moreover, the increase of electrode potentials or cell voltage beyond the limiting current density region usually results in parasitic reactions such as water electrolysis or electrode corrosion.12There are different alternatives to overcome mass transfer limitations in electrochemical flow cells. One is based on the insertion of obstacles in the interelectrode gap. Different geometries of so-called turbulence promoters have been proposed and they are known to produce higher averaged mass transfer coefficients and a more uniform current distribution.13–15 Another strategy is based on the increase of the electrode surface area by introducing roughness or porous electrodes. The latter leads to the highest mass transfer coefficients but might increase pressure drop in the flow channel.7 The third option is to generate gas bubbles at the electrode surface or to sparge the electrolyte with bubbles in the interelectrode gap.16 The mass-transfer coefficient is raised due to the disruption of the mass-transfer boundary layer. However, an increase in ohmic drop and a modification in the current distribution in the electrode surface can take place.17
Finally, mass transfer limitations can be mitigated by flow-guiding shapes in the flow channel. These flow fields have different purposes: to distribute electrolyte on the electrode surface, to structurally support the electrode material, to increase local flow velocity and mixing, and to allow heat management (in large cells or stacks of cells). Each flow field design results in a specific pressure drop at a given flow rate. Some of the channel designs proposed in the literature include: parallel, spiral, serpentine, tubular, interdigitated, fractal, or corrugated geometries.18,19 Conventional fabrication techniques, such as injection-molding of graphite or carbon materials, computer numerically controlled (CNC) machining of graphite plates or stamping metals, can be time-consuming and ill-suited for manufacturing more complex flow field designs.20
3D printing has been developed as a promising manufacturing technology in chemical research,21 and particularly, in electrochemistry.22,23 A wide range of cell components can be 3D printed: flow channels and turbulence promoters,24,25 textured planar electrodes,20,26,27 mesh-like electrodes,28,29 and other porous electrodes.30,31 3D printing is a helpful fast prototyping tool, reducing the costs and lead time associated in making individual pieces, while keeping adequate manufacture tolerances. Moreover, 3D printing enables to investigate complex flow designs, those which cannot be produced with conventional techniques. This is useful in the development of benchtop flow cells, which are increasingly common in organic electrosynthesis.32 Plus, 3D printing can enable the immediate production of cell components in remote or isolated areas or for portable low-cost applications, for example, electrochemical water treatment.8
To the best of our knowledge, differential growth shapes based on space-filling curves have not yet been employed as flow fields in electrochemical flow reactors. These shapes are created in nature by stochastic processes that can be simulated by algorithms.33 Folding geometries in many natural systems follow these patterns, for example, organs such as brains or intestines, rippled surfaces in plants, filling behavior of worms and river meanders.34 Reactors for heterogeneous reactions and heat exchangers can benefit notably from these designs.35,36 In an electrochemical flow cell, the tortuous shapes will cause flow disturbance and promote the boundary layer disruption close to the electrodes. Additionally, by properly adjusting the channel curvatures, an extended-channel length may be set on a tiny area while retaining a high electrode surface utilization. This could be an innovative method for improving fractional conversion in systems that demand long residence-times.
In this work, a novel geometry based on biomimetic space-filling shapes is applied as a flow field in an undivided electrochemical flow cell. Its mass transfer properties are studied through the limiting current technique and compared against a rectangular channel and a serpentine channel; the latter being often used in organic electrosynthesis.32 The pressure drop experienced by the electrolyte as a result of the flow field shapes is also considered. The manufacture of the tortuous and intricate biomimetic flow field was enabled by fast prototyping using resin stereolithography (SLA) 3D printer.
Experimental
Flow field design and 3D printing
The mass transfer performance of three different flow field designs is compared: biomimetic differential growth, serpentine and rectangular (Fig. 1a). The flow fields act both as interelectrode separator and as flow channels in an undivided cell. The three designs occupy a projected rectangular surface area of 25 mm × 50 mm (12.5 cm2). The channel height, which is the interelectrode gap, is the same in the three cases (2 mm), with the electrode (active) geometrical surface area varying in each case, as shown in Table 1. These geometries were built with the software Rhinoceros 6 (McNeel & Assoc.). For the differential growth shape, the Grasshopper software extension and the Kangaroo plug-in were used. An initial curve was divided into 200 nodes and the growing space was adapted to 25 mm × 50 mm. More details about the geometry parametric construction can be found elsewhere.33,37–39 The flow field gaskets were produced in a commercial 3D printer (Anycubic Photon Mono) optimized for 405 nm light. A photopolymerizable liquid resin (Anycubic ABS+ resin) was employed as the precursor material. The printing parameters were previously studied and adjusted, achieving better results with a layer height of 50 μm, exposure of 2 s, off-time of 0.5 s, bottom layer exposure of 40 s on 6 layers, a Z-lift distance of 10 mm, speed of 2 mm s−1 and no anti-aliasing. | ||
| Fig. 1 The concept of a 3D printed biomimetic flow channel along traditional flow configurations in electrochemical flow cells. (a) Flow field designs. (b) Manufacture process by SLA 3D printing. | ||
| Symbol | Property | Rectangular | Serpentine | Differential growth |
|---|---|---|---|---|
| L | Channel length (mm) | 50 | 240 | 308 |
| B | Channel width (mm) | 25 | 2 | 2 |
| S | Electrode spacing (mm) | 2 | 2 | 2 |
| A | Geometrical electrode area (mm2) | 1250 | 481 | 616 |
| d h | Hydraulic diameter dh = 2BS/(B + S) (mm) | 3.7 | 2 | 2 |
| A cross | Cross sectional area Across = BS (mm2) | 50 | 4 | 4 |
Once the flow fields were printed, the excess of resin was removed with isopropyl alcohol, >99% wt (Höfer Chemie), including the resin retained inside the channels. Next, the flow fields were cured by being exposed for 120 s to a 405 nm light source (Fig. 1b). The chemical stability of the 3D printed material gasket was tested prior to the electrochemistry trials, according to the procedure described by Márquez-Montes.40 None of the objects presented variations on mass or length higher than 1% and no deformations of the polymer were observed after the immersion period of 10 days into the electrolyte used in this work. The 3D printed flow fields had sufficient flexibility to be compressed into the electrodes without any electrolyte leakage.
Limiting current technique
The limiting current is an important parameter for the characterization of mass transfer in electrochemical flow reactors. When an electrochemical system operates at its limiting current, the reaction proceeds at the maximum rate. Mass transfer coefficients (km) calculated from the limiting current values (IL) for model redox reactions are frequently used in order to characterize electrochemical cells and reactors. The evaluation of the performance factor (kmA) can be used to compare their behavior across scales and predict their suitability for a particular electrochemical process. For planar electrodes, the value of kmA is given by the expression: | (1) |
Mass transfer to an electrode in the side wall of a rectangular channel can be characterized by four dimensionless groups, namely the Sherwood (Sh), Reynolds (Re), Schmidt (Sc) numbers along with the dimensionless length (Le). These groups can be defined as:41
 | (2) |
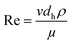 | (3) |
 | (4) |
 | (5) |
 | (6) |
Experimental procedure
As shown in Fig. 2, an undivided flow cell with the filter-press configuration was implemented, similar to the approach used by other authors.42–44 The cell consisted on a 3D printed flow field gasket of 2 mm thickness, compressed between two graphite planar electrodes (Eisenhuth GmbH), which served as working and counter electrodes. One of the electrodes featured orifices as inlet and outlet for the electrolyte. Two copper meshes with 24 mesh count and mesh size 0.80 mm (GKD-Gebr. Kufferath AG) were used as current collectors in contact with the graphite electrodes. These components were assembled together between methacrylate plates (96 × 76 × 11 mm) which worked as casing for the electrochemical cell and provided connections (EM-Technik) for the inlet and outlet. These elements were compressed mechanically by stainless-steel tie-bolts set to a torque of approximately 0.8 N m. This assembly corresponds to the cell design presented by Martin et al.45 | ||
| Fig. 2 Experimental arrangement and electrochemical flow cell for the measurement of limiting currents. | ||
The reduction of the ferricyanide complex in an aqueous and alkaline media was employed as model reaction:46
| (Fe(CN)6)3− + e− → (Fe(CN)6)4− | (7) |
The composition of the electrolyte, diluted into distilled water, is detailed in Table 2. All the reagents were analytical grade (Carl Roth). The ferrocyanide was present in excess with respect to the ferricyanide species in order to ensure that the limiting reaction would be the reduction process.
| Symbol | Property | Value |
|---|---|---|
| T | Temperature (K) | ≈298 |
| ρ | Electrolyte density (kg m−3) | 1098.5 |
| ν | Electrolyte kinematic viscosity (cm2 s−1) | 9.56 × 10−3 |
| D m | Diffusion coefficient of ferricyanide (m2 s−1) | 6.4 × 10−10 |
| Sc | Schmidt number | 1494 |
| Q v | Volumetric flow rate (L h−1) | 10–15 |
| C bulk | Concentration of K3Fe(CN)6, Fe(III) (mol L−1) | 1 × 10−3 |
| C c | Concentration of K4Fe(CN)6, Fe(II) (mol L−1) | 1 × 10−2 |
| C s | Concentration of Na2CO3 (mol L−1) | 1.0 |
As shown in Fig. 2, the electrolyte was stored in a 500 mL reservoir kept dark by aluminum foil to avoid its decomposition and it was prepared fresh for each measurement. A peristaltic pump (G928A, Grothen) recirculated the electrolyte between the cell and the reservoir through 1/4 inch polyethylene tubing at flow rates ranging from 10 to 15 L h−1. A pulsation dampener was used for stabilizing the flow rate and the pressure in the flow circuit. A rotameter was installed for measuring flow rate and the pump speed control vs. desired flow rate was calibrated prior to the experiments. The flow circuit was hydraulically tested with water at the maximum flow rate to ensure that there were no leakages. Pressure drop was measured with a digital manometer connected to the flow cell inlet.
Limiting current measurements were carried out by chronoamperometry, imposing a cell voltage with a power supply (6226, PeakTech), according to the procedure described by Cañizares et al.43 The anode of the cell was connected to the positive terminal of the power supply and the cathode to the negative one. A digital multimeter (OW15E, OWON) measured the cell current every 5 s and sent the data to a PC application (Multimeter BLE4.0, OWON). The current response over time displayed peaks for a few seconds at the beginning of each applied voltage step due to polarization and a change in the concentration profile along the electrode. Since determining the limiting current at fast scan rates or immediately after a potential change may induce to errors in this method,47 sufficient time between voltage steps was given in order to achieve a quasi-steady state (>300 s), calculating the average current for the last ten values of current at a given cell voltage.
Results and discussion
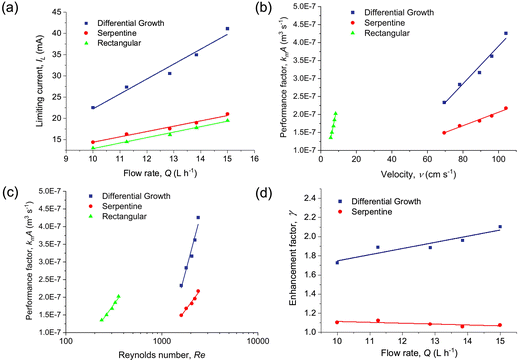
Fig. 3 shows the polarization curves and the mass transfer limitation regions for the ferricyanide reduction at different inlet flow rates for the three flow field geometries. The limiting current is characterized by a plateau, observed at cell voltages between 2.2 V and 2.4 V. There are different methods to determine the limiting current values: direct measurement from I vs. E curve, calculation from the current value at Elim = ΔE/2, (where ΔE is the length of the limiting current plateau), and from the first derivative dI/dE in the I vs. E curve.48 In this work, the limiting current was determined according to the second procedure. The reproducibility of the experiments was evaluated for the biomimetic differential growth shape at all flow rates, obtaining differences in the measured limiting currents lower than 1%. As expected, the limiting current is higher with increasing flow rates. An increase in the fluid velocity promotes mixing, diminishing the boundary layer near the electrode surface, and hence favoring the exchange between reactants and products near the electrodes.Fig. 4a compares the limiting current as a function of volumetric flow rate for the three flow field geometries. The differential growth shape increased the limiting current value in average by 91.2% and 75.8% compared to the rectangular and serpentine geometries, respectively. It should be noted that the differential growth shape achieves higher mass transfer coefficients with 48.8% less electrode surface area in comparison to the rectangular shape. This could be especially beneficial for some applications in electrocatalysis that need expensive electrode materials (e.g., gold sensor electrodes49), as the particles could only be deposited in the projected channel surface into a support material, reducing the total loading of catalyst required.
Fig. 4b and c show the kmA values at different mean linear velocity and Re for each geometry, calculated according to eqn (1). Note that the mean linear velocity is lower in the case of the rectangular channels, because the volumetric flow rates in the experiments in the three geometries were identical. Due to the cell channel configuration, where the entrance of fluid is carried out through electrode perforations, eddies and higher local velocities occur near the inlet and outlet, especially in the rectangular channel.
The biomimetic differential growth flow field exhibits the highest performance, which can be attributed to the increased turbulence in the channel due to the numerous bends and turns. The formation of secondary vortices in these types of channels promotes mixing and enhances mass transfer from the electrodes to the bulk of the solution and vice versa. The fluid near the center of the channel experiences higher centripetal acceleration than the flow at the channel wall, resulting in the superposition on the primary axial flow of a transverse motion. Moreover, it is known that the formation of secondary vortices is influenced by Re and curvature radius.50–52 This could also happen, although to a lesser extent, in the serpentine channel. Another factor to consider is the roughness of the channel induced by SLA 3D printing, which has already been measured for ABS-like materials.53 Surface roughness is thought to disrupt the concentration boundary layer and cause turbulence due to penetration into valleys between roughness peaks.54 Both differential growth and serpentine channels have longer wall contact and hence the fluid can be more influenced by channel roughness than in the rectangular one.
The improvement in mass transfer can be quantified by an enhancement factor, γ, which indicates the ratio of kmA of the differential growth and serpentine flow fields compared to the rectangular channel:
 | (8) |
Here kmA refers to the performance of the rectangular channel and kmA′ to the differential growth or serpentine flow fields. The enhancement factor is 1.9 for the differential growth shape and 1.1 for the serpentine shape on an average taken from all evaluated flow rates. The largest value of γ for the biomimetic flow field is 2.10 (Fig. 4d). Notably, the value of γ increases as a function of flow rate in the case of the differential growth flow field whereas it remains approximately constant, in fact slightly decreasing, in the case of the serpentine flow field. This is likely the result of the greater number of curves in the biomimetic shape, which contribute to higher turbulence gain for a given flow rate increment.
From the experimental values of km and the geometrical electrode surface areas, the Sherwood number was calculated according to eqn (2), and these values are represented in Fig. 5a as a function of Re. The differential growth flow field showed the highest Sh, followed by the serpentine and finally the rectangular flow channel. As the Re number increases, the differences between differential growth and serpentine flow fields become larger due to the higher increase in turbulence in the first geometry.
To facilitate comparison, there are correlations in the literature that relate Sh with the other three dimensionless numbers in electrochemical flow reactors:
| Sh = aRebSccLde | (9) |
| Flow field | a | b | c | d | Re | Ref. |
|---|---|---|---|---|---|---|
| Rectangular | 0.59 | 1.00 | 0.33 | 0.33 | ≈230–350 | This work |
| Serpentine | 0.42 | 0.89 | 0.37 | 0.31 | ≈1500–2400 | This work |
| Differential growth | 0.62 | 1.44 | 0.23 | 0.94 | ≈1500–2400 | This work |
| Electrocell ESC | 0.39 | 0.63 | 0.33 | — | ≈700–800 | 55 |
| Electrocell MFC with turbulence promoter | 0.50 | 0.58 | 0.33 | — | ≈200–1700 | 15 |
| FM01-LC | 0.22 | 0.71 | 0.33 | — | ≈200–1000 | 56 |
| FM01-LC | 0.18 | 0.73 | 0.33 | — | ≈500–2200 | 57 |
Another important parameter in electrochemical flow cell is the pressure drop, ΔP, as it is related to the energy required for pumping the electrolyte. Pressure losses in a channel can be attributed to local losses (such as expansion, narrowing or bending) and frictional losses (for a certain channel length and hydraulic diameter).59 The velocity of the fluid has the greater impact on head loss, but the channel geometry has also a contribution. ΔP as a function of Re is shown in Fig. 5b for the three geometries.
This parameter increases with Re in all cases. The smallest ΔP values were obtained for the rectangular channel, as it showed the lowest velocity on the channel, not suffering obstacles or redirections on the flow. In the case of serpentine and differential growth flow fields, the highest ΔP values corresponded to the latter. The differential growth channel has more bends and turns than the rectangular channel, which increases the local pressure losses for a given mean linear velocity. ΔP in the channel as a function of Reynolds number can be described by a power law:57
| ΔP = pReq | (10) |
| Flow field | p (Pa) | q | Ref. |
|---|---|---|---|
| Rectangular | 0.617 | 1.40 | This work |
| Serpentine | 5.1 × 10−3 | 2.14 | This work |
| Differential growth | 3.7 × 10−3 | 2.38 | This work |
| FM01-LC with empty channel | 5.9 × 10−3 | 1.87 | 57 |
| FM01-LC with turbulence promoter | 6.3 × 10−3 | 1.89 | 57 |
| Flow cell with flat electrode | 9.25 × 10−3 | 0.93 | 47 |
| Flow cell with ‘Kenics’ HCW/HCW electrode | 0.097 | 1.13 | 47 |
Moreover, the flow rates employed in many examples of laboratory organic electrosynthesis are typically in a range of milliliters per hour, so the pressure drop in these conditions decreases significantly. In this kind of applications, mass transfer and residence-time becomes more important than pressure drop and a differential growth geometry can be advantageous. In contrast, pumping costs and design complications due to elevated pressure drop impose a penalty on the operability of electrochemical systems requiring high flow rates or large dimensions, where the biomimetic flow field may not be the most suitable choice.
Conclusions
A novel biomimetic differential growth flow field geometry is demonstrated as a mass transfer enhancing strategy in undivided electrochemical flow cells. Its electrochemical performance was compared to the classic rectangular and serpentine channels. After fabricating these flow fields by SLA 3D printing, mass transfer limitation studies were carried out through the limiting current technique. From their experimental values, the Sherwood number was calculated and pressure drop was measured. The biomimetic flow field enhanced the limiting current value in average 91.2% and 75.8% compared to the conventional rectangular and serpentine geometries, respectively. The differential growth shape exhibited a higher mass transfer coefficient at equal flow rates, affording an enhancement factor of up to 2.10 over the rectangular channel. Due to the tortuous design of the biomimetic channel, an increase in mixing and turbulence takes place, reducing the concentration boundary layers thickness near the electrode. There is a cost in terms of required pumping energy for the differential growth geometry, but the pressure drop values are still typical for laboratory flow cells. Applications in electrosynthesis can benefit from the implementation of this type of parametric flow field designs as they favor long residence-time reactions in a very compact volume.Author contributions
IGL: conceptualization, investigation, experiments, data analysis, resources, writing – original draft. LFA: conceptualization, investigation, methodology, writing – review & editing. TT: resources, writing – review & editing. VIA: supervision, writing – review & editing. AGE: supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
IGL is grateful to Clausthal University of Technology (Germany) for supporting this work through a research stay at the Research Center for Energy Storage Technologies (EST), Goslar. LFA acknowledges a research fellowship granted by the Alexander von Humboldt Foundation (Germany).References
- K. Scott, Renewable Sustainable Energy Rev., 2018, 81, 1406–1426 CrossRef.
- S. A. Grigoriev, V. N. Fateev, D. G. Bessarabov and P. Millet, Int. J. Hydrogen Energy, 2020, 45, 26036–26058 CrossRef CAS.
- M. C. Leech and K. Lam, Nat. Rev. Chem., 2022, 6, 275–286 CrossRef.
- Y. Yuan and A. Lei, Nat. Commun., 2020, 11, 802 CrossRef CAS PubMed.
- E. Butrón, M. E. Juárez, M. Solis, M. Teutli, I. González and J. L. Nava, Electrochim. Acta, 2007, 52, 6888–6894 CrossRef.
- F. A. Rodríguez, M. N. Mateo, J. M. Aceves, E. P. Rivero and I. González, Environ. Technol., 2013, 34, 573–583 CrossRef PubMed.
- F. F. Rivera, C. Ponce de León, J. L. Nava and F. C. Walsh, Electrochim. Acta, 2015, 163, 338–354 CrossRef CAS.
- L. F. Arenas, C. Ponce de León and F. C. Walsh, J. Electrochem. Soc., 2020, 167, 023504 CrossRef CAS.
- C. Y. Cheng and G. H. Kelsall, J. Appl. Electrochem., 2007, 37, 1203–1217 CrossRef CAS.
- D. Pletcher, R. A. Green and R. C. D. Brown, Chem. Rev., 2018, 118, 4573–4591 CrossRef CAS PubMed.
- C. Barbero, M. C. Miras and R. Kötz, Electrochim. Acta, 1992, 37, 429–437 CrossRef CAS.
- B. De Mot, J. Hereijgers, M. Duarte and T. Breugelmans, Chem. Eng. J., 2019, 378, 122224 CrossRef CAS.
- C. J. Brown, D. Pletcher, F. C. Walsh, J. K. Hammond and D. Robinson, J. Appl. Electrochem., 1992, 22, 613–619 CrossRef CAS.
- F. B. Leitz and L. Marinčić, J. Appl. Electrochem., 1977, 7, 473–484 CrossRef CAS.
- S. J. C. Weusten, J. van der Schaaf and M. T. de Groot, J. Electroanal. Chem., 2022, 918, 116481 CrossRef CAS.
- A. Shah and J. Jorne, J. Electrochem. Soc., 1989, 136, 153 CrossRef CAS.
- A. N. Colli, R. Toelzer, M. E. H. Bergmann and J. M. Bisang, Electrochim. Acta, 2013, 100, 78–84 CrossRef CAS.
- M. Sauermoser, N. Kizilova, B. G. Pollet and S. Kjelstrup, Front. Energy Res., 2020, 8, 13 CrossRef.
- M. Marappan, K. Palaniswamy, T. Velumani, K. B. Chul, R. Velayutham, P. Shivakumar and S. Sundaram, Chem. Rec., 2021, 21, 663–714 CrossRef CAS PubMed.
- H. Piri, X. T. Bi, H. Li and H. Wang, Clean Energy, 2020, 4, 142–157 CrossRef.
- V. Saggiomo, Adv. Sci., 2022, 9, 2202610 CrossRef PubMed.
- C.-Y. Lee, A. C. Taylor, A. Nattestad, S. Beirne and G. G. Wallace, Joule, 2019, 3, 1835–1849 CrossRef CAS.
- S. S. Kawale, I. Jang, N. M. Farandos and G. H. Kelsall, React. Chem. Eng., 2022, 7, 1692–1712 RSC.
- C. Ponce De Leon, W. Hussey, F. Frazao, D. Jones, E. Ruggeri, S. Tzortzatos, R. Mckerracher, R. G. A. Wills, S. Yangb and F. Walsh, Chem. Eng. Trans., 2014, 41, 1–6 Search PubMed.
- S. J. C. Weusten, L. C. E. M. Murrer, M. T. de Groot and J. van der Schaaf, AIChE J., 2021, 67, e17263 CrossRef CAS.
- A. Ambrosi, R. R. S. Shi and R. D. Webster, J. Mater. Chem. A, 2020, 8, 21902–21929 RSC.
- G. Chisholm, P. J. Kitson, N. D. Kirkaldy, L. G. Bloor and L. Cronin, Energy Environ. Sci., 2014, 7, 3026–3032 RSC.
- Z. Li, H. Li, X. Zhu, Z. Peng, G. Zhang, J. Yang, F. Wang, Y.-F. Zhang, L. Sun, R. Wang, J. Zhang, Z. Yang, H. Yi and H. Lan, Adv. Sci., 2022, 9, 2105331 CrossRef CAS PubMed.
- K. Hirech, A. Arhaliass and J. Legrand, Ind. Eng. Chem. Res., 2003, 42, 1478–1484 CrossRef CAS.
- T. Chu, S. Park and K. Fu, Carbon Energy, 2021, 3, 424–439 CrossRef.
- J. Hu, Y. Jiang, S. Cui, Y. Duan, T. Liu, H. Guo, L. Lin, Y. Lin, J. Zheng, K. Amine and F. Pan, Adv. Energy Mater., 2016, 6, 1600856 CrossRef.
- R. A. Green, R. C. D. Brown and D. Pletcher, J. Flow Chem., 2016, 6, 191–197 CrossRef CAS.
- I. García-López, V. I. Águeda and A. Garrido-Escudero, Chem. Eng. J. Adv., 2023, 13, 100438 CrossRef.
- T. McNulty, D. Bhate, A. Zhang, M. A. Kiser, L. Ferry, A. Suder, S. Bhattacharya and P. Boradkar, 27th International Solid Freeform Fabrication Symposium, University of Texas at Austin, 2017 Search PubMed.
- M.-O. Coppens, Curr. Opin. Chem. Eng., 2012, 1, 281–289 CrossRef CAS.
- K. Noack, M. F. Eichenauer and D. Lordick, J. Ind. Design Eng. Graphics, 2019, 14, 35–40 Search PubMed.
- Differential Growth – The Different Design, https://thedifferentdesign.com/digitaldownloads/differential-growth/, (accessed November 23, 2022) Search PubMed.
- D. Bachman, in ACM SIGGRAPH 2019 Educators Forum, Association for Computing Machinery, New York, NY, USA, 2019, pp. 1–59 Search PubMed.
- C. Klemmt, I. Pantic, A. Gheorghe and A. Sebestyen, in Ubiquity and Autonomy-Paper Proceedings of the 39th Annual Conference of the Association for Computer Aided Design in Architecture, ACADIA 2019, Association for Computer Aided Design in Architecture (ACADIA), 2019, vol. 39, pp. 542–552 Search PubMed.
- R. A. Márquez-Montes, V. H. Collins-Martínez, I. Pérez-Reyes, D. Chávez-Flores, O. A. Graeve and V. H. Ramos-Sánchez, ACS Sustainable Chem. Eng., 2020, 8, 3896–3905 CrossRef.
- F. J. Recio, P. Herrasti, L. Vazquez, C. Ponce de León and F. C. Walsh, Electrochim. Acta, 2013, 90, 507–513 CrossRef CAS.
- C. N. Brito, M. B. Ferreira, E. C. M. de Moura Santos, J. J. L. Léon, S. O. Ganiyu and C. A. Martínez-Huitle, J. Appl. Electrochem., 2018, 48, 1321–1330 CrossRef CAS.
- P. Cañizares, J. García-Gómez, I. Fernández de Marcos, M. A. Rodrigo and J. Lobato, J. Chem. Educ., 2006, 83, 1204 CrossRef.
- W. Jud, C. O. Kappe and D. Cantillo, Chem.: Methods, 2021, 1, 36–41 CAS.
- J. Martin, K. Schafner and T. Turek, Energy Technol., 2020, 8, 2000522 CrossRef CAS.
- J. R. Selman and C. W. Tobias, in Advances in Chemical Engineering, ed. T. B. Drew, G. R. Cokelet, J. W. Hoopes and T. Vermeulen, Academic Press, 1978, vol. 10, pp. 211–318 Search PubMed.
- J. Hereijgers, J. Schalck and T. Breugelmans, Chem. Eng. J., 2020, 384, 123283 CrossRef CAS.
- C. Ponce de León, C. T. J. Low, G. Kear and F. C. Walsh, J. Appl. Electrochem., 2007, 37, 1261–1270 CrossRef.
- J. A. Hondred, Z. T. Johnson and J. C. Claussen, J. Mater. Chem. C, 2020, 8, 11376–11388 RSC.
- A. Qamareen, M. A. Ansari and S. S. Alam, Chem. Eng. Process., 2022, 176, 108945 CrossRef CAS.
- A. Gigras and S. Pushpavanam, Microfluid. Nanofluid., 2008, 5, 89–99 CrossRef.
- N. Nivedita, P. Ligrani and I. Papautsky, Sci. Rep., 2017, 7, 44072 CrossRef PubMed.
- J. Son and H. Lee, Micromachines, 2020, 11, E843 CrossRef PubMed.
- D. R. Gabe and D. J. Robinson, Electrochim. Acta, 1972, 17, 1129–1137 CrossRef CAS.
- L. Carlsson, B. Sandegren, D. Simonsson and M. Rihovsky, J. Electrochem. Soc., 1983, 130, 342 CrossRef CAS.
- M. Griffiths, C. P. de León and F. C. Walsh, AIChE J., 2005, 51, 682–687 CrossRef CAS.
- C. J. Brown, D. Pletcher, F. C. Walsh, J. K. Hammond and D. Robinson, J. Appl. Electrochem., 1993, 23, 38–43 CrossRef CAS.
- D. J. Schmitt and S. G. Kandlikar, in International Conference on Nanochannels, Microchannels, and Minichannels, 2005, vol. 41855, pp. 281–289 Search PubMed.
- R. Goovaerts, W. Smits, G. Desmet, J. Denayer and W. De Malsche, Chem. Eng. J., 2012, 211–212, 260–269 CrossRef CAS.
- C. J. Brown, F. C. Walsh and D. Pletcher, Chem. Eng. Res. Des., 1995, 73, 196–205 CAS.
- L. Wu, L. F. Arenas, J. E. Graves and F. C. Walsh, J. Electrochem. Soc., 2020, 167, 043505 CrossRef CAS.
- R. C. D. Brown, Chem. Rec., 2021, 21, 2472–2487 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |