Thermal characterization of highly exothermic flash chemistry in a continuous flow calorimeter

Abstract

A key parameter for reactor design and safety evaluation is the reaction enthalpy (ΔH_r). Flash chemistry is a field of chemical synthesis where fast reactions are performed in a precise manner to produce desired compounds with high selectivity. In this paper, we demonstrate that robust calorimetric data for highly exothermic, rapid reactions can be obtained within a modular 3D printed continuous flow calorimeter. This data would be difficult, or impossible, to reliably measure within a batch calorimeter. Initially, the reaction of n-hexyllithium (HexLi) with ethanol was studied using different solvent compositions, with the average enthalpy determined to be −297.6 kJ mol⁻¹. Furthermore, the undesired reaction between HexLi and 2-methyltetrahydrofuran was avoided in continuous flow. Subsequently, the reaction between di-tert-butyldicarbonate and HexLi was conducted. This reaction forms a tert-butyl ester as the desired product and an alcohol as an undesired overreaction product. The influence of mixing efficiency on conversion and product selectivity within the microstructured continuous flow calorimeter was investigated through computational fluid dynamics (CFD) simulations. A tert-butyl ester and alcohol were synthesized with high selectivity after a design of experiments (DoE) study and the reaction enthalpies for generation of these two products were deconvoluted successfully. A lithium–halogen exchange and iodine (I₂) quench were also investigated in the continuous flow calorimeter, which demonstrated that the I₂ quench step is more exothermic than the lithiation step. Overall, the temporal resolution of these organolithium reactions was showcased on a length scale, which corresponded to residence times of seconds (1.1 to 8.9 s).

---

1 Introduction

Flash chemistry is a field of chemical synthesis where extremely fast reactions (milliseconds to seconds) are conducted under controlled conditions.¹ Very reactive reagents or intermediates are usually involved, thus the reaction processes are highly exothermic. In batch reactors, these flash reactions are typically carried out at cryogenic temperatures (typically between −100 and 0 °C) with one reagent slowly feeding into another, to avoid side reactions and decomposition of reagents.² Nevertheless, safety is still a major concern due to the limited heat dissipation rate of batch reactors, especially at large scales.^3–5 The long processing time combined with the requirement of cryogenic conditions also makes it an onerous task to scale-up these reactions.⁶

In recent years, the use of flow technologies has significantly accelerated the development of flash chemistry examples, and new reaction routes have been proposed which were considered impossible in batch due to their short lifetimes.^7,8 Nagaki et al. reported the generation and transformation of o-, m-, p-nitro-substituted aryl lithium compounds in a microflow system.⁹ This chemistry benefited from the high-resolution reaction time control in microchannels, therefore allowing either the kinetically preferred or the thermodynamically preferred aryl lithium reagent to be used selectively. Furthermore, iodophenyl carbamates were successfully functionalized at the ortho position with the use of a customized microfluidic device, which can achieve submillisecond mixing times even at cryogenic temperatures.¹⁰ With the fast mixing and high heat transfer rate in microreactors, the selectivity is increased significantly and higher reaction temperatures are tolerated.^11–13 Moreover, the safety profile is remarkably enhanced in flow, which undoubtedly aids the scalability of flash chemistry, with some examples of scale-up recently reported.^14,15 The field of flash chemistry has been reviewed by a number of researchers.^1,7,8,16,17 However, despite the exciting progress made in performing flash chemistry in a controlled manner within microreactors, the direct thermochemical characterization of these reactions is scarce.¹⁸ Precise and reliable calorimetric data are fundamental to achieve facile scale-up of reaction processes. Furthermore, calorimetric data are indispensable for developing kinetic models which underpins reactor design and process development.^19–21 Thus, the ability to perform reaction calorimetry for flash chemistry examples is of great interest and importance.

Reaction calorimetry is normally performed using stirred batch reactors.²² Commercially available batch calorimeters, such as the RC1 from Mettler-Toledo, are widely used in industrial and academic laboratory settings.^23,24 However, despite the drawbacks of batch calorimetry, such as a significant holdup and safety issues,^25,26 the limitations when applied to flash chemistry are even greater. As mentioned above, flash chemistry is difficult or impossible to perform in batch in a controlled manner due to the extremely short reaction half-life.²⁷ Even though some flash chemistry reactions can be carried out to some extent in batch, the limited mixing rate, poor temperature control, as well as inefficient quenching often results in a low selectivity for the desired product. Hence, thermal characterization by batch calorimetry is likely to be unreproducible and measurements are likely be influenced by side reactions, resulting in an unreliable result. In the light of difficulties for flash chemistry calorimetry in batch, continuous flow calorimetry is a potential alternative which can address many of the challenges.

Continuous flow calorimetry is receiving increasing attention in recent years.²⁸ The miniaturization of calorimeters that operate in a continuous flow fashion potentially enables the safe investigation of fast and highly exothermic reactions at high reactant concentrations along with minimal material consumption.²⁹ There are three types of flow calorimeters based on different calorimetric methods that have been reported:

• Energy balance based on measurements with temperature sensors.^18,30–32 Temperature sensors are used due to their relatively low price and high accuracy. Moser et al. developed a scalable milli-scale continuous flow calorimeter which exploited temperature sensors, which does not need calibration.³¹ A standard neutralization reaction of acetic acid (AcOH) and sodium hydroxide (NaOH) was selected to test the system and the deviation from the literature value was approximately 2%. Furthermore, they presented a procedure to simultaneously decouple the heat of reaction and heat of mixing.³² However, to measure the temperature these sensors have to be embedded into the channel and may influence the flow behavior, and a number of sensors are needed to obtain the temperature profile. Determination of the heat transfer coefficient is usually needed for this type of flow calorimetry.

• Energy balance based on measurements with an infrared camera.^33–37 Infrared thermometry is a non-intrusive method to record the complete temperature profile of the area of interest.³⁵ Zhang et al. developed a microsystem integrated with an infrared camera to measure the reaction enthalpy.³⁶ The system was placed in a vacuum box and operated under an adiabatic environment. A homogeneous neutralization reaction between sulfuric acid (H₂SO₄) and NaOH and a heterogeneous reaction of cyclohexanone oxime protonation were performed. The results were reproducible and in good agreement with literature values. However, for this method an expensive infrared camera is used which needs to be carefully calibrated. In addition, the microchannel must be covered with infrared transparent materials.³⁷ Moreover, reaction temperatures cannot be controlled and calorimetry at low temperatures is difficult or even impossible for this type of calorimeter.^34,36

• Heat flow measurements with thermoelectric elements.^{25,26,38–46} Seebeck elements can be used to directly measure the heat flux with high sensitivity and resolution. For example, Hany et al. developed a microfluidic calorimeter and validated it with the neutralization reaction between hydrochloric acid (HCl) and NaOH.⁴¹ Calorimetric titration was showcased and the esterification reaction between propionic anhydride and 2-butanol was characterized by the determination of the mixing and reaction enthalpy. A plate-type microreactor was used to safely obtain thermokinetic data for exothermic chemical reactions by Reichmann et al.²⁶ The Seebeck elements were calibrated by the Joule effect while its performance was demonstrated in heat transfer and neutralization reaction experiments. Ładosz et al. presented an isothermal flow calorimeter consisted of a Seebeck element for characterization of reaction enthalpy and kinetics.⁴² Hydrolysis of acetic anhydride was selected as a model reaction and the reaction enthalpy, heat of mixing and kinetic rate constants were determined.

In previous work, a modular 3D printed isothermal continuous flow calorimeter designed for direct heat flux measurements was presented.⁴⁵ The calorimeter was validated with a series of experiments and proved to be highly efficient for fast reactions. Subsequently, the system was applied to measure the heat of reaction for a gas–liquid ozonolysis reaction occurring on a very short timescale (0.55 s) in a separate study.⁴⁶ In the work described herein, we investigate the thermal behavior of flash chemistry, specifically organolithium reactions, using this microstructured continuous flow calorimeter. We commence our study with a standard neutralization reaction to benchmark the calorimeter at different temperatures. Subsequently, the calorimetry for a non-selective quench of n-hexyllithium (HexLi) with ethanol (EtOH) is carried out and validated. The reaction between di-tert-butyldicarbonate and HexLi is conducted, which favors different products depending on the conditions used. The reaction is optimized for the ester and alcohol products in the calorimeter and the reaction enthalpies are decoupled. A two-step metal–halogen exchange and subsequent iodine (I₂) quench is investigated. The temporal resolution of these rapid reactions is shown spatially as well. In this manuscript, the implementation and superiority of a continuous flow calorimeter for the thermal characterization of highly exothermic and fast reactions, which are unsuitable to be performed in conventional batch calorimeters due to both chemistry and safety limitations is described.

2 Experimental

2.1 Flow calorimeter system

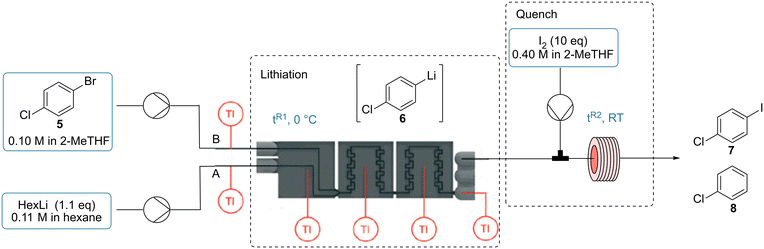
Fig. 1 shows the setup for the 3D printed isothermal heat flow calorimeter system. The calorimeter (part 5) consists of base plate, heating foils, reactor plate, Seebeck elements, Peltier elements, cooling blocks, thermocouples and casing elements (see previous work for more details⁴⁵). The feed solutions (part 1) were introduced into the flow system using syringe pumps (part 2, HiTec Zang, SyrDos2). The reactor plate itself includes a precooling segment and two reaction segments, which utilize split-and-recombine structures (see Fig. S1‡).^47,48 The inner diameter of the channel is 0.8 mm and each reaction segment has a volume of 110 μL. The heat flux generated by reactions in the reactor plate is measured by Seebeck elements using the thermoelectric Seebeck effect. The generated thermoelectric voltages from the Seebeck elements are measured by the microcontroller (part 6) and recorded automatically every 2 or 3 seconds. The real-time data was collected and stored on a laptop computer (part 8). To obtain the actual heat flux, a calibration needs to be carried out with the DC power supply (part 4) and the integrated heating foils. By applying known power inputs, the exothermic reaction can be simulated by these heaters. Then according to the correlation between power inputs of heating foils and the recorded thermoelectric voltages, the heat flux of the reaction can be determined.

Fig. 1 Setup for calorimeter system: 1. feed solutions, 2. syringe pumps, 3. pressure transmitters, 4. DC power supply, 5. flow calorimeter, 6. microcontroller, 7. collection flask, 8. computer, 9. thermostat.

Isothermal conditions are ensured in the designed calorimeter through a PID control of each reactor segment separately. Temperatures of the reactor segments are measured by the attached thermocouples and transmitted to the microcontroller. By comparing the set temperature to the measured values, the supply current to each cooling Peltier element, which acts as a heat sink, is adjusted and the isothermal condition can be maintained. The thermostat (part 9, Huber Ministat 240) is used to cool the hot sides of the Peltier elements which directly contact the cooling blocks to ensure a steady cooling performance. The set temperature of the thermostat is set to a higher temperature than the set temperature of the calorimeter. The pressure was measured using pressure sensors (part 3) incorporated in the tubes prior to the calorimeter.

2.2 Typical procedures for flow calorimetry

The neutralization between AcOH and NaOH was selected to benchmark and verify the performance of the calorimeter. The setup is shown in Fig. S1‡ and the procedures for calorimetry are as follows.

1) Reaction. For example, to perform the calorimetry at 25 °C: initially the temperatures of the thermostat and the calorimeter were set to 28 °C and 25 °C, respectively. After the temperatures and the thermoelectric voltages of the three segments stabilized, the solutions of AcOH (1.0 M) and NaOH (1.0 M) both dissolved in deionized water were introduced into the calorimeter through two syringe pumps in an equimolar ratio. The reaction was run for 15 min and the corresponding temperatures and thermoelectric voltages were recorded automatically. After sufficient data points at steady state were collected, the flow rates were changed and another run was conducted.

2) Calibration. After performing the reaction measurements, a calibration was carried out. At this stage, the pumps were stopped and an output voltage was set to the power supply. As the heating foils were connected in parallel to the power supply, the heat fluxes were generated and delivered to the three Seebeck elements. As a result, thermoelectric voltages with a known power input were obtained. For each set voltage, a 15 min calibration was needed to obtain enough steady data points. Then the voltage was increased step by step. It is better if the detected thermoelectric voltage at the highest power input exceeded the one from the reaction. Finally, correlations between power input and thermoelectric voltage for the three reactor segments were obtained.

3) Calculation. The reaction heat is calculated based on the heat balance as follows:where Q̇_conv is the convective heat fluxes of inlet and outlet streams. Q̇_tr is the transmitted heat flux which is measured directly by the Seebeck elements. According to the correlation in the calibration step, the actual value of Q̇_tr for the reaction can be determined. The reactive heat flux, Q̇_rx, depends on the total volumetric flow rate, V̇, molar reaction enthalpy, ΔH_r, initial concentration, C₀, and conversion X regarding the limiting substance (eqn (2)). At steady state, the change of energy in the calorimeter equals to zero in eqn (1). Finally, the reaction enthalpy can be obtained. Although the reaction selectivity is not considered within the calculation, a high selectivity is always preferred to obtain an accurate enthalpy for a specific reaction process.

Q̇_rx = V̇C₀ΔH_rX (2)

3 Results and discussion

3.1 Neutralization benchmarking

The calorimeter was benchmarked by using the neutralization reaction between AcOH and NaOH at 25 °C (see ESI‡ Section S2.2.1). A value for ΔH_r of −59.6 ± 0.3 kJ mol⁻¹ was obtained at V_total values from 1 mL min⁻¹ to 6 mL min⁻¹. As organolithium chemistry in flow is generally performed between −20 °C to room temperature, we wanted to assess the performance of the calorimeter at lower temperatures. Consistent results to the value collected at 25 °C were expected as the heat of reaction should be independent of temperature. When performing the reaction at lower temperatures (<20 °C), we identified that it is important to perform a blank test with solvents (see ESI‡ Section S2.2.2). A value for ΔH_r of −59.2 ± 1.1 kJ mol⁻¹ was obtained for the data collected at 5 °C. In the case of the blank tests: for the neutralization reaction then water was used and for the organolithium reactions then hexane and 2-methyltetrahydrofuran (2-MeTHF) were used at the setpoint temperature.

3.2 Calorimetry for the reaction of HexLi with EtOH

We commenced our flash chemistry investigations with the deprotonation of ethanol (EtOH) by n-hexyllithium (HexLi), which was previously reported in a flow calorimeter by Mortzfeld et al.¹⁸ This reaction is ultrafast and mixing limited. More importantly, no unstable intermediates are formed and the reaction is non-selective, therefore it served as an excellent starting point for our investigations. HexLi is a cost-effective and industrially safe reagent.⁶n-Butyllithium (n-BuLi) is the most commonly used organolithium base in organic synthesis, but butane is formed as a flammable gaseous byproduct which makes it more challenging to handle than HexLi. Therefore, HexLi was used throughout our study.

In the work by Mortzfeld et al., a jacketed tube heat balance calorimeter based on thermocouples was adopted.¹⁸ Due to the larger inner diameter (i.d. = 7.8 mm) of the reactor, clogging was not likely to happen in the device. However, a limitation of this device is that the measurement is highly dependent on the determination of the heat transfer coefficient. Furthermore, high flow rates were used in this study, which resulted in a large amount of chemical consumption. We selected to use lower reagent concentrations and higher equivalents of EtOH, since the channel was prone to clogging due to its small internal diameter (i.d. 0.8 mm). Much lower flow rates were adopted (1 to 2 mL min⁻¹), so that the consumption of chemicals could be reduced. Furthermore, 2-MeTHF was used as a greener alternative to tetrahydrofuran (THF) since it was more stable for low temperature lithiation.^49,50 The reactor setup is shown in Fig. 2.

Fig. 2 Setup for calorimetric characterization of reaction between HexLi and EtOH.

The reaction was initially performed at room temperature (21 °C). To our delight, a similar reaction enthalpy was obtained, see Table 1, to the reference value by Mortzfeld et al. (−198 kJ mol⁻¹ in flow, −206 kJ mol⁻¹ in batch¹⁸). As can be seen in Table 1, our reaction enthalpies were consistent under different flow rates with a standard deviation of 1.8%. According to the thermoelectric voltages, no heat was detected in the r2 segment showing that the reaction had gone to completion within the r1 segment (≤3.3 s). Subsequently, the reaction was performed at 0 °C (Table 2). However, when compared to our values at 21 °C and the values reported by Mortzfeld et al.,¹⁸ the values at 0 °C were considerably different. We were surprised by this difference, even after repeat experiments were performed (Table S3‡).

Table 1 Reaction enthalpy for the reaction of HexLi with EtOH at 21 °C using different flow rates

Entry	Flow rate [mL min^−1]		ΔHr [kJ mol^−1]	Ave. ± SD [kJ mol^−1]
	EtOH in 2-MeTHF	HexLi in hexane
1	0.51	0.50	−212.5	−218.1 ± 3.9
2	0.62	0.60	−215.0
3	0.72	0.70	−217.0
4	0.82	0.80	−221.7
5	0.92	0.90	−219.6
6	1.03	1.00	−222.5

---

Table 2 Reaction enthalpy for the reaction of HexLi with EtOH at 0 °C using different flow rates

Entry	Flow rate [mL min^−1]		ΔHr [kJ mol^−1]	Ave. ± SD [kJ mol^−1]
	EtOH in 2-MeTHF	HexLi in hexane
1	0.51	0.50	−295.6	−300.4 ± 4.1
2	0.61	0.60	−303.9
3	0.71	0.70	−299.1
4	0.81	0.80	−304.8
5	0.91	0.90	−303.2
6	1.01	1.00	−296.0

---

Thereafter, the focus turned to the reason for the discrepancy at 0 °C. To address this, reactions with different solvents were carried out at room temperature (21 °C). Specifically, an EtOH solution was prepared in 2-MeTHF or hexane, and a HexLi solution was prepared in hexane. The voltages for these two conditions were compared, shown in Fig. 3. In the precooling segment, the voltages were similar and both close to the baseline. This indicated that the convection heat was small for the reactions performed at room temperature. For the r2 segment, the two curves for the reaction were exactly the same as the baseline, which meant no heat was detected in this segment. While for the r1 segment, U was always higher for the reaction with using only hexane as solvent. This was unexpected since the reaction heat should be the same, even though the solvents were different. A reasonable explanation was that the mixing of 2-MeTHF and hexane is an endothermic process. This was further verified by a solvent mixing test in the calorimeter (see Fig. 4). As can be seen in Fig. 4b, voltages for mixing between hexane and hexane were stable and the same as baseline. For the mixing process between 2-MeTHF and hexane, the voltages were lower than the baseline and decreased with the increase of flow rates. Hence, it can be concluded that the mixing of 2-MeTHF and hexane is an endothermic process. This information can also explain the high enthalpy at 0 °C. When we corrected the enthalpy with solvents, the mixing heat was taken away as well; while for the result at room temperature (Table 1), the mixing heat was included. Therefore, if we took away the mixing heat from the result at room temperature, the value should be the same as the one at 0 °C. For the reaction with hexane as the solvent at room temperature, no correction was needed. Table 3 summaries the reaction enthalpy under different conditions. As expected, a consistent value was obtained, with an enthalpy of −297.6 kJ mol⁻¹ with a difference of 3.9%, which indicated the reliability of the calorimeter.

Fig. 3 Comparison of thermoelectric voltages in the reactor segments for the two reaction systems at 21 °C: (a) precooling segment; (b) r1 segment; (c) r2 segment.

Fig. 4 Comparison of thermoelectric voltages in the reactor segments for the two mixing processes at 21 °C: (a) precooling segment; (b) r1 segment; (c) r2 segment.

Table 3 Summary of reaction enthalpy using different conditions

Temperature [°C]	Reactant^a	ΔHr [kJ mol^−1]
a HexLi solution was prepared with hexane.
0	EtOH in 2-MeTHF	−302.9 ± 6.9
21	EtOH in 2-MeTHF	−305.7 ± 8.1
21	EtOH in hexane	−284.1 ± 6.7

---

The mixing heat of the solvents was included in the values reported by Mortzfeld et al.,¹⁸ therefore it is difficult to make a direct comparison. Thus, we attempted to verify our result using a standard batch micro reaction calorimeter μRC (Thermal Hazard Technology Inc.). We compared three different solvent compositions: absolute EtOH, diluted EtOH in 2-MeTHF and diluted EtOH in hexane. A HexLi solution was prepared in hexane. Fig. 5 shows the result for both reaction and mixing. The negative power value validated that the mixing between 2-MeTHF and hexane is an endothermic process. The average enthalpies of reaction before and after taking away the mixing heat were determined to be −210.0 ± 1.1 kJ mol⁻¹ and −239.4 ± 1.4 kJ mol⁻¹, respectively. However, when using the same conditions but using absolute EtOH or diluted EtOH in hexane, the average enthalpy was −272.1 ± 0.5 kJ mol⁻¹ (mixing heat excluded, see ESI‡ Section S3.3.2). We postulated that this discrepancy was caused from the reaction between HexLi and 2-MeTHF.^51,52 To demonstrate this potential reaction, a further titration of 2-MeTHF with HexLi was carried out (see ESI‡ Section S3.3.3). As can be seen in Fig. 6, the power was extremely high for the first injection, which resulted from the reaction between HexLi and any residual moisture in 2-MeTHF; then it decreased remarkably for further injections. The moisture in 2-MeTHF should be consumed in the first three injections. For the fourth to ninth injection, ΔH_r ranged from 52 to 81 kJ mol⁻¹. Moreover, it can be noticed that when HexLi was injected into 2-MeTHF, the power increased immediately but then decreased slowly. Even after 15 min, the power did not reach the baseline. While for the reaction between EtOH and HexLi (Fig. 5, see also Fig. S8 and S9‡), the power decreased sharply to the baseline. These phenomena implied the existence of a reaction between HexLi and 2-MeTHF. Furthermore, this reaction is less exothermic and slower than the reaction between HexLi and EtOH. Based on this information, the lower reaction enthalpy of −239.4 ± 1.4 kJ mol⁻¹ in the 2-MeTHF and hexane system could be explained. When HexLi was dosed to EtOH solution, the reaction between HexLi and EtOH happened as well as the reaction between HexLi and 2-MeTHF due to the limited mixing. Hence, there was less HexLi to react with EtOH and a smaller value was obtained. Therefore, a better estimation of the reaction enthalpy for the quench of HexLi with EtOH in batch is −272.1 kJ mol⁻¹. Compared to the value of −297.6 kJ mol⁻¹ obtained in flow, the deviation of 8.6% indicated a high accuracy of the flow calorimeter. Moreover, a consistent value was obtained with different solvents in flow (Table 3), which also showed the superiority of the flow calorimeter.

Fig. 5 Calorimetric characterization of the reaction and mixing using the titration mode in the μRC at 25 °C, HexLi diluted in hexane (0.5 M) and EtOH diluted in 2-MeTHF (0.5 M), 15 μL per injection × 6 injection times, the first injection was excluded from the calculation as normally the injection volume is smaller than expected.

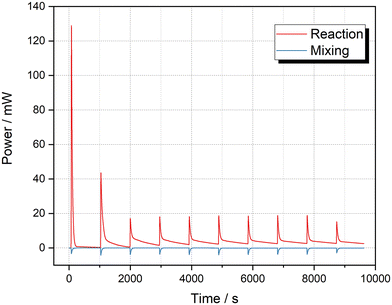Fig. 6 Thermal behavior of 2-MeTHF titrated with 2.5 M HexLi solution at 25 °C and mixing between hexane and 2-MeTHF (10 μL per injection × 10 injection times).

Additionally, the adiabatic temperature rise, ΔT_ad, of the reaction was calculated based on the following equation:⁵³

where C₀ was the initial concentration of the limiting reagent after mixing, ρ was the density of the mixture, c_p was the specific heat capacity of the mixture. According to the setting in the flow calorimeter, ΔT_ad was determined to be 17 °C. As can be seen, even with such a low concentration of HexLi (0.085 M after mixing), a high ΔT_ad was obtained. Hence, continuous flow operation with microreactors is recommended for these highly exothermic organolithium reactions, especially for higher concentration or large-scale applications.

3.3 Calorimetric characterization for preparation of tert-butyl ester and alcohol

tert-Butyl esters are widely used in synthetic organic chemistry, but their preparation is not straightforward.⁵⁴ In recent years, several methodologies have been proposed among which the coupling of di-tert-butyldicarbonate (1), (Boc)₂O, with nucleophilic organometallics in flow microreactors is direct and more sustainable.⁵⁴ The reaction selected in this work was the addition of HexLi to (Boc)₂O (1) which was previously performed in a flow microreactor.⁵⁵ These reactions cannot be conducted under batch conditions, even at cryogenic temperatures, due to the formation of tertiary alcohol (Scheme 1). As a result, a reliable calorimetry measurement for the preparation of tert-butyl ester 2 is difficult to achieve in batch.

Scheme 1 Previously reported batch results for the reaction of (Boc)₂O (1) with HexLi.⁵⁵

The setup for our study is shown in Fig. 7. Before performing the calorimetry, optimization was needed to obtain a high conversion of (Boc)₂O (1) as well as a high selectivity towards the desired ester 2. Some of the results are selected in Table 4 (see Table S4‡ for all results). In addition to the tertiary alcohol 3, a ketone side product 4 was also observed which had not been reported previously. Based on the experimental data, a design of experiment (DoE) analysis was carried out to understand the parameter effects (see ESI‡ Section S4.2). As the selectivity of ketone 4 was low (≤6% in all experiments) and did not change much, it was not included in the DoE models. Models were generated by including all main, square and interaction terms and then non-significant terms were removed. Overall, for the model for ester 2 selectivity, a high level of reproducibility in the data collected in flow was observed with a calculated reproducibility score of 0.98. Gratifyingly, a good fit was achieved for the final model with an R² value of 0.94 and a very good level of predictability was obtained with a Q² value of 0.93. Significant coefficients for the three responses were determined for the main effects of temperature, HexLi equivalent and total volumetric flow rate and for the squared term of total volumetric flow rate.

Fig. 7 Setup for addition of HexLi to (Boc)₂O (1).

Table 4 Optimization for the preparation of tert-butyl ester 2 (partial)

Entry	T [°C]	HexLi^a equiv.	V total [mL min^−1]	Residence time^b [s]	Conv. 1^c [%]	Sel. 2^c [%]	Sel. 3^c [%]	Sel. 4^c [%]
a The concentration of HexLi solution was 0.1 M. b Based on two reaction segments (220 μL) and a 26 cm PFA outlet tubing (i.d. 0.8 mm). c Determined by GC-FID area%. d Average results obtained from calorimetry experiments.
1	21	1.1	1.05	20.0	68	23	70	6
2	21	1.1	2.10	10.0	76	34	62	3
3	21	1.1	3.15	6.7	80	48	50	2
4	21	1.1	5.58	3.8	80	59	38	3
5	21	1.2	5.87	3.6	88	60	38	3
6	21	1.4	5.74	3.7	90	46	51	3
7	0	1.1	6.06	3.5	86	73	25	3
8a	0	1.2	6.13	3.4	88	74	24	3
8b^d	0	1.2	6.13	3.4	89	72	28	—
9	−10	1.1	6.36	3.3	88	78	19	3
10	−10	1.2	6.12	3.4	89	72	25	3

---

The DoE results showed that the reaction performance was significantly influenced by the total volumetric flow rate (V_total) (Table 4, entries 1 to 4), therefore indicating that the reaction is mixing sensitive. To better understand the mixing effects within the microstructured flow calorimeter under different flow rates, computational fluid dynamics (CFD) simulations were carried out (see ESI‡ Section S4.3). As the concentrations of the reagents were relatively low, only the mixing between the two solvents (2-MeTHF and hexane) at 20 °C was considered to simplify the simulation. The mixing index (MI) represented the degree of homogeneity of two fluids and this measure was used to quantify the mixing quality. Fig. 8a shows the geometry of the calorimeter and the allocated positions for MI calculation. As can be seen in Fig. 8b, MI increased linearly at the beginning for all the flow rates and then the rate of increase gradually decreased. Furthermore, the MI was always larger under higher flow rates at the same position (except for the first two positions), even though the residence time is shorter at higher flow rates. This also implied that the mixing gradually changed from a diffusion–convection controlled region to a convection dominant region with an increase in the volumetric flow rate in these split-and-recombine units (see also Fig. S18‡).¹⁰ In Fig. 8c, the streamlines were relatively stratified at 1 mL min⁻¹. While for higher flow rates, the streamlines intertwined and vortices can also be seen, which undoubtedly provided enhanced fluid mixing. As a result, a larger MI was obtained with increasing V_total. This explained the changes in conversion and selectivity at different V_total (residence time) as tertiary alcohol 3 was the main product under low mixing efficiency. However, a higher flow rate than 6.1 mL min⁻¹ was not attempted to further increase the selectivity of ester 2 due to the pressure limit of the device and to minimize potential clogging.

Fig. 8 (a) Allocated position of cross sections for the evaluation of the mixing quality; (b) mixing index at different positions; (c) streamline at different flow rates, colored by velocity magnitude.

In addition, as demonstrated by the DoE study, the used HexLi equivalents was another important parameter for the reaction (entries 4 to 10). Higher equivalents increased the conversion, but were detrimental to the ester 2 selectivity. Slightly better results were also obtained at lower temperatures (entries 4 and 5, 7 to 10, see also Fig. S15‡). However, when operating the reaction at −10 °C, clogging of the calorimeter was observed, which is a commonly reported problem when performing organometallic chemistry within continuous flow reactors.^56,57 On balance we selected to use the conditions shown in entry 8 for the calorimetry. The measurements obtained are depicted in Fig. 9 (see also ESI‡ Section S4.4.1). The U_r2 values from the reaction (Fig. 9e), mixing (Fig. 9f) and calibration at 0 V (Fig. S20,‡ first stair) were the same, thus demonstrating that no heat was generated in the r2 segment. In other words, the reaction was completed in the r1 segment, within only 1.1 s. Therefore, an inline quench was not necessary and not used. Temperatures were well controlled and the thermoelectric voltages were stable during the calorimetry. Based on the calibration data, an average enthalpy of −486.7 ± 6.8 kJ mol⁻¹ was obtained (Table 4, entry 8b, 89% (Boc)₂O 1 conversion and 72% ester 2 selectivity, ketone 4 not included, see also Table S6‡). ΔT_ad was determined to be 15 °C for this process (0.046 M (Boc)₂O 1).

Fig. 9 Calorimetry for preparation of ester 2 at 0 °C: (a) temperatures for reaction at inlets and outlet; (b) temperatures for mixing at inlets and outlet; (c) temperatures of the three segments for reaction; (d) temperatures of the three segments for mixing; (e) thermoelectric voltages for reaction; (f) thermoelectric voltages for mixing.

Although this was the best selectivity of ester 2 we could obtain from our optimization, it was not fully selective since 28% of alcohol 3 formation was observed. The formation of alcohol 3 clearly influenced the precision in the measurement of the reaction enthalpy of ester 2. Therefore, we decided to take one step further and decouple the reaction enthalpies for these two products. Based on the preliminary experiments, it could be deduced that the synthesis of tertiary alcohol 3 could be performed at 21 °C. With 3.0 equiv. of HexLi, full conversion was obtained, but more than 10% of ketone 4 was formed which was undesired (Table 5, entries 1 and 2). A decrease to 2.8 equiv. of HexLi and an increase in flow rates resulted in a decrease in ketone 4 without a drop in conversion (entries 3 and 4); while a further decrease in HexLi equivalents would result in an increase in ester 2 (entry 5). Moreover, increasing above 3 equiv. of HexLi provided no improvement in increasing the amount of alcohol 3 (entries 6 to 8). The conditions shown for entry 4 were selected to do the calorimetry. An inline quench was used to check whether the reaction was completed within the calorimeter (entry 9). By comparing entries 4 and 9, it can be seen that results were very similar, which meant that the reaction had gone to completion within the two reaction segments and all the heat was detected. An average reaction enthalpy of −806.4 ± 1.1 kJ mol⁻¹ was obtained (Table 5, entry 4b, 100% (Boc)₂O 1 conversion and 88% alcohol 3 selectivity, see also Table S7‡). This corresponds to a ΔT_ad for this process of 28 °C (0.053 M (Boc)₂O 1). Finally, based on the yields and reaction enthalpies for these two different processes, the enthalpies for the formation of ester 2 and alcohol 3 were decoupled, shown in Fig. 10. The selectivity towards the ketone 4 was maintained below 5%, therefore the reaction enthalpy of this step was not decoupled from the alcohol 3 formation.

Table 5 Optimization for the preparation of alcohol 3 at 21 °C

Entry	HexLi^a equiv.	Residence time^b [s]	Conv. 1^c [%]	Sel. 2^c [%]	Sel. 3^c [%]	Sel. 4^c [%]
a The concentration of HexLi solution was 0.3 M. b Based on two reaction segments (220 μL) and a 26 cm PFA outlet tubing (i.d. 0.8 mm). c Determined by GC-FID area%. d With inline quench. e Average results obtained from calorimetry experiments.
1	3.0	20.2	100	4	80	16
2	3.0	10.2	100	5	82	13
3	2.8	10.9	100	11	80	9
4a	2.8	3.5	100	11	85	5
4b^e	2.8	3.6	100	12	88	—
5	2.5	3.8	100	20	76	4
6	3.0	3.5	100	8	87	5
7	3.3	3.2	100	7	87	6
8	5.0	3.2	100	6	85	10
9^d	2.8	3.5	100	11	84	5

---

Fig. 10 Decoupled reaction enthalpies for the two main reaction products.

3.4 Calorimetric characterization of a lithium–halogen exchange and its quench with I₂

Lithium–halogen exchange reactions are a well-established method for preparing organolithium compounds and these species serve as valuable intermediates in organic synthesis.^52,58 However, these reactions occur rapidly and their lithiated products are often highly reactive and unstable, thus low temperatures are required for their generation in conventional batch reactors.^59,60 Furthermore, these species are prone to react with any available electrophile in a fast and exothermic manner, which can often lead to a considerable number of side products if not carefully controlled.^61,62 These challenges have been overcome in recent years through the use of continuous flow systems.^11,63,64

We utilized the calorimeter to study a two-step reaction, namely the lithiation of 1-bromo-4-chlorobenzene (5) to form intermediate 6, which can then be reacted in an electrophilic quench with iodine (I₂) to afford product 7. The main side product detected during our optimization of the process was chlorobenzene (8) from the proton quench of the lithiated intermediate 6. Before carrying out the calorimetry test, suitable operating conditions were determined. For the lithiation step, the temperature of the calorimeter was set to 0 °C. I₂ was used in excess (10 equiv.) at room temperature to ensure that the inline quench was performed as fast as possible (Table 6). With a decrease in residence time (t^R1), the conversion of 5 as well as the selectivity towards the desired product 7 increased (Table 6, entries 1 to 3). To ensure that the lithiation step was finished within the calorimeter, an offline quench in batch was compared to the inline quench (entry 4). The same conversion values were obtained for the inline and offline quench, indicating the completion of the lithiation step within 4.4 s (entries 3 and 4), but a better selectivity was obtained with the inline quench. From the thermoelectric voltages, no heat was detected in the r2 segment for the lithiation, which gave further spatially-resolved insight that the reaction was completed within 2.2 s (see Fig. S24‡). The reaction enthalpy was determined to be −151.7 ± 8.0 kJ mol⁻¹ (Table 6, entry 3b, 87% 5 conversion and 86% 7 selectivity on average, see also Table S8‡).

Table 6 Optimization of the lithiation step at 0 °C

Entry	t ^R1 [s]	t ^R2 [s]	Conv. 5^c [%]	Sel. 7^c [%]	Sel. 8^c [%]
a Based on two reaction segments (220 μL). b 98 cm PFA tubing (i.d. 0.8 mm) used for entries 1 to 4, 400 cm tubing for entry 3b. c Determined by GC-FID area%. d Offline quench was used. e Average results obtained from calorimetry experiments.
1	13.3	13.2	86	83	17
2	6.7	6.6	92	85	15
3a	4.4	4.4	94	87	13
3b^e	4.4	17.8	87	86	14
4^d	4.4	10.0	94	78	22

---

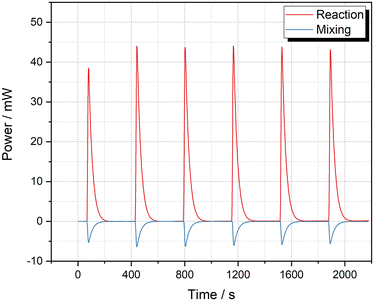
The setup was modified to perform calorimetric measurements for the quench of the lithiated intermediate 6 with I₂. The lithiation step was conducted in PFA tubing (i.d. 0.8 mm) submerged within an ice bath and then the quenching step was carried out in the calorimeter (Table 7). As the goal was to decouple the heat of reaction for quench from the heat of reaction of the lithiation, the reaction between HexLi and I₂ within the calorimeter should be avoided. Therefore, the HexLi was decreased to 1.0 equiv. and a slight decrease of conversion is to be expected. To our delight, good conversion of 5 and selectivity towards 7 was observed (Table 7, entry 1). In order to minimize the energetic contribution of the undesired proton quench to give chlorobenzene (8), higher concentrations were utilized (entries 2 to 4). As expected, the selectivity of the desired product 7 increased and 2.0 equivalent of I₂ was found to be enough for an efficient quench. A 0.5 M solution of starting material 5, 1.0 equiv. HexLi and 2.0 equiv. I₂ was adopted for calorimetry. Another concern was that the heat of the lithiation step should be completed prior to the I₂ stream entering the calorimeter. The performance of the lithiation reaction was compared using three different tubing lengths. Very similar results were obtained using different tubing which demonstrated that the lithiation was complete (entries 5 to 7). The final conditions for the calorimetry used 2 equiv. of I₂ and 17.8 s of residence time for the iodination step (see ESI‡ Section S5.2.2). No heat was detected in the r2 segment (see Fig. S26‡). An average reaction enthalpy of −342.8 ± 11.7 kJ mol⁻¹ was obtained (Table 7, entry 3b, 86% 5 conversion and 91% 7 selectivity on average, see also Table S9‡). This value is 2.3 times high than that of the lithiation enthalpy. This example demonstrates that it is important to consider the entire process as the quench can be even more exothermic than the lithiation step.

Table 7 Optimization of the quenching step at 21 °C

Entry	Concentration [mol L^−1]		t ^R3 [s]	I2^b [equiv.]	t ^R4 [s]	Conv. 5^d [%]	Sel. 7^d [%]	Sel. 8^d [%]
	Substrate 5	HexLi
a 98.0 cm PFA tubing (i.d. 0.8 mm) for entries 1 to 5, 137.5 cm tubing for entry 6, 190.0 cm tubing for entry 7. b The concentration of I2 was 0.3 M for entry 1, 0.4 M for entry 2, 0.6 M for entries 3 to 7. c Based on two reaction segments (220 μL). d Determined by GC-FID area%. e Only the lithiation step in the ice bath. f Average results obtained from calorimetry experiments.
1	0.10	0.10	73.9	3.0	22.0	89	78	22
2	0.30	0.30	73.9	2.0	18.9	90	89	11
3a	0.51	0.51	73.9	2.0	17.8	91	92	8
3b^f	0.50	0.50	103.7	2.0	17.8	86	91	9
4	0.51	0.51	73.9	4.0	12.2	92	92	8
5^e	0.50	0.50	73.9	3.0	—	87	85	15
6^e	0.50	0.50	103.7	3.0	—	89	86	14
7^e	0.50	0.50	143.3	3.0	—	89	87	13

---

4 Conclusion and outlook

Continuous flow calorimetry was used to characterize the reaction enthalpy of a number of flash chemistry examples, namely organolithium transformations. These reactions are particularly challenging to study in batch calorimetry systems due to their short reaction times, mixing sensitivity, highly exothermic nature and the need for cryogenic conditions. Therefore, calorimetric measurements of these reaction systems are seldom performed. Initially, the calorimetry for the reaction of HexLi with EtOH was carried out. Consistent values were obtained with different solvents and at different temperatures, the average enthalpy was determined to be −297.6 kJ mol⁻¹ with a standard deviation of 3.9%, after removal of the mixing heat. The undesired reaction between HexLi and 2-MeTHF could be avoided in flow which showed its superiority over batch calorimetry. In addition, a more challenging reaction between (Boc)₂O and HexLi, which can form the desired tert-butyl ester product and undesired alcohol product, was conducted. The reaction enthalpies for these two reaction processes were successfully decoupled. CFD studies provided an insight into the mixing efficiency at different flow rates within the microstructured flow calorimeter. A Li–Br exchange and its quench with I₂ were also assessed in the flow calorimeter. The result demonstrated that the I₂ quench of the lithiated intermediate was more exothermic than the lithiation step.

We have successfully demonstrated that the continuous flow calorimeter utilized in this study⁴⁵ provides calorimetric and kinetic insight into flash chemistry examples, which are difficult to control under batch conditions. The temporal resolution of these organolithium reactions was showcased on a length scale, which corresponded to reaction times of only seconds (1.1 to 8.9 s). High ΔT_ad values were obtained, demonstrating the need for rapid heat transfer to ensure control over these reactions. This clearly demonstrates that it is very important to obtain these measurements to provide appropriate information for plant design and safety. The temperature could be carefully controlled within the flow calorimeter and the utilization of a microstructured device ensured low material consumption. However, there are also some challenges to characterize reaction enthalpies of these reactions in flow. Higher concentration of reagents could decrease the influence of moisture, however conditions needed to be carefully optimized to prevent clogging by salts at these high concentrations. Furthermore, the reaction of HexLi with water will result in the clogging of the continuous flow system due to the formation of solids, therefore we did not explore measuring the enthalpy of this reaction.

The calorimeter is 3D printed, therefore different structures could easily be identified to provide an even higher level of mixing control. By having additional connector ports, reactions with multiple steps could be carried out and the enthalpy for each step can be determined simultaneously. The internal volume of reactor plates can also be increased to meet the requirement of longer residence time for specific applications. Multiple plates could be placed in series to give better spatially resolved insight. Further studies will investigate reactions which are difficult to study in batch, such as handling reactions involving corrosive reagents, and liquid–liquid and gas–liquid transformations. Apart from thermal characterization, measurements for kinetic model generation and parameter estimation is another interesting topic to be examined within the calorimeter as isothermal conditions can be easily maintained.

Nomenclature

Symbol	Definition	Units
C 0	Initial concentration	mol L^−1
c p	Specific heat capacity	J g^−1 K^−1
Q̇ conv	Convective heat fluxes	W
Q̇ tr	Transmitted heat flux	W
Q̇ rx	Reactive heat flux	W
T	Temperature	°C
U pre	Thermoelectric voltage of precooling segment	mV
U r1	Thermoelectric voltage of r1 segment	mV
U r2	Thermoelectric voltage of r2 segment	mV
V̇	Total volumetric flow rate	mL min^−1
X	Reaction conversion	%
ΔHr	Molar reaction enthalpy	kJ mol^−1
ΔTad	Adiabatic temperature rise	°C
ρ	Density	g mL^−1

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Research Center Pharmaceutical Engineering (RCPE) is funded within the framework of COMET – Competence Centers for Excellent Technologies by BMK, BMDW, Land Steiermark and SFG. The COMET program is managed by the FFG. Gang Fu acknowledges the China Scholarship Council for offering him a scholarship to conduct research at University of Graz (CSC No. 202008320426). We gratefully acknowledge Heidrun Gruber-Woelfler and Sebastian Soritz for helpful discussions.

References

1. J.-i. Yoshida, Flash Chemistry: fast organic synthesis in microsystems, John Wiley & Sons, Ltd, Chichester, UK, 2008.
2. U. Wietelmann, J. Klösener, P. Rittmeyer, S. Schnippering, H. Bats and W. Stam, Org. Process Res. Dev., 2022, 26, 1422–1431.
3. M. Movsisyan, E. I. P. Delbeke, J. K. E. T. Berton, C. Battilocchio, S. V. Ley and C. V. Stevens, Chem. Soc. Rev., 2016, 45, 4892–4928.
4. N. Kockmann, P. Thenée, C. Fleischer-Trebes, G. Laudadio and T. Noël, React. Chem. Eng., 2017, 2, 258–280.
5. J. A. Schwindeman, C. J. Woltermann and R. J. Letchford, J. Chem. Health Saf., 2002, 9, 6–11.
6. M. Power, E. Alcock and G. P. McGlacken, Org. Process Res. Dev., 2020, 24, 1814–1838.
7. J.-i. Yoshida, H. Kim and A. Nagaki, J. Flow Chem., 2017, 7, 60–64.
8. J.-i. Yoshida, Y. Takahashi and A. Nagaki, Chem. Commun., 2013, 49, 9896–9904.
9. A. Nagaki, H. Kim and J.-i. Yoshida, Angew. Chem., Int. Ed., 2009, 48, 8063–8065.
10. H. Kim, K.-I. Min, K. Inoue, D. J. Im, D.-P. Kim and J.-i. Yoshida, Science, 2016, 352, 691–694.
11. A. Nagaki, K. Imai, S. Ishiuchi and J.-i. Yoshida, Angew. Chem., Int. Ed., 2015, 54, 1914–1918.
12. A. Giovine, B. Musio, L. Degennaro, A. Falcicchio, A. Nagaki, J.-i. Yoshida and R. Luisi, Chem. – Eur. J., 2013, 19, 1872–1876.
13. T. von Keutz, J. D. Williams and C. O. Kappe, Org. Process Res. Dev., 2021, 25, 1015–1021.
14. V. Fath, S. Szmais, P. Lau, N. Kockmann and T. Röder, Org. Process Res. Dev., 2019, 23, 2020–2030.
15. J. Y. F. Wong, C. G. Thomson, F. Vilela and G. Barker, Chem. Sci., 2021, 12, 13413–13424.
16. M. Colella, A. Nagaki and R. Luisi, Chem. – Eur. J., 2020, 26, 19–32.
17. A. Nagaki, Y. Ashikari, M. Takumi and T. Tamaki, Chem. Lett., 2021, 50, 485–492.
18. F. Mortzfeld, J. Polenk, B. Guelat, F. Venturoni, B. Schenkel and P. Filipponi, Org. Process Res. Dev., 2020, 24, 2004–2016.
19. M. A. Schneider and F. Stoessel, Chem. Eng. J., 2005, 115, 73–83.
20. C. Zhang, J. Zhang and G. Luo, J. Flow Chem., 2020, 10, 219–226.
21. T. A. Frede, M. Dietz and N. Kockmann, J. Flow Chem., 2021, 11, 321–332.
22. H. Yao, L. Wan, Y. Guo, Y. Mao and Z. Xin, Org. Process Res. Dev., 2022, 26, 1365–1377.
23. W. Litz, Bench Scale Calorimetry in Chemical Reaction Kinetics, Springer, Switzerland, 2015.
24. S. M. Sarge, G. W. H. Höhne and W. Hemminger, Calorimetry: Fundamentals, Instrumentation and Applications, Wiley-VCH, Weinheim, Germany, 2014.
25. G. Glotz, D. J. Knoechel, P. Podmore, H. Gruber-Woelfler and C. O. Kappe, Org. Process Res. Dev., 2017, 21, 763–770.
26. F. Reichmann, S. Millhoff, Y. Jirmann and N. Kockmann, Chem. Eng. Technol., 2017, 40, 2144–2154.
27. T. Westermann and L. Mleczko, Org. Process Res. Dev., 2016, 20, 487–494.
28. T. A. Frede, M. C. Maier, N. Kockmann and H. Gruber-Woelfler, Org. Process Res. Dev., 2022, 26, 267–277.
29. M. N. Kashid, A. Renken and L. Kiwi-Minsker, Microstructured Devices for Chemical Processing, Wiley-VCH, Weinheim, Germany, 2014.
30. K. Wang, Y. C. Lu, H. W. Shao and G. S. Luo, AIChE J., 2010, 56, 1045–1052.
31. M. Moser, A. G. Georg, F. L. Steinemann, D. P. Rütti and D. M. Meier, J. Flow Chem., 2021, 11, 691–699.
32. F. L. Steinemann, D. P. Rütti, M. Moser, A. G. Georg and D. M. Meier, J. Flow Chem., 2022, 12, 389–396.
33. M. Romano, C. Pradere, F. Sarrazin, J. Toutain and J. C. Batsale, Chem. Eng. J., 2015, 273, 325–332.
34. M. Zhang, Y. Feng, L. Lou, H. Zhang, J. Wang and Y. Yang, Org. Process Res. Dev., 2022, 26, 1506–1513.
35. J. Haber, M. N. Kashid, N. Borhani, J. Thome, U. Krtschil, A. Renken and L. Kiwi-Minsker, Chem. Eng. J., 2013, 214, 97–105.
36. J. S. Zhang, C. Y. Zhang, G. T. Liu and G. S. Luo, Chem. Eng. J., 2016, 295, 384–390.
37. G. Hetsroni, A. Mosyak, E. Pogrebnyak and R. Rozenblit, Int. J. Therm. Sci., 2011, 50, 853–868.
38. J. Lerchner, A. Wolf, G. Wolf, V. Baier, E. Kessler, M. Nietzsch and M. Krügel, Thermochim. Acta, 2006, 445, 144–150.
39. F. Reichmann, K. Vennemann, T. A. Frede and N. Kockmann, Chem. Ing. Tech., 2019, 91, 622–631.
40. J. Lerchner, A. Wolf, R. Hüttl and G. Wolf, Chem. Eng. J., 2004, 101, 187–194.
41. C. Hany, H. Lebrun, C. Pradere, J. Toutain and J. C. Batsale, Chem. Eng. J., 2010, 160, 814–822.
42. A. Ładosz, C. Kuhnle and K. F. Jensen, React. Chem. Eng., 2020, 5, 2115–2122.
43. C. Pradere, C. Hany, J. Toutain and J. C. Batsale, Exp. Heat Transfer, 2010, 23, 44–62.
44. T. A. Frede, M. Greive and N. Kockmann, Reactions, 2022, 3, 525–536.
45. M. C. Maier, M. Leitner, C. O. Kappe and H. Gruber-Woelfler, React. Chem. Eng., 2020, 5, 1410–1420.
46. D. Polterauer, D. M. Roberge, P. Hanselmann, P. Elsner, C. A. Hone and C. O. Kappe, React. Chem. Eng., 2021, 6, 2253–2258.
47. S. Schwolow, J. Hollmann, B. Schenkel and T. Röder, Org. Process Res. Dev., 2012, 16, 1513–1522.
48. J. M. Reckamp, A. Bindels, S. Duffield, Y. C. Liu, E. Bradford, E. Ricci, F. Susanne and A. Rutter, Org. Process Res. Dev., 2017, 21, 816–820.
49. D. F. Aycock, Org. Process Res. Dev., 2007, 11, 156–159.
50. V. Pace, P. Hoyos, L. Castoldi, P. Domínguez De María and A. R. Alcántara, ChemSusChem, 2012, 5, 1369–1379.
51. J. Clayden and S. A. Yasin, New J. Chem., 2002, 26, 191–192.
52. S. Zeibi Shirejini and A. Mohammadi, Org. Process Res. Dev., 2017, 21, 292–303.
53. F. Stoessel, Thermal Safety of Chemical Processes: Risk Assessment and Process Design, Wiley-VCH, Weinheim, Germany, 2020.
54. Z. Xin, T. M. Gøgsig, A. T. Lindhardt and T. Skrydstrup, Org. Lett., 2012, 14, 284–287.
55. L. Degennaro, D. Maggiulli, C. Carlucci, F. Fanelli, G. Romanazzi and R. Luisi, Chem. Commun., 2016, 52, 9554–9557.
56. P. Filipponi, B. Guelat, J. Haber, S. Mostarda, R. O'Meadhra, L. Piccioni, J. Polenk, B. Schenkel, S. Schoenebeck, A. Streit, R. Suremann, F. Venturoni and S. Wegmann, Chimia, 2019, 73, 809–816.
57. H. Usutani, T. Nihei, C. D. Papageorgiou and D. G. Cork, Org. Process Res. Dev., 2017, 21, 669–673.
58. M. Ketels, M. A. Ganiek, N. Weidmann and P. Knochel, Angew. Chem., Int. Ed., 2017, 56, 12770–12773.
59. J. Choe, J. H. Seo, Y. Kwon and K. H. Song, Chem. Eng. J., 2008, 135, S17–S20.
60. S. Umezu, T. Yoshiiwa, M. Tokeshi and M. Shindo, Tetrahedron Lett., 2014, 55, 1822–1825.
61. A. Nagaki, Y. Tomida, H. Usutani, H. Kim, N. Takabayashi, T. Nokami, H. Okamoto and J.-i. Yoshida, Chem. – Asian J., 2007, 2, 1513–1523.
62. Q. Tian, S. Shang, H. Wang, G. Shi, Z. Li and J. Yuan, Molecules, 2017, 22, 1952.
63. H. Kim, H. J. Lee and D. P. Kim, Angew. Chem., Int. Ed., 2015, 54, 1877–1880.
64. H. Kim, A. Nagaki and J.-i. Yoshida, Nat. Commun., 2011, 2, 264.

---

Footnotes

† Dedicated to the memory of Jun-ichi Yoshida for his pioneering research on flash chemistry.

‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2re00439a

---