Open Access Article
Open Access ArticleA DFT investigation of lead-free TlSnX3 (X = Cl, Br, or I) perovskites for potential applications in solar cells and thermoelectric devices
Redi Kristian Pingak *a,
Soukaina Bouhmaidib,
Amine Harbic,
Larbi Settib,
Fidelis Nitti
*a,
Soukaina Bouhmaidib,
Amine Harbic,
Larbi Settib,
Fidelis Nitti d,
M. Moutaabbidc,
Albert Z. Johannesa,
Nikodemus U. J. Hauwalie and
Meksianis Z. Ndiif
d,
M. Moutaabbidc,
Albert Z. Johannesa,
Nikodemus U. J. Hauwalie and
Meksianis Z. Ndiif
aDepartment of Physics, Faculty of Science and Engineering, The University of Nusa Cendana, Kupang, Indonesia. E-mail: rpingak@staf.undana.ac.id
bLaboratory of Advanced Science and Technologies, FPL, Abdelmalek Essaadi University, Tetouan, Morocco
cDepartment of Chemistry, Faculty of Sciences Ben M'Sik, Laboratory of Chemistry and Physics of Materials LCPM, University Hassan II of Casablanca, Casablanca, Morocco
dDepartment of Chemistry, Faculty of Science and Engineering, The University of Nusa Cendana, Kupang, Indonesia
eDepartment of Physics Education, The University of Nusa Cendana, Kupang, Indonesia
fDepartment of Mathematics, Faculty of Science and Engineering, The University of Nusa Cendana, Kupang, Indonesia
First published on 20th November 2023
Abstract
In the present study, the Density Functional Theory (DFT) was employed to computationally investigate the potential application of newly developed lead-free perovskites with the formula of TlSnX3 (X = Cl, Br, or I) as absorbers in the perovskite solar cells and as thermoelectric materials. The Quantum Espresso code was implemented to optimize the structural configuration of the perovskites and to compute a range of their properties, including their elasticity, electronic behavior, optical characteristics, and thermoelectric attributes. The findings indicated that these perovskite materials exhibit both chemical and structural stability and that TlSnBr3 and TlSnI3 perovskites possess high dynamic stability. The findings additionally revealed direct (R → R) band gap energy values of 0.87 eV for TlSnCl3, 0.52 eV for TlSnBr3, and 0.28 eV for TlSnI3 using the GGA-PBE functional. Further analysis of their elastic properties suggested that these materials are mechanically stable and displayed overall ductile behaviour. They also demonstrated remarkable optical properties, particularly a high absorption coefficient, ranging from 105 cm−1 to 106 cm−1. Consequently, it is reasonable to infer that these materials exhibit considerable potential for utilization in solar cells. Finally, the evaluation of their thermoelectric properties has revealed the highly promising potential of these materials to be employed in thermoelectric applications.
1 Introduction
The quest for sustainable and renewable energy sources has become a vital global mission, primarily driven by the increasing concerns on the limited supply of fossil fuels and the repercussions of climate change. Solar energy has emerged as a promising solution, with photovoltaic technologies playing a pivotal role in harnessing the power of the sun. Within this array of technologies, lead-based perovskite solar cells (PSCs) have garnered substantial interest for their remarkable potential to revolutionize the solar energy landscape due to their high-power conversion efficiency and cheap production cost.With their unique crystalline structure and exceptional optoelectronic properties, lead-based perovskite materials have also rapidly evolved into a frontrunner in the field of photovoltaic markets, challenging the dominance of traditional silicon-based solar cells.1–6 A recent study reported that the efficiency of lead-based PSCs reached 25.8%,7 which is comparable to that of the conventional silicon based solar cells (26.6%).8 Indeed, if the silicon and perovskite materials are combined in tandem solar cells, much higher efficiency can be achieved. One of the most recent studies reported that the silicon–perovskite tandem solar cells have 29.80% efficiency.9 However, the toxicity associated with the presence of lead in these materials has risen environmental and health concerns, challenging the sustainability and safety of PSCs and thus hampering the large-scale fabrication of the PSCs.10 Considering these challenges, the pursuit of more environmentally and sustainably lead-free perovskite materials ABX3 has emerged as a promising avenue. This initiative has the promise not only to revolutionize the market for perovskite solar cells (PSCs) but also to streamline their large-scale production, thus effectively addressing the urgent demand for cleaner and safer energy.
Recent development in the field of lead free perovskites material has shed the light on the exceptional properties of Sn-based perovskites in comparison to other lead-free perovskites. As evidenced by a recent research by Ke and Kanatzidis (2019), Sn-based perovskites have exhibited remarkable stability and have demonstrated superior performance when utilized in solar cells.11 Notably, some recent studies have underlined the promising optoelectronic properties of Sn-based perovskites ASnX3 include CsSnX3 (X = I, Br, Cl),12 KSnCl3,13 TlSnF3,14 RbSnX3 (X = Cl, Br),15,16 InSnCl3,17 and InSnX3 (X = I, Br, Cl) perovskites.18 Moreover, further investigations of Sn-based double perovskites, such as Cs2SnI6, have unveiled their exceptional and distinct optoelectronic characteristics when compared to other lead-free perovskites.19 These findings highlight the growing significance of Sn-based perovskite materials in various applications, particularly within the domain of solar energy and optoelectronics.
Despite the existing studies, there has been a notable absence of studies on Sn-based halide perovskites where thallium (Tl) acts as the other cation and X represents Cl, Br or I. Indeed, the only existing studies involving such materials were conducted on TlSnF3 by Pingak14 and Zaman et al.20 Their findings revealed that TlSnF3 possesses an indirect band gap (R → M) with energy values of 0.75 eV and 0.63 eV, respectively. However, it is worth noting that the indirect nature of the energy gap in TlSnF3 can be altered into a direct bandgap behavior by substituting F with Cl, Br, or I. Recent investigation by Pingak et al.18 has demonstrated that the replacement of Cl with Br results in a change in the band gap nature of the compounds. Moreover, recent experimental research has highlighted the potential of the TlSnI3/C3N4 nanocomposites as a viable photocatalyst for water treatment.21 A theoretical exploration of TlSnI3 in its orthorhombic structure by Singh22 has also demonstrated that Sn is a promising activator in TlPbI3, conducive to its utilization as low-band-gap scintillators. Therefore, further investigation of the properties of lead-free perovskites TlSnCl3, TlSnBr3, and TlSnI3 is of considerable significance.
The objective of the present study is to conduct a comprehensive investigation into the optoelectronic, elastic, and thermoelectric properties of TlSnX3 (where X can be Cl, Br, or I) perovskite materials. This investigation utilizes the Density Functional Theory (DFT) method, which is known as a highly effective and accurate computational approach for predicting the properties of novel materials. By using DFT method in this research, we aim to obtain the precise material properties prior to the experimental synthesis. This will provide comprehensive information which can streamline the potential application of the studied perovskite materials in various devices and technologies.
2 Computational details
The computation of the properties of the TlSnX3 (X = Cl, Br, I) perovskites was conducted using the Quantum Espresso (QE) code23 based on the DFT approximation,24 with GGA-PBE functional.25 Although the PBE functional generally underestimates materials' band gap energy, Råsander and Moram26 observed that it exhibits relatively comparable accuracy to other functionals, including hybrid functionals in generating materials' lattice constants. Surprisingly, certain elastic properties of the materials derived from the PBE functional are even more accurate than those obtained from other functionals. The procedures involved in the calculation of the properties are as follows. First, the total energy of the compounds as a function of lattice parameters was calculated. Then, the cell relaxation was conducted to optimize the structure of the TlSnX3 (X = Cl, Br, I) perovskites. This was done based on the Birch–Murnaghan equation of states,27,28 using eqn (1).
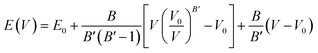 | (1) |
In this self-consistent field calculation, we applied k-points of size 6 × 6 × 6. The optimized lattice parameters of the compounds were then used to perform non-self-consistent calculation, with k-points of size 12 × 12 × 12, to calculate their electronic properties. Energy cut-offs for the wave function and the charge density were 50 Ry and 500 Ry, respectively, while the total energy convergence threshold was set to be 10−8 Ry.
To evaluate the chemical stability of the perovskites, their formation energies were also computed using eqn (2), where the total energy of TlSnX3 (X = Cl, Br, I) unit cell is represented by Etot (TlSnX3) while the energy of Tl, Sn, and X (X = Cl, Br, I) atoms is represented by E(Tl), E(Sn) and E(X) for the respective atoms.
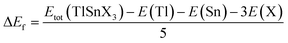 | (2) |
Meanwhile, the optical and elastic properties of the perovskites were computed using the thermo pw program and the thermoelectric properties were calculated using the BoltzTrap code,29 within which the fixed relaxation time approximation is applied. The 3D representation of the Young's modulus, shear modulus, and bulk modulus of the studied compounds are also plotted using the ELATE code. The imaginary part of dielectric function ε2(ω) was calculated using eqn (3) while and the real part ε1(ω) was calculated using eqn (4),30–34 where the electronic charge is represented by e and the unit cell volume is represented by Ω. Meanwhile, ψkV and EKV are the wave functions and the electrons' energy at a particular k in the valence bands, respectively, whereas ψkC and EKC are those in the conduction band, respectively. Finally, U is the unit vector along polarization direction of the electric field of the incident light.
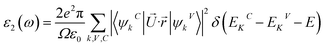 | (3) |
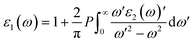 | (4) |
Other optical properties including the refractive index η(ω), the extinction coefficient k(ω), the reflectivity R(ω), the absorption coefficient α(ω), and the loss function L(ω) of the perovskites were calculated using eqn (5)–(9), respectively.34
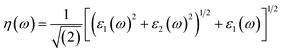 | (5) |
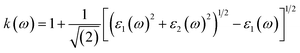 | (6) |
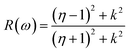 | (7) |
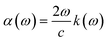 | (8) |
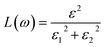 | (9) |
3 Results and discussion
3.1 Structural properties
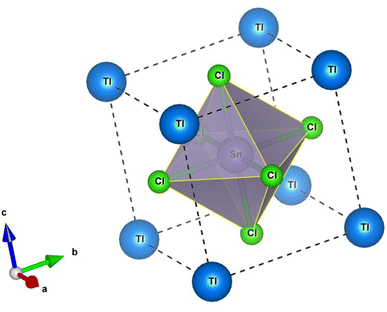
The perovskite crystals TlSnX3 (X = Cl, Br, or I) exhibit a cubic structure, and their crystal structure falls within the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (number 221). The unit cell structure of TlSnCl3 perovskite is visualized in Fig. 1, where the Tl cations are situated at the Wyckoff coordinates of (0, 0, 0) while the Sn atom is located at (0.5, 0.5, 0.5); meanwhile, the remaining three Cl anions are positioned at (0.5, 0.5, 0), (0.5, 0, 0.5), and (0, 0.5, 0.5). The unit cell of TlSnBr3 and TlSnI3 perovskites is identical to that of TlSnCl3, with Cl replaced by Br and I, respectively.
m (number 221). The unit cell structure of TlSnCl3 perovskite is visualized in Fig. 1, where the Tl cations are situated at the Wyckoff coordinates of (0, 0, 0) while the Sn atom is located at (0.5, 0.5, 0.5); meanwhile, the remaining three Cl anions are positioned at (0.5, 0.5, 0), (0.5, 0, 0.5), and (0, 0.5, 0.5). The unit cell of TlSnBr3 and TlSnI3 perovskites is identical to that of TlSnCl3, with Cl replaced by Br and I, respectively.
Total energy as a function of the lattice parameter of TlSnX3 (X = Cl, Br, I) perovskites is shown in Fig. 2. The graph clearly indicates a noticeable shift in the equilibrium lattice parameters of these compounds when the X anions are altered. This outcome was anticipated because of the clear difference in the ionic radii of the respective anions.
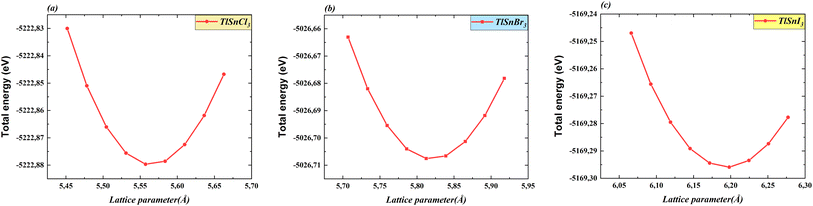 | ||
| Fig. 2 Total energy as a function of the lattice constants of the cubic TlSnCl3 (a), TlSnBr3 (b), and TlSnI3 (c) perovskites. | ||
Table 1 depicts the calculated optimized lattice constants for the studied perovskites. As observed from Table 1, there is a systematic increase in the lattice parameters when Cl is substituted with Br, and then with I. This phenomenon arises from the expansion of the compounds' unit cells, driven by the increased ionic radii resulting from the substitution, which is necessary for achieving stability and minimizing the total energy. This observation is consistent with the findings of a recent study on isoelectronic compounds like InSnX3 (X = Cl, Br, I) perovskites.18 This also corresponds with similar trends reported for a wide range of ABX3 perovskites35–41 and double perovskites.42–49
| Perovskites | a (Å) | ΔEf (eV) | Eg (eV):GGA |
|---|---|---|---|
| TlSnCl3 | 5.58 | −3.11 | 0.87 (R → R) |
| TlSnBr3 | 5.83 | −2.79 | 0.52 (R → R) |
| TlSnI3 | 6.21 | −2.44 | 0.28 (R → R) |
Another important parameter is the formation energy of these compounds, which is closely related to their chemical stability. The formation energy values for the compounds are presented in Table 1. Since the TlSnX3 (X = Cl, Br, I) perovskites have negative formation energy, it can be predicted that these perovskite materials are chemically stable and thus they can be experimentally synthesized under standard ambient condition.
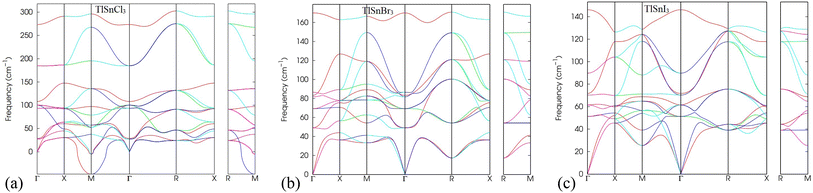
In addition, the analysis of phonon dispersion profiles can be used as valuable tools to study the dynamic stability of materials. Therefore, the phonon dispersion of TlSnX3 (X = Cl, Br, I) perovskites was calculated in the present work and the results were displayed in Fig. 3. As evident from Fig. 3, the lattice vibrational frequency for all phonon modes in TlSnBr3 and TlSnI3 are positive, indicating their dynamic stability. Moreover, the presence of three acoustic branches with zero frequency at the k = 0 point in the reciprocal space further confirms the materials' dynamic stability. This behaviour aligns with the results reported for other perovskites.50,51 In contrast, TlSnCl3 perovskite possesses a negative frequency at the M-point, suggesting that the material is not as stable as the TlSnBr3 and TlSnI3 perovskites. The appearance of imaginary modes in the phonon dispersion might stem from three factors: (i) potential numerical issues during the calculation, (ii) incomplete consideration of certain physical parameters when computing dynamical matrices or force constants, and (iii) inherent dynamic instabilities within the crystal structure.52 Given that the numerical methods and physical parameters used for TlSnCl3, TlSnBr3, and TlSnI3 are identical, factors (i) and (ii) are eliminated, suggesting that the appearance of the imaginary mode in the phonon dispersion of TlSnCl3 corresponds to intrinsic instabilities within the perovskite's crystal. This situation could represent either a local maximum or a saddle point on the Potential Energy Surface (PES) and might be accessed as an average over nearby minima at elevated temperatures.52
3.2 Electronic properties
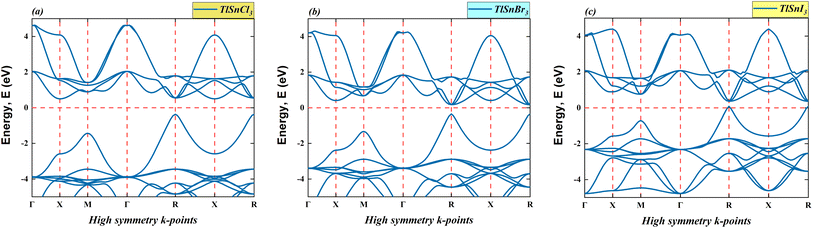
This section provides the calculated energy band diagrams and the electronic density of TlSnX3 (X = Cl, Br, I) perovskites. The band diagrams for these materials are plotted in Fig. 4, where it is obvious that TlSnCl3, TlSnBr3, and TlSnI3 perovskites exhibit direct band gaps (R → R). Furthermore, the band gap reduces as Cl is replaced with Br and I. The specific numerical values of these forbidden energy gaps are summarized in Table 1.As evident from Fig. 4, the overall features of the band diagram of the three perovskites are notably similar, which aligns with the expected characteristics, since these materials are isoelectronic with one another. Nevertheless, a significant change is observed in the size of the forbidden gap between the valence band and conduction band of these materials. This decrease in the band gap of these compounds can be attributed to the distinct orbitals associated with the X anions. This phenomenon was also true for a wide range of halide perovskites and double perovskites. It results from an increase in the lattice parameter and bond length of the compounds, making the valence electrons less tightly bound to their parent atoms.
Moreover, the electronic band gap values of the cubic TlSnCl3, TlSnBr3, and TlSnI3 perovskites are 0.87 eV, 0.52 eV, and 0.28 eV, respectively (Table 1). More importantly, the band gap of the materials is direct in nature. If one compares this with the band gap nature of TlSnF3,14,20 which is indirect, it is apparent that changing the F anion by Cl, Br, or I anions results in the change in the bandgap nature of the perovskites. This is vitally important because direct bandgap materials are better for optoelectronic applications than those with indirect nature electronic bandgap as in general, materials which have direct bandgap experience faster carrier recombination and have better radiative efficiency than those that possess indirect bandgap.53 In their study, Wang et al.53 managed to induce indirect-to-direct bandgap transition in the methylammonium lead iodide via external hydrostatic pressure. Various methods that successfully change indirect nature of bandgap into direct one were also reported in a number of studies, including mechanical strains,54 order-to-disorder transformation,55 mixing of cations,56 and thermal approach.57 The studies observed that the change in the bandgap nature of materials leads to change in their optical properties.
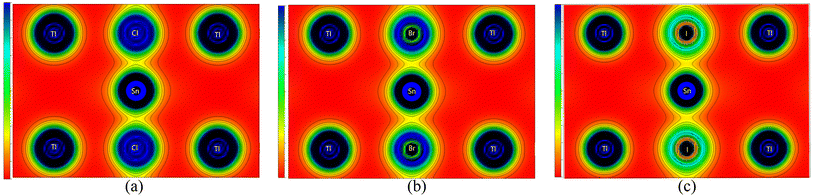
To evaluate the chemical bonds within the compounds, we have plotted their (110) electron density, shown in Fig. 5. The electron density provides information about the charge distribution within the unit cell of the materials, from which the nature of the chemical bonds present in the materials can be determined. These figures clearly indicate that the Tl–Cl, Tl–Br, and Tl–I bonds are mainly ionic in nature. This is evident from the nearly spherical electronic distribution around these atoms. Conversely, the Sn–Cl, Sn–Br, and Sn–I bonds are predicted to be mainly covalent, as evident by an obvious distortion in the electron distribution between the atoms. Consequently, it can be inferred that the replacement of the halogen does not significantly alter the bonding characteristics of these compounds, as Tl–X and Sn–X bonds remain predominantly ionic and covalent, respectively, irrespective of the specific X anion. This observation aligns with the characteristics of other ABX3 perovskites including oxide (X = O),58–60 halide (X = Cl, Br, I) perovskites61 and antiperovskites.62 Across these structures, the A–X bonds generally exhibit an ionic nature,63 consistent with the findings in our study where Tl–X is identified as predominantly ionic. Simultaneously, the B–X bonds predominantly demonstrate a covalent nature, which corresponds to our observations where the Sn–X bond exhibits a mainly covalent character. Notably, these B–X bonds significantly govern the optoelectronic properties of the perovskites and play a pivotal role in their exceptional optical absorption, a critical aspect for their applications in solar cells.63 These bonding characteristics observed in TlSnX3 closely resemble those observed in InSnX3 (X = Cl, Br, I) perovskites,14 where it was reported that the covalent character percentages of Sn–Cl, Sn–Br, and Sn–I are predicted to be approximately 77.11%, 81.06%, and 87.37%, respectively.
3.3 Elastic properties
Table 2 presents the calculated elastic properties of the TlSnCl3, TlSnBr3, and TlSnI3 compounds. Among the most significant elastic properties of the materials are their elastic constants, as they can be used to assess the mechanical stability of the materials using the well-known Born–Huang mechanical stability criteria.64 The mechanical stability of materials is confirmed when their bulk modulus B and elastic constants satisfy specific conditions, which include C11 > 0, C44 > 0, (C11 − C12) > 0, (C11 + 2C12) > 0, and C12 < B < C11. Based on the calculated data presented in Table 2, it is apparent that the elastic constants and the bulk modulus of all the three studied perovskites satisfy these criteria, confirming their mechanical stability.| Parameters | TlSnCl3 | TlSnBr3 | TlSnI3 |
|---|---|---|---|
| Elastic const. C11 (GPa) | 51.52 | 45.44 | 37.99 |
| Elastic const. C12 (GPa) | 8.81 | 6.78 | 4.39 |
| Elastic const. C44 (GPa) | 3.38 | 2.89 | 2.66 |
| Bulk modulus B (GPa) | 22.99 | 19.70 | 15.59 |
| Shear modulus G (GPa) | 7.81 | 6.94 | 6.17 |
| Pugh ratio B/G | 2.94 | 2.84 | 2.53 |
| Anisotropy factor A | 0.16 | 0.15 | 0.158 |
| Young's modulus E (GPa) | 20.82 | 18.39 | 16.14 |
| Poisson ratio ν | 0.33 | 0.32 | 0.31 |
| Kleinman parameter ξ | 0.32 | 0.30 | 0.27 |
| Cauchy pressure (C12 − C44) | 5.43 | 3.89 | 1.73 |
| Debye temperature θD (K) | 128.356 | 107.025 | 93.462 |
| Melting temperature Tm (K) | 857.53 ± 300 | 822.25 ± 300 | 777.56 ± 300 |
| Average sound velocity Vm (m s−1) | 1406.33 | 1226.18 | 1140.30 |
| Longitudinal sound velocity Vl (m s−1) | 2365.767 | 2045.524 | 1788.201 |
| Transverse sound velocity Vt (m s−1) | 1379.006 | 1213.807 | 1124.479 |
| Lamé const. λ | 4.12 | 3.50 | 2.96 |
| Lamé const. μ | 7.83 | 6.96 | 6.16 |
| Total mass (a.m.u) | 429.4433 | 562.7933 | 703.8053 |
| Density (g cm−3) | 4.1083 | 4.7088 | 4.8761 |
The bulk modulus B, provides insights into the perovskites' resistance to applied pressure. From Table 2, it can be seen that TlSnCl3 perovskite has the highest bulk modulus B (22.99 GPa), followed by TlSnBr3 (19.70 GPa) and finally by TlSnI3 (15.59 GPa). This implies that TlSnCl3 is predicted to be more resistant to external pressure compared to its counterparts TlSnBr3 and TlSnI3 perovskites. Interestingly, the decrease in the bulk modulus of these compounds as Cl is replaced by Br and I is also accompanied by a reduction in the materials' energy gap. This linear relationship between bulk modulus and energy gap has been predicted for a large number of materials.65 However, it is worth noting that this relationship might not be applicable universally, as Li et al.66 found that for alloys, this trend is not always true. They argued that various factors, including size and chemical effects, play a major role in the variation of the band structure in alloys.67
The shear modulus G is another important parameter which describes the shear resistance of materials. Similar to the bulk modulus, the TlSnCl3 is expected to have larger shear resistance than TlSnBr3 and TlSnI3. Similarly, concerning the stiffness of the perovskites, represented by their Young's modulus E, TlSnCl3 perovskite is the stiffest material compared to its counterparts.
From the Poisson and the Pugh's ratio, one can predict the ductility of materials. A material is considered ductile if its Poisson ratio is greater than 0.26; and brittle if it is lower than 0.26.68 Moreover, a material is ductile if its Pugh's ratio is larger than 1.75 and is brittle if its Pugh's ratio is lower than 1.75.69 As indicated by Table 2, the studied perovskites are all predicted to possess ductile behaviour since their Poisson ratio and Pugh's ratio are larger than 0.26 and 1.75, respectively. This prediction is also corroborated by the positive values of the Cauchy pressure for these perovskites.
To investigate internal strain within the studied perovskites, their Kleinman parameter ξ was computed, with computed Kleinman parameter of 0.32, 0.30, and 0.27 for TlSnCl3, TlSnBr3, and TlSnI3, respectively. These values suggest that within the perovskites structure, the bond bending is more dominant than the bond stretching. In the context of Kleinman parameters, ξ = 0 corresponds to minimizing bond bending and ξ = 1 corresponds to minimizing bond stretching.70
It is observed that the Debye temperature and the melting temperature of the perovskite materials decrease as Cl is replaced by Br and I. This trend is also reflected in their longitudinal, transverse and average sound velocity. On the other hand, their total mass and density increase following the anion replacement.
Finally, the two Lamé's constants can be used to further investigate the perovskites' elastic behaviour. The first Lamé's constant λ and the second constant μ measure their compressibility and shear stiffness.71,72 It is expected that these two constants should be directly proportional to the values of the Young modulus, which is confirmed in the present study (Table 2). Furthermore, the change in the second Lamé's constant should mirror the variation in the shear modulus, as both represent the shear behaviour of the compounds. As expected, this relationship is also confirmed in the current study, and has been reported for various isoelectronic materials.73–76
Furthermore, the 3D elastic properties such as the linear compressibility, shear modulus and Young's modulus, of the compounds were also calculated and the results are visualized using the ELATE program (Fig. 6). It is clear that TlSnI3 has the largest compressibility, followed by TlSnBr3 and TlSnCl3. This is in good agreement with the values of the bulk modulus as presented in Table 2 since the compressibility is inversely proportional to the bulk modulus. The 3D profiles of the elastic properties can also be used to predict the anisotropy of the mechanical properties of the perovskites. The high degree of deviation from the 3D shapes of their shear modulus and Young's modulus strongly indicates elastic anisotropy and therefore, the materials are predicted to possess interesting elastic anisotropy. The anisotropy can be further analyzed from the minimum and maximum values of the corresponding properties of the materials, which are summarized in Table 3 along with those of the Poisson ratio ν.
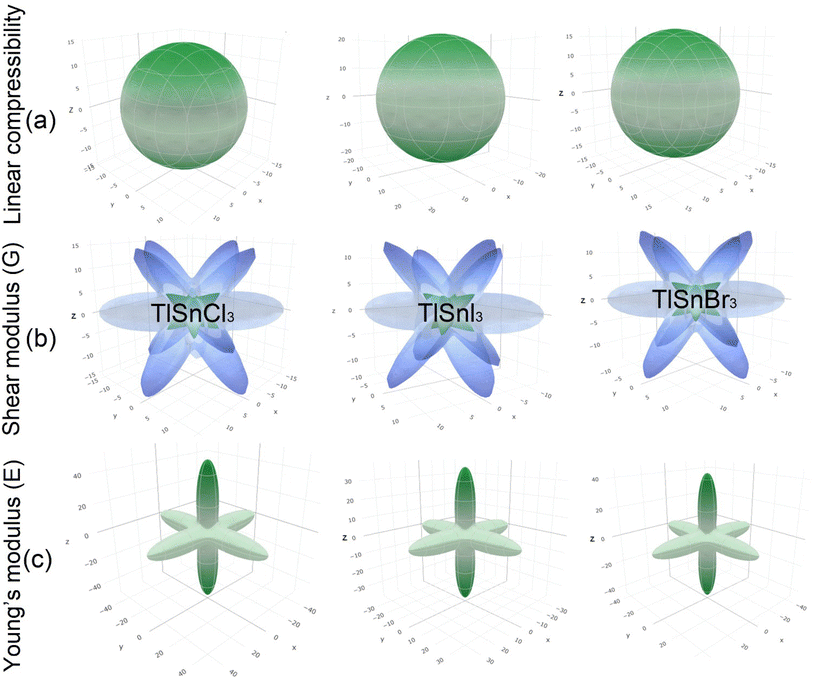 | ||
| Fig. 6 3D elastic properties of the cubic TlSnCl3, TlSnBr3, and TlSnI3 perovskites: linear compressibility (a), shear modulus (b), Young's modulus (c). | ||
| Perovskites | Gmin | Gmax | Emin | Emax | νmin | νmax |
|---|---|---|---|---|---|---|
| TlSnCl3 | 3.38 | 21.36 | 9.67 | 48.95 | 0.04 | 0.79 |
| TlSnBr3 | 2.89 | 19.39 | 8.27 | 43.79 | 0.03 | 0.79 |
| TlSnI3 | 2.66 | 15.57 | 7.58 | 36.50 | 0.03 | 0.78 |
The considerable difference between the minimum and the maximum values of the shear modulus G and the Young's modulus E confirms the high degree of the anisotropy of the two mechanical properties within the studied perovskites. The computed minimum values of the shear modulus of TlSnCl3, TlSnBr3, and TlSnI3 perovskites are 3.38 GPa, 2.89 GPa, and 2.66 GPa, respectively, far lower than its maximum values: 21.36 GPa, 19.39 GPa, and 15.57 GPa for the respective materials. Similarly, the computed minimum (maximum) values of their Young's modulus are 9.67 GPa (48.95 GPa), 8.27 GPa (43.79 GPa), and 7.58 GPa (36.50 GPa) for TlSnCl3, TlSnBr3, and TlSnI3 compounds, respectively. Interestingly, the minimum values of their shear modulus and the maximum values of their Young's modulus are found along the same [001] direction. This implies that the three studied perovskites are predicted to be more resistant to any external pressure along the [001] direction than other crystal orientations within the materials, and at the same time have lower shear resistance in this direction compared to the other directions within the materials.
It is also interesting to note that although our calculated Poisson's ratio in Table 2 indicates that the materials are all ductile in nature, the Poisson's ratio extracted from the 3D profiles of the elastic properties of TlSnCl3, TlSnBr3, and TlSnI3 compounds range from 0.04 to 0.79, 0.03 to 0.79, and 0.03 to 0.78, respectively. This strongly indicates that although it is predicted that the materials exhibit overall ductility, they may show brittleness in some directions within the crystal of the materials. Furthermore, the results also indicate that the materials exhibit similar ductile behaviour even though TlSnCl3 is projected to be slightly more ductile.
The 3D contours of the Young's moduli of materials are also strongly correlated to the types of octahedral connection within them.77–79 The shape of the 3D Young's moduli profiles of the compounds represents Sn–X (X = Cl, Br, I) bonds along the 〈001〉 family planes, which is also closely related to the charge distribution between Sn and X atoms as shown in Fig. 5. Similar finding was also reported for Pb–I bonds in γ-CsPbI3.79
3.4 Optical properties
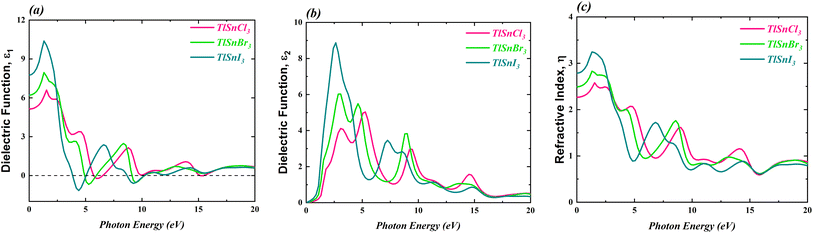
The optical properties of the TlSnX3 (X = Cl, Br, I) perovskites were calculated within photon energy interval [0, 20] eV. The computed real part of the dielectric function ε1(ω), the imaginary part ε2(ω), and the refractive index η(ω) of the perovskite compounds are shown in Fig. 7.It is noticeable from Fig. 7 is that the overall feature of the refractive index of the compounds (Fig. 7c) resembles that of the dielectric function ε1(ω) (Fig. 7a), as expected. It is also obvious from Fig. 7a that the TlSnI3 perovskite has the highest static dielectric function ε1(0) of 7.75, which is followed by TlSnBr3 and TlSnCl3 perovskites with static dielectric function of 6.20 and 5.13, respectively. This indicates that, based on their ε1(0) values, TlSnI3 is expected to exhibit better optoelectronic performance compared to TlSnBr3 and TlSnCl3. This is due to the fact that materials with larger ε1(0) values tend to have lower charge recombination,80,81 which is favourable for optoelectronic applications. In addition, there is an inverse relationship between ε1(0) and the energy band gaps of the TlSnCl3, TlSnBr3, and TlSnI3 compounds, which aligns with the Penn model.82 Similarly, the static refractive index values η(0) also increase when Cl is substituted by Br and I. The η(0) values of TlSnCl3, TlSnBr3, and TlSnI3 perovskites are 2.27, 2.49, and 2.78, respectively.
The imaginary part of the ε2(ω), as shown in Fig. 7b, provides insights into the perovskites' absorption behaviour. The strongest absorption by these studied perovskites can be predicted from the main peaks of their calculated absorption spectra, represented by the ε2(ω) graph. In line discussion of the compounds' band structure in the previous section, where it was found that the band gap of the materials decrease as Cl is replaced by Br and I, Fig. 7b also indicates a shift in the energy threshold of ε2(ω) to lower photon energy due to the anion replacement. Beyond this energy threshold, the absorption of TlSnCl3, TlSnBr3, and TlSnI3 perovskites is predicted to increase, reaching their main absorption peaks at approximately 5.03, 6.03, and 8.87, at approximately 5.28 eV, 3.08 eV, and 2.64 eV, for the respective perovskite materials.
To further investigate the optical properties of the compounds, the dielectric constants were used to calculate the reflectivity R(ω), the absorption coefficient α(ω), the loss function L(ω), and the extinction coefficient k(ω). These properties are important to evaluate the potential application of the materials in optoelectronic devices. The computed corresponding properties are presented in Fig. 8.
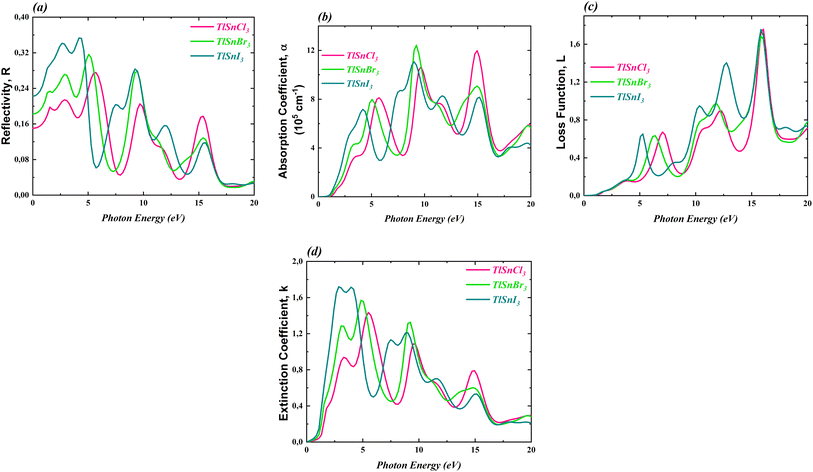 | ||
| Fig. 8 R(ω) (a), α(ω) (b), L(ω) (c) and k(ω) (d) of the cubic TlSnCl3, TlSnBr3, and TlSnI3 perovskites. | ||
Fig. 8a reveals that the reflectivity of the compounds is relatively low. The maximum reflectivity of TlSnCl3, TlSnBr3, and TlSnI3 is 27.52% at 5.72 eV, 31.62% at 5.06 eV, and 35.31% at 4.18 eV, respectively. Additionally, the materials exhibit strong absorption, in the order of 105 cm−1 to 106 cm−1 (Fig. 8b). The threshold energy for absorption aligns with the electronic band gap energy of the compounds as well as the threshold energy for the imaginary part of the dielectric function. This further confirms that TlSnI3 has the lowest optical band gap energy and thus can absorb light of lower energy. The high absorption of the TlSnI3 perovskite was previously predicted by Singh22 for the orthorhombic phase. It is also important to note a significant dissimilarity between the absorption threshold reported by Singh (around 2 eV) and our finding (approximately 0.4 eV). This divergence can be attributed to the different structures considered in the two studies. Recently, Ghaithan et al.83 disclosed that using several functionals, the orthorhombic structure of CsPbBr3 exhibits a marginally larger energy gap compared to its cubic structure. Similar trends were also observed for other perovskites including BaZrS3,84 CH3NH3PbI3,85 and PbZrO3.86 Moreover, the discrepancy between the absorption threshold obtained by Singh and our findings can be attributed to the use of different functionals. While Singh22 employed the TB-mBJ functional, we utilized the GGA-PBE approach, renowned for its tendency to underestimate the band gap, thereby leading to an expected lower absorption threshold in our study. This discrepancy can be further investigated using experimental data such as UV-Vis spectra, from which the optical band gap can be determined using the Tauc plot method.87 The combination of the low reflectivity and the high absorption makes these materials potential candidates for a wide range of applications, including use as absorbers in solar cells.
Regarding the loss function L(ω), which accounts for an inelastic scattering process, Fig. 8c indicated that for low photon energy (between 0 and 3 eV), the inelastic scattering is negligibly small and therefore it does not significantly impact the absorption behaviour of the materials within this photon energy range. The loss function for the TlSnX3 (X = Cl, Br, I) then increases with a similar trend above this energy except that there is a shift of the function of TlSnI3 and TlSnBr3 towards a lower energy between energy range about 3 eV and 10 eV. A similar shift is also observed in the extinction coefficient k(ω) of the studied perovskites, as presented in Fig. 8d. The main peaks of k(ω) of TlSnCl3, TlSnBr3, and TlSnI3 are 1.43 at 5.50 eV, 1.57 at 4.84 eV, and 1.72 at 2.86 eV, respectively.
3.5 Thermoelectric properties
The thermoelectric properties of the cubic TlSnX3 (X = Cl, Br, I) perovskites were also calculated and the computed properties are shown in Fig. 9. The properties include the electrical conductivity, the Seebeck coefficient, the thermal conductivity, and the figure of merit. All these properties were investigated as functions of the temperature.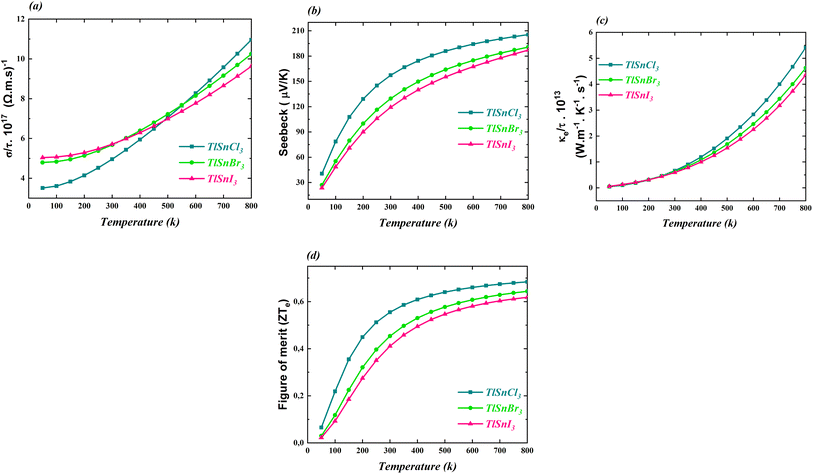 | ||
| Fig. 9 (a) The electrical conductivity, (b) Seebeck coefficient, (c) thermal conductivity, and (d) figure of merit of the cubic TlSnCl3, TlSnBr3, and TlSnI3 perovskites. | ||
It is obvious from Fig. 9a that the electrical conductivity per relaxation time σ/γ of the three studied perovskites increases as the temperature increases. It is also notable that below 500 K, σ/γ values of TlSnI3 and TlSnBr3 are considerably higher than those of TlSnCl3 while for larger temperature, the reverse trend is observed. Similarly, there is an increase in the electronic contribution to the thermal conductivity of the perovskites, as depicted in Fig. 9c. The three compounds exhibit approximately the same thermal conductivity up to the room temperature (300 K). However, for temperatures above 300 K, their thermal conductivity rises considerably, with TlSnCl3 having higher thermal conductivity than TlSnBr3 and TlSnI3 perovskites. The increase in the electrical conductivity and thermal conductivity of the studied perovskites as a function of the temperature was also observed for other isoelectronic compounds of the form InSnX3 (X = Cl, Br, or I).18
Fig. 9b and d illustrate how the Seebeck coefficients S and the figure of merit ZTe, respectively, change with temperature. The Seebeck coefficient measures the potential difference between two different conductors or semiconductors when a temperature gradient exists between the two junctions, while the ZTe = S2Tσ/κ serves as a transport parameter used to assess the performance of thermoelectric materials.88 Here, S, T, σ, and κ stand for the Seebeck coefficient, temperature, electrical and thermal conductivity, respectively. As expected, the general feature of the two parameters is very similar. As observed in both figures, these parameters increase with increasing temperature. Between 50 K and 300 K, there is a significant increase in the parameters, followed by a more gradual increase for higher temperatures. TlSnCl3 has the largest Seebeck coefficient and the figure of merit for the entire temperature range, followed consecutively by TlSnBr3 and TlSnI3 perovskites. Since ZTe describes the thermoelectric performance of materials, with higher ZTe indicating better thermoelectric properties,19 these figures clearly show that TlSnCl3 is expected to have better thermoelectric performance compared to TlSnBr3 and TlSnI3 perovskites. The highest values of the figure of merit for the respective compounds are 0.68, 0.64, and 0.62 at 800 K. These relatively high ZTe values suggest that these materials are promising candidates as thermoelectric materials. Virtually, all materials have positive Seebeck coefficients, indicating that they are highly likely p-type semiconductors.
4 Conclusions
In this study, a comprehensive computational investigation on the structural, elastic, optoelectronic, and the thermoelectric properties of novel lead-free perovskites with the chemical composition TlSnX3 (X = Cl, Br, I) was conducted using the DFT based on the GGA-PBE functional. The results showed that the studied perovskites are structurally and mechanically stable and that TlSnBr3 and TlSnI3 perovskites are also dynamically stable. They were also found to be ductile in nature and possess direct semiconducting behaviour, with GGA-PBE electronic band gaps of 0.87 eV, 0.52 eV, and 0.28 eV for TlSnCl3, TlSnBr3, and TlSnI3, respectively. Moreover, the perovskites have outstanding optical properties making them promising for applications in optoelectronics including perovskite solar cells. Analysis of their thermoelectric properties also suggested that the perovskites can be used as thermoelectric materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Ministry of Education, Culture, Research and Technology of Indonesia through Penelitian Kompetitif Nasional – Penelitian Fundamental – Reguler 2023 with grant number: 147/E5/PG.02.00.PL/2023 and the institution grant number: 406/UN15.22/SP2H/LT/2023. The authors also thank Naldo Alfa Sandi Malelak and Sem Peli Dolu for their technical assistance.Notes and references
- P. Roy, A. Ghosh, F. Barclay, A. Khare and E. Cuce, Coatings, 2022, 12, 1089 CrossRef CAS.
- M. Wang, W. Wang, B. Ma, W. Shen, L. Liu, K. Cao, S. Chen and W. Huang, Nano-Micro Lett., 2021, 13, 62 CrossRef.
- X. Lupa, X. Liu and L. Han, Next Energy, 2023, 1, 100011 CrossRef.
- F. D. Angelis, Nat. Photonics, 2021, 6, 1586–1587 Search PubMed.
- M. A. Green, A. W. Y. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- M. Roknuzzaman, J. A. Alarco, H. Wang, A. Du, T. Tesfamichael and K. K. Ostrikov, Comput. Mater. Sci., 2019, 169, 109118 CrossRef CAS.
- H. M. Ane, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. I. Seok, Nature, 2021, 598, 444–450 CrossRef PubMed.
- K. Yoshikawa, H. Kawasaki, W. Yoshida, T. Irie, K. Konishi, K. Nakano, T. Uto, D. Adachi, M. Kanematsu, H. Uzu and K. Yamamoti, Nat. Energy, 2017, 2, 17032 CrossRef CAS.
- P. Tockhorn, J. Sutter, A. Cruz, P. Wagner, K. Jäger and D. Yoo, Nat. Nanotechnol., 2022, 17, 1214–1221 CrossRef CAS PubMed.
- M. Roknuzzaman, K. Ostrikov, H. Wang, A. Du and T. Tesfamichael, Sci. Rep., 2017, 7, 14025 CrossRef PubMed.
- W. Ke and M. G. Kanatzidis, Nat. Commun., 2019, 10, 965 CrossRef PubMed.
- J. U. Rehman, M. Usman, S. Amjid, M. Sagir, M. B. Tahir, A. Hussain, I. Alam, R. Nazir, H. Alrobei, S. Ullah and M. A. Assiri, Comput. Theor. Chem., 2022, 1209, 113624 CrossRef.
- O. Das, M. Saiduzzaman, K. M. Hossain, I. K. Shuvo, M. M. Rahman, S. Ahmad and S. K. Mitro, Results Phys., 2023, 44, 106212 CrossRef.
- R. K. Pingak, Comput. Condens. Matter, 2022, 33, e00747 CrossRef.
- M. A. Rashid, M. Saiduzzaman, A. Biswas and K. M. Hossain, Eur. Phys. J. Plus, 2022, 137, 649 CrossRef CAS.
- M. H. Rahman, M. Jubair, M. Z. Rahman, M. S. Ahasan, K. K. Ostrikov and M. Roknuzzaman, RSC Adv., 2022, 12, 7497–7505 RSC.
- S. Khan, N. Mehmood, R. Ahmad, A. Kalsoom and K. Hameed, Mater. Sci. Semicond. Process., 2022, 150, 106973 CrossRef CAS.
- R. K. Pingak, A. Harbi, M. Moutaabbid, A. Z. Johannes, N. U. J. Hauwali, M. Bukit, F. Nitti and M. Z. Ndii, Mater. Res. Express, 2023, 10, 095507 CrossRef.
- A. E. Maughan, A. M. Ganose, M. M. Bordelon, E. M. Miller, D. O. Scanlon and J. R. Neilson, J. Am. Chem. Soc., 2016, 138, 8453–8464 CrossRef CAS.
- S. U. Zaman, S. Khan, N. Mehmood, A. U. Rahman, R. Ahmad, N. Sultan, F. Ullah and H. J. Kim, Opt. Quantum Electron., 2022, 54, 396 CrossRef CAS.
- F. Yousefzadeh, Q. A. Yousif, M. Ghanbari and M. Salavati-Niasari, J. Mol. Liq., 2022, 349, 118443 CrossRef CAS.
- D. J. Singh, J. Appl. Phys., 2012, 112, 083509 CrossRef.
- G. Paolo, B. Stefano, B. Nicola, C. Matteo, C. Roberto, C. Carlo, C. Davide, C. Guido, C. Matteo, D. Ismaila, D. C. Andrea, d. G. Stefano, F. Stefano, F. Guido, G. Ralph, G. Uwe, G. Christos, K. Anton, L. Michele, M.-S. Layla, M. Nicola, M. Fransesco, M. Riccardo, P. Stefano, P. Alfredo, P. Lorenzo, S. Carlo, S. Sandro, S. Gabriele, P. S. Ari, S. Alexander, U. Paolo and M. Renata, J. Phys.: Condens.Matter, 2009, 21, 395502 CrossRef PubMed.
- W. Khon and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Råsander and M. A. Moram, J. Chem. Phys., 2015, 143, 144104 CrossRef PubMed.
- F. Birch, Phys. Rev., 1974, 71, 809 Search PubMed.
- D. P. Hastuti, P. Nurwantoro and S. Sholihun, Mater. Today Commun., 2019, 19, 459–463 CrossRef CAS.
- G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- M. A. Green, Y. Jiang, A. M. Soufianj and A. Ho-Baillie, J. Phys. Chem. Lett., 2015, 6, 4774–4785 CrossRef CAS PubMed.
- C. Ambrosch-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1–14 CrossRef CAS.
- S. Bouhmaidi, A. Marjaoui, A. Talbi, M. Zanouni, K. Nouneh and L. Setti, Comput. Condens. Matter, 2022, 31, e00663 CrossRef.
- S. Bouhmaidi, R. K. Pingak, A. Azouaoui, A. Harbi, M. Moutaabbid and L. Setti, Solid State Commun., 2023, 369, 115206 CrossRef CAS.
- M. S. Alam, M. Saiduzzaman, A. Biswas, T. Ahmed, A. Sultan and K. M. Hossain, Sci. Rep., 2022, 12, 8663 CrossRef CAS PubMed.
- R. K. Pingak, S. Bouhmaidi, L. Setti, B. Pasangka, B. Bernandus, H. I. Sutaji, F. Nitti and M. Z. Ndii, Indones. J. Chem., 2023, 23, 843–862 CrossRef CAS.
- Q. Mahmood, F. hedhili, S. Al-Shomar, S. Chebaaneef, T. I. Al-Muhimeed, A. AlObaid, A. Meta and O. A. Alamri, Phys. Scr., 2021, 96, 095806 CrossRef.
- R. K. Pingak, S. Bouhmaidi and L. Setti, Phys. B, 2023, 663, 415003 CrossRef CAS.
- S. Bouhmaidi, A. Azouaoui, N. Benzakour, A. Hourmatallah and L. Setti, Comput. Condens. Matter, 2022, 33, e00756 CrossRef.
- M. Saiduzzaman, T. Ahmed, K. Hossain, A. Biswas, S. Mitro, A. Sultana, M. Alam and S. Ahmad, Mater. Today Commun., 2023, 34, 105188 CrossRef CAS.
- S. Bouhmaidi, M. B. Uddin, R. Pingak, S. Ahmad, M. Rubel, A. Hakamy and L. Setti, Mater. Today Commun., 2023, 37, 107025 CrossRef CAS.
- M. Ahmad, G. Rehman, L. Ali, M. Shafiq, R. Iqbal, R. Ahmad, T. Khan, S. Jalali-Asadabadi, M. Maqbool and I. Ahmad, J. Alloys Compd., 2023, 705, 828–839 CrossRef.
- T. Ou, W. Jiang, Q. Zhuang, H. Yan, S. Feng, Y. Sun, P. Li and X. Ma, Phys. B, 2023, 415050 CrossRef CAS.
- A. Harbi and M. Moutaabbid, Polyhedron, 2023, 233, 116316 CrossRef CAS.
- K. Chen, S. Schunemann, S. Song and H. Tuysuz, Chem. Soc. Rev., 2018, 47, 7045–7077 RSC.
- A. Harbi, A. Aziz and M. Moutaabbid, Inorg. Chem. Commun., 2023, 153, 110842 CrossRef CAS.
- A. Hedhili, B. Hassan, M. S. Rashid, M. Bakr, Q. Mahmood, S. M. Al-Shomar, W. Alahmad, F. Alimi and L. Mechi, Curr. Appl. Phys., 2023, 53, 1–8 CrossRef.
- A. Harbi, S. Bouhmaidi, R. K. Pingak, L. Setti and M. Moutaabbid, Phys. B, 2023, 668, 415242 CrossRef CAS.
- C. Kaewmeechai, Y. Laosiritaworn and A. P. Jaroenjittichai, Results Phys., 2022, 42, 106015 CrossRef.
- S. Bouhmaidi, A. Harbi, R. Pingak, A. Azouaoui, M. Moutaabbid and L. Setti, Comput. Theor. Chem., 2023, 1227, 114251 CrossRef CAS.
- T. Zelai, S. A. Rouf, Q. Mahmood, S. Bouzgarrou, M. A. Amin, A. I. Aljameel, T. Ghrib, H. H. Hegazy and A. Mera, J. Mater. Res. Technol., 2022, 16, 631–639 CrossRef CAS.
- A. Jehan, M. Husain, V. Tirth, A. Algahtani, M. Uzair, N. Rahman, A. Khana and S. M. Khan, RSC Adv., 2023, 13, 28395 RSC.
- I. Pallikara, P. Kayastha, J. M. Skelton and L. D. Whalley, Electron. Struct., 2022, 4, 033002 CrossRef.
- T. Wang, B. Daiber, J. M. Frost, S. A. Mann, E. C. Garnett, A. Walsh and B. Ehrler, Energy Environ. Sci., 2017, 10, 509–515 RSC.
- X. Zhang, Y. Lv, Y. Lv, Y. Liu and Z. Yang, J. Mater. Res. Technol., 2022, 17, 425–432 CrossRef CAS.
- M. A. Hadi, M. N. Islam and J. Podder, RSC Adv., 2022, 12, 15461–15469 RSC.
- A. Karmakar, G. M. Bernard, A. Meldrum, O. A. Oliynyk and V. K. Michaelis, J. Am. Chem. Soc., 2020, 142, 10780–10793 CrossRef CAS PubMed.
- X. Wu, X. Zhang, W. Yu, Y. Zhou, W. Wong, W. He, K. P. Loh, X.-F. Jiang and Q.-H. Xu, J. Mater. Chem. A, 2023, 11, 4292–4301 RSC.
- A. Harbi and M. Moutaabbid, J. Supercond. Novel Magn., 2022, 35, 3447–3456 CrossRef CAS.
- A. Harbi, A. Azouaoui, S. Benmokhtar and M. Moutaabbid, J. Supercond. Novel Magn., 2022, 35, 1405–1412 CrossRef CAS.
- A. Harbi, A. Azouaoui, Y. Toual, A. Hourmatallah and M. Moutaabbid, J. Supercond. Novel Magn., 2023, 36, 1171–1179 CrossRef CAS.
- H. Dong, C. Ran, W. Gao, M. Li, Y. Xia and W. Huang, eLight, 2023, 3, 3 CrossRef.
- S. Bouhmaidi, R. Pingak and L. Setti, Moroccan J. Chem., 2023, 11, 1254–1265 CAS.
- M. Wuttig, C.-F. Schön, M. Schumacher, J. Robertson, P. Golub, E. Bousquet, C. Gatti and J.-Y. Raty, Adv. Funct. Mater., 2022, 32, 2110166 CrossRef CAS.
- M. Born, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160–172 CrossRef CAS.
- R. R. Reddy, K. R. Gopal, K. Narasimhulu, L. S. S. Reddy, K. R. Kumar, G. Balakrishnaiah and M. R. Kumar, J. Alloys Compd., 2009, 473, 28–35 CrossRef CAS.
- K. Li, C. Kang and D. Xue, Mater. Res. Bull., 2012, 47, 2902–2905 CrossRef CAS.
- Z. Song, W. Fan, C. S. Tan, Q. Wang, D. Nam, D. H. Zhang and G. Sun, New J. Phys., 2019, 21, 073037 CrossRef CAS.
- H. M. Ghaithan, Z. A. Alahmed, S. H. M. Qaid and A. S. Aldwayyan, ACS Omega, 2021, 6, 30752–30761 CrossRef CAS PubMed.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- Y. F. Cherif, M. Rouaighia, A. Zaoui and A. Boukortt, Acta Phys. Pol., A, 2017, 131, 406–413 CrossRef.
- M. A. H. Shah, M. Nuruzzaman, A. Hossain, M. Jubair and M. A. K. Zilani, Comput. Condens. Matter, 2023, 34, e00774 CrossRef.
- B. Ghebouli, M. A. Ghebouli, A. Bouhemadou, M. Fatmi, R. Khenata, D. Rached, T. Ouahrani and S. Bin-Omran, Solid State Sci., 2012, 14, 903–991 CrossRef CAS.
- M. E. A. Monir and F. Z. Dahou, SN Appl. Sci., 2020, 2, 465 CrossRef.
- N. Erum and M. A. Iqbal, Acta Phys. Pol., A, 2020, 138, 509–517 CrossRef CAS.
- A. Bakar, A. O. Alrashdi, M. M. Fadhali, A. Afaq, H. A. Yakout and M. Asif, J. Mater. Res. Technol., 2022, 19, 4233–4241 CrossRef CAS.
- A. A. Mubarak and S. Al-Omari, J. Magn. Magn. Mater., 2015, 382, 211–218 CrossRef CAS.
- M. Szafranski and A. Katrusiak, J. Phys. Chem. Lett., 2016, 7, 3458–3466 CrossRef CAS PubMed.
- S. Sun, F. H. Isikgor, Z. Deng, F. Wei, G. Kieslich, P. D. Bristowe, J. Ouyang and A. K. Cheetham, ChemSusChem, 2017, 10, 3740–3745 CrossRef CAS PubMed.
- Z. Li, Y. Qin, L. Dong, K. Li, Y. Qiao and W. Li, Phys. Chem. Chem. Phys., 2020, 22, 12706–12712 RSC.
- A. Biswas, M. S. Alam, A. Sultana, T. Ahmed, M. Saiduzzaman and K. M. Hossain, Appl. Phys. A: Mater. Sci. Process., 2021, 127, 939 CrossRef CAS.
- M. Z. Rahaman and A. Hossain, RSC Adv., 2018, 8, 33010–33018 RSC.
- D. R. Penn, Phys. Rev., 1962, 128, 2093–2097 CrossRef CAS.
- H. M. Ghaithan, Z. A. Alahmed, S. M. H. Qaid, M. Hezam and A. S. Aldwayyan, ACS Omega, 2020, 5, 7468–7480 CrossRef CAS PubMed.
- Y. M. Odeh, S. M. Azar, A. Y. Al-Reyahi, A. A. Mousa, E. K. Jaradat and N. Al Aqtash, AIP Adv., 2023, 13, 075118 CrossRef CAS.
- T. Oku, M. Zushi, Y. Imanishi, A. Suzuki and K. Suzuki, Appl. Phys. Express, 2014, 7, 121601 CrossRef.
- S. Piskunov, A. Gopeyenko, E. Kotomin, Y. Zhukovskii and D. Ellis, Comput. Mater. Sci., 2007, 41, 195–201 CrossRef CAS.
- A. Z. Johannes, R. K. Pingak and M. Bukit, IOP Conf. Ser.: Mater. Sci. Eng., 2020, 823, 012030 CAS.
- Y. Selmani, H. Labrim, A. Jabar and L. Bahmad, Int. J. Mod. Phys. B, 2023, 2450334 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |