 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An energy decomposition and extrapolation scheme for evaluating electron transfer rate constants: a case study on electron self-exchange reactions of transition metal complexes†
Akihiro Mutsuji a,
Kenichiro Saita
a,
Kenichiro Saita b and
Satoshi Maeda
b and
Satoshi Maeda *bcde
*bcde
aGraduate School of Chemical Sciences and Engineering, Hokkaido University, Sapporo, Hokkaido 060-8628, Japan
bDepartment of Chemistry, Graduate School of Science, Hokkaido University, Sapporo, Hokkaido 060-0810, Japan. E-mail: smaeda@eis.hokudai.ac.jp
cInstitute for Chemical Reaction Design and Discovery (WPI-ICReDD), Hokkaido University, Sapporo, Hokkaido 001-0021, Japan
dERATO Maeda Artificial Intelligence for Chemical Reaction Design and Discovery Project, Hokkaido University, Sapporo, Hokkaido 060-0810, Japan
eResearch and Services Division of Materials Data and Integrated System (MaDIS), National Institute for Materials Science (NIMS), Tsukuba, Ibaraki 305-0044, Japan
First published on 1st November 2023
Abstract
A simple approach to the analysis of electron transfer (ET) reactions based on energy decomposition and extrapolation schemes is proposed. The present energy decomposition and extrapolation-based electron localization (EDEEL) method represents the diabatic energies for the initial and final states using the adiabatic energies of the donor and acceptor species and their complex. A scheme for the efficient estimation of ET rate constants is also proposed. EDEEL is semi-quantitative by directly evaluating the seam-of-crossing region of two diabatic potentials. In a numerical test, EDEEL successfully provided ET rate constants for electron self-exchange reactions of thirteen transition metal complexes with reasonable accuracy. In addition, its energy decomposition and extrapolation schemes provide all the energy values required for activation-strain model (ASM) analysis. The ASM analysis using EDEEL provided rational interpretations of the variation of the ET rate constants as a function of the transition metal complexes. These results suggest that EDEEL is useful for efficiently evaluating ET rate constants and obtaining a rational understanding of their magnitudes.
Introduction
Electron transfer (ET) plays a fundamental role in various chemical systems, including artificial photosynthesis, photocatalysis, electrocatalysis, and electronic devices.1–6 Theoretical tools are needed to elucidate and design novel reactivities and functions triggered by ET.7–10 The ET rate constant is given by eqn (1).9,11,12
 | (1) |
 | (2) |
| PLZ = 1 − exp(−2πγ) | (3) |
 | (4) |
 | (5) |
 | ||
| Fig. 1 Crossing of two diabatic potential energy surfaces and the relations among V12, λ, ΔG0, ΔG‡, and ΔG‡na in the rate constant expressions. | ||
The harmonic approximation is often used to describe the diabatic PESs of the initial and final states, which allows one to estimate the Gibbs energy of activation ΔG‡na (subscript “na” means “non-adiabatic”) by the following eqn (6) without explicitly locating the intersection between the two diabatic PESs on the multidimensional coordinate space. Note that the reaction barrier in eqn (1) is ΔG‡, not ΔG‡na (Fig. 1).
 | (6) |
Since the diabatization required to obtain the diabatic PESs and their coupling V12 is not unique, different approaches have been proposed depending on the purpose.14–23 For example, the generalized Mulliken–Hush (GMH) theory is for ET and generates diabatic states based on the assumption that the initial and final diabatic states are charge-localized states at different centers of the donor and acceptor.24,25 Constrained density functional theory (CDFT) is also useful for ET and forms diabatic states by imposing constraints on the partial charge (or spin) of arbitrary molecules or fragments using the Lagrange multiplier.26,27
To go beyond the framework based on the harmonic approximation, it is necessary to consider the anharmonic effect on the reaction coordinate. This requires explicit evaluations of PESs at around the non-adiabatic transition takes place. Molecular dynamics simulations can be performed to obtain accurate transition probabilities by calculating a large number of trajectories passing through such a region.9,28–31 A computationally less demanding alternative approach is to identify the seam-of-crossing (SX) or conical intersection (CI) geometry within the full-dimensional coordinate space.32–38 Simulations of non-adiabatic events based on SX or CI geometries have become increasingly common in recent years.39–45 In this approach, ΔG‡na is estimated as the energy gap between the SX/CI geometry and the initial state equilibrium (EQ) geometry.
This study presents a semi-quantitative yet efficient algorithm for predicting the ET rate constant based eqn (1)–(4) rather than eqn (5) because our scheme tends to give relatively large coupling values as discussed in Results and discussion. The present method directly identifies the SX geometry. A simple diabatization based on energy decomposition and extrapolation schemes46–48 allows one to optimize an SX geometry and evaluate ΔG‡, ΔG‡na, V12, and λ. Rate constants for thirteen electron self-exchange reactions were calculated and compared with experimental49–59 and calculated60–66 values reported in the literature to investigate the performance of the present method. The calculated rate constants showed a good correlation with the experimental values. The energy decomposition scheme provided interpretations of the factors determining the magnitudes of the ET rate constants based on the activation strain model (ASM).67–69
Method
In this study, a simple diabatization scheme called energy decomposition and extrapolation-based electron localization (EDEEL) is proposed. In EDEEL, the diabatic energies for the initial and final states V11 and V22 are given by eqn (7) and (8), respectively.| V11(R) = ECn+m(R) − EDn(RD) + EDn+1(RD) | (7) |
| V22(R) = ECn+m(R) − EAm(RA) + EAm+1(RA) | (8) |
ΔG‡na = (GSX − Ginitial−EQ) is the Gibbs energy gap between the SX and the initial state EQ geometries. Gibbs energy corrections at the EQ and SX are calculated by the normal mode analysis. The coupling V12 is computed as the energy difference V12 = V11−ECn+m+1, where ECn+m+1 is the lower adiabatic energy between those for the two states that contain the contributions of the two diabatic states the most. Thus, at the SX between V11 and V22, i.e., when V11 = V22, the EDEEL scheme reproduces the diabatic–adiabatic relation of the two-state model in eqn (9).
 | (9) |
In the electron self-exchange reactions, ECn+m+1 is the adiabatic energy of the donor–acceptor complex in its electronic ground state. The parameter λ is obtained as eqn (10) based on eqn (6).
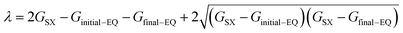 | (10) |
The distance dependence of the ET reaction rate may have a distinct peak.60 This study regards adiabatic ground state at the SX geometry between V11 and V22 as the approximate transition state and maximizes the ET rate constant kET within the SX region to obtain the final kET (=kcalc). This is done by taking the donor–acceptor distance rDA (the metal–metal distance in the transition metal examples below) as the reaction coordinate, evaluating the kET at various rDA, and maximizing the kET along rDA. Details of how the initial rDA(ini) is systematically determined and how the kET is maximized are described in the ESI.†
As shown in Fig. 2, the entire kcalc evaluation workflow consists of the following four steps.
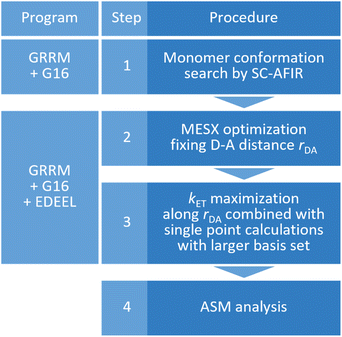 | ||
| Fig. 2 The entire workflow for obtaining an electron transfer rate constant by EDEEL and the calculation programs used in each procedure. | ||
(1) Systematic search for monomer conformations using the SC-AFIR71,72 method implemented in the Global Reaction Route Mapping (GRRM) program.73
(2) Optimization of a minimum energy SX (MESX) geometry74,75 within the SX hypersurface between V11 and V22 while maintaining the donor–acceptor distance to rDA(ini).
(3) kET maximization along rDA by calculating kET for five rDA values near rDA(ini), where line search is done by simple quadratic curve fitting using three kET values in this study. In the calculation of kET with eqn (1)–(4), the Gibbs energies are extrapolated by the electronic energies obtained from single point calculations with larger basis set.
(4) ASM analysis at the geometry of the largest kET (=kcalc) obtained in step 3 (optional).
Results and discussion
The workflow in Fig. 2 was applied to the electron self-exchange reactions of thirteen transition metal complexes listed in Table 1. Electronic structure calculations were performed with the Gaussian 16 program76 and geometry optimization was performed with the GRRM program at the UωB97X-D/Def2-SV(P)77,78 level taking into account the solvent effect of water by the conductor-like polarizable continuum model (C-PCM).,79,80 where UωB97X-D stands for a spin unrestricted DFT calculation using the ωB97X-D functional. kET was maximized using the electronic energy calculated at the UωB97X-D/Def2-TZVP81 level and the Gibbs energy correction at the UωB97X-D/Def2-SV(P) level; the calculation level is represented as UωB97X-D/Def2-TZVP//Def2-SV(P). In the calculation of kET, νn in eqn (1) was approximated as kBT/h, the coefficient of transition state theory rate constant equation. The spin multiplicity was chosen to stabilize each state as much as possible and was set to the values listed in Table 1. The reaction set in Table 1 covers reactions of different timescales with rate constants in the wide range of 10−7 to 109 dm3 mol−1 s−1, and thus would be suitable as a test set. It was assumed that both +3 and +2 charged complexes were in the electronic ground state at SX, although there were possibilities for ET via metal-to-ligand-charge transfer (MLCT) or electronic excited states of each complex.82 Further computational details are presented in Computational section.| Redox couple | Spin multiplicity (3+/2+) | Experimental values | References | |
|---|---|---|---|---|
| kexpt/dm3 mol−1 s−1 | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexpt kexpt |
|||
| a Values for monomer and SX are shown outside and inside the parentheses, respectively. | ||||
| [V(H2O)6]3+/2+ | 3/4 | 3 × 10−3, 1 × 10−2 | −2.0 | 49 and 50 |
| [Cr(H2O)6]3+/2+ | 4/5 | <2 × 10−5 | −4.7 | 51 |
| [Fe(H2O)6]3+/2+ | 6/5 | 1.1 | 0.0 | 51 |
| [Co(H2O)6]3+/2+ | 5/4 | 5 | 0.7 | 49 and 52 |
| [Ru(H2O)6]3+/2+ | 2/1 | (6 ± 4) × 101 | 1.8 | 53 |
| [Co(NH3)6]3+/2+ | 1/4 | >10−7 | −7.0 | 51 |
| [Ru(NH3)6]3+/2+ | 2/1 | 4.3 × 103 | 3.6 | 49 and 54 |
| [Ru(NH3)5py]3+/2+ | 2/1 | 4.7 × 105 | 5.7 | 55 |
| [Co(en)3]3+/2+ | 1/4 | 7.7 × 10−5 | −4.1 | 56 |
| [Ru(en)3]3+/2+ | 2/1 | 2.8 × 104 | 4.4 | 51 |
| [Fe(bpy)3]3+/2+ | 2/1 | 3 × 108 | 8.5 | 57 and 58 |
| [Co(bpy)3]3+/2+ | 1/4 (1/2)a | 18 | 1.3 | 51 |
| [Ru(bpy)3]3+/2+ | 2/1 | 1.2 × 109 | 9.1 | 59 |
Table 2 lists the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcalc, ΔG‡, λ, V12, κel, and rDA values obtained by the present calculations at the UωB97X-D/Def2-TZVP//Def2-SV(P) level. Fig. 3 shows the correlation between the calculated log10
kcalc, ΔG‡, λ, V12, κel, and rDA values obtained by the present calculations at the UωB97X-D/Def2-TZVP//Def2-SV(P) level. Fig. 3 shows the correlation between the calculated log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcalc and the experimental log10
kcalc and the experimental log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexpt,49–59 and that the present calculation reproduces the experimental trend well. Fig. 3 also compares the log10
kexpt,49–59 and that the present calculation reproduces the experimental trend well. Fig. 3 also compares the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcalc values with those obtained by the other theoretical methods.60–66 Despite the simplicity of the algorithm, which does not include a complex diabatization scheme or any empirical factors, the present method provides an accuracy comparable to the other theoretical methods, making EDEEL promising for the semi-quantitative estimation of ET rate constants.
kcalc values with those obtained by the other theoretical methods.60–66 Despite the simplicity of the algorithm, which does not include a complex diabatization scheme or any empirical factors, the present method provides an accuracy comparable to the other theoretical methods, making EDEEL promising for the semi-quantitative estimation of ET rate constants.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcalc, Gibbs energies of activation ΔG‡, reorganization energy λ, diabatic coupling V12, electronic transmission coefficient κel, and donor–acceptor distance rDA by EDEEL at the UωB97X-D/Def2-TZVP//Def2-SV(P) level
kcalc, Gibbs energies of activation ΔG‡, reorganization energy λ, diabatic coupling V12, electronic transmission coefficient κel, and donor–acceptor distance rDA by EDEEL at the UωB97X-D/Def2-TZVP//Def2-SV(P) level
| Redox couple | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcalc kcalc |
ΔG‡/eV | λ/eV | V12/eV | κel | rDA/Å |
|---|---|---|---|---|---|---|
| [V(H2O)6]3+/2+ | 1.1 | 0.77 | 4.02 | 0.23 | 1.00 | 5.76 |
| [Cr(H2O)6]3+/2+ | −4.3 | 1.09 | 5.45 | 0.27 | 1.00 | 5.74 |
| [Fe(H2O)6]3+/2+ | 0.2 | 0.83 | 4.29 | 0.24 | 1.00 | 5.72 |
| [Co(H2O)6]3+/2+ | 1.0 | 0.78 | 4.10 | 0.24 | 1.00 | 5.53 |
| [Ru(H2O)6]3+/2+ | 1.1 | 0.77 | 4.01 | 0.23 | 1.00 | 5.78 |
| [Co(NH3)6]3+/2+ | −6.9 | 1.25 | 5.26 | 0.07 | 0.96 | 7.68 |
| [Ru(NH3)6]3+/2+ | 6.9 | 0.43 | 2.01 | 0.07 | 0.99 | 7.39 |
| [Ru(NH3)5py]3+/2+ | 8.6 | 0.33 | 1.65 | 0.08 | 1.00 | 9.51 |
| [Co(en)3]3+/2+ | −5.5 | 1.16 | 4.86 | 0.05 | 0.91 | 7.96 |
| [Ru(en)3]3+/2+ | 7.1 | 0.42 | 1.90 | 0.06 | 0.98 | 8.02 |
| [Fe(bpy)3]3+/2+ | 11.9 | 0.08 | 0.87 | 0.13 | 1.00 | 9.08 |
| [Co(bpy)3]3+/2+ | 2.2 | 0.71 | 3.24 | 0.10 | 1.00 | 8.75 |
| [Ru(bpy)3]3+/2+ | 11.8 | 0.14 | 0.97 | 0.10 | 1.00 | 8.91 |
 | ||
Fig. 3 A correlation between experimental log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexpt and calculated log10 kexpt and calculated log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcalc by EDEEL at the UωB97X-D/Def2-TZVP//Def2-SV(P) level (filled squares) or by the other method60–66 (red crosses). The red dotted line represents the diffusion-controlled rate constant.49 kcalc by EDEEL at the UωB97X-D/Def2-TZVP//Def2-SV(P) level (filled squares) or by the other method60–66 (red crosses). The red dotted line represents the diffusion-controlled rate constant.49 | ||
In Table 2, the coupling values are relatively large, making κel almost unity. This is because our diabatization constraint assumes that there is no interaction between the electron to be transferred and the acceptor molecule. In other words, our constraint pushes the strong attraction between the negative charge on the moving electron and the +3 positive charge on the acceptor molecule into the coupling value, making the coupling values large. As for the non-adiabaticity, electron transfer reactions in [M(H2O)6]3+/2+, which showed the largest coupling values among the systems in our calculation, are known as non-adiabatic process with smaller actual coupling values (<100 cm−1).83 The log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcalc does not include the diffusion-controlled rate constant, which is estimated to be kdiff = 3 × 109 dm3 mol−1 s−1 for these reactions.49 In other words, kdiff would be a source of the large error seen for fast reactions such as [Fe(bpy)3]3+/2+ and [Ru(bpy)3]3+/2+. In our scheme, the C-PCM environments of the initial and final states are relaxed independently, which does not satisfy the Franck–Condon principle. This would have led to the underestimation of reaction barriers. For example, the outer-sphere reorganization energy of [Ru(H2O)6]3+/2+ was estimated to be 0.68 eV based on dielectric continuum theory.13 This implies additional reaction barrier of 0.17 eV, reducing its log10
kcalc does not include the diffusion-controlled rate constant, which is estimated to be kdiff = 3 × 109 dm3 mol−1 s−1 for these reactions.49 In other words, kdiff would be a source of the large error seen for fast reactions such as [Fe(bpy)3]3+/2+ and [Ru(bpy)3]3+/2+. In our scheme, the C-PCM environments of the initial and final states are relaxed independently, which does not satisfy the Franck–Condon principle. This would have led to the underestimation of reaction barriers. For example, the outer-sphere reorganization energy of [Ru(H2O)6]3+/2+ was estimated to be 0.68 eV based on dielectric continuum theory.13 This implies additional reaction barrier of 0.17 eV, reducing its log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kET from 1.1 to −1.7, which is three-order of magnitude smaller than the experimental value. The simple addition of the outers-sphere reorganization energy correction is not sufficient in our scheme. The better treatment of outer-sphere reorganization in our scheme needs further study in the future. Many other factors such as explicit solvation, dynamic and quantum motion of the atoms, and higher order (or static) electron correlation would contribute to the error. However, further improvement of the accuracy considering these factors is beyond the scope of this study.
kET from 1.1 to −1.7, which is three-order of magnitude smaller than the experimental value. The simple addition of the outers-sphere reorganization energy correction is not sufficient in our scheme. The better treatment of outer-sphere reorganization in our scheme needs further study in the future. Many other factors such as explicit solvation, dynamic and quantum motion of the atoms, and higher order (or static) electron correlation would contribute to the error. However, further improvement of the accuracy considering these factors is beyond the scope of this study.
Thanks to the energy decomposition and extrapolation scheme of EDEEL, the ASM analysis67–69 can be performed using the energy components, i.e., ECn+m, EDn, EDn+1, EAm, and EAm+1, calculated during the EDEEL calculations, without any additional calculations. Note that the ASM analysis was performed using electronic energies rather than Gibbs energies for the SX geometry with the highest kET value. In the ASM/EDEEL analysis, the strain energies in donor ΔE‡Strain(D) and acceptor ΔE‡Strain(A) and their interaction energy ΔE‡Interaction(C) are represented as follows.
| ΔE‡Strain(D) = ED(SX)n+1 − ED(initial−EQ)n+1 | (11) |
| ΔE‡Strain(A) = EA(SX)m − EA(initial−EQ)m | (12) |
| ΔE‡Interaction(C) = EC(SX)n+m − ED(SX)n − EA(SX)m | (13) |
Conclusion
In this article, we have proposed a simple diabatization scheme called EDEEL for the analysis of ET reactions. EDEEL represents the diabatic energies, V11 and V22, by combining the adiabatic energies of the donor, acceptor, and their complex. Such a simple representation allows us to easily optimize the SX geometries between the two diabatic potentials. A scheme for estimating the ET rate constants at the SX geometries has also been introduced. The diabatic coupling V12 is also estimated using the adiabatic energy of the donor–acceptor complex. In other words, the present scheme allows one to obtain all the parameters necessary to estimate ET rate constants using only the adiabatic energies. Numerical tests with electron self-exchange reactions of thirteen transition metal complexes have shown that EDEEL reproduces the trend of the experimental rate constants well and is semi-quantitative.Two advantages of using EDEEL can be suggested. One is that EDEEL can be combined with any ab initio method and program without touching their codes. This is because all diabatic potential elements, i.e., V11, V22 and V12, are represented by the adiabatic energies. The other is that EDEEL provides all the energy components and SX geometries needed in the ASM analysis. The latter is helpful in interpreting the ET efficiency and further designing a system with higher ET efficiency. In the present applications, the EDEEL-based ASM analysis successfully provided rational explanations for the variation of the magnitudes of the ET rate constants depending on the transition metal complexes.
Computational section
The above procedures were implemented in an in-house Python script as an interface program between the GRRM program and the Gaussian 16 program.73,76 The script takes a geometry from GRRM, performs the necessary electronic structure calculations to obtain the EDEEL PES at the geometry using Gaussian 16, and returns the energy and gradient (and Hessian if necessary) of the EDEEL PES at the geometry to GRRM. Geometry optimizations were performed by a developer version of the GRRM program at the UωB97X-D/Def2-SV(P) level. The “Stable = Opt” option was also used to identify the electronic ground state configuration of a given spin multiplicity. The “Int(Grid = 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590)” option was used in DFT calculations. Although some of the aqua-complexes are highly acidic and may not prevail as simple [M(H2O)6]3+/2+ complexes in actual aqueous solution, the metal centers were assumed to be hexa-coordinated in this study as previous reports.60,62,63,65 Solvent water was modeled by the conductor-like polarizable continuum model (C-PCM).79,80 Gibbs energy corrections were obtained from the standard normal mode analysis of 3N−8 dimensions (one direction orthogonal to SX and one direction along the vector between two metal atoms were removed from the full 3N−6 dimensions) at T = 298.15 K and p0 = 1 atm, with normal mode frequencies smaller than 100 cm−1 replaced by 100 cm−1 as suggested in the literature.84 The bases of Gibbs activation energies were calculated as the sum of the extrapolated Gibbs energies of the most stable donor and acceptor monomers, where the most stable structures were identified by a systematic conformation search using SC-AFIR with possible spin multiplicities. An entropy correction −4.3 kcal mol−1 was added to the Gibbs energy of the dimer complex in the activation energy calculation to account for the restriction of their mobility in the water solvent, following the previous studies.85–87 The rate constant maximization was done at the UωB97X-D/Def2-TZVP//Def2-SV(P) level.
590)” option was used in DFT calculations. Although some of the aqua-complexes are highly acidic and may not prevail as simple [M(H2O)6]3+/2+ complexes in actual aqueous solution, the metal centers were assumed to be hexa-coordinated in this study as previous reports.60,62,63,65 Solvent water was modeled by the conductor-like polarizable continuum model (C-PCM).79,80 Gibbs energy corrections were obtained from the standard normal mode analysis of 3N−8 dimensions (one direction orthogonal to SX and one direction along the vector between two metal atoms were removed from the full 3N−6 dimensions) at T = 298.15 K and p0 = 1 atm, with normal mode frequencies smaller than 100 cm−1 replaced by 100 cm−1 as suggested in the literature.84 The bases of Gibbs activation energies were calculated as the sum of the extrapolated Gibbs energies of the most stable donor and acceptor monomers, where the most stable structures were identified by a systematic conformation search using SC-AFIR with possible spin multiplicities. An entropy correction −4.3 kcal mol−1 was added to the Gibbs energy of the dimer complex in the activation energy calculation to account for the restriction of their mobility in the water solvent, following the previous studies.85–87 The rate constant maximization was done at the UωB97X-D/Def2-TZVP//Def2-SV(P) level.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Most part of the computation was performed using Research Center for Computational Science (RCCS), Okazaki, Japan. This work was in part supported by the JST via ERATO grant JPMJER1903. The support was also provided by the Institute for Chemical Reaction Design and Discovery (ICReDD), which was established by the World Premier International Research Center Initiative (WPI), MEXT, Japan. AM is supported by Hokkaido University Ambitious Doctoral Fellowship (Information AI) from Hokkaido University. KS is supported by the Photo-Excitonix Project in Hokkaido University and by the JST via CREST grant JPMJCR1902.References
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2009, 42, 1890 CrossRef CAS PubMed.
- M. H. Shaw, J. Twilton and D. W. C. MacMillan, J. Org. Chem., 2016, 81, 6898 CrossRef CAS PubMed.
- N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075 CrossRef CAS PubMed.
- N. T. Suen, S. F. Hung, Q. Quan, N. Zhang, Y. J. Xu and H. M. Chen, Chem. Soc. Rev., 2017, 46, 337 RSC.
- K. Tvrdy, P. A. Frantsuzov and P. V. Kamat, Proc. Natl. Acad. Sci. U. S. A., 2010, 108, 29 CrossRef PubMed.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595 CrossRef CAS PubMed.
- N. Sutin, Prog. Inorg. Chem., 1983, 30, 441 CrossRef CAS.
- R. Borrelli and A. Peluso, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 542 CAS.
- J. Blumberger, Chem. Rev., 2015, 115, 11191 CrossRef CAS PubMed.
- S. Fletcher, J. Solid State Electrochem., 2010, 14, 705 CrossRef CAS.
- M. D. Newton and N. Sutin, Annu. Rev. Phys. Chem., 1984, 35, 437 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CrossRef CAS.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1982, 77, 6090 CrossRef CAS.
- C. E. Hoyer, X. Xu, D. Ma, L. Gagliardi and D. G. Truhlar, J. Chem. Phys., 2014, 141, 114104 CrossRef PubMed.
- C. E. Hoyer, K. Parker, L. Gagliardi and D. G. Truhlar, J. Chem. Phys., 2016, 144, 194101 CrossRef PubMed.
- H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2001, 115, 10353 CrossRef CAS.
- H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2002, 117, 5576 CrossRef CAS.
- T. Lenzen and U. Manthe, J. Chem. Phys., 2017, 147, 084105 CrossRef PubMed.
- D. M. G. Williams, A. Viel and W. Eisfeld, J. Chem. Phys., 2019, 151, 164118 CrossRef PubMed.
- D. M. G. Williams and W. Eisfeld, J. Chem. Phys., 2018, 149, 204106 CrossRef PubMed.
- Y. Shu and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 6456 CrossRef CAS PubMed.
- Y. Shu, Z. Varga, A. G. S. de O. Filho and D. G. Truhlar, J. Chem. Theory Comput., 2021, 17, 1106 CrossRef CAS PubMed.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15 CrossRef CAS.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213 CrossRef CAS.
- B. Kaduk, T. Kowalczyk and T. V. Voorhis, Chem. Rev., 2012, 112, 321 CrossRef CAS PubMed.
- F. Ding, H. Wang, Q. Wu, T. V. Voorhis, S. Chen and J. P. Konopelski, J. Phys. Chem. A, 2010, 114, 6039 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- A. V. Akimov, A. J. Neukirch and O. V. Prezhdo, Chem. Rev., 2013, 113, 4496 CrossRef CAS PubMed.
- Z. Futera, K. Sodeyama, J. V. Burda, Y. Einaga and Y. Tateyama, Phys. Chem. Chem. Phys., 2014, 16, 19530 RSC.
- H. Nakano and H. Sato, J. Chem. Phys., 2017, 146, 154101 CrossRef PubMed.
- N. Koga and K. Morokuma, Chem. Phys. Lett., 1985, 119, 371 CrossRef CAS.
- M. R. Manaa and D. R. Yarkony, J. Chem. Phys., 1993, 99, 5251 CrossRef CAS.
- F. Bernardi, M. Olivucci and M. A. Robb, Chem. Soc. Rev., 1996, 25, 321 RSC.
- R. Poli and J. N. Harvey, Chem. Soc. Rev., 2003, 32, 1 RSC.
- B. G. Levine and T. J. Martínez, Annu. Rev. Phys. Chem., 2007, 58, 613 CrossRef CAS PubMed.
- D. R. Yarkony, Chem. Rev., 2012, 112, 481 CrossRef CAS PubMed.
- J. N. Harvey, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 1 CAS.
- S. Maeda, T. Taketsugu, K. Ohno and K. Morokuma, J. Am. Chem. Soc., 2015, 137, 3433 CrossRef CAS PubMed.
- Y. Harabuchi, T. Taketsugu and S. Maeda, Phys. Chem. Chem. Phys., 2015, 17, 22561 RSC.
- M. Hatanaka, Y. Hirai, Y. Kitagawa, T. Nakanishi, Y. Hasegawa and K. Morokuma, Chem. Sci., 2017, 8, 423 RSC.
- N. Aizawa, Y. Harabuchi, S. Maeda and Y. J. Pu, Nat. Commun., 2020, 11, 3909 CrossRef CAS PubMed.
- S. Suzuki, S. Sasaki, A. S. Sairi, R. Iwai, B. Z. Tang and G. Konishi, Angew. Chem., Int. Ed., 2020, 59, 9856 CrossRef CAS PubMed.
- E. Pieri, D. Lahana, A. M. Chang, C. R. Aldaz, K. C. Thompson and T. J. Martínez, Chem. Sci., 2021, 12, 7294 RSC.
- Y. Harabuchi, H. Hayashi, H. Takano, T. Mita and S. Maeda, Angew. Chem., Int. Ed., 2023, 62, e202211936 CrossRef CAS PubMed.
- F. Maseras and K. Morokuma, J. Comput. Chem., 1995, 16, 1170 CrossRef CAS.
- L. W. Chung, H. Hirao, X. Li and K. Morokuma, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 327 CAS.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H. B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678 CrossRef CAS PubMed.
- M. Chou, C. Creutz and N. Sutin, J. Am. Chem. Soc., 1977, 99, 5615 CrossRef CAS.
- K. V. Krishnamurty and A. C. Waiil, J. Am. Chem. Soc., 1958, 80, 5921 CrossRef CAS.
- B. S. Brunschwig, C. Creutz, D. H. Macartney, T. K. Sham and N. Sutin, Faraday Discuss. Chem. Soc., 1982, 74, 113 RSC.
- N. A. Bonner and J. P. Hunt, J. Am. Chem. Soc., 1960, 82, 3826 CrossRef CAS.
- W. Bottcher, G. M. Brown and N. Sutin, Inorg. Chem., 1979, 18, 1447 CrossRef CAS.
- T. J. Meyer and H. Taube, Inorg. Chem., 1968, 7, 2369 CrossRef CAS.
- G. M. Brown, H. J. Krentzien, M. Abe and H. Taube, Inorg. Chem., 1979, 18, 3374 CrossRef CAS.
- F. P. Dwyer and A. M. Sargeson, J. Phys. Chem., 1961, 65, 1892 CrossRef CAS.
- I. Ruff and M. Zimonyi, Electrochim. Acta, 1973, 18, 515 CrossRef CAS.
- D. H. Macartney and N. Sutin, Inorg. Chem., 1983, 22, 3530 CrossRef CAS.
- R. C. Young, F. R. Keene and T. J. Meyer, J. Am. Chem. Soc., 1977, 99, 2468 CrossRef CAS.
- H. Oberhofer and J. Blumberger, Angew. Chem., Int. Ed., 2010, 49, 3631 CrossRef CAS PubMed.
- M. D. Newton, J. Phys. Chem., 1991, 95, 30 CrossRef CAS.
- D. Zhang, B. Zhuang, D. Feng and C. Liu, Int. J. Quantum Chem., 2000, 78, 32 CrossRef CAS.
- K. M. Rosso and J. R. Rustad, J. Phys. Chem. A, 2000, 104, 6718 CrossRef CAS.
- R. G. Endres, M. X. LaBute and D. L. Cox, J. Chem. Phys., 2003, 118, 8706 CrossRef CAS.
- X. Zeng, X. Hu and W. Yang, J. Chem. Theory Comput., 2012, 8, 4960 CrossRef CAS PubMed.
- R. L. Kenion and N. Ananth, Phys. Chem. Chem. Phys., 2016, 18, 26117 RSC.
- F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114 CrossRef CAS.
- L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324 CAS.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 CrossRef CAS PubMed.
- F. P. Rotzinger, Inorg. Chem., 2015, 54, 10450 CrossRef CAS PubMed.
- S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki, T. Ichino, Y. Sumiya, K. Sugiyama and Y. Ono, J. Comput. Chem., 2018, 39, 233 CrossRef CAS PubMed.
- S. Maeda, Y. Harabuchi, M. Takagi, T. Taketsugu and K. Morokuma, Chem. Rec., 2016, 16, 2232 CrossRef CAS PubMed.
- S. Maeda, K. Ohno and K. Morokuma, Phys. Chem. Chem. Phys., 2013, 15, 3683 RSC.
- M. J. Bearpark, M. A. Robb and H. B. Schlegel, Chem. Phys. Lett., 1994, 223, 269 CrossRef CAS.
- S. Maeda, K. Ohno and K. Morokuma, J. Chem. Theory Comput., 2010, 6, 1538 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.02, Gaussian, Inc., Wallingford CT, 2019 Search PubMed.
- J. D. Chai and M. H. Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- C. Daniel, Phys. Chem. Chem. Phys., 2021, 23, 43 RSC.
- Y. Bu, Y. Wang, F. Xu and C. Deng, J. Mol. Struct., 1998, 453, 43 CrossRef CAS.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556 CrossRef CAS PubMed.
- R. L. Martin, P. J. Hay and L. R. Pratt, J. Phys. Chem. A, 1998, 102, 3565 CrossRef CAS.
- Y. Liu, Y. Tang, Y. Y. Jiang, X. Zhang, P. Li and S. Bi, ACS Catal., 2017, 7, 1886 CrossRef CAS.
- Z. Xu, Y. Yang, J. Jiang and Y. Fu, Organometallics, 2018, 37, 1114 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Initial SX geometry preparation (S1), rate constant maximization (S2), monomer EQ geometries and energies (S3), and dimer SX geometries and energies (S4–S6). See DOI: https://doi.org/10.1039/d3ra05784d |
| This journal is © The Royal Society of Chemistry 2023 |


