Strategic sampling with stochastic surface walking for machine learning force fields in iron's bcc–hcp phase transitions

Abstract

This study developed a machine learning-based force field for simulating the bcc–hcp phase transitions of iron. By employing traditional molecular dynamics sampling methods and stochastic surface walking sampling methods, combined with Bayesian inference, we construct an efficient machine learning potential for iron. By using SOAP descriptors to map structural data, we find that the machine learning force field exhibits good coverage in the phase transition space. Accuracy evaluation shows that the machine learning force field has small errors compared to DFT calculations in terms of energy, force, and stress evaluations, indicating excellent reproducibility. Additionally, the machine learning force field accurately predicts the stable crystal structure parameters, elastic constants, and bulk modulus of bcc and hcp phases of iron, and demonstrates good performance in predicting higher-order derivatives and phase transition processes, as evidenced by comparisons with DFT calculations and existing experimental data. Therefore, our study provides an effective tool for investigating the phase transitions of iron using machine learning methods, offering new insights and approaches for materials science and solid-state physics research.

---

1 Introduction

Iron is a critical material in both industrial and military applications, and its phase transition has been an evergreen topic in the fields of materials science, condensed matter physics and geoscience.^1–4 Understanding this phase transition and its dynamic evolution is essential for improving material properties and manufacturing processes, as well as deepening our knowledge of the Earth's mantle. Bancroft et al.⁵ discovered in 1956 that when iron is subjected to shock loading, it undergoes a phase transition from bcc to hcp at a pressure of 13 GPa. Since then, scientists have conducted theoretical and experimental research to better understand the microscopic mechanism involved.^6–12

Based on the extended X-ray absorption fine structure (EXAFS) technique, Wang and Ingalls¹³ initially proposed three possible microscopic mechanisms for the phase transition from bcc to hcp. The first two mechanisms involve different paths of bcc-to-hcp transition, while the third mechanism involves a path from bcc to an intermediate fcc phase and then to hcp phase. From an energetic standpoint, the third mechanism presents a more advantageous route for the phase transition. However, research evidence confirming its existence remains scarce. Kadau et al.¹⁴ employed classical molecular dynamics to simulate the phase transition in single-crystal iron under shock compression. They found that the bcc–hcp transition occurs when two adjacent crystal planes slip relative to each other along the [110] crystal direction, consistent with the Burgers relationship. Kalantar et al.¹⁵ directly observed the bcc–hcp phase transition in impaction iron via nanosecond X-ray diffraction (XRD). Moreover, based on first-principles calculations, Lu et al.¹⁶ argued that the transferable fcc state during the transition process is energetically unfavorable. Due to the small size of the unit cell typically employed in first-principles calculations, phase transitions involving larger atomic scales cannot be simulated. Moreover, temperature plays a crucial role in the dynamic phase transition process, and a thermodynamic energy-based description alone is inadequate to provide a comprehensive and accurate depiction of the kinetics of the phase transition. In simulations of phase transitions in iron, atomic-scale information requires molecular dynamics simulations that take into account temperature.^17–24 The accuracy of molecular dynamics simulations heavily relies on the choice of interatomic potential. Quantum-mechanical potentials are computationally expensive for large-scale systems,^25–27 while commonly used empirical potentials may have deviations in describing the high-energy transition region of phase transitions. Therefore, an efficient and high-precision empirical potential will benefit a deeper understanding of the phase transition process in simulations.

In recent years, various new interatomic potentials^28–32 have been applied to simulate the atomic phase transition of iron under different loading conditions and initial microstructures at high pressure. Among them, machine learning force fields (MLFFs), as a typical representative of the new paradigm of “AI for science”, are increasingly being used by researchers in molecular dynamics simulations.^33–38 In MLFF models, the potential energy is described as a function of descriptors representing the atomic structure of the material, and the parameters of the function are optimized to reproduce first-principles (FP) quantities, including the total energy, forces, and stress tensor components, to accurately and efficiently predict interatomic potentials.

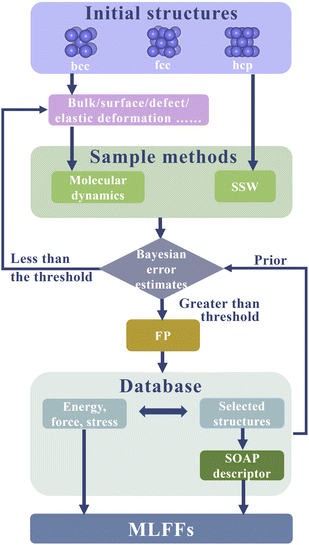
In addition to the robustness of the model itself, the dataset required for fitting the model is crucial. To simulate the phase transition process, the dataset needs to cover the relevant configurations during the phase transition, enabling the model to predict the entire process through interpolation. In this study, we propose a systematic ML approach to construct an Fe interatomic potential, including the sampling process of the dataset, feature analysis of descriptors, and fitting process of the potential function. We demonstrate that this Fe MLFF can achieve close-to-DFT accuracy over a wide range of properties, including energy, forces and stress tensor, elastic properties. Importantly, it can also simulate the phase transition process of iron effectively.

2 Methods

2.1 SOAP descriptor and Bayesian formalism

Machine learning force fields require the establishment of a mapping relationship between atomic arrangements and potential energy surfaces (PES). The atomic arrangements in different materials are complex and varied, but there are often rotational, translational, and permutational symmetries in the materials. To simplify the force field model, it is common practice to transform the atomic arrangements into structural descriptors, and then use machine learning algorithms to fit the mapping relationship between the descriptors and PES. Due to the strong shielding effect within metals, it is a reasonable approximation to neglect long-range interactions when simplifying simulations. Therefore, we adopt atomic local environments as structural descriptors to encode the different configurations of iron. Existing local descriptors include radial distribution functions (RDFs),^39,40 bond-orientational order parameters (BOOPs),^41,42 localized Wannier functions (LWFs),⁴³ and smooth overlap of atomic positions (SOAP).⁴⁴ The recently developed Atomic Cluster Extension (ACE) method⁴⁵ also provides an efficient and complete representation of local atomic environment, most previous descriptors can be regarded as special cases or minor variations of the ACE formalism. Among them, our work specifically focuses on the SOAP descriptor. SOAP uses Gaussian functions to define atomic neighborhood densities and employs spherical harmonics expansion to represent the chemical environment in the atomic neighborhood. This representation method has continuity and differentiability and is invariant to global rotation, reflection, and atomic permutation. Furthermore, SOAP can adjust its parameters to control the smoothness and sensitivity of similarity measurement, making it suitable for various chemical environments in the phase transition of iron.

Once the atomic configurations have been converted into structural descriptors, a labeled dataset is necessary to train the model. In the case of machine learning force fields, the dataset is labeled with the total energies of the configurations and the forces on each atom. At the time of our research, publicly available datasets specifically focused on the structures formed by the Fe element were not identified. However, subsequent to our research work, we came across a recent paper⁴⁶ that provides a dataset on iron clusters. Regrettably, there remains a lack of available data on the bulk structure, which is directly relevant to our work. To efficiently construct the required dataset, we used a Bayesian learning algorithm with diverse sampling methods for real-time data collection and model fitting. After data collection is complete, a post-processing step involves using singular value decomposition to solve the system of linear equations in the ridge regression method to improve the model's accuracy.

2.2 Training data sampling

The accuracy of machine learning predictions for interpolating data is significantly higher than for extrapolating data, thus constructing a dataset for a machine learning force field requires good coverage of the studied problem. In order to efficiently construct the database, we used Bayesian error to estimate the true prediction error of new configurations in all sampling methods (Fig. 1), which was used to determine whether the existing dataset can accurately predict the properties of new configurations. Sampling only occurs when the Bayesian error estimate of one force exceeds the threshold. The initial threshold was set to 0.002 eV Å⁻¹, and then dynamically adjusted based on the average Bayesian errors, typically ranging from 0.02 eV Å⁻¹ to 0.06 eV Å⁻¹. Simultaneously, first-principles calculations were performed to label the total energy and forces on each atom of this new sampled configuration.

Fig. 1 Schematic diagram for constructing the machine learning force fields (MLFFs) combining Bayesian inference and different sampling methods. Sampling is to perform molecular dynamics and SSW simulations on the initial structures, and perform errors based on Bayesian inference for each configuration of the simulation outputs to decide whether to sample.

In this paper, we used two sampling methods to construct a database suitable for phase transition studies. The construction of our training set is a fundamental component of our methodology, and we will provide an extended and more detailed description as follows.

Molecular dynamics (MD) sampling. To collect a sufficiently diverse set of configurations, our initial structures were prepared by randomly perturbing and scaling the 2 × 2 × 2 supercell of relaxed standard crystal structures, including bcc, fcc, and hcp structures. To create a diverse set of structures, we took the following steps in the dataset preparation. We considered three different scales for lattice constants: 101%, 100%, and 95% of the original lattice constant. For each scale, we introduced structural deformations of 0.03 in cell volume and 0.01 in atomic positions, and generated a total of 50 perturbed structures at these three scales. These perturbed structures, along with the original structures, were used to enhance the diversity of the dataset and to ensure that the sampled structures covered a wide range of configurations. Additionally, slabs with (100), (110), (111) and vacancy defect structures were also included as sources of structural diversity. The MD simulations were conducted using both the NVT (constant number of particles, volume, and temperature) and NPT (constant number of particles, pressure, and temperature) ensembles. We performed simulations at temperatures ranging from 300 K to 800 K to ensure coverage across a broad temperature range. When implementing molecular dynamics simulations started from different phase structures, we employed the VASP program, which integrates a real-time force field-based Bayesian inference. This method uses a force field constructed based on the current dataset to evaluate the properties of the current frame structure in molecular dynamics. The Bayesian error, a measure of the discrepancy between the real-time force field's predictions and the observed properties, is calculated for each frame, and if the error fell below a predefined threshold, we collected data for that structure. If, within a 2 ps interval, all structures demonstrated errors below the specified threshold, we concluded the molecular dynamics simulation for that initial configuration and proceeded to sample the next initial configuration. The configurations obtained from the MD-based sampling methods typically cover the potential energy surface near the lowest energy configurations. However, we recognize that MD has limitations in overcoming high potential energy barriers, and as such, the coverage of this dataset in the phase transition state region may be insufficient.

Stochastic Surface Walking (SSW) sampling. To address the limitation of MD in exploring the phase transition state region, we incorporated a second sampling method based on the stochastic surface walking (SSW)^47,48 approach. The SSW method draws inspiration from bias-potential driven dynamics and metropolis Monte Carlo sampling. By introducing bias potentials along a softened random direction, SSW smoothly manipulates the structure on the potential energy surfaces (PES). The resulting SSW trajectories encompass diverse structural configurations on the PES, ranging from minima to saddle points and even fragmented structures with high energy. In this process, we integrated the SSW method with the software LASP⁴⁹ and the VASP program, which includes real-time force field-based Bayesian inference. The data collected from the molecular dynamics simulations served as the initial dataset for the real-time force field. Starting from bcc and hcp phase configurations, we initiated random walks on the potential energy surface. The integration of these two programs served the purpose of significantly improving sampling efficiency. The purely random walking method often results in configurations mostly located near the ground state, and it may suffer from the issue of repetitive sampling of short-distance structures. By integrating a real-time force field, we could bypass a substantial portion of the demanding first-principles calculations, facilitating the acquisition of diverse configurations, particularly in the high-energy range. This integration was a key element in our methodology and played a crucial role in gathering data representative of the entire potential energy surface. This comprehensive sampling efficiently explores the global potential energy surfaces (PES), including the challenging phase transition state region. Sampling these diverse structures is pivotal for constructing machine learning potentials suitable for studying phase transition processes.

In all sampling methods, each configuration was labeled with its energy, stress, and the forces on all atoms in it, which were calculated based on spin-polarized density functional theory (DFT).⁵⁰ The DFT calculations were performed with the Perdew–Burke–Ernzerhof (PBE)⁵¹ exchange-correlation functional with projector-augmented wave (PAW)⁵² pseudopotentials implemented in the VASP code.⁵³ The energy cutoff of 500 eV was used consistently across all configurations, which is much greater than 1.3 times the ENMAX of iron's pseudopotential. The strict condition of 1 × 10⁷ eV was used to break the electronic self-consistent loop, and the Methfessel–Paxton smearing was set for each orbital occupation with 0.1 eV broadening. The k-space sampling of the first Brillouin zone was performed in gamma-centered Monkhorst–Pack grids with a linear density of 0.18 Å⁻¹, the related SOAP descriptor and Bayesian formalism used in this work were implemented in the VASP(Version 6.3.2).⁵³

3 Results and discussion

3.1 Data selection

After obtaining the sampling dataset, analyzing the distribution characteristics of the dataset is beneficial to discuss the sampling efficiency. The dataset contains a total of 9156 configurations. This dataset includes crystal structure information, structural energy, cell stress, and the forces acting on each atom. Out of the total dataset, 8016 configurations were obtained through molecular dynamics (MD) sampling. These configurations were derived as follows: (1) 2800 configurations were obtained from MD sampling initiated from bcc and its perturbed structures. (2) 1915 configurations were obtained from MD sampling initiated from hcp structures. (3) 2988 configurations were obtained from MD sampling initiated from fcc structures. (4) 73 configurations were collected from MD sampling of surface structures. (5) 240 configurations were acquired through MD sampling of defect structures. The remaining 821 configurations were obtained using the stochastic surface walking (SSW) method. In addition to the above configurations, we incorporated 309 configurations obtained from elastic deformation fitting data and 10 configurations representing classic Burgers' reference states, bringing the total number of configurations to 9156.

We first analyzed the distribution characteristics of the data in the energy–volume space. As shown in Fig. 2(a), based on Bayesian inference, the energy distribution of the dataset is reasonable and generally normal. Among them, it should be noted that the number of samples in the low-energy region of the dataset is very rare, and the lower boundary presents a volume–energy relationship curve conforming to the law of the equation of state. This feature reflects the advantage of Bayesian inference in constructing dataset. Based on prior experience of existing data, it can infer whether new structures need to be added to the dataset before first-principles calculation, which avoids the problem of repeated sampling of structures. In the low-energy region, the structural changes are so small that a few samples can cover the typical atomic local environment. With the increase of energy, the degree of chaos of atomic arrangement increases rapidly. At this time, a large number of samples are added to the dataset, which increases the coverage of samples to the energy space, and thus the extrapolation ability of the dataset corresponding to the potential function. In order to analyze the descriptive ability of a dataset on phase transitions, we constructed a classical Burgers phase transition path and embedded it into an energy–volume curve. As shown by the green dotted line in Fig. 2(a), this dataset can essentially cover the region traversed by the phase transition path, and high-energy data still exist in regions with energies higher than the transition state. Therefore, the energy distribution of the dataset is reasonable.

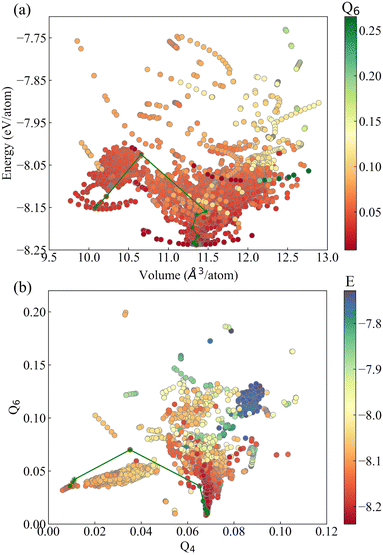Fig. 2 Distribution of the configurations in (a) the energy–volume space and (b) Steinhardt order parameter. The green path represents the classic Burgers phase transition path.

After solving the problem of sample coverage to the energy space, we further analyzed the distribution characteristics of the dataset in the structural phase space. Due to the inherent symmetry of crystal structure, the current common means of machine learning potential function is to transform the structure into a local environment descriptor, and regression modeling is carried out between the descriptor and the energy and force properties of the structure. Therefore, we also adopted atomic local environment characteristics to analyze the distribution characteristics of samples in the structural phase space of the dataset.

The Steinhardt order parameters are a set of parameters that characterizes the local atomic environment and is popularly used to distinguish crystal structures, and its expression is as follows:

where , , the core idea is to use spherical harmonic function group to represent the local coordination environment of atoms. As shown in Fig. 2(b), the data samples based on the Steinhardt order parameter exhibit several clustered distributions, which reflects its advantage in characterizing short-range ordering of crystal structures and distinguishing between different crystal configurations. However, the dataset has a low coverage of the Burgers phase transition path indicated by the green solid line, especially with low distinguishability of configurations in the intermediate region of the phase transition. If the Steinhardt order parameter is used as the structural descriptor to construct a machine learning potential, this potential is not suitable for describing structural phase transitions.

In this article, the descriptor we used is smooth overlap of atomic positions (SOAP), which utilizes a local expansion of a Gaussian-smoothed atomic density with orthonormal functions that are based on spherical harmonics and radial basis functions. When using the typical truncation radius (5 Å), 8 radial basis functions, and 4 spherical harmonics quantum numbers in the construction of the SOAP descriptor, the characteristic dimension of each atom's local environment reached 5000. In order to analyze the distribution characteristics of the data after being mapped by the SOAP descriptor, we performed principal component analysis (PCA) to map the 5000-dimensional features into a 2-dimensional principal component space. To evaluate the sampling efficiency, we split the dataset according to the sampling method and included the number of data samples for each method. As shown in Fig. 3, the distribution of principal components of the SOAP descriptor covers a wide range, completely covering the region traversed by the classical Burgers path, which suggests that mapping the dataset with the SOAP descriptor is reasonable for studying phase transition problems.

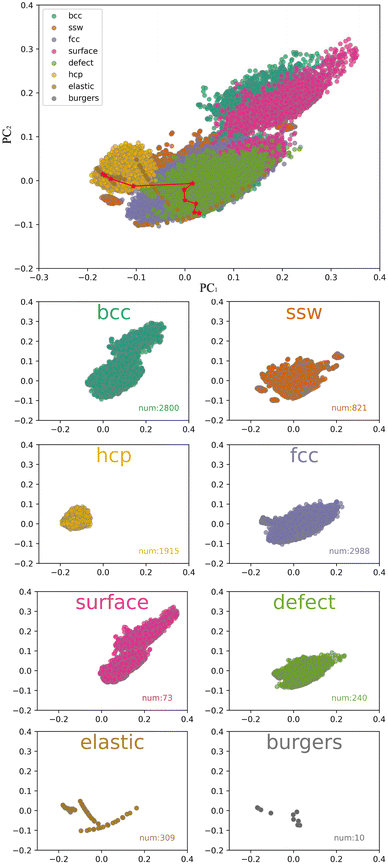Fig. 3 Smooth overlap of atomic positions (SOAP) descriptors combined with principal component analysis. The small figure shows the classification data obtained by different sampling methods.

In addition, principal component analysis (PCA) based on different sampling methods revealed that the data distributions obtained by different methods were relatively concentrated, with significant differences in the coverage areas. The elastic sampling method obtained the fitted equation-of-state (EOS) structures by perturbing the structure through stretching or compressing. The obtained data showed that the SOAP descriptors could reflect the continuity of structural changes when describing structural features, which is necessary for studying phase transitions in variable cell solids.

The trajectory sampling data obtained by performing high-temperature molecular dynamics simulations based on the hcp equilibrium structure were highly concentrated (0.2 < PC₁ < 0.05, 0.05 < PC₂ < 0.1) even though the number of trajectories reached 1915. The trajectory sampling data obtained based on the bcc equilibrium structure had a larger coverage area (0.1 < PC1 < 0.3, 0.1 < PC2 < 0.3), but the overlap between the two types of structures obtained by the bcc and hcp molecular dynamics simulations was small, which was not conducive to accurately describe the phase transition between the two. The trajectory sampling data obtained by performing high-temperature molecular dynamics simulations based on the fcc equilibrium structure had the largest number of trajectories, and the distribution could cover the area between bcc and hcp structures well, which was related to some reports stating that fcc is the intermediate phase in the bcc–hcp phase transition. Nevertheless, the efficiency of the molecular dynamics simulation-based sampling methods was generally low in describing the intermediate processes of the bcc–hcp phase transition, and the dataset may have better coverage of the bcc–fcc phase transition (transition temperature 1180 K) instead. The iron phase diagram shows that the bcc–hcp phase transition can be driven by pressure, which requires considering sampling at different pressures in molecular dynamics simulations. However, the ability of ordinary molecular dynamics simulations to cross high-energy barriers is low, making it difficult to obtain samples near the transition saddle point using this sampling scheme. To quickly and specifically obtain a dataset and a machine learning potential suitable for studying phase transition problems, we also tried the random walk algorithm on the potential energy surface. This algorithm can cross high energy barriers and obtain continuous phase transition paths, which is very helpful for constructing phase transition research dataset. We further added Bayesian inference to the original algorithm to infer whether new samples can be described by the existing dataset while randomly walking. This set can accelerate the construction of the dataset and avoid the collection of duplicate samples. The red data points in Fig. 3 show the data obtained by the sampling method based on the Stochastic Surface Walking (SSW) approach. The random walk started from the bcc ground state structure. It can be seen from the figure that the sampling in the initial stage was in line with the Hamburg path, diverged in the middle area, and finally converged near the hcp ground state. Compared with the molecular dynamics-based sampling methods, the dataset obtained based on the random potential energy surface walking scheme had higher coverage of phase transitions, which is conducive to training potentials with stronger generalization ability and more suitable for phase transition research. Moreover, the surface model and defect model had significant advantages over ideal crystals in obtaining local configurations, which could increase the diversity of sampling data.

3.2 Model training and optimization

MLFF was used in this work to investigate these potentials on the same dataset. MLFF assumes that the potential energy of configuration system can be expressed as a sum of local atomic energies, which are the functional of the local coordination environment around each atom. The local environment is described as a rotation-invariant descriptor. Further, the mapping relationship between descriptors and configurational potential energy can be established using machine learning methods, and the correlation coefficients in the mapping relationship can be fitted using the constructed dataset to finally obtain the available MLFF.

In this work, we applied the kernel-based Bayesian regression model integrated within the VASP code.³⁴ In this model, a variant of the smooth overlap of atomic positions was adopted as the descriptors X_i, and a kernel function K was used to measure the similarity between a local configuration and the reference local configuration. The cutoff radius of radial descriptors and angular descriptors were 8.0 Å with a 0.5 Å Gaussian broadening. The descriptors were expanded by radial basis functions (N = 12) and spherical harmonics (L_max = 4), the weight of radial descriptors in the kernel was set to 0.1. Bayesian linear regression was employed to get the fitting coefficients w_iB in the linear equations for the energies U and kernel functions K,

The threshold for the CUR algorithm used in the sparsification of local reference configurations was 10⁻⁹, the convergence criterion for the optimization of parameters was 10⁻¹⁵.

3.3 Accuracy evaluation

Fig. 4 shows the comparison between the energy, force, and stress components predicted by the DFT and the MLFF using the training dataset. It is worth noting that this comparison based on training data only verifies whether the MLFF can capture the complex relationship between local environmental changes and energy and force. For these three quantities, the MLFF’s predictions are consistent with the DFT results with uniform slopes. For the energy, force and stress components, the root mean square errors (RMSE) between the DFT and MLFF predictions were 4.27 meV per atom, 0.05 eV Å⁻¹ and 0.51 GPa, respectively. The predicted errors indicate that the constructed MLFF exhibits lower overall errors and is suitable for related research within the given error range. To demonstrate the reliability of these errors, we provide some fitting error data for the Fe empirical model. For instance, the GAP-SOAP model presented in ref. 31 has root mean square errors (RMSEs) of 0.92 meV per atom for crystals and defects, and 4.07 meV per atom for liquid structures. While the energy of the Fe EAM potential, as reported by Byggmästar J. et al.,³¹ is found to be 5.29 ± 0.05 meV per atom, with a corresponding RMSE of 0.16 ± 0.06 eV Å⁻¹ in the force predictions. It's important to note that direct comparisons of which model is “better” may not be meaningful due to differences in the characteristics of the testing sets. The performance of models can vary depending on the specific test structures used. For example, the GAP-SOAP model exhibits a higher energy error for liquid structures, primarily due to their greater disorder. Our kernel-based Bayesian regression model demonstrates competitive accuracy in both energy and force predictions.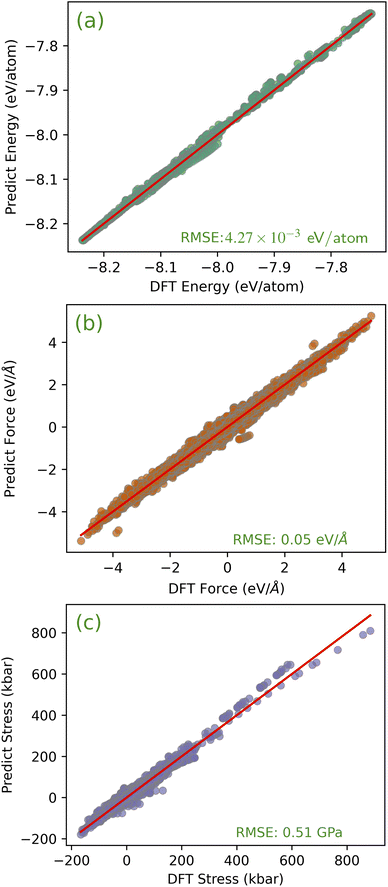

Fig. 4 Kernel-based Bayesian regression model predictions compared with first-principles results for (a) the energy, (b) the force, and (c) the stress.

Table 1 provides a comparison of the Fe MLFF model predictions for the lattice constants and elastic properties of bcc and hcp Fe with experiments. It is found that the calculated lattice constants for bcc and hcp phases by the model are in excellent agreement with DFT and experimental values. The elastic properties of bcc Fe predicted by MLFF are also in good agreement with DFT. For instance, the predicted values of C₁₁, C₁₂, and C₄₄ are 267, 145, and 86 GPa, respectively, with errors of 4.3%, 3.6%, and 7.5% compared to DFT, while the errors of EAM are significantly higher at 10.2%, 3.6%, and 46.3%.^54,55 However, the elastic properties of hcp Fe predicted by MLFF show relatively larger errors compared to DFT. The volume modulus estimated using the Voigt–Reuss–Hill approximation⁵⁶ shows good agreement with DFT, but the volume modulus from the MEAM potential is greatly underestimated.

Table 1 Calculated lattice parameter (a, c), energy (E) elastic constants (c_ij), bulk modulus (B), vacancy formation energy (E_v), migration energy (E_m) with the DFT, MLFF, and experiments

	bcc			hcp
	Exp	DFT	MLFF	Exp	DFT	MLFF
a	2.866	2.832	2.831	2.347	2.458	2.461
c	—	—	—	3.797	3.887	3.863
E	—	−8.237	−8.234	—	−8.153	−8.169
C11		256	267		527	655
C12		140	145		178	219
C44		80	86		164	186
B		180	185		289	347
Ev		2.16	1.91		0.05	0.03
Em		0.69	0.89		1.49	1.64

---

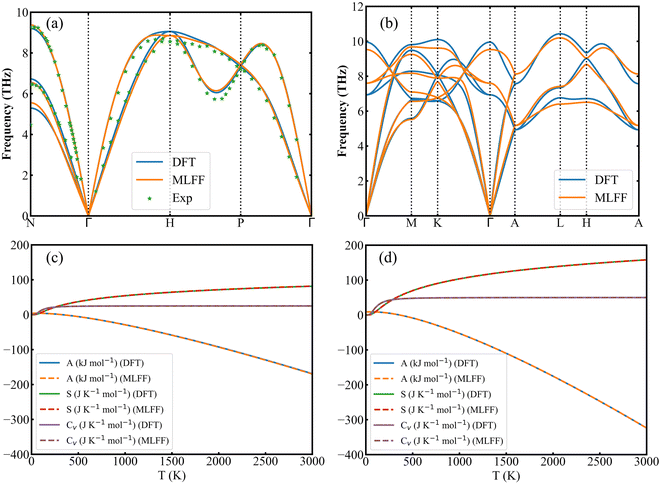
To further investigate predictions of force and lattice dynamics using Fe MLFF, phonon dispersion curves for bcc and hcp Fe 3 × 3 × 3 supercell were calculated by the finite displacement method, as shown in Fig. 5(a and b). The predicted phonon dispersion curves of bcc and hcp Fe are in good agreement with those calculated by DFT and measured by the experiments. The imaginary frequency is not observed, and the lowest frequency is located at the point. The deviation of the results calculated by DFT and MLFF mainly occurs in the range of high-frequency phonons. To determine the effect of these deviations on thermal properties, we calculated the Helmholtz free energy (A), entropy (S) and constant volume molar thermal capacity (C_v) of bcc and hcp Fe by DFT and MLFF. Both methods show nearly identical curves for all three quantities, demonstrating the accuracy of machine-learned potential functions in simulating thermal properties (Fig. 5(c and d)).

Fig. 5 Phonon dispersion curves of (a) bcc and (b) hcp Fe, Helmholtz free energy (A), entropy (S), and constant volume molar thermal capacity (C_v) of (c) bcc and (d) hcp Fe calculated by the MLFF and DFT.

To explore whether the constructed machine learning potential function can simulate the phase transition process, we performed variable-cell double-ended surface walking method simulations⁵⁷ using MLFF to determine the phase transition process. The 32-atom bcc Fe supercell was assumed as initial state, and hcp Fe was the final state. The energy trajectories from bcc to hcp phase was shown in Fig. 6, the phase transition from bcc to hcp needs to overcome a energy barrier of 0.12 eV, which is very close to the previous DFT calculation results (0.132 eV,⁵⁸ 0.156 eV,⁴⁶ 0.112 eV,⁸ 0.185 eV⁵⁹). We also calculated the energies of these intermediate configurations using DFT. The energies of DFT and MLFF on the side of the bcc phase are very consistent, and there is a certain deviation between the two on the side of the hcp phase, and the largest deviation occurs on the transition state structure. This is related to the lack of high-energy region data used in the fitting, although we use the SSW sampling method to avoid this problem. This phenomenon is not unique to our model; the PES calculated by Jana et al.⁴⁶ used Dragoni's GAP potential²⁸ and Mendelev's EAM potential⁶⁰ also exhibit similar behavior. The low weight of transition state structures in the fitting process, owing to their small proportion in the dataset, contributes to the challenges in accurately capturing their energy during the fitting process. To evaluate the impact of potential functions, we employed three publicly available potentials: Dragoni's GAP potential, Mendelev's EAM potential, and Jana's TurboGAP potential. We applied these potentials to compute the energy of these same structures in PES, depicted in Fig. 6(b). Our findings reveal that, while Dragoni's GAP potential and Mendelev's EAM potential offer insights into the relative energy relationship between bcc and hcp structures, they fall short of characterizing the phase transition barrier between them. The most recent Jana's TurboGAP potential and our constructed potential demonstrate comparable predicted energies, both of which are slightly lower than those obtained through DFT calculations. However, it's essential to acknowledge that differences in data sets and variations in force predictions affect the assessment. For Dragoni's GAP potential and Mendelev's EAM potential, the structures near the boundary are not ground states, potentially impacting their ability to describe the potential energy surface for the phase transition. Notably, when comparing these results, it becomes evident that Dragoni's GAP potential, despite its GAP-type nature, is constrained by the limitations of the dataset, making it somewhat inadequate in describing the potential energy surface for the phase transition.

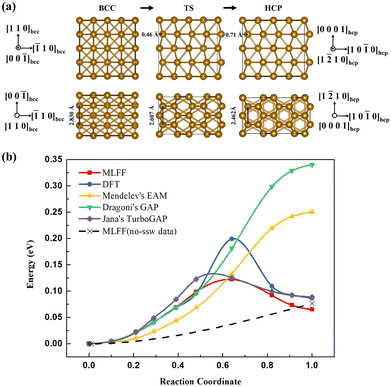Fig. 6 (a)IS, TS, FS structures and (b) reaction energy profile along the Fe bcc-to-hcp phase transition pathway the double-ended surface walking trajectories from bcc to hcp phase, calculated by our MLFF, DFT, Mendelev's EAM potential,⁶⁰ Dragoni's GAP potential²⁸ and the latest Jana's TurboGAP potential⁴⁶ with the same structures based on our MLFF PES. The dashed line represents the barrierless prediction using MLFF trained without SSW data.

To explicitly demonstrated how SSW-added workflow outperforms standard MD sampling in the transition state region, we specifically fitted a machine learning potential using the subset of data collected through MD simulations (8016 data points) with the same parameters as a reference. This reference model, based on the “no-ssw data”, was then utilized to calculate the potential energy barrier between bcc and hcp structures. Simulated by variable-cell double-ended surface walking method simulations, within a system of 32 atoms, the energy of the transition state is only marginally higher (0.001 eV) than that of the bcc structure. Considering numerical errors, this implies the absence of a substantial energy barrier between the two states. This behavior closely resembles the response of the EAM and GAP potential functions, as shown in Fig. 6(b). This phenomenon may be attributed to the complexity of force properties. For each configuration, it necessitates the labeling of one total energy, six stress values, and as many as 3N_atom force values. While machine learning can predict a single total energy value easily using interpolation, it becomes notably challenging for the 3N_atom force values. Interpolation in such cases is intricate, and errors tend to amplify, making accurate force predictions more challenging, particularly when data is limited. When force predictions are inaccurate, it becomes impossible to derive precise phase transition paths. Therefore, in Fig. 6(b), we present a failed schematic representation of the barrierless prediction using MLFF trained without SSW data. In the absence of SSW data, the assessment of forces within the intermediate state encounters limitations. These limitations, in turn, undermine the meaningfulness of calculating the energies associated with these structures. Upon the inclusion of 821 data points generated through the SSW sampling process (comprising only 1/10 of the data from MD sampling), the constructed potential can accurately model the energy barrier between bcc and hcp structures, which means that both the force and the energy predictions are reasonable. This compelling evidence underscores the significance of the SSW sampling strategy and highlights the necessity of SSW in addressing the limitations of traditional MD sampling when studying phase transitions. These additional insights confirm the advantages of our workflow in modeling phase transitions with improved accuracy and efficiency. We have shown that our approach is more efficient, requiring SSW data to achieve comparable or better accuracy in predictions.

Considering the phase transition process from bcc to hcp as a whole, our MLFF model can reasonably reproduce the potential energy surface, energy, and force predictions, providing a reasonable representation of the phase transition behavior and reasonable barrier heights. In addition, due to the limitations of the current machine learning force field model and the large amount of calculation required to construct a database containing atomic oriented magnetic moments, the properties of magnetic moments are not explicitly reflected in the current force field model, which also limits an accurate description of phase transitions in magnetic materials.

4 Conclusions

This paper developed a machine learning force field for predicting the bcc–hcp phase transitions of iron. By employing traditional molecular dynamics sampling methods and SSW sampling methods, combined with Bayesian inference, we construct an efficient machine learning force field. Analyzing the distribution characteristics of the constructed dataset in the energy–volume space and Steinhardt order parameter space, we find that using SOAP descriptors to map structural data exhibits good coverage in the phase transition space through PCA analysis. Subsequently, a machine learning force field is constructed using a Bayesian linear regression model. Through energy, force, and stress evaluations, we find that the RMSE between the machine learning force field and DFT calculations is only 4.27 meV per atom, 0.05 eV Å⁻¹, and 0.51 GPa, indicating excellent reproducibility of the dataset labels by the machine learning force field. With the machine learning force field, we obtain the stable crystal structure parameters, elastic constants, and bulk modulus of bcc and hcp phases of iron. By comparing with DFT calculation results and experimental data, the predictive capability of the machine learning force field for basic structural properties is demonstrated. To evaluate the predictive capability of the force field for higher-order derivatives, we calculate the phonon dispersion relations, which show good agreement between the machine learning force field, DFT calculations, and existing experimental data. Finally, to validate the predictive capability of the force field for phase transition processes, we employ variable-cell double-ended surface walking method simulations, which demonstrate that the machine learning force field can obtain smooth phase transition processes that follow the Burgers pathway.

Data availability

The data that support the findings of this study are available at https://github.com/windysoul-code/MLFF_iron.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China-NSAF (No. U2030117), the Natural Science Foundation of Shanxi Province (20210302123201), and Shanxi Scholarship Council of China (2023-077 and 2023-078).

Notes and references

1. D. Andrews, J. Phys. Chem. Solids, 1973, 34, 825–840.
2. F. Birch, Elastic Properties and Equations of State, 1988, 26, 31–90.
3. J. C. Boettger and D. C. Wallace, Phys. Rev. B, 1997, 55, 2840.
4. M. Ekman, B. Sadigh, K. Einarsdotter and P. Blaha, Phys. Rev. B, 1998, 58, 5296.
5. D. Bancroft, E. L. Peterson and S. Minshall, J. Appl. Phys., 1956, 27, 291–298.
6. L. Stixrude, R. Cohen and D. Singh, Phys. Rev. B, 1994, 50, 6442.
7. L. Vočadlo, G. A. de Wijs, G. Kresse, M. Gillan and G. D. Price, Faraday Discuss., 1997, 106, 205–218.
8. D. F. Johnson and E. A. Carter, J. Chem. Phys., 2008, 128, 104703.
9. B. Dupé, B. Amadon, Y.-P. Pellegrini and C. Denoual, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024103.
10. L. Miyagi, M. Kunz, J. Knight, J. Nasiatka, M. Voltolini and H.-R. Wenk, J. Appl. Phys., 2008, 104, 103510.
11. S. Merkel, A. Lincot and S. Petitgirard, Phys. Rev. B, 2020, 102, 104103.
12. D. Kalantar, J. Belak, G. Collins, J. Colvin, H. Davies, J. Eggert, T. Germann, J. Hawreliak, B. Holian and K. Kadau, et al., Phys. Rev. Lett., 2005, 95, 075502.
13. F. Wang and R. Ingalls, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 5647.
14. K. Kadau, T. C. Germann, P. S. Lomdahl and B. L. Holian, Science, 2002, 296, 1681–1684.
15. D. Kalantar, J. Belak, G. Collins, J. Colvin, H. Davies, J. Eggert, T. Germann, J. Hawreliak, B. Holian and K. Kadau, et al., Phys. Rev. Lett., 2005, 95, 075502.
16. Z. Lu, W. Zhu, T. Lu and W. Wang, Modell. Simul. Mater. Sci. Eng., 2014, 22, 025007.
17. S. Jian-Li, H. An-Min, D. Su-Qing, W. Pei and Q. Cheng-Sen, Acta Phys. Sin., 2010, 59, 4888–4894.
18. H. Djohari, F. Milstein and D. Maroudas, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 174109.
19. L. Ma, S. Xiao, H. Deng and W. Hu, Int. J. Fatigue, 2014, 68, 253–259.
20. G. J. Ackland, A. P. Jones and R. Noble-Eddy, Mater. Sci. Eng., A, 2008, 481, 11–17.
21. B. Wang, J. Shao, G. Zhang, W. Li and P. Zhang, J. Phys.: Condens. Matter, 2010, 22, 435404.
22. J.-L. Shao, X.-X. Guo, G. Lu, W. He and J. Xin, Mech. Mater., 2021, 158, 103878.
23. K. Kadau, T. C. Germann, P. S. Lomdahl and B. L. Holian, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 064120.
24. H.-T. Luu, R. G. Veiga and N. Gunkelmann, Metals, 2019, 9, 1040.
25. J. Bouchet, S. Mazevet, G. Morard, F. Guyot and R. Musella, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094102.
26. A. Belonoshko, S. Arapan and A. Rosengren, J. Phys.: Condens. Matter, 2011, 23, 485402.
27. L. Kong, J. Li, Q. Shi, H. Huang and K. Zhao, Europhys. Lett., 2012, 97, 56004.
28. D. Dragoni, T. D. Daff, G. Csányi and N. Marzari, Phys. Rev. Mater., 2018, 2, 013808.
29. I. Novikov, B. Grabowski, F. Körmann and A. Shapeev, npj Comput. Mater., 2022, 8, 13.
30. J.-B. Maillet, C. Denoual and G. Csányi, AIP Conf. Proc., 2018, 050011.
31. J. Byggmästar, G. Nikoulis, A. Fellman, F. Granberg, F. Djurabekova and K. Nordlund, J. Phys.: Condens. Matter, 2022, 34, 305402.
32. Y. Wang, J. Liu, J. Li, J. Mei, Z. Li, W. Lai and F. Xue, Comput. Mater. Sci., 2022, 202, 110960.
33. C. Chen, Z. Deng, R. Tran, H. Tang, I.-H. Chu and S. P. Ong, Phys. Rev. Mater., 2017, 1, 043603.
34. R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105.
35. C. Zeni, K. Rossi, A. Glielmo and F. Baletto, Adv. Phys.: X, 2019, 4, 1654919.
36. A. M. Goryaeva, J.-B. Maillet and M.-C. Marinica, Comput. Mater. Sci., 2019, 166, 200–209.
37. R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701.
38. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
39. O. A. Von Lilienfeld, R. Ramakrishnan, M. Rupp and A. Knoll, Int. J. Quantum Chem., 2015, 115, 1084–1093.
40. M. P. González, Z. Gándara, Y. Fall and G. Gómez, Eur. J. Med. Chem., 2008, 43, 1360–1365.
41. S. Winczewski, J. Dziedzic and J. Rybicki, Comput. Phys. Commun., 2016, 198, 128–138.
42. L. Zhan, J. Z. Chen and W.-K. Liu, J. Chem. Phys., 2007, 127, 141101.
43. N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419.
44. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.
45. R. Drautz, Phys. Rev. B, 2019, 99, 014104.
46. R. Jana and M. A. Caro, Phys. Rev. B, 2023, 107, 245421.
47. C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845.
48. X.-J. Zhang, C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 3252–3260.
49. S.-D. Huang, C. Shang, P.-L. Kang, X.-J. Zhang and Z.-P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415.
50. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
51. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
52. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
53. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
54. H.-S. Jin, S.-N. Ho, R.-S. Kong and I.-S. Kim, Indian J. Phys., 2021, 95, 1775–1782.
55. W. Hu, X. Shu and B. Zhang, Comput. Mater. Sci., 2002, 23, 175–189.
56. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349.
57. X.-J. Zhang and Z.-P. Liu, J. Chem. Theory Comput., 2015, 11, 4885–4894.
58. J. Liu and D. D. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 134113.
59. N. A. Zarkevich and D. D. Johnson, J. Chem. Phys., 2015, 143, 064707.
60. M. I. Mendelev, S. Han, D. J. Srolovitz, G. J. Ackland, D. Y. Sun and M. Asta, Philos. Mag., 2003, 83, 3977–3994.

---