DOI:
10.1039/D3RA04018F
(Paper)
RSC Adv., 2023,
13, 25007-25017
Determination of the crystalline size of hexagonal La1−xSrxMnO3 (x = 0.3) nanoparticles from X-ray diffraction – a comparative study
Received
15th June 2023
, Accepted 16th August 2023
First published on 22nd August 2023
Abstract
The electronic, magnetic, optical and elastic properties of nanomaterials are governed partially by the crystallite size and crystal defects. Here, the crystalline size of hexagonal La1−xSrxMnO3 (x = 0.3) nanoparticles was determined using various methods. Single-phase La0.7Sr0.3MnO3 nanopowders were produced after 10 h of milling in a commercial high-energy SPEX 8000D shaker mill, and then they were heated at 700 °C and 800 °C to study the effect of calcined temperature on the crystallization of nanoparticles. The modified Scherrer, Williamson–Hall, size–strain, and Halder–Wagner methods were used to determine the crystallite sizes and the elastic properties, such as intrinsic strain, stress, and energy density, from the X-ray diffraction peak broadening analysis. The obtained results were then compared with one another. The difference in crystallite sizes calculated from the different methods was due to the different techniques.
1. Introduction
La1−xSrxMnO3 materials with perovskite structure of the type ABO3 have been the subject of much research interest in solid-state physics for a long time, because they exhibit many interesting physical effects, especially the strong correlation between their magnetic and transport properties.1,2 These properties are closely related to the ionic size effect, which depends on the applied chemical pressure, i.e., whether or not the ion is substituted in site A or B, resulting in modification of the bond distance and thus the bandwidth (or electron hopping interaction).3 The kinetic energy of conduction electrons is controlled by the doping level, which not only drives the metal insulator transition but also governs the competing magnetic interaction.4 Among all perovskite manganites, the La0.7Sr0.3MnO3 (x = 0.3) compound is one of the most promising materials due to the high magnetic moment at room temperature and large Curie temperatures (TC ∼ 370 K).5 Thus, it exhibits significant colossal magneto-resistance (CMR) and magnetocaloric effects, and holds great potential for applications in magnetic refrigeration (MR) and magnetic recording technology.6 However, materials with TC values close to room temperature are important technological requirements.7 Researchers showed that partial substitution of the ions at site A or B by other metal ions and reduction in their particle size to a critical value (usually nanometers) could make the TC values reach close to room temperature, which is beneficial for MR technology.8–11
Considering the crystal structure of the La1−xSrxMnO3 system, most reports indicated that the rhombohedral structure could be observed in the range of 0.2 ≤ x ≤ 0.5.12,13 However, Bindu3 found that the hexagonal structure exists in the samples x = 0.2, 0.3, and 0.4, similar to the observation in the La0.7Sr0.3MnO3 nanopowders fabricated by high-energy ball milling and then calcined at 700 °C, 800 °C, and 900 °C.11 Through appropriate fabrication methods, the La0.7Sr0.3MnO3 manganite could clearly be either a rhombohedral lattice structure or hexagonal and orthorhombic ones. In nanocrystals, size confinement gives rise to large intrinsic strain, and this important elastic characteristic could be tuned by different synthesis parameters, such as pH, calcined temperature, and concentration of pre-chemicals.15 Usually, the crystallinity of a sample could be evaluated by analyzing different peaks of X-ray diffraction (XRD).14 For nanocrystals, a broadening of the XRD peaks could be observed due to the finite size effect and the existence of an intrinsic strain derived from the size confinement. Hence, a physical peak broadening mainly consists of two parts: one is related to size-dependent broadening, and the other is due to the contribution of strain-induced broadening.15 The most ordinary sources of the lattice strain are point defects, contact or sinter stress, grain boundary junction, dislocation density, and stacking faults.16–18 Therefore, the size of nanocrystals; the value of the intrinsic strain; and other elastic properties, such as stress and energy density, which are related to strain, could be determined indirectly through XRD peak broadening analysis. Many methods could be used for this analysis, including the Williamson–Hall (W–H), Warren–Averbach, and Balza methods. Among them, the W–H method utilizes the full-width half-maximum (FWHM) of the diffraction peak. Therefore, this method is very easy to apply and the acceptable one for determining different elastic properties, including strain, and calculating the average crystalline size.
Until now, limited attention has been paid to the microstructural parameters and crystal defects of nanomanganites. Most works only focused on studies related to crystallite size and grain size calculation, without investigating crystal defects and the internal stresses, uniform strain, lattice stress, and deformation energy density of nanomanganites. These structural parameters greatly influence the physical properties of the material. Thus, studying these parameters could not only provide important additional information about the crystal structure of manganites but also show the effect of stress on their crystallite size.
The present work is a continuation of a previous study on the same nanoparticle samples, in which the effect of calcined temperature on the magnetic and AC magnetic heating characteristics of La0.7Sr0.3MnO3 nanopowders have been reported.11 The present work aimed to study the crystallographic properties, microstructural parameters, and crystal defects of these nanoparticles. A comparative study of these microstructural properties of prepared La0.7Sr0.3MnO3 nanopowders based on XRD peak broadening was conducted using different models, such as the modified Scherrer, Williamson–Hall, size–strain plot (SSP), and Halder–Wagner methods. Subsequently, morphological analysis was performed via Field emission scanning electron microscopy (FESEM), and the average size obtained from this method was compared to the obtained results from XRD analysis.
2. Experimental procedures
La0.7Sr0.3MnO3 nanopowders were prepared using reactive milling combined with thermal processing methods as reported in the authors' previous work.11 After 10 h of milling in ambient atmosphere, the resulting powder was calcined at 700 °C and 800 °C for 4 h in air. The samples obtained were denoted as S1 for sample calcined at 700 °C and S2 for sample calcined at 800 °C. The phase purity, homogeneity, and crystal structure were characterized by XRD using a Bruker D8 Advance X-ray diffractometer with CuKα radiation (λ = 1.5406 Å) and an accelerating voltage of 40 kV. The data were recorded at room temperature from 20° to 80° for 2θ at a scanning speed of 2° min−1 and a step size of 0.02°. The XRD patterns were studied by the commercial X'pert Highscore Plus of the PANalytical program for Rietveld refinement analysis. The surface morphology of the samples was observed using scanning electron microphotographs under Field emission scanning electron microscopes (Hitachi S-4800).
3. Results and discussion
The analysis of phase purity and structural properties of samples at room temperature were done using X-ray diffraction (XRD) measurements. Fig. 1(a) displays the XRD patterns of both studied samples La1−xSrxMnO3 (x = 0.3) sintered at 700 °C (S1) and 800 °C (S2). All the samples are single phasic crystallizing in perovskite phase, with no trace of any impurity phases. The experimental data were analyzed using the X'Pert HighScore Plus software, which confirmed that all the samples were crystallized in the hexagonal symmetry and the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C space group. The inset of Fig. 1(a) shows the intensity of the main diffraction peaks of La0.7Sr0.3MnO3 nanopowders. The intensity of the main peak clearly increased as the annealed temperature increased from 700 °C to 800 °C, indicating the improvement of x = 0.3 crystallinity at higher annealed temperature. Besides, the full-width half-maximum (FWHM) of the main x = 0.3 peaks decreased as the annealed temperature increased. As shown in Fig. 1(b) and (c), the Rietveld analysis was applied in samples S1 and S2. The experimental Bragg reflections were consistent with their calculated positions. The a- and c-axis lattice parameters increased slightly with the sintering temperature, which is in very well agreement with the authors' previous report.11 From this diffraction data, the crystal sizes and related structural parameters of the samples were calculated, and the obtained results are discussed in the following section.
C space group. The inset of Fig. 1(a) shows the intensity of the main diffraction peaks of La0.7Sr0.3MnO3 nanopowders. The intensity of the main peak clearly increased as the annealed temperature increased from 700 °C to 800 °C, indicating the improvement of x = 0.3 crystallinity at higher annealed temperature. Besides, the full-width half-maximum (FWHM) of the main x = 0.3 peaks decreased as the annealed temperature increased. As shown in Fig. 1(b) and (c), the Rietveld analysis was applied in samples S1 and S2. The experimental Bragg reflections were consistent with their calculated positions. The a- and c-axis lattice parameters increased slightly with the sintering temperature, which is in very well agreement with the authors' previous report.11 From this diffraction data, the crystal sizes and related structural parameters of the samples were calculated, and the obtained results are discussed in the following section.
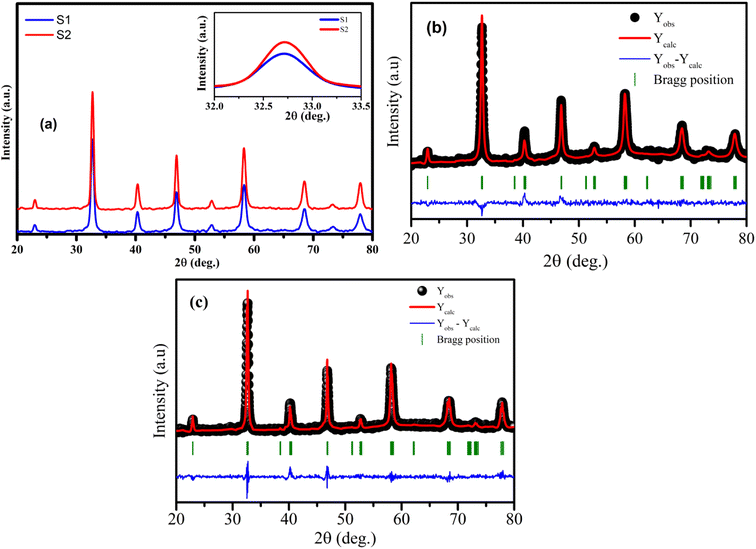 |
| | Fig. 1 (a) XRD patterns of S1 and S2 manganites. The inset shows the diffraction angle of the intense peak. (b) and (c) Rietveld refinement for the S1 and S2 samples. | |
3.1. The modified Scherrer method
The crystalline size of nanomaterials is usually calculated using Scherrer's formula, which is based on the broadening of the diffraction peaks from the size effect and intrinsic strain effect. Given that the diffraction peak broadening includes physical and instrumental broadenings,19,20 it must be corrected using the following equation:where βm is the measured broadening, βi is the instrumental broadening, and βd is the corrected broadening responsible for crystalline size. Here, crystalline silicon was used as the reference material for calibration error from instrumental broadening. The instrumental and physical broadenings of the samples were measured through FWHM, and by utilizing the corrected physical broadening, the average crystallite size could be conveniently calculated using Scherrer's equation as follows:21,22| |
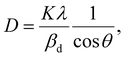 | (2) |
where D is the average crystallite size (nm); K is the shape factor, usually taken as 0.9 for ceramic materials; λ is the wavelength of X-rays; and θ is the Bragg angle.
In most studies, the average crystalline size is determined using only for the sharpest peak, so to reduce the sum of absolute error, 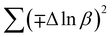 , Monshi et al.23 suggested the modified Scherrer formula to provide a more accurate value of D from all or some of the different peaks.
, Monshi et al.23 suggested the modified Scherrer formula to provide a more accurate value of D from all or some of the different peaks.
| |
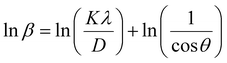 | (3) |
From eqn (3), if the line of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β is drawn in terms of
β is drawn in terms of 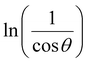 , then the y-intercept could give the value of
, then the y-intercept could give the value of 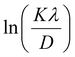 . Thus, the crystal size is as follows:
. Thus, the crystal size is as follows:
| |
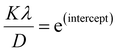 | (4) |
In order to obtain the more accurate value of crystalline for samples, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs.
β vs. 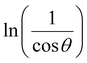 graph has been plotted for all the diffraction peaks. Fig. 2 displays the graph of ln
graph has been plotted for all the diffraction peaks. Fig. 2 displays the graph of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs.
β vs. 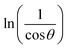 for both samples of LSMO nanoparticles. The fitting lines determined from eqn (3) for S1 and S2 were y = −4.7987 + 2.9748x and y = −4.9937 + 3.1941x, respectively. Therefore, the average crystalline size calculated using eqn (4) was 16.83 nm and 20.45 nm for S1 and S2, respectively.
for both samples of LSMO nanoparticles. The fitting lines determined from eqn (3) for S1 and S2 were y = −4.7987 + 2.9748x and y = −4.9937 + 3.1941x, respectively. Therefore, the average crystalline size calculated using eqn (4) was 16.83 nm and 20.45 nm for S1 and S2, respectively.
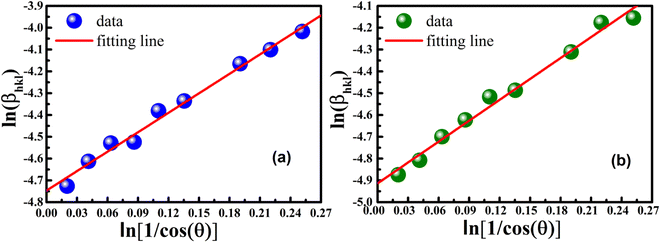 |
| | Fig. 2 Linear plots of modified Scherrer equation and gained intercepts for different LSMO obtained from (a) S1 and (b) S2. | |
The modified Scherrer method is the only method for determining the crystalline sizes in this study that could provide checkpoints to evaluate the accuracy of the obtained results. The slope in eqn (5) should be equal to the theoretical slope, i.e., 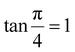 .23 However, due to errors associated with the experimental data, the least squares method gives the best slope value and equal to
.23 However, due to errors associated with the experimental data, the least squares method gives the best slope value and equal to 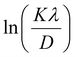 , indicating that some experimental points have to be removed to reduce the error and obtain a more accurate crystalline size. However, for comparison between methods, all the experimental points obtained from the XRD peaks of the samples remained the same.
, indicating that some experimental points have to be removed to reduce the error and obtain a more accurate crystalline size. However, for comparison between methods, all the experimental points obtained from the XRD peaks of the samples remained the same.
3.2. The Williamson–Hall analysis
Scherrer method only considers the effect of crystal size on the broadening of the XRD peaks; therefore, it does not give any information regarding the internal strain of the lattice, which is developed from the point defect, grain boundary, triple junction, and stacking faults in nanocrystals.24,25 Many methods, such as the W–H and Warren–Averbach methods, are utilized to evaluate the effect of the intrinsic strain on the broadening of XRD peaks. Therefore, they could be used to determine the intrinsic strain along the crystal size. Among these methods, the W–H method is an easy, simple, and useful one.26 According to this method, the physical expansion of the XRD peaks occurs due to the influence of the size and the microscopic strain of the nanocrystal. Thus, the total broadening could be calculated as follows:| | |
βtotal = βsize + βstrain
| (5) |
In this study, the W–H method included the uniform deformation model (UDM), uniform stress deformation model (USDM), and uniform deformation energy density model (UDEDM) were used and discussed in the following sections.
3.2.1 Uniform deformation model (UDM). UDM assumes that the strain is uniform in all the crystallographic directions, despite the fact that most of the nanocrystals have imperfect structures. In other words, UDM considers the strain to be isotropic in nature,21 and this intrinsic strain affects the physical broadening of the XRD profile. Therefore, the strain-induced broadening (βstrain) could be calculated as follows:| |
βstrain = 4ε × tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (6) |
The βsize in eqn (5) is given by the Scherrer's expression as follows: 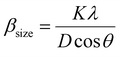 . Therefore, the total resulting broadening due to the strain and size of any diffraction line is
. Therefore, the total resulting broadening due to the strain and size of any diffraction line is
| |
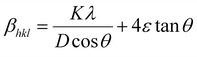 | (7) |
where
ε is the microstrain. By multiplying both sides of
eqn (7) by cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ and when sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ = tan
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ × cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ, the following equation could be obtained:
| |
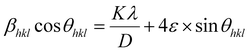 | (8) |
Eqn (8) shows that if the graph is plotted with βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as the y-axis and 4
θ as the y-axis and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as the x-axis, then the relationship between these two quantities is linear and the line has a slope, directly giving the value of the microstrain (ε). Meanwhile, the y-intercept is equal to the value of
θ as the x-axis, then the relationship between these two quantities is linear and the line has a slope, directly giving the value of the microstrain (ε). Meanwhile, the y-intercept is equal to the value of 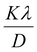 , from which the value of the crystal size could be determined. Fig. 3 shows a plot of βhkl
, from which the value of the crystal size could be determined. Fig. 3 shows a plot of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ versus 4
θ versus 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, and the red line denotes a good fitted line. The average crystal sizes determined from UDM were approximately 22.73 and 26.66 nm for S1 and S2, respectively. From the slope, the intrinsic average strain values were calculated to be 3.00 × 103 and 2.49 × 103 for S1 and S2, respectively. A positive value of the intrinsic strain indicates that this strain is a tensile strain, whereas a negative value indicates compressive strain.24
θ, and the red line denotes a good fitted line. The average crystal sizes determined from UDM were approximately 22.73 and 26.66 nm for S1 and S2, respectively. From the slope, the intrinsic average strain values were calculated to be 3.00 × 103 and 2.49 × 103 for S1 and S2, respectively. A positive value of the intrinsic strain indicates that this strain is a tensile strain, whereas a negative value indicates compressive strain.24
 |
| | Fig. 3 Linear plots of uniform deformation model obtained from (a) S1 and (b) S2. | |
3.2.2 Uniform stress deformation model (USDM). The uniform strain model is based on the assumption that nanocrystals are homogeneous and isotropic in nature, which is not completely true for real crystals. Therefore, to better respond to realistic conditions, the W–H equation must be adjusted so that the lattice deformation strain is anisotropic. This modified model is a USDM, in which the lattice deformation stress is assumed to be uniform along all lattice plane directions and considers a small microstrain present in the particles.Hooke's law relating to strain shows a linear relationship between stress and strain by the expression σ = εYhkl, deducing ε = σ/Yhkl, where σ is the stress of the crystal; ε is the anisotropic microstrain, depending on the crystallographic directions; and Yhkl is the modulus of elasticity or Young's modulus. Therefore, by substituting the value of ε in eqn (8), the W–H equation could be modified as follows:21
| |
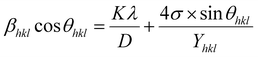 | (9) |
For hexagonal crystals, the Young's modulus is given by the following expression:25,26
| |
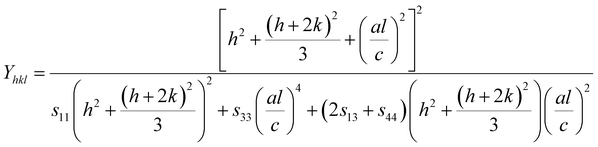 | (10) |
where
h,
k, and
l are the Miller indices, and
a and
c are the lattice constants (these values could be extracted from Rietveld refinement analysis using the X'pert software). In addition,
s11,
s13,
s33, and
s44 refer to the elastic compliance values of hexagonal manganites, and they could be determined from the elastic stiffness constants
c11,
c12,
c33, and
c44 by using the following expression:
27| |
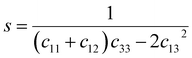 | (11a) |
| |
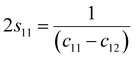 | (11b) |
| |
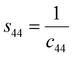 | (11f) |
The values of c11, c12, c33 and c44 for hexagonal manganites are cited in ref. 28. It is to be noted that the value of elastic stiffness constants are common for all the hexagonal manganites. By using these values and those from eqn (11a)–(11f), the elastic coefficients of S1 and S2 were calculated, as shown in Table 1. Furthermore, the Young's modulus (Yhkl) corresponding to the Miller indices of S1 and S2 were calculated using eqn (10), as presented in Table 2. The average Yhkl values for S1 and S2 were 268.358 and 268.364 GPa, respectively.
Table 1 Elastic compliances and stiffness constants of S1 and S2 samples
| Elastic compliances (GPa)28 |
Stiffness constants × 10−3 (GPa−1) |
| c11 |
c12 |
c13 |
c33 |
c44 |
s11 |
s12 |
s13 |
s33 |
s44 |
| 248 |
129 |
106 |
308 |
119 |
4.20 |
−0.91 |
−1.13 |
4.03 |
8.40 |
Table 2 Young's modulus (Yhkl) corresponding to the Miller indices of the samples S1 and S2, respectively
| S1 |
S2 |
| h |
k |
l |
Yhkl (GPa) |
h |
k |
l |
Yhkl (GPa) |
| 0 |
1 |
2 |
271.965 |
0 |
1 |
2 |
271.977 |
| 1 |
0 |
4 |
276.111 |
1 |
0 |
4 |
276.103 |
| 2 |
0 |
2 |
251.638 |
1 |
1 |
3 |
251.648 |
| 0 |
2 |
4 |
271.965 |
0 |
2 |
4 |
271.977 |
| 1 |
1 |
6 |
278.109 |
1 |
1 |
6 |
278.105 |
| 2 |
1 |
4 |
263.215 |
2 |
1 |
4 |
263.228 |
| 2 |
0 |
8 |
276.111 |
2 |
2 |
0 |
276.103 |
| 0 |
3 |
6 |
271.965 |
0 |
3 |
6 |
271.977 |
| 1 |
3 |
4 |
254.144 |
1 |
3 |
4 |
254.155 |
Theoretical studies have shown that Yhkl is closely related to the cohesive force between atoms. Therefore, the variation of Yhkl fairly accurately reflects the information of the lattice variation. Compared with the value of 167 GPa of La0.7Sr0.3MnO3 bulks,29 the high value of Yhkl in the samples of the present study showed that the change in JT-type distortion of the MnO6 octahedron is very large. Normally, the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C space group enforces on the average equal Mn–O bond lengths and thus prevents static coherent JT-type distortions of the MnO6 octahedron. Although neutron diffraction experiments have shown no obvious evidence for the existence of JT-type distortions in hexagonal or rhombohedral La0.7Sr0.3MnO3,30 Louca et al.31 proposed that the local atomic structure could deviate significantly from the average, and thus, the local JT distortion could persist even if the crystallographic structure has no JT distortion. Therefore, in the case of nano La0.7Sr0.3MnO3, the high value of Yhkl indicates that the dynamic incoherent local JT distortion of the lattice is significant in the nanoscale samples and fabricated by reactive milling method.
C space group enforces on the average equal Mn–O bond lengths and thus prevents static coherent JT-type distortions of the MnO6 octahedron. Although neutron diffraction experiments have shown no obvious evidence for the existence of JT-type distortions in hexagonal or rhombohedral La0.7Sr0.3MnO3,30 Louca et al.31 proposed that the local atomic structure could deviate significantly from the average, and thus, the local JT distortion could persist even if the crystallographic structure has no JT distortion. Therefore, in the case of nano La0.7Sr0.3MnO3, the high value of Yhkl indicates that the dynamic incoherent local JT distortion of the lattice is significant in the nanoscale samples and fabricated by reactive milling method.
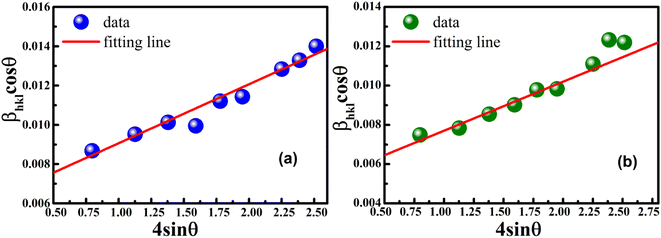
The uniform strain stress (σ) from the slope and the average crystal sizes from the y-intercept of the linear fit of the plotting of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ vs. 4
θ vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/Yhkl could be estimated. Fig. 4 displays the plotting of βhkl
θ/Yhkl could be estimated. Fig. 4 displays the plotting of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as a function of 4
θ as a function of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/Yhkl, and the red line indicates a good fitted line from eqn (9). The values of y-intercept found from the linear fit for S1 and S2 were 0.0062 and 0.0051, respectively, and the average crystal sizes were determined as 22.36 and 27.03 nm, respectively.
θ/Yhkl, and the red line indicates a good fitted line from eqn (9). The values of y-intercept found from the linear fit for S1 and S2 were 0.0062 and 0.0051, respectively, and the average crystal sizes were determined as 22.36 and 27.03 nm, respectively.
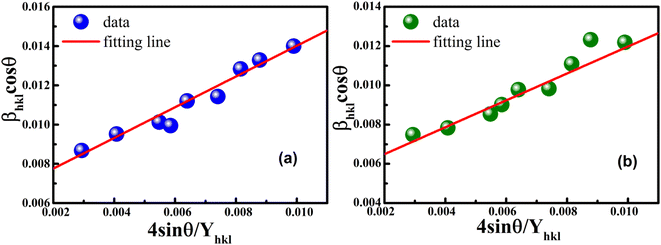 |
| | Fig. 4 Uniform stress deformation model plots for (a) S1 and (b) S2. | |
In addition, from the slope of linear fitting lines for samples S1 and S2, the values of uniform strain stress (σ) were obtained as 0.782 and 0.685 GPa, respectively, and the strain values (ε) were calculated as 2.91 × 10−3 and 2.55 × 10−3, respectively.
3.2.3 Uniform deformation energy density model (UDEDM). In real crystals, various defects, dislocations, and agglomerations produce imperfections of most crystals. So, the hypothesized isotropic nature of the crystal of UDM and the linear relationship between stress and strain of USDM could not be satisfied completely in the real system. Therefore, UDEDM, which assumes that the deformation energy is uniform in all directions of the crystal, was used as an alternative model to investigate the crystal structure parameters of the material.The Hooke's law for an elastic system shows the relationship between energy density (u) and strain by u = (ε2Yhkl)/2. Therefore, eqn (9) could express the maximum as
| |
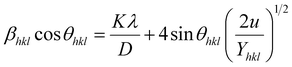 | (12) |
The anisotropic energy density (u) was estimated from the slope of the linear fit and the crystallite size D from the y-intercept of the plot βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl vs. 4
θhkl vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl(2/Yhkl)1/2. Fig. 5 shows a plotting of βhkl
θhkl(2/Yhkl)1/2. Fig. 5 shows a plotting of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl vs. 4
θhkl vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl(2/Yhkl)1/2, and the red line indicates a linear fit. The values of u were determined from the slope of the fitting line to be 0.199 and 0.166 GPa for S1 and S2, respectively. The average crystal sizes determined from the y-intercept were 0.0060 and 0.0050 for S1 and S2, respectively, so the crystal size values were 23.10 nm for S1 and 27.51 nm for S2. Given that σ = εYhkl and u = (ε2Yhkl)/2, the stress (σ) could be determined by the expression u = (σ2/2Yhkl). The results showed that the strain values (ε) were 3.10 × 10−3 and 2.38 × 10−3 (Yhkl ∼ average Young's modulus) for S1 and S2, respectively.
θhkl(2/Yhkl)1/2, and the red line indicates a linear fit. The values of u were determined from the slope of the fitting line to be 0.199 and 0.166 GPa for S1 and S2, respectively. The average crystal sizes determined from the y-intercept were 0.0060 and 0.0050 for S1 and S2, respectively, so the crystal size values were 23.10 nm for S1 and 27.51 nm for S2. Given that σ = εYhkl and u = (ε2Yhkl)/2, the stress (σ) could be determined by the expression u = (σ2/2Yhkl). The results showed that the strain values (ε) were 3.10 × 10−3 and 2.38 × 10−3 (Yhkl ∼ average Young's modulus) for S1 and S2, respectively.
 |
| | Fig. 5 Linear plots of uniform deformation energy density model for (a) S1 and (b) S2. | |
3.3. Size–strain plot (SSP)
The W–H method assumes that the broadening of peaks is essentially isotropic, thus emphasizing that the diffracting domains are isotropic due to the contribution of the effect of size- and microstrain-induced broadenings, which are considered as Cauchy-like profile. However, in the case of isotropic line broadening, better evaluating the size–strain parameters is possible by considering an average SSP.25 The advantage of this method is that less weight is given to the data from reflections at high angles, where accuracy is usually lower. In this approximation, the “crystal size” broadened profile is assumed to be illustrated by the Lorentzian function and the “strain broadened profile” by the Gaussian function. Accordingly,15,22–24| |
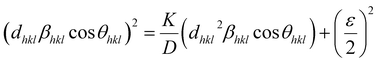 | (13) |
or| |
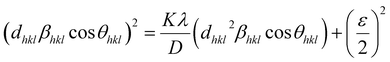 | (14) |
However, the above equations are not appropriate because they do not follow the dimensional homogeneity rule, so the appropriate equation of the SSP method must be as follows:32,33
| |
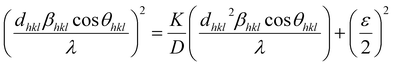 | (15a) |
or
| |
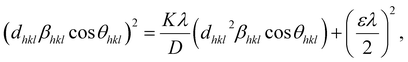 | (15b) |
where
dhkl is the lattice distance between the (
hkl) planes and has a magnitude for the hexagonal crystal as
| |
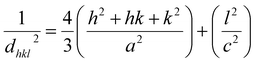 | (16) |
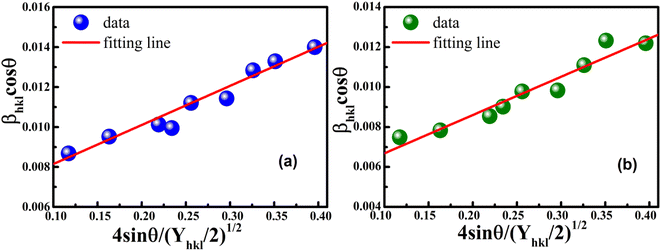
According to eqn (15b), the corresponding SSP for samples was obtained by plotting (dhklβhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl)2 on y-axis with respect to (dhkl2βhkl
θhkl)2 on y-axis with respect to (dhkl2βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl) on the x-axis for all peaks of S1 and S2 samples with the hexagonal phase. Fig. 6 displays that (dhklβhkl
θhkl) on the x-axis for all peaks of S1 and S2 samples with the hexagonal phase. Fig. 6 displays that (dhklβhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl)2 is plotted with respect to (dhkl2βhkl
θhkl)2 is plotted with respect to (dhkl2βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl), and the red line indicates a linear fit. The particle size (D) values were determined from the slope of the linearly fitted data as 18.01 and 20.83 nm for S1 and S2, respectively, whereas the root of the y-intercept provided the strain (ε) values of 3.40 × 10−3 and 2.76 × 10−3 for S1 and S2, respectively.
θhkl), and the red line indicates a linear fit. The particle size (D) values were determined from the slope of the linearly fitted data as 18.01 and 20.83 nm for S1 and S2, respectively, whereas the root of the y-intercept provided the strain (ε) values of 3.40 × 10−3 and 2.76 × 10−3 for S1 and S2, respectively.
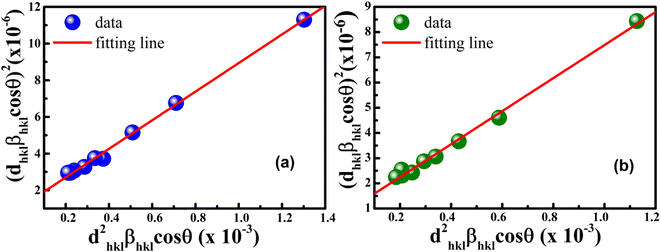 |
| | Fig. 6 Size–strain plot method of (a) S1 and (b) S2. | |
3.4. Halder–Wagner (H–W) method
The SSP method assumes that the crystalline size broadening of the XRD peak profile is described by the Lorentzian function, whereas the strain broadening corresponds to the Gaussian function. However, the XRD peaks actually are neither Lorentzian nor Gaussian functions, so the Halder–Wagner method is a useful alternative method to determine the crystalline size and strain of sample. This method is based on the assumption that the broadening of the XRD peaks is a Voigt symmetric function,34 and that it could be analyzed as deconvolution of two Lorentzian and Gaussian functions. In this case, the FWHM of the physical profile is written as follows:| | |
βhkl2 = βLβhkl + βG2,
| (17) |
where βL and βG are the FWHM of the Lorentzian and Gaussian functions, respectively. The H–W method has the advantage that it offers more weight to the peaks at low and medium diffraction angles and minimizes the overlap of the diffraction peaks.32 According to the Halder–Wagner method, the relation between the crystallite size and lattice strain could be expressed as follows:| |
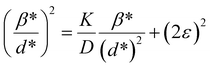 | (18) |
where β* = βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ and d* = 2
θ/λ and d* = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ. So, eqn (18) could be modified as
θ/λ. So, eqn (18) could be modified as| |
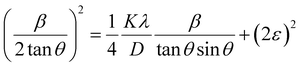 | (19) |
To estimate the values of crystallite size and strain using eqn (19), we fitted a linear equation to the 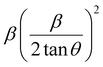 versus
versus 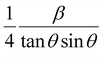 plots (see Fig. 7). The slope of the plotted straight line provides the average crystalline size, whereas the intercept gives the intrinsic strain of the samples. The average particle sizes were calculated from the plot as 17.78 nm for S1 and 21.20 nm for S2, which matched well with those obtained from the SSP model. Meanwhile, the calculated strain values from the Halder–Wagner plot were 3.46 × 10−3 for S1 and 3.12 × 10−3 for S2.
plots (see Fig. 7). The slope of the plotted straight line provides the average crystalline size, whereas the intercept gives the intrinsic strain of the samples. The average particle sizes were calculated from the plot as 17.78 nm for S1 and 21.20 nm for S2, which matched well with those obtained from the SSP model. Meanwhile, the calculated strain values from the Halder–Wagner plot were 3.46 × 10−3 for S1 and 3.12 × 10−3 for S2.
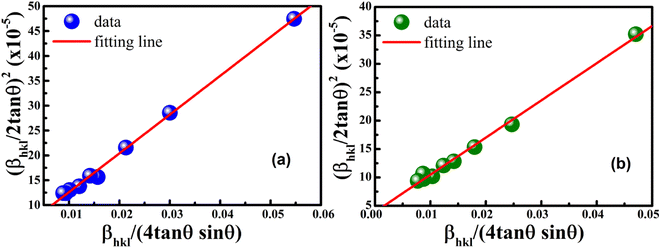 |
| | Fig. 7 Linear plots of Halder–Wagner method for (a) S1 and (b) S2. | |
Table 3 provides all the calculated values of the average crystalline size and the intrinsic strain, including other elastic parameters. The strain (ε) values calculated using the methods were comparable and consistent with one another. Furthermore, the average crystalline size (D) values obtained by Modified-Scherrer, SSP and H–W methods are almost similar, whereas these values are slightly higher for W–H method. Such difference could be attributed to both methods considering the anisotropy nature of the elastic constant are primarily different. USDM shows that deformation stress (σ) is the same in all crystallographic directions, with energy density (u) being anisotropic, whereas UDEDM assumes that deformation energy is uniform in all crystallographic directions, so deformation stress (σ) is anisotropic. According to literature,19,21,24 the SSP and H–W methods are more suitable than W–H, because the data from reflections at high angles are less important, and the data points are located very close to linear fit.
Table 3 Geometric parameters of La0.7Sr0.3MnO3 nanoparticles calcinated at 700 °C (S1) and 800 °C (S2) for 4 h
| Sample |
Modified Scherrer method |
Williamson–Hall method |
Size–strain plot |
Halder–Wagner method |
| UDM |
USDM |
UDEDM |
| Size D (nm) |
Size D (nm) |
Strain ε (10−3) |
Size D (nm) |
Strain ε (10−3) |
Stress σ (GPa) |
Size D (nm) |
Strain ε (10−3) |
Stress σ (GPa) |
Energy density u (GPa) |
Size D (nm) |
Strain ε (10−3) |
Size D (nm) |
Strain ε (10−3) |
| S1 |
16.83 |
22.73 |
3.00 |
22.36 |
2.91 |
0.782 |
23.10 |
3.10 |
0.831 |
0.199 |
18.01 |
3.14 |
17.78 |
3.46 |
| S2 |
20.45 |
26.66 |
2.49 |
27.03 |
2.55 |
0.685 |
27.51 |
2.38 |
0.639 |
0.166 |
20.83 |
2.76 |
21.20 |
3.12 |
3.5. Morphological study
FESEM images are one the best way to study of the morphology of the La1−xSrxMnO3 (x = 0.3) nanoparticles. The FESEM images and the particle-size distribution for the S1 and S2 nanoparticles are presented in Fig. 8. All the samples consisted of agglomerated or interconnected nanoparticles with non-uniform morphology may be due to the magnetic dipole–dipole interactions, which caused the nanoparticles to aggregate.35 The particle sizes were in the range of 20–70 nm for S1 and 25–75 nm for S2. The average particle size was determined by ImageJ software, and the Gaussian function showed that the average particle sizes of S1 and S2 were ∼39 and ∼50 nm, respectively, as shown in Fig. 8(b) and (d).
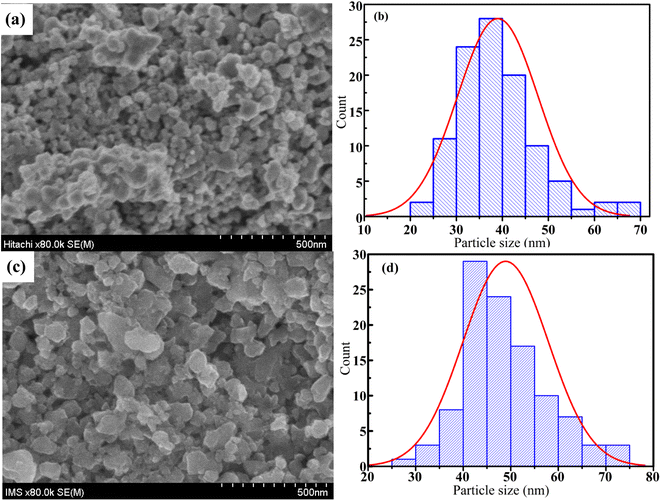 |
| | Fig. 8 FESEM micrograph (a and c) and grain size distribution histograms (b and d) of S1 and S2 samples. | |
4. Conclusions
In this study, nano-polycrystalline La1−xSrxMnO3 (x = 0.3) samples were synthesized using the reactive milling technique with conventional sintering method. The room-temperature X-ray diffraction analysis showed that all the studied compounds possessed a hexagonal structure with a R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C space group. The average crystalline size and the various elastic properties of the La1−xSrxMnO3 (x = 0.3) nanomanganites, such as intrinsic strain, stress, and energy density, were determined by different methods, such as the modified Scherrer, W–H plot, SSP, and Halder–Wagner methods, via XRD peak broadening analysis. The calculation results showed that the SSP and Halder–Wagner methods are the two most suitable methods to accurately determine the crystal size and intrinsic strain of nanomanganites. Finally, the morphology and the distribution of the average particle size were studied via FESEM, which showed that the average size increased from 39 nm for S1 to 49 nm for S2 as the annealing temperature increased from 700 °C to 800 °C.
C space group. The average crystalline size and the various elastic properties of the La1−xSrxMnO3 (x = 0.3) nanomanganites, such as intrinsic strain, stress, and energy density, were determined by different methods, such as the modified Scherrer, W–H plot, SSP, and Halder–Wagner methods, via XRD peak broadening analysis. The calculation results showed that the SSP and Halder–Wagner methods are the two most suitable methods to accurately determine the crystal size and intrinsic strain of nanomanganites. Finally, the morphology and the distribution of the average particle size were studied via FESEM, which showed that the average size increased from 39 nm for S1 to 49 nm for S2 as the annealing temperature increased from 700 °C to 800 °C.
Author contributions
Do Hung Manh: conceptualization, investigation, formal analysis, data curation, writing. Tran Thi Ngoc Nha, Le Thi Hong Phong and Pham Hong Nam: investigation, formal analysis. Tran Dang Thanh and Pham Thanh Phong: conceptualization, investigation, formal analysis, data curation, supervision, project administration, writing – review & editing.
Conflicts of interest
The authors declare that they have no conflict of interest.
Acknowledgements
This work was supported by the excellent research team development program grant funded by Vietnam Academy of Science and Technology (VAST) under Project Code NCXS01.04/22-24.
References
- E. Dagotta, T. Hotta and A. Moreo, Colossal magnetoresistant materials: the key role of phase separation, Phys. Rep., 2001, 344, 1–153, DOI:10.1016/S0370-1573(00)00121-6.
- S. Biswas, P. Wiśniewski and S. Keshri, Study of the Structural, Electrical and Magnetic Properties of the La0.67Sr0.33-xPbxMnO3 Manganite Nanocrystalline Materials, J. Low Temp. Phys., 2022, 206, 400–412, DOI:10.1007/s10909-021-02654-z.
- R. Bindu, Structural studies of La1-xSrxMnO3+δ (x = 0.1–1.0), Eur. Phys. J. B, 2004, 37, 321–327, DOI:10.1140/epjb/e2004-00062-8.
- Y. K. Lakshmi, G. Venkataiaha, M. Vithal and P. V. Reddy, Magnetic and electrical behavior of La1-xAxMnO3 (A= Li, Na, K and Rb) manganites, Phys. B, 2008, 403, 3059–3066, DOI:10.1016/j.physb.2008.03.018.
- A. Rostamnejadi, M. Venkatesan, P. Kameli, H. Salamati and J. M. D. Coey, Magnetocaloric effect in La0.67Sr0.33MnO3 manganite above room temperature, J. Magn. Magn. Mater., 2011, 323, 2214–2218, DOI:10.1016/j.jmmm.2011.03.036.
- P. Dey and T. K. Nath, Effect of grain size modulation on the magneto- and electronic-transport properties of La0.7Ca0.3MnO3 nanoparticles: The role of spin-polarized tunneling at the enhanced grain surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 214425, DOI:10.1103/PhysRevB.73.214425.
- N. Kouki, A. Guedri, S. Hcini, A. Algreiby, R. Charguia and R. K. Alharbi, Structural, magnetic, magnetocaloric and critical studies of Sm-substituted La0.67-xSmxPb0.13Ca0.2MnO3 perovskite manganites, Solid State Commun., 2023, 363, 115104, DOI:10.1016/j.ssc.2023.115104.
- L. T. T. Ngan, N. T. Dang, N. X. Phuc, L. V. Bau, N. V. Dang, D. H. Manh, P. H. Nam, L. H. Nguyen and P. T. Phong, Magnetic and transport behaviors of Co substitution in La0.7Sr0.3MnO3 perovskite, J. Alloys Compd., 2022, 911, 164967, DOI:10.1016/j.jallcom.2022.164967.
- S. Biswas and S. Keshri, Large magnetocaloric effect near room temperature in La0.67(Sr,K/Pb)0.33MnO3 manganite nanomaterials, J. Mater. Sci.: Mater. Electron., 2020, 31, 21896–21912, DOI:10.1007/s10854-020-04694-9.
- K. Abdouli, F. Hassinib, W. Cherif, P. R. Prezas, M. P. F. Graça, M. A. Valent, O. Messaoudie, S. Elgharbi, A. Dhahri and L. Manai, Investigation of the structural, electrical, and dielectric properties of La0.5Sm0.2Sr0.3Mn1-xCrxO3 for electrical application, RSC Adv., 2022, 12, 16805–16822, 10.1039/D2RA01006B.
- D. H. Manh, P. T. Phong, P. H. Nam, D. K. Tung, N. X. Phuc and In-Ja Lee, Structural and magnetic study of La0.7Sr0.3MnO3 nanoparticles and AC magnetic heating characteristics for hyperthermia applications, Phys. B, 2014, 444, 94–102, DOI:10.1016/j.physb.2014.03.025.
- J. Hemberger, A. Krimmel, T. Kurz and H.-A. Krug Von Nidda, Structural, magnetic, and electrical properties of single-crystalline La1−xSrxMnO3 (0.4 < x < 0.85), Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 094410, DOI:10.1103/PhysRevB.66.094410.
- R. Mahendiran, S. K. Tiwary, A. K. Ray Chaudhari and T. V. RamaKrishnan, Structure, electron-transport properties, and giant magnetoresistance of hole-doped LaMnO3 systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 3348, DOI:10.1103/PhysRevB.53.3348.
- C. E. Hintze, D. Fuchs, M. Merz, H. Amari, C. Kubel, M. Huang, A. Powell and H. v. Lohneysen, Size-induced changes of structural and ferromagnetic properties in La1-xSrxMnO3 nanoparticles, J. Appl. Phys., 2017, 121, 214303–214309, DOI:10.1063/1.4984829.
- D. Nath, F. Singh and R. Das, X-ray diffraction analysis by Williamson-Hall, Halder-Wagner and size-strain plot methods of CdSe nanoparticles- a comparative study, Mater. Chem. Phys., 2020, 239, 122021, DOI:10.1016/j.matchemphys.2019.122021.
- M. A. Islam, A. K. M. Akther Hossain, M. Z. Ahsan, M. A. A. Bally, M. Samir Ullah, S. M. Hoque and F. A. Khan, Structural characteristics, cation distribution, and elastic properties of Cr3+ substituted stoichiometric and non-stoichiometric cobalt ferrites, RSC Adv., 2022, 12, 8502, 10.1039/d1ra09090a.
- B. D. Cullity and S. R. Stock, Elements of X-Ray Diffraction, Addison-Wesley Publishing Company, Mass, 2001 Search PubMed.
- A. Guinier, X-ray Diffraction in Crystals, Imperfect Crystals and Amorphous Bodies, Dover, New York, 1994 Search PubMed.
- R. Delhez, T. H. de Keijser and E. J. Mittemeijer, Determination of crystallite size and lattice distortions through X-ray diffraction line profile Analysis, Fresenius' Z. Anal. Chem., 1982, 312, 1–16, DOI:10.1007/BF00482725.
- R. Yogamalara, R. Srinivasan, A. Vinu, K. Ariga and A. C. Bose, X-ray peak broadening analysis in ZnO nanoparticles, Solid State Commun., 2009, 149, 1919–1923, DOI:10.1016/j.ssc.2009.07.043.
- P. Bindu and S. Thomas, Estimation of lattice strain in ZnO nanoparticles: X-ray peak profile analysis, J. Theor. Appl. Phys., 2014, 8, 123–132, DOI:10.1007/s40094-014-0141-9.
- A. Khorsand Zak, W. H. Abd Majid, M. E. Abhrishami and R. Yousef, X-ray analysis of ZnO nanoparticles by Williamson-Hall and size-strain plot methods, Solid State Sci., 2011, 13, 251–256, DOI:10.1016/j.solidstatesciences.2010.11.024.
- A. Monshi, M. R. Foroughi and M. R. Monshi, Modified Scherrer Equation to Estimate More Accurately Nano-Crystallite Size Using XRD, World J. Nano Sci. Eng., 2012, 2, 154–160, DOI:10.4236/wjnse.2012.23020.
- M. Rabiei, A. Palevicius, A. Monshi, S. Nasiri, A. Vilkauskas and G. Janusas, Comparing Methods for Calculating Nano Crystal Size of Natural Hydroxyapatite Using X-Ray Diffraction, Nanomaterials, 2020, 10, 1627, DOI:10.3390/nano10091627.
- D. Balzar and H. Ledbetter, Voigt-function modeling in Fourier analysis of size- and strain-broadened X-ray diffraction peaks, J. Appl. Crystallogr., 1993, 26, 97–103, DOI:10.1107/S0021889892008987.
- B. E. Warren and B. L. Averbach, The separation of cold-work distortion and particle size broadening in X-ray patterns, J. Appl. Phys., 1952, 23, 497, DOI:10.1063/1.1702352.
- R. Thokala and J. Chaudhuri, Calculated elastic constants of wide band gap semiconductor thin films with a hexagonal crystal structure for stress problems, Thin Solid Films, 1995, 266, 189–191, DOI:10.1016/0040-6090(96)80022-8.
- A. Chadli, M. Halit, B. Lagoun, F. Mohamedi, S. Maabe, A. Cheriet, E. Hlil and H. Farh, Structural and Anisotropic Elastic Properties of Hexagonal YMnO3 in Low Symmetry Determined by First-Principles Calculations, Solid State Phenom., 2019, 297, 120–130, DOI:10.4028/www.scientific.net/SSP.297.120.
- D. P. Kozlenko, I. N. Goncharenko and B. N. Savenko, High pressure effects on the crystal and magnetic structure of La0.7Sr0.3MnO3, J. Phys.: Condens. Matter, 2004, 16, 6755–6762, DOI:10.1088/0953-8984/16/37/011.
- P. G. Radaelli, M. Marezio, H. Y. Hwang, S.-W. Cheong and B. Batlogg, Charge localization by static and dynamic distortions of the MnO6 octahedra in perovskite manganites, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 8992, DOI:10.1103/PhysRevB.54.8992.
- D. Louca, T. Egami, E. L. Brosha, H. Roder and A. R. Bishop, Local Jahn-Teller distortion in La1-xSrxMnO3 observed by pulsed neutron diffraction, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R8475, DOI:10.1103/PhysRevB.56.R8475.
- T. Tatarchuk, M. Bououdina, W. Macyk, O. Shyichuk, N. Paliychuk, I. Yaremiy, B. Al-Najar and M. Pacia, Structural, Optical, and Magnetic Properties of Zn-Doped CoFe2O4 Nanoparticles, Nanoscale Res. Lett., 2017, 12, 141, DOI:10.1186/s11671-017-1899-x.
- S. Mangavati, A. Pal, A. Rao, Z. Jiang and Y. Kuo, Reduction in low temperature thermal conductivity of Cu2Se via substitution of Se by Te atoms, J. Phys. Chem. Solids, 2022, 160, 110301, DOI:10.1016/j.jpcs.2021.110301.
- L. Motevalizadeh, Z. Heidary and M. E. Abrishami, Facile template-free hydrothermal synthesis and microstrain measurement of ZnO nanorods, Bull. Mater. Sci., 2014, 37, 397–405, DOI:10.1007/s12034-014-0676-z.
- S. Kumar, G. D. Dwivedi, S. Kumar, R. B. Mathur, U. Saxena, A. K. Ghosh, A. G. Joshi, H. D. Yang and S. Chatterjee, Structural, transport, and optical properties of (La0.6Pr0.4)0.65Ca0.35MnO3 nanocrystals: a wide band-gap magnetic semiconductor, Dalton Trans., 2015, 44, 3109–3117, 10.1039/C4DT03452J.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Tran Thi Ngoc Nhab,
Le Thi Hong Phonga,
Pham Hong Nama,
Tran Dang Thanh*ab and
Pham Thanh Phong
ab,
Tran Thi Ngoc Nhab,
Le Thi Hong Phonga,
Pham Hong Nama,
Tran Dang Thanh*ab and
Pham Thanh Phong *cd
*cd
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C space group. The inset of Fig. 1(a) shows the intensity of the main diffraction peaks of La0.7Sr0.3MnO3 nanopowders. The intensity of the main peak clearly increased as the annealed temperature increased from 700 °C to 800 °C, indicating the improvement of x = 0.3 crystallinity at higher annealed temperature. Besides, the full-width half-maximum (FWHM) of the main x = 0.3 peaks decreased as the annealed temperature increased. As shown in Fig. 1(b) and (c), the Rietveld analysis was applied in samples S1 and S2. The experimental Bragg reflections were consistent with their calculated positions. The a- and c-axis lattice parameters increased slightly with the sintering temperature, which is in very well agreement with the authors' previous report.11 From this diffraction data, the crystal sizes and related structural parameters of the samples were calculated, and the obtained results are discussed in the following section.
C space group. The inset of Fig. 1(a) shows the intensity of the main diffraction peaks of La0.7Sr0.3MnO3 nanopowders. The intensity of the main peak clearly increased as the annealed temperature increased from 700 °C to 800 °C, indicating the improvement of x = 0.3 crystallinity at higher annealed temperature. Besides, the full-width half-maximum (FWHM) of the main x = 0.3 peaks decreased as the annealed temperature increased. As shown in Fig. 1(b) and (c), the Rietveld analysis was applied in samples S1 and S2. The experimental Bragg reflections were consistent with their calculated positions. The a- and c-axis lattice parameters increased slightly with the sintering temperature, which is in very well agreement with the authors' previous report.11 From this diffraction data, the crystal sizes and related structural parameters of the samples were calculated, and the obtained results are discussed in the following section.

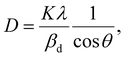
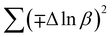 , Monshi et al.23 suggested the modified Scherrer formula to provide a more accurate value of D from all or some of the different peaks.
, Monshi et al.23 suggested the modified Scherrer formula to provide a more accurate value of D from all or some of the different peaks.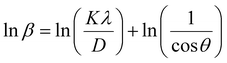
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β is drawn in terms of
β is drawn in terms of 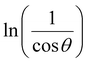 , then the y-intercept could give the value of
, then the y-intercept could give the value of 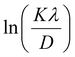 . Thus, the crystal size is as follows:
. Thus, the crystal size is as follows: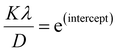
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs.
β vs. 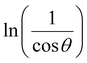 graph has been plotted for all the diffraction peaks. Fig. 2 displays the graph of ln
graph has been plotted for all the diffraction peaks. Fig. 2 displays the graph of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs.
β vs. 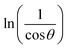 for both samples of LSMO nanoparticles. The fitting lines determined from eqn (3) for S1 and S2 were y = −4.7987 + 2.9748x and y = −4.9937 + 3.1941x, respectively. Therefore, the average crystalline size calculated using eqn (4) was 16.83 nm and 20.45 nm for S1 and S2, respectively.
for both samples of LSMO nanoparticles. The fitting lines determined from eqn (3) for S1 and S2 were y = −4.7987 + 2.9748x and y = −4.9937 + 3.1941x, respectively. Therefore, the average crystalline size calculated using eqn (4) was 16.83 nm and 20.45 nm for S1 and S2, respectively.
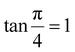 .23 However, due to errors associated with the experimental data, the least squares method gives the best slope value and equal to
.23 However, due to errors associated with the experimental data, the least squares method gives the best slope value and equal to 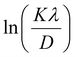 , indicating that some experimental points have to be removed to reduce the error and obtain a more accurate crystalline size. However, for comparison between methods, all the experimental points obtained from the XRD peaks of the samples remained the same.
, indicating that some experimental points have to be removed to reduce the error and obtain a more accurate crystalline size. However, for comparison between methods, all the experimental points obtained from the XRD peaks of the samples remained the same.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ
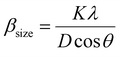 . Therefore, the total resulting broadening due to the strain and size of any diffraction line is
. Therefore, the total resulting broadening due to the strain and size of any diffraction line is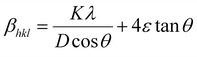
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and when sin
θ and when sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = tan
θ = tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ × cos
θ × cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, the following equation could be obtained:
θ, the following equation could be obtained: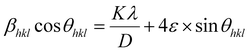
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as the y-axis and 4
θ as the y-axis and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as the x-axis, then the relationship between these two quantities is linear and the line has a slope, directly giving the value of the microstrain (ε). Meanwhile, the y-intercept is equal to the value of
θ as the x-axis, then the relationship between these two quantities is linear and the line has a slope, directly giving the value of the microstrain (ε). Meanwhile, the y-intercept is equal to the value of 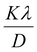 , from which the value of the crystal size could be determined. Fig. 3 shows a plot of βhkl
, from which the value of the crystal size could be determined. Fig. 3 shows a plot of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ versus 4
θ versus 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, and the red line denotes a good fitted line. The average crystal sizes determined from UDM were approximately 22.73 and 26.66 nm for S1 and S2, respectively. From the slope, the intrinsic average strain values were calculated to be 3.00 × 103 and 2.49 × 103 for S1 and S2, respectively. A positive value of the intrinsic strain indicates that this strain is a tensile strain, whereas a negative value indicates compressive strain.24
θ, and the red line denotes a good fitted line. The average crystal sizes determined from UDM were approximately 22.73 and 26.66 nm for S1 and S2, respectively. From the slope, the intrinsic average strain values were calculated to be 3.00 × 103 and 2.49 × 103 for S1 and S2, respectively. A positive value of the intrinsic strain indicates that this strain is a tensile strain, whereas a negative value indicates compressive strain.24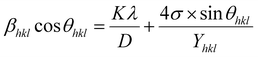
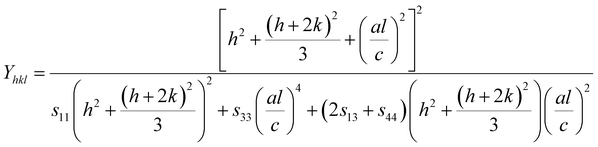
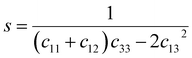
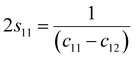
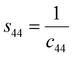
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C space group enforces on the average equal Mn–O bond lengths and thus prevents static coherent JT-type distortions of the MnO6 octahedron. Although neutron diffraction experiments have shown no obvious evidence for the existence of JT-type distortions in hexagonal or rhombohedral La0.7Sr0.3MnO3,30 Louca et al.31 proposed that the local atomic structure could deviate significantly from the average, and thus, the local JT distortion could persist even if the crystallographic structure has no JT distortion. Therefore, in the case of nano La0.7Sr0.3MnO3, the high value of Yhkl indicates that the dynamic incoherent local JT distortion of the lattice is significant in the nanoscale samples and fabricated by reactive milling method.
C space group enforces on the average equal Mn–O bond lengths and thus prevents static coherent JT-type distortions of the MnO6 octahedron. Although neutron diffraction experiments have shown no obvious evidence for the existence of JT-type distortions in hexagonal or rhombohedral La0.7Sr0.3MnO3,30 Louca et al.31 proposed that the local atomic structure could deviate significantly from the average, and thus, the local JT distortion could persist even if the crystallographic structure has no JT distortion. Therefore, in the case of nano La0.7Sr0.3MnO3, the high value of Yhkl indicates that the dynamic incoherent local JT distortion of the lattice is significant in the nanoscale samples and fabricated by reactive milling method.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ vs. 4
θ vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/Yhkl could be estimated. Fig. 4 displays the plotting of βhkl
θ/Yhkl could be estimated. Fig. 4 displays the plotting of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as a function of 4
θ as a function of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/Yhkl, and the red line indicates a good fitted line from eqn (9). The values of y-intercept found from the linear fit for S1 and S2 were 0.0062 and 0.0051, respectively, and the average crystal sizes were determined as 22.36 and 27.03 nm, respectively.
θ/Yhkl, and the red line indicates a good fitted line from eqn (9). The values of y-intercept found from the linear fit for S1 and S2 were 0.0062 and 0.0051, respectively, and the average crystal sizes were determined as 22.36 and 27.03 nm, respectively.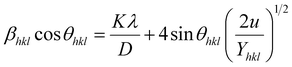
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl vs. 4
θhkl vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl(2/Yhkl)1/2. Fig. 5 shows a plotting of βhkl
θhkl(2/Yhkl)1/2. Fig. 5 shows a plotting of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl vs. 4
θhkl vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl(2/Yhkl)1/2, and the red line indicates a linear fit. The values of u were determined from the slope of the fitting line to be 0.199 and 0.166 GPa for S1 and S2, respectively. The average crystal sizes determined from the y-intercept were 0.0060 and 0.0050 for S1 and S2, respectively, so the crystal size values were 23.10 nm for S1 and 27.51 nm for S2. Given that σ = εYhkl and u = (ε2Yhkl)/2, the stress (σ) could be determined by the expression u = (σ2/2Yhkl). The results showed that the strain values (ε) were 3.10 × 10−3 and 2.38 × 10−3 (Yhkl ∼ average Young's modulus) for S1 and S2, respectively.
θhkl(2/Yhkl)1/2, and the red line indicates a linear fit. The values of u were determined from the slope of the fitting line to be 0.199 and 0.166 GPa for S1 and S2, respectively. The average crystal sizes determined from the y-intercept were 0.0060 and 0.0050 for S1 and S2, respectively, so the crystal size values were 23.10 nm for S1 and 27.51 nm for S2. Given that σ = εYhkl and u = (ε2Yhkl)/2, the stress (σ) could be determined by the expression u = (σ2/2Yhkl). The results showed that the strain values (ε) were 3.10 × 10−3 and 2.38 × 10−3 (Yhkl ∼ average Young's modulus) for S1 and S2, respectively.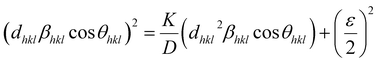
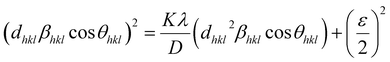
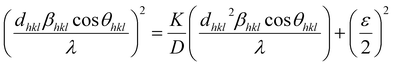
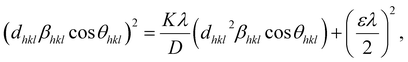
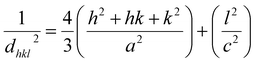
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl)2 on y-axis with respect to (dhkl2βhkl
θhkl)2 on y-axis with respect to (dhkl2βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl) on the x-axis for all peaks of S1 and S2 samples with the hexagonal phase. Fig. 6 displays that (dhklβhkl
θhkl) on the x-axis for all peaks of S1 and S2 samples with the hexagonal phase. Fig. 6 displays that (dhklβhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl)2 is plotted with respect to (dhkl2βhkl
θhkl)2 is plotted with respect to (dhkl2βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl), and the red line indicates a linear fit. The particle size (D) values were determined from the slope of the linearly fitted data as 18.01 and 20.83 nm for S1 and S2, respectively, whereas the root of the y-intercept provided the strain (ε) values of 3.40 × 10−3 and 2.76 × 10−3 for S1 and S2, respectively.
θhkl), and the red line indicates a linear fit. The particle size (D) values were determined from the slope of the linearly fitted data as 18.01 and 20.83 nm for S1 and S2, respectively, whereas the root of the y-intercept provided the strain (ε) values of 3.40 × 10−3 and 2.76 × 10−3 for S1 and S2, respectively.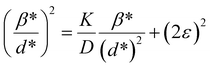
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ and d* = 2
θ/λ and d* = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ. So, eqn (18) could be modified as
θ/λ. So, eqn (18) could be modified as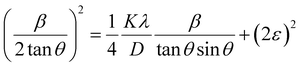
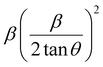 versus
versus 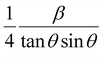 plots (see Fig. 7). The slope of the plotted straight line provides the average crystalline size, whereas the intercept gives the intrinsic strain of the samples. The average particle sizes were calculated from the plot as 17.78 nm for S1 and 21.20 nm for S2, which matched well with those obtained from the SSP model. Meanwhile, the calculated strain values from the Halder–Wagner plot were 3.46 × 10−3 for S1 and 3.12 × 10−3 for S2.
plots (see Fig. 7). The slope of the plotted straight line provides the average crystalline size, whereas the intercept gives the intrinsic strain of the samples. The average particle sizes were calculated from the plot as 17.78 nm for S1 and 21.20 nm for S2, which matched well with those obtained from the SSP model. Meanwhile, the calculated strain values from the Halder–Wagner plot were 3.46 × 10−3 for S1 and 3.12 × 10−3 for S2.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C space group. The average crystalline size and the various elastic properties of the La1−xSrxMnO3 (x = 0.3) nanomanganites, such as intrinsic strain, stress, and energy density, were determined by different methods, such as the modified Scherrer, W–H plot, SSP, and Halder–Wagner methods, via XRD peak broadening analysis. The calculation results showed that the SSP and Halder–Wagner methods are the two most suitable methods to accurately determine the crystal size and intrinsic strain of nanomanganites. Finally, the morphology and the distribution of the average particle size were studied via FESEM, which showed that the average size increased from 39 nm for S1 to 49 nm for S2 as the annealing temperature increased from 700 °C to 800 °C.
C space group. The average crystalline size and the various elastic properties of the La1−xSrxMnO3 (x = 0.3) nanomanganites, such as intrinsic strain, stress, and energy density, were determined by different methods, such as the modified Scherrer, W–H plot, SSP, and Halder–Wagner methods, via XRD peak broadening analysis. The calculation results showed that the SSP and Halder–Wagner methods are the two most suitable methods to accurately determine the crystal size and intrinsic strain of nanomanganites. Finally, the morphology and the distribution of the average particle size were studied via FESEM, which showed that the average size increased from 39 nm for S1 to 49 nm for S2 as the annealing temperature increased from 700 °C to 800 °C.





