Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The alkoxy radical polymerization of N-vinylpyrrolidone in organic solvents: theoretical insight into the mechanism and kinetics†
Quan V. Vo *a,
Truong Le Bich Tram*b,
Loc Phuoc Hoang
*a,
Truong Le Bich Tram*b,
Loc Phuoc Hoang *c,
Nguyen Thi Hoaa and
Adam Mechler
*c,
Nguyen Thi Hoaa and
Adam Mechler d
d
aThe University of Danang—University of Technology and Education, Danang 550000, Vietnam. E-mail: vvquan@ute.udn.vn; vovanquan1980@gmail.com
bDepartment of Science-Technology and Environment, The University of Danang, Danang 550000, Vietnam. E-mail: tlbtram@ac.udn.vn
cQuang Tri Teacher Training College, Dong Ha, Quang Tri 520000, Vietnam. E-mail: loc_hp@qtttc.edu.vn
dDepartment of Biochemistry and Chemistry, La Trobe University, Victoria 3086, Australia
First published on 4th August 2023
Abstract
Poly(N-vinylpyrrolidone) (PVP) is a polymer with many applications in cosmetic, pharmaceutical, and biomedical formulations due to its minimal toxicity. PVP can be synthesized through radical polymerization in organic solvents; this well-known industrial process is thoroughly characterized experimentally, however, quantum chemical modeling of the process is scarce: the mechanism and kinetics have not been thoroughly investigated yet. In this work, the mechanism and kinetics of the alkoxy radical polymerization of N-vinylpyrrolidone in organic solvents, namely isopropanol (IP) and toluene (TL), were successfully modeled by computational chemistry. The initiator radicals di-tert-butyl peroxide (TBO˙) and dicumyl peroxide (CMO˙) as well as the solvents isopropanol and toluene, were shown to be capable of assisting in the initiation reactions. The rate constant was influenced by the combination of initiators and solvent and the values of the rate constant of propagation were approximately 101–103 M−1 s−1. The radical polymerization of NVP with dicumyl peroxide as an initiator was comparable to that of di-tert-butyl peroxide in all of the examined organic solvents, whereas the solvents had less of an effect.
1. Introduction
In cosmetic, pharmaceutical, and biomedical formulations, poly(N-vinylpyrrolidone) (PVP) is frequently used because of its biocompatibility, biodegradability, potent complexing ability, and superior film-forming qualities.1 It is a nonionic, amorphous polymer that is soluble in both organic solvents and water.2,3 In medical formulations, it can be found in a wide range of granules, tablets, soft gelatin capsules, hydrogels, films, palettes, and other medical device coatings.2N-Vinylpyrrolidone (NVP, Fig. 1) is typically polymerized in an aqueous solution with hydrogen peroxide as initiator, or in organic solvents such as isopropanol (IP) or toluene (TL) with organic peroxides such as di-tert-butyl peroxide (TBO)2 or dicumyl peroxide (CMO)2 as initiators (Fig. 1).4–6 The radicals in the organic solvent, such as alcohols or toluene, act as the reaction's initiators when polymerization is carried out with organic peroxides like (TBO)2 or (CMO)2. It was discovered that the PVP made in organic solutions was more stable, and no pyrrolidone impurity production was seen, unlike when polymerization was carried out in aqueous solvents with H2O2 as an initiator.5 The polymerization of NVP in polar media by radicals i.e. HO˙ garnered some attention in the literature,7–16 where the mechanism and kinetics have been investigated.10,11,16 However, the alkoxy radical polymerization in organic solvents was not studied with the same fervor, despite of the fact that the PVP made in organic solutions was more stable and no pyrrolidone impurity production was seen.4,5
In the field of radical reactions and polymerizations, the in silico approach has gained popularity recently as a technique for analyzing the kinetics and mechanism of radical processes. While using the least amount of resources and time possible, new techniques and procedures create dependable data.17–30 In this study, we use a well-established method based on quantum chemistry,16,31,32 to investigate the alkoxy radical (TBO˙ and CMO˙) polymerization of N-vinylpyrrolidone in IP and TL.
2. Computational details
The kinetic calculations were performed using the quantum mechanics-based test for the overall free radical scavenging activity (QM-ORSA) technique,31 which is directly applicable given the chemical analogy between all radical reactions.17,33,34The rate constant (k) was determined by applying eqn (1) to the 1 M standard state at 298.15 K and the transition state theory (TST).35–39
 | (1) |
Those rate constants near the diffusion limit were modified.33 To obtain the apparent rate constants (kapp) for an irreversible bimolecular diffusion-controlled reaction in solvents at 298.15 K, the Collins–Kimball theory43 and the literature were consulted to determine the steady-state Smoluchowski rate constant (kD).33,44
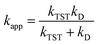 | (2) |
| kD = 4πRABDABNA | (3) |
DAB = DA + DB, where DA or DB is the mutual diffusion coefficient of A and B as calculated using the Stokes–Einstein formulation (4).43,45–47
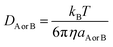 | (4) |
η is the viscosity of the solvents and a is the radius of the solute that was obtained in Gaussian calculations. The viscosity of isopropanol is 20.4 × 10−4 Pa s and that of toluene is 5.60 × 10−4 Pa s. Identifiable transition states had a single imaginary frequency. To ensure that each transition state is accurately associated with the pre- and post-complexes, calculations with intrinsic coordinates were conducted.
All computations for this investigation were performed utilizing the M06-2X/6-311++G(d,p) method from the Gaussian 16 software package.48 This model chemistry yields the most precise thermodynamics and kinetics outcomes.49–53 It is frequently used to assess the radical reactions with small errors in comparison to experimental data (kcalc/kexp ratio = 0.2–2.9).16,32,33,38,54-56 The SMD method was used to model the effects of isopropanol and toluene.57 AIM2000 software was used to conduct atom-in-molecule (AIM) analysis at the M06-2X/6-311++G(d,p) level.58,59
3. Results and discussion
3.1 Initiation reactions of TBO˙/CMO˙ in the organic solvents
To investigate the initiation reaction of the polymerization utilizing organic peroxides such as di-tert-butyl peroxide ((TBO)2) or dicumyl peroxide ((CMO)2) in organic solvents such as IP, or TL, all potential radical reactions could occur following the reactions 5–9 (Fig. 2). The alkoxy radicals are formed by heating peroxides in accordance with reaction 5, while the TBO˙, CMO˙ radicals can react with solvents or NVP at possible reactions, i.e. the formal hydrogen transfer (FHT, reactions 6, 7, and Table 1) and the radical adduct formation (RAF, reaction 8, 9 and Table 1). As shown in Table 1, the FHT mechanism for the IP/TL + TBO˙/CMO˙ reactions is thermodynamically spontaneous (ΔG° = −14.0 to −0.8 kcal mol−1), whereas the RAF mechanism is thermodynamically nonspontaneous (ΔG° > 0) for all of the studied solvents and radicals. Thus the kinetics of the IP/TL + TBO˙/CMO˙ reactions were computed and presented in Table 2 and Fig. 3.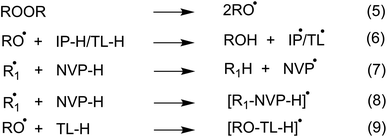 | ||
| Fig. 2 The initiation reaction of the TBO˙/CMO˙ in isopropanol (IP) and toluene (TL) (R:TB, CM; R1˙:TBO˙, CMO˙, IP˙, TL˙). | ||
| Solvents | Mechanisms | Positions | TBO˙ | CMO˙ |
|---|---|---|---|---|
| IP | FHT | C1–H | −5.2 | −5.4 |
| C2–H | −13.8 | −14.0 | ||
| O2–H | −0.8 | −1.0 | ||
| TL | FHT | C7–H | −13.0 | −13.4 |
| RAF | C1 | 11.3 | 12.6 | |
| C2 | 10.9 | 12.2 | ||
| C3 | 9.4 | 10.5 | ||
| C4 | 8.5 | 9.4 |
| Solvents | Mechanisms | TBO˙ | CMO˙ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔG≠ | κ | kapp | Γ | ΔG≠ | κ | kapp | Γ | |||
| a koverall = ∑kapp; Γ = kapp × 100/koverall | ||||||||||
| IP | FHT | C1–H | 16.7 | 13.0 | 2.70 × 102 | 1.2 | 15.2 | 8.4 | 2.10 × 103 | 2.7 |
| C2–H | 11.9 | 2.0 | 2.30 × 104 | 98.5 | 10.9 | 1.3 | 7.60 × 104 | 96.8 | ||
| O2–H | 18.3 | 361.9 | 8.00 × 101 | 0.3 | 16.7 | 107.9 | 3.90 × 102 | 0.5 | ||
| koverall | 2.34 × 104 | 7.85 × 104 | ||||||||
| TL | FHT | C7–H | 14.7 | 8.0 | 8.90 × 102 | 16.4 | 7.5 | 4.60 × 101 | ||
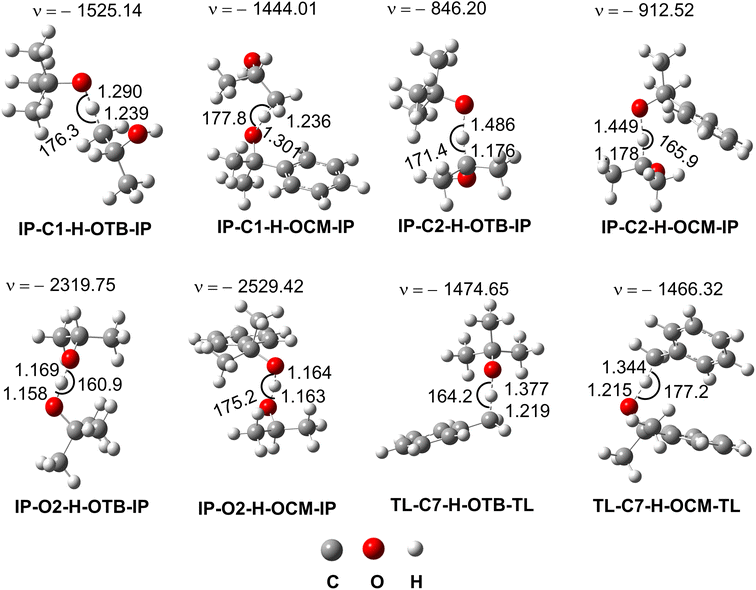
As shown in Table 2, the H-abstraction at the C2–H bond defined the IP + TBO˙/CMO˙ reactions with the kapp = 2.30 × 104 (Γ = 98.5%) and 7.60 × 104 (Γ = 96.8%) M−1 s−1 for the TBO˙ and CMO˙ radicals, respectively, whereas the FHT reaction of the O2–H bond contributed only 0.3–0.5% in the overall rate constant. Thus the IP-C2˙, which was formed by reaction 6 in the IP solvent, is the main radical for the following reactions (i.e. 7 and 8). At the same time, the H-abstraction at the C7–H characterized the TL + TBO˙/CMO˙ reactions and formed the TL-C7˙ radical with kapp = 8.90 × 102 and 4.60 × 101 M−1 s−1 for the TBO˙ and CMO˙ radicals, respectively, however, these are slower than the IP + TBO˙/CMO˙ reactions. Thus in the IP solution, the NVP can react with three main radicals including IP-C2˙, TBO˙ and CMO˙, whereas in the TL solvent, the IP-C2˙ is replaced by the TL-C7˙ radical.
To gain insight into the structure of the TSs, the AIM analysis was used to measure the intermolecular contacts (Table S1, Fig. S2, ESI†). It was found that the TS-IP-C2-H-OTB/OCM-IP are stabilized by intermolecular contacts at the H5⋯C2, H5⋯O13, (TBO)H3⋯O2, (TBO)H3⋯H1, (TBO)H1⋯C1, (CMO)H1⋯O2, (CMO)C4⋯H1 and ring critical points (RCPs) at RCP1, RCP2 and RCP3, whereas those of the C1–H are only defined by intermolecular contacts H7⋯C1, H7⋯O13, (CMO)C6⋯H1 and RCP1, RCP2. Intermolecular contacts and RCPs define the stability of TSs of the TS-IP-O2-H-OTB/OCM-IP; however, the EH–B(O2–H12) values (EH–B(O2–H12) = −87.5 and −90.3 kcal mol−1) are significantly lower than the EH–B(C2–H5) values (EH–B(C2–H5) = −69.3 and −69.9 kcal mol−1). Therefore, the O2–H12 bond may be more difficult to break than the C2–H5 bond when forming the products. This may account for the high stability of TS-IP-C2-H-OTB/OCM-IP and the rapid H-abstraction at the C2–H bond. At the TSs of TL-C7-H + OTB/OCM reactions, the O16–H13 bond at the TS-TL-C7-H-OTB is more stable than that at the TS-TL-C7-H-OCM, which can lead to rapid H-abstraction by the TBO radical.
The reaction of NVP with alkyl radicals i.e. IP-C2˙/TL-C7˙ was first evaluated and the results are presented in Table 3 and Fig. 4. It was found that the RAF reaction at C7 position dominated the NVP + IP-C2˙/TL-C7˙ reactions (Γ = 99.9%), however the rate constant of the NVP + IP-C2˙ reaction (koverall = 6.21 × 103 M−1 s−1) was about 103 times faster than that of the NVP + TL-C7˙ (koverall = 4.50 M−1 s−1). The other reactions had no contributions to the overall rate constant of the alkyl radical scavenging activity of NVP. Thus for the alkoxy radicals i.e. TBO˙ and CMO˙, the NVP + TBO˙/CMO˙ reactions were only focused on the RAF pathway at the C7 position (Table 3 and Fig. 4).
| RAD/Sol. | Mechanism | ΔG≠ | κ | kapp | Γ | |
|---|---|---|---|---|---|---|
| IP-C2˙/IP | FHT | C3–H | 17.7 | 8.1 | 5.70 | 0.1 |
| C4–H | 23.2 | 22.0 | 1.40 × 10−3 | 0.0 | ||
| C5–H | 20.8 | 21.0 | 7.00 × 10−2 | 0.0 | ||
| RAF | C6 | 35.2 | 1.0 | 1.10 × 10−13 | 0.0 | |
| C7 | 12.4 | 1.2 | 6.20 × 103 | 99.9 | ||
| koverall | 6.21 × 103 | |||||
| TL-C7˙/TL | FHT | C3–H | 24.6 | 16.0 | 9.10 × 10−5 | 0.0 |
| C4–H | 26.2 | 21.0 | 8.80 × 10−6 | 0.0 | ||
| C5–H | 22.4 | 18.0 | 4.10 × 10−3 | 0.1 | ||
| RAF | C6 | 22.2 | 1.7 | 6.20 × 10−4 | 0.0 | |
| C7 | 16.7 | 1.4 | 4.50 | 99.9 | ||
| koverall | 4.50 | |||||
| TBO˙/IP | RAF | C7 | 11.4 | 1.1 | 3.10 × 104 | |
| CMO˙/IP | 9.7 | 1.0 | 5.20 × 105 | |||
| TBO˙/TL | 12.7 | 1.2 | 3.40 × 103 | |||
| CMO˙/TL | 10.5 | 1.1 | 1.50 × 105 | |||
As shown in Table 3, the alkoxy radical reactions of NVP in the IP solvent were faster than in the TL solution. The NVP + TBO˙/CMO˙ reactions in the IP solution were about 9.1 and 3.5 times faster than those in the TL solution for TBO˙ and CMO˙ respectively. It is important to notice that in the IP solution, the formed radical from the solvent (IP-C2˙) can react with NVP as fairly fast as the NVP + TBO˙/CMO˙ reactions (k = 103–105 M−1 s−1), thus the IP-C2˙ may also contribute to the propagation reactions. However, in the TL solution, the NVP + TBO˙/CMO˙ reactions were about 103−104 times faster than the NVP + TL-C7˙ reaction.
The AIM analysis (Table S1, Fig. S2, ESI†) indicated that energies (EH–B) of the C7⋯C/O intermolecular contacts of RAF transition states are in the range of −13.1 to −9.8 kcal mol−1. The replacement of the methyl group at TBO˙ by phenyl at CMO˙ could reduce the EH–B(C7⋯O) values, particularly in TL solvent. That may be a reason for the high rate constant of the CMO˙ + NVP reaction.
3.2 The propagation reaction
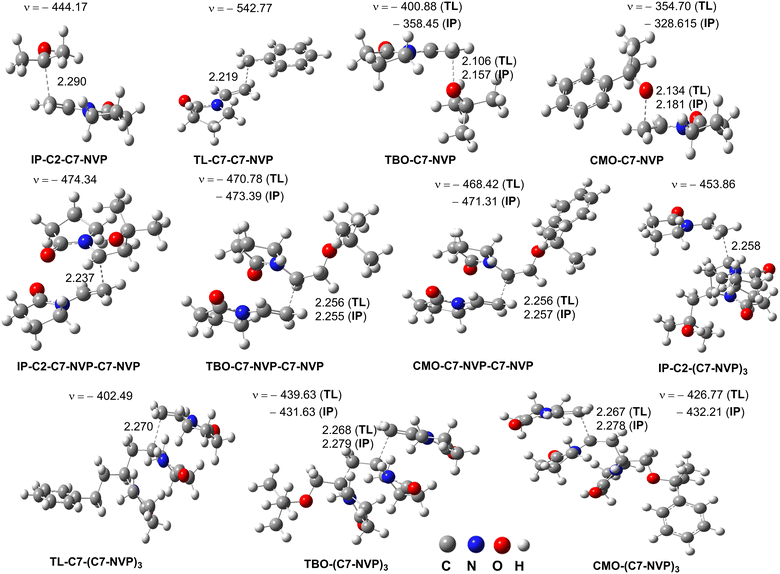
As previously mentioned, the main intermediates of the radical process were IP-C2-C7-NVP, TL-C7-C7-NVP, TBO-C7-NVP, and CMO-C7-NVP (Table 3 and Fig. 3). These radicals were thought to follow the RAF pathway, the basic reaction mechanism of radical chain polymerization, and react with NVP at the most active site (C7). Thus, using the QM-ORSA approach,33 the propagation rate constant (kp) of the reaction between IP-C2-C7-NVP/TL-C7-C7-NVP/TBO-C7-NVP/CMO-C7-NVP and NVP was determined. The results are provided in Table 4, and the TSs are illustrated in Fig. 5.| Reactions | Solvents | ΔG≠ | κ | kp |
|---|---|---|---|---|
| IP-C2-C7-NVP˙ + NVP | IP | 13.4 | 1.2 | 1.20 × 103 |
| TL-C7-C7-NVP˙ + NVP | TL | 12.4 | 1.2 | 6.10 × 103 |
| TBO-C7-NVP˙ + NVP | IP | 13.0 | 1.2 | 2.10 × 103 |
| CMO-C7-NVP˙ + NVP | 15.5 | 1.2 | 3.30 × 101 | |
| TBO-C7-NVP˙ + NVP | TL | 13.5 | 1.2 | 1.10 × 103 |
| CMO-C7-NVP˙ + NVP | 15.7 | 1.2 | 2.50 × 101 | |
| IP-C2-C7-NVP-C7-NVP˙ + NVP | IP | 16.1 | 1.2 | 1.18 × 101 |
| TL-C7-C7-NVP-C7-NVP˙ + NVP | TL | 13.7 | 1.2 | 6.75 × 102 |
| TBO-C7-NVP-C7-NVP˙ + NVP | IP | 12.6 | 1.1 | 3.96 × 103 |
| CMO-C7-NVP-C7-NVP˙ + NVP | 14.4 | 1.0 | 1.73 × 102 | |
| TBO-C7-MVP-C7-NVP˙ + NVP | TL | 13.9 | 1.2 | 4.82 × 102 |
| CMO-C7-NVP-C7-NVP˙ + NVP | 13.7 | 1.0 | 5.63 × 102 |
As shown in Tables 4, in the IP solution, the kp value of the IP-C2-C7-NVP + NVP reaction (kp = 1.20 × 103 M−1 s−1) was similar to that of the TBO-C7-NVP + NVP reaction (kp = 2.10 × 103 M−1 s−1), whereas these values were about 36.4 and 63.6 (for IP-C2-C7-NVP and TBO-C7-NVP, respectively) times higher than that of the CMO-C7-NVP + NVP reaction (kp = 3.30 × 101 M−1 s−1). Therefore, the radical polymerization of NVP in the isopropanol solution with (CMO)2 as an initiator could produce PVP with a solvent molecule (IP-C2). That is in good agreement with the experimental data.4 However, when (TBO)2 is used as an initiator, the PVP may contain both the solvent (IP) and initiator (TB) structures.
A similar trend was also observed in the TL solvent, the TL-C7-C7-NVP/TBO-C7-NVP + NVP reactions were about 24.4 (kp = 6.10 × 103 M−1 s−1) and 4.4 (kp = 1.10 × 103 M−1 s−1) times faster than the CMO-C7-NVP + NVP reaction (kp = 2.50 × 101 M−1 s−1), respectively. Being the solvent, the amount of TL is significantly greater than that of the initiators, i.e. (TBO)2 or (CMO)2, thus the PVP produced this way could contain residues of both the solvent (TL) and initiators (TB, CM), despite the rate constant of the TL-C7˙ + NVP reaction being lower than those of the TBO˙/CMO˙ + NVP reactions (Table 3).
The investigation of the chain extension (adding the second NVP molecule) revealed that the kp values (kp = 101–102 M−1 s−1, Table 4, Fig. 3 and 5) were comparable to those of the initial propagation reactions. It appears that the rate constants of the propagation reactions are in the range of 101–103 M−1 s−1, depending on the performed radicals and solvents.
Since the atoms adjacent to the center of the radicals are identical, the propagation rate constants of CMO-C7-NVP + NVP in both IP and TL were found to be lower than those of other propagation reactions. However, the kp values for the CMO-C7-NVP-C7-NVP + NVP were fairly similar to those of the TBO-C7-NVP-C7-NVP + NVP reactions. This could be due to the steric effects of CMO in the CMO-C7-NVP + NVP reaction.60
4. Conclusion
Using computational chemistry, the mechanism and kinetics of the alkoxy radical polymerization of N-vinylpyrrolidone in organic solvents, namely isopropanol, and toluene, have been successfully determined. It was discovered that both solvents, i.e. isopropanol and toluene could contribute to the initiation reactions alongside the initiator radicals TBO˙ and CMO˙. The rate constant varied as a function of the initiators and solvents used. The values of the constant rate of propagation were approximately 101–103 M−1 s−1. In all of the analyzed organic solvents, the radical polymerization of NVP with (CMO)2 as an initiator occurred fairly similarly with (TBO)2, whereas the solvents could contribute to the radical polymerization of NVP.Author contributions
Quan V. Vo: conceptualization, methodology, investigation, formal analysis, funding acquisition, writing – original draft, supervision. Truong Le Bich Tram, Hoang Phuoc Loc, Nguyen Thi Hoa: formal analysis, data curation, investigation, visualization, writing – original draft. Adam Mechler: project supervision, administration, software, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Vietnamese Ministry of Education and Training under project number B2021-DNA-18 (T. L. B. T.).References
- M. Kurakula and G. K. Rao, J. Drug Delivery Sci. Technol., 2020, 60, 102046 CrossRef CAS PubMed.
- M. Teodorescu and M. Bercea, Polym.-Plast. Technol. Eng., 2015, 54, 923–943 CrossRef CAS.
- Y. Luo, Y. Hong, L. Shen, F. Wu and X. Lin, AAPS PharmSciTech, 2021, 22, 1–16 CrossRef PubMed.
- F. Haaf, A. Sanner and F. Straub, Polym. J., 1985, 17, 143–152 CrossRef CAS.
- R. Awasthi, S. Manchanda, P. Das, V. Velu, H. Malipeddi, K. Pabreja, T. D. Pinto, G. Gupta and K. Dua, in Engineering of Biomaterials for Drug Delivery Systems, Elsevier, 2018, pp. 255–272 Search PubMed.
- J.-C. An, A. Weaver, B. Kim, A. Barkatt, D. Poster, W. N. Vreeland, J. Silverman and M. Al-Sheikhly, Polymer, 2011, 52, 5746–5755 CrossRef CAS.
- A. Davison, D. Sangster, J. Lynn and E. Senogles, J. Polym. Sci., 1976, 249–257 CAS.
- J. Davis, D. Sangster and E. Senogles, Aust. J. Chem., 1981, 34, 1423–1431 CrossRef CAS.
- C. Dispenza, M. A. Sabatino, N. Grimaldi, B. Dahlgren, M. Al-Sheikhly, J. F. Wishart, Z. Tsinas, D. L. Poster and M. Jonsson, Radiat. Phys. Chem., 2020, 174, 108900 CrossRef CAS.
- N. Bartoszek, P. Ulański and J. M. Rosiak, Int. J. Chem. Kinet., 2011, 43, 474–481 CrossRef CAS.
- P. Sawicki, G. Łapienis, S. Kadłubowski, P. Ulański and J. M. Rosiak, Radiat. Phys. Chem., 2023, 202, 110543 CrossRef CAS.
- K. M. Koczkur, S. Mourdikoudis, L. Polavarapu and S. E. Skrabalak, Dalton Trans., 2015, 44, 17883–17905 RSC.
- G. Ghosh, M. K. Naskar, A. Patra and M. Chatterjee, Opt. Mater., 2006, 28, 1047–1053 CrossRef CAS.
- R. Singh and D. Singh, J. Mater. Sci.: Mater. Med., 2012, 23, 2649–2658 CrossRef CAS PubMed.
- M. Wang, L. Xu, H. Hu, M. Zhai, J. Peng, Y. Nho, J. Li and G. Wei, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 265, 385–389 CrossRef CAS.
- Q. V. Vo, T. L. B. Tram, N. T. Hoa, A. N. Au-Duong and A. Mechler, Polym. Degrad. Stab., 2023, 216, 110483 CrossRef CAS.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef.
- B. H. Northrop and R. N. Coffey, J. Am. Chem. Soc., 2012, 134, 13804–13817 CrossRef CAS PubMed.
- V. Fındık, I. Degirmenci, Ş. Çatak and V. Aviyente, Eur. Polym. J., 2019, 110, 211–220 CrossRef.
- E. Frick, C. Schweigert, B. B. Noble, H. A. Ernst, A. Lauer, Y. Liang, D. Voll, M. L. Coote, A.-N. Unterreiner and C. Barner-Kowollik, Macromolecules, 2016, 49, 80–89 CrossRef CAS.
- I. Degirmenci, S. u. k. Eren, V. Aviyente, B. De Sterck, K. Hemelsoet, V. Van Speybroeck and M. Waroquier, Macromolecules, 2010, 43, 5602–5610 CrossRef CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823–1835 CrossRef CAS.
- P. Deglmann, I. Müller, F. Becker, A. Schäfer, K. D. Hungenberg and H. Weiß, Macromol. React. Eng., 2009, 3, 496–515 CrossRef CAS.
- C. Y. Lin, E. I. Izgorodina and M. L. Coote, Macromolecules, 2010, 43, 553–560 CrossRef CAS.
- P. Deglmann, K. D. Hungenberg and H. M. Vale, Macromol. React. Eng., 2017, 11, 1600037 CrossRef.
- P. Deglmann, K. D. Hungenberg and H. M. Vale, Macromol. React. Eng., 2018, 12, 1800010 CrossRef.
- M. Dossi, G. Storti and D. Moscatelli, Macromol. Theory Simul., 2010, 19, 170–178 CrossRef CAS.
- E. Mavroudakis, D. Cuccato and D. Moscatelli, Polymers, 2015, 7, 1789–1819 CrossRef CAS.
- J. A. Kretzmann, D. Ho, C. W. Evans, J. H. Plani-Lam, B. Garcia-Bloj, A. E. Mohamed, M. L. O'Mara, E. Ford, D. E. Tan and R. Lister, Chem. Sci., 2017, 8, 2923–2930 RSC.
- M. D. Nothling, Z. Xiao, N. S. Hill, M. T. Blyth, A. Bhaskaran, M. A. Sani, A. Espinosa-Gomez, K. Ngov, J. White and T. Buscher, Sci. Adv., 2020, 6, eaaz0404 CrossRef CAS PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed.
- Q. V. Vo, N. T. Hoa and A. Mechler, Polym. Degrad. Stab., 2021, 185, 109483 CrossRef CAS.
- M. E. Alberto, N. Russo, A. Grand and A. Galano, Phys. Chem. Chem. Phys., 2013, 15, 4642–4650 RSC.
- N. T. Hoa and Q. V. Vo, Chemosphere, 2023, 314, 137682 CrossRef CAS PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy 1.0.2, Cinvestav, Mérida, Yucatán, 2018 Search PubMed.
- E. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100, 2984–2991 CrossRef CAS.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425–437 CrossRef CAS.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- G. G. Stokes, Mathematical and Physical Papers, University Press, Cambridge, 1905 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, G. Z. J. Bloino, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- M. Carreon-Gonzalez, A. Vivier-Bunge and J. R. Alvarez-Idaboy, J. Comput. Chem., 2019, 24, 2103–2110 CrossRef PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. K. Chandra, P.-C. Nam and M. T. Nguyen, J. Phys. Chem. A, 2003, 107, 9182–9188 CrossRef CAS.
- C. Iuga, J. R. l. Alvarez-Idaboy and N. Russo, J. Org. Chem., 2012, 77, 3868–3877 CrossRef CAS PubMed.
- Q. V. Vo, M. V. Bay, P. C. Nam and A. Mechler, J. Phys. Chem. B, 2019, 123, 7777–7784 CrossRef CAS PubMed.
- Q. V. Vo, M. V. Bay, P. C. Nam, D. T. Quang, M. Flavel, N. T. Hoa and A. Mechler, J. Org. Chem., 2020, 85, 15514–15520 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- F. Biegler-König, AIM 2000, University of Applied Sciences, Bielefeld, Germany, 2000 Search PubMed.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- H. Fischer and L. Radom, Angew. Chem., Int. Ed., 2001, 40, 1340–1371 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra03820c |
| This journal is © The Royal Society of Chemistry 2023 |