Machine learning of atomic force microscopy images of organic solar cells

Abstract

The bulk heterojunction structures of organic photovoltaics (OPVs) have been overlooked in their machine learning (ML) approach despite their presumably significant impact on power conversion efficiency (PCE). In this study, we examined the use of atomic force microscopy (AFM) images to construct an ML model for predicting the PCE of polymer : non-fullerene molecular acceptor OPVs. We manually collected experimentally observed AFM images from the literature, applied data curing and performed image analyses (fast Fourier transform, FFT; gray-level co-occurrence matrix, GLCM; histogram analysis, HA) and ML linear regression. The accuracy of the model did not considerably improve even by including AFM data in addition to the chemical structure fingerprints, material properties and process parameters. However, we found that a specific spatial wavelength of FFT (40–65 nm) significantly affects PCE. The GLCM and HA methods, such as homogeneity, correlation and skewness expand the scope of image analysis and artificial intelligence in materials science research fields.

---

Introduction

Scalable and low-cost solar energy conversion devices are indispensable to fostering sustainability in society. Consequently, lightweight and colour-tunable organic photovoltaics (OPVs) composed of binary and ternary organic semiconductors have assumed a prominent position in scientific inquiry and application to industries.^1–3 Owing to recent advancements in high-performance p-type conjugated polymers and n-type non-fullerene acceptor molecules (NFA),^4–6 the power conversion efficiency (PCE) of OPVs has significantly increased to nearly 20%.^7–11 High performance is achieved through efficient photoenergy conversion processes comprising photoabsorption, exciton diffusion, charge separation and charge transport with minimal loss.^12–15 One of the essential factors in facilitating these multi-physical phenomena is optimising the bulk heterojunction (BHJ) structure of a p/n-blended film, which is fabricated through a solution process, including a p/n blend ratio, solvent, additive and annealing.^16–21 The resulting morphological and crystalline features of the BHJs are characterized by atomic force microscopy (AFM),^22–24 transmission electron microscopy (TEM),^25–27 X-ray diffractometry (XRD)^28–30 and neutron scattering.^31–33 Researchers typically assess the quality of the morphology based on observed domain size, surface roughness and uniformity. Generally, the morphology of BHJ with small and fine domains shows a higher PCE than that with large and coarse ones, owing to the large p/n surface and high charge separation efficiency. However, advanced analyses of massive image data and a deeper understanding have been lacking so far.

Machine learning (ML) empowered by artificial intelligence (AI) has garnered significant attention as an alternative approach to rapidly discovering new materials and scientific principles.^34–37 In this context, ML has been increasingly deployed for the exploration of organic electronic materials, such as OPVs,^38–45 organic light-emitting diodes (OLEDs)^46–48 and organic thin-film transistors (OTFTs).^49–51 Typically, digital fingerprints associated with chemical structures, molecular properties obtained from experiments and quantum chemical calculations and other extracted feature variables are learned in conjunction with the respective objective variables, such as PCE of OPVs, photoluminescence quantum yield of OLEDs and charge carrier mobility of OTFTs. While the film morphology of these thin-film devices is crucial to their performance, attempts to incorporate image analysis data into ML models remain challenging. Some examples of AFM (or TEM) image analysis relating to OPVs include a fast Fourier transform (FFT) analysis of poly(3-hexylthiophene) (P3HT) : [6,6]-phenyl-C₆₁-butyric acid methyl ester (PCBM) film,²² image recognition of fibrous structures of P3HT film,⁵² miscibility of binary/ternary mixture in the framework of Flory–Huggins theory⁵³ and electron spectroscopic imaging to identify polymer and NFA domains.⁵⁴ Despite the informative acquisition of film surface morphology by widely used AFM, quantitative and comprehensive analyses of these images in large datasets have remained unexplored, possibly due to the non-uniformity in image quality, scattered location in digital space and diverse image processing methods.

In this study, we present an approach where AFM images were integrated into an ML model for predicting the PCE of binary (polymer and NFA) BHJ-OPVs. After gathering AFM images from literature sources, we performed data curation and analysis, followed by the construction of an ML model. We examined the combinational effects of material properties such as bandgap (E_g) and highest occupied molecular orbital (HOMO) of both polymers and NFAs. Our results indicate that even though achieving high prediction accuracy of PCEs is challenging, the characteristic FFT wavelength proved to be crucial to PCE prediction. Our study establishes a basis for interpreting AFM images and sets the stage for future exploration of OPV materials.

Results and discussion

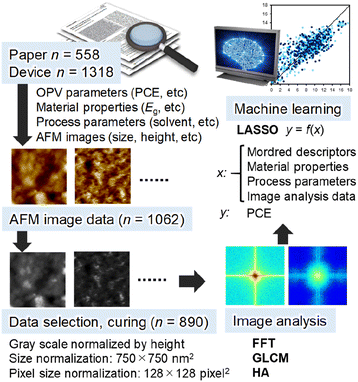
The workflow of this study is illustrated in Fig. 1. The basis data are binary polymer : NFA OPVs (the number of data = 1318), which were previously collected by us from literature (the number of papers, n = 558).^24,55 The dataset comprises simplified molecular input line entry system (SMILES) of chemical structure, HOMO, the lowest unoccupied molecular orbital (LUMO), E_g, weight-averaged molecular weight (M_w) and polydispersity index (PDI) of both polymer (SMILES is a repeating unit) and NFA (M = the molecular weight and PDI = 1), along with the OPV parameters (PCE; short-circuit current density, J_SC; open-circuit voltage, V_OC; fill factor, FF). We define HOMO, LUMO, E_g, M_w (M) and PDI as the material properties and polymer : NFA blend ratio, solvent and additive as the process parameters (Table S1 (ESI†)). SMILES were converted to 2-dimensional Mordred descriptors (1613 descriptors, Table S2 (ESI†))⁵⁶ and used as the inputs. Then, we manually extracted an AFM image (topography and phase) of each OPV device and converted them to a jpg format. The image size (spatial length) and height scale (the minimum height was shifted to zero) were also digitized. Totally, 1062 topography and 649 phase images were obtained. The statistics of spatial size and height scale of topographic images are shown in Fig. S1 (ESI†), where the typical image size is 2 × 2 or 5 × 5 μm², and the typical height scale is 5–20 nm. Subsequently, we selected AFM images by considering (1) no superimposition such as a sample name and scale bar in the active area (750 × 750 nm²) and (2) height scale availability. As a result, 890 images with a spatial size of 750 × 750 nm² and pixel size of 128 × 128 pixel² (5.86 nm per pixel) were extracted and applied to data curing (conversion to a greyscale and brightness normalization by height). We did not make data augmentation of images (e.g. rotation and inversion), which is often used for artificial neural network. Each AFM image corresponds to an individual device, where image extraction at a different position in the same AFM image was not performed. The AFM images in greyscale were analysed by FFT,^57,58 grey-level co-occurrence matrix (GLCM)^59,60 and histogram analysis (HA). The obtained parameters were used in the ML investigation.

Fig. 1 Schematic of the workflow in this study. The example AFM images are taken from a literature²⁴ with permission.

Fig. 2a shows FFT analysis of AFM images for the low (1.03%),⁶¹ middle (8.02%)⁶² and high (17.1%)⁶³ PCE. The 2-dimensional Fourier power spectra (FPS) were converted to isotropic ones (IFPS), which exhibit multiple characteristic peaks at shorter than 100 nm (Fig. 2b). The minimum and maximum spatial wavelengths are 11.72 (= 5.86 × 2) and 1500 (= 750 × 2) nm, respectively. For a comparison of spatial wavelength among different height-scale AFM images, IFPS was normalized by the intensity at 1500 nm. And then, the power values for each spatial wavelength (from 11.72 to 300 nm, 124 points in total) were used as the input parameters in the ML analysis. Instead of losing height information in the normalization and high pass filter (>300 nm⁻¹) process, HA data (the maximum, mean, variance, energy, contrast, entropy, skewness, and kurtosis values shown in Fig. S2 (ESI†)) were incorporated together with IFPS. For example, the variance and skewness of the histogram are related to the surface roughness.

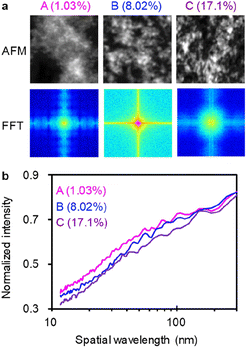Fig. 2 FFT analysis of AFM images. (a) Upper panels: original AFM images (grey-scale); lower panels: their FFT images. The AFM images of BHJ films (A, B, and C) were taken from literature^61–63 with permission and showed PCE of 1.03, 8.02 and 17.1%, respectively. (b) IFPS of A, B, and C.

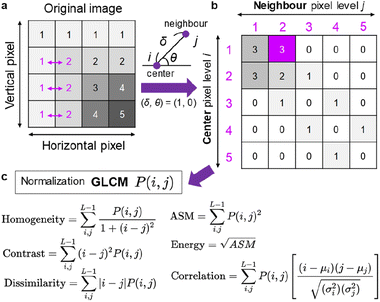
In addition to the FFT and HA analyses, we used GLCM that is a conventional but useful image texture analysis method applied to various images.^59,60 As shown in Fig. 3a, an original grey-scale AFM image, each pixel of which possesses a brightness level (0–255), was analysed by counting the pixel values in the neighbour. The definition of neighbour is given by (δ, θ), where δ (from 1 to the maximum pixel size) is the distance from the centre pixel, and θ (from 0 to 90°) is the angle from the horizontal axis. An example of (δ, θ) = (1, 0°) is illustrated in Fig. 3b, together with the acquired GLCM matrix: P(i, j). The row (i) and column (j) of the matrix correspond to the neighbour pixel level and centre pixel level, respectively. This matrix example indicates high values in the left top, which means that the pixels with low brightness levels (1 or 2) locate at a specific region. The example also shows a convergence along the diagonal line, which indicates that the change in brightness level is moderate. If high counted values appear in the right top and/or left bottom, the change of brightness level is steep. The acquired GLCM with different δ (2–10 pixels) and the horizontal direction (θ = 0°) was then subjected to various statistics such as homogeneity, contrast, dissimilarity, angular second moment (ASM), contrast, energy and correlation (Fig. 3c).

Fig. 3 Schematic of GLCM analysis of AFM image. (a) Original grey scale image (the colour is inverted for an easier looking). (b) Matrix P (i, j) calculated from the original image with (δ, θ) = (1, 0). The purple cell: P (1, 2) is calculated by counting the neighbours indicated by the arrows in (a). (c) Equations (homogeneity, contrast, dissimilarity, ASM, energy, and correlation) for the analysis of GLCM.

A linear regression using least absolute shrinkage and selection operator (LASSO)^64,65 was performed using Mordred descriptors, material properties and process parameters as the input parameters. The correlation of experimental and predicted PCE values are displayed in Fig. 4a, where the train data (n = 623) and test data (n = 267) exhibited the correlation coefficient (r) values of 0.802 and 0.747, respectively. The root-mean-square error (RMSE) values are appended in the caption. The r of train data is lower than those obtained by random forest (RF) regression (r = 0.83–0.85 for 5-fold cross validation) in the previous study using similar explanatory variables.⁵⁵ However, we used LASSO in this study to discuss the polarity of variable coefficients. The negative and positive coefficients (top 30 for each sorted in decent order) are shown in the left and right panels of Fig. 4b, respectively (the list is provided in Table S3 (ESI†)). Most of the important variables are Mordred descriptors derived from the chemical structures, while the material properties of LUMO of NFA, PDI of polymer and E_g of NFA along with the process parameter of 1,2,4-trimethylbenzene solvent (Solvent_TMB) are ranked on the high level. The most important positive and negative parameters are averaged and centred Moreau-Broto autocorrelation of lag 0 weighted by ionization potential (AATSC0i) of polymer and Geary coefficient of lag 6 weighted by intrinsic state (GATS6s) of NFA, respectively.^66,67 They are obtained by calculating autocorrelation and quantifying the clustering in 2-dimensional space, although their meaning is difficult to correlate directly with a physical property. However, multi-collinearity calculations of these parameters revealed that AATSC0i appears to correlate with AMID_X (averaged molecular ID on halogen atoms) and nF (number of F atoms) with r = 0.881 and 0.863, respectively (Table S4 (ESI†)). The addition of halogen atoms (typically fluorine) in the polymer is thought to fine-tune its energy level and improve the BHJ morphology. GATS6s was also found to correlate with NtN (the sum of nitrogen atoms) and C1SP1 (sp carbon bound to 1 other carbon) with r = −0.753 Table S5 (ESI†). This is linked to the cyano substituent (–CN) widely appended to efficient NFAs. Meanwhile, the positive, large coefficient of –LUMO of NFA indicates that the deepened LUMO level of NFA contributes to the increase of PCE, which is understood from the increased offset for efficient electron transfer from LUMO of polymer to that of NFA.

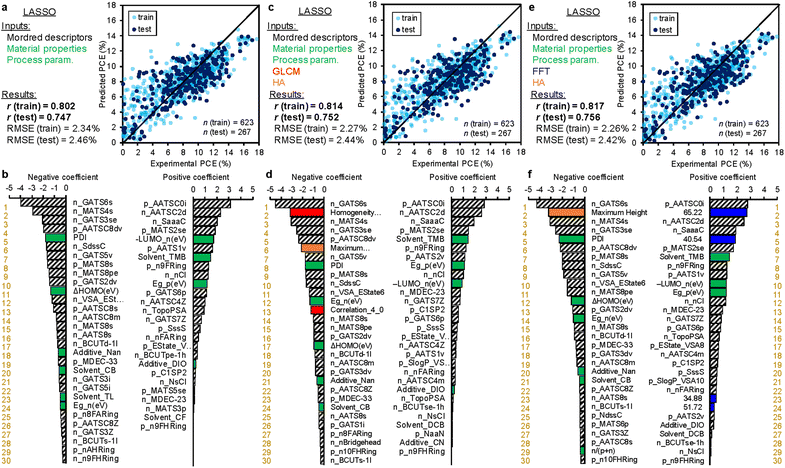Fig. 4 Results of LASSO regression. (a) and (b) The explanatory variables are chemical structures (Mordred descriptors), material properties (bandgap, etc.), and process parameters (solvent, etc.). (c) and (d) The aforementioned parameters plus GLCM and HA data. (e) and (f) The aforementioned parameters plus FFT and HA data. The upper panels (a, c, and e) are the regression plots of experimental (horizontal) and predicted (vertical) PCE. The white-blue (n = 623) and dark blue (n = 267) circles are the train and test data, respectively. The correlation coefficient (r) values of the train and test data are appended. The lower panels (b, d, and f) are the feature importance in decent order. The green, red, orange, and blue bars correspond to the material properties and process parameters, GLCM parameters, HA parameters, and FFT parameters, respectively. A complete list of rankings is provided in Tables S3, S6, and S7 (ESI†).

Even after additional inclusion of GLCM and HA data into the explanatory variables, the prediction accuracy was not improved. As shown in Fig. 4c, the r values of train and test data are 0.814 and 0.752, respectively, similar to those of Fig. 4a. The ranking of coefficients in Fig. 4d was also very similar, while the GLCM parameters were ranked on the 2nd (homogeneity of δ = 2) and 13th (correlation of δ = 4) in the negative polarity (the list is provided in Table S6 (ESI†)). In addition, the maximum height of HA was ranked the 6th in the negative polarity. These parameters represent the smoothness of a film, and thus, their negative impact on PCE (the smaller, the better) is readily reasonable.

As shown in Fig. 4e, the additional use of FFT and HA data as the explanatory variables exhibited almost unchanged, but marginal improvement in the r values of train (0.817) and test data (0.756). Notably, FFT parameters appeared on the high rank in their coefficient intensities (Fig. 4f). The spatial wavelengths of 65.22 and 40.54 nm were ranked the 2nd and 5th in the positive polarity, respectively. Interestingly, the positive impact of 40–65 nm spatial wavelength (their half-pitch is 20–33 nm) is consistent with the exciton diffusion length in OPV (∼20 nm),^68,69 where a narrow bicontinuous network of BHJ maximizes the efficiencies of exciton diffusion and charge separation that benefit the OPV performance. Meanwhile, a spatial distance much larger than the exciton diffusion length causes a radiative and non-radiative loss of exciton, leading to the decrease in J_SC and PCE. This finding is the same as the previous FFT study on P3HT : PCBM films with different thermal annealing process;²² however, it should be emphasized that the general importance of fine bicontinuous network shorter than ∼30 nm was found in a large data set (n = 890) comprising various types of polymers and NFAs.

Additionally, we examined RF algorithm instead of LASSO by using the same explanatory variables (Fig. S3†). The r values of train data were high (0.947–0.968), whereas those of test data showed a large decrease (0.814–0.781), possibly due to some overfitting. Similarly to the previous report⁵⁵ and LASSO results, the most important feature was StN of Mordred descriptor for all models (Tables S9–S11 (ESI†)), which is associated with the number of triple bonds nitrogen of the cyano substituent. In the GLCM and HA-based model, the correlation of δ = 2 of GLCM was ranked the 22nd. In the case of FFT and HA-based models, no FFT spatial wavelength was ranked in the top 30th. This indicates that LASSO is more suitable than RF to focus on AFM-derived parameters.

Since LASSO is a sparse model and reduces the parameters after optimization, detailed examination over the whole spatial wavelength of FFT is unable to access. We, therefore, performed Ridge regression by using FFT and HA descriptors. Fig. 5a displays the results for the train and test data, of which r values are 0.844 and 0.755, respectively, mostly identical to those of LASSO. However, the ranking features appear to drastically change (Fig. 5b). Many material properties and process parameters are ranked on the top level in both positive and negative coefficients. In addition, HA parameters such as maximum height, mean, skewness and variance are ranked higher than 20th. These parameters are associated with the height scale roughness of a BHJ film.

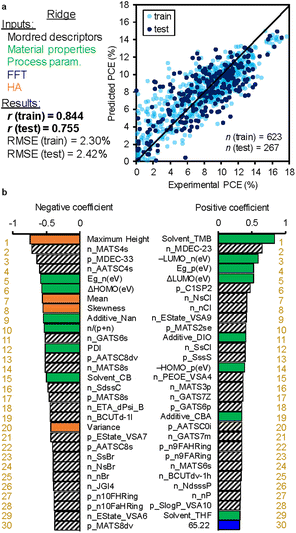Fig. 5 Results of Ridge regression. The explanatory variables are chemical structures (Mordred descriptors), material properties (bandgap, etc.), process parameters (solvent, etc.), and FFT and HA data. (a) Regression plot of experimental (horizontal) and predicted (vertical) PCE. The white blue (n = 623) and dark blue (n = 267) circles are the train and test data, respectively. The correlation coefficient (r) values of the train and test data are appended. (b) Regression coefficient ranking in decent order. The green, orange, and blue bars correspond to the material properties and process parameters, HA parameters, and FFT parameters, respectively. A complete list of rankings is provided in Table S8 (ESI†).

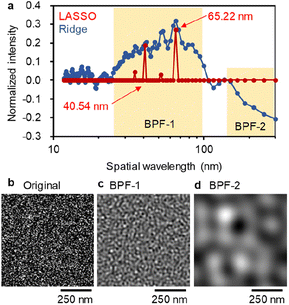
An in-depth comparison of LASSO and Ridge results about the FFT spatial wavelength is provided in Fig. 6a. The continuous Ridge spectrum is very similar to the discrete LASSO spectrum, where the wavelength regions at 25–100 nm exhibit a positive impact on PCE. In the Ridge model, negative coefficients are observed at >150 nm. Such a large-scale structure is much larger than the exciton diffusion length and would deteriorate the device performance.

Fig. 6 LASSO (red) and Ridge (blue) regression coefficient spectra of FFT. The vertical value is normalized by the maximum, while the horizontal values correspond to the spatial wavelength of FFT. The yellow part is the region of BPF used in (c) and (d). (b) Original noise image generated for demonstration. Reconstructed image after applying FFT to the original image with (c) BPF-1 (25–100 nm) or (d) BPF-2 (>150 nm) and inverse FFT.

We next demonstrate a generation of virtual BHJ morphology suitable for an efficient OPV. An original grey-scale image generated by applying noise (Fig. 6b) was processed by FFT with a band pass filter (BPF), and new images were reconstructed by inverse FFT. The IFPS with/without BPF are appended in Fig. S4 (ESI†). As shown in Fig. 6c, a narrow fibrous network was acquired after applying BPF-1 that corresponds to the preferred wavelength at 25–100 nm. In contrast, wide and rough features are observed after applying BPF-2 at the un-preferred wavelength at >150 nm (Fig. 6d). We thus exemplified the importance of high frequency (wavelength: 40–65 nm and their half-pitch is 20–33 nm) bicontinuous network in BHJ, which is general regardless of the polymers and NFAs. To examine the direct effect of AFM images on the solar cell performance, we performed LASSO, Ridge and RF by solely using AFM data (GLCM, HA, FFT and their combinations) as the explanatory variables (Fig. S5 (ESI†)). The r values of LASSO and Ridge were very low (0.3–0.4) for both train and test data. The RF model showed a high r of ∼0.85 for train, but a significantly low r of 0.3–0.5 for test, due to overfitting. Accordingly, the PCE prediction with moderate accuracy needs material properties and process parameters. Given the almost unchanged r values irrespective of using AFM data, the chemical structures and material properties may implicitly involve miscibility and BHJ information for a target polymer : NFA blend. This envisions a complete virtual screening of OPV materials without explicitly considering the BHJ structure.

Conclusions

We conducted a study on binary BHJ-type polymer : NFA OPVs using ML techniques. This involved the incorporation of AFM images (n = 890) collected from device data (n = 1318) found in existing literature (n = 558). Our analysis, utilizing the LASSO regression model, resulted in moderate, yet mostly consistent accuracy (r = 0.80–0.82 for training and 0.75–0.76 for testing) regardless of GLCM, FFT and HA parameters obtained from the AFM image analysis. Importantly, we discovered that the spatial wavelength of FFT, specifically 40–65 nm (their half-pitch is 20–33 nm), had a positive and significant impact on the PCE of OPVs, while longer wavelengths beyond 150 nm had a negative effect on performance. The former wavelength corresponded with the typical exciton diffusion length, providing support for the validity of our findings. Other parameters, such as homogeneity, correlation and skewness, also demonstrated some impact, which could be related to the smoothness of the film. While we did not achieve an improvement in ML prediction accuracy for the AFM-included dataset, our work successfully identified crucial spatial wavelengths among a large dataset and demonstrated a path toward more efficient BHJ OPVs.

Experimental

The solar cell performance (maximum PCE), chemical structures (SMILE), material properties (E_g, HOMO, LUMO and molecular weight), and process parameters (solvent, additive and p/n ratio) of binary polymer : NFA OPVs were based on our previous report that collected these data from the literature (n = 1318, available free of charge in American Chemical Society website).⁵⁵ The AFM images were manually collected from corresponding papers and processed, giving n = 890 dataset in a normalized size (750 × 750 nm²) and resolution (128 × 128 pixel²; 5.86 nm per pixel). No data augmentation (rotation and inversion) on the images was applied. FFT (IFPS), GLCM and HA analyses were performed using Numpy (OpenCV), Scikit-image and Numpy in Python, respectively. ML modelling (LASSO, Ridge, and RF) was implemented by the Scikit-learn package in Python. A sample code of LASSO is provided in ESI.†. The hyperparameters for LASSO, Ridge and RF were optimised by Bayesian optimisation using Optuna with a 5-fold cross validation score (LASSO and Ridge: 100 trials, RF: 300 trials).

Data availability

The dataset of polymer : NFA OPV is available in our previous report.⁵⁵ Feature importance lists are provided in ESI.†

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

We acknowledge financial support from Core Research for Evolutional Science and Technology (CREST) (JPMJCR2107 for A.S.), MIRAI (JPMJMI22E2 for A.S.), and PRESTO (JPMJPR21A2 for F.I.) from the Japan Science and Technology Agency (JST), the Green Innovation Project (JP21578854 for A.S.) from the New Energy and Industrial Technology Development Organization (NEDO) and KAKENHI from the Japan Society for the Promotion of Science (JSPS) (JP20H05836 and JP20H00398 for A.S. and JP22H04541, JP21H00400, JP20H02784 for F. I.). We thank Dr Ryosuke Nishikubo at Osaka University for fruitful discussion. Y. K. acknowledges the Interactive Materials Science CADET program at Osaka University for the financial support and exchange research opportunity.

Notes and references

1. R. F. Service, Science, 2022, 378, 588–591.
2. N. Camaioni, C. Carbonera, L. Ciammaruchi, G. Corso, J. Mwaura, R. Po and F. Tinti, Adv. Mater., 2023, 35, 2210146.
3. W. Heng, L. Weihua and K. Bachagha, J. Mater. Chem. A, 2023, 11, 1039–1060.
4. J. Cao, L. Yi, L. Zhang, Y. Zou and L. Ding, J. Mater. Chem. A, 2023, 11, 17–30.
5. X. Xu, Y. Li and Q. Peng, Adv. Mater., 2022, 34, 202107476.
6. W. Deng, W. Liu, R. Qian and H. Wu, J. Phys. Chem. Lett., 2022, 13, 544–551.
7. L. Hong, H. Yao, Y. Cui, P. Bi, T. Zhang, Y. Cheng, Y. Zu, J. Qin, R. Yu, Z. Ge and J. Hou, Adv. Mater., 2021, 33, 2103091.
8. K. Chong, X. Xu, H. Meng, J. Xue, L. Yu, W. Ma and Q. Peng, Adv. Mater., 2022, 34, 2109516.
9. L. Zhu, M. Zhang, J. Xu, C. Li, J. Yan, G. Zhou, W. Zhong, T. Hao, J. Song, X. Xue, Z. Zhou, R. Zeng, H. Zhu, C.-C. Chen, R. C. I. MacKenzie, Y. Zou, J. Nelson, Y. Zhang, Y. Sun and F. Liu, Nat. Mater., 2022, 21, 656–663.
10. J.-W. Lee, C. Sun, C. Lee, Z. Tan, T. N.-L. Phan, H. Jeon, D. Jeong, S.-K. Kwon, Y.-H. Kim and B. J. Kim, ACS Energy Lett., 2023, 8, 1344–1353.
11. H. Chen, S. Y. Jeong, J. Tian, Y. Zhang, D. R. Naphade, M. Alsufyani, W. Zhang, S. Griggs, H. Hu, S. Barlow, H. Y. Woo, S. R. Marder, T. D. Anthopoulos, I. McCulloch and Y. Lin, Energy Environ. Sci., 2023, 16, 1062–1070.
12. B. M. Savoie, N. E. Jackson, L. X. Chen, T. J. Marks and M. A. Ratner, Acc. Chem. Res., 2014, 47, 3385–3394.
13. S. Few, J. M. Frost and J. Nelson, Phys. Chem. Chem. Phys., 2015, 17, 2311–2325.
14. J. Yuan, T. Huang, P. Cheng, Y. Zou, H. Zhang, J. L. Yang, S.-Y. Chang, Z. Zhang, W. Huang, R. Wang, D. Meng, F. Gao and Y. Yang, Nat. Commun., 2019, 10, 57.
15. Y. Tamai, Adv. Energy Sustainability Res., 2023, 4, 2200149.
16. A. J. Moulé and K. Meerholz, Adv. Funct. Mater., 2009, 19, 3028–3036.
17. A. J. Heeger, Adv. Mater., 2014, 26, 10–28.
18. N. D. Treat and M. L. Chabinyc, Annu. Rev. Phys. Chem., 2014, 65, 59–81.
19. X. Liu, Y. Yan, Y. Yao and Z. Liang, Adv. Funct. Mater., 2018, 28, 1802004.
20. A. Karki, A. J. Gillett, R. H. Friend and T.-Q. Nguyen, Adv. Energy Mater., 2020, 11, 2003441.
21. G. Zhang, R. R. Lin, F. Qi, T. Heumüller, A. Distler, H.-J. Egelhaaf, N. Li, P. C. Y. Chow, C. J. Brabec, A. K.-Y. Jen and H.-L. Yip, Chem. Rev., 2022, 122, 14180–14274.
22. W. Ma, C. Yang and A. J. Heeger, Adv. Mater., 2007, 19, 1387–1390.
23. C. J. Takacs, S. D. Collins, J. A. Love, A. A. Mikhailovsky, D. Wynands, G. C. Bazan, T.-Q. Nguyen and A. J. Heeger, ACS Nano, 2014, 8, 8141–8151.
24. K. Kranthiraja and A. Saeki, Adv. Funct. Mater., 2021, 31, 2011168.
25. J. S. Moon, C. J. Takacs, S. Cho, R. C. Coffin, H. Kim, G. C. Bazan and A. J. Heeger, Nano Lett., 2010, 10, 4005–4008.
26. M. Pfannmöller, W. Kowalsky and R. R. Schröder, Energy Environ. Sci., 2013, 6, 2871–2891.
27. J. J. van Franeker, G. H. L. Heintges, C. Schaefer, G. Portale, W. Li, M. M. Wienk, P. van der Schoot and R. A. J. Janssen, J. Am. Chem. Soc., 2015, 137, 11783–11794.
28. J. Rivnay, S. C. B. Mannsfeld, C. E. Miller, A. Salleo and M. F. Toney, Chem. Rev., 2012, 112, 5488–5519.
29. E. Al-Naamani, A. Gopal, M. Ide, I. Osaka and A. Saeki, ACS Appl. Mater. Interfaces, 2017, 9, 37702–37711.
30. I. Osaka and K. Takimiya, Adv. Mater., 2017, 30, 1605218.
31. H. Chen, J. Peet, Y.-C. Hsiao, B. Hu and M. Dadmun, Chem. Mater., 2014, 26, 3993–4003.
32. M. Shao, J. K. Keum, R. Kumar, J. Chen, J. F. Browning, S. Das, W. Chen, J. Hou, C. Do, K. C. Littrell, A. Rondinone, D. B. Geohegan, B. G. Sumpter and K. Xiao, Adv. Funct. Mater., 2014, 24, 6647–6657.
33. Y. Yan, X. Liu and T. Wang, Adv. Mater., 2017, 29, 1601674.
34. K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555.
35. A. Saeki and K. Kranthiraja, Jpn. J. Appl. Phys., 2020, 59, SD0801.
36. S. M. Moosavi, K. M. Jablonka and B. Smit, J. Am. Chem. Soc., 2020, 142, 20273–20287.
37. G. Restrepo, Digital Discovery, 2022, 1, 568–585.
38. S. Nagasawa, E. Al-Naamani and A. Saeki, J. Phys. Chem. Lett., 2018, 9, 2639–2646.
39. M.-H. Lee, Adv. Energy Mater., 2019, 9, 1900891.
40. Z.-W. Zhao, Y. Geng, A. Troisi and H. Ma, Adv. Intell. Syst., 2022, 4, 2100261.
41. A. Mahmood, A. Irfan and J.-L. Wang, Chin. J. Polym. Sci., 2022, 40, 870–876.
42. P. Friederich, A. Fediai, S. Kaiser, M. Konrad, N. Jung and W. Wenzel, Adv. Mater., 2019, 31, 1808256.
43. R. Pollice, G. d. P. Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-D’Addario, A. K. Nigam, C. T. Ser, Z. Yao and A. Aspuru-Guzik, Acc. Chem. Res., 2021, 54, 849–860.
44. X. Rodríguez-Martínez, E. Pascual-San-José and M. Campoy-Quiles, Energy Environ. Sci., 2021, 14, 3301–3322.
45. G. H. Gu, J. Noh, I. Kim and Y. Jung, J. Mater. Chem. A, 2019, 7, 17096–17117.
46. Y. Shu and B. G. Levine, J. Chem. Phys., 2015, 142, 104104.
47. R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D. −G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127.
48. Y. Zhuo and J. Brgoch, J. Phys. Chem. Lett., 2021, 12, 764–772.
49. S. Atahan-Evrenk and F. B. Atalay, J. Phys. Chem. A, 2019, 123, 7855–7863.
50. C. Kunkel, J. T. Margraf, K. Chen, H. Oberhofer and K. Reuter, Nat. Commun., 2021, 12, 2422.
51. Q. Ai, V. Bhat, S. M. Ryno, K. Jarolimek, P. Sornberger, A. Smith, M. M. Haley, J. E. Anthony and C. Risko, J. Chem. Phys., 2021, 154, 174705.
52. N. E. Persson, J. Rafshoon, K. Naghshpour, T. Fast, P. –H. Chu, M. McBride, B. Risteen, M. Grover and E. Reichmanis, ACS Appl. Mater. Interfaces, 2017, 9, 36090–36102.
53. X. Du, X. Jiao, S. Rechberger, J. D. Perea, M. Meyer, N. Kazerouni, E. Spiecker, H. Ade, C. J. Brabec, R. H. Fink and T. Ameri, Macromolecules, 2017, 50, 2415–2423.
54. W. Köntges, P. Perkhun, J. Kammerer, R. Alkarsifi, U. Würfel, O. Margeat, C. Videlot-Ackermann, J.-J. Simon, R. R. Schröder, J. Ackermann and M. Pfannmöller, Energy Environ. Sci., 2020, 13, 1259–1268.
55. Y. Miyake and A. Saeki, J. Phys. Chem. Lett., 2021, 12, 12391–12401.
56. H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminf., 2018, 10, 4.
57. A. Saeki, T. Kozawa and S. Tagawa, Appl. Phys. Lett., 2009, 95, 103106.
58. K. J. Lachowski, K. Vaddi, N. Y. Naser, F. Baneyx and L. D. Pozzo, Digital Discovery, 2022, 1, 427–439.
59. D. Chen, M. Pan, W. Huang, W. Luo and C. Wang, Anal. Methods, 2018, 10, 4053–4062.
60. I. Pantic, J. Cumic, S. Dugalic, G. A. Petroianu and P. R. Corridon, Sci. Rep., 2023, 13, 4025.
61. Y. Kim, C. E. Song, S. J. Moon and E. Lim, RSC Adv., 2015, 5, 62739–62746.
62. T. J. Aldrich, W. Zhu, S. Mukherjee, L. J. Richter, E. Gann, D. M. DeLongchamp, A. Facchetti, F. S. Melkonyan and T. J. Marks, Chem. Mater., 2019, 31, 4313–4321.
63. G. Chai, Y. Chang, J. Zhang, X. Xu, L. Yu, X. Zou, X. Li, Y. Chen, S. Luo, B. Liu, F. Bai, Z. Luo, H. Yu, J. Liang, T. Liu, K. S. Wong, H. Zhou, Q. Peng and H. Yan, Energy Environ. Sci., 2021, 14, 3469–3479.
64. R. Tibshirani, J. Roy. Stat. Soc. B, 1996, 58, 267–288.
65. N. Ishida, A. Wakamiya and A. Saeki, ACS Photonics, 2016, 3, 1678–1688.
66. R. C. Geary, Inc. Statistician, 1954, 5, 115–145.
67. L. Anselin and S. Rey, Geogr. Anal., 1991, 23, 112–131.
68. O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888.
69. Y. Tamai, H. Ohkita, H. Benten and S. Ito, J. Phys. Chem. Lett., 2015, 6, 3417–3428.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary Tables S1–S11 and Fig. S1–S5. See DOI: https://doi.org/10.1039/d3ra02492j

---