How organic switches grafting on TiO₂ modifies the surface potentials: theoretical insights

Abstract

Hybrid organic switch-inorganic semiconductor systems have important applications in both photo-responsive intelligent surfaces and microfluidic devices. In this context, herein, we performed first-principles calculations to investigate a series of organic switches of trans/cis-azobenzene fluoride and pristine/oxidized trimethoxysilane adsorbed on low-index anatase slabs. The trends in the surface–adsorbate interplay were examined in terms of the electronic structures and potential distributions. Consequently, it was found that the cis-azobenzene fluoride (oxidized trimethoxysilane)-terminated anatase surface attains a lower ionization potential than the trans-azobenzene fluoride (pristine trimethoxysilane)-terminated anatase surface due to its smaller induced (larger intrinsic) dipole moment, whose direction points inwards (outwards) from the substrate, which originates from the electron charge redistribution at the interface (polarity of attached hydroxyl groups). By combining the induced polar interaction analysis and the experimental measurements in the literature, we demonstrate that the ionization potential is an important predictor of the surface wetting properties of adsorbed systems. The anisotropic absorbance spectra of anatase grafted with azobenzene fluoride and trimethoxysilane are also related to the photoisomerization and oxidization process under UV irradiation, respectively.

---

1 Introduction

Reversible photochemical processes on photosensitive materials enable a switchable change in their surface properties, e.g., wettability, adhesion and color, under the influence of external stimuli in an environmentally friendly, non-contact and convenient manner,^1–6 and thus have found significant applications in chemical sensors,⁷ artificial intelligent surfaces,⁵ and microfluidic devices.³ One well-known strategy to obtain dynamically modifiable surface properties exploits the changes in geometry and dipole moment resulting from photochromism in surface-confined organic molecules, including azobenzene (AZB),^8,9 diarylethene (DTE),¹⁰ spiropyran (SP)¹¹ and their derivatives. Another approach toward more pronounced and switchable property changes exploits the reversible property of some semiconductor oxides such as ZnO,^12–14 WO₃,¹⁵ and TiO₂.^16–18 Recently, many studies, mainly from an experimental viewpoint, have been directed toward combining organic switches with inorganic materials^19–21 given that the resulting hybrid systems are believed to be the key to expanding the applicability of the subsystems in realistic devices. The corresponding investigations include the study of the colorless-colored isomerization of SP derivatives on porous TiO₂,²² cis–trans isomerization of azobenzene fluoride derivatives adsorbed on metal oxide nanoparticles,²³ and trimethoxy(alkyl)silane grafted on TiO₂ nanoparticles.^24,25 Moreover, artificial joint systems (e.g., metal/ZnO, metal/insulator/semiconductor and bipyridine-complexes/TiO₂) have also been found to be a promising solution for integrated and efficient solar-to-chemical conversion,^26–30 indicating their potential applications in the field of energy utilization. These investigations confirm that immobilized organic switches and inorganic semiconductor oxide substrates may retain their photosensitive and modifiable properties in joint systems.^19,31,32

In this case, a good understanding of hybrid systems is crucial to quantify the interplay between the organic switches and inorganic substrates during the photochemical process. To explore the optoelectronic properties of these hybrid systems, numerous studies have carried out, including density functional theory (DFT)/time-dependent density functional theory (TDDFT) investigation of a series of photochromic derivatives of trans/cis-AZB,³³ open/closed-SP³⁴ and open/closed-DTE^33,35 adsorbed onto anatase and rutile slabs. To explain the switchable wettability of TiO₂ nanoparticles modified with trimethoxysilane under UV illumination, a series of experiments was carried out to confirm the oxidization process for the degradation of trimethoxysilane.^24,25 However, complementary computational efforts to model the surface of these systems and interface properties are lacking.

Surface potential is one of the basic physical characteristics of a material surface, which is related to its surface properties (through the Fermi energy), given that it can dictate the direction of charge transfer, and thereby significantly affect the stability and surface chemistry of surfaces with adsorbates.^36–38 Particularly, the work function (ionization potential) of the metallic (semiconducting or insulating) surface is one of the most important technological parameters of the surface potential^39,40 in developing new field-emitter cathodes or photo-responsive superhydrophobic surfaces for applications in light-emitting diodes and smart fluid control. By using the surface polarizability approach and performing contact angle measurements, the surface polarizability, which has been observed to exhibit a significant inverse relationship with respect to the ionization potential,^41–43 was found to be closely related to the surface free energy and wettability.⁴⁴ By combining first-principle calculation with contact angle measurement, the work function was demonstrated to be a critical quantity in understanding the wettability of silane coatings.⁴⁵ Based on first-principles density functional theory, low-dimensional materials with a low work function have been demonstrated to have a considerable impact on the power efficiency for field-emission applications.⁴⁶ However, a limited number of studies has been conducted on the surface potentials of joint systems that incorporate organic switches in inorganic surfaces. In this case, how the functional organic switch configuration, low-index semiconductor surface and surface–adsorbate interplay influence the electronic properties and surface potential barriers of the joint system remains an unsolved issue. Furthermore, the difference in surface potentials between a series of organic switches grafted on various inorganic semiconductor surfaces still needs to be studied in depth.

Herein, we used DFT to investigate the electronic properties and surface potentials of hybrid organic/inorganic systems with different organic adsorbates and various low-index TiO₂ surfaces. We show that the change in the ionization potential during the photoisomerization and oxidization processes of the organic switch configuration is correlated with the changes in the surface dipole moments. We demonstrate that the ionization potentials play an important role in determining the potential barriers, and consequently justify their surface-wetting properties. This work is organized as follows: the Computational methods section provides the physical model and the computational methodology. The results and their interpretations are presented in the Results and discussion section. Finally, the Conclusions section provides a general summary of this work.

2 Computational methods

To quantify the mutual influence between organic and inorganic subsystems, we performed a DFT study on two commonly used organic coatings, i.e., azobenzene fluoride (FAZB) and 1H,1H,2H,2H-perfluorooctyl(trimethoxy)silane (PFOS), grafted on anatase TiO₂ surfaces modeled as a periodic slab, as shown in Fig. 1 and S1.† To ensure immobilization of the coating to the surface, the trans-FAZB and cis-FAZB isomers were anchored on surfaces with strong binding by adding carboxyl groups on one side of the isomer,^33,47 while the oxygen atom in the siloxane groups of PFOS binds to the surface the titanium atom.⁴⁵ We considered the perpendicular configuration of the organic switches adsorbed on anatase slabs given that the present work aimed to explore the changes in the polarity and surface potentials of immobilized organic switches in the perpendicular direction during the photoisomerization and photo-induced oxidization process, which proceeded via rotation or inversion mechanisms in sufficient space. The perpendicular configuration was also demonstrated to be the optimal adsorption mode in terms of energetic and dynamical stability.^30,47–50 The effectiveness of adding anchor groups was predicted through both experimental and theoretical studies,^34,47,49 while the covalent bonding of trimethoxysilane refers to a grafting reaction with silanes in the real synthesis process.^50,51 To consider the effect of the oxidization of PFOS due to UV illumination, one of the fluorine atoms at the end of the carbon chain of pristine PFOS (labeled as PFOS-F) was replaced by a hydroxyl group, which was labeled as PFOS-OH. Considering their widespread use as photoelectrode substrates, we selected two types of commonly used stable anatase TiO₂ faces, i.e., (100) and (101), as the inorganic surfaces.⁵² Particularly, there are two inequivalent anatase (101) surfaces (Fig. S1†), and thus for clarity, they will be referred to as (101)-I and (101)-II herein.

Fig. 1 Adsorbed structures of (left to right) trans-FAZB, cis-FAZB, PFOS-F and PFOS-OH on anatase TiO₂ (100) surface viewed along (a) y-axis and (b) x-axis. The white, gray, blue, red, gold, light-gray and light-blue spheres represent hydrogen, carbon, nitrogen, oxygen, silicon, titanium and fluorine atoms, respectively.

We carried out DFT calculations with the Perdew–Burke–Ernzerhof (PBE)⁵³ form of the generalized gradient approximation (GGA) for the exchange-correlation functional to optimize the atomic structures and calculate the electronic structures, as implemented in the Vienna ab initio simulation package (VASP).^54,55 The ion–electron interactions were treated using the projector augmented wave (PAW) method⁵⁶ with a cutoff energy of 400 eV. The two-dimensional joint system was modeled by using the supercell approximation with at least a 25 Å vacuum space along the direction perpendicular to the surface, which was taken to be the z-axis, to eliminate interactions between periodic images. From the bulk anatase cell, a four-layer 4 × 1 and 1 × 4 slab was cut in the (100) and (101) directions, presenting dimensions of 11.36 × 9.87 Ų and 10.57 × 11.36 Ų in the x–y plane, respectively, and the bottom layer along the z direction was fixed. All the selected atoms were fully relaxed using the conjugate gradient method until the magnitude of the force on each atom became less than 0.01 eV Å⁻¹ in the optimized structures and the total energies were converged within 10⁻⁵ eV per cell. For the structural optimization (static calculations), the Brillouin zone was sampled using a set of 2 × 2 × 1 (4 × 4 × 1) Monkhorst–Pack k points.⁵⁷ The Gaussian smearing scheme was applied with a smearing width of 0.14 eV. The adsorption coverage in our calculation corresponded to one organic adsorbate per TiO₂ 4 × 1 (1 × 4) supercell for the (100) [(101)] surface, i.e., ∼8.9 × 10¹³ cm⁻² (∼8.3 × 10¹³ cm⁻²) for (100) [(101)] surface. The coverage we considered is in the reasonable range reported in previous experimental and theoretical studies.^48,49,58

The ionization potential (work function) for a semiconductor (metal) was derived from the energy difference between the vacuum level and the valence band maximum (Fermi energy). Generally, the Fermi level is located between the conduction band minimum and the valence band maximum depending on the hybrid and surface states. Given that the adsorption is on only one side of the hybrid organic/inorganic surface, in the calculation of surface potentials, we put two joint systems with mirror symmetry in the supercell to create two vacuum regions with constant vacuum potentials to obtain two independent vacuum levels of the two sides of the surface. It is noteworthy that our computational approach was validated by performing sets of work function calculations on silane-modified substrates⁴⁵ and graphene edges.³⁷

3 Results and discussion

We begin our discussion by focusing on the structures of the adsorbed systems. Examples of the relaxed atomic structures of FAZB and PFOS chemisorbed on the anatase (100) surface are shown in Fig. 1 [adsorption on anatase (101)-I and (101)-II surfaces is depicted in Fig. S1†]. To determine the stability of hybrid systems, we investigated the adsorption energies of organic/inorganic interfaces. The adsorption energy E_a of the organic switch can be expressed as E_a = E_hybrid − (E_o + E_ino), where E_hybrid is the total energy of the hybrid system with organic adsorbates, E_o is the energy of an isolated organic functional group, and E_ino is the energy of an inorganic substrate with a clean surface. According to this definition, exothermic adsorption corresponds to negative values. Table 1 presents the adsorption energies of 12 species of the considered hybrid systems. We found that all the organic adsorbates are chemisorbed on the (100), (101)-I and (101)-II TiO₂ surfaces with large adsorption energies. The adsorption energies were at least −2.14 and −2.73 eV for the FAZB- and PFOS-grafted surfaces, respectively, which are much higher than the thermal energy at room temperature (i.e., 0.026 eV), indicating the very stable adsorption of FAZB and PFOS. It is instructive to compare the adsorption energies of organic hybrid systems with inorganic group-grafted anatase surfaces given that the nitrate groups were successfully grafted on a rutile TiO₂ surface.⁵⁹ We found that the nitrate groups are also chemisorbed on the anatase surfaces stably with adsorption energies slightly smaller than that of the organic hybrid systems.

Table 1 Total energies and adsorption energies of 12 species of considered hybrid systems in comparison to inorganic group-grafted anatase surfaces

Structure (as labeled in Fig. 1 and S1)	Total energy (eV)	Adsorption energy (eV)
trans-FAZB/(100)	−834.80	−2.68
cis-FAZB/(100)	−834.32	−2.59
trans-FAZB/(101)-I	−826.50	−2.63
cis-FAZB/(101)-I	−825.94	−2.54
trans-FAZB/(101)-II	−835.04	−2.14
cis-FAZB/(101)-II	−834.68	−2.15
PFOS-F/(100)	−839.55	−3.05
PFOS-OH/(100)	−845.91	−3.09
PFOS-F/(101)-I	−832.01	−3.37
PFOS-OH/(101)-I	−838.37	−3.68
PFOS-F/(101)-II	−840.90	−2.73
PFOS-OH/(101)-II	−849.15	−3.16
NO3/(100)	−654.78	−1.08
NO3/(101)-I	−642.26	−2.00
NO3/(101)-II	−652.64	−1.07

---

Given that all the surface properties of the organic/inorganic hybrid systems were derived by truncation of the bulk systems and modification of the initial surfaces, in Fig. S2† and 2 we reported the electronic structures of the TiO₂ bulk and three different pristine anatase surfaces. An indirect band gap of 2.13 eV between the Γ and X points was found for bulk anatase TiO₂, which is significantly smaller than the experimental band gap value of 3.2 eV (ref. 60) but in agreement with the theoretical studies (2.0 ∼ 2.37 eV).^61,62 Our PBE-computed band gaps for the unbound (100), (101)-I and (101)-II anatase slabs are 2.11, 2.18 and 2.46 eV, respectively, in agreement with the previous studies on TiO₂ slab systems (1.75 ∼ 2.5 eV).³³ Fig. 2(d) shows the typical potential energy distribution across the unbound TiO₂ surface. The vacuum potential at a remote location far away from the surface in the z direction is an asymptotic constant. Given that the valence band maximum was set to zero in our calculation, the vacuum level, which is determined from the electrostatic potential in the vacuum region far enough away from the slab surface, is equal to the ionization potential. For each unbound surface, the difference in ionization potentials between the fixed bottom side and the relaxed top side is influenced by surface relaxation. It is clear that the unbound (101)-II [(101)-I] surface has the highest (lowest) ionization potential.

Fig. 2 (a–c) Electronic band structure of unbound anatase (100), (101)-I and (101)-II surface along the high-symmetry path, respectively. (d) Potential energy distribution for unbound anatase (100), (101)-I and (101)-II surface. It is plotted along a line perpendicular to the surface. The Fermi energy is set to the valence band maximum (VBM) for comparison.

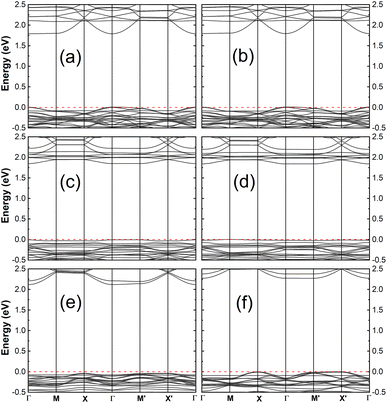
Here, we consider the impact of adsorption on the electronic structure of the hybrid systems as given by the energy band. The band structures, as depicted in Fig. 3 for the FAZB/TiO₂ systems and Fig. 4 for the PFOS/TiO₂ systems, show the contribution of the organic adsorbates. For a given TiO₂ substrate, all the joint systems are semiconductors with band gaps that are smaller than that of the unbound surface. A comparison of the energy gaps between the hybrid and unbound systems is presented in Table 2, where we notice that for each type of TiO₂ substrate, the band gap of the hybrid system with cis-FAZB adsorption is smaller than that with trans-FAZB adsorption, while the band gaps of the hybrid systems with PFOS-F and PFOS-OH adsorption show small differences.

Fig. 3 Electronic band structure of (a) trans-FAZB/(100), (b) cis-FAZB/(100), (c) trans-FAZB/(101)-I, (d) cis-FAZB/(101)-I, (e) trans-FAZB/(101)-II and (f) cis-FAZB/(101)-II. The Fermi energy is set to the valence band maximum (VBM) for comparison.

Fig. 4 Electronic band structure of (a) PFOS-F/(100), (b) PFOS-OH/(100), (c) PFOS-F/(101)-I, (d) PFOS-OH/(101)-I, (e) PFOS-F/(101)-II and (f) PFOS-OH/(101)-II. The Fermi energy is set to the valence band maximum (VBM) for comparison.

Table 2 Energy bandgaps and ionization potentials of the 12 considered hybrid systems

Structure (as labeled in Fig. 1 and S1)	Energy gap (eV)	Ionization potential (eV)
		Modified side (relaxed side)	Clean side (fixed side)
(100)	2.11	5.86	4.62
(101)-I	2.18	5.76	3.96
(101)-II	2.46	6.23	5.47
trans-FAZB/(100)	1.77	5.17	4.90
cis-FAZB/(100)	1.62	4.61	4.88
trans-FAZB/(101)-I	1.62	5.48	3.92
cis-FAZB/(101)-I	1.54	5.00	3.85
trans-FAZB/(101)-II	1.84	5.07	5.69
cis-FAZB/(101)-II	1.54	4.44	5.68
PFOS-F/(100)	1.78	6.24	4.61
PFOS-OH/(100)	1.79	5.79	4.69
PFOS-F/(101)-I	1.86	6.75	3.85
PFOS-OH/(101)-I	1.84	6.02	3.88
PFOS-F/(101)-II	2.16	6.05	5.55
PFOS-OH/(101)-II	2.27	5.46	6.08

---

Given that both the FAZB/TiO₂ and PFOS/TiO₂ hybrid systems are semiconductors, we explored their ionization potential to quantify the energy barrier to free space that prevents an electron at the valence band maximum from escaping the solid. Fig. 5(a) and (c) show the potential energy distribution of FAZB and PFOS adsorbed on different anatase surfaces, respectively. We plotted the electrostatic potential energy along a line that crosses the adsorbates and is perpendicular to the slab. It is clear that the potential energy in the vicinity of the surface increases gradually as the distance increases for both the adsorbed side and the clean side [Fig. 5(a and c), respectively], but the variation in the potential energy is not monotonous in the former case due to the existence of adsorbates. We found that the vacuum level of the adsorbed side is different from that of the clean side. The difference in the vacuum levels between the adsorbed side and the clean side is determined by the adsorbate type. It is obvious that the vacuum levels of the clean sides are independent of the type of organic adsorbate on the other side and similar to that of the unbound surfaces without relaxation. To further investigate the potential barriers of the TiO₂ surface with different organic switch modifications, we plotted the potential energy curves along the forward path, which is the line perpendicular to the surface, with the origin at the outermost atoms, as shown in Fig. 5(b and d), respectively. The corresponding ionization potentials obtained from the vacuum levels in Fig. 5(b and d) are summarized in Table 2. We noted that the ionization potentials of the FAZB/TiO₂ hybrid systems follow the order of trans-FAZB/(101)-I > trans-FAZB/(100) > trans-FAZB/(101)-II > cis-FAZB/(101)-I > cis-FAZB/(100) > cis-FAZB/(101)-II. We found that the adsorption on a semiconducting substrate with each given FAZB configuration changes the relative order of the ionization potential between the different TiO₂ surfaces compared to that without adsorption. For example, the relative order of the ionization potential for the (100), (101)-I and (101)-II hybrid surfaces grafted with trans-FAZB is different from that for the (100), (101)-I and (101)-II unbound surfaces. Clearly, regardless of the type of anatase surface, the ionization potential of the TiO₂ surface grafted with trans-FAZB is always larger than that with cis-FAZB. Alternatively, the ionization potential of the TiO₂ surface modified with various short carbon chain silanes follows the order of PFOS-F/(101)-I > PFOS-F/(100) > PFOS-F/(101)-II > PFOS-OH/(101)-I > PFOS-OH/(100) > PFOS-OH/(101)-II. It is clear that ionization potentials of the different types of TiO₂ surfaces modified with a given silane exhibit the same relative order as that of the TiO₂ surfaces modified with a given FAZB. The PFOS-F-grafted TiO₂ surface also shows a larger ionization potential than the PFOS-OH-grafted TiO₂ surface. Notably, the hierarchy of the ionization potential of the hybrid systems predicted by our numerical calculations was found to follow the same trend of hydrophobicity in experimental measurements [105° (23°) contact angle for the trans-state (cis state) FAZB-grafted silica-encapsulated nanoparticles²³ and 165° (<10°) contact angle for PFOS-F (PFOS-OH)-grafted TiO₂ nanoparticles²⁵], which can be explained by the induced polar interaction model at the liquid/solid interfaces.⁴⁴ When a polar liquid (e.g., water) is in contact with a polarizable solid surface, the induced solid/liquid polar interaction, and thereby the surface hydrophilicity increases with the solid surface polarizability monotonously, which is inversely related to the ionization potential.^41–43 Thus, we can expect that the equilibrium contact angle for contacting a polar liquid will increase with an increase in the ionization potential of solid surface, i.e., the surface hydrophobicity of trans-FAZB (PFOS-F)-grafted TiO₂ is larger than that of cis-FAZB (PFOS-OH)-grafted TiO₂.

Fig. 5 Potential energies (a) along a line that crosses the adsorbates and is perpendicular to the slab and (b) along the forward path that is perpendicular to the surface with the origin at the outermost atoms of adsorbate for the cis-FAZB/(100) (■), trans-FAZB/(100) (□), cis-FAZB/(101)-I (●), trans-FAZB/(101)-I (○), cis-FAZB/(101)-II (▲) and trans-FAZB/(101)-II (△), (c, d) are the same as (a and b) but for PFOS-F/(100) (▼), PFOS-OH/(100) (▽), PFOS-F/(101)-I (◆), PFOS-OH/(101)-I (◇), PFOS-F/(101)-II (★) and PFOS-OH/(101)-II (☆), respectively.

To understand how the organic adsorbates affect the surface potential, we considered in detail the redistributions of the electron charges between the inorganic substrate and the organic adsorbate, as shown in Fig. 6 and 7. A common feature is that the charge redistributions are locally confined in the vicinity of the interface between the TiO₂ surface and the adsorbates. In the case of the FAZB/TiO₂ (PFOS/TiO₂) hybrid system, the positive charges accumulate on the top layer of the TiO₂ substrate [indicated in Fig. 6 (Fig. 7)], while negative charges accumulate at the binding site of FAZB (PFOS) [indicated in Fig. 6 (Fig. 7)]. However, the end-to-end distance and the linear distribution of transferred electron charge for the planar rod-like trans-FAZB is larger than that of nonplanar cis-FAZB, suggesting that the trans-FAZB receives more electrons from the interface and induces a larger dipole moment whose direction points inwards from the TiO₂ substrate. It had been reported that the adsorbate on the substrate reduces (enhances) the electron binding capability, i.e., work function or ionization potential, by forming a plane of dipoles, whose direction points outwards (inwards) from the substrate.³⁷ Therefore, compared to the case of the cis-FAZB-grafted TiO₂ surface, the higher ionization potential for the trans-FAZB-grafted TiO₂ surface can be attributed to the larger electron charge transfer caused by chemical functionalization and structural relaxation effect. Alternatively, the relative order of ionization potential between the PFOS-F- and PFOS-OH-grafted TiO₂ surfaces cannot be explained by the effect of the induced dipole moment derived from charge transfer only. As shown in Fig. 7, for a given TiO₂ surface, the linear distribution of transferred electron charge of PFOS with hydroxyl substitution is almost the same as that of pristine PFOS. It is widely known that the hydroxyl group is a polar chemical group with an intrinsic dipole moment pointing from oxygen to hydrogen. Fig. 7(d) shows the dipole moment contributions of the PFOS-F and PFOS-OH adsorbates. The contribution of the OH dipole moment to the potential barrier is negative given that its direction points outwards to the anatase slab [Fig. 7(d)]. This explains why the OH-substituted PFOS exhibits exceptionally low ionization potentials. The effect of the intrinsic dipole moments of the functional groups was also predicted with an increase or decrease in the potential barriers of several surfaces.^46,63

Fig. 6 (a) Linear distribution of transferred electron charge for FAZB-grafted anatase (100) surface. (b and c) Same as (a) but for FAZB-grafted anatase (101)-I and (101)-II surface, respectively. The hybrid system with adsorbate of trans-(cis-) FAZB is represented with red solid (blue dashed) lines. The vertical dashed lines indicate the encompassing regions of positive (1) and negative charges (2) near the interfaces. The transferred electron charge at the coordinate z is obtained by averaging the transferred electron charge on the corresponding x–y plane.

Fig. 7 (a) Linear distribution of transferred electron charge for PFOS-grafted anatase (100) surface. (b and c) Same as (a) but for PFOS-grafted anatase (101)-I and (101)-II surface, respectively. The hybrid system with adsorbate of PFOS-OH (PFOS-F) is represented with red solid (blue dash) lines. The vertical dashed lines indicate the encompassing regions of positive (1) and negative charges (2) near the interfaces. The transferred electron charge at the coordinate z is obtained by averaging the transferred electron charge on the corresponding x–y plane. (d) Mulliken charge distributions on adsorbate of PFOS-OH (○) and PFOS-F (■). The horizontal axis is the coordinate of the atom in the z-direction.

Also, we calculated the UV-vis absorbance spectra of the hybrid organic/inorganic systems to probe the grafting-induced changes in their optical properties. Consequently, a significant anisotropic absorbance was found for the bare and hybrid surfaces. The first absorption bands in Fig. 8 are 3.02, 2.74 and 3.39 eV for the (100), (101)-I and (101)-II unbound TiO₂ surfaces, respectively. Our computed first absorption band of the (101)-I unbound surface is consistent with other theoretical calculations (2.56 eV)³⁴ but is underestimated compared with the experimental measurements, which is located between 3.4 and 4.9 eV performed on TiO₂ films with different thicknesses.⁶⁴ To obtain the exact optical properties in the UV-vis range, the scissors operation⁶⁵ of 0.66 eV, which corresponds to the difference between the experimental measurement of the thinnest TiO₂ films (∼15 nm) considered in a previous study and our theoretical result, was carried out in an optical absorbance of the hybrid system. As shown in Fig. 9(a), we found that the absorbance spectra of the TiO₂ surface grafted with trans-FAZB are slightly different from that with cis-FAZB, except for the case of TiO₂ surface grafted with trans-FAZB in the z polarization direction, which exhibits an additional absorption peak at about 3.2 eV, corresponding to the conformational switch of azobenzene-containing units from the apparent wetting state (i.e., trans isomer) to the fully wetting state (i.e., cis isomer) under UV irradiation.²³ In addition, the absorbance spectra of the (101)-II TiO₂ surface grafted with PFOS-F are also slightly different from that with PFOS-OH [Fig. 9(b)], while the absorbance spectra of PFOS-F- and PFOS-OH-grafted TiO₂ surfaces are similar for the (100) and (101)-I surfaces. The absorption peak at about 3.6 eV for the PFOS-grafted TiO₂ surface can be assigned to the oxidization of PFOS upon UV illumination.²⁵

Fig. 8 Absorbance spectra of unbound anatase (100) (top panel), (101)-I (middle) and (101)-II (bottom panel) surface when the polarization direction of incident light is along the x- (black), y- (red) and z (blue)-directions.

Fig. 9 (a) Absorbance spectra of cis-FAZB- (solid) and trans-FAZB (dash)-grafted anatase (100) (top panel), (101)-I (middle) and (101)-II (bottom panel) surface when the polarization direction is along the x- (black), y- (red) and z (blue)-directions. (b) Absorbance spectra of PFOS-F (solid)- and PFOS-OH (dash)-grafted anatase (100) (top panel), (101)-I (middle) and (101)-II (bottom panel) surface when the polarization direction of incident light is along the x- (black), y- (red) and z (blue)-directions. The scissors operation of 0.66 eV is applied.

4 Conclusions

Density functional theory calculations were performed on hybrid systems containing organic switches adsorbed on low-index TiO₂ anatase surfaces. We considered the trans-FAZB and cis-FAZB isomers anchored by carboxyl groups on one side of the isomer, while the pristine PFOS-F and oxidized PFOS-OH bonded by the oxygen atoms in the siloxane groups. The reliability of our models was demonstrated by examining the chemically intuitive parameter, i.e., adsorption energies. To understand how the different conformations of the organic switches interact with the inorganic surface, we investigated their electronic structures and surface potentials and analyzed their charge redistributions. The band gaps of the hybrid systems are reduced upon adsorption. For each type of TiO₂ surface, while the trans-FAZB-grafted TiO₂ surface exhibits a larger band gap than the cis-FAZB-grafted TiO₂ surface, both the PFOS-F- and PFOS-OH-grafted TiO₂ surfaces have similar band gaps. The effect of organic switch modifications was found to be crucial to determine the relative order of the ionization potentials among the different TiO₂ surfaces. Moreover, we systematically studied the organic switch configuration dependence of the ionization potentials of the functionalized TiO₂ surfaces with FAZB and PFOS adsorbates and found that regardless of the type of TiO₂ surface, the cis-FAZB (PFOS-OH)-grafted TiO₂ exhibits a lower ionization potential than the trans-FAZB (PFOS-F)-grafted TiO₂. By considering the two important factors in tuning the surface dipole moments, as follows: (i) the electron charge redistribution at the interface caused by chemical functionalization and structural relaxation effect and (ii) the polarity of attached chemical groups, we successfully explained the different behaviors of the ionization potentials for the trans-/cis-FAZB- and PFOS-F/PFOS-OH-terminated TiO₂ surfaces. By combining the induced polar interaction analysis and the experimental measurements in the literature, we demonstrated that the ionization potential is an important predictor of the surface wetting properties of the adsorbed systems. Anisotropic absorbance for the considered hybrid surfaces was also found. The first absorption peak of TiO₂ grafted with trans-FAZB (PFOS-F) was assigned to the conformational switch (oxidization) under UV irradiation. This study represents the first effort to rationalize the surface potentials of organic/inorganic systems via first-principles modeling, which can be helpful for the proper design and selection of organic coatings with controllable surface properties for photosensitive material applications, such as chemical sensors, artificial intelligent surfaces, and microfluidic devices.

Author contributions

Haiming Huang: conceptualization, methodology, validation, investigation, formal analysis, visualization, writing – review & editing. Mingquan Ding, Yu Zhang, Shuai Zhang and Yiyun Ling: investigation, formal analysis, visualization. Weiliang Wang: methodology, validation, supervision, project administration, writing – review & editing. Shaolin Zhang: conceptualization, supervision, project administration, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the National Natural Science Foundation of China (12004083 and 51972069), the Science and Technology Projects in Guangzhou (202102020350, 202102010470 and 202102080361), the National Key R&D Program of China (2016YFB0200800), the Key-Area Research and Development Program of Guangdong Province (2019B030330001), the College Students Innovation and Entrepreneurship Training Program of Guangdong Province (s202211078135), Key Discipline of Materials Science and Engineering, Bureau of Education of Guangzhou (202255464), the National Supercomputer Center in Guangzhou, and the Network Center of Guangzhou University.

References

1. Y. B. Zheng, B. K. Pathem, J. N. Hohman, J. C. Thomas, M. Kim and P. S. Weiss, Adv. Mater., 2013, 25, 302–312.
2. M. M. Russew and S. Hecht, Adv. Mater., 2010, 22, 3348–3360.
3. S. L. Oscurato, M. Salvatore, P. Maddalena and A. Ambrosio, Nanophotonics, 2018, 7, 1387–1422.
4. E. Pantuso, G. De Filpo and F. P. Nicoletta, Adv. Opt. Mater., 2019, 7, 1900252.
5. V. Y. Chang, C. Fedele, A. Priimagi, A. Shishido and C. J. Barrett, Adv. Opt. Mater., 2019, 7, 1900091.
6. S. L. Oscurato, F. Borbone, P. Maddalena and A. Ambrosio, ACS Appl. Mater. Interfaces, 2017, 9, 30133–30142.
7. B. Ziolkowski, M. Czugala and D. Diamond, J. Intell. Mater. Syst. Struct., 2013, 24, 2221–2238.
8. H. M. D. Bandara and S. C. Burdette, Chem. Soc. Rev., 2012, 41, 1809–1825.
9. L. Zhang and J. M. Cole, ACS Appl. Mater. Interfaces, 2014, 6, 3742–3749.
10. M. Irie, Chem. Rev., 2000, 100, 1685–1716.
11. R. Klajn, Chem. Soc. Rev., 2014, 43, 148–184.
12. X. J. Feng, L. Feng, M. H. Jin, J. Zhai, L. Jiang and D. B. Zhu, J. Am. Chem. Soc., 2004, 126, 62–63.
13. Q. T. H. Ta, S. Park and J. S. Noh, J. Colloid Interface Sci., 2017, 505, 437–444.
14. M. Hilal and W. Yang, Nano Convergence, 2022, 9, 14.
15. S. T. Wang, X. J. Feng, J. N. Yao and L. Jiang, Angew. Chem., Int. Ed., 2006, 45, 1264–1267.
16. D. S. Kommireddy, A. A. Patel, T. G. Shutava, D. K. Mills and Y. M. Lvov, J. Nanosci. Nanotechnol., 2005, 5, 1081–1087.
17. X. J. Xie and E. Bakker, J. Am. Chem. Soc., 2014, 136, 7857–7860.
18. Q. Q. Ding, R. Li, M. D. Chen and M. T. Sun, Appl. Mater. Today, 2017, 9, 251–258.
19. D. P. Hoffman, O. P. Lee, J. E. Millstone, M. S. Chen, T. A. Su, M. Creelman, J. M. J. Frechet and R. A. Mathies, J. Phys. Chem. C, 2013, 117, 6990–6997.
20. M. Zuleta, T. Edvinsson, S. Yu, S. Ahmadi, G. Boschloo, M. Gothelid and A. Hagfeldt, Phys. Chem. Chem. Phys., 2012, 14, 10780–10788.
21. Y. P. Zhang, Y. S. Wang, Z. Q. Xu, J. Y. Liu, J. C. Song, Y. Z. Xue, Z. Y. Wang, J. L. Zheng, L. C. Jiang, C. X. Zheng, F. Z. Huang, B. Q. Sun, Y. B. Cheng and Q. L. Bao, ACS Nano, 2016, 10, 7031–7038.
22. S. B. Ma, H. K. Ting, Y. Z. Ma, L. L. Zheng, M. W. Zhang, L. X. Xiao and Z. J. Chen, AIP Adv., 2015, 5, 057154.
23. S. Pan, R. Guo and W. Xu, Soft Matter, 2014, 10, 9187–9192.
24. Y. Ito, M. Heydari, A. Hashimoto, T. Konno, A. Hirasawa, S. Hori, K. Kurita and A. Nakajima, Langmuir, 2007, 23, 1845–1850.
25. Y. Pan, W. Kong, B. Bhushan and X. Zhao, Beilstein J. Nanotechnol., 2019, 10, 866–873.
26. J. W. Zhao, L. Xue, Z. J. Niu, L. Huang, Y. D. Hou, Z. Z. Zhang, R. S. Yuan, Z. X. Ding, X. Z. Fu, X. Lu and J. L. Long, J. Power Sources, 2021, 512, 230532.
27. J. W. Zhao, L. Huang, L. Xue, Z. J. Niu, Z. Z. Zhang, Z. X. Ding, R. S. Yuan, X. Lu and J. L. Long, J. Energy Chem., 2023, 79, 601–610.
28. J. W. Zhao, B. Q. Liu, L. S. Meng, S. He, R. S. Yuan, Y. D. Hou, Z. X. Ding, H. X. Lin, Z. Z. Zhang, X. X. Wang and J. L. Long, Appl. Catal., B, 2019, 256, 117823.
29. H. W. Zhang, P. Zhang, J. W. Zhao, Y. Liu, Y. Huang, H. W. Huang, C. Yang, Y. B. Zhao, K. F. Wu, X. L. Fu, S. Y. Jin, Y. D. Hou, Z. X. Ding, R. S. Yuan, M. B. J. Roeffaers, S. C. Zhong and J. L. Long, Angew. Chem., Int. Ed., 2021, 60, 16009–16018.
30. P. Zhang, X. Y. Sui, Y. Wang, Z. Wang, J. W. Zhao, N. Wen, H. L. Chen, H. W. Huang, Z. Z. Zhang, R. S. Yuan, Z. X. Ding, W. X. Dai, X. Z. Fu, Y. X. Weng and J. L. Long, J. Am. Chem. Soc., 2023, 145, 5769–5777.
31. L. Dworak, M. Zastrow, G. Zeyat, K. Ruck-Braun and J. Wachtveitl, J. Phys.: Condens. Matter, 2012, 24, 394007.
32. P. Bluemmel, A. Setaro, C. Maity, S. Hecht and S. Reich, J. Phys.: Condens. Matter, 2012, 24, 394005.
33. K. J. Chen, A. Charaf-Eddin, B. Selvam, F. Boucher, A. D. Laurent and D. Jacquemin, J. Phys. Chem. C, 2015, 119, 3684–3696.
34. A. Belhboub, F. Boucher and D. Jacquemin, J. Phys. Chem. C, 2016, 120, 18281–18288.
35. K. J. Chen, F. Boucher and D. Jacquemin, J. Phys. Chem. C, 2015, 119, 16860–16869.
36. Z. Deng, Z. Li and W. Wang, Chem. Phys. Lett., 2015, 637, 26–31.
37. W. Wang and Z. Li, J. Appl. Phys., 2011, 109, 114308.
38. C. Q. Sun, Nano Mater. Sci., 2020, 2, 333–345.
39. J. L. Freeouf and J. M. Woodall, Appl. Phys. Lett., 1981, 39, 727.
40. Y. Ando, Y. Gohda and S. Tsuneyuki, Surf. Sci., 2012, 606, 1501–1506.
41. I. K. Dmitrieva and G. I. Plindov, Phys. Scr., 1983, 27, 402–406.
42. K. R. S. Chandrakumar, T. K. Ghanty and S. K. Ghosh, J. Phys. Chem. A, 2004, 108, 6661–6666.
43. P. Politzer, P. Jin and J. S. Murray, J. Chem. Phys., 2002, 117, 8197–8202.
44. A. Carre, J. Adhes. Sci. Technol., 2007, 21, 961–981.
45. H. Huang, W. Wang and L. Wang, Phys. Chem. Chem. Phys., 2019, 21, 8257–8263.
46. M. Khazaei, M. Arai, T. Sasaki, A. Ranjbar, Y. Y. Liang and S. Yunoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075411.
47. W. Li, L. G. C. Rego, F. Q. Bai, C. P. Kong and H. X. Zhang, RSC Adv., 2014, 4, 19690–19693.
48. F. De Angelis, S. Fantacci and R. Gebauer, J. Phys. Chem. Lett., 2011, 2, 813–817.
49. A. G. Thomas and K. L. Syres, Chem. Soc. Rev., 2012, 41, 4207–4217.
50. G. Pilania, K. Slenes and R. Ramprasad, J. Appl. Phys., 2013, 113, 064316.
51. A. Y. Fadeev and T. J. McCarthy, J. Am. Chem. Soc., 1999, 121, 12184–12185.
52. F. Labat, P. Baranek and C. Adamo, J. Chem. Theory Comput., 2008, 4, 341–352.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
55. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
56. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
57. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
58. S. C. Li, Y. Losovyj, V. K. Paliwal and U. Diebold, J. Phys. Chem. C, 2011, 115, 10173–10179.
59. H. Wang, X. T. Hu, Y. J. Ma, D. J. Zhu, T. Li and J. Y. Wang, Chin. J. Catal., 2020, 41, 95–102.
60. S. P. Kowalczyk, F. R. McFeely, L. Ley, V. T. Gritsyna and D. A. Shirley, Solid State Commun., 1977, 23, 161–169.
61. R. Asahi, Y. Taga, W. Mannstadt and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7459–7465.
62. S. Mo and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 13023–13032.
63. P. C. Rusu and G. Brocks, J. Phys. Chem. B, 2006, 110, 22628–22634.
64. A. Mills, G. Hill, S. Bhopal, I. P. Parkin and S. A. O'Neill, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 160, 185–194.
65. M. R. Pederson and B. M. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10319–10331.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00537b

---