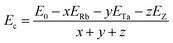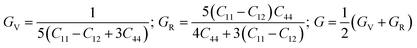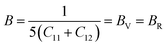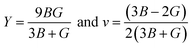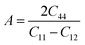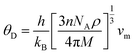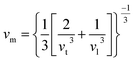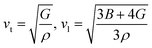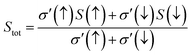Tantalum half-Heusler alloys RbTaSi and RbTaGe: potential candidates for desirable thermoelectric and spintronic applications

Abstract

Heusler alloys have drawn the interest of researchers due to their possible technical significances and multifunctional use. Herein, a thorough theoretical analysis using “density functional theory (DFT)” is performed to investigate the general physical features of RbTaSi and RbTaGe alloys. The “generalised gradient approximation (GGA)” and “Tran–Blaha modified Becke–Johnson (TB-mBJ) potential” has been incorporated to model the electronic structures of RbTaSi and RbTaGe. The structural optimization results signify that these materials are stable in the ferromagnetic phase with a cubic F4̄3m structure, which is supported by the computed elastic parameters. In addition, cohesive energy and microhardness signify strong bonding. The spin-polarisation bands and density of states indicate the half-metallic nature of these materials. These materials have spin magnetic moment 2μ_B, thereby emphasizing the use of these alloys for spintronic applications. Transport and thermodynamic properties have been calculated, and their temperature dependence is illustrated. The behavior of transport coefficients with temperature futher implies the presence of half-metallic nature.

---

Introduction

Global energy crises have surely heightened research interest in the development of clean energies and novel electrochemical energy storage systems.^1–6 On one side, fossil fuels are currently on the verge of disappearing as a result of extreme exploitation, while both global energy demand and consumption are still rising. Moreover, a significant amount of energy is dissipated due to the low efficiency of current state-of-the-art devices.⁷ Thermoelectric devices have the ability to reconvert dissipated thermal energy to a useable form. The goal and critical needs are to improve the effectiveness of thermoelectric devices. This can be achieved by synthesizing or modelling materials with valuable applications, particularly in transforming squandered heat into a useable form of energy.^8,9 The search for such novel materials and the tunability of their properties creates significant momentum in unlocking various applications. Besides thermoelectrics, the current progress in electronics which combines spin magnetic characteristics with conventional electronic devices, has pushed half-metallic ferromagnets to the forefront.¹⁰ The half-metallic magnetic metals depict semiconducting band structure in one spin state while the other spin-state band structure is metallic. Thus, these materials exhibit 100% spin polarization around the Fermi level.

Heusler alloys offer a great prospect of achieving such performances and possess potential technological applicability.^11,12 In the past three decades, a huge number of Heusler alloys have been shown to depict half-metallic characteristics.^13–15 Their tunability in electronic structure, spin coupling phenomena, charge distributions, and subsequent multidimensional and multifunctional properties have drawn the interest of researchers worldwide. The ternary half Heusler alloys (XYZ), including MnCrP,¹⁶ Ti_0.5Zr_0.5NiSn,¹⁷ CrZSi (Z = Sc, Ti),¹⁸ LiMnZ (Z = N, P, Si),¹⁹ XCrZ (X = Li, K, Rb, Cs; Z = S, Se, Te),²⁰ TaXY (X = Ru, Rh; X = Sb, Bi, Sn, and Pb)²¹ and many others possess some novel properties, including good optical absorbance, high figure of merit, and half-metallicity. Recently, half-Heusler compounds with 8 valence electrons, due to their compatible electronic structure and thermal stability, are regarded as prospective materials for spintronic applications.²² Motivated by the aforementioned characteristics and multi-dimensional applications, cubic half-metallic RbTaZ (Z: Si, Ge) Heusler alloys have been selected in the present work. There are no detailed results regarding the mechanical characteristics, thermodynamic and transport properties of these alloys; therefore, our results would pose their future applications in energy harvesting and spintronic technologies.

The setup of the paper is: in the “Computational details” section, a brief report of the process and computational parameters is provided. In the “Results and discussion” section, the results are described and thoroughly explored. In the “Conclusion section”, the main findings are summarized.

Computational details

Using Wien2k,²³ a full potential linearized augmented plane wave based software, the ground state properties of RbTaSi and RbTaGe have been investigated. Perdew–Burke–Ernzerhof form of GGA²⁴ has been adopted as an exchange–correlation functional to estimate the energies and determine equilibrium geometries. To ensure no charge leakage from the muffin tin spheres and to achieve better energy convergence, non-overlapping muffin-tin radii were used. The energy and charge convergence constraints are set to 10⁻⁴ e and 10⁻⁴ Ry, respectively. The parameters R_MTK_MAX and l_max are set to 7 and 10, respectively, which controls the size of the basis set. The tetrahedral method,²⁵ along with a dense k-mesh of 4000 k-points within the Monkhorst and Pack convention, is used. In order to have accurate electronic properties (e.g., band gaps and magnetic moments), modified Becke–Johnson potential (mBJ)²⁶ has been implemented with GGA. Gibbs2 code, which is based on quasi-harmonic approximation, has been used to invigilate the thermodynamic properties,²⁷ while transport characteristics are obtained using the BoltzTrap code.²⁸ Structural optimization data is used as input for determining the thermodynamic properties, while transport properties are obtained from band distribution around the Fermi level (E_F). Because the estimation of thermoelectric properties is highly dependent on the electronic structure, a precise forecast of the electronic band gap is necessary. So, GGA + mBJ results and 10⁵ k-points are used to deliver transport properties.

Results and discussion

Structural properties

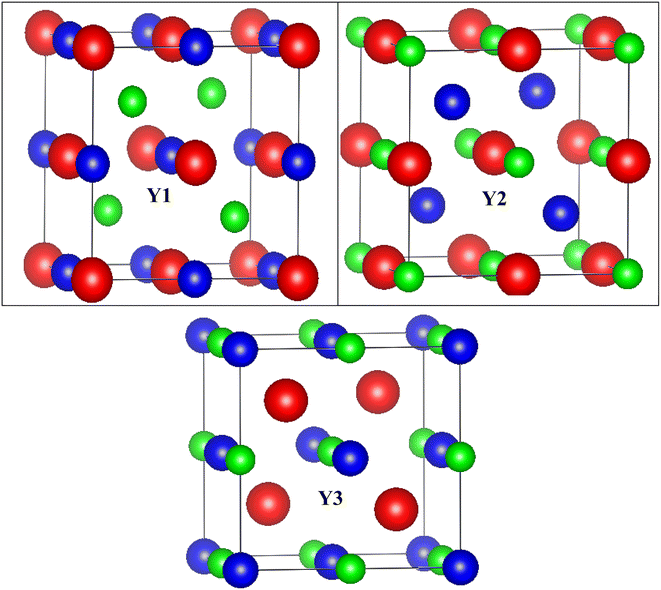
Conventional cubic half Heusler unit cell has three interpenetrating face-centered cubic (fcc) sub-lattices, which together form a crystal structure with F4̄3m (#216) symmetry. It is possible to generate the three inequivalent atomic structures Y1, Y2, and Y3 by permuting the constituents X, Y, and Z over the Wyckoff locations 4a (0,0,0), 4b (1/2,1/2,1/2), and 4c (1/4,1/4,1/4). The difference in configuration is self-explained in Table 1. The structures of the three phases are depicted in Fig. 1.

Table 1 Atomic occupancy in different half Heusler structures

Arrangement	Rb	Ta	Z
Y1	4a	4b	4c
Y2	4b	4c	4a
Y3	4c	4a	4b

---

Fig. 1 Representation of structures in Y1, Y2, and Y3 phases. Red – Rb, blue-Ta, and green-Ge/Si.

The half Heusler alloys RbTaZ have a non-metal p-block element Si and Ge at the Z position. Structural optimization has been carried out to predict the stable structural configuration of RbTaSi and RbTaGe compounds out of all three arrangements (Y1, Y2, Y3). The structure was optimised by fitting the total energy as a function of volume using the Birch–Murnaghan equation of state.^29,30 From the optimization plots demonstrated in Fig. 2, it is clear that RbTaSi and RbTaGe are the most stable Y1 phase. In the Y1 phase, further a stable magnetic configuration is determined. The ferromagnetic states owe comparatively more negative energy and thus are the most stable states, as shown in Fig. 3. The relaxed parameters determined at the optimum volume of the ferromagnetic states are given in Table 2. The obtained values of lattice constants are compatible with already reported values in the literature.²² The observed increment in lattice parameter from RbTiSi to RbTiGe is related to the increase in the atomic radius of the elements.

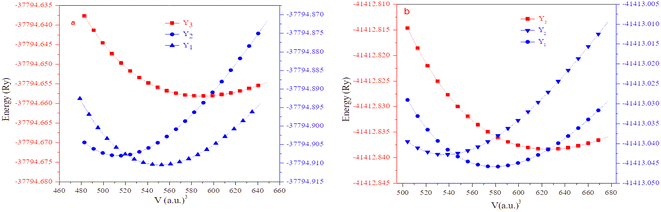Fig. 2 Calculated total energy as a function of unit cell volume of Y1, Y2, and Y3 configurations of (a) RbTaSi and (b) RbTaGe, respectively.

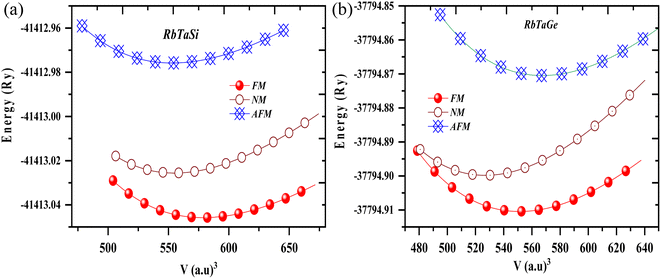Fig. 3 Total energy vs. volume in ferromagnetic (FM), antiferromagnetic (AFM), and non-magnetic (NM) phases of (a) RbTaSi and (b) RbTaGe compounds.

Table 2 Lattice parameter a₀ (Å), V (volume in (a.u.)³), B (bulk modulus in GPa), B′ (dB/dP), E₀ (total energy in Ry), and cohesive energy (E_c in eV) RbTaSi and (b) RbTaGe in FM phase

Alloys	a0	V	B	B′	E0 (Ry)	Ec
RbTaSi	6.88; 6.89 (ref. 22)	551.20	42.75	4.40	−37794.910463	5.51
RbTaGe	7.00; 6.99 (ref. 22)	578.96	39.34	4.67	−41413.045816	4.45

---

Further, the cohesive energy (E_c) is also determined using relation;²¹

Here, E₀ represent the total optimized energy, E_Rb, E_Ta and E_Z are energies of isolated Rb, Ta, and Z atoms, respectively. While x, y, and z are the number of Rb, Ta, and Z constituents in a conventional unit cell, respectively. E_c measures the difference between the optimized energy and the energy of its constituent atoms.³¹ The cohesive energy characterizes the strength of bonds. The calculated values of E_c are presented in Table 2. The overall results indicate that these materials are stable and constituents are strongly held.

Electronic and magnetic properties

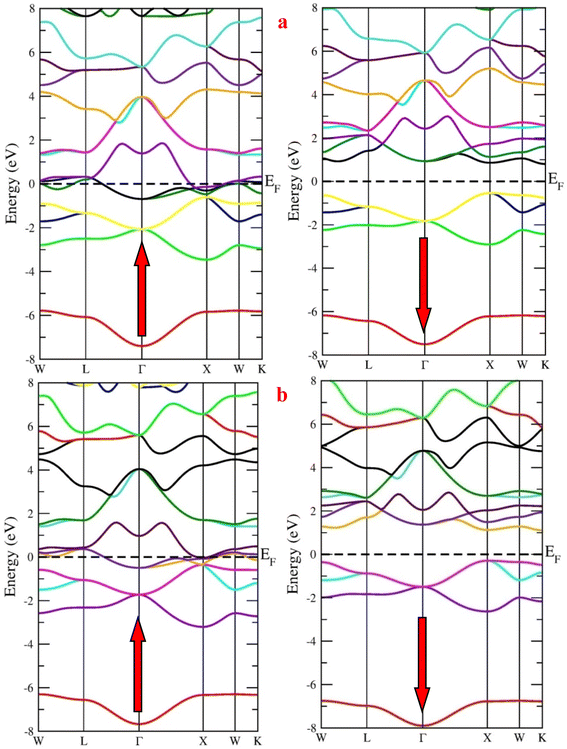
First, we calculated the spin-polarized band structure along the high symmetry directions of the Brillouin zone using the GGA approximation. The results reported in Fig. 4 make it evident that there exist several energy states at the Fermi level (E_F) in the spin-up channel, indicating that the relevant state has a metallic characteristic while the Fermi level is unoccupied in the opposite spin channel, demonstrating indirect band profile. The band gaps of RbTaSi and RbTaGe along K–X symmetric points are 0.58 eV and 0.66 eV, respectively, resulting in the overall half-metallic characteristics of these alloys. However, GGA typically underestimates the energy gap of semiconductors, notably in systems with d-electrons. Keeping this in view and to overcome this uncertainty, we have employed the mBJ scheme to obtain a more precise band structure. The band structures obtained from the mBJ method are profiled in Fig. 5. The band gap in the semiconducting channel expands by adding the mBJ potential in GGA. The new values are 1.33 eV and 1.39 eV for RbTaSi and RbTaGe, respectively. The obtained values of band gaps are consistent with the reported values.²² However, the bands at the Fermi level of spin up states do not shift, thereby validating the half-metallicity in these alloys.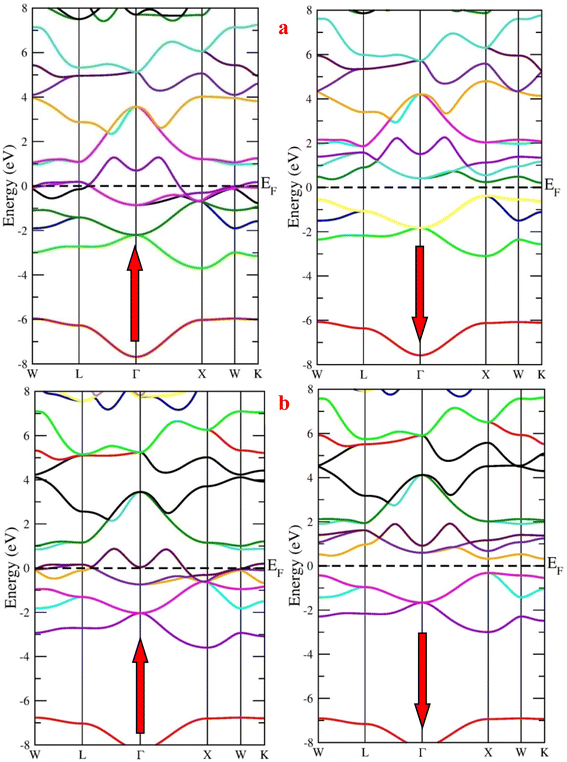

Fig. 4 Band structure of (a) RbTaSi and (b) RbTaGe alloys through GGA approximation (Fermi level is set at 0 eV).

Fig. 5 Spin polarized band structure of (a) RbTaSi (b) RbTaGe alloys via mBJ method.

The half-metallic composition in these alloys is further explored via calculation of the total, atomic, and individual density of states (DOS) around E_F, as shown in Fig. 6 and 7. It is clear from the total atomic DOS in the spin up state that there is adequate DOS at the Fermi level, which is strong evidence of metallic nature in the relevant state. While in the spin down state, there is a splitting of energy levels at the Fermi level, resulting in a gap at the Fermi level. There are no energy states at the Fermi level, suggesting semiconducting nature. Also, from Fig. 7, in spin up channel, all the atoms have their contribution to DOS at the Fermi level (tantalum has the majority contribution), but in spin down state, neither conduction nor valence band touches the Fermi level due to the splitting of energy states. So, atomic and total DOS also signify half-metallicity in these alloys.

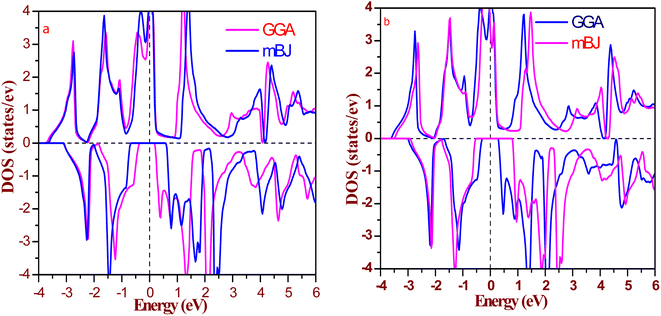Fig. 6 Calculated total density of states for (a) RbTaSi and (b) RbTaGe by GGA and mBJ (Fermi level is set at 0 eV).

Fig. 7 Atomic density of states (DOS) at equilibrium lattice constant of (a) RbTaSi and (b) RbTaGe.

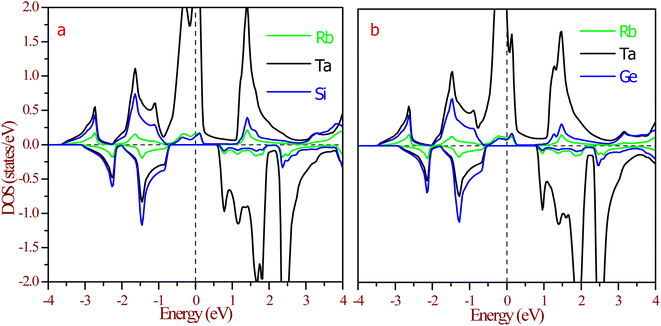
The half-metallic nature can be understood more from the partial density of states (pDOS), as shown in Fig. 8. The origin of gaps in half-Heusler alloys mostly came from d–d hybridization among the transition elements. The RbTaZ (Z = Si, Ge) alloys under investigation have only one transition metal atom (Ta), so the gap originates via d–d hybridization happening via the p-orbitals of Z. The constituents can be thought to be in Rb⁺¹Ta⁺³Z⁻⁴ oxidation states. Among the constituents, Rb is the most electropositive, transferring its s-electron to the Z constituent. The outer shell electronic configuration of Z after accepting the electron from Rb becomes 4s²4p³. The Y and Z atoms are positioned in such a way that they form a ZnS-type lattice with Y at the centre of the tetrahedron. The d-state of Ta has 5-fold degenerate d-orbitals; d_xy, d_yz, d_zx lie in between the axis and d_x²−y², d_z² lie on the axis. The Z-atom acts as a ligand, approaches along the cubic axes, lifts the degeneracy of d-orbitals. The d-state splits into d_xy, d_yz, d_xz referred as d-t_2g states and d_x²−y², d_z² labelled as d-e_g states. In a tetrahedral environment of ligands, d-t_2g states are at higher energy compared to the d-e_g states.³² The p-states of ligands do side-wise hybridization with t_2g and direct with e_g-state. In this way, d–d hybridization happens via the p-orbitals of the ligand. The bonding dt_2g–p–de_g states have their contribution at the Fermi level, as illustrated in Fig. 8. The non-bonding dt_2g–p–de_g states give DOS peaks above the Fermi level. In the Rb⁺¹Ta⁺³Z⁻⁴ oxidation state, Ta has two unpaired electrons that partially fill hybridized bonding d–d orbitals in the spin up channel, thereby giving rise to metallic nature. The pDOS further clarifies that in the minority spin channel, valence band minima are constituted by dt_2g–p–de_g hybridized states. Lack of unpaired electrons in spin down channels results in semiconducting nature. This also leads to 100% spin polarization of materials at the Fermi level.

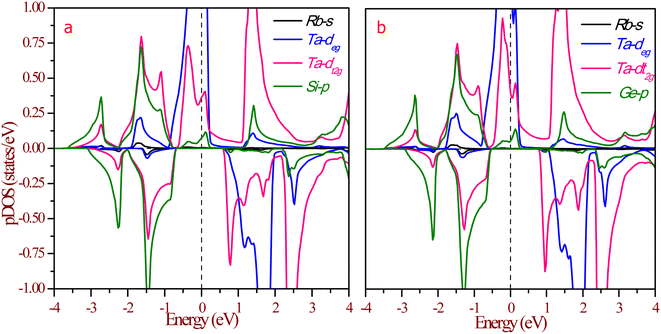Fig. 8 Partial density of states (pDOS) at equilibrium lattice constant for (a) RbTaSi and (b) RbTaGe. The Fermi level is set at zero energy.

The magnetic properties were examined only after these materials had indeed been found to be stable in the ferromagnetic phase via proper optimization in different magnetic states. Half-metallic alloys possess an integer value of the magnetic moment. As both alloys have 2μ_B magnetic moment, these follow the Slater–Pauling rule.²² Ta element contributes the most to the magnetization, with a small impact from the Rb and Z (Si, Ge) atoms. In the Rb⁺¹Ta⁺³Z⁻⁴ oxidation state, only Ta exhibits two unpaired electrons, thereby giving rise to 2μ_B magnetic moment. From the pDOS displayed in the Fig. 8, the highest peak corresponds to d-e_g, and d-t_2g state of Ta at the Fermi level gives ferromagnetic character to alloys. We have further plotted susceptibility (χ) vs. temperature, as shown in Fig. 9. The output data χ from the BoltzTrap code is used to plot the graph. The curves indicate the presence of ferromagnetic nature.

Fig. 9 Variation in the molar susceptibility (χ) and inverse of susceptibility (χ⁻¹) with the temperature.

Charge density and chemical bonding

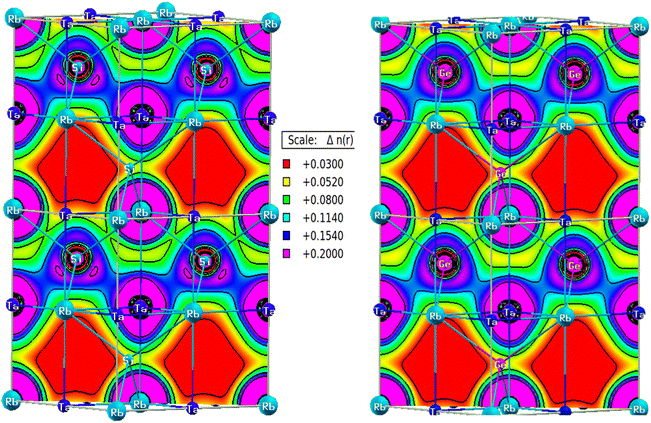
Charge distribution predicts the bonding behaviour between constituents. Covalent bonds are generated by electron sharing, which is achievable if the orbitals overlap to a certain extent to form hybrid (molecular) orbitals. As a result, there will always be a non-zero charge in inter-atomic distances. While there is an entire charge transfer in the case of ionic bonding leaving interstitial space free from charge density.³³ Fig. 10 depicts charge density maps for RbTaSi and RbTaGe along (110) planes. There is a large accumulation of charge between Ta and Z (Si, Ge) with dumbbell shape type charge distribution, indicating covalent bonding between Ta and Z. The bonding electrons between Ta and Z are contributed solely by Ta. The charge density around Rb atom is spherical for both alloys, as depicted from the charge density plot. Z is more electronegative and is the nearest neighbour to Rb, leading to ionic bonding between Rb and Z.

Fig. 10 Charge density plots along [110] plane of RbTaSi and RbTaGe.

Elastic properties

Elastic properties of a material are closely associated with many diverse solid-state properties.³⁴ From elastic properties, we can determine the mechanical stability, bonding feature between the neighbouring atomic planes, and the anisotropic nature of bonding in a compound.³⁵ For the determination of these elastic constants, the energy-strain relation³⁶ is followed i.e., elastic constants are determined by distorting the equilibrium cubic structure at constant volume constraint. This is accomplished by applying minor strains to the optimized structure and evaluating the change in the total energy, from which the second-order elastic constants (C_ij) and elastic moduli are calculated. Because these alloys have cubic symmetry, only C₁₁, C₁₂, and C₄₄ are required to investigate mechanical integrity. C₁₁ denotes length flexibility, while C₁₂ and C₄₄ reflect shape elasticity. The transverse strain on material causes it to alter shape; C₁₂ represents resistance to transverse expansion, whereas C₄₄ represents resistance to shear deformation. For the cubic structure, if the elastic constants are positive and satisfy Born–Huang (BH) stability criteria C₁₁ > 0, C₁₄ > 0, C₁₂ < B < C₁₁, C₁₁ − C₁₂ > 0, C₁₁ + 2C₁₂ > 0, then the material is mechanically stable.³⁷ The C_ij values obtained are provided in Table 3, and it is evident that RbTaSi and RbTaGe satisfy all the conditions and hence are mechanically stable. The mechanical behaviour of the alloy is further elucidated by determining different parameters. The average shear modulus is an indicator of reversible deformation resistance to shear stress and represents plastic deformation resistance. As a result, the hardness of a material can be determined more precisely by computing the shear modulus G and bulk modulus (B). The B and G moduli are determined through Hill's approximation,³⁸ which is the average of Voigt's and Reuss's values of B and G. In this way, the moduli for the cubic structure are defined as:

Table 3 Elastic parameters at 0 K and 0 GPa^a

Alloy	C11	C12	C44	B	GV	GR	G	Y	B/G	CP	A	V	H
a Cij's, B, GV, GR, G, Y, CP, and H are in units of GPa while B/G, A, and v are dimensionless quantities.
RbTaSi	80.63	24.62	21.37	43.29	24.02	23.60	23.81	60.36	1.81	3.25	0.76	0.27	9.36
RbTaGe	68.12	24.95	16.43	39.02	18.49	18.16	18.32	47.57	2.14	8.52	0.76	0.29	7.21

---

Young's modulus (Y) and Poisson's ratio (ν) are related to the bulk modulus B and the shear modulus G by the following equations;³⁹

With these elastic parameters in hand, the ductile and brittle behaviour can be estimated. Poisson's ratio (v),³⁹ Pugh's ratio (B/G),⁴⁰ and Cauchy pressure (C_P = C₁₂ − C₄₄)⁴¹ are all essential criteria in determining whether a solid is ductile or brittle. The key value of v to distinguish between brittle and ductile materials is 0.26. Above this, materials are expected to be ductile, while materials with ν < 0.26 are considered to be brittle. According to the Pugh criterion, B/G ratio could be used as a metric to quantify whether a material has a ductile or brittle character. The key value separating ductile from brittle material is 1.75. Specifically, when B/G > 1.75, the material is ductile, and when B/G < 1.75, the material is brittle. If C₁₂ > C₄₄ i.e., C_P is positive, and the alloy is ductile and possesses central bonding. The measured value of v, B/G, and C_P confirms the ductile character of these alloys.

Another important parameter that has an important implication in industrial science to detect micro-cracks in materials is the anisotropy factor (A).⁴²

It demonstrates the directional dependence of physical qualities, whether they have the same value in all directions (isotropic) or not (anisotropic). For A = 1, a material is entirely isotropic and anisotropic for any value less or larger than unity. The greater a system's divergence from unity, the greater the degree of anisotropy. The obtained value of A shows the alloys are anisotropic. The microhardness (H) test is used to determine the mechanical strength of solids. H can be related to both bulk and shear moduli to indicate an alloy's strength. However, for covalent and ionic materials, shear modulus (G_V) is proven to be a stronger predictor of hardness than bulk modulus.⁴³ The microhardness can be calculated using the expression H = 0.39G_V. The calculated value of H for RbTaSi and RbTaGe alloys are 9.36 GPa and 7.21 GPa.

The Debye temperature is an important thermo-elastic characteristic that indicates the temperature at which collective oscillatory behaviour changes to individual thermal vibration. The Debye temperature⁴⁴ can be calculated by the following relation

where ‘h’ is Planck's constant, ‘k_B’ is Boltzmann's constant, ‘N_A’ is Avogadro's number, ‘ρ’ is mass per unit volume (density), ‘M’ is molecular weight, and ‘v_m’ is mean sound velocity, the mean sound velocity v_m is obtained, as depicted in Table 4, using mean longitudinal ‘v_l’ and transverse ‘v_t’ velocities.
v_t and v_l can be determined from Navier's equation

Table 4 Calculated density (ρ in g m⁻³), transverse, longitudinal, and average sound velocities (v_t, v_l, and v_m in m s⁻¹), Debye temperature (θ_D in K) and melting temperature (T_m in K)

Alloys	ρ	vt	vl	vm	θD	Tm
RbTaSi	4500	2300	4080	2570	222	1029.52
RbTaGe	4920	1920	3600	2146	189	955.58

---

The melting temperature is very important in predicting the stability of material over a wider range of temperatures. It is calculated by the following relation; T_m (K) = {553 + 5.11(C₁₁) ± 300}.

Thermodynamic properties

In order to understand the behaviour of RbTaSi and RbTaGe with increasing temperature and pressure, thermodynamic properties like thermal expansion (α), specific heat (C_v), Gruneisen parameter (γ), and entropy (S) are studied using quasi-harmonic model.^27,45

Fig. 11 clearly shows that volume does not alter appreciably with temperature. However, as the pressure rises, the volume of the alloys shrinks dramatically. Moreover, large variations in volume are evident at low pressures, and virtually minor variations can be seen at high pressures. So, pressure has a considerable influence on material volume. Variation in thermal expansion coefficient (α) is presented in Fig. 12 for RbTaSi and RbTaGe. α is proportional to an increase in the mean amplitude of oscillating atoms. α is related to numerous thermal properties, including melting point, specific heat, and also explains the strength of atomic bonds, which characterises a material's thermal shock behaviour. Materials with high α demonstrate low thermoelastic strength. As is evident from the graph, α grows dramatically at low temperatures up to 150 K for RbTaSi and 130 K for RbTaGe and approaches saturation at high temperatures. Furthermore, as the temperature rises, it significantly drops, owing to an increase in bond energy. At zero pressure and 300 K, the thermal expansion is low for RbTaSi and RbTaGe being 4.12 × 10⁻⁵ K⁻¹ and 3.6 × 10⁻⁵ K⁻¹.

Fig. 11 Graphical variation of volume with temperature at different pressures for (a) RbTaSi and (b) RbTaGe.

Fig. 12 Graphical variation of thermal expansion coefficient with temperature at different pressures for (a) RbTaSi (b) RbTaGe.

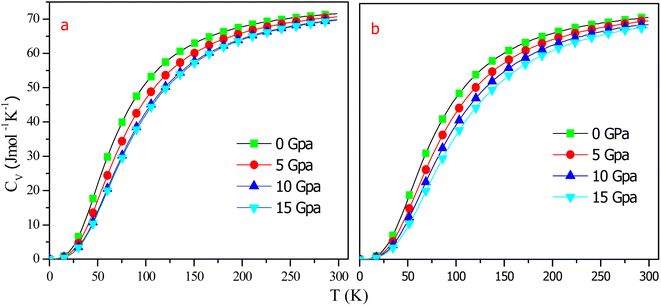
The heat capacity at fixed volume (C_V) is characterized as a substance's ability to absorb heat and increase its temperature. As a result of heat, intake atomic vibrations rise. The heat capacity approaches zero at around T ∼ 0 K and exhibits temperature dependency with the rise in temperature. The variations in C_V were calculated as a function of temperature at some fixed pressures, as shown in Fig. 13. Obviously, the C_V increases strongly up to 150 K, after which it increases incredibly slowly for both alloys. At high temps, C_V tends to a threshold limit referred to as the Dulong–Petit limit,⁴⁶ indicating that thermal energy stimulates all phonon modes. Fig. 13 clearly shows that at low temperatures, C_V is proportional to T³. Also, as seen in the graph, pressure and temperature have opposing effects on C_V, with temperature having a greater impact than pressure. The computed C_V values for RbTaSi and RbTaGe at zero pressure and 300 K are 71.6 J mol⁻¹ K⁻¹ and 70.90 J mol⁻¹ K⁻¹, respectively.

Fig. 13 Behaviour of specific heat with temperature at different pressures (a) RbTaSi (b) RbTaGe.

Fig. 14 illustrates the temperature's impact on the Grüneisen parameter (γ) at elevated stress, demonstrating a drastic fall with rising stress but a moderate increase with increasing temperature. Like other dynamic properties, an increase in temperature and pressure have opposite effects, but the pressure effect outweighs the temperature influence. The Gruneisen parameter for RbTaSi and RbTaGe is 2.19 and 2.05, respectively, at 0 K and 0 GPa and declines to 1.89 and 1.82 at 0 K and 15 GPa pressure.

Fig. 14 Variation of Gruneisen parameter with temperature at different pressures (a) RbTaSi (b) RbTaGe.

Entropy (S) is a measure of chaos and randomness in a system, and it can be used to accurately forecast the physical state of the system. At 0 K, the entropy is zero for all pressure values, as shown in Fig. 15. S increases exponentially with temperature while decreasing moderately with the application of pressure. As pressure increased, volume decreased, thereby constituents being concentrated in a smaller space and being less spread out. Entropy is calculated to be 96.611 J mol⁻¹ K⁻¹ at room temperature and 0 GPa pressure for RbTaSi and 105.43 J mol⁻¹ K⁻¹ for RbTaGe. This shift in entropy is due to a rise in the vibrational motion of the atoms when the temperature rises, resulting in an increase in the system's internal energy. Finally, there is no discontinuity in the entropy curve, indicating that the material maintains a single phase over the given range of temperature.

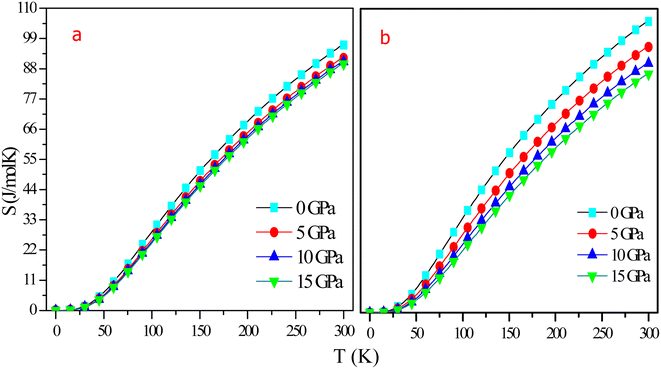Fig. 15 Graphical variation of entropy with temperature at different pressures of (a) RbTaSi and (b) RbTaGe.

Thermoelectric properties

Thermoelectric coefficients are calculated by BoltzTraP code that works on semi-classical Boltzmann theory.^28,47 The Boltzmann equation is solved under the constraint of constant relaxation time with a dense mesh of 100 000 k-points to obtain thermoelectric coefficients.

Electrical conductivity

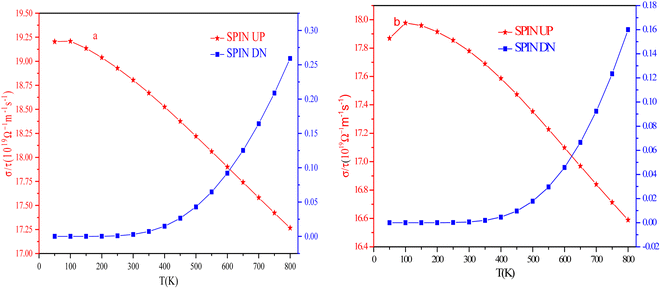
It is a characteristic feature of materials that quantifies the current carrying ability. Mathematical, σ = neμ, where ‘σ is the electrical conductivity coefficient, ‘n’ is the number of carriers’, ‘e’ is the charge on electron’, and ‘μ’ is the mobility of carriers. Both n and μ depend on temperature and can be determined from experiments through resistivity and Hall coefficient determination.⁴⁸ Each material is associated with some impurities that can act as a barrier to the flow of electric current and scatter the electrons inside the materials.⁴⁹ The graphical illustration of σ vs. T at the chemical potential (in the vicinity of Fermi level) is depicted in Fig. 16. In the spin-up channel, σ declines from 19.20 × 10¹⁹ Ω m⁻¹ s⁻¹ and 17.86 ×10¹⁹ Ω m⁻¹ s⁻¹ to 17.26 × 10¹⁹ Ω m⁻¹ s⁻¹ and 16.58 × 10¹⁹ Ω m⁻¹ s⁻¹ as the temperature rises from 100 K to 800 K for RbTaSi and RbTaGe, respectively. This decreasing conductivity with increasing temperature depicts the metallic nature of alloys in the spin up channel, thereby consistent with band structure. In the spin down channel, the conductivity shows no change up to ∼400 K for both alloys. The conductivity shows a sharp increase from 0.0146 × 10¹⁹ (0.00461 × 10¹⁹) Ω m⁻¹ s⁻¹ at 400 K to 0.25 × 10¹⁹ (0.16 × 10¹⁹) Ω m⁻¹ s⁻¹ at 800 K for RbTaSi and RbTaGe, respectively, indicating the semiconducting nature in respective channels. The total conductivity is the sum of the conductivities of two spin channels. The conductivity of a metallic channel is much larger than that of a semiconducting channel. Therefore, its behaviour would control the nature of total conductivity.

Fig. 16 Graphical variation of electrical conductivity with temperature (a) RbTaSi (b) RbTaGe.

Seebeck coefficient

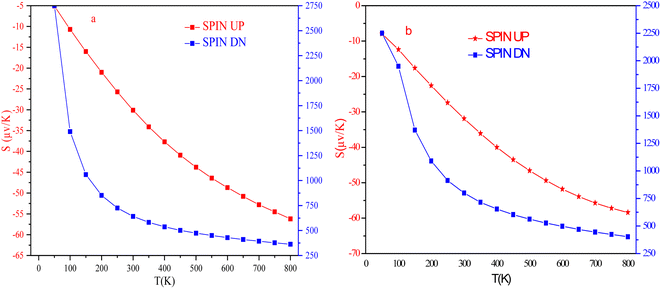
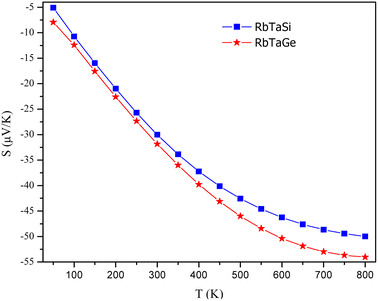
The temperature-led variations in Seebeck coefficient (S) are plotted in Fig. 17. The graph clearly indicates that the absolute value of S in the spin-up channel increases from 10 μV K⁻¹ and 12 μV K⁻¹ at 100 K to 56 μV K⁻¹ and 58 μV K⁻¹ at 800 K for Si and Ge-based alloys, respectively. In the spin-down channel, it decreases from 1490 μV K⁻¹ and 1950 μV K⁻¹ at 100 K to 363 μV K⁻¹ and 402 μV K⁻¹ at 800 K, correspondingly for RbTaSi and RbTaGe alloys. The S-value in the semiconducting channel is larger for RbTaGe. This is due to a larger bandgap in the spin minority channel of RbTaGe than RbTaSi. The negative sign of S in the spin up channel indicates electron carriers whilst the positive sign in the spin-down channel specifies holes as majority charge carriers. Further, the S_tot value is calculated with the help of the relation given below – two current model.⁵⁰

Fig. 17 Variation of Seebeck coefficient in spin up and spin down states (a) RbTaSi and (b) RbTaGe.

The behaviour of S_tot with temperature is given in Fig. 18. The graph reveals that there is a linear negative change with temperature, indicating that the spin-up channel is dominating. Thus, in half-metallic materials, the transport properties are more dominated by the metallic channel. The absolute value of S_tot gradually increases as the temperature rises, increasing from 12.42 μV K⁻¹ and 10.74 μV K⁻¹ at 100 K to 54.03 and 49.97 μV K⁻¹ at 800 K for RbTaSi and RbTaGe, respectively.

Fig. 18 Variation of total Seebeck coefficient with temperature for RbTaSi and RbTaGe.

Electronic thermal conductivity

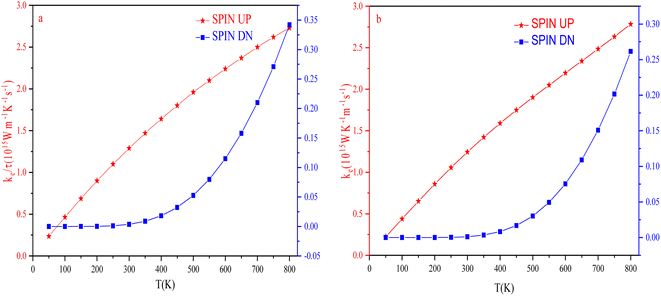
The temperature-led variations in electronic thermal conductivity (κ_e) of both the spin channels are shown in Fig. 19. For the spin-up channel, the thermal conductivity increases linearly with an increase in temperature, increasing from 0.23 × 10¹⁵ W m⁻¹ K⁻¹ s⁻¹ and 0.22 × 10¹⁵ W m⁻¹ K⁻¹ s⁻¹ at 50 K to 2.73 × 10¹⁵ W m⁻¹ K⁻¹ s⁻¹ and 2.78 × 10¹⁵ W m⁻¹ K⁻¹ s⁻¹ at 800 K for RbTaSi and RbTaGe, respectively. For the spin-down channel, it increases from 0.016 × 10¹⁵ W m⁻¹ K⁻¹ s⁻¹ and 0.032 × 10¹⁵ Ω m⁻¹ s⁻¹ at 450 K to 0.35 × 10¹⁵ W m⁻¹ K⁻¹ s⁻¹ and 0.26 × 10¹⁵ Ω m⁻¹ s⁻¹ at 800 K for RbTaSi and RbTaGe, respectively. The higher value of the thermal conductivity in the spin-up channel than the spin-down channel is due to the metallic nature of the spin-up state.

Fig. 19 Variation of thermal conductivity with temperature (a) RbTaSi (b) RbTaGe.

Power factor

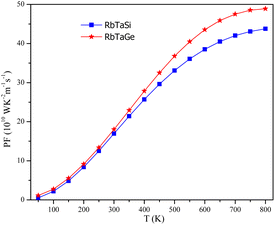
Power factor (PF = S_tot²σ) determines the utility of any materials for thermopower generation. PF enables us to comprehend the utmost efficiency that a material can have in relation to the supplied input. The power factor is dependent on both the Seebeck coefficient and conductivity. So, both S and σ should have reasonable values in order to achieve a high-power factor. The power factor of the alloys increases as the temperature rises, as depicted in Fig. 20. This is due to the fact that S_tot at lower temperatures is very low even though conductivity is high, generating a very low (∼0) power factor. However, conductivity decreases marginally with increasing temperature but S_tot increases; therefore S_tot²σ turns out to be substantial towards higher temperatures. The PF increases from 9.15 (8.38) 10¹⁰ W m⁻¹ K⁻² s⁻¹ at 200 K to 43.76 (48.90) 10¹⁰ W m⁻¹ K⁻² s⁻¹ for Si and Ge-based alloys respectively. The increasing nature of PF in both alloys hints that these could be used for high-temperature thermoelectric applications.

Fig. 20 Behaviour of total power factor with temperature for RbTaSi and RbTaGe.

Conclusion

The investigation of RbTaSi and RbTaGe using density functional theory by incorporating the functionals, namely GGA and GGA + mBJ, has been summed up. Both GGA and GGA + mBJ schemes show half-metallic character for the alloys. The majority spin channel turns out to be metallic and the minority spin channel as semiconductor. The half-metallic nature originates due to de_g–dt_2g hybridization happening via p-orbitals of the Z-constituent. Both alloys have 2μ_B magnetic moment with the utmost contribution from Ta-d electrons. These materials are mechanically stable, demonstrating good elastic and mechanical durability. Moreover, the cohesive energies portray that constituents of RbTaSi and RbTaGe are strongly bounded. The computed thermodynamic parameters ensure thermodynamic stability. The temperature-led variations in transport coefficients, including Seebeck coefficients and conductivities, certify the presence of the half-metallic nature. The increasing nature of PF in both alloys hints that these could be used for high-temperature thermoelectric applications. Thereby, the overall features of these materials render them suitable in solid-state device applications such as thermoelectric and spintronics.

Author contributions

Mr Nisar Ahmad Ganie performed all the calculations and wrote the manuscript. Dr Shabir A. Mir and Dr Dinesh C. Gupta reviewed and modified the manuscript.

Conflicts of interest

There is no conflict of interest among the authors.

References

1. M. G. Walter, et al., Solar water splitting cells, Chem. Rev., 2010, 110(11), 6446–6473.
2. S. W. Boettcher, et al., Photoelectrochemical hydrogen evolution using Si microwire arrays, J. Am. Chem. Soc., 2011, 133(5), 1216–1219.
3. S. A. Mir and D. C. Gupta, Analysis of cage structured halide double perovskites Cs2NaMCl6 (M= Ti, V) by spin polarized calculations, J. Alloys Compd., 2021, 854, 156000.
4. Y. W. Chen, et al., Atomic layer-deposited tunnel oxide stabilizes silicon photoanodes for water oxidation, Nat. Mater., 2011, 10(7), 539–544.
5. J. Zhang, et al., A metal-free bifunctional electrocatalyst for oxygen reduction and oxygen evolution reactions, Nat. Nanotechnol., 2015, 10(5), 444–452.
6. M. A. Green and S. P. Bremner, Energy conversion approaches and materials for high-efficiency photovoltaics, Nat. Mater., 2017, 16(1), 23–34.
7. S. A. Khandy and D. C. Gupta, Study of ferromagnetism, spin-polarization, thermoelectrics and thermodynamics of layered perovskite Ba2FeMnO6 under pressure and temperature, J. Phys. Chem. Solids, 2019, 135, 109079.
8. S. A. Khandy and D. C. Gupta, Magneto-electronic, mechanical, thermoelectric and thermodynamic properties of ductile perovskite Ba2SmNbO6, Mater. Chem. Phys., 2020, 239, 121983.
9. S. A. Sofi, S. Yousuf and D. C. Gupta, Prediction of robustness of electronic, magnetic and thermoelectric properties under pressure and temperature variation in Co2MnAs alloy, Comput. Condens. Matter, 2019, 19, e00375.
10. R. A. De Groot, et al., New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024.
11. K. Elphick, et al., Heusler alloys for spintronic devices: review on recent development and future perspectives, Sci. Technol. Adv. Mater., 2021, 22(1), 235–271.
12. Z. Bai, et al., Data storage: review of Heusler compounds, Spin, 2012, 2(4), 1230006.
13. Ab Q. Seh and D. C. Gupta, Quaternary Heusler alloy CoZrMnAs competent candidate for spintronics and thermoelectric technologies, Energy Storage, 2022, 4(4), e324.
14. Ab Q. Seh and D. C. Gupta, Exploration of highly correlated Co-based quaternary Heusler alloys for spintronics and thermoelectric applications, Int. J. Energy Res., 2019, 43(14), 8864–8877.
15. N. Naghibolashrafi, et al., Synthesis and characterization of Co-Ti-Sn alloys: Co1. 5TiSn as half-metal based on the Fe1. 5TiSb layered Heusler prototype, J. Alloys Compd., 2022, 924, 166501.
16. A. O. Alrashdi, et al., First principles calculations to investigate electronic, magnetic anisotropy energy and optical properties of MnCrP half-Heusler alloy, J. Mater. Res. Technol., 2022, 4220–4230.
17. G. Rogl, et al., Half-Heusler alloys: Enhancement of ZT after severe plastic deformation (ultra-low thermal conductivity), Acta Mater., 2020, 183, 285–300.
18. D. Vishali and J. Rita, Structural, electronic and magnetic properties of the Half-Heusler alloy CrZSi (Z= Sc, Ti), J. Cryst. Growth, 2022, 583, 126556.
19. L. Damewood, et al., Spintronic properties and stability of the half-Heusler alloys LiMnZ (Z = N, P, Si), arXiv, 2013, preprint, arXiv:1301.6367.
20. X. Wang, Z. Cheng and G. Liu, Largest magnetic moments in the half-Heusler alloys XCrZ (X= Li, K, Rb, Cs; Z= S, Se, Te): A first-principles study, Materials, 2017, 10(9), 1078.
21. D. M. Hoat, Electronic structure and thermoelectric properties of Ta-based half-Heusler compounds with 18 valence electrons, Comput. Mater. Sci., 2019, 159, 470–477.
22. M. A. Sattar, et al., First-principles prediction of magnetically ordered half-metals above room temperature, J. Materiomics, 2019, 5(3), 404–412.
23. P. Blaha, et al., Introduction to WIEN2K, An augmented plane wane plus local orbitals program for calculating crystal properties, Vienna University of Technology, Vienna, Austria, 2001, vol. 2001.
24. J. P. Perdew, K. Burke and M. Ernzerhof., Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
25. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188.
26. F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102(22), 226401.
27. A. Otero-de-la-Roza, D. Abbasi-Pérez and V. Luaña, Gibbs2: a new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation, Comput. Phys. Commun., 2011, 182(10), 2232–2248.
28. G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71.
29. F. Birch, Finite elastic strain of cubic crystals, Phys. Rev., 1947, 71(11), 809.
30. F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244–247.
31. S. A. Mir and D. C. Gupta, Scrutinizing the stability and exploring the dependence of thermoelectric properties on band structure of 3 d-3 d metal-based double perovskites Ba2FeNiO6 and Ba2CoNiO6, Sci. Rep., 2021, 11(1), 10506.
32. B. R. K. Nanda and I. Dasgupta, Electronic structure and magnetism in half-Heusler compounds, J. Phys.: Condens. Matter, 2003, 15(43), 7307.
33. S. A. Mir and D. C. Gupta, Exploration of uranium double perovskites Ba2MUO6 (M = Co, Ni) for magnetism, spintronic and thermoelectric applications, J. Magn. Magn. Mater., 2020, 493, 165722.
34. H. Fu, et al., Ab initio calculations of elastic constants and thermodynamic properties of NiAl under high pressures, Comput. Mater. Sci., 2008, 44(2), 774–778.
35. J. Wang and Y. Zhou, Dependence of elastic stiffness on electronic band structure of nanolaminate M 2 AlC (M = Ti, V, Nb, and Cr) ceramics, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(21), 214111.
36. G. V. Sin'Ko and N. A. Smirnov, Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure, J. Phys.: Condens. Matter, 2002, 14(29), 6989.
37. S. Yip, et al., Mechanistic aspects and atomic-level consequences of elastic instabilities in homogeneous crystals, Mater. Sci. Eng., 2001, A317(1–2), 236–240.
38. S. A. Mir and D. C. Gupta, New ferromagnetic half-metallic perovskites for spintronic applications: BaMO 3 (M= Mg and Ca), RSC Adv., 2020, 10(60), 36241–36252.
39. S. Cherid, et al., Theoretical prediction of half metallic ferromagnetic full-Heusler alloys Cs2CrGe, Solid State Commun., 2017, 260, 14–18.
40. S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Lond. Edinb. Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843.
41. D. G. Pettifor, Theoretical predictions of structure and related properties of intermetallics, Mater. Sci. Technol., 1992, 8(4), 345–349.
42. D. C. Gupta and S. Ghosh., First-principal study of full Heusler alloys Co2VZ (Z= As, In), J. Magn. Magn. Mater., 2017, 435, 107–116.
43. J. M. Leger, et al., Hardness and elasticity in cubic ruthenium dioxide, Appl. Phys. Lett., 2001, 79(14), 2169–2171.
44. O. L. Anderson, A simplified method for calculating the Debye temperature from elastic constants, J. Phys. Chem. Solids, 1963, 24(7), 909–917.
45. E. Francisco, et al., Quantum-mechanical study of thermodynamic and bonding properties of MgF2, J. Phys. Chem. A, 1998, 102(9), 1595–1601.
46. R. Fox, The background to the discovery of Dulong and Petit's law, Br. J. Hist. Sci., 1968, 4(1), 1–22.
47. E. S. Toberer, A. F. May and G. Jeffrey Snyder, Zintl chemistry for designing high efficiency thermoelectric materials, Chem. Mater., 2010, 22(3), 624–634.
48. P. Pichanusakorn and P. Bandaru, Nanostructured thermoelectrics, Mater. Sci. Eng., R, 2010, 67(2–4), 19–63.
49. M. H. Elsheikh, et al., A review on thermoelectric renewable energy: principle parameters that affect their performance, Renewable Sustainable Energy Rev., 2014, 30, 337–355.
50. H. J. Xiang and D. J. Singh, Suppression of thermopower of Na_xCoO₂ by an external magnetic field: Boltzmann transport combined with spin-polarized density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(19), 195111.

---