Open Access Article
Open Access ArticleOptical properties of nanostructured antiviral and anticancer drugs†
Alessandra Angela Pisu‡
a,
Francesco Siddi‡a,
Giancarlo Cappellini *ab and
Roberto Cardia
*ab and
Roberto Cardia *a
*a
aDepartment of Physics, University of Cagliari, S.P. Monserrato-Sestu Km 0,700, Monserrato, CA I-09042, Italy. E-mail: giancarlo.cappellini@dsf.unica.it; roberto.cardia@dsf.uinica.it
bEuropean Theoretical Spectroscopy Facility (ETSF), Italy
First published on 1st August 2023
Abstract
We present a computational study on the optical absorption properties of some systems of interest in the field of drug delivery. In particular we considered as drug molecules favipiravir (T705, an antiviral molecule) and 5-fluorouracil (5FU, an anticancer molecule) and, on the other hand, pure fullerenes (C24, B12N12, Ga12N12) and doped fullerenes (C23B, CB11N12) are considered as nanocarriers. Some combined configurations between the drug molecules and the carrier nanostructures have been then studied. The optical absorption properties of the above mentioned drug molecules and their carrier nanostructures in the free and bound states are obtained by a TD-DFT method, in gas phase and in aqueous solution. We perform a detailed analysis of the modifications arising in the absorption spectra that take place in some linked configurations between the drug molecules and the carrier nanostructures. These changes could be of importance as an optical fingerprint of the realized drug/carrier link.
1. Introduction
In recent years, the nanostructures based on carbon, boron nitride, gallium nitride and derivatives have been subject of great interest in the scientific community. These systems can be promising candidates to face several issues and emerging challenges in technological fields, ranging from the biological to medical and electronics ones.1–8 In this work we focus our attention on small fullerenes based on C, BN e GaN, here considered as potential carriers of the drugs T705 and 5FU.Favipiravir (T705 for short, C5H4FN3O2) is a molecule of strong pharmacological interest, developed in Japan in 1999, that is used in different kinds of biological areas for its antiviral proprieties. Favipiravir acts as broad-spectrum inhibitor against many different RNA viruses. Its action is based on the inhibition of the RNA polymerase and as a consequence it blocks the replication of the virus.9–11 Its first significant application was in the cure of Ebola outbreak,12 and today its effects are studied as possible cure against SARS-CoV-2 virus.13
5-Fluorouracil (shortly 5FU and chemical formula C4H3FN2O2) is a fluorinate analogue of pyrimidine.6 It has uracil-like structure, with a peripheral fluorine atom in place of a hydrogen atom. This biomolecule is often used in chemotherapeutic drugs to attack certain types of cancer (e.g., skin, breast, stomach, colon cancers).6,14–18 Its mechanism of action is based on entering and interfering in the synthesis process of nucleic acids (DNA, RNA) of the tumoral cells. Therefore, the replication of tumoral cells is inhibited.
The carbon based fullerenes (C2n) can be formed by 2n C atoms linked together with covalent bonds.4 The most famous and representative carbon fullerene is C60, discovered in 1985 by Kroto19 (Nobel Prize in Chemistry, 1996).20 After the discovery of C60, researchers have shown increasing interest in finding new fullerenes. During the years, several studies on the stability of fullerenes with 2n < 60 and 2n > 60 have been done. Many of these systems have been also synthesized21–23 within several techniques like arc-melting, laser ablation and electron beam irradiation technique.4,24–29 In recent years, small fullerenes (such as the C24 considered in this work) have gained the attention of the researchers. The fullerene C24 has been studied in several works to prove its stability and to understand its properties.21,30 In 2002, C24 has been synthesized within the electron beam irradiation technique.31,32 Boron nitride fullerenes can be formed by the same number of B and N atoms (BnNn), linked together with polar B–N bonds. Boron nitride fullerenes are isoelectronic with respect the carbon fullerenes formed of the same number of atoms. Their interesting chemical, physical, optical, electronics properties are different from the ones of their C counterparts. Boron nitride fullerenes are widely studied in several theoretical works30,33,34 and most of them have been also synthesized.31,35–37 The most stable system of the BnNn family is B12N12,33,34 which has been synthesized in 1998 within the electron beam irradiation.36,37
Gallium nitride nanocages (GaxNx, with 10 ≤ x ≤ 20) have been analyzed theoretically in ref. 7, to demonstrate their stability and physical properties. In this work we consider the GaN fullerene of 24 atoms, Ga12N12.
The unique chemical and physical properties of C and BN fullerenes are manifold: good adsorption capacity and interaction with bio/pharmaceutical molecules, high chemical stability, easiness of functionalization, biocompatibility, low toxicity and low poisonous quality.1,2,9,38,39 These properties make the C/BN fullerenes interesting for potential applications in biomedical fields as sensors (drug detectors) and transporter of drugs (drug carriers).1,2,9,39 Moreover, the good adsorption propriety allows the fullerenes to capture small molecules and to interact with them with high energy bond. Therefore, several researchers investigated the possibility to use them as gas sensors for the detection of harmful and polluting substances.2,33,38–41 Furthermore, GaN nanostructures are promising candidate for new nanotechnology applications.7 Gallium nitride systems are used in some optoelectronic devices and applications. For example, they can be used in light-emitting devices.7,8
An emerging challenge in the biomedical field is the research of systems based on nanostructures for the drug delivery. This is a promising modality to face and to overcome some problems related to the traditional way of drug administration.1,42 This innovative way of delivery consists in using nanostructures, such as functionalized fullerenes, as support system for bio/pharmaceutical molecules: the loaded drug will be transported by the carrier toward a specific target and will be released in the desired zone. As a consequence, the side effects are reduced and the quality of the therapy improves. The release mechanism can happen in several ways, for example through the action of enzymes or for particular pH conditions.1,6,42,43 In antiviral and antitumoral therapy there are needs of research and development in the drug delivery field. In particular, the efficiency of some clinical antiviral drugs is limited because of several factors: drug resistance, poor bioavailability, weak solubility and permeability, release off target, harmful side effects.9,44,45 Concerning the antitumoral therapy, the chemotherapy performed with traditional mechanism can be very harmful for the patient. The limitations are related to: drug toxicity and low solubility, degradation of drug before reaching the target, tumoral cell drug resistance, lack of selectivity between healthy and sick cells and release off target.46–48 In antiviral and antitumoral therapy a suitable drug delivery based on nanostructures (fullerenes, nanotubes, graphene-like structures), can improve the selectivity, facilitate the penetration of polar drugs through the cells, increase the drug release at the target.9,43–45 Moreover, they permit lower dosage and, therefore, less side effects6,9 and less damage to the healthy cells.6,46
Regarding the drug delivery based on fullerenes, the best known involves the C60, and in scientific literature there are several works concerning in vitro and in vivo tests.1,49,50 In particular, in these experiments, functionalized C60 is considered as a carrier of biomolecules that can be either adsorbed on the external surface of the carrier1,50 or loaded inside the C60.49 For smaller fullerenes like C24 and B12N12, several DFT and TD-DFT studies are being conducted to evaluate their potential applicability in this field.9,33,38,43,51 Concerning the gallium nitride Ga12N12 nanocage, in recent years its potential action as carrier for anticancer drugs 5-fluorouracil6 and cisplatin52 has been studied.
The aim of this work is to investigate the optical absorption properties obtained by TD-DFT calculations, of some proposed drug delivery systems (carrier + drug). In particular, we built four combined configurations of C/BN fullerenes (C24, B12N12, C23B, CB11N12) covalently bonded to 5FU. We considered as potential carrier also two substituted systems (C23B and CB11N12). This procedure is justified by the existence of some works in the literature in which it has been demonstrated that the doping process can enhance the interaction between carrier and drug.1,9,33,43
To validate our methods we considered some configurations from the scientific literature (C/BN clusters-T705 and Ga12N12-5FU).6,9 Please consider that it is out of the scope of this work to enter in the complex mechanism of drug delivery made by different steps as the drug/carrier bond creation, the drug transportation and the drug release at the target. Moreover, we do not consider here the issue related to the formation of drug/carrier systems starting from the free components. We focus here on the differences arising in the absorption spectra of the drug/carrier systems considered in their ground-state (either here calculated or obtained from literature) in comparison with the spectra of the free drug and carrier. These differences can be interpreted as an optical fingerprint of the occurred molecular bond between the carrier and the drug molecules.
2. Computational details
In this work we performed density functional theory (DFT) and time dependent-DFT (TD-DFT)53–57 calculations within the Gaussian16 computational code,58 an all-electron Gaussian-based software package. For all calculations we used a localized Gaussian basis-set (6-31+G*)59 combined with a hybrid exchange correlation (XC) functional (Becke-3-parameter-Lee–Yang–Parr, B3LYP).60,61 The chosen basis-set is composed by a valence double-ζ set including d polarization functions (indicated with the symbol “*”) and diffuse functions (“+”) for each atom other than H. The selected couple of XC potential and basis-set has been successfully tested for many different atomic systems, both organic and inorganic, with different sizes and degrees of complexity.62–77 Moreover, in several works (which studied nanostructures similar to ours)6,9,41,51,78 the B3LYP XC functional or the 6-31+G* basis-set have been used.We performed all the calculations for all systems under study both in gaseous phase and in aqueous solution. For the gas phase calculations we used the default self-consistency field (SCF) method. We investigated the solvent effect of water using the self-consistency reaction field (SCRF) method based on the conductor-like polarizable continuum model (CPCM).79 In this calculation scheme, the solvent is treated as a conductor-like polarizable continuous medium, described by a dielectric constant other than 1, i.e. 78.3553 for water.58
In more detail, we have performed geometry optimization of all the structures, in free and bound state, both in gaseous phase and aqueous solution. The configurations obtained from the literature were already optimized, so we did not perform the structural optimization in those cases. In particular for the systems studied in ref. 9 we started from their equilibrium geometry obtained in vacuum. For the systems (drug + carrier) considered in ref. 6 we used their equilibrium geometries obtained in water solution. We used the default convergence criteria as implemented in Gaussian16:58 maximum force 0.000450 Ha bohr−1, RMS force 0.000300 Ha bohr−1, maximum displacement 0.001800 Å e RMS displacement 0.001200 Å.
As mentioned in the introduction, in this work we studied some systems of interest for drug delivery. In particular the antiviral drug is the favipiravir (T705) and the anticancer drug is the pyrimidine analogue 5-fluorouracil (5FU), shown in Fig. 1a and b. The nanostructures here analyzed are the carbon-based fullerene C24, the boron nitride one B12N12, the substituted systems C23B and CB11N12 and the gallium nitride nanocage Ga12N12 (Fig. 1c–g). We considered three sets of combined systems (Fig. 2), two sets obtained from the literature6,9 and one set original calculated in the present work.
 | ||
| Fig. 2 Optimized geometries of combined systems: (a–d) T705 with pure and doped C/BN carrier after ref. 9 (e and f) 5FU with Ga12N12 as carrier after ref. 6, (g–j) 5FU with pure and doped C/BN carrier. | ||
In particular, we analyzed:
• four configurations after ref. 9: the most stable configurations of T705 adsorbed on the surface of the pure and doped carbon/boron–nitride fullerenes (Fig. 2a–d);
• two configurations after ref. 6: one linked system Ga12N12-5FU (Fig. 2e) and one covalent bonded system (Fig. 2f);
• four original configurations: these systems have been obtained by the removal of a hydrogen atom of the 5-fluorouracil molecule to create a covalent bond with the pure and doped C/BN clusters (Fig. 2g–j). Take in consideration that the removal of H atoms in the adsorption of molecules at solid surfaces has been demonstrated in different cases.80–83
It is worth mentioning that the systems C23B-T705, CB11N12-T705, C24-5FU and B12N12-5FU (respectively shown in Fig. 2c, d, g and h), show states with different multiplicity (and free radical character) due to the presence of unpaired electrons.
Through the DFT we obtained also HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) energies, their spatial distribution and their energy gap.
Moreover, the time-dependent counterpart (TD-DFT) of this method has allowed us to obtain the adsorption spectra of the systems. All the TD-DFT calculations were performed in the frequency space within the Casida scheme55 implemented in the Gaussian16 code. In all DFT and TD-DFT calculations we used the default integration grid and the default convergence criteria for SCF cycles (10−6 Hartree for energy differences).
It is well known (for example after ref. 84) that the use of (semi)-local XC (even hybrid) functionals in the standard DFT framework provides a sub-optimal description in the case of transitions with charge transfer (CT) character which need more advanced techniques (e.g., generalized KS framework with tuned range-separated hybrid XC functionals). We decided to maintain this level of theory because we consider this work as a first approach to the problem and because there is only a small number of excitations with CT character. In the future, we will extend the present study with other calculations, e.g., with more advanced schemes.
3. Optical properties
In the present study we considered, for the first two groups of molecules (Fig. 2a–f), six combined clusters which have been demonstrated stable after the computational studies by other groups (ref. 9 and 6). The remaining four combined clusters (Fig. 2g–j) result as stable geometries after the present study. We stress again that the present research is focused on the optical absorption properties of the clusters and not on the search of their particular ground-state configurations. In particular we are interested in the differences in optical absorption properties between free and combined clusters, in case these differences could be considered as optical signature of the realized drug/carrier link.To this aim, from Fig. 3 to 5we have reported the absorption spectra of the particular combined systems compared to those of the free molecules (carrier and drug), as obtained after TD-DFT calculations in gas phase. In each plot we showed also the spectra of the combined system in aqueous solution to investigate the solvent effect. In Tables 1 and 2 we analyzed some details of two important peaks of the spectra of the free and bound systems: the first peak (optical onset) and the main peak in the region under study (MP).§ In particular, we have reported: the excitation energy (E, eV) and wavelength (λ, nm) of the transition; the corresponding oscillator strength (O.S.); the occupied and virtual molecular orbitals contributing significantly to the transition (with the corresponding weight in brackets); the character of charge-transfer (CT) or locally-excited (LE) depending on whether or not there is charge transfer upon the transition (Table 2, gas phase column).
 | ||
| Fig. 3 Absorption spectra of the combined systems (a) C24-T705, (b) B12N12-T705, (c) C23B-T705, (d) CB11N12-T705 after ref. 9, compared to those of the free molecules (C/BN-carrier and T705). The spectra reported in solid line are calculated in gas phase while in dotted red line is shown the one of combined clusters in aqueous solution. The color bars in the (b–d) figures represent the visible region. | ||
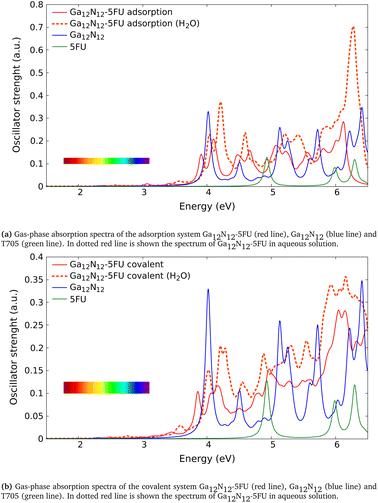 | ||
| Fig. 4 Absorption spectra of the combined systems Ga12N12-5FU (a) with adsorption interaction and (b) with covalent bond after ref. 6, compared to those of the free molecules (Ga12N12 carrier and 5FU). The spectra reported in solid line are calculated in gas phase while in dotted red line is shown the one of combined clusters in aqueous solution. The color bars in the figures represent the visible region. | ||
| Gas phase | Aqueous solution | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Systems | E (eV) | λ (nm) | O.S. | MO contributions | Systems | E (eV) | λ (nm) | O.S. | MO contributions |
| T705 | 4.26 | 291.4 | 0.127 | H-1 → L (0.39) | T705 | 4.22 | 293.8 | 0.206 | H → L (0.48) |
| 5.83 | 212.7 | 0.135 | H-1 → L + 1 (0.33) | 5.74 | 215.8 | 0.163 | H → L + 1 (0.44) | ||
| 7.94 | 156.2 | 0.248 | H-3 → L + 3 (0.12) | 6.63 | 186.9 | 0.246 | H-5 → L (0.36) | ||
| H-2 → L + 5 (0.10) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| 5FU | 4.93 | 251.5 | 0.127 | H → L (0.46) | 5FU | 4.85 | 255.4 | 0.182 | H → L (0.47) |
| 7.46 | 166.2 | 0.143 | H-1 → L + 4 (0.25) | 7.37 | 168.3 | 0.345 | H-2 → L + 1 (0.29) | ||
| H-2 → LA + 1 (0.14) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| C24 | 3.67 | 337.5 | 0.010 | H-1 → L + 3 (0.24) | C24 | 3.66 | 338.8 | 0.017 | H → L + 3 (0.29) |
| H → L + 4 (0.19) | H-2 → L + 4 (0.23) | ||||||||
| H-2 → L + 4 (0.16) | H-1 → L + 4 (0.19) | ||||||||
| 5.39 | 230.0 | 0.418 | H-10 → L (0.23) | 5.31 | 233.7 | 0.531 | H-9 → L + 2 (0.31) | ||
| H-9 → L + 2 (0.15) | H-10 → L (0.16) | ||||||||
| H-9 → L + 1 (0.14) | H-10 → L + 1 (0.15) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| B12N12 | 6.35 | 195.3 | 0.035 | H-2 → L + 5 (0.19) | B12N12 | 6.39 | 194.0 | 0.052 | H-1 → L + 5 (0.21) |
| H-1 → L + 4 (0.16) | H-2 → L + 4 (0.18) | ||||||||
| 7.14 | 173.8 | 0.119 | H-6 → L + 2 (0.14) | 7.16 | 173.1 | 0.155 | H-7 → L + 1 (0.14) | ||
| H-8 → L + 2 (0.12) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| C23B | 2.16 | 574.6 | 0.002 | HA-2 → LA + 2 (0.61) | C23B | 2.17 | 570.8 | 0.002 | HA-2 → LA + 2 (0.63) |
| 5.47 | 226.5 | 0.144 | HA-10 → LA + 1 (0.19) | 5.23 | 237.3 | 0.194 | HA-10 → LA + 2 (0.20) | ||
| HB-11 → LB + 2 (0.17) | HA-3 → LA + 3 (0.17) | ||||||||
| HB-2 → LB + 7 (0.12) | HA-9 → LA (0.12) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| CB11N12 | 3.95 | 314.1 | 0.009 | HA → LA + 2 (0.81) | CB11N12 | 4.01 | 309.0 | 0.012 | HA → LA + 2 (0.81) |
| 7.00 | 177.1 | 0.045 | HB-1 → LB + 8 (0.21) | 7.04 | 176.0 | 0.081 | HA-1 → LA + 8 (0.21) | ||
| HA-1 → LA + 7 (0.18) | HB → LB + 8 (0.21) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Ga12N12 | 2.31 | 537.7 | 0.001 | H → L (0.50) | Ga12N12 | 2.45 | 505.3 | 0.001 | H → L (0.5) |
| 4.02 | 308.6 | 0.109 | H-14 → L (0.43) | 4.08 | 304.0 | 0.188 | H-15 → L (0.45) | ||
| Gas phase | Aqueous solution | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Systems | E (eV) | λ (nm) | O.S. | MO contributions | Systems | E (eV) | λ (nm) | O.S. | MO contributions |
| C24-T705 | 3.26 | 380.3 | 0.008 | H-3 → L + 1 (0.49) (CT) | C24-T705 | 3.22 | 384.8 | 0.0003 | H → L + 3 (0.23) |
| H-1 → L + 3 (0.22) | |||||||||
| 5.39 | 229.9 | 0.333 | H-14 → L + 2 (0.13) (LE) | 5.28 | 234.8 | 0.609 | H-14 → L (0.19) | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| B12N12-T705 | 2.69 | 461.3 | 0.009 | H → L (0.49) (CT) | B12N12-T705 | 3.59 | 345.1 | 0.006 | H → L (0.43) |
| 4.10 | 302.5 | 0.196 | H-7 → L (0.42) (CT) | 4.03 | 307.6 | 0.299 | H-3 → L (0.49) | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| C23B-T705 | 2.15 | 577.0 | 0.002 | HB-1 → LB + 5 (0.24) (CT) | C23B-T705 | 2.09 | 593.0 | 0.001 | HB-1 → LB + 3 (0.20) |
| HA → LA + 4 (0.18) (CT) | HA-1 → LA + 2 (0.16) | ||||||||
| HA → LA + 3 (0.15) | |||||||||
| 4.10 | 302.1 | 0.139 | HA-10 → LA (0.26) (CT) | 2.14 | 578.8 | 0.002 | HA → LA + 3 (0.32) | ||
| HB-9 → LB (0.24) (CT) | HB-1 → LB + 4 (0.32) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| CB11N12-T705 | 2.32 | 534.9 | 0.049 | HA → LA + 9 (0.82) (LE) | CB11N12-T705 | 2.21 | 560.1 | 0.062 | HA → LA + 3 (0.88) |
| 3.91 | 317.4 | 0.158 | HA-1 → LA (0.30) (CT) | 3.79 | 326.7 | 0.245 | HA → LA + 11 (0.52) | ||
| HA → LA + 15 (0.28) (CT) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Ga12N12-5FU (ads) | 2.34 | 530.1 | 0.001 | H-1 → L (0.29) (CT) | Ga12N12-5FU (ads) | 2.55 | 486.0 | 0.001 | H → L (0.48) |
| H → L (0.16) (CT) | |||||||||
| 3.91 | 317.3 | 0.121 | H-13 → L + 1 (0.42) (LE) | 4.03 | 307.4 | 0.177 | H-14 → L (0.40) | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Ga12N12-5FU (cov) | 2.33 | 531.8 | 0.001 | H → L (0.49) (LE) | Ga12N12-5FU (cov) | 2.60 | 477.8 | 0.001 | H → L (0.49) |
| 3.85 | 321.8 | 0.081 | H-12 → L (0.36) (LE) | 4.29 | 289.3 | 0.119 | H-15 → L (0.34) | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| C24-5FU | 2.27 | 546.2 | 0.006 | HB-2 → LB (0.45) (LE) | C24-5FU | 2.28 | 542.9 | 0.002 | HB-3 → LB (0.34) |
| HA → LA + 2 (0.21) | |||||||||
| 5.25 | 236.2 | 0.103 | HA-2 → LA + 9 (0.15) (LE) | 5.18 | 239.4 | 0.203 | HA → LA + 9 (0.12) | ||
| HA-1 → LA + 9 (0.08) (LE) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| B12N12-5FU | 0.65 | 1894.0 | 0.059 | HB → LB (0.88) (CT) | B12N12-5FU | 0.82 | 1518.8 | 0.018 | HB-1 → LB (0.95) |
| 6.29 | 197.0 | 0.060 | HB-11 → LB + 1 (0.36) (CT) | 7.36 | 168.5 | 0.183 | HA-12 → LA + 1 (0.19) | ||
| HB-11 → LB + 2 (0.19) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| C23B-5FU | 2.03 | 610.9 | 0.005 | H → L + 2 (0.30) (LE) | C23B-5FU | 2.40 | 517.3 | 0.029 | H-3 → L (0.48) |
| H-2 → L + 1 (0.18) (LE) | |||||||||
| 4.83 | 256.9 | 0.140 | H-1 → L + 8 (0.17) (LE) | 4.65 | 266.4 | 0.182 | H-1 → L + 7 (0.39) | ||
| H-11 → L + 2 (0.12) (LE) | |||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| CB11N12-5FU | 4.56 | 272.2 | 0.149 | H → L (0.47) (LE) | CB11N12-5FU | 4.56 | 272.0 | 0.215 | H → L (0.48) |
| 7.48 | 165.7 | 0.111 | H-14 → L (0.26) (LE) | 6.08 | 204.0 | 0.241 | H → L + 6 (0.45) | ||
| H-4 → L + 10 (0.13) (CT) | |||||||||
For the implicit solvent calculations is important to highlight that in the classical linear response scheme of the polarizable continuum model (PCM) the TD-DFT transition densities are easily available in all conventional TD-DFT calculation schemes and are used to predict the PCM modifications in charges upon excitation. Hence, within this framework the bulk solvent effects for excited states present a moderate computational cost. However, this linear response model is not always accurate in the cases in which are present strong variations of the electronic cloud between the two states involved in a transition; this is the typical case of states with significant charge-transfer as in some of the systems under study in this work (See ESI†). For such cases, more elaborated models to determine the polarization of the cavity in the excited states are used even if is well known that these models are significantly more expensive, from the computational point of view, with respect to the simplest standard PCM scheme. One of the most employed models is the so called vertical excitation model (VEM) which is justified in the cases large-size compounds. Actually, the vibrational effects are important in determining both the position of the absorption maxima and the shape of the absorption structures. It has been shown that absorption bands in the spectra of simple organic compounds are typically redshifted between 0.1 and 0.2 eV in comparison to the vertical excitations.85 Some recent studies investigated the origin of this red-shift, and found that the main reason can be ascribed to the frequency change between the ground and excited states in multidimensional systems, where vibrational frequencies in the excited states are systematically smaller than those of the ground states.85 In all cases, in order to correctly consider this issue in our modeling, a numerical Hessian of the excited state in solution is needed, which is by no means practical for medium to large size molecules. It should be pointed out, however, that the vertical approximation is adopted in many previous studies dealing with relatively large-size molecular systems.85
Finally, for the excitations reported in Table 2 (gas phase column) we have also calculated the orbitals involved in the transitions in order to evaluate the possible charge transfer. The orbitals for the onset transitions are reported in the final section of the ESI.†
3.1 C and BN clusters – T705 with adsorption
The first molecules that we analyze here are the ones first proposed in ref. 9, shown in Fig. 2a–d. As mentioned above, in this work we calculated the absorption spectra only of the molecules within TD-DFT. The calculations of the absorption spectra for all the molecules have been performed both in gas phase and in aqueous solution. The spectra obtained for those molecules are shown in Fig. 3. The comparison between the energies of the peaks calculated in this work (Gaussian16, B3LYP/6-31+G*) and the ones after ref. 9 (Gaussian09, B3LYP/6-31G**) are shown in Table 3.In Fig. 3a is reported the absorption spectrum of the combined system in gas phase C24-T705 (red line) and in aqueous solution C24-T705 (H2O) (red dotted line) in comparison with those of the free molecules in gas phase (the blue line is C24 and the green line is T705). The energies of the peaks calculated for the combined system are shown in Table 2 and the ones for the free molecules are shown in Table 1. The first notable difference between combined molecule and free ones is the onset peak position, which is at 3.26 eV for the combined system in gas phase (3.22 eV in aqueous solution), 3.67 eV for C24 in gas phase (3.66 eV in aqueous solution) and 4.26 eV for T705 in gas phase (4.22 eV in aqueous solution). We notice the presence of two peaks in the spectrum of the combined system positioned near the onset of the spectra for each free molecules. There are no notable differences in the energy of the main peak, that is near to the one of C24. The main peak relative to the combined molecule results shifted passing from the gas phase to the aqueous solution (from 5.39 eV to 5.28 eV).
In Fig. 3b are reported the spectra of the combined system B12N12-T705 in gas phase and in aqueous solution B12N12-T705 (H2O) and the spectra of the free molecules in gas phase only. At 2.69 eV in the spectrum of B12N12-T705 a small structure appears. In the proximity of the onset peak of T705 we still observe a peak in the spectrum of the combined molecule, shifted towards smaller energies (redshifted). We notice major overlaps towards larger energies.
In Fig. 3c are shown the spectra of the combined system C23B-T705 in gas phase and in aqueous solution C23B-T705 (H2O) and the spectra of the free molecules in gas phase. The onset peak corresponding to C23B-T705 is near the onset peak of the free C23B (2.15 eV for the combined system and 2.16 eV for the free C23B). We notice at 3.23 eV a peak in the C23B-T705 that is not present in the other cases. We observe a redshift in the onset peak of the T705, more clear for C23B-T705 (H2O). At larger energies there are no notable differences.
In Fig. 3d are shown the spectra of the combined system CB11N12-T705 in gas phase and in aqueous solution CB11N12-T705 (H2O) and the spectra of the free molecules in gas phase. In both phases, the spectrum of the combined molecule shows an onset peak at much smaller energies than the ones of the free molecules. In the region where the onset peak of the free molecule is, we observe a peak in the combined system too. In the case of the combined molecule there is no evident difference between the spectrum for CB11N12-T705 and CB11N12-T705 (H2O). In conclusion, in the analyzed configurations some peaks are present only for the combined systems and some notable differences take place between the absorption spectra of the free molecules and the ones of the combined molecules. Those differences can be used as an optical fingerprint to deduct if the molecules are truly combined. Furthermore, as shown in Table 3, the energies of the peaks for the combined molecule in gas phase here calculated are in fair agreement to those present in ref. 9. In fact we have a maximum deviation of 2% for the molecule in gas phase and of 5% for the molecule in aqueous solution.
3.2 GaN clusters-5FU
We analyze now the proposed molecules after ref. 6. Unlike the above analyzed molecules, in those clusters we have a carrier formed of gallium and nitrogen atoms. In the following we present the absorption spectra calculated in this work of two systems made of Ga12N12 combined with 5FU, the first via an adsorption (Fig. 2e) and the second via a covalent bond (Fig. 2f), both in gas phase and aqueous solution. In Table 4 has been reported the comparison between the energies of the peaks presented in ref. 6 (Gaussian09, BMK/6-31++G**) and the correspondent ones calculated in the present work (Gaussian16, B3LYP/6-31+G*).In Fig. 4a we show the absorption spectrum of the adsorbed system Ga12N12-5FU. No large difference is present between the spectra of the combined molecule in gas phase and the free molecule Ga12N12. On the other hand, for the spectrum of combined molecule in aqueous solution Ga12N12-5FU (H2O) we notice a blueshift of the main peak of the carrier and the presence of peaks at smaller energies that are not present for the Ga12N12. In the high energies region, the spectra of all the systems are similar.
In Fig. 4b we show the spectra of the covalent bonded system Ga12N12-5FU. As above, we notice small differences between the spectra of bonded molecule and free carrier in gas phase and we observe a blueshift of the peaks for the bonded molecule in aqueous solution. In the higher energies region we notice that the peaks present in the Ga12N12 spectrum are replaced by a single wide peak.
In conclusion, we find a good agreement in comparing the energies of the peaks calculated in the present work with the ones after ref. 6. The small differences in the data present in Table 4 can be ascribed to the different basis-set used for the calculations and to the different exchange–correlation functional used.
3.3 C and BN clusters – 5FU with covalent bond
Finally, we analyze the optical absorption spectra of the four original systems after this work (Fig. 5). We have obtained these systems (Fig. 2g–j) by forcing a covalent bond between the drug molecule (5FU) and the carrier (C/BN nanocluster). In Tables 1 and 2 we show some important details of the optical onset transitions and the main peaks of all the spectra of free and bound systems, in gas phase and aqueous solution.In Fig. 5a we note that the spectrum of the combined system C24-5FU is quite different from the ones of free C24 and 5FU, for both energy position and height of the peaks. In particular, the absorption of C24-5FU begins in the visible region at the energy of 2.27 eV, a value redshifted with respect to that of both the carrier (3.67 eV, NUV) and the drug (4.93 eV, MUV). The main feature of Fig. 5a is the strong reduction in height of the main peak of C24 after its binding with 5FU. At this energy, 5.39 eV, we can find a peak of the combined system with a considerable smaller oscillator strength (from 0.418 to 0.064). Moreover, the nature of the transition is different because the involved molecular orbitals are not the same as for C24. In particular, the transition for the combined system is between the orbitals HA-14 and LA, with a weight of 0.16, while those for C24 are reported in Table 1. The main peak for C24-5FU is located at 5.25 eV (in Table 2 more details about it). In this case the solvent effect in the spectrum of the combined system is not relevant. The onset and main peak for C24-5FU (H2O) are at similar energy than those in gas phase, with small differences in the O.S. and in the MO involved in the transitions (see Table 2). This fact can be of importance for applicative reasons: in fact the absence of the peak at 5.39 eV in the absorption spectrum can be interpreted as a clear optical fingerprint of the occurred molecular bond between C24 and 5FU clusters.
In Fig. 5b we note that the absorption spectrum of B12N12-5FU is very different from that of the free B12N12 and 5FU systems. The combined system here analyzed is characterized by very different absorption structures, especially in the low energies region. In particular, the absorption of B12N12-5FU takes place in a range that cover the IR, the visible and the UV, while the absorption of free systems presents spectra mainly located in the UV region. In more detail, for the gas phase, the onset energy of the combined system is at 0.65 eV, very distant from the one of the drug (4.93 eV, MUV) and of the carrier (6.35 eV, FUV). For energies larger than 6 eV we can see similarities between the spectra. For example the main peak of B12N12-5FU in gas phase (6.29 eV) is at the same energy of a peak of the drug (6.29 eV, O.S. = 0.114, H → L + 2, weight = 0.44) and it is near to the onset of the carrier (6.35 eV). Moreover, the combined system presents a major peak at 7.44 eV¶ near to the main peaks of the free systems B12N12 (7.14 eV) and 5FU (7.46 eV). We see from Table 2 that the nature of these transitions is different. On the other hand, the solvent effect in the TD-DFT calculations leads to some differences in the onset and in the main peak of the combined system with respect to the gas phase. The onset peak is blueshifted (from 0.65 eV to 0.82 eV) and its oscillator strength is reduced (from 0.059 to 0.018); the main peak is at higher energies (from 6.29 eV to 7.36 eV) near to the before mentioned peak at 7.44 eV. Also in this case, the presence of structures in a more than 4 eV extended region below the absorption edge of 5FU is a clear optical fingerprint of the occurred molecular bond between B12N12 and 5FU.
In Fig. 5c we note that, for the combined system C23B-5FU, the initial part of the spectrum is similar to that of the carrier C23B. This behavior occurs up to 4.5 eV, for an energy range in which the free biomolecule is not absorbing. The onset energy for both the combined system and the carrier is in the visible region, respectively at 2.03 eV and 2.16 eV. The spectrum of C23B-5FU at energies larger than 4.5 eV differs slightly from the spectra of free molecules. In particular, it presents some new absorption structures. The main peak of C23B-5FU (4.83 eV) is only 0.1 eV redshifted with respect to the energy of the onset for the drug (4.93 eV). Moreover, near the carrier MP energy position (5.47 eV), there is a peak of the combined system (E = 5.42 eV, O.S. = 0.097, H-11 → L + 3, weight = 0.33). The spectrum of C23B-5FU (H2O) presents peaks at energies slightly different from those for the gas phase. In more detail, the onset peak is blueshifted (from 2.03 eV to 2.40 eV) while the main peak results redshifted (from 4.83 eV to 4.65 eV). In this case no clear and distinguishable optical difference could be found for the considered clusters either in gas phase and in aqueous solution.
In Fig. 5d we see that the CB11N12-5FU begins its absorption in the MUV at 4.56 eV. This is the only case, with respect to the here studied clusters, in which the onset energy lies in the UV region at a value placed in the middle between the peaks of free molecules. In the three previous cases instead, the onset for the combined system was always at lower energy than for the free molecules and it lied in the visible or IR region. Here, otherwise, the onset of CB11N12-5FU is blueshifted of +15% and redshifted of −7% as compared, respectively, to those of the cluster (3.95 eV, NUV) and the drug (4.93 eV, MUV). In the regions around 6 eV and 7 eV we find also some overlaps of peaks of the free and bound systems. In this case the solvent effect is more significant in the region beyond 5.5 eV. The onset results at the same energy (4.56 eV) as that found for the gas phase. However, the oscillator strength is almost double (from 0.149 to 0.215). Beyond 5.5 eV, for CB11N12-5FU (H2O) we observe a shift of the peaks (for example that around 6.25 eV) and to an average increase of the oscillator strengths. In this particular case the presence of the peak at 4.56 eV can be considered as the optical evidence of the realised drug/carrier bond.
3.4 Long-range corrected optical properties
We have performed some test calculations for 5FU systems using the long-range corrected CAM-B3LYP exchange–correlation functional.As we show in Fig. 6, the corresponding spectra presents basically just an almost rigid shift of the order of ∼0.1 to ∼0.4 eV and some small amplitude variations in the absorption features. The shift appears of the same order of those found in ref. 86 using CAM-B3LYP.
 | ||
| Fig. 6 Absorption spectra calculated with different exchange–correlation functional; comparison for (a) B12N12-5FU and (b) C23B-5FU. | ||
For the scope and the level of this work the differences between the two calculations are small enough to guarantee the low energy same pattern. For this reason we can still consider valid our previous B3LYP results.
4. Additional computational details, tests, and open issues
To give a more general (and chemical) insight in the results of the present paper, the MOs for the onset transitions relative to a large subset of the studied systems, along with a description of the CT transitions, have been reported in the ESI.† Moreover, the details of the transitions have been extensively reported in Tables 1 and 2. Take in consideration that we also made the comparison of our results with those after ref. 6 and 9. We have found a good agreement with the calculations of those references, proving that our method is valid and can be used for studying similar drug delivery systems, as the ones original from our work. In addition, we calculated some properties that are not present in the literature that can be used to provide other information on the systems of interest, e.g., full spectra representation and some additional peaks information.We performed also different additional convergence tests: the average number of states included in the calculations are 350 for each system, using the Casida formalism to calculate the absorption spectra.
In the cases of CT character, the theory here adopted presents some limitations (as reported, e.g., in ref. 84) and for this reason some CT states may be affected by an unfair description. Moreover, the number of states calculated may be not sufficient to completely characterize the high energy region of the absorption spectra of some molecules. On the other hand, it is out of the scope of this work a in depth study of the high energy or Rydberg transitions.
To validate further our method, we have performed additional calculations with a larger basis set for the wave-function representation in some configurations and the resulting spectra are almost identical to the ones we reported in this article produced with the smaller basis set.
Considering the possible discrepancies arising for some CT transitions after the use of the TDDFT-B3LYP scheme, we performed additional TDDFT CAM-B3LYP spectra calculation (Section 3.4). The comparison with the TDDFT-B3LYP spectrum demonstrates that the CAM-B3LYP absorption spectrum present the same structure and main peaks with a small blue-shift. We reached these conclusions after comparing tha absorption spectra for some systems, e.g., the B12N12-5FU and the C23B-5FU systems, (reported respectively in Fig. 6a and b).
All the spectra have been obtained by the convolution of Lorentzian curves (FHWM of 0.05 eV) with the single eigenvalues' peaks obtained by the output of Gaussian16. The broadening value is obtained by a trade-off between the plots readability and the need to ensure that most of the peaks are resolved.
Moreover, we decided to add in the ESI† the coordinates for some important cases in order to guarantee the reproducibility of the results. Hereby we confirm that the here proposed method permits to know for the first time, for several different molecular systems of importance for the drug delivery, how their electronic and optical properties change following the establishment of a bond between the carrier and the drug molecule. Moreover, the possibility to compare to previous works for some systems confirmed the validity of the methodology we applied.
Finally, in some of the studied systems there is the occurrence of possible multireference character (MC) states. However, since this phenomenon occurs only in a very limited number of the molecules under study, this fact does not affect dramatically the general conclusions of the paper. We have already planned a new computational campaign in which we will address in a deeper way this particular issue using more refined computational schemes.
5. Conclusions
We propose in the present work a computational study of the optical absorption of nanostructured clusters of interest for drug delivery applications. We considered a group of combined drug/carrier clusters which have been demonstrated stable after previous computational studies. The remaining systems show stable geometries after the present study. We, in some cases, observed the appearance of new peaks in the spectra of the combined systems or red or blue shift effects in the already existing structures. The changes in the absorption spectra could play the role of an optical signature helping to verify the correct occurred bonding needed for drug delivery and for tracking the combined clusters once formed in solution. Possible future developments of the present work could be the study of the release mechanisms of the drug at the target, the application of more refined models for the water solvent, the extension of the same analysis to different solvents.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. C. acknowledges collaboration with “Progetti biennali d’Ateneo UniCa finanziati dalla Fondazione di Sardegna annualità 2020: molecular simulations and machine learning in bio- and medical physics”. G. C., A. A. P., F. S. acknowledge partial financial support from the IDEA-AISBL-Bruxelles. The authors acknowledge ISCRA-CINECA facility within the ISCRA-C 2021 projects HP10CDZJIB/HP10CS0OT2/HP10C8WASP. F. S. acknowledges that this article was produced while attending the PhD programme in Physics at the University of Cagliari, Cycle XXXVIII, with the support of a scholarship financed by the Ministerial Decree no. 351 of 9th April 2022, based on the NRRP – funded by the European Union – NextGenerationEU – Mission 4 ”Education and Research”, Component 1 ”Enhancement of the offer of educational services: from nurseries to universities” – Investment 4.1 “Extension of the number of research doctorates and innovative doctorates for public administration and cultural heritage”.Notes and references
- P. Wang, G. Yan, X. Zhu, Y. Du, D. Chen and J. Zhang, Nanomaterials, 2021, 11, 115 CrossRef CAS PubMed.
- B. T. Tomić, C. S. Abraham, S. Pelemiš, S. J. Armaković and S. Armaković, Phys. Chem. Chem. Phys., 2019, 21, 23329–23337 RSC.
- M. Moradi, A. A. Peyghan, Z. Bagheri and M. Kamfiroozi, J. Mol. Model., 2012, 18, 3535–3540 CrossRef CAS PubMed.
- T. Dinadayalane and J. Leszczynski, in Fundamental Structural, Electronic, and Chemical Properties of Carbon Nanostructures: Graphene, Fullerenes, Carbon Nanotubes, and Their Derivatives, Springer, 2012, pp. 793–867 Search PubMed.
- D. S. Sabirov, A. D. Zakirova, A. A. Tukhbatullina, I. M. Gubaydullin and R. G. Bulgakov, RSC Adv., 2013, 3, 1818–1824 RSC.
- N. Wazzan, K. Soliman and W. Abdel Halim, J. Mol. Model., 2019, 25, 265 CrossRef PubMed.
- A. Zerenturk and S. Berber, Europhys. Lett., 2013, 103, 16003 CrossRef.
- Y. Arakawa and S. Kako, Phys. Status Solidi A, 2006, 203, 3512–3522 CrossRef CAS.
- K. A. Soliman and S. A. Aal, Diamond Relat. Mater., 2021, 117, 108458 CrossRef CAS PubMed.
- Y. Furuta, K. Takahashi, K. Shiraki, K. Sakamoto, D. F. Smee, D. L. Barnard, B. B. Gowen, J. G. Julander and J. D. Morrey, Antiviral Res., 2009, 82, 95–102 CrossRef CAS PubMed.
- Y. Furuta, B. B. Gowen, K. Takahashi, K. Shiraki, D. F. Smee and D. L. Barnard, Antiviral Res., 2013, 100, 446–454 CrossRef CAS PubMed.
- S. J. Smither, L. S. Eastaugh, J. A. Steward, M. Nelson, R. P. Lenk and M. S. Lever, Antiviral Res., 2014, 104, 153–155 CrossRef CAS PubMed.
- Y.-X. Du and X.-P. Chen, Clin. Pharmacol. Ther., 2020, 108, 242–247 CrossRef CAS PubMed.
- Y. Furuta, B. B. Gowen, K. Takahashi, K. Shiraki, D. F. Smee and D. L. Barnard, Antiviral Res., 2013, 100, 446–454 CrossRef CAS PubMed.
- M. Milczarek, K. Wiktorska, L. Mielczarek, M. Koronkiewicz, A. Dąbrowska and K. Lubelska, Food Chem. Toxicol., 2018, 111, 1–8 CrossRef CAS PubMed.
- H. Uetsuka, M. Haisa, M. Kimura, M. Gunduz, Y. Kaneda, T. Ohkawa, M. Takaoka, T. Murata, T. Nobuhisa, T. Yamatsuji, J. Matsuoka, N. Tanaka and Y. Naomoto, Exp. Cell Res., 2003, 289, 27–35 CrossRef CAS PubMed.
- L. Metterle, C. Nelson and N. Patel, J. Am. Acad. Dermatol., 2016, 74, 552–557 CrossRef CAS PubMed.
- Sauraj, V. Kumar, B. Kumar, F. Deeba, S. Bano, A. Kulshreshtha, P. Gopinath and Y. S. Negi, Int. J. Biol. Macromol., 2019, 128, 204–213 CrossRef CAS PubMed.
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- H. W. Kroto, Angew. Chem., Int. Ed. Engl., 1997, 36, 1578–1593 CrossRef.
- H. W. Kroto, Nature, 1987, 329, 529–531 CrossRef CAS.
- A. Popov, in Structures and Stability of Fullerenes, Metallofullerenes, and Their Derivatives, Springer, 2017, pp. 1031–1096 Search PubMed.
- Y. Chang, J. Zhang, H. Sun, B. Hong, Z. An and R. Wang, Int. J. Quantum Chem., 2005, 105, 142–147 CrossRef CAS.
- E. A. Rohlfing, D. M. Cox and A. Kaldor, J. Chem. Phys., 1994, 81, 3322–3330 CrossRef.
- F. Diederich, R. Ettl, Y. Rubin, R. L. Whetten, R. Beck, M. Alvare, S. Anz, D. Sensharma, F. Wudl, K. C. Khemani and A. Koch, Science, 1991, 252, 548–551 CrossRef CAS PubMed.
- K. Kikuchi, N. Nakahara, T. Wakabayashi, M. Honda, H. Matsumiya, T. Moriwaki, S. Suzuki, H. Shiromaru, K. Saito, K. Yamauchi, I. Ikemoto and Y. Achiba, Chem. Phys. Lett., 1992, 188, 177–180 CrossRef CAS.
- T. Kimura, T. Sugai, H. Shinohara, T. Goto, K. Tohji and I. Matsuoka, Chem. Phys. Lett., 1995, 246, 571–576 CrossRef CAS.
- Y. Miyake, T. Minami, K. Kikuchi, M. Kainosho and Y. Achiba, Mol. Cryst. Liq. Cryst., 2000, 340, 553–558 CrossRef CAS.
- R. Taylor, G. J. Langley, A. G. Avent, T. J. S. Dennis, H. W. Kroto and D. R. M. Walton, J. Chem. Soc., 1993, 2, 1029–1036 Search PubMed.
- F. Jensen and H. Toflund, Chem. Phys. Lett., 1993, 201, 89–96 CrossRef CAS.
- T. Oku, M. Kuno, H. Kitahara and I. Narita, Int. J. Inorg. Mater., 2001, 3, 597–612 CrossRef CAS.
- V. Mahamiya, A. Shukla and B. Chakraborty, J. Alloys Compd., 2022, 897, 162797 CrossRef CAS.
- S. Kaviani, S. Shahab, M. Sheikhi, V. Potkin and H. Zhou, Comput. Theor. Chem., 2021, 1201, 113246 CrossRef CAS.
- G. Seifert, P. Fowler, D. Mitchell, D. Porezag and T. Frauenheim, Chem. Phys. Lett., 1997, 268, 352–358 CrossRef CAS.
- T. Oku, A. Nishiwaki, I. Narita and M. Gonda, Chem. Phys. Lett., 2003, 380, 620–623 CrossRef CAS.
- O. Stéphan, Y. Bando, A. Loiseau, F. Willaime, N. Shramchenko, T. Tamiya and T. Sato, Appl. Phys. A: Mater. Sci. Process., 1998, 67, 107–111 CrossRef.
- D. Golberg, Y. Bando, O. Stéphan and K. Kurashima, Appl. Phys. Lett., 1998, 73, 2441–2443 CrossRef CAS.
- M. Javan, A. Soltani, Z. Azmoodeh, N. Abdolahi and N. Gholami, RSC Adv., 2016, 6, 104513–104521 RSC.
- E. Tazikeh, A. Soltani, M. T. Baei, M. Javan and S. Moazen Rad, Adsorption, 2018, 24, 585–593 CrossRef.
- E. Vessally, S. A. Siadati, A. Hosseinian and L. Edjlali, Talanta, 2017, 162, 505–510 CrossRef CAS PubMed.
- A. Soltani, M. T. Baei, E. Tazikeh and A. Pahlevani, Superlattices Microstruct., 2014, 75, 716–724 CrossRef CAS.
- M. R. Mohammadi, A. Nojoomi, M. Mozafari, A. Dubnika, M. Inayathullah and J. Rajadas, J. Mater. Chem. B, 2017, 5, 3995–4018 RSC.
- A. Hosseinian, E. Vessally, S. Yahyaei, L. Edjlali and A. Bekhradnia, J. Cluster Sci., 2017, 28, 2681–2692 CrossRef CAS.
- L. Wang, Z. Wang, L. Cao and K. Ge, Biosaf. Health, 2022, 4, 161–170 CrossRef PubMed.
- R. Delshadi, A. Bahrami, D. J. McClements, M. D. Moore and L. Williams, J. Controlled Release, 2021, 331, 30–44 CrossRef CAS PubMed.
- R. Bolskar, in Fullerenes for Drug Delivery, Springer, 2016, pp. 1267–1281 Search PubMed.
- H. Kazemzadeh and M. Mozafari, Drug Discovery Today, 2019, 24, 898–905 CrossRef CAS PubMed.
- E. Giusto, L. Žárská, D. F. Beirne, A. Rossi, G. Bassi, A. Ruffini, M. Montesi, D. Montagner, V. Ranc and S. Panseri, Nanomaterials, 2022, 12, 2372 CrossRef CAS PubMed.
- H. Wang, P. Agarwal, S. Zhao, J. Yu, X. Lu and X. He, Nat. Commun., 2015, 6, 10081 CrossRef CAS PubMed.
- J. Shi, H. Zhang, L. Wang, L. Li, H. Wang, Z. Wang, Z. Li, C. Chen, L. Hou, C. Zhang and Z. Zhang, Biomaterials, 2013, 34, 251–261 CrossRef CAS PubMed.
- A. Soltani, A. Sousaraei, H. Balakheyli, M. Eskandari and M. Javan, New J. Chem., 2016, 40, 7018–7026 RSC.
- M. Alpater, Z. Al-Sawaff and F. Kandemirli, Global J. Eng. Technol. Adv., 2021, 9, 77–85 CrossRef.
- W. Kohn, Rev. Mod. Phys., 1999, 71, S59–S77 CrossRef CAS.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- M. E. Casida, in Time-Dependent Density Functional Response Theory for Molecules, World Scientific Publishing, 1995, vol. 1, ch. 5, pp. 155–192 Search PubMed.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- M. Palummo, C. Hogan, F. Sottile, P. Bagalá and A. Rubio, J. Chem. Phys., 2009, 131, 084102 CrossRef PubMed.
- M. Frisch, et al., Gaussian16, 2016 Search PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- R. Cardia, G. Malloci, A. Mattoni and G. Cappellini, J. Phys. Chem. A, 2014, 118, 5170–5177 CrossRef CAS PubMed.
- N. Dardenne, R. Cardia, J. Li, G. Malloci, G. Cappellini, X. Blase, J.-C. Charlier and G.-M. Rignanese, J. Phys. Chem. C, 2017, 121, 24480–24488 CrossRef CAS.
- P. Mocci, R. Cardia and G. Cappellini, Phys. Chem. Chem. Phys., 2019, 21, 16302–16309 RSC.
- G. Cappellini, A. Bosin, G. Serra, J. Furthmüller, F. Bechstedt and S. Botti, ACS Omega, 2020, 5, 13268–13277 CrossRef CAS PubMed.
- A. Kumar, R. Cardia and G. Cappellini, Cellulose, 2017, 25, 2191–2203 CrossRef.
- L. Stagi, D. Chiriu, M. Scholz, C. M. Carbonaro, R. Corpino, A. Porcheddu, S. Rajamaki, G. Cappellini, R. Cardia and P. C. Ricci, Spectrochim. Acta, Part A, 2017, 183, 348–355 CrossRef CAS PubMed.
- R. Cardia, G. Malloci, G.-M. Rignanese, X. Blase, E. Molteni and G. Cappellini, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 235132 CrossRef.
- R. Cardia, G. Cappellini, M. Valentini and E. Pieroni, Phys. Chem. Chem. Phys., 2022, 24, 25547–25554 RSC.
- R. Cardia, G. Malloci, A. Bosin, G. Serra and G. Cappellini, Chem. Phys., 2016, 478, 8–13 CrossRef CAS.
- E. Pinna, C. Melis, A. Antidormi, R. Cardia, E. Sechi, G. Cappellini, M. d'Ischia, L. Colombo and G. Mula, Int. J. Mol. Sci., 2017, 18, 1567 CrossRef CAS PubMed.
- A. Antidormi, G. Aprile, G. Cappellini, E. Cara, R. Cardia, L. Colombo, R. Farris, M. d'Ischia, M. Mehrabanian, C. Melis, G. Mula, A. Pezzella, E. Pinna and E. Redolfi Riva, J. Phys. Chem. C, 2018, 122, 28405–28415 CrossRef CAS.
- A. Kumar, G. Cappellini and F. Delogu, Cellulose, 2019, 26, 1489–1501 CrossRef CAS.
- P. Mocci, R. Cardia and G. Cappellini, J. Phys.: Conf. Ser., 2019, 1226, 012016 CrossRef CAS.
- P. Mocci, R. Cardia, A. Bosin and G. Cappellini, J. Phys.: Conf. Ser., 2020, 1548, 012028 CrossRef CAS.
- P. Mocci, R. Cardia and G. Cappellini, New J. Phys., 2018, 20, 113008 CrossRef CAS.
- P. Mocci, R. Cardia and G. Cappellini, J. Phys.: Conf. Ser., 2018, 956, 012020 CrossRef.
- B. X. Vuong, N. Hajali, A. Asadi, A. A. Baqer, S. K. Hachim and G. Canli, Inorg. Chem. Commun., 2022, 141, 109558 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- E. Molteni, G. Cappellini, G. Onida and G. Fratesi, Phys. Rev. B, 2017, 95, 075437 CrossRef.
- E. Molteni, G. Fratesi, G. Cappellini and G. Onida, Phys. Status Solidi B, 2017, 255, 1700497 CrossRef.
- K. Seino, W. G. Schmidt, M. Preuss and F. Bechstedt, J. Phys. Chem. B, 2003, 107, 5031–5035 CrossRef CAS.
- K. Seino, W. G. Schmidt and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 245309 CrossRef.
- S. Kümmel, Adv. Energy Mater., 2017, 7, 1700440 CrossRef.
- Q. Alkhatib, W. Helal and A. T. Afaneh, New J. Chem., 2022, 46, 7682–7694 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00061c |
| ‡ These authors contributed equally to this work. |
| § Please note that for T705 we reported three peaks instead of two because depending on the spectral region under study the main peak could be at higher energy. |
| ¶ Around this energy there are several roots that determined a broad Lorentzian structure. The root with larger oscillator strength is characterized by: E = 7.44 eV, O.S. = 0.032, HA-5 → LA + 6, weight = 0.08. |
| This journal is © The Royal Society of Chemistry 2023 |