Open Access Article
Open Access ArticleIntegrated exploration of experimentation and molecular simulation in ester-containing polyimide dielectrics†
Jinpeng Luoab,
Hui Tong *b,
Song Moc,
Fei Zhoua,
Song Zuoa,
Chuanqiang Yina,
Ju Xubd and
Xiaomin Li
*b,
Song Moc,
Fei Zhoua,
Song Zuoa,
Chuanqiang Yina,
Ju Xubd and
Xiaomin Li *a
*a
aInstitute of Photovoltaics, Nanchang University, Nanchang, 330031, China. E-mail: lixiaomin@ncu.edu.cn
bInstitute of Electrical Engineering, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: tonghui@mail.iee.ac.cn
cKey Laboratory of Science and Technology on High-tech Polymer Materials, Institute of Chemistry, Chinese academy of Sciences, Beijing, 100190, China
dSchool of Engineering Science, University of Chinese Academy of Sciences, Beijing, 100049, China
First published on 4th January 2023
Abstract
With the growing development of film capacitors in various applications, the requirements for polymer dielectrics have increased accordingly. In this work, a series of ester-cotaining polyimide (EPI) dielectrics were designed and fabricated. Futhermore, integrated exploration of experimentation and molecular simulation is proposed to achieve polymer dielectrics with advanced comprehensive performance, as well as to analyze the dielectric mechanism in-depth. The EPIs show superior thermal resistance and dielectric properties. A Weibull breakdown strength of 440–540 MV m−1, permittivity of 3.52–3.85, dissipation factor of 0.627–0.880% and theoretical energy density of 3.13–4.90 J cm−3 were obtained for the EPIs. The relationship between microscopic parameters and dielectric behavior was investigated in detail. According to the experimental and calculated results, there is close correlation between dipolar moment density (μ/Vvdw) and dielectric permittivity (εr). It is deduced that the integrated research of experiments and molecular simulation would be an effective strategy to reveal the dielectric mechanism as well as assist in the molecular design of polymer dielectrics.
Introduction
It is well known that there is continuous growing demand for film capacitors used in applications such as advanced propulsion systems, hybrid electric vehicles (HEVs), and underground oil/gas exploration.1–7 As the basis of capacitors, dielectric materials need further improvement because it is increasingly difficult for the state-of-the-art dielectric of biaxially oriented polypropylene (BOPP) to meet the requirements of high energy density.8,9 Among the various kinds of dielectrics, “dipolar polymer glass” proposed by Zhu et al.10 has attracted plenty of attention due to the feasible designability of its molecular architecture and the achievable manipulation of its dielectric properties. Dipolar polymer glass belongs to a class of amorphous polar polymers with high glass transition temperature. The isolated dipoles are added into polymer chains and the interactions among the dipoles and between the dipoles and polymer matrix are weak. Consequently, the dielectric loss of polymer dipolar glass is relatively low. What is more, the permittivity can be enhanced by molecular tailoring.As a kind of typical polymer dipolar glass, polyimides indicate superior mechanical, thermal and electrical insulating performance, as well as excellent processability and molecular designability. Polyimide dielectrics have been intensively investigated via introducing polar groups such as ether, cyano, bipyridine, bipyrimidine, carbonyl and sulfonyl groups into molecular chains.11–18 Particularly, polyimides derived from polar aromatic dianhydrides and aliphatic ether-containing diamines18 exhibit high energy density of 15 J cm−3 while poor thermal resistance (Tg = 53–174 °C). In other researches, the dielectric permittivity was enhanced to 4.9 (190 °C, 1 kHz) when cyano groups15 were attached to polyimide backbones, and to 5.5–7.2 when bipyridine units17 were brought into the mainchains, while their dissipation factors were also increased to a high level of 0.04–0.08 due to the difficulty of frictionless dipole switching.
The flexible ester group is considered to facilitate the frictionless orientation of dipoles, resulting in low dielectric loss.19–23 For instance, polyethylene glycol terephthalate (PET)20 with ester group in each repeating unit shows dielectric loss as low as 0.3%. In addition, the polar ester group would also be beneficial to enhancing the dielectric permittivity by strengthen the orientational polarization. Consequently, dielectric permittivity of 3.1 was obtained in PET. Therefore, it is deduced that introducing ester group into polyimide to prepare ester-containing polyimide would be an effective way to acquire advanced polymer dielectrics. In addition, the oxygen-rich ester group also facilitates self-healing process,24–27 which will improve the reliability of film capacitor.
On the other hand, computational simulation on theoretical basis28–34 is regarded as a helpful means for mechanism analysis and molecular design in the study of dielectric materials. Different theoretical models such as density functional theory (DFT) and molecular dynamics (MD) are adopted in the existing multi-dimensional molecular simulation to connect the micro-structure and macro-property. Consequently, it greatly improves the efficiency of molecular design, material selection and experimental research. Arun et al.32 used DFT to calculate band gap and permittivity of polymers containing groups such as –CH2–, –CO–, –NH–, –C6H4–, –C4H2S–, –CS–, and –O–. Based on the simulation results, polymers containing –NH–CO–NH–C6H4–, –CO–NH–CO–C6H4– and –NH–CS–NH–C6H4– are considered to be promising for practical applications. According to this conclusion, polythiourea was chosen by Rui Ma et al.29 as the experimental object with enhanced energy storage capacity. The simulation method can also be applied to study the trap energy level in polymer dielectrics. For example, in Takada's work,31 locations of traps in the chemical structures of polymer were determined in order to facilitate understanding the complex charge accumulation behaviour. With the assistance of molecular simulation, microstructural information such as aggregation density of the macromolecular chains, dipolar moment and polarizability of polyimide can be calculated. For instance, in the research of Tian et al.28 it is discovered that polarizability in per unit volume can predict the dielectric permittivity appropriately in fluorinated polyimides. Coincidentally, high correlation between the dielectric permittivity and volume polarizability with a correlation coefficient of 0.90 is also found in 36 kinds of polyimides at a high frequency of 10 GHz in research of Ueda et al.33
In this work, a series of ester-containing polyimides (EPI) derived from ester-containing dianhydride and different diamines were synthesized. The molecular structure, as well as thermal and dielectric properties were characterized. The influence of molecular structure on dielectric properties was discussed in detail. What is more, to reveal the relationship between microstructure and dielectric properties in EPIs, the electronic properties and microscopic volume parameters were obtained based on the density functional theory (DFT) and molecular dynamics (MD). The correlation between microscopic properties and dielectric behaviour in ester-containing polyimides was analysed.
Experimental
Materials
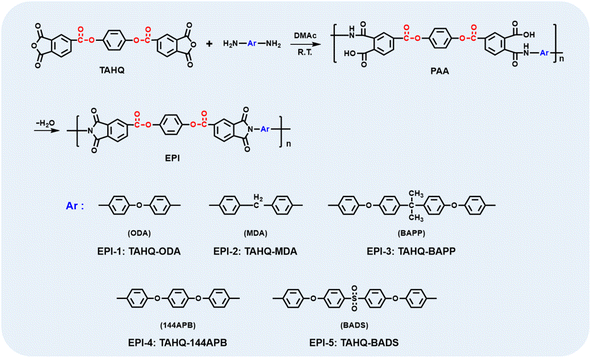
Bis(1,3-dioxo-1,3-dihydroisobenzofuran-5-carboxylate) (TAHQ) and N,N-dimethylacetamide (DMAc) was obtained from Shanghai Macklin Biochemical Co., Ltd. 4,4′-Oxydianiline (ODA), 4,4′-methylenedianiline (MDA), 4,4'-(4,4′-isopropylidenediphenyl-1,1′-diyldioxy)diamidine (BAPP), 1,4-bis(4-aminophenoxy)benzene (144APB) and bis[4-(4-aminophenoxy)phenyl] sulfone (BADS) were purchased from Shanghai Aladdin Biochemical Technology Co., Ltd. DMAc was purified by distillation under reduced pressure and dehydrated with 4 Å molecular sieves prior to use.Preparation of ester-containing polyimides
A series of ester-containing polyimides were prepared from dianhydride TAHQ and aromatic diamines, i.e., ODA, MDA, BAPP, 144APB and BADS, respectively. In a typical experiment, EPI-1, which derived from TAHQ and ODA was synthesized according to the following procedure. ODA (0.6553 g, 3.27 mmol) and DMAc (9.2 ml) were added to a three-necked flask equipped with a mechanical stirrer under nitrogen atmosphere. Then, TAHQ (1.5000 g, 3.27 mmol) was poured into the solution when ODA was dissolved completely. After continuously stirring for 8 h, the viscous poly (amic acid) (PAA) precursor was obtained. Afterwards, the as-prepared PAA solution was cast onto the clean glass plate with a knife gap of 200 μm on the automatic film applicator of BEVS 1818 GV. The wet film was thermally baked in an oven at 60 °C for 2 h, 180 °C for 1 h, 250 °C for 1 h and 300 °C for 0.5 h, successively. During the process, the solvent was removed and complete imidization occurred. The free-standing polyimide film with the thickness of about 25 μm was acquired by immersion the glass plate in hot water followed by dying in an oven at 120 °C overnight. The other polymer films derived from ester-containing polyimide, i.e., EPI-2 (TAHQ/MDA), EPI-3 (TAHQ/BAPP), EPI-4 (TAHQ/144APB), EPI-5 (TAHQ/BADS) were prepared by the similar procedure, except ODA was replaced by the other aromatic diamines as shown in Scheme 1.Characterizations
FTIR spectra were recorded on a Bruker Vertex 70 spectrophotometer, and the infrared wavelengths ranged from 400 to 4000 cm−1. The X-ray diffraction (XRD) measurements were conducted on the D8 Advance Bruker X-ray diffractometer with Cu/K radiation, operated at 40 kV and 40 mA from 5° to 70°. The UV-vis spectra were obtained from UV-vis spectrophotometer 2910 with the spectral range of 200–800 nm. The apparent density was tested by buoyancy method. Five pieces of samples from different batches were taken to calculate the average. In addition, heating treatment of 100 °C for 2 h was conducted to remove the residual solvent. The solubility of EPIs was tested with reagents including N-methylpyrrolidone (NMP), N,N-dimethylacetamide (DMAc), N,N-dimethylformamide (DMF), dimethyl sulfoxide (DMSO), ethanol and acetone. Put 0.05 g films into clean glass containers, separately. Then, the result of solubility was obtained under ultrasonic oscillation with 20 mL testing solution after 48 h.Thermal gravimetric analysis (TGA) was carried out using Mettler Toledo TGA/DSC 3+ in nitrogen atmosphere with a heating rate of 10 °C min−1. Thermomechanical analysis (TMA) measurements were conducted on a waters instrument of discovery TMA 450 EM, with a preload force of 0.05 N from room temperature to 200 °C. The average CTE values were calculated from the length variation in the range of 50−200 °C and can be described as:
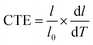 | (1) |
Electrical breakdown measurements were performed on a breakdown instrument (CS9920B, China) using the electrostatic pull-down method under a direct-current voltage ramp of 500 V s−1. The breakdown strength is analysed within the framework of a two-parameter Weibull statistic described as:
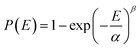 | (2) |
ln[−ln(1 − P)] = β(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E − ln E − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α) α)
| (3) |
| P = (i − 0.44)/(n + 0.25) | (4) |
The permittivity and dissipation factor were investigated using an Keysight LCR meter (E4980A) from 20 Hz to 2 MHz at room temperature. Silver electrodes of 20 mm diameter and 60 nm thickness were evaporated on both sides of the sample by using high vacuum electron beam evaporation method for the electric measurements.
Molecular simulation details
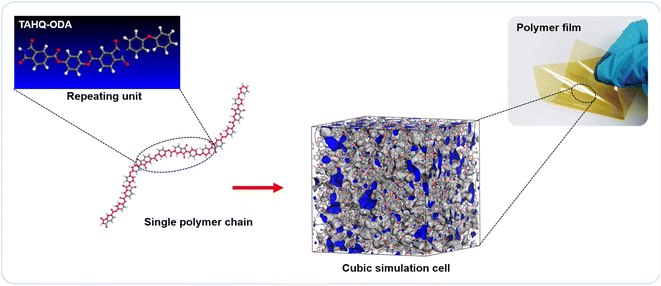
The Gaussian program was used to construct the EPIs basic repeating unit and calculated the electronic properties, including dipolar moment (μ) and polarizability (α), by using density functional theory (DFT). Dipolar moment and polarizability were calculated at the B3LYP level with the 6-31G(d) basis set (DFT (B3LYP/6-31G(d))). Material studio was used for molecular dynamics (MD) simulations to calculate the microparameters of fraction of free volume (FFV) and theoretical density of the steady-state of the ester-containing polyimides. In the modeling stage, 10 polyimide chains each containing 20 repeating units were assessed in the COMPASS force field. The amorphous cell module was employed to construct a cubic simulation cell for each polyimide (EPI-1/EPI-2/EPI-3/EPI-4/EPI-5) matrix. In the Forcite module, all the molecular models were treated with geometry optimization to obtain a stable structure with an energy minimization process over 1000 iterations. Subsequently, a series of dynamic optimization were performed on the cubic cells. First, a pressure of 0.5 GPa was used in NPT (fixed number of atoms, pressure and temperature) ensemble to compress the cubic cell. Then, an annealing step of NVT (fixed number of atoms, cell volume and temperature) ensemble was adopted to seek the conformation with minimum energy. Then, another NPT process was conducted to release the cell at the pressure of 10−4 GPa. Finally, the cubic cell underwent a relaxation process of NVT ensemble for 500 ps in order to obtain the state of equilibrium and acquire the conformation of steady state. Snapshots in the molecular simulation process of all the EPIs are shown in Fig. S1–S20.† Atom volume & surface tools were applied to calculate the volume parameters, e.g., occupied volume and free volume. The FFV value can be calculated by the following equation:
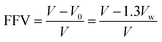 | (5) |
Results and discussion
Characterizations of ester-containing polyimides
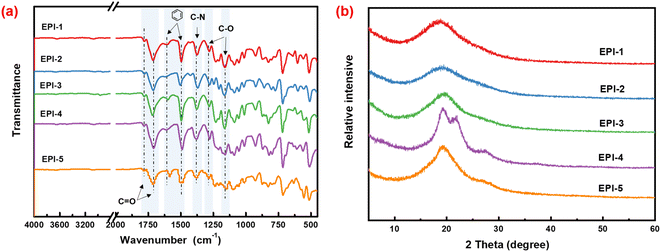
The chemical structures of ester-containing polyimides were identified by FTIR and their spectra were shown in Fig. 1a. The characteristic absorptions of imide rings are observed at 1774 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, asymmetric stretching), 1716 cm−1 (symmetric stretching), 720 cm−1 (C
O, asymmetric stretching), 1716 cm−1 (symmetric stretching), 720 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, bending) and 1380 cm−1 (C–N stretching). Moreover, the absence of the characteristic stretching vibration around 3300–3500 cm−1 of N–H bond derived from amino group indicates the complete imidization of poly(amic acid) to polyimide. Meanwhile, the peaks at 1501 cm−1 and 1598 cm−1 are usually regarded as the stretching of aromatic rings. The characteristic peaks of C–O bond in ester group are observed at 1163 cm−1 (asymmetric stretching) and 1280 cm−1 (symmetric stretching). Furthermore, the absorption peak of C
O, bending) and 1380 cm−1 (C–N stretching). Moreover, the absence of the characteristic stretching vibration around 3300–3500 cm−1 of N–H bond derived from amino group indicates the complete imidization of poly(amic acid) to polyimide. Meanwhile, the peaks at 1501 cm−1 and 1598 cm−1 are usually regarded as the stretching of aromatic rings. The characteristic peaks of C–O bond in ester group are observed at 1163 cm−1 (asymmetric stretching) and 1280 cm−1 (symmetric stretching). Furthermore, the absorption peak of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in ester group superimposes with that of carbonyl bond in imide group. Consequently, the absorption peak around 1716 cm−1 is wide and strong. Therefore, the ester-containing polyimide were successfully synthesized.
O bond in ester group superimposes with that of carbonyl bond in imide group. Consequently, the absorption peak around 1716 cm−1 is wide and strong. Therefore, the ester-containing polyimide were successfully synthesized.
The X-ray diffraction patterns of EPIs are illustrated in Fig. 1b. Broad halos are observed in most XRD patterns, which indicate the typical amorphous characteristics of EPIs. However, there is an exception of EPI-4, which exhibited two shoulder peaks. The partial crystallinity of EPI-4 is considered to derive from the continuous aromatic ether bond in the diamine moieties facilitating the ordered packing the molecular chains. Furthermore, the crystalline phase will be benefit to the exclusion of impurities in polymer matrix, so as to reduce conductivity loss and maintain high breakdown strength.
As shown in Table 1, EPIs are soluble in most polar organic solutions such as NMP, DMAc, DMF, DMSO, acetone and ethanol. The good solubility of EPIs may be due to the flexibility of molecular chains. The ester-containing polyimides exhibit outstanding thermal properties. As shown in Fig. S21, S22 and Table S1,† the 5% thermal decomposition temperature (T5%) of EPIs is higher than 442 °C. EPI-2 started to begin thermal decomposition earlier than others because of the methylene bridge linkage in the diamine moiety with lower bond energy. EPI-3 decomposes faster due to the larger fragment and lower bond energy derived from the tert-butyl structure in molecular chains compared to the other counterparts. Meanwhile, excellent glass transition temperatures (Tg) ranged from 200 °C to 316 °C are obtained in EPIs. The long segments containing flexible ether bond in the diamine part will improve the molecular chain mobility, so as to decrease the values of Tg. Consequently, EPI-3, EPI-4 and EPI-5 reveal lower Tg than EPI-1 and EPI-2. Moreover, the EPIs manifest pleasant dimensional stability up to 200 °C. Specifically, the coefficient of thermal expansion (CTE) ranges from 30.0 ppm °C−1 to 51.2 ppm °C−1.
| EPIs | Solvent | |||||
|---|---|---|---|---|---|---|
| NMP | DMAc | DMF | DMSO | Acetone | Ethanol | |
| a “+”: soluble by stirring; “−”: insoluble. | ||||||
| EPI-1 | + | + | + | + | + | − |
| EPI-2 | + | + | + | + | + | − |
| EPI-3 | + | + | + | + | + | − |
| EPI-4 | + | + | + | + | + | − |
| EPI-5 | + | + | + | + | + | − |
Dielectric properties of ester-containing polyimides
It is known that the band gap can be determined by linear extrapolation of the curve of absorbance utilizing the following equation:
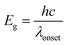 | (6) |
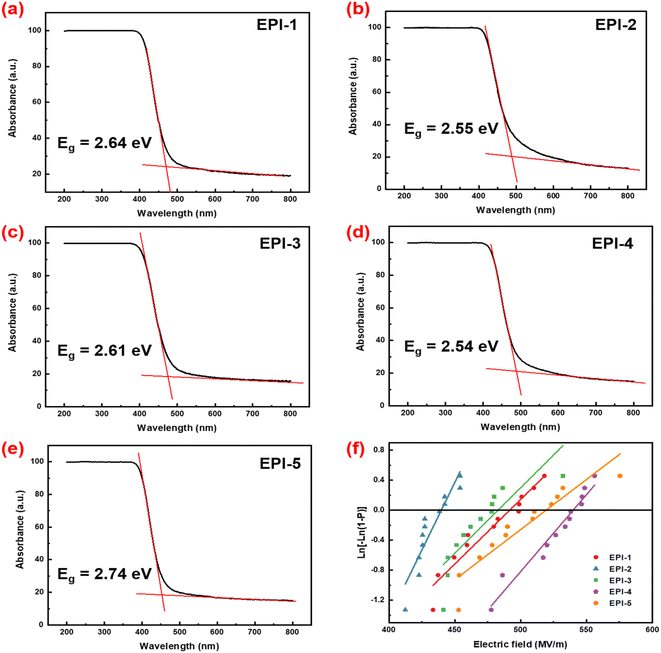 | ||
| Fig. 2 (a)–(e) UV-vis curves and calculated band gaps of EPIs; (f) Weibull plot with 95% confidence interval of electrical breakdown strength. | ||
| PI | Eb (MV m−1) | εr | tan δ (%) | Ue,max (J cm−3) | ρa (g cm−3) | ρc (g cm−3) | FFV (%) | Vvdw (Å3) | α | α/Vvdw | μ (Debye) | μ/Vvdw (Debye Å−3) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a ρa: the apparent density from experiment; ρc: the calculated density. | ||||||||||||
| EPI-1 | 492 | 3.78 | 0.748 | 4.05 | 1.272 | 1.313 | 18.29 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 981 |
410.3 | 0.829 | 3.58 | 0.00724 |
| EPI-2 | 440 | 3.65 | 0.880 | 3.13 | 1.199 | 1.286 | 18.41 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0622 0622 |
434.3 | 0.863 | 3.12 | 0.00620 |
| EPI-3 | 483 | 3.52 | 0.690 | 3.64 | 1.165 | 1.246 | 18.60 | 138![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 998 |
589.6 | 0.848 | 3.60 | 0.00518 |
| EPI-4 | 540 | 3.80 | 0.645 | 4.90 | 1.202 | 1.297 | 18.35 | 114![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939 939 |
464.7 | 0.809 | 4.24 | 0.00739 |
| EPI-5 | 519 | 3.85 | 0.627 | 4.59 | 1.266 | 1.310 | 18.55 | 135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728 728 |
564.9 | 0.824 | 4.68 | 0.00690 |
The variation of permittivity (εr) and dissipation factor (tan δ) as function of frequency at room temperature for EPIs are shown in Fig. 3. The values of permittivity drop slightly with the increasing frequency because of the lagging dipolar orientation in alternating current field. The permittivity of EPIs falls in the range of 3.52 to 3.85 at 103 Hz (Table 2). EPI-4 and EPI-5 exhibit higher values of εr than others. Besides the ester and imide groups, the polar structures of sulfonyl group and the ether linkage in the diamine moieties in EPI-4 and EPI-5 would facilitate the dipolar polarization considerably, so as to enhance the permittivity. While in EPI-1 and EPI-2, there are shorter diamine units and less amounts of polar groups so that the permittivity indicates only a small increase compared with the commercial polyimide of Kapton (εr = 3.1).20 EPI-1 reveals a higher εr than EPI-2 because the polarity of ether bond in EPI-1 is higher than that of methylene group in EPI-2, although they have similar backbones. EPI-3 presents the lowest permittivity despite the facts that there are polar structures of both ether and isopropyl groups in the repeating unit. It is deduced that the bulky isopropyl group in EPI-3 would inhibit the tight packing of molecular chains and yield a large fraction of free volume of 18.60% (Table 2), so as to dilute the density of polar groups. Therefore, the permittivity of EPI-3 decreases accordingly. It is not difficult to discover that only qualitative conclusions can be drawn by analysing the correlation between molecular structure and permittivity of intrinsic polymer dielectrics. It will be more challenging when multiple factors must be taken into accounts. Hence, quantitative methodology of theoretical simulation can be considered to evaluate the relationship between microstructures and macroscopic permittivity, as discussed in detail in Section 3.3.
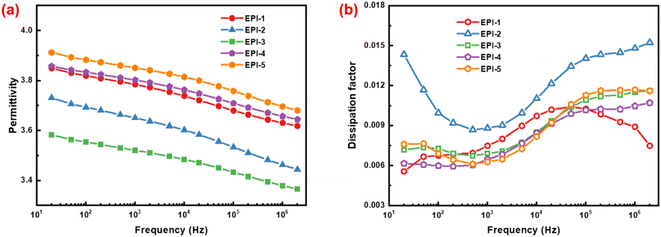 | ||
| Fig. 3 .Dependence of (a) permittivity and (b) dissipation factor on frequency of ester-containing polyimides at room temperature. | ||
As can be seen from Fig. 3b, the dissipation factors of EPIs decrease firstly and then increase with the increase of frequency. In addition, at 103 Hz, the values of tan δ range from 0.627% to 0.880% (Table 2). Polyimides with longer diamine moieties (EPI-3, EPI-4 and EPI-5) indicate lower dissipation factors. The reason is that long-range flexible structures of is favourable to the “frictionless” orientation, thus reducing the dielectric loss. Compared with EPI-1 and EPI-2 with similar molecular backbones, the methylene structure in EPI-2 would yield larger internal frictional resistance when orientates in an alternating electric field and its dissipation factor is higher than that of EPI-1. The analogous situation also occurs in EPI-3 and EPI-5. Consequently, EPI-5 shows the lowest dissipation factor of 0.627%.
The maximum energy densities of EPIs are calculated by the following equation:
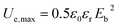 | (7) |
Consequently, excellent comprehensive performances, i.e., enhanced permittivity and breakdown strength, reduced dissipation factor, as well as outstanding thermal properties are obtained in ester-containing polyimides. Therefore, the polymer dielectrics based on ester-containing polyimides would be the potential candidates for film capacitors applied in harsh conditions such as high temperature.
Comparative investigation on dielectric permittivity from experimentation and molecular simulation
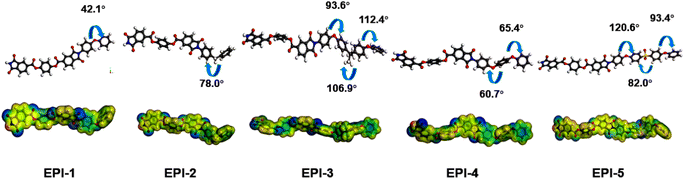
Theoretical simulation is an effective method to assist the analysis of dielectric mechanism. Herein, the electronic properties (electrostatic potential surface, polarizability and dipolar moment) and microscopic volume parameters (fractional free volume, van der Waals volume) were obtained by molecular simulation. The optimized geometries and the ESP surfaces of ester-containing polyimides are shown in Fig. 4. Obvious electron localization is observed surrounding the polar groups such as imide and ester groups, which would facilitate the electronic polarization and in further increase the permittivity. Other polar groups, e.g., methyl and sulfonyl, also contribute much to electronic polarization. It is worth mentioning that these polar structures and the electron localization would offer a non-negligible effect on the strengthen of orientational polarization and subsequent the enhancement of permittivity.The density and fractional free volume (FFV) from simulation of the EPIs are presented in Table 2, so as the apparent density from experiments. It is found that the sequence of the apparent and calculated density is exactly identical, which is EPI-1 > EPI-5 > EPI-4 > EPI-2 > EPI-3 (Table 2 and Fig. S23†). Although the calculated values are slightly higher than that from experimental due to the systematic deviation, molecular simulation is still an effective method to predict polymer properties. The sequence of FFV is EPI-3 > EPI-5 > EPI-2 > EPI-4 > EPI-1. It is noted that the values of FFV are exactly inversely correlated with density except EPI-5. Owing to the existence of the heavy sulfonyl atom, EPI-5 indicates relatively high density though there is a great deal of free volume in the corresponding film.
Polarization and the van der Waals volumes of the repeating unit in EPIs are calculated by simulating method to evaluate the correlations between the microparameters and dielectric properties. The polarization in per volume (α/Vvdw), or polarization density is shown in Table 2. The sequence of α/Vvdw is EPI-2 > EPI-3 > EPI-1 > EPI-5 > EPI-4, while that of practical permittivity at 1 kHz is EPI-5 > EPI-4 > EPI-1 > EPI-2 > EPI-3. Different from the conclusion that the dielectric permittivity is positively related to the polarizability density drawn from previous research,28,30,33 there is a significant discrepancy between α/Vvdw and εr in EPIs (Fig. 5a). According to the Clausius–Mossitti equation:
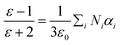 | (8) |
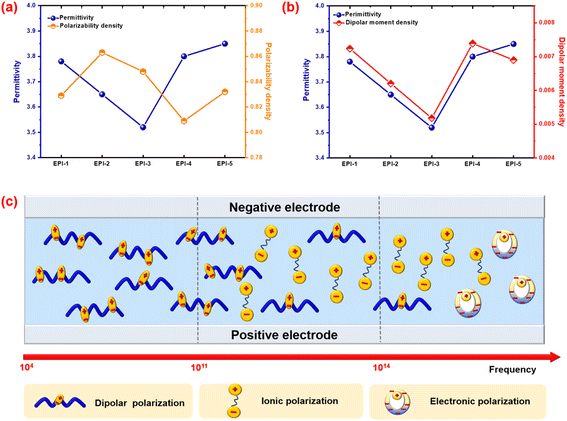 | ||
| Fig. 5 Comparison between (a) permittivity vs. polarization density and (b) permittivity vs. dipolar moment density; (c) schematic diagram of the polarization mechanism in polar polymers. | ||
As the main influencing factor of dielectric permittivity, dipolar polarization is studied then. The dipolar moment, as well as the density of dipolar moment is calculated in Table 2. As all the ester-containing polyimides have similar backbones and close fraction of free volume, a hypothesis that all the EPIs exhibit approximative orientation ability under an applied electric field is established here. As a result, the permittivity seems to be proportional to the density of dipolar moments (μ/Vvdw). As displayed in Table 2, the sequence of dipolar moment density is EPI-4 > EPI-1 > EPI-5 > EPI-2 > EPI-3. In general, the μ/Vvdw shows a positive correlation to permittivity with one exception of EPI-5. Compared to EPI-4, EPI-5 exhibits lower μ/Vvdw (0.00690) but higher permittivity (3.85). From Table 2, it can be seen that the repeating unit of EPI-5 with strong sulfonyl group indicates high dipolar moment of 4.68 Debye, while the value of μ/Vvdw is reduced because of the large free space which can be confirmed by FFV and Vvdw. At this case, the orientation ability of dipoles in EPI-5 may be underestimated in the hypothesis above because there are more linkages (sulfonyl and ether bonds) between phenyl rings in single repeating unit. Therefore, EPI-5 reveals larger εr although the μ/Vvdw is lower than EPI-4. Another possible reason is that besides μ/Vvdw and the orientation capability of dipoles, permittivity is also influenced by the interactions among the dipoles, which cannot be evaluated in this study. In summary, the microparameter of μ/Vvdw is illustrated an appropriate method to predict the dielectric behavior especially in the cases of polymer dielectrics with similar backbones.
Conclusions
In summary, a series of ester-containing polyimides (EPIs) were fabricated derived from dianhydride with ester group in molecular structure and different diamines. The ester-containing polyimides show superior thermal resistance and dielectric properties. In particular, the EPIs presented Weibull breakdown strength of 440–540 MV m−1, dielectric permittivity of 3.52–3.85, dissipation factor of 0.627–0.880% and theoretical energy density of 3.13–4.90 J cm−3. In addition, the electronic properties, i.e., electrostatic potential surface, dipolar moment and polarizability as well as microscopic volume parameters, i.e., fractional free volume and van der Waals volume were calculated on theoretical basis of density functional theory (DFT) and molecular dynamics (MD). Based on these experimental and calculated results, it can be found that the dipolar moment density (μ/Vvdw) is closely correlated to dielectric permittivity. The reason is that dipolar polarization is the predominant polarization mode in ester-containing polyimides in the studied frequency range. The nontrivial correlation between microscopic parameters from theoretical simulation and dielectric behaviour from experimental results demonstrates that μ/Vvdw is an appropriate parameter to predict dielectric behaviour in polar polymers dominated by dipolar polarization. The integrated research of molecular simulation and experimentation help to discover an effective micro-parameter to predict the variation tendency of the macroscopic permittivity, as well as reveal the dielectric mechanism and assist molecular design of polymer dielectrics.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors would like to acknowledge the financial supports from the National Natural Science Foundation (Grant no: 51907187) and the Institute of Electrical Engineering, CAS (Grant no: E155440301) and the Youth Long-term Project of Jiangxi Province to Introduce Leading Innovative Talents, China (Grant no: jxsq2018106023).Notes and references
- C. Racles, M. Alexandru, V. E. Musteata, M. Cazacu and D. M. Opris, RSC Adv., 2014, 4, 37620–37628 RSC.
- S. J. Dünki, M. Tress, F. Kremer, S. Y. Ko, F. A. Nüesch, C. D. Varganici, C. Racles and D. M. Opris, RSC Adv., 2015, 5, 50054–50062 RSC.
- W. Y. Zhou, T. Li, M. X. Yuan, B. Li, S. L. Zhong, Z. Li, X. R. Liu, J. J. Zhou, Y. Wang, H. W. Cai and Z. M. Dang, Energy Storage Mater., 2021, 42, 1–11 CrossRef.
- J. Y. Pei, S. L. Zhong, Y. Zhao, L. J. Yin, Q. K. Feng, L. Huang, D. F. Liu, Y. X. Zhang and Z. M. Dang, Energy Environ. Sci., 2021, 14, 5513–5522 RSC.
- X. J. Liu, M. S. Zheng, G. Chen, Z. M. Dang and J. W. Zha, Energy Environ. Sci., 2022, 15, 56–81 RSC.
- J. P. Cao, J. Zhao, X. D. Zhao and Z. M. Dang, Compos. Sci. Technol., 2021, 209, 108792 CrossRef CAS.
- G. Zhang, Q. Li, E. Allahyarov, Y. Li and L. Zhu, ACS Appl. Mater. Interfaces, 2021, 13, 37939–37960 CrossRef CAS PubMed.
- X. P. Yuan, Y. C. Matsuyama and T. C. M. Chung, Macromolecules, 2010, 43, 4011–4015 CrossRef CAS.
- G. Picci and M. Rabuffi, Status quo and future prospects for metallized polypropylene energy storage capacitors[C]//PPPS-2001 Pulsed Power Plasma Science 2001, in 28th IEEE International Conference on Plasma Science and 13th IEEE International Pulsed Power Conference. Digest of Papers (Cat. No. 01CH37251), IEEE, 2001, vol. 1, pp. 417–420 Search PubMed.
- J. J. Wei, Z. B. Zhang, J. K. Tseng, I. Treufeld, X. B. Liu, M. Litt and L. Zhu, Interfaces, 2015, 7, 5248–5257 CAS.
- Y. H. Lu, J. H. Zhang, G. Y. Xiao, L. Li, M. J. Hou, J. Y. Hu and T. H. Wang, RSC Adv., 2020, 10, 17461–17472 RSC.
- X. W. Peng, W. H. Xu, L. L. Chen, Y. C. Ding, T. R. Xiong, S. L. Chen and H. Q. Hou, React. Funct. Polym., 2016, 106, 93–98 CrossRef CAS.
- T. W. Zhu, Q. X. Yu, W. W. Zheng, R. X. Bei, W. H. Wang, M. M. Wu, S. W. Liu, Z. G. Chi, Y. Y. Zhang and J. R. Xu, Polym. Chem., 2021, 12, 2481–2489 RSC.
- H. Tong, J. Fu, A. Ahmad, T. Fan, Y. D. Hou and J. Xu, Macromol. Mater. Eng., 2019, 304, 1800709 CrossRef.
- D. H. Wang, B. A. Kurish, I. Treufeld, L. Zhu and L. S. Tan, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 422–436 CrossRef CAS.
- H. Tong, A. Ahmad, J. Fu, H. Y. Xu, T. Fan, Y. D. Hou and J. Xu, J. Appl. Polym. Sci., 2019, 136, 47883 CrossRef.
- X. W. Peng, Q. Wu, S. H. Jiang, M. Hanif, S. L. Chen and H. Q. Hou, J. Appl. Polym. Sci., 2014, 131, 40828 Search PubMed.
- R. Ma, A. F. Baldwin, C. Wang, I. Offenbach, M. Cakmak, R. Ramprasad and G. A. Sotzing, ACS Appl. Mater. Interfaces, 2014, 6, 10445–10451 CrossRef CAS PubMed.
- J. T. Bendler, D. A. Boyles, C. A. Edmondson, T. Filipova, J. J. Fontanella, M. A. Westgate and M. C. Wintersgill, Macromolecules, 2013, 46, 4024–4033 CrossRef CAS.
- J. M. Luo, L. Zhu, W. J. Wang, S. Wang, J. L. Mao, L. L. Tian, Y. Chen and Y. H. Cheng, Macromol. Chem. Phys., 2021, 222, 2100049 CrossRef CAS.
- J. J. Fontanella, D. A. Boyles, T. S. Filipova, S. Awwad, C. A. Edmondson, J. T. Bendler, M. C. Wintersgill, J. F. Lomax and M. Schroeder, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 289–304 CrossRef CAS.
- P. Yang, F. Q. Tian and Y. Ohki, IEEE Trans. Dielectr. Electr. Insul., 2014, 21, 2310–2317 CAS.
- J. T. Bendler, C. A. Edmondson, M. C. Wintersgill, D. A. Boyles, T. S. Filipova and J. J. Fontanella, Eur. Polym. J., 2012, 48, 830–840 CrossRef CAS.
- B. Walgenwitz, J. H. Tortai, N. Bonifaci and A. Denat, Self-healing of metallized polymer films of different nature, in Proceedings of the 2004 IEEE International Conference on Solid Dielectrics, 2004. ICSD 2004, IEEE, 2004, vol. 1, pp. 29–32 Search PubMed.
- M. Rabuffi and G. Picci, IEEE Trans. Plasma Sci., 2002, 30, 1939–1942 CrossRef CAS.
- C. W. Reed and S. W. Cichanowskil, IEEE Trans. Dielectr. Electr. Insul., 1994, 1, 904–922 CrossRef CAS.
- J. S. Ho and S. G. Greenbaum, ACS Appl. Mater. Interfaces, 2018, 10, 29189–29218 CrossRef CAS PubMed.
- H. Zhou, H. Y. Lei, J. H. Wang, S. L. Qi, G. F. Tian and Z. D. Wu, Polymer, 2019, 162, 116–120 CrossRef CAS.
- R. Ma, V. Sharma, A. F. Baldwin, M. Tefferi, I. Offenbach, M. Cakmak, R. Weiss, Y. Cao, R. Ramprasad and G. A. Sotzing, J. Mater. Chem. A, 2015, 3, 14845–14852 RSC.
- X. L. Li, H. Y. Lei, J. C. Guo, J. H. Wang, S. L. Qi, G. F. Tian and D. Z. Wu, J. Appl. Polym. Sci., 2019, 136, 47989 CrossRef.
- T. Takada, H. Kikuchi, H. Miyake, Y. Tanaka, M. Yoshida and Y. Hayase, IEEE Trans. Dielectr. Electr. Insul., 2015, 22, 1240–1249 CAS.
- A. Mannodi-Kanakkithodi, G. M. Treich, H. Tran Doan, R. Ma, M. Tefferi, Y. Cao, G. A. Sotzing and R. Ramprasad, Adv. Mater., 2016, 28, 6277–6291 CrossRef CAS PubMed.
- C. C. Kuo, Y. C. Lin, Y. C. Chen, P. H. Wu, S. J. Ando, M. Ueda and W. C. Chen, ACS Appl. Polym. Mater., 2020, 3, 362–371 CrossRef.
- R. Ma, A. F. Baldwin, C. C. Wang, I. Offenbach, M. Cakmak, R. Ramprasad and G. A. Sotzing, ACS Appl. Mater. Interfaces, 2014, 6, 10445–10451 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06376j |
| This journal is © The Royal Society of Chemistry 2023 |