 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
2-Formylphenoxyacetic acid Schiff bases: a promising ligand scaffold for readily available trigonal prismatic Co(II) single-ion magnets†
Kamil
Kotrle
 a,
Ivan
Nemec
a,
Ivan
Nemec
 a,
Peter
Antal
a,
Kamila
Petrželová
a,
Peter
Antal
a,
Kamila
Petrželová
 a,
Erik
Čižmár
a,
Erik
Čižmár
 b and
Radovan
Herchel
b and
Radovan
Herchel
 *a
*a
aDepartment of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, CZ-771 46 Olomouc, Czech Republic. E-mail: radovan.herchel@upol.cz
bInstitute of Physics, Faculty of Science, P.J. Šafárik University in Košice, Park Angelinum 9, SK-041 54 Košice, Slovakia
First published on 26th October 2023
Abstract
This article presents a series of six mononuclear Co(II) complexes 1–6 featuring ligands derived from a hexadentate Schiff base family, originating from the condensation of (2-formylphenoxy)acetic acid with various diamines. Notably, these complexes uniquely prefer a trigonal prism geometry, presenting a novel approach to synthesizing complexes with this distinctive shape. The compounds were characterized by elemental analysis, FT-IR spectroscopy, and single-crystal and powder XRD techniques. Furthermore, the magnetism was investigated by DC and AC magnetic measurements and also complemented by X-band EPR spectroscopy. The results reveal that the prepared complexes behave as field-induced single-molecule magnets, characterized by a substantial negative axial zero-field splitting D-parameter and spin reversal energetic barrier Ueff reaching values up to 72 K. The theoretical methods based on CASSCF/NEVPT2 calculations were applied to rationalize their magnetic properties. Moreover, these complexes hold promising potential for further functionalization, offering opportunities to enhance their properties, particularly towards developing zero-field single-molecule magnets as evidenced by the slow relaxation of magnetization in zero static magnetic field observed for the zinc-diluted complex 1Zn.
Introduction
In recent years, there has been significant development in the field of single-molecule magnets (SMMs), a class of materials that exhibit intriguing magnetic properties, including magnetic hysteresis and slow relaxation of magnetization at the molecular level. This progress began with discovering and studying these effects in large manganese polynuclear clusters, such as the renowned Mn12ac.1 Subsequent research has explored a wide range of systems, with one notable subclass of SMMs known as single-ion magnets. These magnets consist of only one paramagnetic ion,2 thereby minimizing the influence of any magnetic exchange interactions. Among this class of compounds, an important group, particularly within the first transition metals row, comprises complexes containing Co(II) as the central ion. Co(II) exhibits interesting magnetic properties due to its spin S = 3/2, making it a Kramers ion, and its relatively large spin–orbit coupling resulting from its occupation of the d-orbital.3Although leveraging spin–orbit coupling is key to designing single-molecule magnets with significant magnetic anisotropy, another crucial characteristic of 3d single ion magnets is ligand field splitting, which is usually stronger than spin–orbit coupling.
In six-coordinated Co(II) complexes, the orbital contribution is usually substantial due to the nature of the ground state, which is T1g for an octahedron (Oh), and 4E′ for a trigonal prism (D3h). It is common for the (pseudo)octahedral symmetry to result in large and positive values of the axial zero-field splitting parameter D.4 Positive D-parameter frequently leads to the easy-plane type anisotropy, and only significant rhombicity (E/D ratio) can provide the axial type anisotropy.5 In the case of trigonal prism symmetry, the D-parameter is typically large and negative.4 The relationship between the D-parameter and magnetic anisotropy barrier for half-integer spin complexes, such as Co(II), is defined as:6
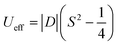 | (1) |
It is worth noting that a significant number of complexes with a trigonal prismatic shape exhibit slow relaxation of magnetization even in the absence of an external magnetic field, earning them the designation of zero-field SMMs. Table 1 lists notable examples of trigonal prismatic and trigonally distorted hexacoordinate complexes showing the slow relaxation of magnetization.
| Name | D (cm−1) | E (cm−1) | U eff (cm−1) | τ 0 (s) | B (T) | CSM TP | CSM OH | Ref. |
|---|---|---|---|---|---|---|---|---|
| tppm = 6,6′,6′′-(methoxymethanetriyl)tris(2-(1H-pyrazol-1-yl)pyridine); hpy = tris(2,2′-bipyrid-6-yl)methanol; PzOx = pyrazoloximate, AcimOx = acetylmethylimidazole-oximate, AcPyOx – acetylmethylpyridine-oximate, Chdc – 6,6′-{cyclohexane-1,3,5-diyltris[nitrilo(E)methylylidene]}dipyridine-3-carboxamide; H2hpmp = R-4-bromo-2-((2-hydroxy-1-phenylethylimino)methyl)phenol; neo = neocuproine, piv = pivalate, 4OH-benz = 4-hydroxybenzoate. | ||||||||
| [Co(tppm)][BPh4]2 | −97.2(2) | 9.3(1) × 10−3 | 192 | 2.6(2) × 10−12 | 0 | 0.554 | 15.893 | 8 |
| [Co(hpy)][BPh4]2·3CH2Cl2 | −107.5(4) | 3.5(3) | 20 | 1.2(1) × 10−3 | 0 | 2.471 | 8.237 | 8 |
| [Co(PzOx)3(BC6H5)]Cl·CHCl3 | −82 | 0.246 | 152 | 2.07 × 10−9 | 0 | 0.828 | 16.272 | 9 |
| [Co(AcimOx)3(BC6H5)]ClO4 | −102.5 | 101 | 2.56 × 10−6 | 0 | 0.905 | 13.462 | 10 | |
| [Co(AcPyOx)3BC6H5]ClO4 | −86 | 194.6 | 3.55 × 10−10 | 0 | 2.006 | 10.042 | 11 | |
| {Na[(Chdc)Co]}(BPh4)3 | −75.8 | 9.1 × 10−4 | 52.6 | 0.1 | 1.793 | 9.293 | 12 | |
| [Co(tppm)][ClO4]2·2CH3CN·H2O | −80.7 | 0.6 | 39.2 | 1.7 × 10−4 | 0 | 0.588 | 14.920 | 13 |
| (HNEt3)[CoIICoIII3(hpmp)6] | −115 | 2.8 | 76.3 | 1 × 10−7 | 0 | 2.341 | 9.284 | 14 |
| [Co(neo)(CH3COO)2] | 26.3 | 1.361 × 10−7 | 0.1 | 3.761 | 11.893 | 15 | ||
| [Co(neo)(piv)2] | 13.2 | 6.2 × 10−6 | 0.1 | 9.801 | 7.650 | 15 | ||
| [Co(neo)(4OH-benz)2]·2CH3OH | 12.2 | 1.04 × 10−6 | 0.1 | 10.110 | 6.352 | 15 | ||
It is evident that focusing on the design of Co(II) complexes as potential candidates for SMMs holds intriguing possibilities, including the potential for zero-field single-molecule magnets. However, such magnets are still relatively rare among Co(II) complexes as a whole due to the common occurrence of quantum tunneling of magnetization in the ground state. In the case of six-coordinated Co(II) complexes, the pseudo-octahedral shape is the most commonly observed coordination polyhedron. Therefore, efforts must be made to achieve the trigonal prism shape. Various strategies have already been applied as can be observed in Table 1. An effective approach, seen in most cases,8–13 involves the use of three heterocyclic binding sites, each with two donor atoms, designed to prevent distortion and maintain the desired shape. In another instance,14 the trigonal prismatic shape is achieved through bridging oxygen atoms in a tetranuclear core, where Co(II) is surrounded by three diamagnetic Co(III) cores. In the last case,15 the desired shape is attained through steric hindrance caused by neocuproine methyl groups.
This work presents a series of six complexes (Scheme 1) that employ Schiff base ligands with similar structural motifs. These ligands induce a distorted coordination environment, compelling the Co(II) complexes to adopt shapes that closely resemble trigonal prismatic geometry. The ligands are derived from (2-formylphenoxy)acetic acid, and by incorporating different diamines, we observed a modulation of both the structural and magnetic properties. While analogous structures have been reported previously for Ni(II), Cu(II), Zn(II), and even Co(II), their magnetic properties have not been studied in detail.16–20
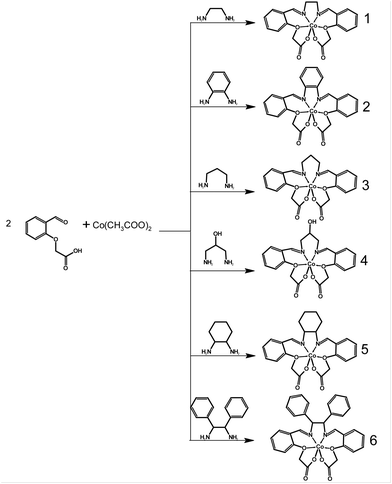 | ||
| Scheme 1 General scheme for the synthesis of Co(II) complexes [CoL] of 1–6 with respective in situ prepared Schiff base ligands H2L. | ||
Results and discussion
Synthesis and characterisation
The methods employed for the preparation of these complexes are described in the Experimental section below. The Co(II) compounds 1–6 were synthesized by reacting a mixture of cobalt(II) acetate and (2-formylphenoxy)acetic acid with the corresponding amine.Among these complexes, all except for 2 exhibit good solubility in methanol (MeOH); however, only complex 1 yielded a crystalline product from this solvent. As 3, 5, and 6 did not crystallize from methanol due to their high solubility, a mixture of propanol and methanol was chosen as the solvent. For insoluble complex 2, crystals were obtained from dimethylsulfoxide (DMSO). Complex 3 presented a challenge during its preparation, as it often resulted in the formation of orange powder. Ultimately, this problem was resolved by conducting the reaction without heating the solution to the reflux temperature. Unfortunately, complex 4 could not be obtained in the required quantity and purity for bulk characterization due to the formation of undesired byproducts. However, a small number of single crystals of complex 4 were successfully prepared, and its structure was determined through X-ray analysis. This allowed us to characterize complex 4 at least with theoretical methods. The composition of the prepared complexes was verified through elemental analysis, infrared spectrometry (Fig. S1†), and X-ray powder diffraction (Fig. S2†). For complex 6, X-ray crystallography indicated the presence of co-crystallized methanol solvent molecules, which displayed notable disorder, likely stemming from solvent loss during the experiment. It was not possible to model the solvent molecules properly and a solvent masking procedure was applied.21 The resultant masked electron density corresponded to 1.25 methanol molecules per complex molecule. Of note here is that the single crystal measured had been promptly transferred from the solution to high viscosity oil. This action very likely contributed to the reduced rate of solvent loss. Thus, the observed alignment between the outcomes of elemental analysis and the assumption of a solvent-free complex is unsurprising.
Magnetically diluted complex 1Zn was prepared by using Co(II) and Zn(II) acetate in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 molar ratio. Sample purity was verified by PXRD (Fig. S2†) and CHNS elemental analysis. The composition was studied by the AAS method, which showed a mass fraction of Co of 0.32%, which means that the diluted sample has formula C21H22N2O7Co0.026Zn0.974.
9 molar ratio. Sample purity was verified by PXRD (Fig. S2†) and CHNS elemental analysis. The composition was studied by the AAS method, which showed a mass fraction of Co of 0.32%, which means that the diluted sample has formula C21H22N2O7Co0.026Zn0.974.
Crystal structure description
Complexes 1, 4, and 5 crystallize in the monoclinic space group P21/n, while 2 and 3 crystallize in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . Complex 6 crystallizes in the orthorhombic space group Iba2. All diffraction experiments were conducted at room temperature. Each compound consists of a [CoL] neutral complex accompanied by co-crystallized solvent molecules of MeOH in the case of 1, 3, 4, and 5, and DMSO in the case of 2. In each complex, the cobalt atom is bonded to four oxygen atoms and two nitrogen atoms. Notably, complexes 5 and 6 contain two symmetrically inequivalent molecules of the complex [CoL] in the asymmetric unit, labeled 5a/6a and 5b/6b, respectively (Fig. 1). Additional details about X-ray crystallographic experiments are listed in Table S1.†
. Complex 6 crystallizes in the orthorhombic space group Iba2. All diffraction experiments were conducted at room temperature. Each compound consists of a [CoL] neutral complex accompanied by co-crystallized solvent molecules of MeOH in the case of 1, 3, 4, and 5, and DMSO in the case of 2. In each complex, the cobalt atom is bonded to four oxygen atoms and two nitrogen atoms. Notably, complexes 5 and 6 contain two symmetrically inequivalent molecules of the complex [CoL] in the asymmetric unit, labeled 5a/6a and 5b/6b, respectively (Fig. 1). Additional details about X-ray crystallographic experiments are listed in Table S1.†
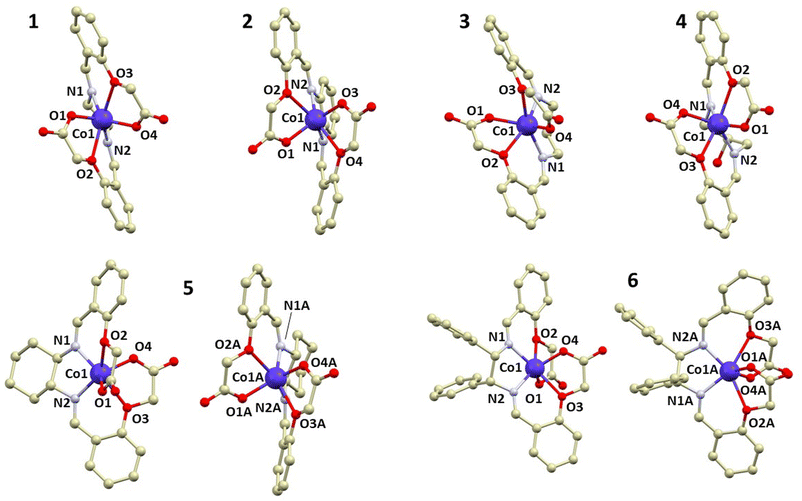 | ||
| Fig. 1 A perspective view of the crystal structures of 1–6, with hydrogen atoms omitted for the sake of clarity. | ||
The shape of the cobalt coordination polyhedron in all complex molecules is closest to a trigonal prism (D3h), as confirmed by calculations of continuous shape measures (CSMs) using SHAPE software.7 The minimal distortion pathway between a trigonal prism and an octahedron, as well as the deviation of the prepared complexes’ structures from the pathway, is shown in Fig. S3.† It is apparent that all complexes exhibit significant deviations from an octahedron (Oh), except for 3, which is nearly on the border between an octahedron and a trigonal prism.
In addition to CSM, the shape of the geometry of the coordination environment was also investigated using the newly proposed structural parameter τ6, a geometry index ranging from 0 (ideal octahedron) to 1 (ideal trigonal prismatic shape).22 This index is analogous to previously published τ5 and τ4 indices for penta- and tetracoordinate complexes, respectively.23 The parameter τ6 is defined as
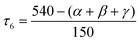 | (2) |
| Co–N1 | Co–N2 | Co–O1 | Co–O2 | Co–O3 | Co–O4 | CSM TP | CSM OH | τ 6 | |
|---|---|---|---|---|---|---|---|---|---|
| a N1 and N2 for these structures are marked as N3 and N4 in Fig. 1. Same way, O1–O4 are marked as O7–O10. b Labeled in a similar way as in Fig. 1, in the HOMFOF cif file, N1 is N1, N2 is N2, O1 is O1, O2 is O3, O3 is O4 and O4 is O5. | |||||||||
| 1 | 2.0829(19) | 2.0736(18) | 1.9911(14) | 2.3176(14) | 2.2822(15) | 1.9848(16) | 1.631 | 16.812 | 0.802 |
| 2 | 2.0883(13) | 2.0681(13) | 1.9922(12) | 2.2846(12) | 2.2688(11) | 1.9759(12) | 1.882 | 13.748 | 0.777 |
| 3 | 2.0770(15) | 2.0929(15) | 2.0370(13) | 2.2257(13) | 2.2451(13) | 2.0110(13) | 4.727 | 5.626 | 0.525 |
| 4 | 2.130(2) | 2.092(2) | 1.983(2) | 2.335(2) | 2.299(2) | 1.993(1) | 1.481 | 12.924 | 0.794 |
| 5a | 2.0667(19) | 2.0739(19) | 1.9861(17) | 2.2963(15) | 2.3525(15) | 1.9879(16) | 1.911 | 17.842 | 0.802 |
| 5b | 2.083(2) | 2.081(2) | 1.9946(17) | 2.2755(18) | 2.2164(16) | 2.0099(18) | 1.472 | 12.663 | 0.785 |
| 6a | 2.066(6) | 2.107(8) | 1.951(5) | 2.336(5) | 2.383(5) | 1.970(7) | 2.612 | 18.154 | 0.760 |
| 6b | 2.052(6) | 2.065(8) | 1.998(5) | 2.399(6) | 2.375(5) | 1.978(6) | 4.714 | 15.726 | 0.694 |
| Co–N1 | Co–N2 | Co–O1 | Co–O3 | Co–O4 | Co–O5 | ||||
| HOMFOF | 2.063(2) | 2.055(2) | 2.042(2) | 2.192(2) | 2.184(2) | 2.032(2) | 10.644 | 1.530 | 0.320 |
Furthermore, a previously known similar complex, [Co(fpa-pn)]·6H2O (CSD code HOMFOF),17 was included in the SHAPE analysis, which is a conformational isomer to 3 and exhibits a structure much closer to an ideal octahedron. Interestingly, the use of different solvents (HOMFOF synthesis used a mixture of ethanol and water) for synthesis results in entirely different structures, which are expected to possess distinct properties, especially from a magnetic standpoint.
The distances between the metal and ligand donor atoms, as listed in Table 2, reveal that in most cases, the four bonds between the central atoms and the Schiff base N-atoms or carboxylic group O-atoms have very similar lengths ranging between 2.0 and 2.1 Å. However, the bonds between Co and the etheric group O-atoms (O2 and O3) are longer, ranging between 2.2 and 2.4 Å. Furthermore, structures that differ from others in terms of their shape (CSM), such as 3 and its isomer with the CSD code HOMFOF, do not appear to differ significantly in their bond lengths, except for a shorter distance between the Co atom and the etheric O atom in the HOMFOF structure.
Complexes 1–5 crystallize as crystal solvates, with dimethyl sulfoxide as the solvent in structure 2, and methanol in all other cases. Methanol is bound to the complex molecule through a hydrogen bond. In structures 1, 4, and 5, it is bound to the carboxylic group oxygen, which is not connected to the central cobalt atom. In structure 3, methanol is bound to the coordinating carboxylic oxygen atom. Moreover, structure 4 contains a ligand with a hydroxyl group, which forms a hydrogen bond with the carboxyl group oxygen, resulting in a supramolecular structure mediated by hydrogen bridges. Details about observed significant hydrogen bonds are shown in the ESI (Fig. S5†).
Magnetic measurements
DC magnetic measurements were conducted for compounds 1–3 and 5–6. The measurements consisted of recording the magnetization as a function of temperature under a magnetic field of 0.2 T and as a function of the magnetic field (Fig. 2) at temperatures of 1.8, 5, and 10 K (or 2 and 5 K for compound 1).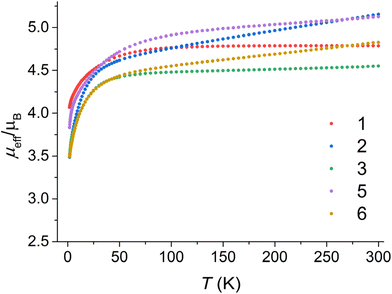 | ||
| Fig. 2 The effective magnetic moment dependence on temperature for all studied compounds 1–3 and 5–6. | ||
The effective magnetic moments of the prepared compounds at a temperature limit of 300 K are as follows: 4.79μB for compound 1, 5.15μB for compound 2, 4.55μB for compound 3, 5.13μB for compound 5, and 4.83μB for compound 6. The spin-only value for S = 3/2 with g = 2.0 is 3.87μB. The observed larger values of the magnetic moment can be attributed to an increased g-factor resulting from orbital contribution and temperature-independent paramagnetism.24
DC magnetic data were analyzed using the following spin Hamiltonian:
| Ĥ = D(Ŝz2 − Ŝ2/3) + E(Ŝx2 − Ŝy2) + μBBgŜ | (3) |
The best-fitted spin Hamiltonian parameters are listed in Table 3 with the standard deviations listed in Table S2,† and calculated magnetic data compared to the experimental ones are depicted in Fig. S6–S10.†
| g | D (cm−1) | E/D | TIP (cm3 mol−1) | |
|---|---|---|---|---|
| a Written either as giso, or gz; gxy. | ||||
| 1 | 2.724; 2.299 | −30.3 | 0.173 | 0 |
| 2 | 2.344 | −13.2 | 0.281 | 2.55 × 10−3 |
| 3 | 2.357; 2.271 | −17.0 | 0.195 | 3.34 × 10−4 |
| 5 | 2.641; 2.395 | −30.5 | 0.207 | 1.33 × 10−3 |
| 6 | 2.148; 2.326 | 15.5 | 0.274 | 1.67 × 10−3 |
For complexes 5 and 6, the fits neglected the inclusion of two symmetrically inequivalent molecules in the asymmetric unit. Instead, the fits were performed to obtain the same parameters for both molecules in order to prevent over-parameterization of the fit. In the case of complex 6, a positive D-parameter was used in the fit, which was suggested by theoretical calculations for one of its symmetrically inequivalent molecules.
AC susceptibility measurements were performed on compounds 1–3 and 5–6 in the presence of a static magnetic field of 0.15 T (0.1 T for 1), because the tunneling of the magnetization was too fast to observe the out-of-phase signal of AC susceptibility at zero static magnetic field. Under such circumstances, all the measured complexes exhibited out-of-phase signals, indicating the presence of field-induced slow relaxation of magnetization. For the fitting of the AC in-phase and out-of-phase susceptibilities, the Havriliak–Negami model was used25
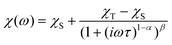 | (4) |
This model is also derived for two relaxation processes:
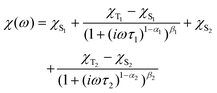 | (5) |
For complexes 1, 2, and 5, the inspection of the Argand (Cole–Cole) plot revealed the presence of two relaxation processes. Consequently, the experimental AC data were fitted by considering this observation. Subsequently, the temperature dependence of the relaxation times was analyzed using the following equation:
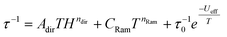 | (6) |
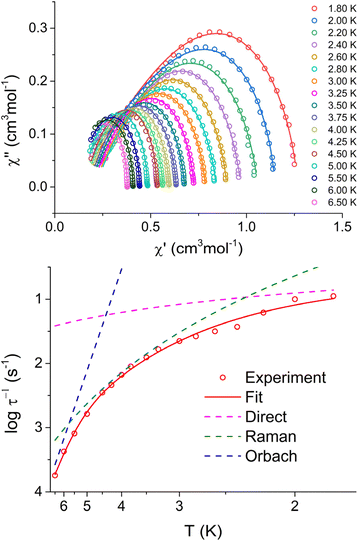 | ||
| Fig. 3 Argand (Cole–Cole) diagram of in-phase and out-of-phase AC susceptibility (upper panel), and fit of relaxation time for 1 with eqn (6) and parameters listed in Table 4. | ||
| Complex | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ0−1 (s−1) τ0−1 (s−1) |
U eff (K) | C (s−1 K−5) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Adir (s−1 K−1 T−4) Adir (s−1 K−1 T−4) |
|---|---|---|---|---|
| 1 | 8.45 ± 0.86 | 72.89 ± 12.59 | 0.14 ± 0.01 | 4.60 ± 0.05 |
| 2 | 6.26 ± 0.16 | 33.63 ± 1.64 | 0 | 4.58 ± 0.02 |
| 3 | 9.31 ± 0.17 | 50.53 ± 1.28 | 0 | 3.32 ± 0.03 |
| 5sa | 0 | 0 | 0.15 ± 0.01 | 3.81 ± 0.07 |
| 5f | 0 | 0 | 78.28 ± 12.24 | 5.89 ± 0.39 |
| Complex | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ0−1 (s−1) τ0−1 (s−1) |
U eff (K) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Adir (s−1 K−1 T−4) Adir (s−1 K−1 T−4) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B1 (s−1) B1 (s−1) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2 (s−1 T−2) B2 (s−1 T−2) |
|---|---|---|---|---|---|
| a As both processes were analyzed for 5, they are marked as slower (s) and faster (f). | |||||
| 1Zn | 5.79 ± 0.10 | 27.16 ± 0.75 | 3.52 ± 0.03 | 3.66 ± 0.06 | 6.11 ± 0.20 |
In the case of complexes 1 and 2, only a small range of temperatures (2.2 K–2.6 K for 1 and 2.8 K–3.0 K for 2) exhibited two clearly distinguishable processes that could be fitted. Consequently, we did not attempt to further analyze this minor process due to insufficient data. For complex 5, two processes were observable throughout the entire temperature range, allowing us to analyze both of them. However, the data for the faster process was not of sufficient quality to provide a convincing analysis. Two options were tested for its analysis, the combination of Orbach + direct processes, and the combination of Raman + direct processes. The first choice (Raman + direct model) was chosen, because it provided reasonable values of fitted parameters, whereas the second option resulted in unrealistic small values of Ueff.
In the case of compounds 1, 2, and 3, values of Ueff reasonably correlate with fitted D-parameters from the magnetic data. However, this correlation is not evident in the case of complex 5 for which we assume that the relaxation through the Raman process is too fast to observe Orbach relaxation.
To further study the relaxation of prepared compounds, complex 1 was selected as the most promising one and prepared again as a metal diluted sample with Zn(II), leading to complex 1Zn. Magnetic measurements (in the range of temperatures 1.8–4.5 K for B = 0.1 T, and range of magnetic fields 0–0.5 T for T = 2 K) show quite a different relaxation profile from non-diluted 1. We were able to fit the main relaxation process, but there seem to be other minor relaxation processes (some data seem to indicate even three relaxation channels) that we could not analyze in detail due to the insufficient resolution of these additional processes in 1Zn. Therefore, we have focused only on fitting the most prominent process with clearly visible maxima. The following equation was used for fitting temperature and field-dependent data simultaneously:
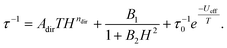 | (7) |
The coefficient for direct relaxation was fixed (ndir = 4) according to the literature as was done in eqn (6) for undiluted samples. However, the fitted Ueff for the diluted complex is significantly lower than Ueff of 1 (Table 4). The most striking difference between the relaxation in 1 and 1Zn is the signature of zero-field relaxation observed in AC data suggested by the decrease of the in-phase and increase of the out-of-phase component of AC susceptibility close to the upper measurement frequency limit at 2 K. The relaxation time at zero static magnetic field of 1Zn is 0.63 ms at 2 K, confirming thus that complex 1 can behave as zero-field SMM.
X-band EPR spectroscopy
The X-band EPR spectra of 1, 1Zn, 2, 3, 5, and 6 were measured using powdered samples; the temperature evolution of the EPR spectra (Fig. S17†) shows a decrease of the signal intensity and a significant line broadening with increasing temperature with the lack of spectral details above 30 K. The spin-Hamiltonian and an effective Seff = 1/2 Hamiltonian were used for the analysis of the experimental spectra obtained at 2.3 K. While spin Hamiltonian is often used to describe the two lowest Kramers doublets in Co(II), it is not possible to estimate the value of the D-parameter from X-band EPR for such large values as suggested from the analysis of magnetic data, only the sign of D and E/D ratio. On the other hand, for a large splitting between the ground and first excited Kramers doublet, highly anisotropic effective g-factors obtained from an effective Seff = 1/2 Hamiltonian reflect the influence of higher electronic states and the anisotropy of the crystal field. The spectra were analyzed within the EasySpin Toolbox,27 including hyperfine interaction (if resolved or necessary for the description) and an anisotropic convolutional broadening ΔB (full-width at half-height, which might reflect the unresolved hyperfine splitting). The splitting due to the hyperfine coupling parameter A was clearly identified only in the experimental EPR spectra of 1Zn and 2 (see Fig. 4, S17, and S18†).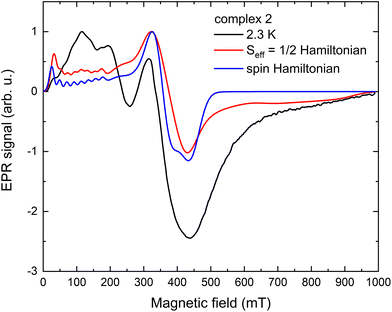 | ||
| Fig. 4 X-band EPR spectra of 2 obtained at 2.3 K, including simulated spectra, an effective Seff = 1/2 Hamiltonian and spin Hamiltonian models. | ||
First, the analysis using spin Hamiltonian formalism was performed, clearly showing D < 0 for 2, 3, and 5 (see Fig. S17†). For the simulation, the D-parameter was tentatively set to ±10 cm−1, and the obtained parameters are summarised in Table 5. Only one set of parameters was used to simulate the EPR spectra of 5, but one cannot exclude the presence of a second Co(II) site with similar parameters. Regarding the analysis of 6, the main component of the spectra at ∼200 mT is clearly compatible with D > 0. The experiment did not resolve a possible contribution of the predicted Co(II) site with a negative D-parameter (vide infra); it might be due to the reduced signal intensity or different line broadening. Interestingly, the E/D ratio for 2, 5, and 6 well agrees with the analysis of magnetic data, while for 3 it seems closer to the CASSCF/NEVPT2 prediction. We could not reasonably reproduce the experimental EPR data of 1 and 1Zn using the spin Hamiltonian approach, most probably due to a significant influence of hyperfine splitting; therefore, an effective Seff = 1/2 Hamiltonian was used.
| D | E/D | g x , gy, gz | ΔBx, ΔBy, ΔBz (mT) | A z (MHz) | |
|---|---|---|---|---|---|
| 2 | − | 0.295 | 2.12, 2.25, 2.35 | 50, 45, 55 | 700 |
| 3 | − | 0.056 | 2.15, 2.18, 2.38 | 40, 40, 180 | |
| 5 | − | 0.155 | 2.11, 2.16, 2.28 | 140, 130, 250 | |
| 6 | + | 0.180 | 2.40, 2.20, 2.00 | 70, 400, 120 |
The results of the analysis of the EPR spectra using an effective Seff = 1/2 Hamiltonian are summarised in Table 6. They can be understood in the frame of the model that includes spin–orbit coupling and a trigonal crystal field parameter δ to split the 4T1 orbital triplet state originating from the cubic crystal field.28 The obtained effective g-factors in the case of δ < 0 equivalent to easy-axis anisotropy yield highly anisotropic g′z ≫ g′x, g′y for |δ| > 1000 cm−1, similar to the ones obtained for 1, 1Zn, 2, 3, and 5. Unlike our previous studies, the two lower g-factor components do not reach the theoretical predictions of the quasi-degenerate perturbation theory.29 In the case of 6, a strong central resonance line was assigned to g′ = 3.39 characteristic for δ > 0 (easy-plane anisotropy). Interestingly, for 1 and 1Zn, slightly different g-factors and hyperfine interaction parameters were needed to simulate the two datasets (Fig. S17†). The full hyperfine splitting pattern was not resolved even in the diluted sample. Differences in obtained parameters might suggest that the Co(II) dilution also leads to minor changes in its electronic spectra.
| g′x, g′y, g′z | A′x, A′y, A′z (MHz) | ΔB1, ΔB2, ΔB3 (mT) | |
|---|---|---|---|
| 1 | 0.68, 2.40, 7.17 | 110, 580, 650 | 50, 45, 55 |
| 1Zn | 0.71, 2.50, 7.17 | 110, 720, 630 | 20, 22, 22 |
| 2 | 0.83, 1.77, 6.45 | 350, 290, 1800 | 40, 55, 65 |
| 3 | 0.82, 1.79, 6.15 | 400, 300, 650 | 20, 80, 100 |
| 5 | 0.74, 1.00, 6.10 | 120, 160, 180 | |
| 6 | —, 3.39, — |
Theoretical calculations
Theoretical CASSCF/NEVPT calculations were conducted to provide additional insights into the electronic structure of the prepared complexes and to potentially identify structural correlations and elucidate the magnetic behavior of the studied compounds. The calculations were performed using molecular structures derived from the X-ray data, and only the atomic positions of the hydrogen atoms were optimized using the DFT method.The energy levels and zero-field splitting (ZFS) parameters of the studied complexes were calculated using the complete active space self-consistent field method (CASSCF) with a 7-electron in 5-orbital active space (CAS(7,5)), which corresponds to the Co(II) 3d7 electron configuration. The treatment of dynamic electron correlation was performed using the N-electron valence perturbation theory (NEVPT2) method. The energy of the active metal d-orbitals was calculated using the AILFT (Ab Initio Ligand Field Theory) module in ORCA.
In the case of an ideal trigonal prismatic geometry, the d-orbitals are split into three energy levels. The lowest level corresponds to the dz2 orbital, followed by two degenerate orbitals, dxy and dx2–y2, and the highest level consists of two degenerate orbitals, dxz and dyz. Such ordering of orbitals is clearly visible for all complexes except for 3 and 6b, suggesting that most of the prepared complexes have crystal field splitting similar to the trigonal prism (Fig. 5).
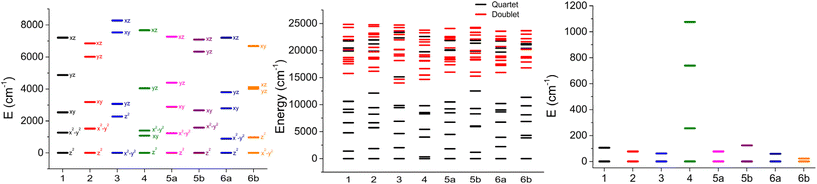 | ||
| Fig. 5 Ab initio energy of d-orbitals (left panel), ligand field terms (center panel), and ligand field multiplets (right panel) for studied complexes. | ||
In a free Co(II) ion, its ground atomic term is 4F, which is then followed by two excited states 4P and 2G. In ideal Oh symmetry, 4F is split into 4T1 + 4T2 + 4A1 ligand field terms, 4P into the 4T1 ligand field term, and 2G into 2T1 + 2T2 + 2A1 ligand field terms. If symmetry is reduced further to D3, each 4T term splits into 4E and 4A, therefore ground term 4F is split into 4E + 4E + 4A2 + 4A14A2, as is observed in the trigonal prism Tanabe Sugano diagram.30 After further reduction of symmetry by distortion from the ideal shape, 4E terms are split into 2 levels. Therefore, the 4F term splits into 7 non-degenerate levels (ligand field terms) in non-ideal symmetry. Thus, if the coordination polyhedron is close to the trigonal prism shape, it should be theoretically possible to see distribution similar to original terms – two close-lying levels from the ground 4E term, another two levels from the first excited 4E term, and finally three levels from 4A terms. It is possible to spot this energy level distribution on prepared complexes, mainly 1 and 4 (Fig. 5). Above ground term levels, 3 quartet levels are visible, which are originating in 4E and 4A2 from 4P first excited term, and also a large number of doublet states, which are from 2G and also higher doublet terms.
The spin–orbit interaction further splits the 4Γ ground term into two ligand field multiplets. Theoretically, the D3h symmetry is expected to yield large and negative D-parameters. Our calculations have confirmed this assumption, and all the relevant parameters for the studied compounds are listed in Table 7 and Table S8†
| D (cm−1) | E/D | g x | g y | g z | Δ (cm−1) | |
|---|---|---|---|---|---|---|
| a For 4, spin Hamiltonian parameters are not completely relevant, because it is not possible to fully describe its energy level splitting with spin Hamiltonian formalism. b The parameter Δ is defined as the energy difference of the two lowest Kramers doublets. | ||||||
| 1 | −52.54 | 0.074 | 2.216 | 2.096 | 2.760 | −103.41 |
| 2 | −38.40 | 0.050 | 2.128 | 2.188 | 2.602 | −77.07 |
| 3 | −30.70 | 0.054 | 2.153 | 2.177 | 2.505 | −61.67 |
| 4 | −127.73 | 0.022 | 1.849 | 2.000 | 3.377 | −255.66 |
| 5a | −37.62 | 0.129 | 2.113 | 2.250 | 2.623 | −77.1 |
| 5b | −61.87 | 0.014 | 2.099 | 2.147 | 2.823 | −123.78 |
| 6a | −27.43 | 0.232 | 2.120 | 2.294 | 2.532 | −59.13 |
| 6b | 10.83 | 0.075 | 2.159 | 2.290 | 2.305 | 21.83 |
Based on the results, it can be observed that among the studied complexes, 5b and 1 exhibit the most favorable characteristics due to their large negative D-parameter. However, it is worth noting that this is a common feature among almost all the complexes, except for the unusual case of 6b, which appears to have an easy-plane anisotropy with its positive D-parameter and significant rhombic components of the g-tensor. The ZFS and g-factor parameters for complex 4 are approximate because its low-lying excited states (Fig. 5) exclude the application of spin Hamiltonian formalism. Additionally, this is often associated with a larger anisotropy, as evidenced by the significant splitting of the crystal field multiplets (Fig. 5).
Moreover, we analyzed the variation of the calculated D-parameter within the series for complexes with a geometry close to the trigonal prism, namely, we took into account complexes 1, 2, 4, 5a, 5b, and 6a that all have the splitting of d-orbitals resembling the expected one for non-ideal D3h symmetry. In such a case, the largest contribution to the D-parameter stems from the electron excitation from ground state electronic configuration dz22dx2–y22dxy1dyz1dxz1 to the first excited state electronic configuration dz22dx2–y21dxy2dyz1dxz1, which corresponds to the electron transfer between dx2–y2 and dxy orbitals. Note that in the case of complex 4, the ordering of these two orbitals is interchanged. Anyway, these two orbitals have the same |ml| values and thus such excitation (dx2–y2 ↔ dxy) has a large contribution to the Dzz part of the D-tensor, which induces a large negative value of the D-parameter.31 The slight energy difference between these orbitals in 4 results in a configuration that closely resembles the orbitally degenerate 4E′ ground state term. Thus, it is not surprising that calculated anisotropy is huge and axial, with limited validity of spin Hamiltonian formalism (Table 7).
Indeed, the respective correlation was established between the D-parameter and the energy difference of two d-orbitals Δεd = |ε(dxy) − ε(dx2–y2)| as depicted in Fig. 6. Evidently, the magnetic anisotropy parameters are very sensitive to the changes in the shape of the coordination polyhedron reflected in d-orbitals splitting induced by the respective ligand field.
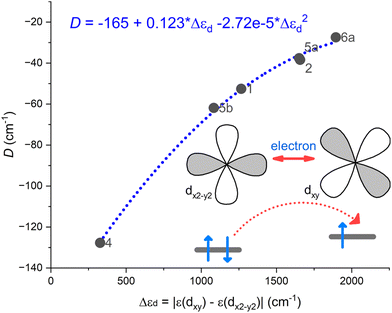 | ||
| Fig. 6 A correlation established between the D-parameter and the energy difference of two d-orbitals Δεd = |ε(dxy) − ε(dx2–y2)| using CASSCF/NEVPT2 results for complexes 1, 2, 4, 5a, 5b, and 6a. | ||
To gain a deeper understanding of magnetic behavior, we utilized the computational module SINGLE_ANISO, which enabled us to visualize the anisotropic energy barrier and calculate transition rates as magnetic moment matrix elements. These transition rates provide valuable insights into the probability of relaxation processes and help identify the pathways for magnetization reversal transitions. In the case of a Co(II) system with a spin of 3/2, there are only two Kramers doublets that could potentially be involved in the relaxation. Of particular importance is the transition rate associated with the ground state quantum tunneling of magnetization, as it determines whether the higher Kramers doublet will play a major role in the relaxation mechanism. The output of the SINGLE_ANISO module is depicted in Fig. 7 for 2, and in Fig. S19† for the rest of the complexes.
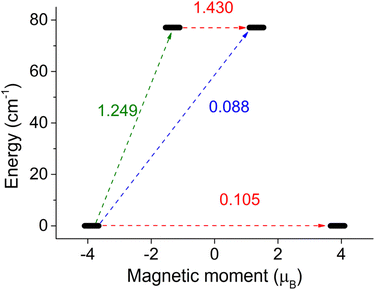 | ||
| Fig. 7 SINGLE_ANISO description of the magnetic moment matrix elements between Kramers doublets for complex 2. | ||
Thus, it is evident that complexes 4 and 5b exhibit the smallest tunneling probabilities in their ground state, which aligns with previous findings describing these complexes as highly anisotropic. These complexes demonstrate tunneling probabilities below 0.1, which render them potential zero-field SMMs. On the other hand, complexes 1, 2, and 3 exhibit tunneling probabilities above 0.1, suggesting that quantum tunneling of magnetization (QTM) is likely to play a significant role in their relaxation. However, it is possible to suppress QTM by applying a magnetic field, which transforms these compounds into field-induced single-molecule magnets (SMMs). Finally, complexes 5a and 6a show a high probability of QTM, while complex 6b is predicted to have typical easy-plane spin level splitting, indicating no potential for slow relaxation of magnetization.
To assess the preference of ligand scaffold in complexes 1–6 for trigonal geometry, we chose to perform additional DFT optimizations on their molecular structures in a vacuum with the help of the well-established B3LYP functional. This approach allows us to explore their optimal arrangement while excluding the influence of crystal packing effects. Indeed, the coordination polyhedra in the optimized geometries of all the complexes exhibit a tendency to adopt trigonal symmetry, characterized by relatively modest TP CSM values ranging between 1.6 and 3.7, and τ6 values found between 0.62 and 0.86 (Table S9†). Remarkably, this inclination persists despite the substantial relaxation observed in the calculated molecular geometries. Evidently, this relaxation is reflected in the elongation of metal–ligand bond lengths, particularly those with the etheric oxygen atoms (O2 and O3), which extend well beyond 2.35 Å (Table S9†). Thus, it seems that the herein utilized ligand motif is rigid enough to provide CoII complexes with a ligand field close to D3 symmetry and certainly deserves further exploration.
We opted to compare our findings also with the data available in CSD. Our search yielded eight crystal structures of complexes containing the Co, Ni and Zn metal centers coordinated with the 2-formylphenoxyacetic acid based Schiff base ligands. Notably, all these complexes incorporate either identical or their methoxy derivatives as those used in the synthesis of 1 and 3. Specifically, these ligands feature either ethylene (en) or propylene (pr) linkers in their structures.
Upon examining their coordination polyhedra, we observed that these complexes primarily adopt coordination environments that closely resemble either octahedral (Oh) or trigonal prismatic (TP) geometries – Table S10.† Complexes with en linkers tend to favor a trigonal prismatic coordination. Even when the lowest CSM values indicate an octahedral geometry, these values are notably high (>5; CSD codes: RUJNES,20 SIRMOX32), comparable to those calculated for a TP geometry. This suggests significant distortion from an idealized octahedral shape.
Conversely, complexes featuring pr linkers and adopting an Oh geometry (CSD codes: HOMFOF,17 QEBBIL,19 SIRMUD32) exhibit low CSM values (below 1.56), implying minimal deviation from an ideal octahedral shape. Given that a TP geometry would induce a doubly degenerate ground state for the Co(II) central atom—subject to strong Jahn–Teller distortion—it is reasonable to conclude that ligand rigidity, particularly in ligands with shorter en linkers, plays a key role in stabilizing this geometry.33
These observations are consistent with the crystal structures presented in this study. The most significant deviation from a TP geometry was observed in 3 featuring a pr linker (Table 2; CSM TP = 4.727, CSM Oh = 5.626). Interestingly, complex 4 featuring a 2-hydroxypropyl linker closely approximated an ideal TP geometry, even though its linker length is very similar to that of the pr linker. However, this complex also incorporates a hydroxyl group, which influences the overall structure not only through steric hindrance but also by enabling intermolecular hydrogen bonding.
These findings lead to a consideration of the somewhat unpredictable effects of crystal packing and non-covalent interactions. For example, the cobalt coordination environments in solvatomorph 3 and HOMFOF differ markedly. Solvatomorph 3 is a methanol solvate, while HOMFOF contains six co-crystallized water molecules per complex in its structure. Notably, complexes approximating an Oh geometry frequently feature extensive solvation in their second coordination spheres, as evidenced by the examples of HOMFOF, SIRMOX, and SIRMUD.
In summary, we may conclude that DFT calculations can predict the geometry of these complexes with reasonable accuracy – Fig. S20.† A general guideline could be that rigid linkers in Schiff base ligands based on 2-formylphenoxyacetic acid contribute to the stabilization of a TP geometry in Co(II) complexes. However, this conclusion must be interpreted with caution, as non-covalent interactions, and particularly the co-crystallization of solvent molecules, can significantly influence the geometry of complex molecules in the solid state.
Experimental
General methods
(2-Formylphenoxy)acetic acid was prepared by a previously published method.34 All the complexes were prepared by in situ reactions of (2-formylphenoxy)acetic acid, respective amine, and cobalt(II) acetate. The reagents were purchased from commercial sources. The CHNS elementary analysis was done using a Thermo Scientific Flash 2000 analyzer (Thermo Scientific, Waltham, MA, USA). The IR spectra were recorded using a Jasco FT/IR-4700 spectrometer (Jasco, Easton, MD, USA) using the ATR technique on a diamond plate in the spectral range of 400–4000 cm−1. The powder XRD patterns were measured using a Rigaku MiniFlex600 diffractometer (Rigaku, Austin, TX, USA) equipped with the Bragg–Brentano geometry and using Cu Kα radiation. EPR spectra were measured on powdered samples using a Bruker ELEXSYS II E500 spectrometer.Synthesis
Anal. calcd for C21H22N2O7Co (1): Mmol = 473.35 g mol−1 – C 53.29; H 4.68; N 5.92%. Found: C 53.08; H 5.08; N 5.88%.
FTIR (ATR, cm−1): 3262 (m), 3053 (w), 2940 (w), 1620 (s), 1494 (s), 1383 (s), 1341 (s), 1244 (s), 1132 (m), 1015 (s), 940 (m), 891 (m), 753 (s), 598 (w), 528 (w).
Anal. calcd for C26H24N2O7SCo (2): Mmol = 567.48 g mol−1 – C 55.03; H 3.91; N 4.94; S 5.65%. Found: C 54.51; H 4.15; N 4.94; S 5.07%.
FTIR (ATR, cm−1): 3033 (w), 2991 (w), 2911 (s), 2165 (w), 1981 (w), 1638 (s), 1485 (s), 1380 (s), 1282 (s), 1237 (s), 1161 (m), 939 (m), 822 (m), 751 (s), 614 (w), 518 (w).
Anal. calcd for C22H24N2O7Co(3): Mmol = 487.38 g mol−1 – C 54.22; H 4.55; N 5.75%. Found: C 53.45; H 4.87; N 5.70%.
FTIR (ATR, cm−1): 3725 (w), 3630 (w) 3276 (m), 3080(w), 2930 (m), 2820 (w), 2297 (w), 2165 (w), 1618 (s), 1493 (s), 1437 (s), 1247 (m), 1128 (m), 1018 (s), 937 (m), 887 (m), 817 (m), 759 (s), 708 (m), 521 (w), 454 (w), 362 (w).
Anal. calcd for C25H28N2O7Co(5): Mmol = 527.44 g mol−1 – C 56.93; H 4.97; N 5.31%. Found: C 56.57; H 4.79; N 5.11%.
FTIR (ATR, cm−1): 3411 (w), 3062 (w), 2929 (m), 2859 (m), 2166 (w), 1628 (s), 1497 (s), 1449 (s), 1381 (s), 1286 (s), 1128 (m), 1004 (s), 939 (m), 894 (m), 821 (m), 759 (s), 614 (w), 515 (w), 453 (w), 400 (w), 353 (w).
Anal. calcd for C32H26N2O7Co(6): Mmol = 593.51 g mol−1 – C 64.76; H 4.08; N 4.72%. Found: C 64.23; H 4.41; N 4.53%.
FTIR (ATR, cm−1): 3724 (m), 3598 (w), 3398 (m), 3031 (w), 2913 (w), 2360 (w), 2298 (w), 2113 (w), 1982 (w), 1619 (s), 1492 (s), 1376 (s), 1293 (s), 1131 (s), 1027 (s), 937 (m), 827 (m), 754 (s), 702 (s), 596 (m), 519 (w), 458 (w).
Anal. calcd for C21H22N2O7Co0.027Zn0.974 (1Zn): Mmol = 479.66 g mol−1 – C 52.59; H 4.20; N 5.84%. Found: C 52.35; H 4.49; N 5.72%.
Theoretical calculations
All theoretical calculations were performed with the use of the ORCA 5.0.2. program package.35 Initial molecular structures, obtained from X-ray data were treated by DFT hydrogen optimization, with the BP86 functional,36 with basis sets from Ahlrich def2 basis set,37 QZVP basis for Co, SVP for C and H atoms, and TZVP for other atoms, and def2/J auxiliary basis. Fully optimized molecular structures reported in Table S9† were obtained with the B3LYP38 hybrid DFT functional with the help of D4 dispersion correction,39 and the vibrational analyses confirmed proper convergence for complexes at local energy minimum as there were no imaginary frequencies.CASSCF calculations were done with the TZVPP basis for Co and the TZVP basis for all other atoms and with def2/J and def2-TZVP/C auxiliary basis sets. The dynamic electron correlation was treated by the RI-NEVPT2 method,40 and spin–orbit coupling by RI-SOMF(1×) approach.41 CASSCF was performed for 7 electrons in 5 d-orbitals (selected by ORCA keyword “actorbs dorbs”), which corresponds to the Co(II) valence electron configuration. The number of calculated roots responds to a maximal number of possible roots, 10 states with multiplicity MS = 4 and 40 roots with MS = 2. For further analysis of Kramers doublets, the SINGLE_ANISO module42 was used and set up to calculate with two Kramers doublets. CASSCF calculations were done with the “NoFrozenCore” keyword.
All calculations were performed with the help of the RIJCOSX approximation,43 with improved integral precision, enabled by “DEFGRID3” ORCA keyword, and strict convergence “TightSCF” settings.
For visualization, the software Avogadro44 and Mercury45 were used. Magnetic data were analyzed with the help of software PHI46 and RELACS.47 In some parts of the text, ChatGPT 348 was used for grammar and stylistic corrections.
Conclusions
A series of six novel complexes were synthesized and characterized using a combination of theoretical and experimental methods, focusing on magnetic properties. These complexes exhibit a notable inclination towards adopting a trigonal prismatic geometry, as confirmed by both experimental observations and theoretical DFT calculations. This inclination is influenced by the building blocks employed in constructing the Schiff base ligand. This observation suggests the potential for further adjustments and fine-tuning of the system to enhance its performance in potential applications. Overall, this system demonstrates remarkable versatility and holds substantial promise for further molecular optimization.The magnetic properties of the studied complexes were investigated using DC and AC magnetometry, as well as EPR spectroscopy. The obtained results were used to extract the parameters of the spin Hamiltonian. Four of the studied complexes were experimentally confirmed to have large and negative D-parameter, indicating axial anisotropy, while complex 6 showed a positive D-parameter. These experimental findings were also supported by theoretical calculations.
AC magnetic measurements revealed that the prepared complexes exhibit characteristics of field-induced single-molecule magnets, as evidenced by the significant quantum tunneling of magnetization in the ground state even without the presence of a magnetic field. In the presence of a magnetic field, all of the prepared complexes demonstrate a slow relaxation of magnetization, including also complex 6 which exhibits easy-plane magnetic anisotropy. The observed field induced magnetic relaxation of 6 can be attributed either to the Raman relaxation process or to the presence of complex 6a within the asymmetric unit which possesses the axial type magnetic anisotropy suitable for the Orbach relaxation process as suggested by theoretical calculations.
The most interesting results were obtained for zinc-diluted sample 1Zn, for which the slow relaxation of magnetization was observed already at zero static magnetic field. Interestingly, the dilution of the sample resulted in changes in spin Hamiltonian parameters as evidenced by EPR analysis and also in changes in the parameters describing the magnetization relaxation processes. Nevertheless, these results make the utilized ligand scaffold promising for future preparation of zero-field SMMs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the Palacký University Olomouc project IGA_PrF_2022_006. E. Č. was supported by the Slovak Research and Development Agency, contract no. APVV-22-0172 and APVV-18-0197. We also thank Mrs. Pavla Richterová for performing elemental analysis.References
- A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, Alternating Current Susceptibility, High Field Magnetization, and Millimeter Band EPR Evidence for a Ground S = 10 State in [Mn12O12(CH3COO)16(H2O)4]· 2CH3COOH·4H2O, J. Am. Chem. Soc., 1991, 113(15), 5873–5874, DOI:10.1021/ja00015a057.
- M. Feng and M. L. Tong, Single Ion Magnets from 3d to 5f: Developments and Strategies, Chem. – Eur. J., 2018, 24(30), 7574–7594, DOI:10.1002/chem.201705761.
- F. A. Cotton, Progress in Inorganic Chemistry (Vol.6), Interscience Publishers, 1964 Search PubMed.
- A. Sarkar, S. Dey and G. Rajaraman, Role of Coordination Number and Geometry in Controlling the Magnetic Anisotropy in FeII, CoII, and NiII Single–Ion Magnets, Chem. – Eur. J., 2020, 26(62), 14036–14058, DOI:10.1002/chem.202003211.
- (a) R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Slow Magnetic Relaxation in Octahedral Cobalt(II) Field-Induced Single-Ion Magnet with Positive Axial and Large Rhombic Anisotropy, Inorg. Chem., 2014, 53(12), 5896–5898, DOI:10.1021/IC500916U; (b) I. Nemec, R. Herchel, M. Kern, P. Neugebauer, J. van Slageren and Z. Trávníček, Magnetic Anisotropy and Field–Induced Slow Relaxation of Magnetization in Tetracoordinate CoII Compound [Co(CH3−im)2Cl2], Materials, 2017, 10(3), 249, DOI:10.3390/MA10030249.
- G. A. Craig and M. Murrie, 3d Single-Ion Magnets, Chem. Soc. Rev., 2015, 44(8), 2135–2147, 10.1039/C4CS00439F.
- (a) S. Alvarez, Polyhedra in (Inorganic) Chemistry, Dalton Trans., 2005,(13), 2209, 10.1039/b503582c; (b) S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape Maps and Polyhedral Interconversion Paths in Transition Metal Chemistry, Coord. Chem. Rev., 2005, 249(17–18 SPEC. ISS.), 1693–1708, DOI:10.1016/j.ccr.2005.03.031; (c) D. Casanova, P. Alemany, J. M. Bofill and S. Alvarez, Shape and Symmetry of Heptacoordinate Transition-Metal Complexes: Structural Trends, Chem. – Eur. J., 2003, 9(6), 1281–1295, DOI:10.1002/chem.200390145; (d) A. Ruiz-Martínez, D. Casanova and S. Alvarez, Polyhedral Structures with an Odd Number of Vertices: Nine-Atom Clusters and Supramolecular Architectures, J. Chem. Soc., Dalton Trans., 2008,(19), 2583–2591, 10.1039/b718821h.
- B. Yao, M. K. Singh, Y.-F. Deng, Y.-N. Wang, K. R. Dunbar and Y.-Z. Zhang, Trigonal Prismatic Cobalt(II) Single-Ion Magnets: Manipulating the Magnetic Relaxation Through Symmetry Control, Inorg. Chem., 2020, 59(12), 8505–8513, DOI:10.1021/acs.inorgchem.0c00950.
- V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M.-E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, A Trigonal Prismatic Mononuclear Cobalt(II) Complex Showing Single-Molecule Magnet Behavior, J. Am. Chem. Soc., 2015, 137(31), 9792–9795, DOI:10.1021/jacs.5b05739.
- A. A. Pavlov, D. Y. Aleshin, S. A. Savkina, A. S. Belov, N. N. Efimov, J. Nehrkorn, M. Ozerov, Y. Z. Voloshin, Y. V. Nelyubina and V. V. Novikov, A Trigonal Prismatic Cobalt(II) Complex as a Single Molecule Magnet with a Reduced Contribution from Quantum Tunneling, ChemPhysChem, 2019, 20(8), 1001–1005, DOI:10.1002/cphc.201900219.
- A. A. Pavlov, S. A. Savkina, A. S. Belov, Y. V. Nelyubina, N. N. Efimov, Y. Z. Voloshin and V. V. Novikov, Trigonal Prismatic Tris-Pyridineoximate Transition Metal Complexes: A Cobalt(II) Compound with High Magnetic Anisotropy, Inorg. Chem., 2017, 56(12), 6943–6951, DOI:10.1021/acs.inorgchem.7b00447.
- T. J. Ozumerzifon, I. Bhowmick, W. C. Spaller, A. K. Rappé and M. P. Shores, Toward Steric Control of Guest Binding Modality: A Cationic Co(II) Complex Exhibiting Cation Binding and Zero-Field Relaxation, Chem. Commun., 2017, 53(30), 4211–4214, 10.1039/C7CC01172E.
- B. Yao, Y.-F. Deng, T. Li, J. Xiong, B.-W. Wang, Z. Zheng and Y.-Z. Zhang, Construction and Magnetic Study of a Trigonal-Prismatic Cobalt(II) Single-Ion Magnet, Inorg. Chem., 2018, 57(22), 14047–14051, DOI:10.1021/acs.inorgchem.8b02692.
- Y. Y. Zhu, Y. Q. Zhang, T. T. Yin, C. Gao, B. W. Wang and S. Gao, A Family of CoIICoIII3 Single-Ion Magnets with Zero-Field Slow Magnetic Relaxation: Fine Tuning of Energy Barrier by Remote Substituent and Counter Cation, Inorg. Chem., 2015, 54(11), 5475–5486, DOI:10.1021/ACS.INORGCHEM.5B00526.
- I. Nemec, O. F. Fellner, B. Indruchová and R. Herchel, Trigonally Distorted Hexacoordinate Co(II) Single-Ion Magnets, Materials, 2022, 15(3), 1064, DOI:10.3390/ma15031064.
- J. Wang, D.-S. Zhu, K.-Z. Shao and L. Xu, {2,2′-[Ethane-1,2-Diylbis(Nitrilomethylidyne)]Diphenoxyacetato}zinc(II) Methanol Solvate, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62(8), m1884–m1886, DOI:10.1107/S1600536806026791.
- Z. L. Wang, D. S. Zhu and R. S. Wang, Crystal Structure of [N,N′-(Bis(2-Phenoxyacetic)Formylidene)Propane- 1,3-Diaminecobalt(II)] Hexahydrate, [Co(C21H20N2O6)] · 6H2O, Z. Kristallogr. – New Cryst. Struct., 2008, 223(3), 217–218, DOI:10.1524/NCRS.2008.0091.
- Z. L. Wang, D. S. Zhu and R. S. Wang, Crystal Structure of [N,N′-(Bis(2-Phenoxyacetic)Formylidene)Propane- 1,3-Diamine-Zinc(II)] - Water - Ethanol (1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25), [Zn(C21H 20N2O6)] · H2O · 0.25C2H6O, Z. Kristallogr. – New Cryst. Struct., 2008, 223(3), 215–216, DOI:10.1524/NCRS.2008.0090/DOWNLOADASSET/1267-2227.CFF.
0.25), [Zn(C21H 20N2O6)] · H2O · 0.25C2H6O, Z. Kristallogr. – New Cryst. Struct., 2008, 223(3), 215–216, DOI:10.1524/NCRS.2008.0090/DOWNLOADASSET/1267-2227.CFF. - L. Yan and C. L. Liu, Synthesis, Structure Characterization, Antibacterial Activity and Fluorescence Studies of a Ni(II) Compound with Schiff-Base Ligand, Jiegou Huaxue, 2017, 36(8), 1315–1320, DOI:10.14102/J.CNKI.0254-5861.2011-1522.
- L. Yan, W. Liu, M. J. Wang, Y. Xu and K. Z. Shi, Synthesis, Characterization, Oxygen Respiratory, Antibacterial Activity, and Photoluminescent Property Studies of One Novel Complex with Schiff-Base Ligand, Jiegou Huaxue, 2020, 39(5), 895–900, DOI:10.14102/J.CNKI.0254-5861.2011-2585.
- P. van der Sluis and A. L. Spek, BYPASS: An Effective Method for the Refinement of Crystal Structures Containing Disordered Solvent Regions, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46(3), 194–201, DOI:10.1107/S0108767389011189.
- J. Moncol, Geometry index for 6-coordinate compounds, Czech Chem. Soc. Symp. Ser., 2023, 21, 147 Search PubMed.
- (a) A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, Synthesis, Structure, and Spectroscopic Properties of Copper(II) Compounds Containing Nitrogen–sulphur Donor Ligands; the Crystal and Molecular Structure of Aqua[1,7-Bis(N-Methylbenzimidazol-2′-Yl)-2,6-Dithiaheptane]Copper(II) Perchlorate, J. Chem. Soc., Dalton Trans., 1984, 1349–1356, 10.1039/DT9840001349; (b) L. Yang, D. R. Powell and R. P. Houser, Structural Variation in Copper(I) Complexes with Pyridylmethylamide Ligands: Structural Analysis with a New Four-Coordinate Geometry Index, τ 4, Dalton Trans., 2007, 955–964, 10.1039/B617136B.
- O. Kahn, Molecular magnetism, VCH, 1993 Search PubMed.
- S. Havriliak and S. Negami, A Complex Plane Representation of Dielectric and Mechanical Relaxation Processes in Some Polymers, Polymer, 1967, 8(C), 161–210, DOI:10.1016/0032-3861(67)90021-3.
- R. Boča and C. Rajnák, Unexpected Behavior of Single Ion Magnets, Coord. Chem. Rev., 2021, 430, 213657, DOI:10.1016/j.ccr.2020.213657.
- S. Stoll and A. Schweiger, EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR, J. Magn. Reson., 2006, 178(1), 42–55, DOI:10.1016/j.jmr.2005.08.013.
- M. Suzuki, I. S. Suzuki and J. Walter, Magnetism and superconductivity in McTa2S2C (M=Fe, Co, Ni, and Cu), Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(22), 224407, DOI:10.1103/PhysRevB.71.224407.
- (a) N. Malinová, J. Juráková, B. Brachňaková, J. D. Midlíková, E. Čižmár, V. T. Santana, R. Herchel, M. Orlita, I. Mohelský, J. Moncol, P. Neugebauer and I. Šalitroš, Magnetization Slow Dynamics in Mononuclear Co(II) Field-Induced Single-Molecule Magnet, Cryst. Growth Des., 2023, 23(4), 2430–2441, DOI:10.1021/acs.cgd.2c01388; (b) J. Juráková, J. Dubnická Midlíková, J. Hrubý, A. Kliuikov, V. T. Santana, J. Pavlik, J. Moncoľ, E. Čižmár, M. Orlita, I. Mohelský, P. Neugebauer, D. Gentili, M. Cavallini and I. Šalitroš, Pentacoordinate Cobalt(II) Single Ion Magnets with Pendant Alkyl Chains: Shall We Go for Chloride or Bromide? Inorg, Chem. Front., 2022, 9(6), 1179–1194, 10.1039/D1QI01350E.
- R. A. D. Wentworth, Trigonal Prismatic vs. Octahedral Stereochemistry in Complexes Derived from Innocent Ligands, Coord. Chem. Rev., 1972, 9(1–2), 171–187, DOI:10.1016/S0010-8545(00)80227-1.
- D. Dai, H. Xiang and M.-H. Whangbo, Effects of Spin-Orbit Coupling on Magnetic Properties of Discrete and Extended Magnetic Systems, J. Comput. Chem., 2008, 29(13), 2187–2209, DOI:10.1002/jcc.21011.
- L. Yan and M.-J. Wang, Synthesis, Crystal Structures and Fluorescence of Two Zn(II) Complexes with Schiff Base Ligands, Chin. J. Inorg. Chem., 2013, 29(11), 2370–2374, DOI:10.3969/j.issn.1001-4861.2013.00.351.
- M. Gruden-Pavlović, M. Perić, M. Zlatar and P. García-Fernández, Theoretical Study of the Magnetic Anisotropy and Magnetic Tunnelling in Mononuclear Ni(Ii) Complexes with Potential Molecular Magnet Behavior, Chem. Sci., 2014, 5(4), 1453, 10.1039/c3sc52984c.
- H.-S. Lv, S.-Y. Huang, Y. Xu, X. Dai, J.-Y. Miao and B.-X. Zhao, A New Fluorescent PH Probe for Imaging Lysosomes in Living Cells, Bioorg. Med. Chem. Lett., 2014, 24(2), 535–538, DOI:10.1016/j.bmcl.2013.12.025.
- (a) F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78, DOI:10.1002/wcms.81; (b) F. Neese, Software Update: The ORCA Program System, Version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327, DOI:10.1002/wcms.1327; (c) F. Neese, Software Update: The ORCA Program System—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606, DOI:10.1002/wcms.1606.
- A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A, 1988, 38(6), 3098–3100, DOI:10.1103/PhysRevA.38.3098.
- (a) F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305, 10.1039/b508541a; (b) F. Weigend, A Fully Direct RI-HF Algorithm: Implementation, Optimised Auxiliary Basis Sets, Demonstration of Accuracy and Efficiency, Phys. Chem. Chem. Phys., 2002, 4(18), 4285–4291, 10.1039/b204199p.
- (a) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623–11627, DOI:10.1021/j100096a001; (b) A. D. Becke, Density–functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652, DOI:10.1063/1.464913; (c) C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789, DOI:10.1103/PhysRevB.37.785; (d) S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58(8), 1200–1211, DOI:10.1139/p80-159.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A Generally Applicable Atomic-Charge Dependent London Dispersion Correction, J. Chem. Phys., 2019, 150(15), 154122, DOI:10.1063/1.5090222.
- Y. Guo, K. Sivalingam, E. F. Valeev and F. Neese, Explicitly Correlated N-Electron Valence State Perturbation Theory (NEVPT2-F12), J. Chem. Phys., 2017, 147(6), 064110, DOI:10.1063/1.4996560.
- F. Neese, Efficient and Accurate Approximations to the Molecular Spin-Orbit Coupling Operator and Their Use in Molecular g-Tensor Calculations, J. Chem. Phys., 2005, 122(3), 034107, DOI:10.1063/1.1829047.
- (a) L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Interplay of Strongly Anisotropic Metal Ions in Magnetic Blocking of Complexes, Inorg. Chem., 2013, 52(11), 6328–6337, DOI:10.1021/ic302568x; (b) L. F. Chibotaru and L. Ungur, Ab Initio Calculation of Anisotropic Magnetic Properties of Complexes. I. Unique Definition of Pseudospin Hamiltonians and Their Derivation, J. Chem. Phys., 2012, 137(6), 064112, DOI:10.1063/1.4739763; (c) L. Ungur, W. Van Den Heuvel and L. F. Chibotaru, Ab Initio Investigation of the Non-Collinear Magnetic Structure and the Lowest Magnetic Excitations in Dysprosium Triangles, New J. Chem., 2009, 33(6), 1224–1230, 10.1039/b903126j; (d) L. F. Chibotaru, L. Ungur and A. Soncini, The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment, Angew. Chem., Int. Ed., 2008, 47(22), 4126–4129, DOI:10.1002/anie.200800283; (e) L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pilet and D. Luneau, Structure, Magnetism, and Theoretical Study of a Mixed-Valence Co II3CoIII4 Heptanuclear Wheel: Lack of SMM Behavior despite Negative Magnetic Anisotropy, J. Am. Chem. Soc., 2008, 130(37), 12445–12455, DOI:10.1021/ja8029416; (f) L. F. Chibotaru, L. Ungur and A. Soncini, The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment, Angew. Chem., Int. Ed., 2008, 47(22), 4126–4129, DOI:10.1002/anie.200800283.
- (a) A. K. Dutta, F. Neese and R. Izsák, Accelerating the Coupled-Cluster Singles and Doubles Method Using the Chain-of-Sphere Approximation, Mol. Phys., 2018, 116(11), 1428–1434, DOI:10.1080/00268976.2017.1416201; (b) R. Izsák and F. Neese, An Overlap Fitted Chain of Spheres Exchange Method, J. Chem. Phys., 2011, 135(14), 144105, DOI:10.1063/1.3646921; (c) F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, Approximate and Parallel Hartree–Fock and Hybrid DFT Calculations. A ‘Chain-of-Spheres’ Algorithm for the Hartree–Fock Exchange, Chem. Phys., 2009, 356(1–3), 98–109, DOI:10.1016/j.chemphys.2008.10.036.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform, J. Cheminf., 2012, 4(1), 17, DOI:10.1186/1758-2946-4-17.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, Mercury : Visualization and Analysis of Crystal Structures, J. Appl. Crystallogr., 2006, 39(3), 453–457, DOI:10.1107/S002188980600731X.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A Powerful New Program for the Analysis of Anisotropic Monomeric and Exchange-Coupled Polynuclear d - and f -Block Complexes, J. Comput. Chem., 2013, 34(13), 1164–1175, DOI:10.1002/jcc.23234.
- M. Liberka, M. Zychowicz, W. Zychowicz and S. Chorazy, Neutral Dicyanidoferrate(ii) Metalloligands for the Rational Design of Dysprosium(III) Single-Molecule Magnets, Chem. Commun., 2022, 58(44), 6381–6384, 10.1039/D2CC02238A.
- OpenAI ChatGPT (2023). https://chat.openai.com/. ChatGPT 12 May version Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2288033–2288038. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3qi01691a |
| This journal is © the Partner Organisations 2023 |
