Searching for silicate nonlinear optical materials by combining calculation and experiment†
Jingjing
Zhang
,
Ruqing
Wei
,
Daqing
Yang
 ,
Ying
Wang
,
Ying
Wang
 and
Bingbing
Zhang
and
Bingbing
Zhang
 *
*
College of Chemistry and Materials Science, Key Laboratory of Medicinal Chemistry and Molecular Diagnosis of the Ministry of Education, Key Laboratory of Analytical Science and Technology of Hebei Province, Hebei University, Baoding 071002, China. E-mail: zhangbb@hbu.edu.cn
First published on 10th July 2023
Abstract
Nonlinear optical (NLO) materials have been applied in many high technology fields. In this work, the first-principles high-throughput screening pipeline (FHSP) has been used for searching NLO materials from the silicate system. 253 silicates collected in the Inorganic Crystal Structural Database (ICSD) have been successfully calculated. Among them, 8 crystals were screened out after two-step evaluation. Finally, 3 compounds were selected for synthesis after comprehensive investigation. The SHG intensities tested using the Kurtz–Perry method of KNbSi2O7, PbZnSiO4, and Na2TiSiO5 are 6.7, 2.9, and 2.8 times that of KDP, respectively. Their UV absorption edges are 243 nm, 276 nm, and 280 nm, respectively. This work provides a full view of silicates as NLO materials and obtains excellent candidates for the next step of development.
Introduction
Nonlinear optical (NLO) crystals are key materials in laser systems owing to their functions of frequency conversion, generation of entangled photon pairs, attosecond pulse generation, etc.1–5 Frequency conversion through NLO materials is a convenient and efficient approach to generate laser beams in a wider range.6–8 β-BaB2O4 (BBO),9 LiB3O5 (LBO),10 AgGaSe2 (AGSe),11 AgGaS2 (AGS),12 and ZnGeP2 (ZGP)13 are commercialized materials that are widely used in the ultraviolet (UV) and mid-far-infrared (M-F-IR) wavelength range.14 With the development of laser technology, NLO crystals with optimal performance are urgently required.Silicates have wide transmission ranges from ultraviolet to mid-IR such as those of Bi12SiO20 (0.37–6.0 μm),15,16 Ba2TiOSi2O7 (0.3–5.0 μm),17 Y2SiO5 (0.2–5.0 μm), Gd2SiO5 (0.2–5.0 μm), and Lu2SiO5 (0.2–5.0 μm).18 In addition, the silicate system has potential to generate large SHG coefficients, such as those of Li2K4[(TiO)Si4O12] (4.5 × KDP) and Li2Rb4[(TiO)Si4O12] (4.5 × KDP),19 Ba2TiOSi2O7 (5.5 × KDP),17 PbSrSiO4 (5.8 × KDP),20 Sr2TiSi2O8 (8.0 × KDP),21 and Cs2B4SiO9 (4.6 × KDP).22 Besides, silicates usually exhibit large band gaps and correspondingly high laser-induced damage thresholds (LDTs), as well as stability in open air.
In this work, non-centrosymmetric silicate crystals collected in the Inorganic Crystal Structural Database (ICSD) are comprehensively investigated using the first-principles high-throughput screening pipeline for NLO materials (FHSP-NLO) and experimental confirmation.23 Finally, three silicates, KNbSi2O7, PbZnSiO4, and Na2TiSiO5, meeting strict multiple criteria are screened out and synthesized using a high-temperature solid-state method. They possess excellent properties, including large SHG coefficients, suitable birefringence, and short cut-off edges. In addition, statistical analysis based on the different classification of cations shows that d0-transition metal (TM) and lone pair (LP) cations play a vital role in birefringence and SHG response.
Methods
Synthesis
KNbSi2O7, PbZnSiO4, and Na2TiSiO5 were synthesized by the conventional solid-state method. The initial reagents including SiO2 (Aladdin, 99%), K2CO3 (Aladdin, 99.5%), Nb2O5 (Aladdin, 99.9%), PbO (Aladdin, 99.9%), ZnO (Aladdin, 99%), NaOH (Aladdin, 95%) and TiO2 (Aladdin, 99%) were used without further purification. Stoichiometric amounts of reactants were mixed thoroughly and heated in the corundum crucibles. The reactants, reaction time, and temperature for each compound are listed below.Powder XRD
KNbSi2O7, PbZnSiO4, and Na2TiSiO5 were tested using a Bruker-D8 X-ray diffractometer. The experimental XRD spectra of the title compounds were measured using X-rays with Cu Kα radiation (λ = 1.541 Å) at room temperature, and then compared with the theoretical XRD pattern.Infrared spectroscopy
The IR spectra of KNbSi2O7, PbZnSiO4, and Na2TiSiO5 were recorded on an IR Affinity-1 Fourier transform infrared spectrometer (Nicolet iS10, America) in the range of 400–3000 cm−1. The silicates were ground and mixed with KBr.UV-vis-NIR diffuse-reflectance spectra
The UV-vis-NIR diffuse reflectance spectra of KNbSi2O7, PbZnSiO4, and Na2TiSiO5 were measured at room temperature with a SolidSpec-3700DUV spectrophotometer. The wavelengths of the spectra were in the range 190–1100 nm.SHG measurement
Through the Kurtz-Perry method,24 the powder SHG (PSHG) responses of KNbSi2O7, PbZnSiO4, and Na2TiSiO5 were investigated using a Q-switch laser at 1064 nm. Silicates and KDP were ground and sieved into different particle size ranges: 20–38, 38–55, 55–88, 88–125, 125–160, 160–200, and 200–250 μm.Computational method
Theoretical calculations were performed using the CASTEP package based on density functional theory (DFT).25 The CASTEP package has been used to perform self-consistent field (SCF) and optical calculations with normal conserved pseudopotentials (NCPs). The exchange correlation energy is described by the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).26,27 The energy cutoff of the plane-wave base was set to 750 eV. The SCF calculations were performed with a convergence criterion of 1 × 10−6 eV per atom on total energy. Numerical integration of the Brillouin zone was performed using the Monkhorst–Pack scheme with k-point separation set as 0.07 Å−1 in the Brillouin zone for SCF and 0.04 Å−1 for optics calculation. The empty band was set to 3 times the valence band in the optical calculation to ensure the convergence of the refractive index and SHG coefficients.Results and discussion
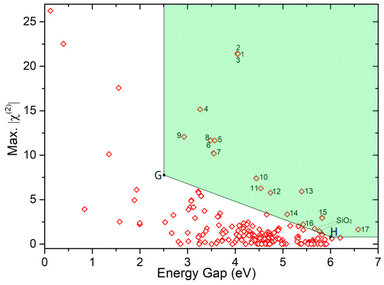
First, 279 noncentrosymmetric (NCS) structures containing Si and O elements were obtained from the Inorganic Crystal Structural Database (ICSD). Then, the band gap, birefringence, and second-order susceptibility χ(2) of these silicates were calculated using FHSP-NLO. Finally, 253 structures were calculated successfully. The chemical formula, ICSD collection-code, space group, band gap (Eg), birefringence (Δn), second-order susceptibility (χ(2)), and the maximum χ(2) tensor of all 253 structures are listed in the ESI.† As shown in Fig. 1, the maximum χ(2) tensors of these silicate crystals are plotted against their band gaps Eg-GGA. One can easily find that the maximum χ(2) obviously decreases with the increase in the band gap, which is consistent with the theory.As we mentioned above, silicates have a wide transmission window from UV to mid-IR and accordingly they can be used as NLO materials working in a wide wavelength range. In order to screen the materials that meet the conditions from UV to mid-IR, we adopted a new screening method. Firstly, we screened out the structures that meet the criteria for UV NLO crystals, i.e. Eg > 6.0 eV and χ(2) > 0.78 pm V−1. Secondly, the structures that meet the criteria for IR NLO crystals (Eg > 2.5 eV and χ(2) > 7.8 pm V−1) were screened out. Thirdly, we joined the two points (marked as G (2.5, 7.8) and H (6, 0.78)) with a straight line. Then, the materials located to the top-right of this line were screened out. Finally, 17 structures (located in the green shading of Fig. 1) with excellent properties were selected.
The calculated properties of the selected 17 structures are listed in Table 1. There are 14 materials because some structures are duplicated. It is well known that the PBE functional tends to underestimate the band gap. To obtain accurate predictions of the band gap, a HSE (hybrid screened exchange) functional was used to perform the band structure calculation.28–30 Both the values, Eg-GGA and Eg-HSE, are listed in Table 1. Based on our previous calculations, it is found that the sum-over-states method cannot precisely predict the birefringence of materials that contain Ti or Nb element, such as Ba2TiGe2O8.31 To improve the accuracy of the birefringence calculation, the density-functional perturbation theory (DFPT) method was adopted for the selected structures. Then we screened the materials with birefringence calculated using the DFPT method greater than 0.04. Subsequently, 8 materials were selected from the above 14 materials, namely PbZn(SiO4),32 Na2TiSiO5,33 Ca2(SiO4),34 KNbSi2O7,35 CaZr(Si2O7),36 BaY6(Si3B6O24)F2,37 Ba2Y3(SiO4)2F5,38 and CsSiB3O7.39 After investigation and experimental verification, we chose three materials for further synthesis and characterization, i.e. KNbSi2O7, PbZnSiO4, and Na2TiSiO5. For the other materials, Ca2(SiO4) shows a virtual vibration frequency that demonstrates the dynamic instability of its structure. Indeed, a centrosymmetric structure that is more reasonable than this NCS structure had been reported.40 Actually, when we synthesized this material the obtained phase was a centrosymmetric structure. The synthesis temperature of CaZr(Si2O7) is too high, and our laboratory conditions cannot meet the requirements. BaY6(Si3B6O24)F2 and Ba2Y3(SiO4)2F5 are multiphase structures, and the pure phase products are difficult to obtain. The NLO properties of CsSiB3O7 have been reported by Sun and Lin et al.,39 and its SHG effect is 0.8 times that of KDP.
| No. | Formula | ICSD | SG | E g-GGA (eV) | E g-HSE (eV) | Δn-SOS | Δn-DFPT | χ (2) (+scissor) (pm V−1) |
|---|---|---|---|---|---|---|---|---|
| 1 | Ba2TiSi2O8 | 201![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844 844 |
P4bm | 4.05 | 5.82 | 0.060 | 0.034 | χ 113 = χ223 = −3.064, χ333 = 10.654 |
| 2 | Ba2TiSi2O8 | 201![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 845 |
P4bm | 4.05 | 5.83 | 0.061 | 0.035 | χ 113 = χ223 = −3.039, χ333 = 10.631 |
| 3 | Ba2TiSi2O8 | 4451 | P4bm | 4.06 | 5.78 | 0.060 | 0.033 | χ 113 = χ223 = 3.077, χ333 = −10.835 |
| 4 | PbZn(SiO4) | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
Pna21 | 3.26 | 4.21 | 0.033 | 0.045 | χ 113 = −1.811, χ223 = −1.134, χ333 = 8.959 |
| 5 | Pb4Zn2[(SO4)(SiO4)(Si2O7)] | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 296 |
P21 | 3.57 | 4.69 | 0.011 | 0.009 | χ 112 = 0.513, χ123 = 1.074 |
| χ 222 = −7.164, χ233 = 0.766 | ||||||||
| 6 | Na2TiSiO5 | 259![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 048 |
Pmc21 | 3.48 | 5.30 | 0.026 | 0.046 | χ 113 = −1.787, χ223 = −0.194, χ333 = 5.454 |
| 7 | Ca2(SiO4) | 182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
P63mc | 3.55 | 4.07 | 0.078 | 0.057 | χ 113 = χ223 = −1.017, χ333 = −7.814 |
| 8 | Na2TiSiO5 | 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
Pmc21 | 3.48 | 5.24 | 0.026 | 0.049 | χ 113 = −1.872, χ223 = −0.178, χ333 = 5.582 |
| 9 | KNbSi2O7 | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111 111 |
P4bm | 2.93 | 5.32 | 0.125 | 0.071 | χ 113 = χ223 = 2.971, χ333 = −0.81 |
| 10 | Ba(Li2SiO4) | 260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 259 259 |
P63mc | 4.44 | 5.72 | 0 | 0.001 | χ 113 = χ223 = 0.085, χ333 = −4.369 |
| 11 | CaZr(Si2O7) | 203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 131 131 |
C2 | 4.5 | 6.59 | 0.062 | 0.052 | χ 112 = −0.799, χ123 = −1.858 |
| χ 222 = −1.075, χ233 = 1.562 | ||||||||
| 12 | BaBe(SiO4) | 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792 792 |
Cm | 4.74 | 5.66 | 0.020 | 0.019 | χ 111 = −0.027, χ113 = −2.262, χ122 = 1.720 |
| χ 133 = −2.666, χ223 = −0.980, χ333 = 3.162 | ||||||||
| 13 | BaY6(Si3B6O24)F2 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674 674 |
P3 | 5.40 | 6.73 | 0.033 | 0.045 | χ 111 = −χ122 = −0.494, χ113 = χ223 = 2.517 |
| χ 333 = −3.105 | ||||||||
| 14 | Ba2Y3(SiO4)2F5 | 290![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
Pba2 | 5.09 | 6.58 | 0.035 | 0.046 | χ 113 = −0.371, χ223 = 0.401, χ333 = −2.173 |
| 15 | BaBe2(Si2O7) | 263![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133 133 |
Pmn21 | 5.83 | 7.58 | 0.017 | 0.006 | χ 113 = 0.384, χ223 = 0.643, χ333 = −1.620 |
| 16 | CsSiB3O7 | 255![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
Pna21 | 5.43 | 7.27 | 0.044 | 0.056 | χ 113 = −0.400, χ223 = −0.962, χ333 = 1.150 |
| 17 | LiB(SiO4) | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 536 |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) |
6.58 | 8.51 | 0.004 | 0.008 | χ 113 = −0.158, χ123 = 0.705, χ223 = 0.158 |
The powder XRD spectra of KNbSi2O7, PbZnSiO4, and Na2TiSiO5 match well with the simulated ones derived from the CIF data (see Fig. 2(a)–(c)). The Rietveld refinement of PXRD data of pure polycrystalline samples was performed (Fig. S1–S3†). The details of the Rietveld refinement of PXRD are provided in Table S1.† It verified the phase purity of the title compounds. In addition, the existence of the fundamental building blocks (FBBs) was confirmed using the experimental IR spectra.41 The IR spectra of KNbSi2O7, PbZnSiO4, and Na2TiSiO5 samples in the wavenumber range 400–3000 cm−1 are shown in Fig. 2(d)–(f). According to calculated IR spectrum and the experimental results of IR spectroscopy, the IR absorption band near 900 cm−1 belongs to the stretching vibration of SiO4 tetrahedra. The IR absorption band from 600 to 400 cm−1 belongs to the bending vibration of SiO4 tetrahedra.42 In particular, in the compound KNbSi2O7, the IR spectral characteristic peak at 1234 cm−1 belongs to the Si–O–Si stretching vibration in the Si2O7 dimer. The peak at 706 cm−1 is due to the Nb–O stretching modes of NbO6 octahedra. The above infrared results can confirm the existence of fundamental building blocks (FBBs) in the title compounds.
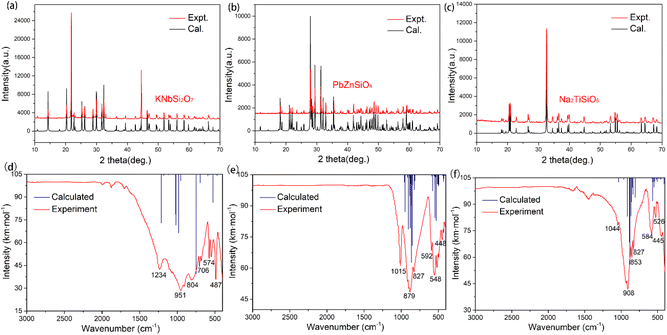 | ||
| Fig. 2 Powder XRD of (a) KNbSi2O7, (b) PbZnSiO4, and (c) Na2TiSiO5. Infrared spectroscopy of (d) KNbSi2O7, (e) PbZnSiO4, and (f) Na2TiSiO5. | ||
The crystal structure of KNbSi2O7 belongs to NCS polar space group P4bm with a = b = 8.7404(8) Å, c = 8.136(1) Å, α = β = γ = 90°, Z = 2. In its structure, NbO6 octahedrons are connected to each other by sharing para-position O atoms to form chains. The chains are further connected by a Si2O7 dimer to form a three-dimensional (3D) skeleton with channels where K atoms are located (see Fig. 3(a)). The UV-vis-NIR diffuse reflectance spectra of KNbSi2O7, PbZnSiO4, and Na2TiSiO5 are shown in Fig. 4(a)–(c). The spectra indicate that KNbSi2O7 has a short UV cutoff edge of 243 nm, and the absorption edge of KNbSi2O7 is 4.31 eV, which is larger than those of Li2K4[(TiO)Si4O12] and Li2Rb4[(TiO)Si4O12].19 KNbSi2O7 exhibits a strong SHG intensity of 6.7 times that of KDP under 1064 nm fundamental wave laser radiation (Fig. 4(d)). It is larger than those of recently reported silicate NLO materials, such as Li2K4[(TiO)Si4O12] (4.5 × KDP) and Li2Rb4[(TiO)Si4O12] (4.5 × KDP),19 Ba2TiOSi2O7 (5.5 × KDP),17 PbSrSiO4 (5.8 × KDP),20 and Sr2ZnSi2O7 (35 × α-SiO2).43 It is worth noting that Crosnier et al. has tested the SHG effect of KNbSi2O7 to get an estimate of the phase transition temperature and identify it as a good candidate for a nonlinear optical material.35 Subsequently, Gopalakrishnan et al. measured the SHG intensity of KNbSi2O7 as 200 times that of α-SiO2.44 The above results support our calculations and experimental results. Afterwards, single crystals of KNbSi2O7 with a size of 10 × 10 × 1 mm3 were fabricated.45 In order to investigate the structure–property relationship, the NLO-related properties were calculated by using DFT method. The partial density of states (PDOS) (see Fig. 5(a)) reveals that the valence band maximum (VBM) is predominantly contributed by the orbitals of O nonbonding 2p. The main components of the conduction band minimum (CBM) are the 4d orbitals of Nb. The SHG-weighted densities presented in Fig. 5(b) and (c) illustrate that the electron densities that mainly contribute to SHG arise from O and Nb atoms in occupied and unoccupied states, respectively.
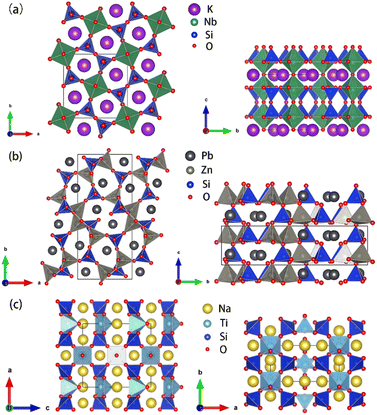 | ||
| Fig. 3 (a) Crystal structures of KNbSi2O7. (b) Crystal structures of PbZnSiO4. (c) Crystal structures of Na2TiSiO5. | ||
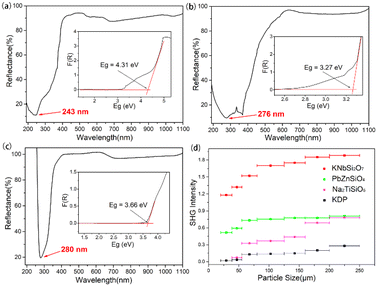 | ||
| Fig. 4 UV–vis–NIR diffuse reflectance spectra of (a) KNbSi2O7, (b) PbZnSiO4, and (c) Na2TiSiO5. (d) Phase-matching measurement results for KNbSi2O7, PbZnSiO4, Na2TiSiO5 and KDP. | ||
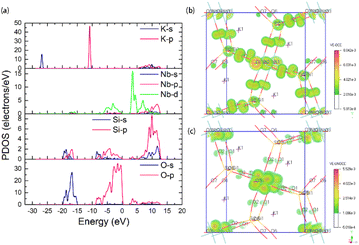 | ||
| Fig. 5 (a) Partial DOS of KNbSi2O7, SHG density in the (b) occupied state and (c) unoccupied state of KNbSi2O7. | ||
PbZnSiO4 compound crystallizes in a NCS polar space group Pna21 and the cell parameters are a = 8.2441(1) Å, b = 18.96259(20) Å, c = 5.06(1) Å, α = β = γ = 90°, Z = 8. In PbZnSiO4, the 3D network is constructed by the ZnO4 and the SiO4 tetrahedron through shared corner O atoms. The Pb atoms are located in the vacancies of the network (see Fig. 3(b)). PbZnSiO4 exhibits a UV cutoff edge of 276 nm and an absorption edge of 3.27 eV. The measured SHG response of PbZnSiO4 is about 2.9 times that of KDP (Fig. 4(d)). The PDOS (see Fig. S4(a)†) reveals that the VBM is predominantly contributed by the nonbonding 2p orbitals of O. The main components of the CBM are predominantly contributed by the Pb 6p orbitals. One can easily find that the 6s orbitals of Pb appear at the VBM. This is the obvious character of the stereochemical active lone pair (SCALP) effect of the Pb atom. The SHG weighted density shows that the main source of electron density is the O atom in the occupied state (see Fig. S5(a)†) and Pb atoms and O atoms in the unoccupied state (see Fig. S5(b)†).
Na2TiSiO5 crystallizes in the crystal system and belongs to the Pmc21 space group with the cell parameters a = 9.1222(5) Å, b = 4.8040(3) Å, c = 9.8293(5) Å, α = β = γ = 90°, Z = 4. The structural unit of Na2TiSiO5 is composed of two independent Na atoms, one Ti atom, two Si atoms and five O atoms. Each Si atom is coordinated by four O atoms to form a SiO4 tetrahedron. Each Ti atom is coordinated by five O atoms to form a TiO5 quadrangular pyramid. The compressed TiO5 square pyramid connects with the SiO4 group by sharing four bottom O atoms of TiO5 to form a 3D network. The top O atoms are only coordinated with the Ti atom. The sodium ions are located in the voids of the structure to balance the charge of this anionic framework (see Fig. 3(c)). The short UV cutoff edge of Na2TiSiO5 is determined to be about 280 nm and its absorption edge is 3.66 eV. Na2TiSiO5 shows a SHG intensity 2.8 times that of KDP at 1064 nm laser irradiation (Fig. 4(d)). The PDOS (see Fig. S4(b)†) reveals that the VBM is predominantly contributed by the 2p orbitals of O. The main components of the CBM are predominantly contributed by the 3d orbitals of Ti. The SHG weighted density shown in Fig. S6 (a) and (b)† indicates that O atoms, especially the top O atoms in the TiO5 quadrangular pyramid, are the main source in the occupied state. In the unoccupied state, the main sources are Ti atoms.
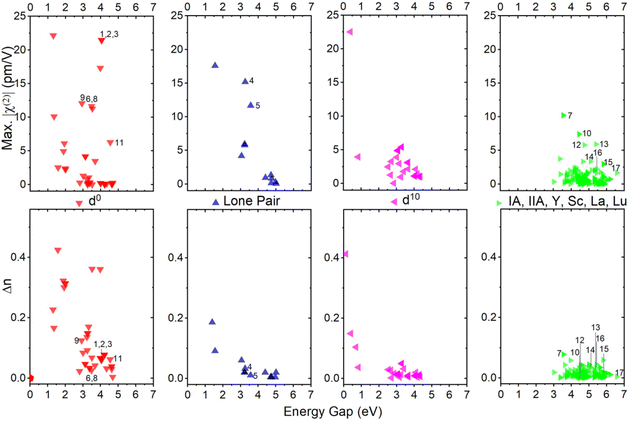
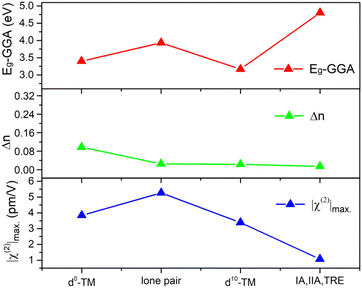
As shown in Table 1, one can find that cations have a significant effect on the band gap, birefringence, and SHG coefficients. In order to clarify the influence of different cation types on NLO-related properties, the 253 structures are divided into four categories according to their cation types: (1) d0-TM cations, (2) lone pair (LP) cations, (3) d10-TM cations, and (4) alkalis and alkaline-earth metal cations as well as trivalent rare-earth (TRE) cations. If the crystal contains more than one kind of cation, the crystal will be classified as the former categories as listed above. As show in Fig. 6, the χ(2) and Δn dispersions of different cations are obviously different. We count the average performance of 253 silicates according to the cation kinds. The duplicate structures are excluded from the statistic. As shown in Fig. 7, one can find that cation types have an obvious influence on the Eg, Δn, and χ(2) values. The d0-TM, LP, and d10-TM cations reduce the band gap compared to the alkali/alkaline-earth/TRE metal cations. In contrast, they can induce larger χ(2) and Δn. In particular, d0-TM and LP cations can significantly improve the χ(2) values.
Conclusion
In summary, an effective first-principles high-throughput screening pipeline (FHSP) based on the DFT method is adopted for the silicate system for searching for excellent NLO materials. Subsequently, 8 compounds are screened out by two-step calculation. Finally, KNbSi2O7, PbZnSiO4, and Na2TiSiO5 are selected and synthesized successfully using the conventional solid-state method. KNbSi2O7 exhibits a large birefringence of 0.071 and a strong phase-matchable SHG intensity of 6.7 times that of KDP. PbZnSiO4 and Na2TiSiO5 exhibit SHG intensities of 2.9 and 2.8 × KDP at 1064 nm, respectively. The UV absorption edges of the three title compounds are 243 nm, 276 nm, and 280 nm, respectively. Based on the statistic results of all the 253 silicates we calculated, one can find that the d0-TM and LP cations are significant sources for SHG and birefringence and are the preferred choice for exploring new NLO materials in silicates. This work provides a full view of silicates to search for new NLO materials and obtain excellent candidates for the next step of development.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant No. 52072109, 21975062, and 22101069) and the Science and Technology Project of Hebei Education Department (grant No. BJK2023029 and QN2023234).References
- M. Mutailipu, K. R. Poeppelmeier and S. L. Pan, Borates: A rich source for optical materials, Chem. Rev., 2021, 121, 1130–1202 CrossRef CAS PubMed.
- J. Chen, C. L. Hu, F. F. Mao, J. H. Feng and J. G. Mao, A facile route to nonlinear optical materials: three-site aliovalent substitution involving one cation and two anions, Angew. Chem., Int. Ed., 2019, 58, 2098–2102 CrossRef CAS PubMed.
- C. F. Wu, J. W. Feng and F. Yu, Na: A new lanthanum sodium borate with infinite 2D layer 2 and moderate birefringence, New J. Chem., 2021, 45, 13592–13598 RSC.
- W. Zhang, H. Yu, H. Wu and P. S. Halasyamani, Phase-matching in nonlinear optical compounds: A materials perspective, Chem. Mater., 2017, 29, 2655–2668 CrossRef CAS.
- L. Gao, J. Huang, S. Guo, Z. Yang and S. Pan, Structure–property survey and computer-assisted screening of mid-infrared nonlinear optical chalcohalides, Coord. Chem. Rev., 2020, 421, 213379 CrossRef CAS.
- F. Liang, L. Kang, Z. Lin, Y. Wu and C. Chen, Analysis and prediction of mid-IR nonlinear optical metal sulfides with diamond-like structures, Coord. Chem. Rev., 2017, 333, 57–70 CrossRef CAS.
- X. F. Lu, Z. H. Chen, X. R. Shi, Q. Jing and M. H. Lee, Two pyrophosphates with large birefringences and second-harmonic responses as ultraviolet nonlinear optical materials, Angew. Chem., Int. Ed., 2020, 59, 17648–17656 CrossRef CAS PubMed.
- L. Qi, Z. H. Chen, X. R. Shi, X. D. Zhang, Q. Jing, N. Li, Z. Q. Jiang, B. B. Zhang and M. H. Lee, A3BBi(P2O7)2 (A = Rb, Cs; B = Pb, Ba): Isovalent cation substitution to sustain large second-harmonic generation responses, Chem. Mater., 2020, 32, 8713–8723 CrossRef CAS.
- C. Chen, Y. Wang, Y. Xia, B. Wu, D. Tang, K. Wu, Z. Wenrong, L. Yu and L. Mei, New development of nonlinear optical crystals for the ultraviolet region with molecular engineering approach, J. Appl. Phys., 1995, 77, 2268–2272 CrossRef CAS.
- C. Chen, Y. Wu, A. Jiang, B. Wu, G. You, R. Li and S. Lin, New nonlinear-optical crystal: LiB3O5, J. Opt. Soc. Am. B, 1989, 6, 616–621 CrossRef CAS.
- R. L. Byer, M. M. Choy, R. L. Herbst, D. S. Chemla and R. S. Feigelson, Second harmonic generation and infrared mixing in AgGaSe2, Appl. Phys. Lett., 1974, 24, 65–68 CrossRef CAS.
- S. C. Abrahams and J. L. Bernstein, Crystal structure of piezoelectric nonlinear-optic AgGaS2, J. Chem. Phys., 1973, 59, 1625–1629 CrossRef CAS.
- G. D. Boyd, E. Buehler and F. G. Storz, Linear and nonlinear optical properties of ZnGeP2 and CdSe, Appl. Phys. Lett., 1971, 18, 301–304 CrossRef CAS.
- M. C. Ohmer and R. Pandey, Emergence of chalcopyrites as nonlinear optical materials, MRS Bull., 2013, 23, 16–22 CrossRef.
- V. M. Skorikov, I. S. Zakharov, V. V. Volkov and E. A. Spirin, Transmission and absorption spectra of Bi12GeO20, Bi12SiO20 and Bi12TiO20 single crystals, Inorg. Mater., 2002, 38, 172–178 CrossRef CAS.
- E. Burattini, G. Cappuccio, M. Grandolfo, S. M. Efendiev, P. Vecchia and M. C. Ferrari, Medium infrared transmittance and reflectance spectra of Bi12GeO20, Bi12SiO20, and Bi12TiO20 single crystals, J. Opt. Soc. Am. B, 1988, 5, 714–720 CrossRef CAS.
- W. Zhao, F. Zhang, J. Liu, B. Hao, S. Pan, F. Zhang and L. Liu, Flux crystal growth of Ba2TiOSi2O7, J. Cryst. Growth, 2015, 413, 46–50 CrossRef CAS.
- M. J. Weber and P. D. Webber, Handbook of optical materials, CRC Press LLC, 2003 Search PubMed.
- T. L. Chao, W. J. Chang, S. H. Wen, Y. Q. Lin, B. C. Chang and K. H. Lii, Titanosilicates with strong phase-matched second harmonic generation responses, J. Am. Chem. Soc., 2016, 138, 9061–9064 CrossRef CAS PubMed.
- S. Jiang, J. Zhou, H. Wu, H. Yu, Z. Hu, J. Wang and Y. Wu, PbSrSiO4: A new ultraviolet nonlinear optical material with a strong second harmonic generation response and moderate birefringence, Chem. Commun., 2020, 56, 7104–7107 RSC.
- J. Yuan, P. Fu, J. Wang, F. Guo, Z. Yang and Y. Wu, A new nonlinear optical material Sr2TiSi2O8, Prog. Cryst. Growth Charact. Mater., 2000, 40, 103–106 CrossRef CAS.
- H. Wu, H. Yu, S. Pan, Z. Huang, Z. Yang, X. Su and K. R. Poeppelmeier, Cs2B4SiO9: A deep-ultraviolet nonlinear optical crystal, Angew. Chem., Int. Ed., 2013, 52, 3406–3410 CrossRef CAS PubMed.
- B. Zhang, X. Zhang, J. Yu, Y. Wang, K. Wu and M.-H. Lee, First-principles high-throughput screening pipeline for nonlinear optical materials: Application to borates, Chem. Mater., 2020, 32, 6772–6779 CrossRef CAS.
- S. K. Kurtz and T. T. Perry, A powder technique for the evaluation of nonlinear optical materials, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- V. Milman, K. Refson, S. J. Clark, C. J. Pickard, J. R. Yates, S. P. Gao, P. J. Hasnip, M. I. J. Probert, A. Perlov and M. D. Segall, Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation, J. Mol. Struct.: THEOCHEM, 2010, 954, 22–35 CrossRef CAS.
- R. W. Godby, M. Schluter and L. J. Sham, Trends in self-energy operators and their corresponding exchange-correlation potentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 6497–6500 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd and G. E. Scuseria, Assessment and validation of a screened Coulomb hybrid density functional, J. Chem. Phys., 2004, 120, 7274–7280 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- Z. Lin, X. Jiang, L. Kang, P. Gong, S. Luo and M.-H. Lee, First-principles materials applications and design of nonlinear optical crystals, J. Phys. D: Appl. Phys., 2014, 47, 253001 CrossRef.
- J. Yu, B. Zhang, X. Zhang, Y. Wang, K. Wu and M. H. Lee, Finding optimal mid-infrared nonlinear optical materials in germanates by first-principles high-throughput screening and experimental verification, ACS Appl. Mater. Interfaces, 2020, 12, 45023–45035 CrossRef CAS PubMed.
- F. G. Layman, Unit cell and space group of larsenite, PbZnSiO4, Am. Mineral., 1957, 42, 910–912 CAS.
- G. Bayer, O. W. Florke and W. Hoffman, et al., Demixing and crystallization in glasses of the system Na2O–TiO2–SiO2, Glastech. Ber., 1966, 39, 242–261 CAS.
- W. Eysel and T. Hahn, Polymorphism and solid solution of Ca2GeO4 and Ca2SiO4, Z. Kristallogr. – Cryst. Mater., 1970, 131, 322–341 CrossRef CAS.
- M. P. Crosnier, D. Guyomard, A. Verbaere, Y. Piffard and M. Tournoux, K2(NbO)2Si4O12: A new material for non-linear optics, Ferroelectrics, 1991, 124, 61–66 CrossRef CAS.
- J. Gittins, E. L. Gasparrini and S. G. Fleet, The occurrence of vlasovite in Canada, Can. Mineral., 1973, 12, 211–214 Search PubMed.
- J. C. Shen and P. B. Moore, Crystal structure of cappelenite, Ba(Y, RE)6[Si3B6O24]F2: A silicoborate sheet structure, Am. Mineral., 1984, 69, 190–195 CAS.
- C. D. McMillen, M. Emirdag-Eanes, J. T. Stritzinger and J. W. Kolis, Hydrothermal synthesis of new rare earth silicate fluorides: A novel class of polar materials, J. Solid State Chem., 2012, 195, 155–160 CrossRef CAS.
- Z. Zhou, Y. Qiu, F. Liang, L. Palatinus, M. Poupon, T. Yang, R. Cong, Z. Lin and J. Sun, CsSiB3O7: A beryllium-free deep-ultraviolet nonlinear optical material discovered by the combination of electron diffraction and first-principles calculations, Chem. Mater., 2018, 30, 2203–2207 CrossRef CAS.
- W. Eysel and H. Theo, Polymorphism and solid solution of Ca2GeO4 and Ca2SiO4, Z. Kristallogr., 1970, 131, 322–341 CrossRef CAS.
- H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Expanding frontiers in materials chemistry and physics with multiple anions, Nat. Commun., 2018, 9, 772 CrossRef PubMed.
- R. A. Nyquist and R. O. Kagel, Infrared spectra of inorganic compounds (3800–45 cm−1), Academic Press, New York, 1971 Search PubMed.
- M. Mutailipu, Z. Li, M. Zhang, D. Hou, Z. Yang, B. Zhang, H. Wu and S. Pan, The mechanism of large second harmonic generation enhancement activated by Zn2+ substitution, Phys. Chem. Chem. Phys., 2016, 18, 32931–32936 RSC.
- J. Gopalakrishnan, K. Ramesha, K. Kasthuri Rangan and S. Pandey, In search of inorganic nonlinear optical materials for second harmonic generation, J. Solid State Chem., 1999, 148, 75–80 CrossRef CAS.
- A. Sahashi, T. Hoshina, H. Takeda and T. Tsurumi, Fabrication of ferroelectric silicate KNbSi2O7 single crystal, J. Ceram. Soc. Jpn., 2014, 122, 389–392 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Calculated band structure and partial density of states (PDOS) of PbZnSiO4 and Na2TiSiO5. The chemical formula, ICSD collection-code, space group, band gap (Eg), birefringence (Δn), second-order susceptibility (χ(2)), and maximum χ(2) tensor (|χ(2)|max) of all 253 silicates. Database is accessed by visiting https://nlo.hbu.cn. See DOI: https://doi.org/10.1039/d3qi00979c |
| This journal is © the Partner Organisations 2023 |