Raman analysis of inverse vulcanised polymers

Abstract

Inverse vulcanised polymers have received significant research attention on account of their easy, modifiable, and low-cost synthesis. These polymers are synthesized from the industrial by-product, elemental sulfur, resulting in a high sulfur content, which has many influences on the polymers’ behavior, and gives them their wide variety of valuable properties. Because of this, inverse vulcanised polymers have many industrially attractive applications, however the high sulfur content that is directly responsible for this, also makes the polymers challenging to analyse. As such, the structure of inverse vulcanised polymers is poorly understood, and although sensible theories exist, there is a lack of direct evidence derived from a complete understanding of the polymers’ bonding level structure. Presented here is the use of Raman spectroscopy to scrutinise better the nature of inverse vulcanised polymers. Several Raman spectroscopic techniques have been compared and contrasted, revealing what information can be obtained from Raman spectroscopy in regard to these otherwise difficult to analyse polymers. Method optimisations are presented alongside computational studies and model compounds, all of which benefit the understanding of spectral information obtained from Raman spectroscopy. It was found that Raman spectroscopy is capable of providing several key pieces of information about inverse vulcanised polymers in a rapid and non-destructive way. These include, calculating the amorphous elemental sulfur content, assessing the homogeneity, tracking reactions in progress, and most crucially, identifying the proportions of different sulfur ranks of the polymer, which has thus far eluded all other analytical techniques.

---

Introduction

In 2013, Chung et al., reported that the reaction of molten sulfur with an organic comonomer containing at least two carbon–carbon double bonds, afforded a new class of polymeric materials, which have become known as inverse vulcanised polymers.¹ These potentially low-cost polymers are hypothesized to be highly crosslinked networks of organic units interconnected with chains of sulfur atoms. Since the Pyun group's seminal discovery, the field has flourished, giving rise to many alternative organic comonomers, which in turn provides inverse vulcanised polymers with broad ranges of properties that make them applicable for different uses. Such applications that inverse vulcanised polymers may find include water purification, highly refractive infrared optical components, and cathode materials in lithium sulfur batteries, amongst many others.^2–9 Since sulfur is a by-product of the petroleum refining industry, currently available in vast excesses, and the organic comonomer can derived be from a renewable source, inverse vulcanised polymers can adhere to the principles of green chemistry.^10–13 Furthermore, these polymers have several properties that add to their attractiveness in the aforementioned applications, such as a combination of thermoplastic and thermoset properties, which can allow them to be shape persistent but also be recyclable and melt processable.¹ Some display self-healing capabilities, which is particularly exciting in the field of infrared optics as it means lenses can be repaired after damage, rather than being discarded and replaced.¹⁴

Inverse vulcanised polymers then, have a wide range of properties that are often tuneable with the synthetic conditions, or modifiable with post-processing techniques. These properties which make inverse vulcanised polymers so versatile and attractive, are often a direct result of their high weight percentage of sulfur, which is typically between 20 and 80%. For example, the melt processing and self-healing characteristics of these polymers are thought to be a direct result of the reversible cleavage of the sulfur–sulfur bonds in the bridges between the organic units.¹⁴ Another setting in which the high sulfur content of these polymers is important is in their infrared transparency, as the high proportion of highly polarisable sulfur atoms gives rise to the low infrared absorbance.^4,14 The sulfur bridges between the organic units in inverse vulcanised polymers are also thought to be of great importance in electrochemical applications of inverse vulcanised polymers, as it is thought that different chain lengths have different susceptibilities to the shuttle effect.^15–17

Clearly, the high weight percentage of sulfur in inverse vulcanised polymers is integral to their unique complement of characteristics. However, it is also the high weight percentage of sulfur that makes these materials hard to analyse. For the most part, analysis of inverse vulcanised polymers is limited to differential scanning calorimetry, to determine thermal characteristics and identify unreacted crystalline sulfur in the form of S₈; thermogravimetric analysis, to identify the decomposition profiles; and powder X-ray diffraction, again to identify unreacted crystalline sulfur as S₈. Other complementary techniques include dynamic mechanical analysis, thin layer chromatography, and mass spectrometry, though the latter can be difficult to perform and is destructive.

Several other commonplace analytical techniques encounter significant complications when applied to inverse vulcanised polymers. Combustion microanalysis suffers from a lack of suitable high sulfur content calibration standards and so only estimates the sulfur content. Gel permeation and size exclusion chromatographies are limited by solubility and give dubious results that rely on assuming that the analyte is of similar molecular nature to the comparison standard of known molecular weight; a difficult assumption for inverse vulcanised polymers due to their uniquely high sulfur content and many polysulfide bridges. Solution phase nuclear magnetic resonance spectroscopy is rarely applicable as these polymers are often insoluble. Infrared (IR) spectroscopy is easy to perform, but provides limited information, which is unsurprising given that some inverse vulcanised polymers may see application on account of their high IR transparency.^4,14 IR spectroscopy is typically only useful in identifying the consumption of carbon–carbon double bonds, indicating the extent of reaction, and proving or disproving that the organic comonomer skeleton has remained intact. Certainly, IR spectroscopy struggles to provide information on the sulfurous component of inverse vulcanised polymers on account of its selection rule that vibrations must cause a change in dipole moment, and the sulfur–sulfur bond has little to no dipole moment.¹⁸

None of the aforementioned techniques can readily provide information on what is arguably the most crucial component of inverse vulcanised polymers: their bridging sulfur chains. To this end, Raman spectroscopy may be an ideal solution as the sulfur–sulfur bond and the carbon–sulfur bond are both highly Raman active, but in the ten years since inverse vulcanisation's original publication, the technique has seen limited use. If Raman spectroscopy could successfully be performed, it could provide highly desirable information that is otherwise challenging to access, such as the average number of atoms in a sulfur chain and the distribution of chain lengths, which could then be related to the physical properties, providing a better understanding of why they arise.

To date, only a few publications have included a Raman study of their inverse vulcanised polymers.^12,19–21 Berk et al., used Raman spectroscopy as a complementary technique to IR spectroscopy, but derived little information from their spectra.²² Najmah et al., used Raman spectroscopy despite the fluorescence of their polymers to identify the presence of unreacted sulfur, which gave sufficiently strong signals to be seen through the fluorescent background. Unfortunately, that same fluorescent background precluded a detailed analysis of the polymer peaks.²³

It is hypothesized here that Raman spectroscopy may have the potential to be remarkably beneficial in the analysis of these otherwise hard to study polymers. Therefore this work focused upon the different Raman spectroscopic techniques (1064 nm Raman spectroscopy, Fourier transform Raman spectroscopy, Kerr-Gated Raman spectroscopy, and UV Raman spectroscopy) that can circumvent fluorescence, comparing and contrasting them in the study of inverse vulcanised polymers. Several different techniques have been implemented in the analysis of a representative panel of inverse vulcanised polymers, demonstrating what information can be obtained and how to obtain it. Presented here is an account of the advantages and method optimisations for Raman spectroscopic analysis of inverse vulcanised polymers. This work covers the study of the range and distribution of different sulfur ranks, which is defined as the number of sulfur atoms in a linear sulfur chain, something which cannot easily be measured directly by other techniques at this time, as alternatives such as mass spectrometry can be time consuming and troublesome.²⁴ Also included is an assessment of the homogeneity of the polymers, which can be difficult to scrutinise by other means. It has been found that there are several means by which the progress of reactions can be tracked, and a method has been developed to quantify how much sulfur within the polymer remains unreacted, which has the advantage that it does not rely on the sulfur being crystalline, a common drawback of other techniques. This study also presents step by step guides on how to perform these valuable analyses, as well as applying them in some proof-of-concept examples.

Experimental

To give an array of polymer samples to analyse by Raman spectroscopy, the inverse vulcanisation of several different organic crosslinkers was performed. These crosslinkers were chosen to be representatives of different broad families of crosslinker, to test the range of applicability of Raman spectroscopy, with their structures shown in Fig. 1. Divinylbenzene (DVB) was chosen as the main crosslinker of study, on account of its great success in forming well defined polymers with physical properties that make them straightforward to handle.^25,26 1,3-diisopropenylbenzene (DIB) was chosen on account of its structural similarity to DVB, therefore providing an interesting comparison.¹ Dicyclopentadiene (DCPD) was chosen on account of its rigid polycyclic structure, that is not aromatic like DVB or DIB. DCPD is particularly prevalent to be tested because it can be blended with other crosslinkers to modify the final polymer's properties, though such ternary systems were not studied here on account of their complexity in this flagship study.²⁷ Squalene was chosen as a representative of aliphatic crosslinkers with flexible backbones.^28,29 Although plant oils have flexible backbones and are receiving significant attention on account of their renewability, squalene is a more well defined chemical that was predicted to be easier to analyse by Raman spectroscopy, in contrast to plant oils which normally consist of a complex mixture of related compounds.³⁰

Fig. 1 Molecular structures of divinylbenzene (DVB), 1,3-diisopropenylbenzene (DIB), dicyclopentadiene (DCPD), and squalene, as well as a photograph of a thin piece of DVB50-S50, displaying visual evidence of laser damage in the form of black spots near its centre.

As such, inverse vulcanised polymers of DVB, DIB, DCPD, and squalene (Fig. 1) were synthesized and then analysed by differential scanning calorimetry (DSC) and combustion microanalysis, as tabulated in the ESI (Section IIA. Table S1†). The synthesis was performed by standard literature methods and is detailed in the ESI (Section IIA.†). Briefly, sulfur (3, 5 or 7 g) was heated, melted, and allowed to thermally equilibrate at a desired temperature before an amount of the desired crosslinker, sufficient to bring the scale of the reaction to 10 g, was added to the reaction vial. The reaction was monitored by dip testing: when an aliquot of the reaction was removed on the end of a spatula, and the aliquot remained a single phase upon cooling, (that is no sulfur precipitated) the reaction solution was poured into a preheated mould and left in the oven at 135 °C overnight to cure. From here on, the polymer samples will be referred to by the following abbreviation system: NAME α-Sβ, where α is the mass percentage of crosslinker in the feed ratio, and β is the mass percentage of crosslinker in the feed ratio. In the case of DCPD where two different synthesis temperatures were used, an extra notation, -Tγ, will be added to the end of the abbreviation, where γ is the synthesis temperature in °C. As an example, a polymer of DCPD and sulfur in a 70 : 30 feed ratio, synthesized at 160 °C would have the following abbreviation: DCPD70-S30-T160.

Results and discussion

Conventional Raman analysis

Initial attempts at conventional Raman analysis of inverse vulcanised polymers using either a 532 nm laser or a 785 nm laser, displayed fluorescent backgrounds that obscured all Raman signals (see the ESI, Section IV, Fig. S5 to S7†). A 785 nm laser is generally less prone to fluorescence than other shorter laser wavelengths because its lower photon energy is less likely to be sufficiently energetic to excite an electronic transition, which would then allow subsequent fluorescent transitions. In an attempt to enhance the Raman signals, surface enhanced Raman scattering was attempted (see the ESI Section IIIA, for the synthesis and characterisation of the gold nanoparticles†), but unfortunately was not successful (see the ESI, Section IV, Fig. S8†). This failure of conventional Raman techniques highlights the necessity for Raman spectroscopy variants that can avoid or significantly reduce fluorescent backgrounds. For the representative panel of polymers, fluorescence was observed in every case, suggesting that the absence of fluorescence, such as that in Berk's work is uncommon, and most inverse vulcanised polymers will require measures to avoid fluorescence.²² As a sidenote, as depicted in Fig. 1, it was found that inverse vulcanised polymers can be susceptible to laser damage during Raman spectroscopy, and this should be considered when analysing the polymers: the laser power should be kept as low as possible whilst still acquiring a good signal to noise ratio. In that regard, techniques that minimize the chances of laser damage due to long excitation wavelengths may be particularly valuable.

UV/Vis and fluorescence spectroscopy

It is likely that inverse vulcanisation literature has seen limited contributions from Raman spectroscopy due to the fluorescent background which occurs in several polymer samples. Therefore, it is prudent to characterise this fluorescence; the UV/Vis spectra, and subsequently, the fluorescence spectra of inverse vulcanised polymers were obtained and analysed. More information on this can be found in the ESI, section VII.† The main conclusions were: that leftover unreacted crosslinker was not responsible for the fluorescence; that the polymers in films no thicker than 100 μm, show little absorbance at long wavelengths, but show rapidly rising absorbance at shorter wavelengths that quickly reach the detector limit in the UV, making them potentially good UV blocking materials; that despite the very poor absorbance at 785 nm for DVB and DIB polymers, they still showed fluorescence in 785 nm Raman spectroscopy, so inverse vulcanised polymers are likely very efficient at fluorescence; that polymers of DVB and DIB show negligible absorbance at 1064 nm, suggesting this may be an effective probe wavelength for Raman, but polymers of DCPD and squalene may be still be difficult to analyse at this wavelength as they did show nominal absorbance; that the polymers fluoresced under a wide range of wavelengths, though less effectively at long wavelength, and were capable of emitting at wavelengths much longer than the excitation wavelength, and because of this Raman analysis should be carried out in the dark, to prevent stray ambient light from exciting fluorescence; and that the polymers degrade under UV light and so should be stored in the dark. This final conclusion was reinforced when trialling different Raman probe wavelengths, as with deep UV wavelengths (266 and 300 nm) rapid sample decomposition occurred, making them unviable for analysis of inverse vulcanised polymers.

1064 nm Raman analysis

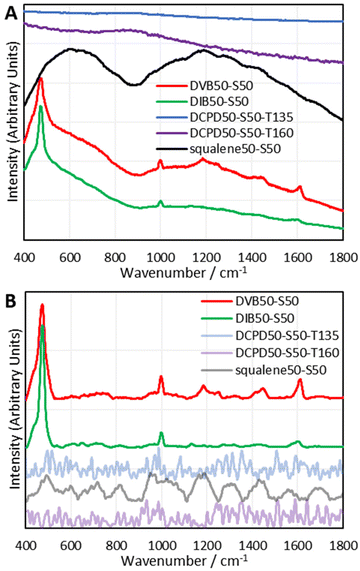
To establish which Raman spectroscopic techniques were deserving of more in-depth investigation, each was briefly trialled at providing Raman spectra on a panel of representative polymers. A full description of the results can be found in the ESI Section IX.†; in brief, 1064 nm Raman spectroscopy was found to be the most promising, with FT-Raman and Kerr-Gated Raman spectroscopy also being successful.^30,31 Kerr-Gated Raman spectroscopy is not a widespread technique, but was capable of providing Raman spectra of highly fluorescent samples, like DCPD and squalene polymers, that 1064 nm Raman spectroscopy and FT-Raman spectroscopy could not provide spectra of.³² Raman spectra could be obtained using a 488 nm excitation wavelength, but this had complications of laser damage and sometimes fluorescent backgrounds.

Since 1064 nm Raman spectroscopy is an accessible technique which showed significant promise, it became the subject of study for further detailed analysis. The instrument used for these initial studies was a handheld instrument (Snowy Range Instruments model CBex 1064), and with baseline correction it was capable of providing easily interpretable spectra that yielded plentiful information (Fig. 2). Trivially, for DVB and DIB polymers, aromatic modes appeared at 1000 and 1600 cm⁻¹. Broad peaks between 600 and 800 cm⁻¹ have been assigned to the carbon–sulfur bond. It was thought initially that the bands between 1025–1060 cm⁻¹ and 1050–1210 cm⁻¹ could be assigned to sulfonic acids and sulfones respectively, indicating some degree of oxidation, however a more detailed study which compared the spectra of polymers reacted under air and nitrogen atmospheres could not find evidence of this, (see the ESI, Section X.†) and the computational analyses performed later provided alternative, more convincing assignments. Most critically, the sulfur–sulfur bond region (425 cm⁻¹ 550 cm⁻¹) was obvious in the spectra of DVB and DIB, and displayed a peak consisting of several overlapping peaks, all contributing to the band. This alludes to different sulfur–sulfur vibrational modes, as it has been shown that the greater the sulfur rank, the progressively weaker the central sulfur–sulfur bond becomes.¹⁶ Band deconvolution was performed upon these compound peaks to elucidate the contributions of the smaller component peaks, however, the analysis of these deconvolutions is far more complex than simply assigning one contributor peak to one sulfur rank. There are numerous complications to take into account when analysing these bands, including, but not limited to: multiple bands arising from the same sulfur rank due to different vibrational modes; overlapping signals from dark sulfur; the accuracy of baseline correction across the sulfur–sulfur band; whether the Raman laser cut off limit is encroaching upon and attenuating the low Raman shift end of the sulfur–sulfur band; and the accuracy of the band deconvolution. Several measures were needed to gain a thorough understanding of this complex, yet information rich band, including the use of model compounds and computational chemistry. Note that dark sulfur is used here as a general term for non-crystalline elemental sulfur, which therefore cannot be detected by DSC or powder X-ray diffraction, as set out in a previous paper.³³ Dark sulfur refers to any allotrope, though it is assumed here that dark sulfur comprises primarily of cyclooctasulfur, the most thermodynamically favourable form of elemental sulfur.

Fig. 2 (A) raw and (B) baseline corrected spectra from a handheld 1064 nm Raman spectrometer (snowy range instruments model CBex 1064) for selected inverse vulcanised polymers. Offsets have been applied to the intensities.

Method optimisation for 1064 nm Raman spectroscopy

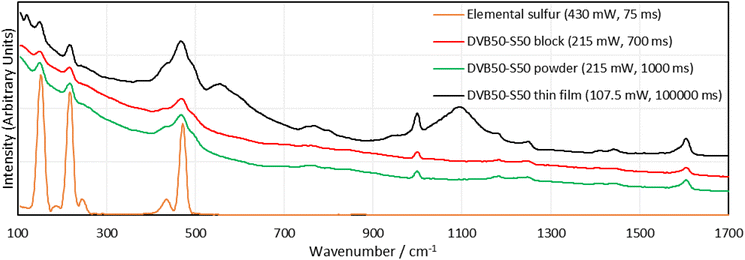
As mentioned previously, several complications were identified in the analysis of the Raman spectra of inverse vulcanised polymers. The most easily solved was the cut off limit of the spectrometer employed (400 cm⁻¹). An alternative 1064 nm Raman spectrometer, with a lower cut off limit of 100 cm⁻¹, and generally better performance was used for all following measurements (Metrohm i-Raman EX 1064). Lowering the cut off limit to the spectra had two other advantages. The first was that it allowed for more accurate baseline correction, since the baseline could be identified on either side of the signal, rather than on one side and not the other. The second relates to the presence of dark sulfur. Molecules of sulfur produce several Raman signals, and some of these peaks occur inside the sulfur–sulfur band region. Therefore, dark sulfur contributes to sulfur–sulfur band (Fig. 3). However, sulfur molecules also provide signals at much lower Raman shifts, below 400 cm⁻¹, and it was theorised that if one of these signals could be identified, free of any other overlapping signals, then by means of relative intensities, it could be used to calculate the contribution of dark sulfur to the compound peak in the sulfur–sulfur region. This would allow the other peaks to be certified as being related to the polymer, but would also allow the quantification of the proportional presence of dark sulfur within the polymer, which currently is only possible by extracting the sulfur into a solvent and then applying HPLC.³³

Fig. 3 Raman spectra of DVB polymers in different morphologies, as well as the Raman spectrum of elemental sulfur, taken on a Metrohm i-Raman EX 1064 nm Raman spectrometer, which has superior specifications to the previously used handheld spectrometer. Offsets have been applied to the intensities. Numbers with the units mW and ms are the laser powers and integration times used to obtain a particular spectrum, respectively.

With this more advanced instrument, method optimisation was performed to examine the effect of spectrometer settings, and sample morphology (solid block, powder, or thin film). With regards to spectrometer settings, the greater the laser power, the greater the signal intensity, but the greater the chances of laser damage. The chance of damage can be reduced by reducing the exposure time, which also makes the measurement more convenient, and minimises the contribution of dark noise. For samples such as DVB, their resistance to laser damage was high, and this permitted higher laser intensities (up to 322.5 mW, 75% laser power). Contrastingly, darker samples, like DCPD and squalene, were very vulnerable to laser damage, and showed significant decomposition at only 20% laser power (86 mW). This was expected, since these polymers were found to have nominal absorbance of 1064 nm light, and would therefore be more effective at heating up when irradiated at this wavelength. Additionally, DCPD and squalene polymers showed no interpretable signals at any laser power or integration time, regardless of whether the sample was a powder, block, or thin film. It seems that DCPD and squalene polymers are highly effective at fluorescence at 1064 nm excitation wavelengths, since even at 1% laser power, the detection system could still be swamped with signal unless the integration time was short.

In terms of morphology, blocks of DVB polymers gave the worst, though still easily interpretable signals. Powders gave better signals and thin films of polymer between glass slides gave the best signal intensity in comparison to the background, though concerns can be raised regarding some peaks. New peaks appeared in the spectra of the thin films that were not present in the spectra of either the blocks or the powders. The powders and the blocks are the polymer in its pure form, whereas the thin film has the polymer between two glass slides. It is possible that the glass has some contribution to the spectrum, and the new peaks are the result. As a final note, it was difficult to focus the Raman laser on the thin film sample, and when it was focused, much longer integration times, as well as high laser intensities were required to obtain a signal, which could be explained as a result of the thin sample providing less Raman active material in the laser irradiation zone. Surprisingly, there was no sign of laser damage, which might be explained by the glass slides acting as a heat sink.

With the method optimisation complete, Raman spectra of the panel of representative polymers were required, ready for in depth analysis of the spectral bands. Rather than acquire the spectra of the initial batch of polymers which had been subject to aging, it was decided to synthesize a fresh batch of polymers. Observing Table S1 (ESI, Section IIA.†), it is clear that the initial batch of polymers suffered from crosslinker evaporation during their syntheses which explains why their sulfur percentages were much higher than expected. This also yielded polymers that were much more similar than desired. For example, DVB30-S70 actually contained 76.9% sulfur, and DVB50-S50 actually contained 71.4% sulfur, meaning these two polymers were quite similar by their compositions, and as a result the differences in their Raman spectra may have been less pronounced. Therefore, the method to synthesize this second batch of polymers was modified, to minimise crosslinker evaporation. The method was the same as the general method in the ESI Section IIA.†, except once the crosslinker was added to the reaction vial, a septum with an air balloon affixed was added to the reaction vial. In this new method, the polymer was not poured into a mould, nor cured in the oven, and instead was cured on the hotplate with the balloon affixed. Unfortunately, squalene was not amenable to this method of synthesis as the reaction auto-accelerated during the curing step despite all method optimisations. The squalene polymers were reacted with the balloon present, but were cured without it. Squalene polymers were also cured at the higher temperature of 145 °C, as this gave polymers with more convenient physical properties. The polymers were then analysed by DSC and CHNS combustion microanalysis, as shown in Table 1, which indicates that the septum had the desired effect, as the actual values for sulfur, mirror more closely their expected values. See the ESI Section XI.†, for DSC traces. This second batch of polymers was analysed by 1064 nm Raman spectroscopy in the form of blocks as this was convenient and minimised the chances of sample contamination, as there was no post-synthetic processing required (Fig. 4).

Fig. 4 The 1064 nm Raman spectra, obtained using the optimised method on the Metrohm i-Raman EX instrument, of inverse vulcanised polymers of (A) DVB and DIB, (B) DCPD and Squalene, synthesized under better controlled conditions than the first batch of inverse vulcanised polymers. Offsets have been applied to the intensities. Numbers with the units mW and ms are the laser powers and integration times used to obtain a particular spectrum, respectively.

Table 1 Synthetic conditions and analyses of the second batch of inverse vulcanised polymers

Chemical structure
Synthesis at	135 °C			135 °C			135 °C			160 °C			170 °C
Feed ratio crosslinker (%)	30	50	70	30	50	70	30	50	70	30	50	30	30	50	70
Sulfur (%)	70	50	30	70	50	30	70	50	30	70	50	70	70	50	30
Microanalysis C expected (%)	27.7	46.1	64.6	27.3	45.5	63.8	27.3	45.4	63.6	27.3	45.4	63.6	26.3	43.9	64.4
C actual (%)	25.4	43.6	60.7	24.9	43.1	60.4	23.3	43.2	59.2	25.7	42.8	59.7	26.5	43.6	60.9
H expected (%)	2.3	3.9	5.4	2.7	4.5	6.2	2.8	4.6	6.4	2.8	4.6	6.4	3.7	6.1	8.6
H actual (%)	2.6	4.0	5.8	2.5	4.2	5.7	2.4	4.3	5.7	2.7	4.3	5.8	3.7	5.9	8.2
S expected (%)	70.0	50.0	30.0	70.0	50.0	30.0	70.0	50.0	30.0	70.0	50.0	30.0	70.0	50.0	30.0
S actual (%)	72.5	52.5	32.9	73.4	52.5	32.3	74.2	52.1	33.7	72.0	52.8	33.4	70.1	50.1	29.8
Glass transition temperature from DSC/°C	53.0	99.0	84.1	11.3	42.2	47.0	76.7	101.3	19.0	66.0	75.9	17.6	14.8	30.6	16.1

---

Once again, DVB and DIB polymers gave clear sulfur–sulfur bands and aromatic bands. The intensity and shape of the sulfur–sulfur band in the DVB and DIB polymers varied with sulfur loading, which implies that this band is indeed dependent upon the quantity of sulfur in the polymer. Also, elemental sulfur signals can be observed in the Raman spectra of DVB and DIB polymers, indicating that dark sulfur is present in these polymers. This interesting result suggests many polymers that have previously been assumed to contain no elemental sulfur, may in fact contain undetected elemental sulfur. This further advocates the use of Raman spectroscopy in the field of inverse vulcanisation, as it is a rapid and convenient technique to identify the presence of elemental sulfur in inverse vulcanised polymers, that works where other techniques fail. Further points to note regarding the spectra of DVB and DIB polymers include: that the elemental sulfur signals become weaker when less sulfur is used in the synthesis; that the aromatic signals become more intense in comparison to the sulfur–sulfur band when less sulfur is used in the synthesis; and that the polymers require higher laser powers or integration times in their measurements when less sulfur is used in the synthesis.

Unfortunately, as seen in Fig. 4, polymers of DCPD and squalene failed to produce 1064 nm Raman spectra through their fluorescent baselines. As an attempt to remedy this, 1064 nm surface enhanced Raman spectroscopy (SERS) was performed upon the polymers of DCPD, squalene, and DVB (see the ESI, Section IIIB., for the synthesis and characterisation of the gold nanorods, and the 1064 nm SERS spectra†). Unfortunately, SERS could not provide a signal for polymers of DCPD and squalene through their fluorescent backgrounds, however, polymers of DVB did show a signal enhancement with SERS.

Understanding the Sulfur–Sulfur band

With the aforementioned issues resolved, an attempt to understand the meaning of the different contributor peaks in the sulfur- sulfur band, could be made. To assist in the understanding of this complex spectral region, computational chemistry was employed. See the ESI Section XIII.,† for the optimisation of the calculation method, and level of theory, as well as how the experimental spectra of real molecules were used to parameterise and improve the accuracy of the calculated spectra.³⁴

With an appropriate method for calculating Raman spectra found, the spectra for the polymers could then be calculated. Modelling an entire inverse vulcanised polymer network with DFT is far too computationally expensive to be viable with the current level of technology, therefore a simplified model of the polymer system was needed. The focus of this system was divinylbenzene, because it provided the clearest signals in 1064 nm Raman spectroscopy. To simulate a polymer network, two faux divinylbenzene units were connected by sulfur chains as shown in Table 2. This model system left several possible ways to connect up the faux divinylbenzene units: each included two chiral carbons, and cis or trans type regiochemistry, as shown in Table 2. Thus, every combination of RS or SS stereochemistry with cis or trans regiochemistry had its Raman spectrum predicted, in order to understand the effects of varying these factors upon the calculated spectrum. Additionally, conformer searches provided the five lowest energy conformations of the RR trans models, allowing determination of how conformation affects the calculated spectrum. Sulfur rank 1 was not modelled because it has no sulfur–sulfur bonds.

Table 2 Structures of the models for computational chemistry, and the obtained bond lengths. Blue numbers are for the RS isomers, red numbers are for the RR isomers. All bond length data is for the lowest energy conformer. The calculation for rank 6 Trans RS failed due to insufficient memory on the supercomputer

Sulfur rank	Cis	Trans
2
3
4
5
6

---

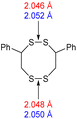
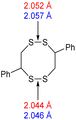
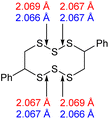
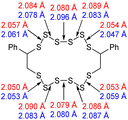
The computational chemistry quantified sulfur–sulfur bond lengths. It is shown in the literature that the bonds in a sulfur chain become longer and weaker towards the centre of the chain, with this effect increasingly obvious for greater sulfur rank chains.²¹ The data in Table 2 agree with this trend with the exception of the central bond in rank 6 which is shorter than the bonds adjacent to it. In addition, though rank 4 shows the longest sulfur–sulfur bond (the weakest single bond length), rank 5 and rank 6 give weaker overall sulfur chains. This is because, even though rank 5 and rank 6 do not have any single bond that is weaker than the weakest bond of rank 4, they possess a greater population of reasonably weak bonds, and with this greater population, it is statistically more likely to break one of them, which leads to a weaker chain overall.

The computational experiments yielded calculated Raman spectra for each model, as shown in Fig. 5. As mentioned previously, Raman spectra were predicted for each combination of RR and RS stereochemistry, with cis and trans regiochemistry, for every sulfur rank from 2 to 6. To simplify the presentation of the results, only the rank 2 and rank 6 data will be displayed here. All data is available in Section XIV. of the ESI.† For the purposes of studying the sulfur rank of inverse vulcanised polymers, the focus in analysing Fig. 5 will be the sulfur–sulfur region which is normally taken to be between 425 cm⁻¹ to 550 cm⁻¹, though with the computational modes having been calculated, the vibrational motion of each mode can be visualised, to determine which peaks correspond to a sulfur–sulfur mode, irrespective of whether the peak occurs within the usual sulfur–sulfur region. See the ESI, Table S3 in Section XIV.†, for the analysis of sulfur bond vibrations to each vibrational mode.

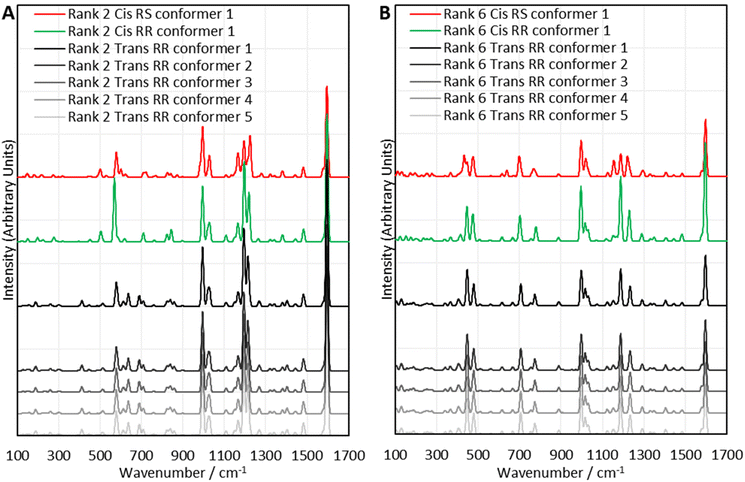Fig. 5 Comparisons between selected sets of calculated Raman spectra for the polymer model compounds of (A) rank 2, and (B) rank 6. Offsets have been applied to the intensities.

Encouragingly, Fig. 5 reveals that in many cases, varying the stereochemistry and regiochemistry does not have a large effect on the spectra though the differences are most pronounced in the sulfur–sulfur region, which suggests that the way in which the atoms are connected up in the polymers has some effect on the sulfur chains, whilst having minimal effect on the organic units. Although it is difficult to suggest reasons why the stereochemistry and regiochemistry affect the spectra, it appears the effects of these structural variations are less pronounced at longer sulfur ranks. Encouragingly, Fig. 5 suggests that the conformation of the sulfur chains has no significant effect on the spectra. It can be seen in all cases that the spectra of the five lowest energy conformers of each polymer model analysed, are nearly identical, and this was stringently true for every sulfur rank calculated. Close analysis of the raw data shows that there are very minor differences in the calculated spectral data of each conformer, but these differences have far too small an effect to cause any tangible difference to the analysis, which is encouraging because it suggests that when analysing the sulfur rank, the conformation can be ignored, vastly simplifying the analysis. The fact that inverse vulcanisation reactions are typically cured in order to provide time and energy for the polymers to reach their thermodynamic minimum, provides more confidence that analysis of the lowest energy conformations is the most appropriate method as, during curing, the polymer chains will likely relax toward these minimum energy conformations in the majority of the population.

The most important feature of the calculated data is that it can be carried forward to be used in the analysis of real polymers, in an attempt to determine their sulfur rank. In this application, it will be appropriate to average together RR and RS data, and separately cis and trans data, because statistically there should be a 50 : 50 distribution of both stereochemistries, and both regiochemistries within the polymer. Parameterisation was attempted and applied as detailed in Section XV. of the ESI† using the experimental spectra of real molecules. Using these parameterisation functions for Raman shifts and intensities, the polymer model data were parameterised and then averaged together as appropriate to give one spectrum for each sulfur rank. These spectra were then used to analyse the sulfur–sulfur band of the experimental Raman spectra of sulfur polymers. Additionally, the computational work also elucidated the assignments of other Raman shift regions. The region of 580 cm⁻¹ to 900 cm⁻¹ is assigned to carbon–sulfur vibrations with contributions from the aromatic modes. What was initially hypothesized to be sulfur–oxygen modes between 1100 cm⁻¹ and 1300 cm⁻¹ is more likely to be carbon–hydrogen vibrations with contributions from the aromatic and carbon–sulfur bonds.

Method for analysing the sulfur–sulfur band: dark sulfur quantification

As seen in Fig. 4, elemental sulfur makes a contribution to the sulfur–sulfur band, as well as providing two free standing signals at about 217 and 150 cm⁻¹. The two free standing signals can be used to predict the intensity of the signals that occur within the sulfur–sulfur band, as well as allowing the quantification of dark sulfur, which is difficult by other means as most other methods can only detect crystalline elemental sulfur.

DVB50-S50 was chosen to be the first polymer to have this analysis performed upon it. In order to quantify the dark sulfur in DVB50-S50, a spectrum of elemental sulfur was necessary. This spectrum was acquired under the same laser power as DVB50-S50, to eliminate the effects of laser power upon signal intensities. Next, to make the spectra comparable, they were both divided by the integration time used to acquire the Raman spectra, which is appropriate because signal intensity varies linearly with integration time. Next, the 217 cm⁻¹ elemental sulfur signal in the DVB50-S50 spectrum was made subject to a linear baseline correction, to eliminate the fluorescent background, and then integrated to find its intensity. The 217 cm⁻¹ peak in the elemental sulfur spectrum was also integrated to find its intensity. According to the elemental analysis, the DVB50-S50 polymer contained 52.5% sulfur by mass. Therefore, the elemental sulfur spectrum intensity was multiplied by 0.525 to correct for this. Comparing the intensity of the elemental sulfur signals between the polymer spectrum and the elemental sulfur spectrum, it was found that that elemental sulfur (present as S₈) in the DVB50-S50 polymer gave signals that were 0.43% as intense as the elemental sulfur spectrum itself, indicating that 0.43% of the sulfur in the polymer was in fact not polymerised, but elemental. This analysis was repeated for DVB30-S70 and DVB70-S30, revealing that DVB30-S70 had an elemental sulfur content of 4.46% of its total sulfur content, and that DVB70-S30 had too little elemental sulfur present to quantify accurately. Using the same method, it was determined that DIB30-S70 had 11.6% of its total sulfur content unpolymerised, and that the analogous value for DIB50-S50 was 1.7%. The elemental sulfur signals in DIB70-S30 were too weak for accurate analysis. See the ESI Section XVI.†, for a step-by-step guide on how to quantify dark sulfur in an inverse vulcanised polymer by Raman spectroscopy.

Method for analysing the sulfur–sulfur band: sulfur rank

One of the most valuable pieces of information that Raman spectroscopy has the potential to provide, is the proportion of different sulfur ranks within inverse vulcanised polymers. This information should be contained within the sulfur–sulfur band; specifically, it should be made up by the smaller bands which contribute to the sulfur–sulfur band. Before this analysis can be attempted, the elemental sulfur contribution to the sulfur–sulfur band must be taken into account. This is done by the same method as before: the baseline corrected intensity of the elemental sulfur peak at roughly 217 cm⁻¹ in the polymer spectrum must first be measured, though in this scenario, there is no need to divide by the integration time. Separately the spectrum of elemental sulfur must be acquired, though in this scenario, the conditions under which it is measured do not need to match that of the polymer spectrum. In the elemental sulfur spectrum, the intensities of the 434 cm⁻¹ and 471 cm⁻¹ peaks, must be measured in comparison to the intensity of the 217 cm⁻¹ peak. In this example, the intensity ratios were as follows: intensity₄₃₄/intensity₂₁₇ = 0.0891 and intensity₄₇₁/intensity₂₁₇ = 0.7492. Returning to the polymer spectrum, in this case DVB50-S50 will be used as the example, the intensity of the 217 cm⁻¹ peak must be multiplied by the aforementioned ratios in order to obtain the intensities of the 434 cm⁻¹ and 471 cm⁻¹ peaks in the polymer spectrum. The baseline corrected intensity of the 217 cm⁻¹ peak in DVB50-S50 was 1675.96 counts. Therefore, by multiplying 1675.96 counts by 0.0891 and 0.7492 separately, the intensity of the 434 cm⁻¹ and 471 cm⁻¹ peaks were found to be 149.33 counts and 1255.63 respectively. With the intensity of these elemental sulfur peaks in the polymer spectrum known, their contributions in the later stages of the analysis can be accounted for.

The first attempt to extract the sulfur rank from the sulfur–sulfur band was performed on DVB50-S50, with the initial method being to use the computational data to explicitly fit the bands. The first attempt used the strategy of applying every explicit peak of the computational data set to the experimental sulfur region, and then varying the proportions of the intensities of the different sulfur ranks. Unfortunately, this method was unsuccessful due to several reasons. Trying to fit the peak data explicitly resulted in as many as thirty different contributor peaks in the band deconvolution process, which was very difficult to manage. Secondly, there were multiple different combinations of contributor peaks that would yield a mathematically acceptable fit, and it was impossible to decide which one was correct. Thirdly, this method was very vulnerable to inaccuracies in the computational data.

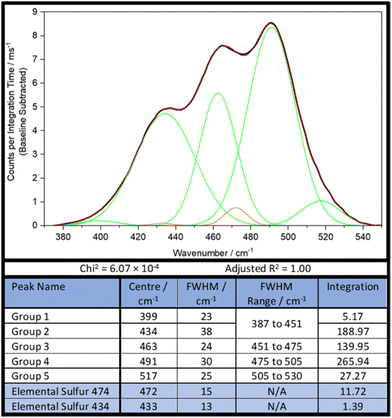
As such, a new, simpler strategy, less constrained by parameters was necessary. Firstly, the sulfur–sulfur band of DVB50-S50 was analysed by band deconvolution without the computational data, using the minimum number of Gaussian peaks necessary to get a mathematically acceptable fit, whilst also incorporating the peaks of elemental sulfur (Fig. 6). In the case of DVB50-S50, besides the elemental sulfur peaks, five Gaussian peaks were needed to complete band deconvolution, though Group 1 and Group 2 will be treated as a single group, Group 1,2, since Group 2 is much larger than Group 1, and Group 1 occurs almost entirely inside Group 2. It was found later that for other polymers, this was treatment not appropriate. Therefore, the sulfur–sulfur band of DVB50-S50 was described in terms of four peaks, which will be referred to as groups (Fig. 6).

Fig. 6 Band deconvolution of the sulfur–sulfur band of DVB50-S50, with selected peak information. Peaks resulting from elemental sulfur are coloured in orange, while peaks in green are the Gaussians assigned to polymer sulfur–sulfur vibrational modes. The black line is the linear baseline corrected experimental spectrum, while the red line is the sum of the green and orange Gaussians.

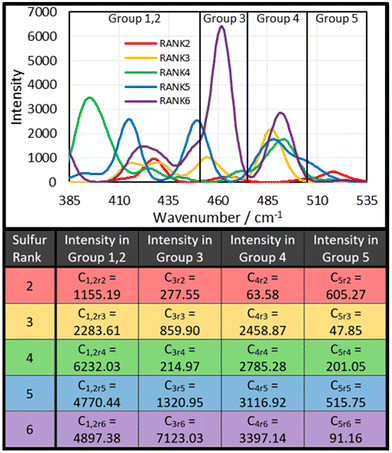
The next step was to use the computational data to determine how much intensity each sulfur rank would contribute to each group. To do this, the peak data shown in the ESI, Section XIV., Table S3,† was sorted by the following protocol: the Raman peak data would be sorted into a group if its parameterised harmonic frequency fell within the FWHM Range of that group (Fig. 6). The FWHM Range was simply the Centre value ± half the FWHM. In the case that a peak occurred within 5 cm⁻¹ of a boundary between two groups, the parameterised intensity of that peak would be halved, and it would be placed into both groups. This was done separately for each sulfur rank, yielding series of peak data for each group by sulfur rank. Finally, the intensities contained within each group by each sulfur rank were summed together to give a total intensity value. Thus, the intensity that each sulfur rank would contribute to each group was then known, as shown in Fig. 7. This approach is more resilient to errors in the computational data, because the band deconvolution becomes less dependent on the harmonic frequency being completely correct.

Fig. 7 The sulfur–sulfur region of the calculated Raman Spectra for each sulfur rank when the Cis, Trans, RR, and RS components are average together to give one spectrum for each sulfur rank, and the intensities per mole that each sulfur rank should contribute to each group in the spectrum of DVB50-S50, according to the computational chemistry and the sorting method.

The next step was to apply the theoretical group data to the real group data, in order to determine the contribution of each sulfur rank to each group, and therefore determine the proportional population of each sulfur rank. The initial approach was to solve the following set of simultaneous equations:

G₁ = r₂C_1r2 + r₃C_1r3 + r₄C_1r4 + r₅C_1r5 + r₆C_1r6

G₂ = r₂C_2r2 + r₃C_2r3 + r₄C_2r4 + r₅C_2r5 + r₆C_2r6

G₃ = r₂C_3r2 + r₃C_3r3 + r₄C_3r4 + r₅C_3r5 + r₆C_3r6

G₄ = r₂C_4r2 + r₃C_4r3 + r₄C_4r4 + r₅C_4r5 + r₆C_4r6

G₅ = r₂C_5r2 + r₃C_5r3 + r₄C_5r4 + r₅C_5r5 + r₆C_5r6

where g_n is the intensity of the group from the experimental data, C_n,rm is the intensity that sulfur rank m should contribute to group n (Fig. 7), and r_m are the populations of sulfur ranks 2, 3, 4, 5, and 6 respectively. For DVB50-S50, because two of its peaks were treated as one, G₁ and G₂ were combined into G_1,2, with constant C_1,2rm. To simplify solving these equations, r₅ and r₆ were considered to be negligible, therefore eliminating the last two terms from the equations. Note that where this analysis was performed here, the experimental G_n values were normalised, and then arbitrarily multiplied by a thousand to make the numbers easier to work with.

If the computational data were flawless, then solving these simultaneous equations for r₂, r₃, r₄, and r₅, would explicitly yield the correct proportions of the sulfur ranks. However this is not the case, and when the equations were solved for r₂, r₃, and r₄, the results were r₂ = 0.18, r₃ = 0.60, and r₄ = −0.17. This implies that sulfur rank 4 would have a population of less than zero, which is of course, impossible. Therefore, explicitly solving these simultaneous equations cannot yield the populations of the sulfur ranks until more accurate computational methods for this analysis are developed. This does not however mean, that a good measure of the populations cannot be obtained. The values for r₂, r₃, and r₄ were used as starting points in an iterative trial and error approach to determine the sulfur rank proportions.

To do this, the values of r₂, r₃, r₄, and r₅ were varied manually, until a minimum difference between the experimental G_n values and the calculated G_n values was achieved. This process revealed why explicitly solving the simultaneous equations failed: the computational data overestimates the intensity of peaks in Group 1,2, forcing one of the sulfur ranks to have a negative population in order to bring the intensity of G_1,2 down (Fig. 9). Therefore, when performing the iterative approach, the difference between the experimental G_1,2 and the calculated G_1,2 was not considered when trying to achieve a minimum error scenario. From this approach, it was determined that for DVB50-S50, r₂ = 0.134, r₃ = 0.357, r₄ = 0.030, r₅ = 0.010. In other words, the proportional populations were 25.2% sulfur rank 2, 67.2% sulfur rank 3, 5.6% sulfur rank 4, and 1.9% sulfur rank 5, with the average sulfur rank being 2.84. For DVB50-S50, based only on its sulfur content (taking into account the evaporation of DVB during synthesis and the presence of unpolymerised sulfur) the expected sulfur rank is 2.24 (see ESI, Section XVII., for the details of this calculation†). The difference between the extracted sulfur rank of 2.84 and the expected sulfur rank of 2.24 is that the expected sulfur rank cannot take into account a biased distribution of sulfur ranks, which is entirely expected from Boltzmann theory. Even still, the extracted and expected values for the average sulfur rank are not vastly different and this provides confidence that the Raman spectroscopic analysis has provided a sensible number for the average sulfur rank. What provides further confidence in the conclusion given by the Raman spectroscopy analysis is that the populations of each sulfur rank that have been obtained roughly follows the Boltzmann distribution, giving a theoretical basis for the results.

To further demonstrate the success of this analysis, the process was repeated for DVB70-S30. Analysis found five distinct peaks within the sulfur band, which could not be combined into fewer peaks as was the case for DVB50-S50. Processing of the data revealed that DVB70-S30 had an average sulfur rank of 2.66, with the following populations: 56.8% rank 2, 21.4% rank 3, and 21.8% rank 4. In this case the population of rank 4 is slightly higher than rank 3, which is difficult to rationalize with theory, and so it is likely the result of error in the computational and analysis method. However, given that the population of rank 4 is only 0.4% higher than rank 3, it seems this error is quite small. The predicted average sulfur rank for DVB70-S30 is 1.00 based on the theory in the (ESI, Section XVII†), significantly lower than the calculated value of 2.66. This suggests that sulfur rank 1 does not occur, and that incomplete consumption or crosslinking of the double bonds may be the case in the DVB70-S30 polymer, which would explain its lower T_g value. What is very interesting in these data, is that the average sulfur rank for DVB50-S50 was found to be 2.86, and the average sulfur rank for DVB70-S30 was found to be 2.66, only marginally lower. Yet, the Raman analysis indicates that despite the similarity in the average sulfur rank values, the individual populations of the sulfur ranks in these two polymers differs significantly. DVB70-S30 was found to contain no rank 5 chains at all, in comparison to DVB50-S50 which contained a small population. Additionally, DVB50-S50 contained less rank 2 than rank 3 chains, whereas the opposite is true for DVB70-S30. This insight into the distribution of sulfur ranks is unobservable from the average sulfur rank which would suggest these polymers are very similar, however Raman analysis shows clearly how different these two polymers are by elucidating the individual proportions of sulfur ranks, not just the average value. This makes clear, the advantages of Raman analysis in comparison to other methods which can only indicate the average sulfur rank, and so do not provide this fascinating in-depth scrutiny of the polymers’ molecular structure. The ability to distinguish between sulfur ranks has tremendous importance in the characteristics of inverse vulcanised polymers. One such example is in the field of recyclability of inverse vulcanized polymers, where Yan et al., found that disulfide bridges and trisulfide bridges behaved vastly differently in their polymer, with trisulfide bridges promoting recyclability, and disulfide bridges hindering recyclability.³⁵ This however, is just one example, and the distribution of sulfur ranks has almost ubiquitous importance throughout the different applications of inverse vulcanised polymers, with another example being lithium sulfur batteries.

Unfortunately, accurate results for DVB30-S70 could not be obtained. The expected average sulfur rank was 5.11, which would suggest that the majority of chain lengths were sulfur rank 5 or higher. This made it impossible to analyse the sulfur rank for this polymer, because the greatest sulfur rank predicted in the quantum calculations, was sulfur rank 6. It is likely that sulfur ranks as high as 10 might need to be calculated for the accurate analysis of polymers with such high sulfur loadings, which therefore makes their analysis impossible here, though with further calculations this would be possible. These calculations were not performed here because the supercomputer used did not have sufficient resources to calculate sulfur rank 7 in a reasonable amount of time (72 hours) and at such a high level of theory. A decrease in the level of theory would be required, which would require all of the calculations to be redone. As such, fine tuning of the computational model for higher sulfur ranks will be left to future work.

An additional limitation to be addressed in future work, was that since the computational simulations were centred on a DVB system, the computational data were not transferrable to the analysis of DIB polymers. This could be solved by performing calculations on model systems for each polymer to be analysed, in whichever specific example is of study. It would be convenient for future applications of this analysis, if a generalised calculation method could be produced that was insensitive to the molecular system under scrutiny. However, even in the absence of calculated data, the sulfur ranks can be qualitatively analysed by the form of their sulfur–sulfur band. It is suggested here that researchers wishing to apply this analysis have two options: they can generate their own computational data to analyse their polymers with, which is time consuming and challenging, but will provide the most accurate results; or they can use a more qualitative approach to analyse the sulfur band. See the ESI, Section XVIII.,† for a step-by-step guide for determining the sulfur rank by Raman spectroscopy.

Admittedly, the in-depth analysis of the sulfur rank is time consuming and difficult, however, this Raman analysis has also opened up the possibility of an extremely rapid and convenient qualitative analysis of the sulfur rank. Observing Fig. 8–10 several general conclusions can be made about the sulfur–sulfur band. According to Fig. 9, the different groups in the band do roughly correspond to different sulfur ranks. Group 5 mostly receives contributions from rank 2, with some smaller contributions from rank 5. Group 4 receives significant contributions from all sulfur ranks except rank 2. Group 3 receives strong contributions from rank 6, however rank 6 should be proportionally uncommon according to Boltzmann theory, so intensity in the group 3 region can be assigned to rank 3 and 5, with lesser contributions from rank 2 and rank 4. Group 1,2 receives strongest contributions from rank 4, with rank 5 and 6 contributing significantly as well, and rank 2 and 3 providing only small contributions. To summarise, intensity in the group 5 region can be assigned to the presence of sulfur rank 2, whereas intensity in the group 1,2 region can be assigned to longer sulfur ranks of 4 and upward, whilst intensity in the group 4 region can be assigned to all sulfur ranks besides rank 2, which makes group 4 a useful comparison to group 1,2 and group 5. These assignments can be used to qualitatively compare the sulfur ranks of the polymers, as shown in Fig. 8. Since this qualitative analysis does not require calculated data, it is adaptable to systems other than polymers based upon DVB.

Fig. 8 Band deconvolutions of the Raman spectra of the sulfur–sulfur band region for different inverse vulcanised polymers. Note that DIB60-S40 was obtained in place of DIB70-S30 because the sulfur–sulfur band of DIB70-S30 did not appear clearly through the fluorescent baseline. Peaks resulting from elemental sulfur are coloured in orange, while peaks in green are the Gaussians assigned to polymer sulfur–sulfur vibrational modes. The black line is the linear baseline corrected experimental spectrum, while the red line is the sum of the green and orange Gaussians.

Fig. 9 The 1064 nm Raman spectra of the top and bottom faces of inhomogeneous polymer of DVB (700 ms integration time) and DIB (500 ms integration time) collected at 430 mW laser power, and information about these different faces of the polymers, derived from their spectra. Offsets have been applied to the intensities.

Fig. 10 Regions of interest from the 1064 nm Raman spectra of DVB50-S50-τ polymers, where τ is the time in minutes that the polymers were left to cure, and accompanying analyses of the spectral regions of interest. A1 shows an elemental sulfur peak, B1 shows the sulfur–sulfur band, and C1 shows the aromatic region. A2 shows the integration of the 220 cm⁻¹ sulfur peak with curing time with an exponential fit, B2 shows the changes in sulfur rank with curing time, and C2 shows the integration of the polymer and DVB aromatic modes with curing time, with a logarithmic and exponential fit, respectively. Samples were measured soon after removing them from the heat source, but long enough afterward that they had cooled to room temperature. Note that for A1, B1, and C1, the intensities have been offset by arbitrary values for clarity.

Observing Fig. 8, the aforementioned assignments can be used to make qualitative statements about the sulfur ranks. Comparing across DVB30-S70 to DVB50-S50 to DVB70-S30, it can be seen that as the proportion of crosslinker increases, the intensity of group 5 (centred at roughly 520 cm⁻¹) increases, suggesting a greater population of rank 2 sulfur chains. Meanwhile, as the proportion of crosslinker in the polymer increases, the intensity of groups 1 (centred at roughly 415 cm⁻¹) and 2 (centred at roughly 435 cm⁻¹) falls in comparison to group 4, indicating that sulfur ranks of 4 and higher make up a smaller proportion of the population as the proportion of crosslinker is increased. Thus, Raman analysis gives an extremely simple and convenient way of qualitatively analysing which sulfur ranks are present in a polymer. Besides the ease of application, this qualitative analysis has one further advantage over the explicit method: it is not limited to polymers of DVB. As can be seen in Fig. 8, the same general trends that were observed for DVB polymers, also hold true for DIB polymers, though the Raman shift ranges of the groups are shifted in comparison to DVB, a potential reason why the in-depth analysis failed. Regardless, it can be seen in the DIB spectra, that as the proportion of crosslinker is increased, the groups in the lower Raman shift end of the spectra (below 450 cm⁻¹), decrease in intensity compared to the higher Raman shift end of the spectrum (above 490 cm⁻¹). According to the aforementioned principles of qualitative analysis, this indicates an increasing presence of rank 2 chains in comparison to rank 4 and higher chains as the proportion of crosslinker is increased, which holds true to both theory and the basis of this analysis. Thus, even though Raman analysis cannot yet provide explicit information on the sulfur rank of polymers other than those of DVB, it appears that Raman analysis can offer qualitative insight into any polymer's sulfur ranks, provided a sulfur–sulfur band can be isolated.

Applications of Raman spectroscopy to inverse vulcanised polymers: homogeneity analysis

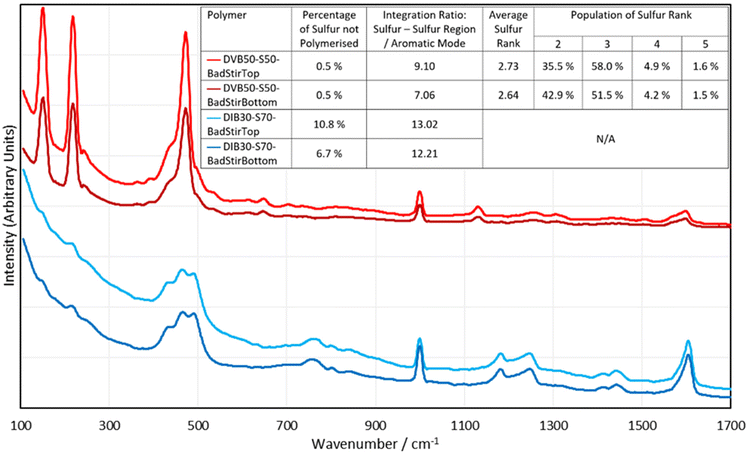
One very rapid, simple, and valuable application that Raman spectroscopy may see in the field of inverse vulcanisation, is assessment of the homogeneity of polymers, which is not easily observed by other bulk analysis techniques. This is because Raman analysis focuses its probe on a very small spot size (60 μm in the case of the i-Raman EX), and so can be used for analysing different locales. By comparing the different spectra obtained in different regions of the polymer, the homogeneity of the sample can be assessed. To this end, DIB30-S70 and DVB50-S50 were synthesized by the aforementioned standard method, but this time they received only 200 rpm stirring, and a few minutes after the reaction mixture became a single phase, stirring was ceased entirely. This allowed the denser phases to sink toward the bottom of the polymer, creating an intentional inhomogeneity, that was analysed by Raman analysis, wherein the spectrum of the top and the bottom of the polymers was acquired (Fig. 9).

As can be seen in Fig. 9, there are clear differences between the spectra of the top and bottom faces of the polymers, even though there was no visibly distinguishable difference. For both the DVB polymer and the DIB polymer, there is a greater fluorescent background in the top face spectra, which suggests Raman analysis can easily give a pass-fail assessment of whether the different regions of the same polymer are homogeneous. This inhomogeneity analysis can be taken further: it is easy to analyse the percentages of dark sulfur in these top and bottom spectra, allowing for the determination of whether there are different amounts of elemental sulfur in the different regions of the polymer. Another easy analysis that can be performed, is to integrate the sulfur–sulfur band in comparison to the aromatic modes, which can give a more quantitative estimate of how much organic versus sulfurous component exists in each region of the polymer. Note that when integrating the sulfur–sulfur region, contributions from elemental sulfur were not counted. The 1000 cm⁻¹ aromatic peak was chosen to represent the integration of the aromatic component. Finally, it is possible for the DVB polymer, to extract the sulfur rank from the top and bottom spectra, to indicate if the sulfur rank varies by region. The results of these analyses can be seen in Fig. 9. These results suggest that the top of both polymers contained more sulfur than the bottoms. Though there is no statistical difference between the dark sulfur content of the top and bottom of the DVB polymer, all other data supports the conclusion that the top of these polymers are richer in sulfur. The DIB polymer indicated a greater presence of elemental sulfur in its top face compared to its bottom, and both polymers showed that the integration of their sulfur–sulfur band compared to that of their 1000 cm⁻¹ aromatic band was greater on the top face than the bottom face. Additionally, the sulfur rank data supports this conclusion that the top face of the polymer is more sulfur rich than the bottom, as the average sulfur rank is higher for the top face of the DVB polymer, and shows higher populations of sulfur ranks 3, 4 and 5, whilst showing less sulfur rank 2 in comparison to the bottom face. Therefore, these data suggest that Raman spectroscopy is effective in showing the differences in homogeneity between different regions of inverse vulcanised polymers.

Applications of Raman spectroscopy to inverse vulcanised polymers: reaction tracking

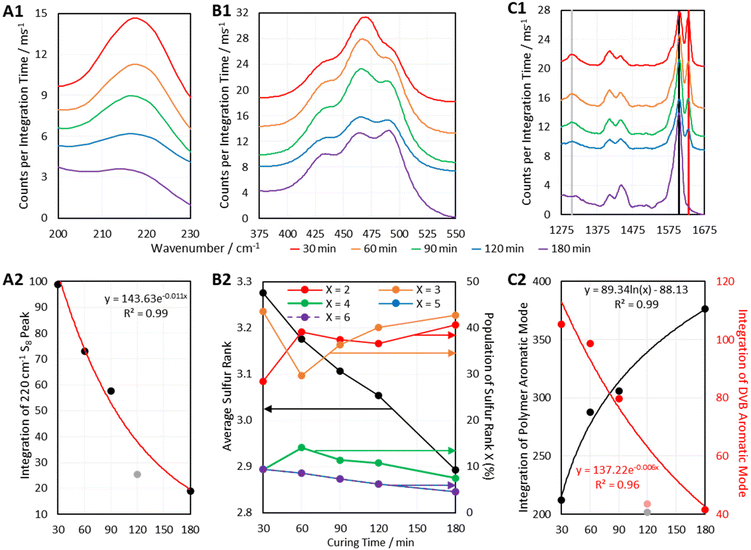
Another way in which Raman Spectroscopy may be applied in the field of inverse vulcanisation is in tracking the progression of reactions. Many Raman spectrometers can be fitted with long lens attachments that allow the Raman probe to collect spectral data while positioned at a sizeable distance from a sample of interest. This would allow the sampling of real time data from a reaction that is in progress. Although this equipment was not available here, it was still possible to track the progress of the curing step of inverse vulcanisation. Six batches of DVB50-S50 were synthesized by the aforementioned method used for the second batch of polymers, but this time, the duration of the curing step was controlled. DVB polymers, cured for different amounts of time were then analysed by 1064 nm Raman spectroscopy, the results of which are given in Fig. 10.

Fig. 10 indicates that as predicted, the polymers show several changes in their spectra as the curing step proceeds. Firstly, a peak at 1630 cm⁻¹ decreases in intensity as curing proceeds, to the point where it is no longer present in the fully cured polymer (Fig. 10 C1). This peak is assigned to the aromatic signal of unreacted DVB. Therefore, the intensity of this peak decreases as DVB is consumed, whilst the aromatic signal of reacted DVB (1605 cm⁻¹) increases over the course of the reaction. Thus, the intensities of peaks associated with reacted DVB and unreacted DVB can be used a measure The 1305 cm⁻¹ peak which decreases in intensity is also assigned to unreacted DVB, though its lower initial intensity makes it a less attractive candidate for reaction monitoring.

The depletion of elemental sulfur signals seen at Raman shifts below 300 cm⁻¹ can also be used to track the reaction (Fig. 10 A1). However, since the low Raman shift end of the spectrum seems to be the most prone to suffering a fluorescent background, there could be an additional error in measuring the intensity of these signals, thus, it may be more accurate to use higher Raman shift signals. It has been identified previously in this work that many polymers do still contain elemental sulfur in their fully cured state, so it cannot always be expected that the elemental sulfur signals will disappear in their entirety, but they can still be a useful measure of the reaction's progress. The elemental sulfur signals can also provide a measure of how much elemental sulfur remains as curing time progresses, which in itself is a point of interest.

Most importantly, Fig. 10 B1 shows that the sulfur–sulfur region of the polymers changes significantly as the curing step progresses. As previously mentioned, intensity at about 495 cm⁻¹ is indicative of sulfur rank 2, and intensity at Raman shifts below 450 cm⁻¹ is indicative of longer sulfur ranks. Thus, Fig. 10 B1 indicates that as the curing step progresses, there is a loss of longer sulfur chains, and an increase in the proportion of shorter sulfur chains. This may be explained by the fact that when elemental sulfur is heated to higher temperatures in its molten state, longer sulfur homopolymer chains will form, much longer than two sulfur atoms. These homopolymers are what initially react with crosslinker units, forming an early-stage structure where crosslinking units are connected by longer chains of sulfur atoms. Then during the curing step, the polymer structure progresses toward its thermodynamic minimum, which entails rearranging the structure and fully crosslinking by reacting any leftover vinyl bonds (Fig. 10 C1). This can be done by breaking longer sulfur chains and using some of their sulfur atoms to form new crosslinks, such that longer sulfur chains are sacrificed in order to form more shorter chains, which can be as short as rank 2. Thus, as the curing step proceeds, the initially present longer chains decrease in population as the shorter chains increase in population. This conclusion is supported by Fig. 10 B2 which, shows how the average sulfur rank and the populations of the different sulfur ranks, obtained by the aforementioned analysis method, change with time. Fig. 10 B2 shows that as the curing time increases, the average sulfur rank decreases, as expected. Fig. 10 B2 also shows a steady decline in the populations of sulfur ranks 4, 5, and 6, while sulfur ranks 2 and 3 increase in population, particularly sulfur rank 3, in line with the Boltzmann distribution. Initially sulfur rank 2 increases rapidly from 30 min to 60 min of curing, but then decreases, which may be due to sulfur atoms being added to rank 2 chains to convert them into rank 3, the population of which was simultaneously increasing. It is worth noting that the data in Fig. 10 B2 may be less accurate at the shorter curing times, because sulfur ranks longer than 6 may have been present, and the current computational data cannot take into account sulfur ranks longer than this. Such an inaccuracy might explain why the data in Fig. 10 B2 for curing time 30 min shows difficult to explain changes in the populations of the sulfur ranks.

Note also that a case study where the curing time and curing conditions of DIB polymers was performed, and this can be found in the ESI, section XX.†, This case study demonstrated how the Raman spectrum can vary drastically for polymers that are produced under different synthetic conditions, which relates to how the polymers can show very different physical properties depending on their synthetic conditions as well. This case study suggested that 1,2-dithiole-dithiones in relation to this Raman analysis should be investigated through a combination of experimental and computational methods.³⁶

Conclusions

Raman spectroscopy has been shown to be a valuable technique in the analysis of inverse vulcanised polymers. It was found that inverse vulcanised polymers fluoresce, and this fluorescence must be avoided in order to obtain a Raman signal. Even stray ambient light may be sufficient to incite fluorescence so Raman analyses must be carried out in the dark. Several Raman techniques were found to be capable of providing well-defined polymer signals, including 1064 nm Raman spectroscopy, FT-Raman spectroscopy, and Kerr-Gated Raman spectroscopy for the most highly fluorescent samples. UV Raman was unsuitable due to the polymers’ high UV absorption, which could make them useful as UV blocking materials. 488 nm Raman spectroscopy showed promise but needed optimisation to avoid laser damage.

Raman spectroscopy was shown to easily quantify unpolymerized elemental sulfur in the polymers in a rapid, convenient, and non-destructive way, even if the sulfur is amorphous and therefore undetectable by DSC and PXRD. Thus, Raman spectroscopy suggests that polymers which were otherwise expected not to contain elemental sulfur, do in fact have this impurity. Raman spectroscopy was also able to assess the homogeneity of polymers, which is not so readily accessible by other techniques. Raman spectroscopy also successfully tracked the progress of a reaction, though in the future this process could be improved by the use of long lens attachments, allowing for easy, real-time, in situ measurements. Most importantly, Raman spectroscopy was able to determine not only the average sulfur rank of a polymer, but also the distribution of the population of different sulfur ranks present, an insight that cannot be obtained by any other means at this time, and one that has tremendous impacts on the polymer properties. Quantitative analysis of the sulfur rank was possible, but needs further work to become applicable to a wider variety of polymers. This stems from the limitations of the quantum calculations used to assign the spectra. These calculations need to be performed for longer sulfur ranks and a broader range of crosslinker molecules in the future. Even so, a broadly applicable qualitative analysis method was developed for drawing conclusions about the sulfur rank of any inverse vulcanised polymer, which is faster and more convenient than the quantitative analysis method.

Outlook

Future work may look toward finding more techniques that can circumvent the fluorescence of inverse vulcanised polymers, as although Kerr-gated Raman spectroscopy was capable of obtaining fluorescence free spectra for polymers of sulfur and dicyclopentadiene or squalene where other techniques could not, it is not a widespread nor easily accessible technique. Nevertheless, Kerr-gated Raman should receive more attention in the future, as it is the only technique that this work found to be capable of providing Raman spectra of highly fluorescent inverse vulcanised polymers, a merit that cannot be overlooked. The core focus of the future work should be placed upon the computational aspect of this analysis. Because the computations performed here focused solely on divinylbenzene, the results were not entirely applicable to other polymer systems, preventing quantitative analysis of the sulfur rank in polymers other than divinylbenzene. If such calculations could be performed for more model systems, or even better, a generally applicable system, then all polymers would be subject to quantitative analysis of their sulfur rank, rather than just qualitative analysis. Further aspects for computational chemistry to observe, would be calculations for higher sulfur ranks, allowing quantitative analysis of polymers with greater sulfur contents. To this end, it would also likely be worthwhile investigating more reliable methods of parameterisation, as it is recognised here that the strategy used in this work may limit how well the parameterisation extends to molecules that were not used to generate the parameterisation model. Finally, something that was not considered here, is whether computational chemistry could provide insights on the carbon–sulfur bonds: the connection point of organic and inorganic in these polymers, and what information this could hold. It is advocated here that Raman spectroscopy should become a widespread analysis technique for inverse vulcanised polymers, which may become preferred for publication of novel inverse vulcanised.

Author contributions

All experimental and computational work was performed by Liam James Dodd under the supervision of Tom Hasell, except where otherwise specified. Cassio Lima performed the initial measurement of 1064 nm Raman with the handheld instrument under the supervision of Royston Goodacre. David Costa-Milan, Alex R. Neale, and Igor Sazanovich at the central laser facility obtained the Kerr-Gated and Fourier Transform Raman under the supervision of Laurence J. Hardwick. Andrei Sarua and Martin Kuball obtained the UV Raman data as well as attempting Raman spectroscopy with a 488 nm laser. Benedict Saunders performed the conformer search under the supervision of Martijn Zwijnenberg, and both advised Liam Dodd on performing the rest of the calculations.

Conflicts of interest

There are no conflicts to declare.

References

1. W. J. Chung, J. J. Griebel, E. T. Kim, H. Yoon, A. G. Simmonds, H. J. Ji, P. T. Dirlam, R. S. Glass, J. J. Wie, N. A. Nguyen, B. W. Guralnick, J. Park, A. Somogyi, P. Theato, M. E. Mackay, Y. E. Sung, K. Char and J. Pyun, Nat. Chem., 2013, 5, 518–524.
2. M. P. Crockett, A. M. Evans, M. J. H. Worthington, I. S. Albuquerque, A. D. Slattery, C. T. Gibson, J. A. Campbell, D. A. Lewis, G. J. L. Bernardes and J. M. Chalker, Angew. Chem., Int. Ed., 2015, 55, 1714–1718.
3. D. J. Parker, H. A. Jones, S. Petcher, L. Cervini, J. M. Griffin, R. Akhtarb and T. Hasell, J. Mater. Chem. A, 2017, 5, 11682–11692.
4. T. S. Kleine, R. S. Glass, D. L. Lichtenberger, M. E. Mackay, K. Char, R. A. Norwood and J. Pyun, ACS Macro Lett., 2020, 9, 245–259.
5. P. T. Dirlam, A. G. Simmonds, T. S. Kleine, N. A. Nguyen, L. E. Anderson, A. O. Klever, A. Florian, P. J. Costanzo, P. Theato, M. E. Mackay, R. S. Glass, K. Char and J. Pyun, RSC Adv., 2015, 5, 24718–24722.
6. A. G. Simmonds, J. J. Griebel, J. Park, K. R. Kim, W. J. Chung, V. P. Oleshko, J. Kim, E. T. Kim, R. S. Glass, C. L. Soles, Y. Sung, K. Char and J. Pyun, ACS Macro Lett., 2014, 3, 229–232.
7. Y. Zhang, R. S. Glass, K. Char and J. Pyun, Polym. Chem., 2019, 10, 4078–4105.
8. J. M. Chalker, M. J. H. Worthington, N. A. Lundquist and L. J. Esdaile, Top. Curr. Chem., 2019, 377, 16.
9. M. J. H. Worthington, R. L. Kuceraa and J. M. Chalker, Green Chem., 2017, 19, 2748–2761.
10. R. J. Angelici, Acc. Chem. Res., 1988, 21, 387–394.
11. A. L. Kohl and R. B. Nielsen, Sulfur Recovery Processes In Gas Purification, Gulf Publishing, Houston, Texas, 5th ed, 1997, pp. 670–730.
12. D. A. Boyd, Angew. Chem., Int. Ed., 2016, 55, 15486–15502.
13. J. J. Griebel, R. S. Glass, K. Char and J. Pyun, Prog. Polym. Sci., 2016, 58, 90–125.
14. J. J. Griebel, N. A. Nguyen, S. Namnabat, L. E. Anderson, R. S. Glass, R. A. Norwood, M. E. Mackay, K. Char and J. Pyun, ACS Macro Lett., 2015, 4, 862–866.
15. A. Hoefling, D. T. Nguyen, P. Partovi-Azar, D. Sebastiani, P. Theato, S. W. Song and Y. J. Lee, Chem. Mater., 2018, 30, 2915–2292.
16. U. Münchberg, A. Anwar, S. Mecklenburg and C. Jacob, Org. Biomol. Chem., 2007, 5, 1505–1518.
17. J. A. Smith, R. Mulhall, S. Goodman, G. Fleming, H. Allison, R. Raval and T. Hasell, ACS Omega, 2020, 5, 5229–5234.
18. S. H. Je, H. J. Kim, J. Kim, J. W. Choi and A. Coskun, Adv. Funct. Mater., 2017, 27, 1703947.
19. M. J. H. Worthington, M. Mann, I. Y. Muhti, A. D. Tikoalu, C. T. Gibson, Z. Jia, A. D. Miller and J. M. Chalker, Phys. Chem. Chem. Phys., 2022, 24, 12363–12373.
20. S. Tonkin, L. N. Pham, J. Gascooke, M. Johnston, M. Coote, C. Gibson and J. Chalker, ChemRxiv, 2022 DOI:10.26434/chemrxiv-2022-bzzd3.
21. P. W. Atkins and J. De Paula, in Atkins’ Physical Chemistry, Oxford University Press, Oxford, 10th ed, 2014.
22. H. Berk, B. Balci, S. Ertan, M. Kaya and A. Cihaner, Mater. Today Commun., 2019, 19, 336–341.
23. I. B. Najmah, N. A. Lundquist, M. K. Stanfield, F. Stojcevski, J. A. Campbell, L. J. Esdaile, C. T. Gibson, D. A. Lewis, L. C. Henderson, T. Hasell and J. M. Chalker, ChemSusChem, 2021, 14, 2352–2359.
24. J. M. Scheiger, C. Direksilp, P. Falkenstein, A. Welle, M. Koenig, S. Heissler, J. Matysik, P. A. Levkin and P. Theato, Angew. Chem., Int. Ed., 2020, 59, 18639–18645.
25. L. J. Dodd, O. Omar, X. Wu and T. Hasell, ACS Catal., 2021, 11, 4441–4455.
26. K. Orme, A. H. Fistrovich and C. L. Jenkins, Macromolecules, 2020, 53, 9353–9361.
27. J. A. Smith, S. J. Green, S. Petcher, D. J. Parker, B. Zhang, M. J. H. Worthington, X. Wu, C. A. Kelly, T. Baker, C. T. Gibson, J. A. Campbell, D. A. Lewis, M. J. Jenkins, H. Willcock, J. M. Chalker and T. Hasell, Chem. – Eur. J., 2019, 25, 10433–10440.
28. X. Wu, J. A. Smith, S. Petcher, B. Zhang, D. J. Parker, J. M. Griffin and T. Hasell, Nat. Commun., 2019, 10, 647.
29. T. S. Sahu, S. Choi, P. Jaumaux, J. Zhang, C. Wang, D. Zhou and G. Wang, Polyhedron, 2019, 162, 147–154.
30. J. H. Worthington, R. L. Kucera, I. Albuquerque, C. T. Gibson, A. Sibley, A. D. Slattery, J. A. Campbell, S. F. K. Alboaiji, K. A. Muller, J. Young, N. Adamson, J. R. Gascooke, D. Jampaiah, Y. M. Sabri, S. K. Bhar-gava, S. J. Ippolito, D. A. Lewis, J. S. Quinton, A. V. Ellis, A. Johs, G. J. L. Bernardes and J. M. Chalker, M. Chem. Eur. J., 2017, 23, 16219–16230.
31. B. Chase, Anal. Chem., 1987, 59, 881A.
32. L. Cabo-Fernandez, A. R. Neale, F. Braga, I. V. Sazanovich, R. Kosteckic and L. J. Hardwick, Phys. Chem. Chem. Phys., 2019, 21, 23833–23842.
33. J. J. Dale, S. Petcher and T. Hasell, ACS Appl. Polym. Mater., 2022, 4, 3169–3173.
34. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
35. P. Yan, W. Zhao, S. J. Tonkin, J. M. Chalker, T. L. Schiller and T. Hasell, Chem. Mater., 2022, 34, 1167–1178.
36. Y. Onose, Y. Ito, J. Kuwabara and T. Kanbara, Polym. Chem., 2022, 13, 5486–5493.

---

Footnote

† Electronic supplementary information (ESI) available: I. General considerations, II. Polymer syntheses, III. Synthesis and characterisation of gold nanoparticles, IV. Raman spectra of polymer samples using conventional Raman methods and SERS, V. UV/Vis spectra of the crosslinkers, VI. Fluorescence spectra of the crosslinkers, VII. Absorption spectra and tauc plots of the polymer thin films, VIII. Fluorescence spectra of the polymer thin films, IX. Screening of different Raman spectroscopic techniques, X. Evidence of oxidation of inverse vulcanised polymers, XI. DSC thermograms for the second batch of polymers, XII. 1064 nm SERS spectra for DVB polymers, XIII. Density functional theory calculation method, XIV. additional calculated data for the polymer models, XV. parameterisation of the calculated spectra, XVI. Step by Step guide for the quantification of dark sulfur by Raman spectroscopy, XVII. Calculation of the expected sulfur rank, XVIII. Step by Step guide for determining the sulfur rank by Raman spectroscopy, XIX. DIB case study band deconvolution data, XX. DIB case study, XXI. References. Further data, such as the determination of the best calculation method and level of theory, comparisons of the results for different levels of theory, and the computational output files for the polymer models are available on request from the authors. See DOI: https://doi.org/10.1039/d2py01408d

---