Open Access Article
Open Access ArticleDouble asymmetric synthesis: faster reactions are more selective and a model to estimate relative rate†
Christopher J.
Richards
 * and
O.
Stephen Ojo
* and
O.
Stephen Ojo
School of Chemistry, University of East Anglia, Norwich, NR4 7TJ, UK. E-mail: Chris.Richards@uea.ac.uk
First published on 27th July 2023
Abstract
The catalysed reaction of an enantiopure substrate with formation of a new chirality element may result in higher diastereoselectivity with one enantiomer of a catalyst (matched pair) than with the other (mismatched pair). The hypothesis that the matched reaction is faster was investigated using literature examples of kinetic resolution procedures that result in the formation of a new stereogenic centre. With one exception from fifteen examples, the selectivity factor (s = kfast/kslow) = kmatched/kmismatched. A model to estimate the relative rate of a fast-matched reaction vs. the corresponding slow-mismatched reaction is proposed. This model also provides insight into the basis of the selectivity displayed in the kinetic resolution procedures studied.
Introduction
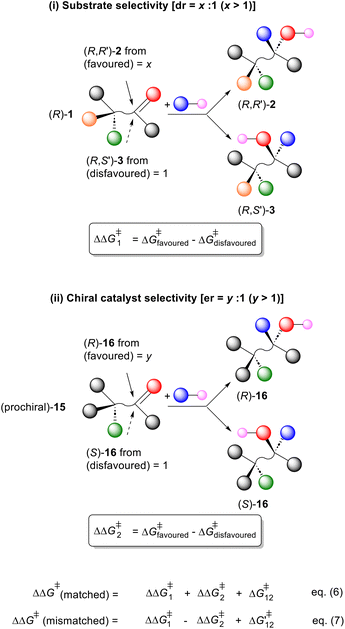
A common occurrence in asymmetric synthesis is the reaction of an enantiopure substrate [e.g. (R)-1] using an enantiopure catalyst (or reagent)1 that results in the formation of a new chirality element (Scheme 1). If the ratio of the resulting diastereoisomers [(R,R′)-2/(R,S′)-3] is independent of the configuration of the catalyst employed, the reaction is under complete substrate control. Conversely, if the ratio of diastereoisomers inverts on swapping the catalyst configuration the reaction is under complete catalyst control. In many cases the resulting ratio of diastereoisomers is frequently much higher with one enantiomer of the catalyst than is observed with the opposite enantiomer; the former being matched and the latter mismatched using the terms introduced by Masamune et al. in their seminal account on double asymmetric synthesis.2,3 Although widely exemplified, an analysis of the relative kinetics of these matched and mismatched reactions was not discussed, as is the case in another review on double asymmetric synthesis,4 and in many subsequent publications.5 There are some instances where a matched reaction is noted to be faster,6,7 but there appear to be just four examples of double asymmetric synthesis where the relative rate of the two diastereomeric reactions has been determined.8,9 One of these does not fit the expected outcome, where as noted by Sharpless, “from a kinetic perspective, one would expect matched double asymmetric reactions, where the intrinsic diastereofacial selectivities of each component are mutually reinforced, to be fast compared to their mismatched counterparts.”9 | ||
| Scheme 1 Schematic representation of enantiopure substrate (R)-1 and conversion into diastereisomers (R,R′)-2 and (R,S′)-3. | ||
In this paper we describe our investigations to confirm, using multiple examples, this correlation between rate and selectivity in double asymmetric synthesis. The data generated is used to validate a model for the estimation of the relative rate of a matched reaction compared to its mismatched counterpart. In addition, this model may also be used to estimate the selectivity factor (s) of a kinetic resolution reaction that results in the generation of a new element of chirality.
Results and discussion
Determination of the rate/selectivity correlation
In light of the paucity of data comparing the rates of matched and mismatched reactions, it was reasoned that the required information may be obtained from kinetic resolution procedures that result in the formation of an additional chirality element (Scheme 2).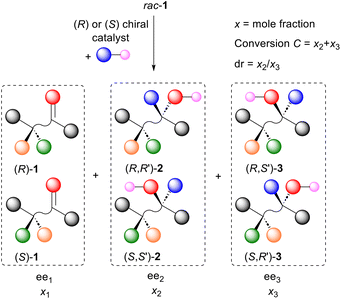 | ||
| Scheme 2 Schematic representation of the kinetic resolution of rac-1 and conversion into diastereisomers (R,R′)-2/(S,S′)-2 and (R,S′)-3/(S,R′)-3. | ||
In such a reaction, in addition to the recovered enantioenriched starting material 1 (ee1), two product diastereoisomers 2 and 3 may be formed (ee2 and ee3 respectively). The selectivity factor s (kfast/kslow), readily calculated from a knowledge of conversion C and ee1 [eqn (1)],8a,10 is the same as the relative rate of reaction of a single enantiomer of substrate with both enantiomers of a catalyst or reagent (i.e. the relative rate of the more-selective matched and less-selective mismatched outcomes as defined in Scheme 1). In addition, using mass balance equations [eqn (2) and (3)],11 the product diastereomeric ratio (dr = x2/x3, where x2 and x3 are the mole fractions of diastereoisomers 2 and 3 respectively) and the enantiomeric excess of each diastereoisomer (ee2 and ee3) may be used to calculate the diastereomeric ratios for the reaction of (R)-1 and (S)-1. These values are the same as those for the reaction of a single enantiomer of the substrate with both enantiomers of a reagent or catalyst (i.e. the dr values for the more-selective matched and less-selective mismatched outcomes as defined in Scheme 1). In this way the correlation between relative rate and diastereoselectivity may be determined.
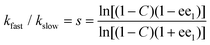 | (1) |
| [R,R′]/[R,S′] = dr[(1 + ee2)/(1 + ee3)] | (2) |
| [S,S′]/[S,R′] = dr[(1 − ee2)/(1 − ee3)] | (3) |
| Y = x1ee1 + x2ee2 + x3ee3 | (4) |
| x2ee2 + x3ee3 = 0 when C = 1 | (5) |
Starting with an examination of the many reviews on kinetic resolution,12 eleven examples of the procedure outlined in Scheme 2 were identified that contained sufficient data to determine the selectivity factor s, [R,R′]/[R,S′] and [S,S′]/[S,R′] (Scheme 3, Table 1, and see ESI†).13
 | ||
Scheme 3 A representative kinetic resolution14 reaction used to study the relationship between s (kfast/kslow) and kmatched/kmismatched. aFrom eqn (1) with C = 0.52 and ee1 = 0.37 (no sign convention for ee1 in this calculation). bFrom eqn (2) and (3) with ee2 = 0.86, ee3 = −0.97 and dr = 3. cDetermined from the values of s, [R,R′]/[R,S′] and [S,S′]/[S,R′]. dFrom eqn (10). eFrom eqn (9). fFrom eqn (12). gFrom the er value (66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) obtained using the same catalyst with a related prochiral substrate.15hFrom eqn (8) with xest and yest. iFrom eqn (8) with xpred and ypred. 1) obtained using the same catalyst with a related prochiral substrate.15hFrom eqn (8) with xest and yest. iFrom eqn (8) with xpred and ypred. | ||
Entry 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 17 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| s = kmatched/kmismatched | drmatched/drmismatched | [R,R′]/[R,S′] | [S,S′]/[S,R′] | x est | x pred | y est | y pred | s est | s pred |
| 4 | 32 | 135 | 4.2 | 24 | 21 | 6 | 2 | 5 | 2 |
Entry 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| s = kmatched/kmismatched | drmatched/drmismatched | [R,R′]/[R,S′] | [S,S′]/[S,R′] | x est | x pred | y est | y pred | s est | s pred |
| 19 | 1332 | 1653 | 1.2 | 45 | 42 | 37 | 56 | 20 | 24 |
Entry 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 23 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| s = kmatched/kmismatched | drmatched/drmismatched | [R,R′]/[R,S′] | [S,S′]/[S,R′] | x est | x pred | y est | y pred | s est | s pred |
| 14 | 51 | 93 | 1.8 | 13 | 29 | 7 | 28 | 5 | 14 |
Entry 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 25 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| s = kmatched/kmismatched | drmatched/drmismatched | [R,R′]/[R,S′]c | [S,S′]/[S,R′] | x est | x pred | y est | y pred | s est | s pred |
| a Values of s, [R,R′]/[R,S′], [S,S′]/[S,R′], xest, yest, xpred, sest and spred determined as given in Scheme 3, and details of the determination of the values for ypred are given in the ESI.† b Selectivity factor s quoted to nearest integer for values <50.26 c For values <1 the inverse value is shown in parenthesis. | |||||||||
| 36 | 44 | 0.017 (59) | 1.3 | 7 | 31 | 9 | 199 | 4 | 26 |
As a representative example the asymmetric epoxidation of benzopyran rac-4 with an iminium salt catalyst will be discussed in detail (Scheme 3).14 At 52% conversion this reaction gave recovered (S)-4 (37% ee) and a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of product diastereoisomers. These diastereoisomers are assigned using first the configuration of the stereogenic centre of the starting material from which it is derived (R or S), followed by the configuration of the closest new stereogenic centre in the product (R′ or S′). Thus the major diastereoisomer with an ee of 86% is (R,R′), and the minor diastereoisomer with an ee of 97% is (S,R′). Using the sign convention where the ee value of the starting material and compounds derived from it is +ve if R, and −ve if S, ee1 = −0.37, ee2 = 0.86 and ee3 = −0.97, with x1 = 0.48, x2 = 0.39 and x3 = 0.13. The validity of these data was checked using eqn (4),11 a further mass balance relationship where ideally Y = 0. In this instance Y = 0.03, and for all the examples used in this study Y ≤ ±0.05. From these data application of eqn (1) with C = x2 + x3 gave s = 3, application of eqn (2) with dr = x2/x3 gave [R,R′]/[R,S′] = 186, and application of eqn (3) gave [S,S′]/[S,R′] = 0.21. Thus the faster reacting (R) enantiomer is significantly more selective (dr = 186
1 ratio of product diastereoisomers. These diastereoisomers are assigned using first the configuration of the stereogenic centre of the starting material from which it is derived (R or S), followed by the configuration of the closest new stereogenic centre in the product (R′ or S′). Thus the major diastereoisomer with an ee of 86% is (R,R′), and the minor diastereoisomer with an ee of 97% is (S,R′). Using the sign convention where the ee value of the starting material and compounds derived from it is +ve if R, and −ve if S, ee1 = −0.37, ee2 = 0.86 and ee3 = −0.97, with x1 = 0.48, x2 = 0.39 and x3 = 0.13. The validity of these data was checked using eqn (4),11 a further mass balance relationship where ideally Y = 0. In this instance Y = 0.03, and for all the examples used in this study Y ≤ ±0.05. From these data application of eqn (1) with C = x2 + x3 gave s = 3, application of eqn (2) with dr = x2/x3 gave [R,R′]/[R,S′] = 186, and application of eqn (3) gave [S,S′]/[S,R′] = 0.21. Thus the faster reacting (R) enantiomer is significantly more selective (dr = 186![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) than the slower reacting (S) enantiomer (dr = 4.8
1) than the slower reacting (S) enantiomer (dr = 4.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, i.e. 1/0.21
1, i.e. 1/0.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) such that kmatched/kmismatched = s (with drmatched/drmismatched = 40).
1) such that kmatched/kmismatched = s (with drmatched/drmismatched = 40).
This positive correlation between rate and diastereoselectivity was observed in all the other ten examples studied (Table 1).16–25 In many cases the example used (Scheme 3 and Table 1 entries 1, 2, 5 and 10) is one of several related kinetic resolution procedures. These were also analysed and found to give the same positive correlation (32 examples in total, see ESI†).
The assumptions made in this analysis are those required for the application of eqn (1) for the calculation of s: namely that each reaction proceeds with pseudo first-order kinetics in the substrate, there are no non-linear effects, and that no side reactions take place (none are reported for the examples used in Scheme 3/Table 1).27 Reactions of this type have been classified by Kagan as ‘divergent reactions on a racemic mixture’.11b If run to completion the minor diastereoisomer will have the higher ee, a consequence of mass balance as formulated by the Horeau equation, eqn (5).28 In a kinetic resolution procedure this is not necessarily so and the minor diastereoisomer may have the lower ee (e.g. see entries 7 and 10). Using the calculated values for s, [R,R′]/[R,S′] and [S,S′]/[S,R′], the relative rate of formation of each stereoisomer may be determined. For the example illustrated in Scheme 3 these values are: kR,R′ = 186, kS,R′ = 53 and kS,S′ = 11, relative to kR,S′ = 1. In turn this may be used to predict reaction mixture composition as a function of conversion.29
As a hypothetical example of the alternative scenario where the matched reaction is slower (kmatched/kmismatched = 1/s), the progress of rac-4 epoxidation (Scheme 3) was calculated with the same value of s (3) but where [R,R′]/[R,S′] = 1/([S,S′]/[S,R′]) and [S,S′]/[S,R′] = 1/([R,R′]/[R,S′]). This revealed that at 52% conversion, in addition to remaining (S)-4 (37% ee), the major (R,R′, 99% ee) and minor (S,R′, 47% ee) products would form with dr = 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Thus in addition to the same enantiomer of recovered starting material, kinetic resolution where the matched reaction is slower may also result in the same major and minor product diastereoisomers, albeit with different product ee and dr values to that of the actual case where the matched reaction is faster. This highlights the viability of such an outcome, and the significance of the positive correlation between rate and selectivity observed in all the examples summarised in Scheme 3 and Table 1.
1. Thus in addition to the same enantiomer of recovered starting material, kinetic resolution where the matched reaction is slower may also result in the same major and minor product diastereoisomers, albeit with different product ee and dr values to that of the actual case where the matched reaction is faster. This highlights the viability of such an outcome, and the significance of the positive correlation between rate and selectivity observed in all the examples summarised in Scheme 3 and Table 1.
A model to account for the rate/selectivity correlation
Underpinning the concept of double asymmetric synthesis were studies on the stereoselectivity of the two corresponding single asymmetric syntheses;2 specifically the diastereoselectivity (x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of the reaction of a chiral substrate (e.g. (R)-1) with an achiral catalyst (Scheme 4(i)), and the enantioselectivity (y
1) of the reaction of a chiral substrate (e.g. (R)-1) with an achiral catalyst (Scheme 4(i)), and the enantioselectivity (y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of the reaction of a related prochiral substrate (e.g.15) with an enantiopure catalyst (Scheme 4(ii)). The differences in the free energy of activation giving rise to these selectivities may be expressed as ΔΔG1‡ and ΔΔG2‡, respectively. Then for a double asymmetric reaction, the selectivity of the matched pair (ΔΔG1‡ + ΔΔG2‡) = xy and the mismatched pair (ΔΔG1‡ − ΔΔG2‡) = x/y. The additional perturbation terms ΔG12‡ and ΔG‘12‡ of eqn (6) and (7) account for conformational differences in the transition states of the double asymmetric reactions compared to the corresponding single asymmetric reactions.2 Provided these are relatively small, summation and subtraction of the values for ΔΔG1‡ and ΔΔG2‡ works well for the prediction of the diastereoselectivities observed in the matched and mismatched double asymmetric syntheses.
1) of the reaction of a related prochiral substrate (e.g.15) with an enantiopure catalyst (Scheme 4(ii)). The differences in the free energy of activation giving rise to these selectivities may be expressed as ΔΔG1‡ and ΔΔG2‡, respectively. Then for a double asymmetric reaction, the selectivity of the matched pair (ΔΔG1‡ + ΔΔG2‡) = xy and the mismatched pair (ΔΔG1‡ − ΔΔG2‡) = x/y. The additional perturbation terms ΔG12‡ and ΔG‘12‡ of eqn (6) and (7) account for conformational differences in the transition states of the double asymmetric reactions compared to the corresponding single asymmetric reactions.2 Provided these are relatively small, summation and subtraction of the values for ΔΔG1‡ and ΔΔG2‡ works well for the prediction of the diastereoselectivities observed in the matched and mismatched double asymmetric syntheses.
Extension to the reaction of (R)-1/(S)-1 with an enantiopure catalyst gives four scenarios, exemplified by the formation of (R,R′)-2, (S,S′)-2, (R,S′)-3 and (S,R′)-3 (where (R)-1 is the fast reacting enantiomer favouring (R,R′)-2, Scheme 5).
 | ||
| Scheme 5 Schematic representation of the reaction of (R) and (S)-1 with an enantiopure catalyst and the resulting relative rates as a function of substrate (x) and catalyst (y) selectivities. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,30 and the catalyst enantioselectivity er = y
1,30 and the catalyst enantioselectivity er = y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (x and y > 1), then to a first approximation the relative rates of reaction to give the following are: (R,R′)-2 = xy, (R,S′)-3 = 1, (S,S′)-2 = x and (S,R′)-3 = y. The ΔΔG‡ value of the matched/matched reaction is given by the sum of the ΔΔG1‡ and ΔΔG2‡ values (Scheme 4) relative to ΔΔG‡ = 0 for the mismatched/mismatched reaction. Then the relative rate of reaction of (R)-1 and (S)-1 is given by eqn (8), such that then s = kmatched/kmismatched > 1. The faster double asymmetric synthesis reaction is more selective.
1 (x and y > 1), then to a first approximation the relative rates of reaction to give the following are: (R,R′)-2 = xy, (R,S′)-3 = 1, (S,S′)-2 = x and (S,R′)-3 = y. The ΔΔG‡ value of the matched/matched reaction is given by the sum of the ΔΔG1‡ and ΔΔG2‡ values (Scheme 4) relative to ΔΔG‡ = 0 for the mismatched/mismatched reaction. Then the relative rate of reaction of (R)-1 and (S)-1 is given by eqn (8), such that then s = kmatched/kmismatched > 1. The faster double asymmetric synthesis reaction is more selective.
Determination of the substrate and catalyst selectivity terms xest and yest
By extension from eqn (8), then [R,R′]/[R,S′] = xy/1 and [S,S′]/[S,R′] = x/y, and from these are derived31 eqn (9) and (10). The values of x and y calculable from these equations are designated as xest and yest, i.e. estimated values for the contributing substrate and catalyst stereoselectivities, respectively. For the example in Scheme 3, the already determined values of [R,R′]/[R,S′] = 186 (= a) and [S,S′]/[S,R′] = 0.21 (= b) are used in eqn (10) and (9) to give xest = 6 and yest = 30. This reveals that the substrate facial selectivity is relatively low (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), but the catalyst facial selectivity is high (30
1), but the catalyst facial selectivity is high (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). From these xest and yest values, use of eqn (8) gives sest, an estimated value of the selectivity factor, which for this example results in sest = 5. This, and several of the examples in Table 1 approximate to this model (s ≈ sest, entries 1–6), in other cases the selectivity factor is significantly higher than that estimated using eqn (8)–(10) (entries 7–10).32
1). From these xest and yest values, use of eqn (8) gives sest, an estimated value of the selectivity factor, which for this example results in sest = 5. This, and several of the examples in Table 1 approximate to this model (s ≈ sest, entries 1–6), in other cases the selectivity factor is significantly higher than that estimated using eqn (8)–(10) (entries 7–10).32 | (11) |
 | ||
| Scheme 6 Matched and mismatched (S,S)-bisoxazoline-copper catalysed Diels–Alder reactions of (R) and (S)-17 with cyclopentadiene, and estimation of the relative rate. | ||
Determination of the substrate and catalyst selectivity terms xpred and ypred
As an alternative to estimating the substrate selectivity term using dr values with eqn (9) and (10), it may determined using eqn (12) from the experimentally determined relative rate values for kR,R′, kS,R′ and kS,S′, with kR,S′ = 1. This provides a predictive value for x, designated xpred. Here xpred is equal to the diastereoselectivity at the start of the reaction (i.e. conversion ≪ 1%, before any significant kinetic resolution can take place), a value which is the same as the diastereoselectivity resulting from the reaction of the racemic catalyst with either the racemic or non-racemic substrate (where kinetic resolution cannot take place).30 In an ideal case kS,S′ = xest = xpred![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 and kS,R′ = yest. However, as xpred captures deviations from ideality36 it may be used in eqn (8) to provide spred, a predictive value of the selectivity factor. For this calculation an experimentally determined value of ypred is required, and this is provided by the known product er ratio resulting from the reaction of a closely related prochiral substrate with the same catalyst. For the example in Scheme 3, use of the same catalyst and conditions with 6-cyano-2,2-dimethylbenzopyran, a prochiral substrate similar to 4, resulted in an er of 98.5
35 and kS,R′ = yest. However, as xpred captures deviations from ideality36 it may be used in eqn (8) to provide spred, a predictive value of the selectivity factor. For this calculation an experimentally determined value of ypred is required, and this is provided by the known product er ratio resulting from the reaction of a closely related prochiral substrate with the same catalyst. For the example in Scheme 3, use of the same catalyst and conditions with 6-cyano-2,2-dimethylbenzopyran, a prochiral substrate similar to 4, resulted in an er of 98.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5.15 Thus ypred = 66, and with xpred = 4, then use of eqn (8) gives spred = 4. Unlike sest, which can underestimate the selectivity factor s in some cases (entries 7–10), the value of spred is in good agreement with s in most cases. Overall, this analysis reveals that the use of eqn (8), with x and y values as defined in Scheme 5, is applicable as at least an approximate model for the relative kinetics of the matched and mismatched reactions arising from a double asymmetric synthesis procedure.
1.5.15 Thus ypred = 66, and with xpred = 4, then use of eqn (8) gives spred = 4. Unlike sest, which can underestimate the selectivity factor s in some cases (entries 7–10), the value of spred is in good agreement with s in most cases. Overall, this analysis reveals that the use of eqn (8), with x and y values as defined in Scheme 5, is applicable as at least an approximate model for the relative kinetics of the matched and mismatched reactions arising from a double asymmetric synthesis procedure. | (12) |
Understanding the outcome of a kinetic resolution using substrate and catalyst selectivity terms
A successful kinetic resolution, where reaction of the substrate results in an additional chirality element in the product, requires not only a high level of catalyst selectivity, but also a high level of substrate selectivity. Dihydroxylation of rac-6 (Table 1, entry 2) proceeds with a high level of substrate control (xest = 24, xpred = 21) but with less selective catalyst control (yest = 6). Therefore the relative inefficiency of this kinetic resolution is a consequence of cis-alkenes being comparatively poor substrates for Sharpless asymmetric dihydroxylation.37It is instructive to compare two examples of the kinetic resolution of a planar chiral aryl/methyl ketone by CBS catalysed reduction. Table 1, entry 3 summarises the use of a [2.2]paracyclophane substrate rac-7,18 and Table 1, entry 4 the use of 1-tetralone-Cr(CO)3rac-8 as substrate.19 With prochiral aryl/alkyl ketones the CBS catalyst results in high reduction enantioselectivity (ypred = 56 from the 96.5% ee observed with acetophenone),38 and a high level of catalyst control is maintained in the two planar chiral examples (yest = 37 and 46, entries 3 and 4). In contrast, the reaction of rac-7 is much more diastereoselective than the reaction of rac-8 (xest = 45 vs. 8 and xpred = 42 vs. 4) accounting for the inefficient kinetic resolution of the latter. As discussed above, the value xpred corresponds to the diastereomeric ratio resulting from the reaction of a chiral substrate with a racemic catalyst.30 Therefore a diastereomeric ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is expected for the reduction of 8 with racemic CBS. This is in contrast to the very high diastereoselectivity observed with this substrate on reduction with LiAlH4 or NaBH4 (also favouring formation of the cis-product).39 This highlights that the diastereoselectivity with a racemic chiral catalyst or reagent can be significantly different to that of an achiral alternative.40
1 is expected for the reduction of 8 with racemic CBS. This is in contrast to the very high diastereoselectivity observed with this substrate on reduction with LiAlH4 or NaBH4 (also favouring formation of the cis-product).39 This highlights that the diastereoselectivity with a racemic chiral catalyst or reagent can be significantly different to that of an achiral alternative.40
The predictive use of this analysis is further illustrated by studies on dihydronaphthalene hydroboration. Regioselective reaction of racemic 18 with rac-QUINAP/Rh followed by amination gave a 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of product diastereoisomers such that xpred = 19 (Scheme 7(i)).41 The corresponding reaction of the related prochiral substrate 1,2-dihydronaphthalene 19 with (R)-QUINAP resulted, after H2O2 oxidation, in the (R)-alcohol with an er of 98
1 ratio of product diastereoisomers such that xpred = 19 (Scheme 7(i)).41 The corresponding reaction of the related prochiral substrate 1,2-dihydronaphthalene 19 with (R)-QUINAP resulted, after H2O2 oxidation, in the (R)-alcohol with an er of 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, such that ypred = 49 (Scheme 7(ii)).42 Thus for the kinetic resolution of 18, using these data with eqn (8) gives spred = 14. These data can also be used to predict the dr ratio and ee values for the products.43 For comparison, from the experimental kinetic resolution of rac-18 with (R)-QUINAP/Rh,41 using the reported value for ee1 and an approximate value of C (0.60), the selectivity factor calculated with eqn (1) is 19 (Scheme 7(iii)). This example further illustrates that provided a catalyst is known to result in high enantioselectivity with a related prochiral substrate, xpred, the substrate selectivity term, may be used to provide a good indication of the suitability of a racemic substrate for divergent kinetic resolution.
2, such that ypred = 49 (Scheme 7(ii)).42 Thus for the kinetic resolution of 18, using these data with eqn (8) gives spred = 14. These data can also be used to predict the dr ratio and ee values for the products.43 For comparison, from the experimental kinetic resolution of rac-18 with (R)-QUINAP/Rh,41 using the reported value for ee1 and an approximate value of C (0.60), the selectivity factor calculated with eqn (1) is 19 (Scheme 7(iii)). This example further illustrates that provided a catalyst is known to result in high enantioselectivity with a related prochiral substrate, xpred, the substrate selectivity term, may be used to provide a good indication of the suitability of a racemic substrate for divergent kinetic resolution.
Additional examples
We next applied this model to the four reactions mentioned in the introduction for which the relative rate of the matched/mismatched reactions have been determined, in these instances due to the selectivity factor s having been calculated for the kinetic resolution of the racemic substrate.8,9 For these examples, the [R,R′]/[R,S′] and [S,S′]/[S,R′] ratios were obtained by either reaction of one enantiomer of the substrate with both enantiomers of the catalyst, or by reaction of one enantiomer of the catalyst with both enantiomers of the substrate (Table 2).Entry 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8b 8b |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| s = kmatched/kmismatched | drmatched/drmismatched | [R,R′]/[R,S′] | [S,S′]/[S,R′] | x est | x pred | y est | y pred | s est | s pred |
| 80 | 53 | 1.9 | 100 | 7 | 55 | 14 | 19 | 5 | 14 |
| Entry 5 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| s = kmatched/kmismatched | drmatched/drmismatched | [R,R′]/[R,S′]c | [S,S′]/[S,R′]c | x est | x pred | y est | y pred | s est | s pred |
a Values of s, xest, yest, xpred, sest and spred determined as given in Scheme 3, and details of the determination of the values for ypred are given in the ESI.†
b Selectivity factor s quoted to nearest integer for values <50 and to the nearest 10 for values between 50–200, except for entries 4 and 5.26
c For values <1 the inverse value is shown in parenthesis.
d Diastereoselectivity measured in the early stages of the reaction = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
e AD-mix-β.
f AD-mix-α.
g Value for AD-mix-α not available therefore value obtained with AD-mix-β used. 1.
e AD-mix-β.
f AD-mix-α.
g Value for AD-mix-α not available therefore value obtained with AD-mix-β used.
|
|||||||||
| 5e | 0.3 | 2.4 | 0.123 (8.1) | 0.54 | 1.6 | 4.4 | 24e | 0.7 | 1.5 |
| 3f | 0.4 | 0.13 (7.5) | 2.8 | 0.61 | 1.4 | 4.6 | 24g | 0.7 | 1.4 |
The efficient kinetic resolution of rac-20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8a and rac-218b (entries 1 and 2) is in part a consequence of the excellent diastereoselectivity of the reactions used with these substrates (xpred = 38 and 55 respectively). Indeed, the DHQD/anthracene based ligand used for the dihydroxylation of 21 was designed to achieve high diastereoselectivity with chiral allylic 4-methoxybenzoates.8b For entry 3 the [S,S′]/[S,R′] and [R,R′]/[R,S′] values used are the ratio of products obtained from the reaction of (R)-22 with AD-mix-α and AD-mix-β, these containing quasi-enantiomeric (DHQ)2PHAL and (DHQD)2PHAL ligands respecively.8c This difference results in two s values for the kinetic resolution of rac-22 with these mixtures, and in turn two values for xpred and spred (entry 3). Similarly, two s values were obtained for the kinetic resolution of rac-23 by Sharpless asymmetric dihydroxylation, with AD-mix-β again being more efficient (entry 4).9 In this work the two enantiomers of 23 were also dihydroxylated with both AD-mix-α and β revealing essentially complete catalyst control and therefore no expected kinetic resolution (sest ≈ 1).
8a and rac-218b (entries 1 and 2) is in part a consequence of the excellent diastereoselectivity of the reactions used with these substrates (xpred = 38 and 55 respectively). Indeed, the DHQD/anthracene based ligand used for the dihydroxylation of 21 was designed to achieve high diastereoselectivity with chiral allylic 4-methoxybenzoates.8b For entry 3 the [S,S′]/[S,R′] and [R,R′]/[R,S′] values used are the ratio of products obtained from the reaction of (R)-22 with AD-mix-α and AD-mix-β, these containing quasi-enantiomeric (DHQ)2PHAL and (DHQD)2PHAL ligands respecively.8c This difference results in two s values for the kinetic resolution of rac-22 with these mixtures, and in turn two values for xpred and spred (entry 3). Similarly, two s values were obtained for the kinetic resolution of rac-23 by Sharpless asymmetric dihydroxylation, with AD-mix-β again being more efficient (entry 4).9 In this work the two enantiomers of 23 were also dihydroxylated with both AD-mix-α and β revealing essentially complete catalyst control and therefore no expected kinetic resolution (sest ≈ 1).
The exception to the rule
In light of this dichotomy we reinvestigated these reactions, first by performing the dihydroxylation of rac-23 with a reaction mixture containing quinuclidine in place of the cinchona alkaloid-based ligands. This resulted in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.3 ratio of diastereoisomers 24 and 25 (previous report (ref. 9) = 1
5.3 ratio of diastereoisomers 24 and 25 (previous report (ref. 9) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) with equatorial dihydroxylation dominating. Kinetic resolution of rac-23 with AD-mix-α gave (Ra)-23 (93% ee, C = 0.90, s = 3) and with AD-mix-β gave (Sa)-23 (98% ee, C = 0.85, s = 5). In our hands subsequent use of both enantioenriched substrates with AD-mix-α and β revealed much lower levels of diastereoselectivity than reported previously (Table 2, entry 5). Significantly, a degree of substrate control was observed with (Ra)-23/α and (Sa)-23/β = matched (24
6) with equatorial dihydroxylation dominating. Kinetic resolution of rac-23 with AD-mix-α gave (Ra)-23 (93% ee, C = 0.90, s = 3) and with AD-mix-β gave (Sa)-23 (98% ee, C = 0.85, s = 5). In our hands subsequent use of both enantioenriched substrates with AD-mix-α and β revealed much lower levels of diastereoselectivity than reported previously (Table 2, entry 5). Significantly, a degree of substrate control was observed with (Ra)-23/α and (Sa)-23/β = matched (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 ≈ 1
25 ≈ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 dr) and (Sa)-23/α and (Ra)-23/β = mismatched (24
8 dr) and (Sa)-23/α and (Ra)-23/β = mismatched (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 ≈ 3
25 ≈ 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dr). Unexpectedly, the more selective combinations were slower (sest = 0.7 for both α and β). In the previous investigation into this reaction it was noted that the fastest forming diol in the kinetic resolution experiments is the axial diastereoisomer 24, i.e. the alternative to that formed preferentially using quinuclidine as ligand.44 As the ratio of diols formed is a function of conversion in the kinetic resolutions,45 this axial preference may be quantified by the values of xpred (1.4 and 1.6 for AD-mix-α and β respectively). This low diastereoselectivity explains, at least in part, the poor efficiency of the corresponding kinetic resolution procedures. It is possibly significant that this one exception to the rule of ‘matched reactions are faster’ is in an example where the diastereoselectivity inverts on changing from a catalyst with an achiral ligand to a catalyst containing a related chiral ligand.
1 dr). Unexpectedly, the more selective combinations were slower (sest = 0.7 for both α and β). In the previous investigation into this reaction it was noted that the fastest forming diol in the kinetic resolution experiments is the axial diastereoisomer 24, i.e. the alternative to that formed preferentially using quinuclidine as ligand.44 As the ratio of diols formed is a function of conversion in the kinetic resolutions,45 this axial preference may be quantified by the values of xpred (1.4 and 1.6 for AD-mix-α and β respectively). This low diastereoselectivity explains, at least in part, the poor efficiency of the corresponding kinetic resolution procedures. It is possibly significant that this one exception to the rule of ‘matched reactions are faster’ is in an example where the diastereoselectivity inverts on changing from a catalyst with an achiral ligand to a catalyst containing a related chiral ligand.
Conclusions
The reaction of an enantiopure substrate with formation of a new chirality element results in a fast-matched outcome with one enantiomer of a catalyst, and a slow-mismatched outcome with the other enantiomer of the catalyst, when not under complete catalyst or substrate control. This was established primarily by examination of known literature kinetic resolution procedures that result in the formation of a new stereogenic centre. A model is proposed accounting for the fast-matched/slow-mismatched outcomes, and from the diastereomeric ratio values (relative to 1) of these two reactions the individual substrate (xest) and catalyst (yest) selectivity contributions may be estimated. These values may then be used to estimate the relative rate of the two reactions (kmatched/kmismatched = sest), and in the context of kinetic resolution the values for xest and yest provide insight into the efficiency of this process. Also of utility is the additional substrate selectivity number (xpred), a value which is also the diastereomeric ratio for the reaction of the racemic catalyst with the substrate. Use of this, in conjunction with the enantiomeric ratio for the reaction of a related prochiral substrate with the enantiopure catalyst (ypred), provides a good prediction of the kinetic resolution selectivity factor (spred). Values obtained for xest and xpred highlight the change in diastereoselectivity that can occur by switching from an achiral catalyst or reagent to a chiral counterpart.Experimental
General information
Silica gel (60 Å pore size, 40–63 μm technical grade) was used for chromatography. Compound rac-23 was prepared essentially as reported previously.46Dihydroxylation of rac-23 with quinuclidine-based AD-mix
Quinuclidine (29.2 mg, 0.26 mmol, 0.1 eq.) was added to a stirred light-brown solution of K2OsO4·2H2O (19.4 mg, 0.053 mmol, 0.02 eq.) in H2O (33 mL) at room temperature. The resulting cloudy-white brown solution was stirred for 15 min, then t-BuOH (33 mL), K3Fe(CN)6 (865.9 mg, 2.63 mmol, 1.0 eq.), K2CO3 (363.2 mg, 2.63 mmol, 1.0 eq.) and MeSO2NH2 (250 mg, 2.63 mmol, 1.0 eq.) were added simultaneously. After 5 min, rac-23 (600 mg, 2.63 mmol, 1.0 eq.) was added to the yellow solution which was then stirred for 48 h at room temperature. The resulting mixture was concentrated in vacuo (40 torr, 50 °C) to dryness and the crude material was purified by silica gel chromatography using 20% EtOAc/hexane. Compound rac-24 and rac-25 were isolated together in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.3 ratio as a crystalline colourless solid (400 mg, 1.52 mmol, 58% yield). Further purification by silica gel chromatography using 5–10% EtOAc/hexane enabled the isolation of both diastereoisomers as a colourless solid.
5.3 ratio as a crystalline colourless solid (400 mg, 1.52 mmol, 58% yield). Further purification by silica gel chromatography using 5–10% EtOAc/hexane enabled the isolation of both diastereoisomers as a colourless solid.
Data for rac-24:47 Mp: 162–168 °C; 1H NMR (400 MHz, CDCl3) δ 7.35–7.28 (m, 5H), 4.37 (s, 1H), 2.48 (s, 1H), 1.82–1.78 (m, 1H), 1.72 (s, 1H), 1.56–1.46 (m, 2H), 1.44–1.39 (m, 1H), 1.32–1.13 (m, 5H), 0.76 (s, 9H). 13C NMR (101 MHz, CDCl3) δ 140.4, 127.9, 127.8, 127.7 81.4, 73.4, 47.7, 34.8, 32.4, 32.2, 27.5, 22.2, 22.0. IR (cm−1) ν: 3407, 2933, 2864, 2359, 1450, 1389, 1012. HRMS (ASAP-TOF) m/z: [M + H]+ calcd for C17H26O2 262.1933; found 262.1930.
Data for rac-25: Mp: 162–168 °C; 1H NMR (400 MHz, CDCl3) δ 7.36–7.22 (m, 5H), 4.77 (d, J = 6.0 Hz, 1H), 2.37–2.31 (m, 2H), 1.89 (s, 1H), 1.77–1.70 (m, 1H), 1.56–1.50 (m, 1H), 1.48 (s, 1H), 1.37–1.02 (m, 5H), 0.83 (s, 9H). 13C NMR (101 MHz, CDCl3) δ 140.6, 128.3, 128.0, 127.6, 77.2, 74.0, 47.3, 35.8, 35.7, 32.8, 27.6, 24.2, 23.8. IR (cm−1) ν: 3333, 2941, 2865, 2360, 1453, 1364, 1061, 1042.
Kinetic resolution of rac-23 with AD-mix-α
AD-mix alpha (5.00 g, 0.0016 eq. Os) was added all at once to a stirred solution of rac-23 (1.000 g, 4.38 mmol, 1.0 eq.) and methanesulfonamide (1.000 g, 10.51 mmol, 2.40 eq.) in t-BuOH/H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (300 mL) at room temperature. The resulting yellow solution was stirred at room temperature for 14 days. The reaction was monitored by HPLC and stopped when the ee of 23 reached 93% ee. The solvents were removed in vacuo (40 torr, 50 °C) and the crude material was purified using 0–20% EtOAc/hexane. Compound (Ra)-23 was obtained as a light-yellow oil (75 mg, 0.33 mmol, 7.5% yield, 93% ee) and compounds 24 and 25 were obtained as a colourless solid as a ≈ 1
1) (300 mL) at room temperature. The resulting yellow solution was stirred at room temperature for 14 days. The reaction was monitored by HPLC and stopped when the ee of 23 reached 93% ee. The solvents were removed in vacuo (40 torr, 50 °C) and the crude material was purified using 0–20% EtOAc/hexane. Compound (Ra)-23 was obtained as a light-yellow oil (75 mg, 0.33 mmol, 7.5% yield, 93% ee) and compounds 24 and 25 were obtained as a colourless solid as a ≈ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of diastereoisomers (0.82 g, 3.125 mmol, 71% yield). Conversion ≈ 90%, s = 3 (valid for a conversion range of 87–94%). The absolute configuration of (Ra)-23 was confirmed by polarimetry [α]22D = −15.4 (c 0.13, CHCl3) [Lit.
1 mixture of diastereoisomers (0.82 g, 3.125 mmol, 71% yield). Conversion ≈ 90%, s = 3 (valid for a conversion range of 87–94%). The absolute configuration of (Ra)-23 was confirmed by polarimetry [α]22D = −15.4 (c 0.13, CHCl3) [Lit.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 = −37.4 (c 0.59, MeOH)].
47 = −37.4 (c 0.59, MeOH)].
Kinetic resolution of rac-19 with AD-mix-β
AD-mix beta (5.00 g, 0.0016 eq. Os) was added all at once to a stirred solution of rac-23 (1.000 g, 4.38 mmol, 1.0 eq.) in t-BuOH/H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (300 mL) at room temperature. The resulting yellow solution was stirred at room temperature for 7 days. The reaction was monitored by HPLC and stopped when the ee of 21 reached 98% ee. The solvents were removed in vacuo (40 torr, 50 °C) and the crude material was purified using 0–20% EtOAc/hexane. Compound (Sa)-23 was obtained as a light-yellow oil (122 mg, 0.534 mmol, 12% yield, 98% ee) and compounds 24 and 25 were obtained as a colourless solid as a ≈ 1
1) (300 mL) at room temperature. The resulting yellow solution was stirred at room temperature for 7 days. The reaction was monitored by HPLC and stopped when the ee of 21 reached 98% ee. The solvents were removed in vacuo (40 torr, 50 °C) and the crude material was purified using 0–20% EtOAc/hexane. Compound (Sa)-23 was obtained as a light-yellow oil (122 mg, 0.534 mmol, 12% yield, 98% ee) and compounds 24 and 25 were obtained as a colourless solid as a ≈ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of diastereoisomers (0.78 g, 2.97 mmol, 68% yield). Conversion ≈ 85%, s = 5 (valid for conversion range of 82–86%). The absolute configuration of (Sa)-23 was confirmed by polarimetry [α]22D = +28.6 (c 0.84, CHCl3) [Lit.48 = +32.8 (c 1.39, MeOH)].
1 mixture of diastereoisomers (0.78 g, 2.97 mmol, 68% yield). Conversion ≈ 85%, s = 5 (valid for conversion range of 82–86%). The absolute configuration of (Sa)-23 was confirmed by polarimetry [α]22D = +28.6 (c 0.84, CHCl3) [Lit.48 = +32.8 (c 1.39, MeOH)].
General procedure for the dihydroxylation of (Ra)-23 and (Sa)-23
AD-mix-α or β (150 mg, 0.0016 eq. Os) was added all at once to a stirred solution of either (Ra)-23 or (Sa)-23 (30 mg, 0.13 mmol, 1.0 eq.) and methanesulfonamide (30 mg, 0.32 mmol, 2.4 eq.) in t-BuOH/H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (10 mL) at room temperature. The resulting yellow solution was stirred at room temperature for 3 days. After the reaction had reached completion, the solvent was removed in vacuo (40 torr, 50 °C) and the crude material was purified using 0–20% EtOAc/hexane to give a mixture of 24 and 25 as a colourless solid.
1) (10 mL) at room temperature. The resulting yellow solution was stirred at room temperature for 3 days. After the reaction had reached completion, the solvent was removed in vacuo (40 torr, 50 °C) and the crude material was purified using 0–20% EtOAc/hexane to give a mixture of 24 and 25 as a colourless solid.
Using AD-mix-α and (Ra)-23 (93% ee) gave 24 and 25 as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.5 mixture of diastereoisomers (29 mg, 0.111 mmol, 84% yield).
7.5 mixture of diastereoisomers (29 mg, 0.111 mmol, 84% yield).
Using AD-mix-β and (Ra)-23 (93% ee) gave 24 and 25 as a 2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of diastereoisomers (30 mg, 0.114 mmol, 85% yield).
1 mixture of diastereoisomers (30 mg, 0.114 mmol, 85% yield).
Using AD-mix-α and (Sa)-23 (98% ee) gave 24 and 25 as a 2.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of diastereoisomers (20 mg, 0.076 mmol, 58% yield).
1 mixture of diastereoisomers (20 mg, 0.076 mmol, 58% yield).
Using AD-mix-β and (Sa)-23 (98% ee) gave 24 and 25 as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 mixture of diastereoisomers (18 mg, 0.069 mmol, 53% yield).
8 mixture of diastereoisomers (18 mg, 0.069 mmol, 53% yield).
Author contributions
The manuscript was written through contributions of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Leverhulme Trust (RPG-2018-270) (O. S. O.) is thanked for financial support. We also thank Prof. David Andrews for mathematical assistance.References
- In this study all of the examples are based on the use of chiral enantiopure catalysts, but the analysis is also applicable to the use of chiral enantiopure reagents.
- S. Masamune, W. Choy, J. S. Petersen and L. R. Sita, Double Asymmetric Synthesis and a New Strategy for Stereochemical Control in Organic Synthesis, Angew. Chem., Int. Ed. Engl., 1985, 24, 1–30 CrossRef.
- The use of the terms matched and mismatched in this work is with respect to the stereochemical selectivity of a reaction as defined by Masamune.2 This should not be confused with the looser use of these terms where matched and mismatched refer to faster and slower reacting enantiomers where selectivity is not a consideration.
- O. I. Kolodiazhnyi, Multiple stereoselectivity and its applications in organic synthesis, Tetrahedron, 2003, 59, 5953–6018 CrossRef CAS.
- For further selected recent examples of double asymmetric synthesis see: (a) M. Ocejo, L. Carrillo, J. L. Vicario, D. Badía and E. Reyes, Role of Pseudoephedrine as Chiral Auxiliary in the “Acetate-Type” Aldol Reaction with Chiral Aldehydes; Asymmetric Synthesis of Highly Functionalized Chiral Building Blocks, J. Org. Chem., 2011, 76, 460–470 CrossRef CAS PubMed; (b) S. Lühr, J. Holz, O. Zayas, V. Wendisch and A. Börner, Synthesis of chiral β2-amino acids by asymmetric hydrogenation, Tetrahedron: Asymmetry, 2012, 23, 1301–1319 CrossRef; (c) M. Chen and W. R. Roush, Enantioselective Synthesis of anti- and syn-Homopropargyl Alcohols via Chiral Brønsted Acid Catalyzed Asymmetric Allenylboration Reactions, J. Am. Chem. Soc., 2012, 134, 10947–10952 CrossRef CAS PubMed; (d) S. G. Davies, E. M. Foster, J. A. Lee, P. M. Roberts and J. E. Thomson, Doubly diastereoselective conjugate additions of the antipodes of lithium N-benzyl-N-(α-methylbenzyl)amide to enantiopure ε-O-protected α,β-unsaturated esters derived from D-ribose, Tetrahedron: Asymmetry, 2014, 25, 534–546 CrossRef CAS; (e) A. Pujol and A. Whiting, Double Diastereoselective Approach to Chiral syn- and anti-1,3-Diol Analogues through Consecutive Catalytic Asymmetric Borylations, J. Org. Chem., 2017, 82, 7265–7279 CrossRef CAS PubMed; (f) F. Gelat, S. Lebrun, N. Henry, F. Agbossou-Niedercorn, C. Michon and E. Denlau, Total Synthesis of (-)-Herbaric Acid through Organocatalyzed Asymmetric Halolactonization of Acrylate-Type Benzoic Acids, Synlett, 2017, 225–230 CAS; (g) T. P. Varner, A. J. Teator, Y. Reddi, P. E. Jacky, C. J. Cramer and F. A. Leibfarth, Mechanistic Insight into the Stereoselective Cationic Polymerization of Vinyl Ethers, J. Am. Chem. Soc., 2020, 142, 17175–17186 CrossRef CAS PubMed; (h) M. De Angelis, C. Sappino, E. Mandic, M. D'Alessio, M. G. De Dominicis, S. Sannino, L. Primitivo, P. Mencarelli, A. Ricelli and G. Righi, Stereodivergent synthesis of piperidine iminosugars 1-deoxy-D-nojirimycin and 1-deoxy-D-altronojirimycin, Tetrahedron, 2021, 79, 131837 CrossRef CAS.
- For examples in double asymmetric synthesis, as outlined in Scheme 1. See: (a) D. A. Evans, S. J. Miller and T. Lectka, Bis(oxazoline)copper(II) Complexes as Chiral Catalysts for the Enantioselective Diels-Alder Reaction, J. Am. Chem. Soc., 1993, 115, 6460–6461 CrossRef CAS; (b) J. A. Marshall, B. M. Seletsky and G. P. Luke, Synthesis of Protected Carbohydrate Derivatives through Homologation of Threose and Erythrose Derivatives with Chiral γ-Alkoxy Allylic Stannanes, J. Org. Chem., 1994, 59, 3413–3420 CrossRef CAS; (c) P. V. Ramachandran, G.-M. Chen and H. C. Brown, Chiral Synthesis via Organoboranes. 43. Selective Reductions. 58. Reagent-Controlled Diastereoselective Reduction of (+)- and (-)-α-Chiral Ketones with (+)- and (-)-B-Chlorodiisopinocampheylborane, J. Org. Chem., 1996, 61, 95–99 CrossRef CAS.
- Examples in other areas of asymmetric or site-selective synthesis: (a) A. V. Malkov, L. Gouriou, G. C. Lloyd-Jones, I. Starý, V. Langer, P. Spoor, V. Vinader and P. Kočovský, Asymmetric Allylic Substitution Catalyzed by C1-Symmetrical Complexes of Molybdenum: Structural Requirements of the Ligand and the Stereochemical Course of the Reaction, Chem. – Eur. J., 2006, 12, 6910–6929 CrossRef CAS PubMed; (b) D. Liu, S. Sarrafpour, W. Guo, B. Goulart and C. S. Bennett, Matched/Mismatched Interactions in Chiral Brønsted Acid-Catalyzed Glycosylation Reactions with 2-Deoxy-Sugar Trichloroacetimidate Donors, J. Carbohydr. Chem., 2014, 33, 423–434 CrossRef CAS; (c) J. Li, S. Grosslight, S. J. Miller, M. S. Sigman and F. D. Toste, Site-Selective Acylation of Natural Products with BINOL-Derived Phosphoric Acids, ACS Catal., 2019, 9, 9794–9799 CrossRef CAS PubMed; (d) K. Stier, M. P. Checinski, S. N. R. Witte and R. Mahrwald, Matched/Mismatched Cases in Proline-Catalysed Cascade Reactions with Carbohydrates: A Computational Insight into the Role of D- and L-Proline, J. Org. Chem., 2019, 84, 1201–1217 CrossRef CAS PubMed.
- (a) V. S. Martin, S. S. Woodard, T. Katsuki, Y. Yamada, M. Ikeda and K. B. Sharpless, Kinetic Resolution of Racemic Allylic Alcohols by Enantioselective Epoxidation. A Route to Substances of Absolute Enantiomeric Purity, J. Am. Chem. Soc., 1981, 103, 6237–6240 CrossRef CAS; (b) E. J. Corey, M. C. Noe and A. Guzman-Perez, Kinetic Resolution by Enantioselective Dihydroxylation of Secondary Allylic 4-Methoxybenzoate Esters Using a Mechanistically Designed Cinchona Alkaloid Catalyst, J. Am. Chem. Soc., 1995, 117, 10817–10824 CrossRef CAS; (c) T. Yokomatsu, T. Yamagishi, T. Sada, K. Suemune and S. Shibuya, Asymmetric Dihydroxylation of 1-Acyloxy-2(E)-Alkenylphosphonates with AD-mix Reagents. Effects of 1-Acyloxy Functional Groups on the Asymmetric Dihydroxylation, Tetrahedron, 1998, 54, 781–790 CrossRef CAS.
- M. S. VanNieuwenhze and K. B. Sharpless, Kinetic Resolution of Racemic Olefins via Asymmetric Dihydroxylation, J. Am. Chem. Soc., 1993, 115, 7864–7865 CrossRef CAS . The only other examples noted where the relative kinetics of matched vs. mismatched reactions are discussed are ref. 17, 19, 20 and 25.
- H. B. Kagan and J. C. Fiaud, Kinetic Resolution, Top. Stereochem., 1988, 18, 249–330 CAS.
- (a) S. El-Baba, J.-C. Poulin and H. B. Kagan, Partial resolution through chiral synthesis using a racemic mixture, Tetrahedron, 1984, 40, 4275–4284 CrossRef CAS; (b) H. B. Kagan, Various aspects of the reaction of a chiral catalyst or reagent with a racemic or enantiopure substrate, Tetrahedron, 2001, 57, 2449–2468 CrossRef CAS.
- (a) J. M. Keith, J. F. Larrow and E. N. Jacobsen, Practical Considerations in Kinetic Resolution Reactions, Adv. Synth. Catal., 2001, 343, 5–26 CrossRef CAS; (b) D. E. J. E. Robinson and S. D. Bull, Kinetic resolution strategies using non-enzymatic catalysts, Tetrahedron: Asymmetry, 2003, 14, 1407–1446 CrossRef CAS; (c) E. Vedejs and M. Jure, Efficiency in Nonenzymatic Kinetic Resolution, Angew. Chem., Int. Ed., 2005, 44, 3974–4001 CrossRef CAS PubMed; (d) H. Pellissier, Catalytic Non-Enzymatic Kinetic Resolution, Adv. Synth. Catal., 2011, 353, 1613–1666 CrossRef CAS; (e) R. Gurubrahamam, Y.-S. Cheng, W.-Y. Huang and K. Chen, Recent Advances in Organocatalytic Kinetic Resolution for the Synthesis of Functionalized products, ChemCatChem, 2016, 8, 86–96 CrossRef CAS.
- Many more examples of this type of kinetic resolution procedure are known that result in two product diastereoisomers, but insufficient data is available for use in this study (typically the ee for one or both product diastereoisomers was not determined).
- P. C. B. Page, L. F. Appleby, Y. Chan, D. P. Day, B. R. Buckley, A. M. Z. Slawin, S. M. Allin and M. J. McKenzie, Kinetic Resolution in Asymmetric Epoxidation using Iminium Salt Catalysis, J. Org. Chem., 2013, 78, 8074–8082 CrossRef PubMed.
- P. C. B. Page, B. R. Buckley, H. Heaney and A. J. Blacker, Asymmetric Epoxidation of cis-Alkenes Mediated by Iminium Salts: Highly Enantioselective Synthesis of Levcromakalim, Org. Lett., 2005, 7, 375–377 CrossRef PubMed.
- W. Adam, H.-U. Humpf, K. J. Roschmann and C. R. Saha-Möller, Enantioselective Epoxidation with Chiral MnIII(salen) Catalysts: Kinetic Resolution of Aryl-Substituted Allylic Alcohols, J. Org. Chem., 2001, 66, 5796–5800 CrossRef CAS PubMed.
- M. A. Brimble and A. D. Johnston, Kinetic resolution in the asymmetric dihydroxylation of 1,7-dioxaspiro[5.5]undec-4-enes, Tetrahedron: Asymmetry, 1997, 8, 1661–1676 CrossRef CAS.
- P. Dorizon, C. Martin, J.-C. Daran, J.-C. Fiaud and H. B. Kagan, A practical kinetic resolution of 4-acetyl[2.2]paracyclophane, Tetrahedron: Asymmetry, 2001, 12, 2625–2630 CrossRef CAS.
- H.-G. Schmalz and H. Jope, On the Oxazaborolidine-Catalyzed Borane Reduction of 1-Tetralone-Cr(CO)3 Complexes: The Control of Reagent over a Strong Substrate, Tetrahedron, 1998, 54, 3457–3464 CrossRef CAS.
- J. Yun and S. L. Buchwald, Efficient Kinetic Resolution in the Asymmetric Hydrosilylation of Imines of 3-Substituted Indanones and 4-Substituted Tetralones, J. Org. Chem., 2000, 65, 767–774 CrossRef CAS PubMed.
- H. Mihara, Y. Sohtome, S. Matsunaga and M. Shibasaki, Chiral-Catalyst-Based Convergent Synthesis of HIV Protease Inhibitor GRL-06579A, Chem. – Asian J., 2008, 3, 359–366 CrossRef CAS PubMed.
- M. Takagi and K. Yamamoto, Carbamate-Directed Stereoselective Hydrogenation and Kinetic Resolution of N-Protected α-(α-Aminoalkyl)acrylates, Tetrahedron, 1991, 47, 8869–8882 CrossRef CAS.
- C. Fehr, J. Galindo and O. Etter, An Efficient Enantioselective Synthesis of (+)-(R,Z,)-5-Muscenone and (-)-(R)-Muscone – An Example of a Kinetic Resolution and Enantioconvergent Transformation, Eur. J. Org. Chem., 2004, 1953–1957 CrossRef CAS.
- T. Soeta, K. Selim, M. Kuriyama and K. Tomioka, Kinetic resolution of 5-substituted cycloalkenones by peptidic amidophosphane-copper-catalyzed conjugate addition of dialkylzinc, Tetrahedron, 2007, 63, 6573–6576 CrossRef CAS.
- A. Jaganathan, R. J. Staples and B. Borhan, Kinetic Resolution of Unsaturated Amides in a Chlorocyclization Reaction: Concomitant Enantiomer Differentiation and Face Selective Alkene Chlorination by a Single Catalyst, J. Am. Chem. Soc., 2013, 135, 14806–14813 CrossRef CAS PubMed.
- M. D. Greenhalgh, J. E. Taylor and A. D. Smith, Best practice considerations for using the selectivity factor, s, as a metric for the efficiency of kinetic resolutions, Tetrahedron, 2018, 74, 5554–5560 CrossRef CAS.
- Kinetic resolution reactions displaying other orders of magnitude are known. See for example: (a) M. Tokunaga, J. Kiyosu, Y. Obora and Y. Tsuji, Kinetic Resolution Displaying Zeroth Order Dependence on Substrate Consumption: Copper-Catalyzed Asymmetric Alcoholysis of Azlactones, J. Am. Chem. Soc., 2006, 128, 4481–4486 CrossRef CAS PubMed; (b) B. Dominguez, N. S. Hodnett and G. C. Lloyd-Jones, Testing Racemic Chiral Catalysts for Kinetic Resolution Potential, Angew. Chem., Int. Ed., 2001, 40, 4289–4291 CrossRef CAS; (c) D. G. Blackmond, N. S. Hodnett and G. C. Lloyd-Jones, Mechanistic Implications of Pseudo Zero Order Kinetics in Kinetic Resolutions, J. Am. Chem. Soc., 2006, 128, 7450–7451 CrossRef CAS PubMed; (d) K. Nishimoto, H. Taue, T. Ohji, S. Funakoshi, Y. Ohki and M. Ogasawara, Diastereo- and Enantioselective Metathesis Dimerization/Kinetic Resolution of Racemic Planar-Chiral Vinylferrocenes, Org. Lett., 2022, 24, 7355–7360 CrossRef CAS PubMed.
- J. P. Guetté and A. Horeau, Asymmetric synthesis by action of an optically active reagent on a substrate having at least one asymmetric centre - relation between quantities of 4 enantiomers formed, Bull. Soc. Chim. Fr., 1967, 1747 Search PubMed.
- The relative rates are given for each example in the ESI,† and the progress of the reaction with respect to each stereoisomer is plotted for the example given in Scheme 3. For the basis of the calculation used to derive this plot see: G. Balavoine, A. Moradpour and H. B. Kagan, Preparation of Chiral Compounds with High Optical Purity by Irradiation with Circularly Polarized Light, a Model Reaction for the Prebiotic Generation of Optical Activity, J. Am. Chem. Soc., 1974, 96, 5152–5158 CrossRef CAS.
- The diastereomeric ratio (x
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is defined as follows. For the reaction of a racemic catalyst with a racemic substrate: with the (R)-catalyst component, and where the configuration of the product is in square brackets, dr = (R[R,R′] + R[S,S′])/(R[R,S′] + R[S,R′]) and with (S)-catalyst component, dr = (S[R,R′] + S[S,S′])/(S[R,S′] + S[S,R′]). For a racemic catalyst, as R[R,R′] = S[S,S′] etc., then dr = (2R[R,R′] + 2R[S,S′])/(2R[R,S′] + 2R[S,R′]) = (R[R,R′] + R[S,S′])/(R[R,S′] + R[S,R′]) = x. For the reaction of a racemic catalyst with the (R)-substrate: dr =
(R[R,R′] + S[R,R′])/(R[R,S′] + S[R,S′]) = x as S[R,R′] = R[S,S′] etc. For the reaction of a racemic substrate with a single enantiomer of the catalyst, at the start of the reaction dr = (kR,R′ + kS,S′)/(kR,S′ + kS,R′) = x.
1) is defined as follows. For the reaction of a racemic catalyst with a racemic substrate: with the (R)-catalyst component, and where the configuration of the product is in square brackets, dr = (R[R,R′] + R[S,S′])/(R[R,S′] + R[S,R′]) and with (S)-catalyst component, dr = (S[R,R′] + S[S,S′])/(S[R,S′] + S[S,R′]). For a racemic catalyst, as R[R,R′] = S[S,S′] etc., then dr = (2R[R,R′] + 2R[S,S′])/(2R[R,S′] + 2R[S,R′]) = (R[R,R′] + R[S,S′])/(R[R,S′] + R[S,R′]) = x. For the reaction of a racemic catalyst with the (R)-substrate: dr =
(R[R,R′] + S[R,R′])/(R[R,S′] + S[R,S′]) = x as S[R,R′] = R[S,S′] etc. For the reaction of a racemic substrate with a single enantiomer of the catalyst, at the start of the reaction dr = (kR,R′ + kS,S′)/(kR,S′ + kS,R′) = x. - See the ESI for more details.†.
- In these cases kR,R′ is larger than expected relative to kS,R′ and kS,S′. This could be due to additional factors favouring formation of the R,R′ isomer, or disfavouring the reaction of the S substrate (to give S,R′ and S,S′ products), or a combination of the two.
- drmatched/drmismatched = ([R,R′]/[R,S′])/([S,S′]/[S,R′)] = (xy/1)/(x/y) = y2 where x > y. Similarly where x < y drmatched/drmismatched = x2.
- W. R. Roush, L. K. Hoong, M. A. J. Palmer, J. Straub and A. D. Palkowitz, Asymmetric Synthesis Using Tartrate Ester Modified Allylboronates. 2. Single and Double Asymmetric Reactions with Alkoxy-Substituted Aldehydes, J. Org. Chem., 1990, 55, 4117–4126 CrossRef CAS.
- As xpred = ([R,R′] + [S,S′])/([R,S′] + [S,R′]) = (xy + x)/(1 + y) = xest.
- The combination of an enantiopure catalyst with both enantiomers of the substrate may result in additional interactions not captured in the values of ΔΔG1‡ (x
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and ΔΔG2‡ (y
1) and ΔΔG2‡ (y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). By increasing or decreasing the values of one or more of kR,R′, kS,S′, kR,S′ and kS,R′, this may result in an increase or decrease in the value of xpred. This is related to the perturbation terms ΔG12‡ and ΔG‘12‡ of eqn (6) and (7), the conformational differences these account for leading to non-ideal values of ΔΔG‡(matched) and ΔΔG‡(mismatched).
1). By increasing or decreasing the values of one or more of kR,R′, kS,S′, kR,S′ and kS,R′, this may result in an increase or decrease in the value of xpred. This is related to the perturbation terms ΔG12‡ and ΔG‘12‡ of eqn (6) and (7), the conformational differences these account for leading to non-ideal values of ΔΔG‡(matched) and ΔΔG‡(mismatched). - H. C. Kolb, M. S. VanNieuwenhze and K. B. Sharpless, Catalytic Asymmetric Dihydroxylation, Chem. Rev., 1994, 94, 2483–2547 CrossRef CAS.
- E. J. Corey, R. K. Bakshi and S. Shibata, Highly Enantioselective Borane Reduction of Ketones Catalyzed by Chiral Oxazaborolidines. Mechanism and Synthetic Implications, J. Am. Chem. Soc., 1987, 109, 5551–5553 CrossRef CAS.
- W. R. Jackson and T. R. B. Mitchell, The Stereochemistry of Organometallic Compounds. Part VIII. Stereochemistry of Reduction of Some Tricarbonyl(arylcycloalkanone)chromiums, J. Chem. Soc. B, 1969, 1228–1230 RSC.
- In addition to the different steric and electronic properties of a racemic chiral vs. achiral catalyst, the former has four rather than two components to consider as x = ([R,R′] + [S,S′])/([R,S′] + [S,R′]).30 If [R,R′] is greater than expected (xpred > xest)32 then the dr is improved, conversely if [R,R′] is less than expected (xpred < xest as is the case for entry 4, Table 1) the dr is impaired.
- K. Maeda and J. M. Brown, Efficient kinetic resolution in hydroboration of 1,2-dihydronaphthalenes, Chem. Commun., 2002, 310–311 RSC.
- H. Doucet, E. Fernandez, T. P. Layzell and J. M. Brown, The Scope of Catalytic Asymmetric Hydroboration/Oxidation with Rhodium Complexes of 1,1′-(2-Diarylphosphino-1-naphthyl)isoquinolines, Chem. – Eur. J., 1999, 5, 1320–1330 CrossRef CAS.
- Predicted recovered (R)-alkene of 97% ee requires C = 0.63, major (S,R′) product x2 = 0.53, ee2 = −0.86, minor (R,R′) product x3 = 0.10, ee3 = 0.99. Observed dr = 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (ref. 41), product ee values not determined.
1 (ref. 41), product ee values not determined. - It was this observation that dihydroxylation of the fast reacting olefin in the kinetic resolution is preferentially from the “intrinsically disfavored diastereoface” that lead to the statement quoted in the introduction to this paper.9.
- For the kinetic resolution with AD-mix-β using the values of [R,R′]/[R,S′], [S,S′]/[S,R′] and s obtained in this work, the ratio of 24
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 at the start of the reaction is calculated as 1.6
25 at the start of the reaction is calculated as 1.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and at the end of the reaction as 1
1, and at the end of the reaction as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4.
1.4. - K. I. Jeong, H. D. Kim, J.-J. Shim and C. S. Ra, Reaction of Phosphorus Ylides with Carbonyl Compounds in Supercritical Carbon Dioxide, J. Korean Chem. Soc., 2004, 48, 28–32 CrossRef CAS.
- Although previously reported9 no characterisation data is available for diols 24 and 25. The assignment of these as ‘equatorial’ and ‘axial’ is in excellent agreement with NMR data reported for closely related seleno alcohols. See: S. Nakamura, T. Aoki, T. Ogura, L. Wang and T. Toru, Highly Enantioselective Reaction of α-Selenoorganolithium Compounds with Chiral Bis(oxazoline)s and Preparation of Enantioenriched Benzylidencyclohexanes, J. Org. Chem., 2004, 69, 8916–8923 CrossRef CAS PubMed.
- S. Hanessian and S. Beaudoin, Studies in asymmetric olefinations – the synthesis of enantiomerically pure allylidene, alkylidene, and benzylidene cyclohexanes, Tetrahedron Lett., 1992, 33, 7655–7658 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental detail, copies of the 1H and 13C spectra, and HPLC traces. See DOI: https://doi.org/10.1039/d3ob01048a |
| This journal is © The Royal Society of Chemistry 2023 |