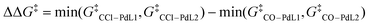Highly chemoselective ligands for Suzuki–Miyaura cross-coupling reaction based on virtual ligand-assisted screening

Abstract

Ligand screening is a crucial step in the development of transition metal catalysis, as it involves identifying the optimal ligand for a particular reaction from a large pool of candidate molecules. Conventionally, this process is performed through an experimental trial-and-error, which can be time-consuming and resource-intensive in many cases. One of the ideal strategies for streamlining this process is a transition state theory (TST)-based approach, which aims to design optimal catalysts that results in the best energy profile for the desired reaction. However, the implementation of TST-based ligand screening remains challenging mainly due to the large number of potential ligands that need to be individually evaluated through quantum chemical calculations. In this study, we experimentally demonstrated a practical TST-based ligand screening in accordance with our virtual ligand-assisted (VLA) screening strategy. As a case study, the electronic anc steric features of phosphine ligands that maximize chemoselectivity in the Suzuki–Miyaura cross-coupling (SMC) reaction of p-chlorophenyl triflate were determined through quantum chemical calculations using virtual ligands, and several phosphine ligands were suggested to exhibit high chemoselectivity. Based on this suggestion, we successfully found that tri(1-adamantyl)phosphine and tri(neopentyl)phosphine show high to excellent selectivity for the C–Cl bond activation. This case study suggests that the VLA screening strategy could be a useful tool for ligand screening.

---

Introduction

Homogeneous transition metal catalysis, including hydroformylation,¹ olefin metathesis,² and cross-coupling reactions,³ has been established as one of the most important reactions in synthetic chemistry. Recently, the development of catalysts with high efficiency and selectivity for a desired chemical transformation, as well as unprecedented chemical bond recombination ability, has been a central research topic in organic chemistry. Generally, the performance of a transition metal catalyst is largely influenced by auxiliary ligands, such as organophosphorus compounds and N-heterocyclic carbenes (NHCs).⁴ Therefore, identifying the optimal ligand for a particular reaction, a process known as ligand screening, is crucial for the development of superior catalysts. Conventionally, ligand screening is performed through an empirical trial-and-error approach (Fig. 1a, left), which can be time-consuming and resource-intensive in many cases. Therefore, several approaches have been developed to streamline this process. One of the early examples is a high-throughput experiment,⁵ in which chemical libraries of representative ligands are prepared in advance, and the performance of each candidate is evaluated in a high throughput fashion. Recently, an in silico approach using informatics techniques has been intensively studied (Fig. 1a, center).⁶ This approach involves using experimental performances of certain ligands as a training dataset and investigating the relationship between their structural features and performances to build a prediction model. Many successful examples, where important but nonintuitive ligand features were rapidly revealed by this approach, have been recently reported.⁶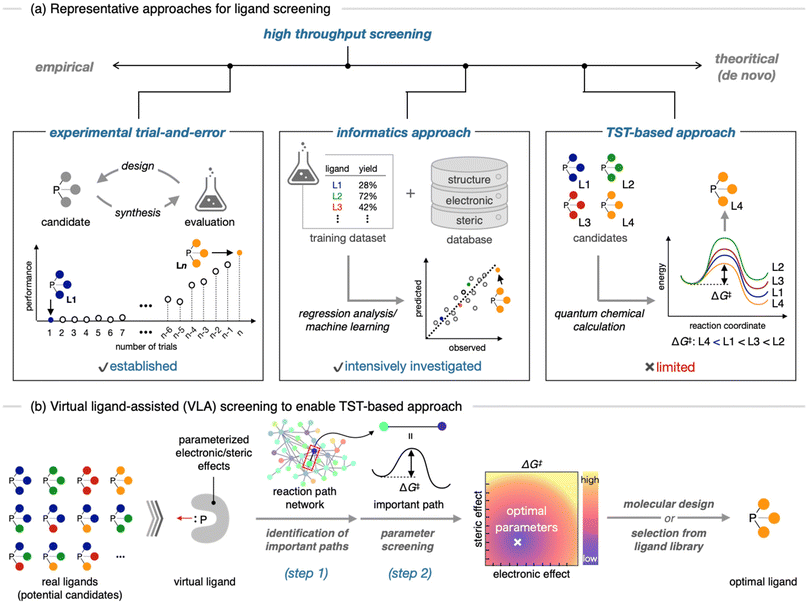

Fig. 1 Schematic illustration of ligand screening approaches. (a) Representative approaches. (b) Virtual ligand-assisted (VLA) screening to enable a practical TST-based approach.

One of the most theoretical and potentially non-empirical strategies is the transition state theory (TST)-based approach (Fig. 1a, right).^7–10 In this approach, the performance of a ligand candidate is evaluated based on the assessment of the potential energy surface (PES), rather than experimental results, and the optimal ligand is identified as the candidate which results in the best energy profile for the desired reaction. Because TST-based ligand screening can be hypothetically performed by quantum chemical calculations, without relying on experimental works, this approach can be not only a time- and resource-efficient way, but also a logical strategy for enabling de novo catalyst design, which is often described as a “holy grail” in computational chemistry.⁸ However, in reality, this approach often suffers from the elusive nature of reaction mechanisms and trade-off between accuracy and computational cost.⁹ Additionally, because a large number of ligand candidates needs to be evaluated by quantum chemical calculations including conformation sampling of corresponding transition states (TSs),¹⁰ which is a huge task even for a single candidate, this tedious procedure makes TST-based approach impractical. Hence, examples of TST-based ligand screening are limited.⁷

Recently, we developed a quantum chemical calculation method called virtual ligand-assisted (VLA) screening to realize practical TST-based ligand screening (Fig. 1b).¹¹ The virtual ligand is a dummy ligand employed in quantum chemical calculations to approximate the electronic and steric effects of real ligands.^11,12 The use of a virtual ligand enables the implicit treatment of most parts of a real ligand in the quantum chemical calculations, significantly reducing the computational cost for transition metal complexes. This facilitates the application of automated reaction path search calculations¹³ to transition metal catalysis, thereby enabling rapid and comprehensive assessments of PES. Therefore, reaction mechanisms including TSs that determine the reaction outcomes can be easily elucidated (Fig. 1b, step 1). In addition, by tuning the electronic and steric parameters of the virtual ligand to optimize the energy profile of the desired reaction, rather than reproducing a specific real ligand, the optimal features of ligands for the reaction can be rapidly identified without individually computing a large number of real ligands (step 2). Once the optimal electronic and steric features are identified by VLA screening, they can be used as a guide for selecting or designing real ligands. We previously developed a virtual ligand for phosphorus(III) ligands and computationally demonstrated the VLA screening for the regioselective hydroformylation.¹¹ In this study, we report the first experimental implementation of the catalyst design guided by VLA screening. We chose a well-known chemoselective Suzuki–Miyaura cross-coupling (SMC) reaction of p-chlorophenyl triflate as the model case and used VLA screening to investigate the effect of electronic and steric features of phosphine ligands on the chemoselectivity. Based on the obtained results, we successfully identified several ligands with high chemoselectivity. These results suggest that VLA screening can be a valuable tool for in silico ligand screening and potential de novo design of transition metal catalysts.

Theory and methods

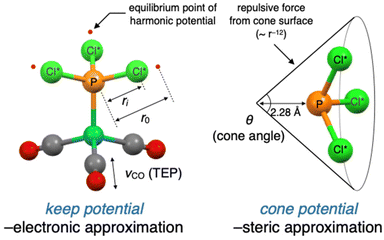
In this section, we describe the modification and improvement of the virtual ligand. We previously developed a virtual ligand for phosphorus(III) ligands¹¹ that reproduces the electronic and steric effects of real ligands gauged by the Tolman's electronic parameter (TEP) and the cone angle, respectively.¹⁴ These properties are reproduced in quantum chemical calculations by a dummy PCl₃ ligand and two independent potential functions (denoted as PCl*₃ in Fig. 2). The electronic effect can be reproduced by tuning the harmonic potentials (keep potential) between the phosphorus and chlorine atoms in the PCl*₃ ligand to match the TEP value of a real ligand. The steric effect can be simulated by a cone-shaped repulsive potential (cone potential), with an apex angle that corresponds to the cone angle of a real ligand.¹¹

Fig. 2 General design of the virtual ligand for phosphorus(III) ligands.

While the accuracy of the approximations made by the virtual ligand was validated in the previous study,¹¹ there were still concerns about the robustness of the calculations and the quantitativity of approximations. To address these issues, we developed some modified versions of the virtual ligand. The original and modified virtual ligands are compared in Table 1. All virtual ligands utilized the keep potential without modifications to approximate the electronic effects. VL1 employed a steric approximation based on the 12-6 Lennard-Jones (LJ) potential from Cl* atoms in a virtual ligand rather than the cone potential. This virtual ligand was developed to eliminate the instability of calculation caused by the cone inversion which may happen during automated explorations (see ESI,† section 5.3 for details) and is primarily used for automated reaction path search calculations using the single component-artificial force induced reaction (SC-AFIR) method (Fig. 1b, step 1).^13a–cVL2 was developed to improve the accuracy of the steric approximation, where the modified version of the cone potential was employed. The original version of the cone potential described the interactions between the virtual ligand and substrates (L–S interactions) through the repulsive term of the 12-6 LJ potential (Fig. 2, right). VL2 improved this approach by optimizing and using the full 12-6 LJ potential, including the attractive term, to describe L–S interactions. Additionally, VL2 employed another 12-6 LJ potential optimized to describe interactions between two ligands (L–L interactions). VL2_PR3 and VL2_PAr3 differ in the way they describe L–L interactions, with one version optimized to reproduce L–L interactions of PR₃ (R ≠ Ar) and the other optimized for PAr₃. These virtual ligands were mainly used for precise geometry optimizations of the TSs in the parameter screening step of VLA screening (Fig. 1b, step 2). Further implementation details and performance of VL1 and VL2 can be found in the ESI.†

Table 1 Summary of original and modified virtual ligands

	Description of electronic effect	Description of L–S interaction	Description of L–L interaction	Usage
Original^11	Keep potential	Cone-shaped repulsive potential optimized for L–S interaction	Cone-shaped repulsive potential optimized for L–S interaction	—
VL1	Keep potential	Spherical 12–6 LJ potential from Cl* atoms	Spherical 12–6 LJ potential from Cl* atoms	Automated reaction path search (SC-AFIR)
VL2PR3	Keep potential	Cone-shaped 12-6 LJ potential optimized for L–S interaction	Cone-shaped 12–6 LJ potential optimized for L–L interaction of PR3	Parameter screening for PR3- and PR2Ar-type ligands
VL2PAr3	Keep potential	Cone-shaped 12-6 LJ potential optimized for L–S interaction	Cone-shaped 12–6 LJ potential optimized for L–L interaction of PAr3	Parameter screening for PAr3- and PAr2R-type ligands

---

Results and discussion

Target reaction of VLA screening

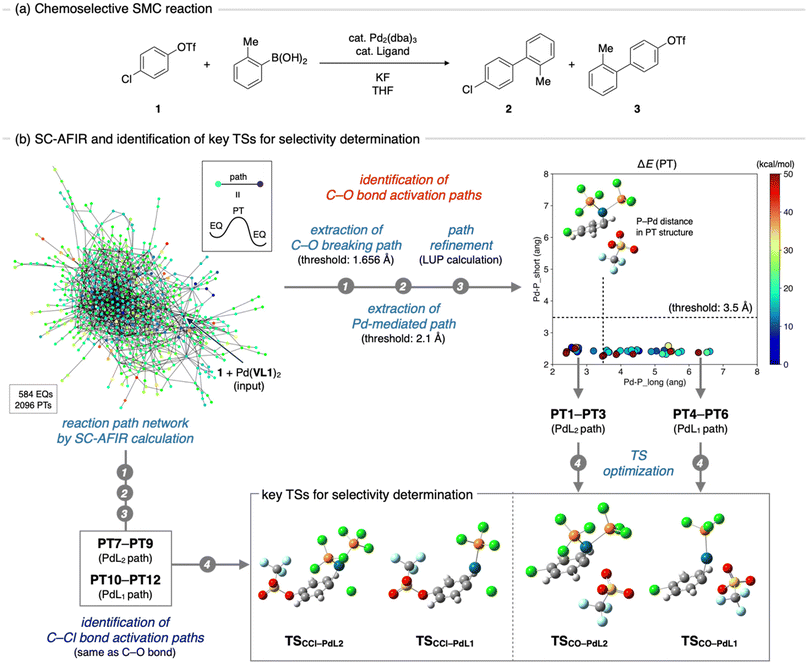
The SMC reaction between 4-chlorophenyl triflate (1) and 2-methylphenylbronic acid was chosen as the target system for VLA screening (Fig. 3a). This reaction, originally reported by Fu et al.,¹⁵ yields two different products depending on the phosphine ligands used. Compound 2 is the major product when the PCy₃ (Cy = cyclohexyl) ligand is employed, whereas compound 3 is exclusively obtained when P^tBu₃ is used. As the electronic and steric effects of these ligands were similar, the observed difference in chemoselectivity prompted further mechanistic studies.^16–18 To date, the origin of chemoselectivity has been investigated through experimental,¹⁶ theoretical,¹⁷ and informatics approaches,¹⁸ and has been recognized as the reactivity difference between monoligated and bis-ligated palladium complexes (PdL₁ and PdL₂, L = ligand). While activation of the C–Cl bond of 1 occurs at the PdL₁ complex (PdL₁ path) in the case of using P^tBu₃, the activation of the C–O bond proceeds at the PdL₂ complex (PdL₂ path) when the slightly smaller PCy₃ ligand is used.^17a,18 Considering the significant importance in carefully choosing ligands to achieve high chemoselectivity, as well as availability of plenty mechanistic insights to validate outcome of the VLA screening, this reaction was considered as an ideal example.

Fig. 3 Identification of important TSs for a chemoselective SMC reaction. (a) General scheme of the chemoselective SMC coupling reaction. (b) Schematic illustration of the procedure for the identification of TSs that determines chemoselectivity.

Step 1: identification of important transition states

VLA screening involves two distinct steps, namely identification of the key TSs that determine the reaction outcome (Fig. 1b, step 1) and parameter screening to find the optimal ligand features that maximize the reaction outcome (step 2). Although the key TS structures for the chemoselective SMC reaction have already been reported,¹⁷ we initiated the VLA screening process from step 1 with minimal experimental knowledge to demonstrate the versatility and applicability of our protocol for a range of reactions. First, we performed an automated reaction path search by the SC-AFIR method,^13a–c starting from 1 and the Pd(VL1)₂ complex. The calculations were performed using the B3LYP functional and Lanl2DZ (for Pd), 6-31G(d) (for S), and 6-31G (for other atoms) basis sets (see ESI,† section 1.2 for details). The electronic and steric parameters of the virtual ligand (VL1) were set to match those of the commonly used phosphine ligand, PPh₃. This resulted in the reaction path network shown in Fig. 3b, where each node represents a locally stable equilibrium (EQ) structure on the PES and each edge corresponds to a path top (PT) structure (i.e., an approximate TS connecting two EQs). To identify the key TSs that determine the chemoselectivity of the reaction, we firstly extracted all reaction paths in which the C–O or C–Cl bond in compound 1 extended beyond the thresholds (1.686 and 2.088 Å, respectively) from the entire network. Then, with the aim of excluding paths where the bond breaking was not facilitated by the palladium complex, we filtered the obtained paths based on the distance between the palladium atom and the carbon atom that was bonded to the leaving group (OTf or Cl). Specifically, we measured the distance between the palladium atom and the carbon atom in the EQ on the product side of each path and excluded paths in which the carbon atom did not coordinate to the palladium atom (threshold 2.1 Å). This resulted in 61 C–O bond cleavage paths and 69 C–Cl bond cleavage paths. All of these paths were then refined at the ωB97X-D/def2-SVP level using the locally updated plane (LUP) method,¹⁹ and classified based on the refined structure of the PT. Taking C–O bond cleavage paths as an example, the distances between the Pd atom and two phosphorus atoms in each PT structure were measured, and all paths were plotted against these distances (Fig. 3b, right top). Based on this plot, the paths were classified into PdL₂, PdL₁, and PdL₀ paths using a threshold of 3.5 Å for the Pd–P distances. All C–O bond cleavage paths were classified as either PdL₂ or PdL₁ paths, and no PdL₀ paths, where bond cleavage occurs at the palladium center with no coordinated phosphine ligands, were obtained. From each group (PdL₂ path and PdL₁ path), we identified three PTs with the lowest electronic energies (PT1–PT3 for the PdL₂ path and PT4–PT6 for the PdL₁ path) and performed geometry optimizations of these PTs using VL2_PAr3, instead of VL1. From the three TSs obtained for each group of PdL₁ and PdL₂ paths, we identified one representative TS as the TS with the lowest Gibbs free energy (TS_CO–PdL2 for the PdL₂ path and TS_CO–PdL1 for the PdL₁ path). Representative TSs for C–Cl bond activation through the PdL₂ path (TS_CCl–PdL2) and PdL₁ path (TS_CCl–PdL1) were also determined by the same process.

Step 2: parameter screening

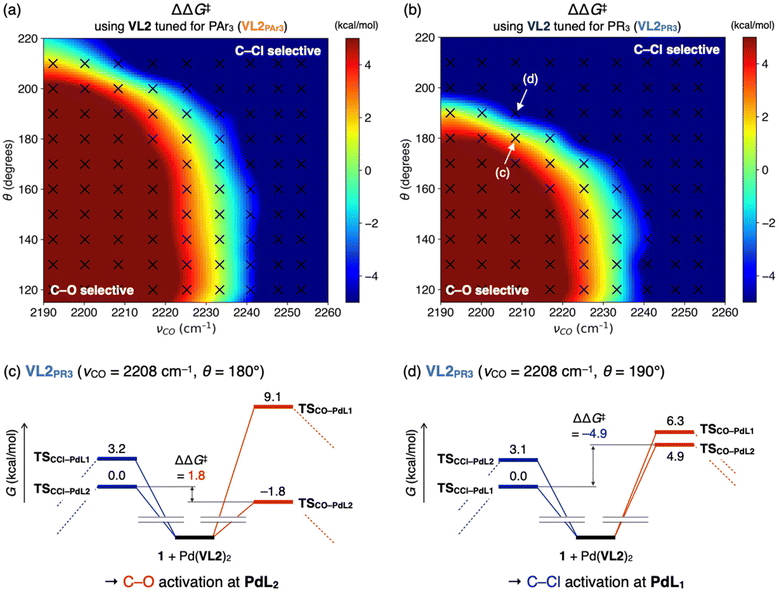
Once the key TSs for chemoselectivity were identified, we conducted parameter screening (Fig. 1b, step 2). The chemoselectivity of the reaction was quantified using ΔΔG^‡, which was defined as follows:
where G^‡_X is the Gibbs free energy of TS_X. We investigated the effect of the electronic and steric parameters of the virtual ligand on the ΔΔG^‡. Geometry optimizations and harmonic vibrational frequency analyses of TS_CO–PdL1, TS_CO–PdL2, TS_CCl–PdL1, and TS_CCl–PdL2 were performed using VL2_PAr3 with 90 combinations of electronic and steric parameters (see ESI,† Section 1.2, for details). ΔΔG^‡ was calculated for each combination of parameters, and a contour map showing the relationship between these parameters of the virtual ligand and ΔΔG^‡ was constructed (Fig. 4a). In this plot, the x- and y-axes represent the TEP values and cone angles of the ligands, respectively, and the color indicates the predicted ΔΔG^‡ value. Each cross represents a data point from the calculations, and the contour map was constructed by interpolating these data points using the radial basis function (Rbf) from the scipy.interpolate.rbf module in Python with the linear function as the basis.²⁰ As a result, ΔΔG^‡ values were found to be positive on the left side of the contour map, indicating preferential activation of the C–O bond when using electron-donating ligands. In contrast, ΔΔG^‡ was expected to be negative when electron-withdrawing ligands were employed in the reaction. This trend of chemoselectivity, along with the electronic effect (represented on the x-axis) has rarely been observed experimentally, probably due to the insufficient reactivity of palladium catalysts with electron-withdrawing ligands in the oxidative addition of aryl (pseudo)halides. Calculations were also performed using VL2_PR3, which was optimized to describe PR₃-type (R ≠ Ar) ligands. The resulting contour map is shown in Fig. 4b. In this case, negative values of ΔΔG^‡ were expected for electron-donating, bulky ligands (ν_CO < 2220 cm⁻¹ and θ = 180°) such as P^tBu₃. Fig. 4c illustrates the energy diagram associated with the data point of ν_CO = 2208 cm⁻¹ and θ = 180°, while Fig. 4d represents that corresponding to ν_CO = 2208 cm⁻¹ and θ = 190°. With a subtle increase in the cone angle, the lowest energy paths switched sharply from the bis-ligated C–O bond activation path (TS_CO–PdL2 in Fig. 4c) to the monoligated C–Cl bond activation path (TS_CCl–PdL1 in Fig. 4d), leading to a marked reversal in the sign of ΔΔG^‡. This result is consistent with the observed difference in chemoselectivity between P^tBu₃ and PCy₃,¹⁵ as well as with previous computational studies.¹⁷ The trend of ΔΔG^‡ along the x-axis was also observed in this contour map in the region of small ligands (θ = 170°), as with the contour map prepared using VL2_PAr3 (Fig. 4a).

Fig. 4 Results of the parameter screening. (a) Results obtained using VL2_PAr3, which is optimized to describe PAr₃-type ligands. (b) Result obtained using VL2_PR3, which is optimized to reproduce PR₃-type ligands. (c) Energy diagram and estimated ΔΔG^‡ value for the virtual ligand tuned to θ = 180°, ν_CO = 2208 cm⁻¹. (d) Energy diagram and estimated ΔΔG^‡ value for the virtual ligand tuned to θ = 190°, ν_CO = 2208 cm⁻¹. Each cross in the contour maps indicate a data point from the calculation.

Validation by experimental data

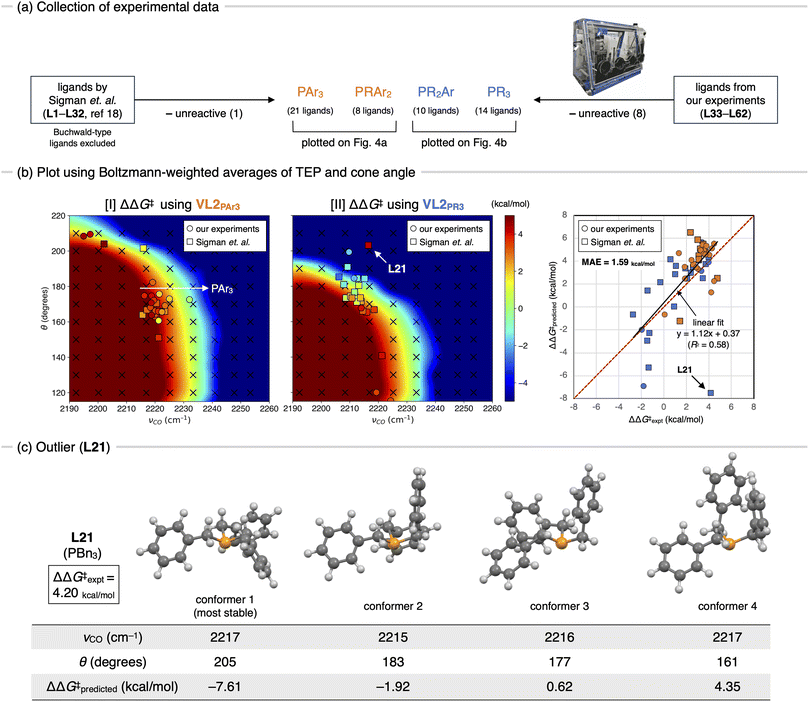
With the contour maps showing the chemoselectivity of the SMC reaction in hand, the accuracy of these contour maps was validated using experimental data. As shown in Fig. 5a, the experimental data for 62 phosphine ligands, including 32 ligands tested by Sigman et al. (L1–L32, see ESI Fig. S2†)¹⁸ and 30 commercially available ligands from our experiments (L33–L62, see ESI Fig. S3†), were used in this study. The original data reported by Sigman et al. include data for six Buchwald-type ligands (SPhos, JhonPhos, Cy-JhonPhos, XPhos, RuPhos, and Cy-vBRIDP), which can coordinate to a metal center in a bidentate manner.²¹ However, Buchwald-type ligands are clearly distinct from typical monodentate phosphine ligands and cannot be properly described by our virtual ligand.¹¹ Therefore, the data for these ligands were not used in this study. Experiments with 30 commercially available ligands (L33–L62) were quickly performed using a robotic synthesizer (see ESI,† Section 2 for the reaction conditions and procedure). ΔΔG^‡ values were calculated using the Curtin-Hammett principle based on the observed ratio of the products (2/3). Out of the experimental data obtained for 62 ligands (L1–L62), the data for nine ligands (one from Sigman's experiment and eight from our experiment) were excluded due to insufficient product yield for selectivity measurements (<1% yield). Therefore, validation was performed using data for the remaining 53 ligands. The TEP and cone angle for each of the 53 phosphine ligands were then calculated. Because these parameters, particularly the cone angle, can vary significantly due to conformational changes in the ligand, a representative combination of these parameters that properly reflects the effective electronic and steric effects of the ligand should be carefully chosen. To this end, we systematically explored the conformational isomers of each ligand using the SC-AFIR method with LNi(CO)₃ (L = ligand) as a reference complex at the GFN1-xTB level. Geometry optimizations and harmonic vibrational frequency analyses of all obtained conformers were then performed at the ωB97X-D/def2-SVP level (see ESI,† Section 1.1, for a detailed procedure). Based on the obtained results, representative combinations of the TEP and the cone angle for each ligand were calculated (ESI Tables S2 and S3†). We then examined the correlation between the predicted and observed values of ΔΔG^‡. Fig. 5b shows the results using the Boltzmann-weighted averages of the TEP values and cone angles as representative parameters. The experimental ΔΔG^‡ values were plotted on the contour maps obtained through parameter screening (Fig. 4a and b) against the TEP and cone angle of the corresponding ligands. The 53 ligands used in this study include not only “pure” PR₃ (R = alkyl) or PAr₃ ligands but also “mixed” phosphine ligands such as PR₂Ar or PRAr₂. As shown in Fig. 5a (center), PAr₃- and PRAr₂-type ligands were plotted on the contour map prepared using VL2_PAr3 (Fig. 4a), whereas PR₂Ar- and PR₃-type ligands were plotted on the contour map prepared using VL2_PR3 (Fig. 4b). The resulting plots are shown in Fig. 5b (left and center). The ΔΔG^‡ values for each ligand were then estimated from the contour maps and plotted against the experimental values (Fig. 5b, right panel). In all plots, the data reported by Sigman et al.¹⁸ (L1–L32) were plotted as squares, whereas the data prepared in this study (L33–L62) were plotted using circles. The predicted ΔΔG^‡ values for most ligands demonstrated a moderate correlation with the experimental values, except for one outlier (L21, discussed below). The regression line (y = 1.12x + 0.37, solid black line) was close to the diagonal (y = x, red dotted line), and the coefficient of determination (R²) was 0.58 after the exclusion of the outlier (L21). The mean absolute error (MAE) was calculated to be 1.59 kcal mol⁻¹. Although the prediction accuracy of the contour maps is moderate, especially compared to the prediction model built using regression analyses,¹⁸ this result is still valuable considering that all ligands were described using two parameters (TEP and cone angle) and no experimental data were used to construct the contour maps. The aforementioned trend of ΔΔG^‡ along the x-axis (electronic effect) was supported by several triarylphosphines, where the most electron-withdrawing P(C₆F₅)₃ showed the lowest value of ΔΔG^‡ (Fig. 5b, left, white arrow). Other typical strategies for determining the TEP and cone angle of a ligand, such as using parameters derived from the minimum cone angle conformer or the lowest Gibbs free energy conformer, were tested but did not significantly improve the prediction accuracy (ESI Table S5†).

Fig. 5 Validation of the prediction performance of the contour maps prepared by the parameter screening. (a) Collection of experimental data. (b) Result using Boltzmann-weighted averages of TEP values and cone angles over all conformers. (c) Outlier (L21) and its conformational dependency of parameters. Each circle and square in the contour maps represent the experimental ΔΔG^‡ value for a ligand. In (c), Ni(CO)₃ moiety was omitted for clarity.

On the other hand, L21 showed poor prediction accuracy (ΔΔG^‡_predicted = −7.51 kcal mol⁻¹, ΔΔG^‡_expt = 4.20 kcal mol⁻¹). This is likely due to the inability of the calculated cone angle, which were based on the LNi(CO)₃ reference complex, to accurately describe the steric features of the ligand in the actual reaction environment. L21 is a flexible ligand, and according to the calculation of (L21)Ni(CO)₃, one of the most sterically demanding conformers (θ = 205°) was the most stable (Fig. 5c, conformer 1). However, in the actual reaction environment, a more compressed conformer might be more feasible due to steric repulsions from the substrates and other ligands. Indeed, several conformers with significantly smaller cone angles were thermally accessible (e.g., conformers 2–4), and using parameters derived from these conformers significantly improved the prediction accuracy (ΔΔG^‡_predicted = −1.92, 0.62 and 4.35 kcal mol⁻¹ for conformers 2, 3, and 4, respectively). Future work will involve developing strategies that consider the flexibility and conformational changes in the actual reaction environment when determining their parameters.

Catalyst selection from phosphine database

Finally, we anticipated to use the contour maps as guides for the selection of catalysts with high chemoselectivities. For this purpose, we exploited the kraken database (Fig. 6a).²² The kraken database, developed by Gensch, Sigman, Aspuru-Guzik, and co-workers, contains information on the electronic and steric properties of over 300 000 monodentate phosphorus(III) ligands. These properties were either derived from DFT calculations or from a machine learning model trained by the DFT-derived data. Furthermore, for ligands with DFT-derived properties, Cartesian coordinates for all accessible conformers are available. To identify appropriate ligands for our purposes, we extracted phosphine ligands from the kraken database based on the following criteria: (1) it is a C₃ symmetric trialkyl phosphine, (2) Cartesian coordinates of conformers are available, and (3) the number of accessible conformers is sufficiently small (less than 20). The first criterion was based on the ease of synthesizing symmetric ligands. Although C₃ symmetric triaryl phosphines could also be potential candidates, we chose to exclude them owing to the low likelihood of finding ligands with high C–Cl selectivity while maintaining sufficient electron-donating ability for oxidative addition to occur (Fig. 4a, ν_CO < 2230 cm⁻¹). The second criterion was set to ensure the efficiency of the parameter calculations. To predict the ΔΔG^‡ value of a given ligand using contour maps, the TEP and cone angle of the ligand are required. While the cone angle is available in the kraken database, the TEP value must be computed at the same level as the parameter screening (the ωB97X-D/def2-SVP level in this study). Assuming the Cartesian coordinates of all accessible conformers of a given ligand are available, TEP can be rapidly calculated without conducting conformational sampling. Although this criterion might exclude certain optimal ligands from the machine learning model, it is still beneficial to avoid the time-consuming process of conformational sampling. The third criterion was implemented to eliminate conformationally flexible ligands, which may not be accurately predicted by contour maps, as showcased in Fig. 5c. Consequently, we obtained 18 trialkyl phosphine ligands (K1–K18) (Fig. 6b). The TEP values and cone angles of these ligands were calculated as the Boltzmann-weighted average among all conformers obtained from the kraken, and ΔΔG^‡ values were predicted using the contour map prepared by VL2_PR3 (Fig. 6a, center and Fig. 6b, ΔΔG^‡_predicted). The predictions showed that ligands K1–K7 would exhibit positive ΔΔG^‡ values, resulting in C–O bond selective activation. This was supported by experimental results for four of these ligands presented in Fig. 5 (i.e., K1, K3, K4, and K5 are the same ligands as L58, L19, L62, and L20, respectively). In contrast, out of the remaining 11 ligands predicted to exhibit some extent of C–Cl selectivity (K8–K18), only P^tBu₃ (K11) has been experimentally evaluated. Therefore, we decided to synthesize and evaluate several of the remaining ligands (K8–10 and K12–18) to identify other optimal ligands for C–Cl bond activation. Synthetic methods for four of these ligands (K9,²³K14,²⁴K17,²⁵ and K18²⁵) have already been reported. Given the expected low reactivity of electron-deficient palladium(0) complexes with K17 or K18 towards oxidative addition, we chose ligands K9 and K14 as the target compounds. We synthesized these ligands following reported procedures,^23,24 and evaluated their chemoselectivity in the SMC reaction (Fig. 6c). To our delight, K14 was found to exhibit excellent C–Cl selectivity (over 99%), while K9 also showed high chemoselectivity (91%). The experimental ΔΔG^‡ values were estimated to be −1.62 kcal mol⁻¹ for K9 and −3.44 kcal mol⁻¹ for K14, which are qualitatively consistent with the predicted values (−0.37 kcal mol⁻¹ for K9 and −7.55 kcal mol⁻¹ for K14). These ligands have already been reported as active ligands for the cross-coupling reactions of aryl halides, including aryl chlorides.²⁶ However, to the best of our knowledge, chemoselectivity in the oxidative addition of chloroaryl triflates, including compound 1, has not been previously reported. Considering well-known success of P^tBu₃ in achieving C–Cl bond activation¹⁵ and the availability of mechanistic insights on this specific reaction,^16–18 ligands K9 and K14 would appear to be intuitive candidates for chemists. However, our protocol of VLA screening did not utilize any experimental data, including those shown in Fig. 5, in selecting these ligands as candidates. Therefore, these results and the success of our protocol in predicting C–O selective ligands (K1, K3, K4 and K5, Fig. 6b) suggest that VLA screening can be a useful strategy for in silico ligand screening.

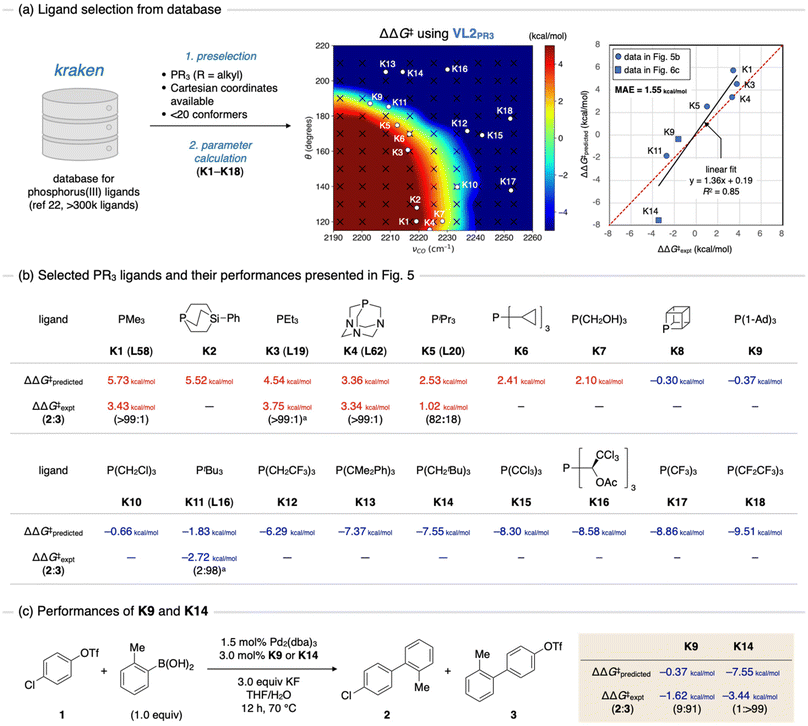Fig. 6 Ligand discovery using the contour maps as a guiding principle. (a) Extraction of candidates from ligand database, kraken. (b) The chemical structures of candidate ligands and their performance shown in Fig. 5. (c) Performance of synthesized ligands K9 and K14. Ad: adamantyl. ^aCalculated at 70 °C based on reported values of ΔΔG^‡.

Conclusions

In this study, the VLA screening, an in silico strategy for ligand screening, was experimentally demonstrated. The chemoselective SMC reaction of p-chlorophenyl triflate (1) was chosen as a model case, and the impact of electronic and steric effects of phosphine ligands on the chemoselectivity were investigated through quantum chemical calculations using virtual ligands. The results were visualized by the contour map and validated with experimental data for 53 phosphine ligands. Then, the contour map was employed to predict performances of phosphine ligands selected from a database. As a result, we successfully found that tri(1-adamantyl)phosphine (K9) and tri(neopentyl)phosphine (K14) show high to excellent selectivity for the C–Cl bond activation. This case study indicates the utility of the VLA screening as a potentially valuable approach for ligand screening and catalyst design.

On the other hand, the scope of VLA screening is still severely limited by the design and performance of virtual ligands. The current virtual ligands (VL1 and VL2) are only applicable for screening of simple phosphine ligands as they describe real ligands only by two parameters (i.e., electronic and steric). This resulted in the suggestion of somewhat “obvious” optimal ligands from chemical viewpoint (K9 and K14). To apply VLA screening for more complicated ligands such as Buchwald-type ligands, more sophisticated virtual ligands which reproduce and parameterize other important aspects of real ligands including functional group-specific interactions need to be developed. Furthermore, the development of virtual ligands for other classes of ligands such as pyridines, amino acids, NHCs and multi-dentate ligands would greatly expand the scope of VLA screening. Therefore, the development of new virtual ligands, thereby generalizing its concept, is an urgent task.

Data availability

The data that support the findings of this study are available in the ESI.†

Author contributions

W. M. conducted all DFT calculations and experiments. Y. H. and S. M. supervised the computational work. Y. N. supervised the experimental work. All authors contributed to write the manuscript and ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JST via the ERATO grant JPMJER1903. Support was also provided by the Institute for Chemical Reaction Design and Discovery (ICReDD), established by the World Premier International Research Initiative (WPI), MEXT, Japan.

References

1. For selected reviews, see: (a) M. Beller, B. Cornils, C. D. Frohning and C. W. Kohlpaintner, J. Mol. Catal. A: Chem., 1995, 104, 17–85; (b) F. Agbossou, J.-F. Carpentier and A. Mortreux, Chem. Rev., 1995, 95, 2485–2506; (c) B. Breit, Acc. Chem. Res., 2003, 36, 264–275; (d) R. Franke, D. Selent and A. Börner, Chem. Rev., 2012, 112, 5675–5732; (e) S. Chakrabortty, A. A. Almasalma and J. G. de Vries, Catal. Sci. Technol., 2021, 11, 5388–5411.
2. For selected reviews, see: (a) R. R. Schrock and A. H. Hoveyda, Angew. Chem., Int. Ed., 2003, 42, 4592–4633; (b) R. H. Grubbs, Tetrahedron, 2004, 60, 7117–7140; (c) T. J. Donohoe, A. J. Orr and M. Bingham, Angew. Chem., Int. Ed., 2006, 45, 2664–2670; (d) A. H. Hoveyda and A. R. Zhugralin, Nature, 2007, 450, 243–251; (e) S. P. Nolan and H. Clavier, Chem. Soc. Rev., 2010, 39, 3305–3316; (f) G. C. Vougioukalakis and R. H. Grubbs, Chem. Rev., 2010, 110, 1746–1787; (g) O. M. Ogba, N. C. Warner, D. J. O'Leary and R. H. Grubbs, Chem. Soc. Rev., 2018, 47, 4510–4544.
3. For selected reviews, see: (a) N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483; (b) C. C. C. Johansson Seechurn, M. O. Kitching, T. J. Colacot and V. Snieckus, Angew. Chem., Int. Ed., 2012, 51, 5062–5085; (c) J. Magano and J. R. Dunetz, Chem. Rev., 2011, 111, 2177–2250; (d) C. S. Yeung and V. M. Dong, Chem. Rev., 2011, 111, 1215–1292; (e) P. Ruiz-Castillo and S. L. Buchwald, Chem. Rev., 2016, 116, 12564–12649; (f) Y.-F. Zhang and Z.-J. Shi, Acc. Chem. Res., 2019, 52, 161–169.
4. For selected reviews focusing on specific classes of organic ligands, see: (a) M. Berthod, G. Mignani, G. Woodward and M. Lemaire, Chem. Rev., 2005, 105, 1801–1836; (b) R. G. Arrayás, J. Adrio and J. C. Carretero, Angew. Chem., Int. Ed., 2006, 45, 7674–7715; (c) R. Martin and S. L. Buchwald, Acc. Chem. Res., 2008, 41, 1461–1473; (d) C. Valente, S. Çalimsiz, K. H. Hoi, D. Mallik, M. Sayah and M. G. Organ, Angew. Chem., Int. Ed., 2012, 51, 3314–3332; (e) B. Ye and N. Cramer, Acc. Chem. Res., 2015, 48, 1308–1318; (f) Q. Zhao, G. Meng, S. P. Nolan and M. Szostak, Chem. Rev., 2020, 120, 1981–2048.
5. For selected reviews focusing on chemical libraries and the high-throughput screening of ligands, see: (a) P. E. Goudriaan, P. W. N. M. van Leeuwen, M.-N. Birkholz and J. N. H. Reek, Eur. J. Inorg. Chem., 2008, 2939–2958; (b) K. D. Collins, T. Gensch and F. Glorius, Nat. Chem., 2014, 6, 859–871; (c) M. Renom-Carrasco and L. Lefort, Chem. Soc. Rev., 2018, 47, 5038–5060.
6. For selected examples, see: (a) K. Wu and A. G. Doyle, Nat. Chem., 2017, 9, 779–784; (b) A. V. Brethomé, R. S. Paton and S. P. Fletcher, ACS Catal., 2019, 9, 7179–7187; (c) S. H. Newman-Stonebraker, S. R. Smith, J. E. Borowski, E. Peters, T. Gensch, H. C. Johnson, M. S. Sigman and A. G. Doyle, Science, 2021, 374, 301–308; (d) J. A. Hueffel, T. Sperger, I. Funes-Ardoiz, J. S. Ward, K. Rissanen and F. Schoenebeck, Science, 2021, 374, 1134–1140; (e) J. Xu, S. Grosslight, K. A. Mack, S. C. Nguyen, K. Clagg, N.-K. Lim, J. C. Timmerman, J. Shen, N. A. White, L. E. Sirois, C. Han, H. Zhang, M. S. Sigman and F. Gosselin, J. Am. Chem. Soc., 2022, 144, 20955–20963.
7. For selected examples, see: (a) A. Uhe, M. Hölscher and W. Leitner, Chem. – Eur. J., 2012, 18, 170–177; (b) M. Hölscher, A. Uhe and W. Leitner, J. Organomet. Chem., 2013, 748, 13–20; (c) M. C. Nielsen, K. J. Bonney and F. Schoenebeck, Angew. Chem., Int. Ed., 2014, 53, 5903–5906; (d) G. Jindal and R. B. Sunoj, Org. Biomol. Chem., 2014, 12, 2745–2753; (e) R. N. Straker, Q. Peng, A. Mekareeya, R. S. Paton and E. A. Anderson, Nat. Commun., 2016, 7, 10109; (f) Y. Guan and S. E. Wheeler, Angew. Chem., Int. Ed., 2017, 56, 9101–9105; (g) D.-H. Kwon, J. T. Fuller, U. J. Kilgore, O. L. Sydora, S. M. Bischof and D. H. Ess, ACS Catal., 2018, 8, 1138–1142.
8. (a) K. N. Houk and F. Liu, Acc. Chem. Res., 2017, 50, 539–543; (b) S. Hammes-Schiffer, Acc. Chem. Res., 2017, 50, 561–566; (c) C. Poree and F. Schoenebeck, Acc. Chem. Res., 2017, 50, 605–608.
9. (a) I. Funes-Ardoiz and F. Schoenebeck, Chem, 2020, 6, 1904–1913; (b) N. Fey and J. M. Lynam, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1590.
10. For selected reviews focusing on automated or high-throughput computations, see: (a) M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354–2377; (b) A. Nandy, C. Duan, M. G. Taylor, F. Liu, A. H. Steeves and H. J. Kulik, Chem. Rev., 2021, 121, 9927–10000; (c) For selected examples, see: E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, J. Comput. Chem., 2016, 37, 2106–2117; (d) Y. Guan, V. M. Ingman, B. J. Rooks and S. E. Wheeler, J. Chem. Theory Comput., 2018, 14, 5249–5261; (e) A. R. Rosales, J. Wahlers, E. Limé, R. E. Meadows, K. W. Leslie, R. Savin, F. Bell, E. Hansen, P. Helquist, R. H. Munday, O. Wiest and P.-O. Norrby, Nat. Catal., 2019, 2, 41–45.
11. W. Matsuoka, Y. Harabuchi and S. Maeda, ACS Catal., 2022, 12, 3752–3766.
12. (a) Y. Ohnishi, Y. Nakao, H. Sato and S. Sakaki, J. Phys. Chem. A, 2008, 112, 1946–1955; (b) N. Koga and K. Morokuma, Chem. Phys. Lett., 1990, 172, 243–248; (c) S. Kozuch and S. Shaik, J. Mol. Catal. A: Chem., 2010, 324, 120–126.
13. For selected examples of our contribution, see: (a) S. Maeda, T. Taketsugu and K. Morokuma, J. Comput. Chem., 2014, 35, 166–173; (b) S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki, T. Ichino, Y. Sumiya, K. Sugiyama and Y. Ono, J. Comput. Chem., 2018, 39, 233–250; (c) S. Maeda and Y. Harabuchi, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1538; (d) For other examples, see: L. P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Nat. Chem., 2014, 6, 1044–1048; (e) Y. V. Suleimanov and W. H. Green, J. Chem. Theory Comput., 2015, 11, 4248–4259; (f) C. A. Grambow, A. Jamal, Y. P. Li, W. H. Green, J. Zádor and Y. V. Suleimanov, J. Am. Chem. Soc., 2018, 140, 1035–1048; (g) P. M. Zimmerman, J. Comput. Chem., 2013, 34, 1385–1392; (h) P. M. Zimmerman, J. Comput. Chem., 2015, 36, 601–611; (i) G. N. Simm, A. C. Vaucher and M. Reiher, J. Phys. Chem. A, 2019, 123, 385–399.
14. C. A. Tolman, Chem. Rev., 1977, 77, 313–348.
15. A. F. Littke, C. Dai and G. C. Fu, J. Am. Chem. Soc., 2000, 122, 4020–4028.
16. F. Barrios-Landeros, B. P. Carrow and J. F. Hartwig, J. Am. Chem. Soc., 2009, 131, 8141–8154.
17. (a) F. Schoenebeck and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 2496–2497; (b) M. Ahlquist and P.-O. Norrby, Organometallics, 2007, 26, 550–553; (c) C. L. McMullin, J. Jover, J. N. Harvey and N. Fey, Dalton Trans., 2010, 39, 10833–10836; (d) S. Kozuch and J. M. L. Martin, ACS Catal., 2011, 1, 246–253; (e) C. L. McMullin, N. Fey and J. N. Harvey, Dalton Trans., 2014, 43, 13545–13556; (f) E. Lyngvi, I. A. Sanhueza and F. Schoenebeck, Organometallics, 2015, 34, 805–812.
18. Z. L. Niemeyer, A. Milo, D. P. Hickey and M. S. Sigman, Nat. Chem., 2016, 8, 610–617.
19. C. Choi and R. Elber, J. Chem. Phys., 1991, 94, 751–760.
20. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, I. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272.
21. For selected examples, see: (a) T. E. Barder, S. D. Walker, J. R. Martinelli and S. L. Buchwald, J. Am. Chem. Soc., 2005, 127, 4685–4696; (b) D. S. Surry and S. L. Buchwald, Chem. Sci., 2011, 2, 27–50.
22. T. Gensch, G. dos Passos Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D'Addario, M. S. Sigman and A. Aspuru-Guzik, J. Am. Chem. Soc., 2022, 144, 1205–1217.
23. L. Chen, P. Ren and B. P. Carrow, J. Am. Chem. Soc., 2016, 138, 6392–6395.
24. (a) R. B. King, J. C. Cloyd Jr. and R. H. Reimann, J. Org. Chem., 1976, 41, 972–977; (b) F. Rampf and H.-C. Militzer, European Pat., EP1354886A1, 2003.
25. M. B. Murphy-Jolly, L. C. Lewis and A. J. M. Caffyn, Chem. Commun., 2005, 4479–4480.
26. For selected examples, see: (a) B. P. Carrow and L. Chen, Synlett, 2017, 280–288; (b) S. M. Raders, J. N. Moore, J. K. Parks, A. D. Miller, T. M. Leißing, S. P. Kelley, R. D. Rogers and K. H. Shaughnessy, J. Org. Chem., 2013, 78, 4649–4664; (c) L. L. Hill, J. M. Smith, W. S. Brown, L. R. Moore, P. Guevera, E. S. Pair, J. Porter, J. Chou, C. J. Wolterman, R. Craciun, D. A. Dixon and K. H. Shaughnessy, Tetrahedron, 2008, 64, 6920–6934.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and computational details, analytical data, additional discussions, and GC spectra (PDF); optimized cartesian coordinates (XYZ). See DOI: https://doi.org/10.1039/d3ob00398a

---