Turning on hotspots: supracolloidal SERS probes made brilliant by an external activation mechanism

Abstract

We achieved external activation of local hot-spot sites in supracolloidal assembly structures. The concept was demonstrated by boosting surface-enhanced Raman scattering (SERS) efficiency by one order of magnitude through a heating-induced process. Our approach involves assembling gold nanoparticles with distinct dimensions, i.e. 16 and 80 nm, into well-defined planet–satellite-type arrangement structures using thermoresponsive (poly(N-isopropylacrylamide)) star polymer linkers. Insights into the assembly process were obtained by calculations within the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory framework. We observe one order of magnitude increase in SERS enhancement by a heating-induced volume-phase transition. This magnification aligns with simulations run using the finite-difference time-domain (FDTD) method. The implications of this adaptive supracolloidal concept are twofold: Firstly, our approach bypasses limitations of existing systems that are associated with the limited accessibility of electromagnetic hot-spot sites in strongly coupled, static assemblies of plasmonic nanoparticles, by providing the capability of dynamic hot-spot re-configuration. Second, these externally activated probes offer promising opportunities for the development of messenger materials and associated sensing strategies.

---

Introduction

The interaction between metal nanoparticles (NPs) and electromagnetic radiation of a suitable frequency leads to the excitation of localized surface plasmon resonance (LSPR) modes.¹ Concomitantly with this excitation, an intense electromagnetic near-field emerges, which is significantly enhanced compared with the incident field intensity.² This field enhancement can be amplified further through electrodynamic coupling interactions, that occur when two or more metal NPs are positioned in close proximity, giving rise to electromagnetic “hot-spots” in the inter-NP gaps.³ Clusters of metal NPs with short interparticle separations can therefore be used to drastically enhance light–matter interactions, for example in surface-enhanced vibrational spectroscopic methods, such as surface-enhanced Raman spectroscopy (SERS).⁴ Consequently, supracolloidal clusters of metal NPs hold great promise as field-enhanced biosensors for applications at the point of care.⁵ Substrate-based approaches⁶ that involve the patterning of surfaces with plasmonic NP clusters⁷ provide a versatile platform in this regard and paved the way to (bio-)sensor chips.^8,9 For solution-based SERS, different strategies were developed, involving for example enhancement from cross-linked NP networks¹⁰ and NP chain assemblies.¹¹ In this domain, achieving consistent SERS is essential. Part of the appeal of structurally well-defined so-called planet–satellite-type clusters is this capability of providing consistent SERS signals,^12–14 making them proper candidates for quantitative SERS. Moreover, their architecture makes the concentration of many electromagnetic “hot-spots” in a small volume possible,¹⁵ giving rise to strong SERS enhancement (that scales with the number of attached satellites).¹⁶ Notably, comparably large SERS enhancement can be achieved using planet–satellite-type clusters,^12,17 which allows the spectrum collection from single clusters,¹² and the in situ chemical imaging of living cells.^18,19 Although hot-spot-dominated SERS probes can typically fulfill the above-mentioned requirements of defined and consistent spectroscopic signals, ensuring the accessibility of the hot-spot sites for analyte molecules can be challenging. This accessibility of hot-spot sites in planet–satellite nanostructures depends on the synthetic route that is used for their fabrication, particularly on the choice of the particle-linking entities that connect the planet with the satellite NPs. These are typically chosen to produce small interparticle gap distances, leading to strong SERS enhancement. Among the different types of spacers, silica shell spacers provide a permanent barrier blocking the hot-spot sites. Therefore, the SERS reporter molecules must be placed within the hot-spots during planet–satellite-assembly.^20,21 The use of folded and, therefore, highly compacted protein spacers¹⁵ can significantly impede analyte adsorption,¹⁷ greatly reducing the practicability of the produced SERS probes. Small molecule spacers typically result in dense surface grafted layers, which may also restrict analyte access toward the hot-spot. This is why in related studies^22–24 they typically serve as SERS-active reporter molecules themselves. In contrast, synthetic macromolecular linkers²⁵ represent planet–satellite linking entities that form swollen brush layers that are not dense in a good solvent environment.²⁶ These solvent-swollen brush layers typically lead to relatively large planet–satellite separations resulting in decreased field enhancement in the hot-spots. However, it is possible to endow these macromolecular linkers with responsive features,²⁷ such that conformational transitions in the linking brush layers lead to on-demand reduction of planet–satellite spacings upon application of suited external stimuli.²⁸ RAFT (Reversible Addition–Fragmentation chain Transfer)²⁹ polymers of N-isopropylacrylamide (NIPAM) with linear^26,30,31 and star topology^26,28,32,33 have recently been introduced as such responsive linkers in planet–satellite nanostructures.

Based on this precedent, we developed a planet–satellite-type SERS platform with responsive polymer linkers that provide hot-spot accessibility under conditions in which the polymer linker is solvent-swollen, with the possibility to reduce the planet– satellite separation after successful analyte adsorption. Thus, we present a prototype platform for activating electromagnetic hot-spots in plasmonic nanoparticle clusters on-demand via an external activation mechanism. We submit that this platform can be adapted to other kinds of external stimuli by adjusting the chemical nature of the linking polymer,²⁷ thereby offering potential for applications in e.g. process-control or biosensing.

Experimental section

Materials

Hydrogen tetrachloroaurate(III) trihydrate (≥99.9%, HAuCl₄·3H₂O), sodium citrate tribasic dihydrate (≥99%), pentaerythritol tetrakis[2-(dodecylthiocarbonothioylthio)-2-methylpropionate] (4-arm star RAFT agent), 2,2′-azobis(2-methylpropionitril) (AMPN), pure Tween 20 solution, and sodium chloride (≥99%) were purchased from Sigma-Aldrich and used as received. Toluene (≥99%), N,N-dimethylformamide (DMF, ≥99%), acetone (≥99%), and methanol (≥99%) were purchased from Acros Organics (Germany), and n-hexane (≥99%) was purchased from Merck KGaA (Germany). N-isopropylacrylamide (NIPAM) was recrystallized before use from toluene/n-hexane (1 : 3), including hot filtration, cooling, and supernatant removal, after which the needle-like crystals were washed with hexane, dried under vacuum, and stored refrigerated in a sealed container. The other chemicals were used as received. Milli-Q water was used in all experiments. All glassware for preparation of AuNPs was cleaned with aqua regia and rinsed extensively with Milli-Q water before use.

Methods

Synthesis of 4-arm-star RAFT poly(NIPAM). The polymerization of the NIPAM monomer was performed by the RAFT method.²⁹ Commercial 4-arm star RAFT agent, thermal initiator AMPN, NIPAM monomer and N,N-dimethylformamide were mixed according to the molar ratio of 1.0 : 0.072 : 200 : 600 and purged with nitrogen for 10 min before being heated to 65 °C for 120 min. The polymer was purified by repeated precipitation. Size exclusion chromatography revealed a number–average molar mass M_n of 30 kg mol⁻¹ (see Table S1 and Fig. S1, ESI†).

Synthesis of citrate-stabilized AuNPs. Quasi-spherical citrate-stabilized gold nanoparticles (AuNPs) with an average diameter of ∼16 nm were synthesized by the citrate-reduction method.³⁴ Briefly, in a 1 L Erlenmeyer flask, aqueous HAuCl₄ solution (1.88 mL, 0.1 M) was added to 750 mL of Milli-Q water and heated to boiling. Aqueous sodium citrate solution (18 mL, 1 wt%) was rapidly injected under vigorous stirring, resulting in a color change of the solution from clear to blue, gray, finally to a wine-red hue. The 16 nm-AuNP solution was allowed to cool down to room temperature. A portion was stored to be used as satellite building blocks in colloidal assembly (citrate@Au₁₆). For the generation of larger particles, 300 mL of the 16 nm AuNP solution was heated to 90 °C in a three-neck round bottom flask. Sodium citrate solution (2.4 mL, 0.1 M) and HAuCl₄ (2 mL, 25 mM) were added, and the solution was stirred for 30 min. This procedure was repeated nine times to achieve a particle diameter of ∼80 nm for use as building blocks (planets) in the following experiments of colloidal assembly (see Fig. S2, ESI†).

Colloidal assembly. The 80 nm AuNP planets were collected from 1 mL colloidal solution by centrifugation (3500 rpm, 10 min) and re-dispersed in a solution of poly(NIPAM) in methanol (2 mg mL⁻¹). After overnight incubation and three cycles of centrifugation/ re-dispersion in methanol, the polymer-coated planets (poly(NIPAM)@Au₈₀) were re-dispersed into 1 mL Milli-Q water. The assembly into planet–satellite nanostructures was performed using surfactants as previously described.³⁰ Briefly, 25 μL Tween 20 aqueous solution (2.5 wt%) and 63 μL NaCl aqueous solution (0.2 M) were added into 912 μL aqueous solution of collected AuNP satellites (citrate@Au₁₆). The polymer-coated planet particles (poly(NIPAM)@Au₈₀) in water were added dropwise to the described satellite solution under vigorous stirring. After incubation for three days, the resultant planet–satellite assemblies were collected by sedimentation and twice re-dispersed into 1 mL Milli-Q water containing 25 μL Tween 20 solution (2.5 wt%) for further purification via sedimentation/re-dispersion.

DLVO calculations. The electrostatic double layer interaction energy between two differently charged particles was calculated according to:³⁵

Here, ε is the dielectric constant, ε₀ the vacuum permittivity, κ the inverse Debye length, ψ_i the surface potential of phase i, and p is a regulation parameter that quantifies the extent of the charge variation of the surface as they approach each other; p₁ = p₂ = 1 yields the classic boundary condition of constant charge. We assume the assumption of low potentials for 1 : 1 electrolyte, that the satellite-to-satellite interactions are negligible, and we neglect effects mediated by the intervening polymer. We convert W(L) to an interaction force, F_e, via the Derjaguin approximation, where F = 2πRW(L), and R is the effective radius given by R = R₁R₂/(R₁ + R₂), where R_i is the radius of particle i. The DLVO relation is obtained with a combination of the van der Waals attraction,

F = F_vdW + F_e

where F_vdW is the van der Waals attraction, given within the framework of Lifshitz theory, as F_vdW = −AR/6L², where A is the Hamaker constant, taken for Au-to-Au interactions across a water medium as 10 to 40 × 10⁻²⁰ J.³⁶

Finite-difference time-domain (FDTD) simulations. Finite-difference time-domain (FDTD) based numerical calculations were performed using a commercial-grade electromagnetic solver (Ansys Lumerical FDTD: 3D Electromagnetic Simulator, version 8.16). To investigate the Mie scattering-based optical responses of AuNP-based planet–satellite structures in water, Total-Field Scattered-Field (TFSF) sources were used with PML boundary conditions along the X, Y, and Z coordinates with an FDTD background index of 1.33. For the dielectric properties of gold, data from Johnson and Christy³⁷ were fitted using six coefficients with an RMS error of 0.2, whereas refractive index data from Brasse et al.³⁸ were used for the poly(NIPAM) layer. Electric fields and corresponding intensity profiles are obtained using frequency domain field and power monitors passing through the diametric cross-section of the core and the satellites. To enhance accuracy, an additional fine mesh with dx = 0.4 nm, dy = 0.4 nm, and dz = 0.4 nm was implemented.

Characterization

Transmission electron microscopy (TEM). TEM images were obtained using a Zeiss TEM Libra 200 at an accelerating voltage of 200 kV. Samples were prepared by placing ∼8 μL droplets of diluted nanoparticle solution on TEM grids (copper, 200 mesh, carbon coated; Science Services GmbH) and solvent evaporation under ambient pressure.

UV-Vis extinction spectroscopy. UV-Vis-NIR spectra were acquired with a spectrophotometer Cary 5000 (Agilent Technologies Deutschland GmbH). The extinction at the wavelength of 400 nm (interband transitions), which is assumed to have a size-independent absorption coefficient,³⁹ was used to normalize the spectra and calculate the gold-atom content in the nanoparticle solution. In addition, temperature-dependent visible light extinction spectra were measured with a spectrometer SPECORD 40 (Analytik Jena GmbH) equipped with temperature control. Spectra were recorded repeatedly at 25 °C and 40 °C after 15 minutes of temperature equilibration time, and the maxima were determined by a second-degree polynomial fit between 520 and 600 nm.

Size-exclusion chromatography (SEC). Molar mass characterization was performed using a size-exclusion chromatography (SEC) system consisting of a high-performance liquid chromatography pump 1200 (Agilent Technologies, US) and a PolarGel-M column (300 × 7.5 mm², Polymer Labs, UK) coupled to a differential refractive index detector K-2301 (Knauer, DE) and a multiangle light scattering detector TREOS II (Wyatt Technology, US). As an eluent, N,N-dimethylacetamide with 3 g L⁻¹ LiCl at a flow rate of 1.00 mL min⁻¹ was used.

Temperature-dependent dynamic light scattering (DLS) and zeta-potential. The temperature-dependent DLS was performed using a Malvern Panalytical Nano ZS Zetasizer with a laser wavelength of 633 nm and temperature control for measurements at 25 °C and 40 °C. Reported data are averages from 3 repeated measurements at every temperature, where each measurement consists of 50 acquisitions over 5 s, respectively, up to 5 cycles in total. After the temperature change an equilibration time of 10 minutes was applied to ensure homogenous temperature distribution. Zeta-potential measurements were performed using the same instrument with a Folded Capillary Zeta Cell (Malvern Panalytical) in a 6.3 mM NaCl solution. Reported data are averages from 3 measurements per sample, and the Z-average value represents the diameter.

Surface-enhanced Raman scattering. Surface-enhanced Raman scattering (SERS) measurements were recorded with a WITec alpha300 RS confocal Raman microscope (Ulm, Germany) equipped with a 785 nm laser. The Raman scattered light was collected through a 10× objective lens with the laser on the sample was 80 mW. SERS spectra were recorded employing a 300 g mm⁻¹ grating, an integration time of 1 s, and a single cumulation. Prior to the SERS measurement, 500 μL nanoparticles underwent centrifugation at 8500 rpm for 15 min. This process was undertaken to eliminate excess ligands. Following this, the nanoparticles were dispersed in 100 μL of 10^–4 M 4-mercaptobenzonitrile (4-MBN) aqueous solution and left to incubate overnight at 4 °C before direct measurement. For each measurement, 20 μL of the prepared sample were added into an aluminum crucible and rested on a heating plate for 2 min before the spectral acquisition was initiated.

Results and discussion

Formation of planet–satellite-type clusters

For this work, 4-arm star-poly(NIPAM) was synthesized following a core-first R-group approach,⁴⁰ where the star topology is already implemented in the commercial RAFT agent (Fig. 1) and the polymer average molar mass was confirmed with size exclusion chromatography (Table S1, and Fig. S1†). Gold nanospheres of about 80 nm diameter were synthesized by a modified Frens method.³⁴ The nanospheres were functionalized with the RAFT 4-arm star-poly(NIPAM) following a “grafting-to” strategy⁴¹ that involved immersing overnight in methanol solution (see Experimental section). Subsequently, we attempted the binding of citrate-stabilized satellite particles (citrate@Au₁₆) to the free sulfur-containing RAFT end groups.^26,32 In pure MilliQ water, this step did not yield the targeted planet–satellite clusters, and we speculated that surface charges represent a major inhibiting factor. Han et al.³⁰ successfully tethered satellite nanoparticles to poly(NIPAM)-stabilized planets by adding NaCl and the non-ionic surfactant Tween20.

Fig. 1 Synthesis scheme of 4-arm star RAFT poly(NIPAM), functionalization of gold 80 nm particles and tethering of 16 nm gold nanoparticles as satellites.

To achieve an understanding of the involved colloidal interactions, we performed electrophoretic (zeta-potential) measurements for the involved colloidal building blocks in both MilliQ water (pH = 5.3) and a solution of NaCl (6.3 mM) (Table 1). These measurements use the movement of charged nanoparticles as a reaction to an external electrical field and provide an experimental approach to estimate the surface charges.⁴² Following the approach of Trefalt et al.,³⁵ the electrostatic double layer free energy from differently charged particles was calculated (for details, see Methods section). This approach neglects structuring forces in water,⁴³ and interfacial interactions that differ from bulk,⁴⁴ as well as any effects from the polymer, but nonetheless, it was observed that in the solution with no added salt, repulsive forces dominate for all but very close distances (Fig. 2a, red) meaning that the particles will repel each other unless forced together, and that no strong Au-to-Au interactions contribute to the assembly. Therefore, particles are not inclined to approach each other toward shorter distances, a prerequisite for satellite tethering. Only with increased ionic strength the curve is pushed towards the negative regime, where attractive forces dominate at all length scales and allow the particles to get in sufficient proximity for the tethering of satellites (Fig. 2a, blue). Therefore, NaCl (6.3 mM) was added to the satellite solution prior to tethering to increase the ionic strength and allow for this assembly to occur. Additionally, the non-ionic surfactant Tween 20 was used to stabilize the satellite particles against electrolyte-induced aggregation, as reported by Han et al.³⁰ The functionalized planets were then added to the satellite solution, and after immersion overnight and removal of unbound excess satellite particles (see Experimental section), the final planet–satellite clusters formed (Fig. 2b–d). While there is a dispersion with regard to the number of satellite particles attached, we find that on average 3 satellite particles are grabbed by the polymer layer surrounding the central “planet” particle (Fig. S3†).

Fig. 2 (a) Force–distance functions resulting from DLVO theory calculations with and without addition of 6.3 mM NaCl electrolyte solution. The upper and lower bounds in each curve correspond to variations in the Hamaker constant. (b–d) TEM images of final planet–satellite clusters with 80 nm Au cores, poly(NIPAM) linker and 16 nm Au satellites, taken at different magnifications.

Table 1 Nanoparticle size from TEM images and zeta potentials of functionalized planets and citrate-stabilized satellites in water and 6.3 mM electrolyte solution

	Poly(NIPAM)@Au80 (planets)	Citrate@Au16 (satellites)
Size [nm]	80 ± 12.0	16 ± 2.3
ζ no salt [mV]	−10.3 ± 0.5	−32.9 ± 2.0
ζ 6.3 mM [mV]	−1.4 ± 2.3	−15.3 ± 1.3

---

Dynamic hot-spot re-configuration

When heated above the lower critical solution temperature (LCST), the poly(NIPAM) spacer undergoes a phase transition,⁴⁵ resulting in a globular state with reduced spacing between planets and satellites.^28,30 The distance change between the plasmonic nanoparticles results in a change of the extinction profile at visible frequencies.^3,30 Therefore, extinction spectroscopy can be used to study the magnitude and reversibility of the distance change.³⁰

The optical extinction properties can be modulated reversibly over several heating/cooling cycles (Fig. 3a and c, Fig. S4a†). Upon heating, we find reduced extinction values at the original peak maximum and increased extinction toward higher wavelengths, apparent in a tailing of the spectra toward the red (Fig. 3a, and Fig. S4a†). The simulated extinction spectra, although showing more narrow resonances, show similar behavior (Fig. 3b, and Fig. S4b†). The simulated spectra furthermore reveal increased absorbance toward higher wavelengths (Fig. S4c†) and a decreased scattering contribution at higher temperature (Fig. S4d†). Because of the observed reversibility, we attribute the tailing in the experimentally observed extinction spectra (Fig. 3a, and Fig. S4a†) to the dispersity of the experimental system,³ rather than uncontrolled aggregation, which would be expected to be irreversible. The temperature-dependent size-switching behavior of the clusters was revealed using dynamic light scattering, which provided the hydrodynamic diameter of the entire cluster assembly (see Fig. S5† for the intensity-distributions). The overall cluster dimension in the expanded state is reasonable considering the distribution in the “planet” particle dimension (Fig. S2†) and the expected polymer shell dimension together with the bias of the DLS method toward larger sizes. Repeated switching of the particle dimension can be observed for several heating/cooling cycles, while the count rate of scattered photons shows no significant changes (Fig. 3d). Thereby, strong aggregation during the heating/cooling cycles can be ruled out, as this would (i) result in an increase in the scattering intensity and (ii) change of the Z-average to significantly larger dimension, as the dimensions determined by DLS are intensity-weighted and therefore highly sensitive to large aggregates.

Fig. 3 Reversible switching behaviour revealed: (a) Experimental extinction spectra below and above LCST; (b) FDTD simulation of extinction spectra at 25 °C and 40 °C; (c) change in absorption maximum from visible light extinction spectroscopy over multiple cycles; and (d) change in cluster diameter estimated from dynamic light scattering. (e) SERS signal of the clusters with 4-MBN as marker molecule at 25 °C and 40 °C.

The DLS results reveal a reversible swelling/contraction of the hydrodynamic diameter of the overall nanostructures by ∼30 nm, i.e. a change in polymer layer thickness of ∼15 nm. To put this value into perspective with regard to particle spacings, we can rely on previously determined²⁶ end-monomer distributions and satellite-particle distributions. It is established that the former decays to zero ∼5 nm farther from the planet particle than the latter distribution.²⁶I.e., in the solvent-swollen state, the satellite particles can penetrate roughly 5 nm into the brush. Thus, the reversible diameter change relates to a change in the planet–satellite particle spacing of ∼10 nm. Furthermore, it is verified that switching occurs on time scales that are smaller than those of one light scattering measurement (few minutes), which is in line with the very fast (∼10 to 100 ns) switching dynamics⁴⁶ observed for simpler gold–core–poly(NIPAM)–shell structures.

In the next step, we evaluated the SERS capabilities of the produced nanostructures. For the SERS experiments, 4-mercaptobenzonitrile (4-MBN) was chosen, structurally closely related to 4-mercaptobenzoic acid (4-MBA), known as a strongly adsorbing, universal SERS reporter molecule⁴⁷ that is commonly used in colloidal systems.¹⁵ Incubation with 4-MBN was done at 25 °C so that the polymer spacer is in a swollen state and analyte access is facilitated. SERS spectra were then recorded at 25 °C and 40 °C using excitation at 785 nm. The pure clusters without 4-MBN were first recorded to observe Raman vibrations that might be present from adsorbed carbonaceous species. As no distinct peaks were observed, the respective spectra of the pure clusters at different temperatures were used for background correction. The data shown in Fig. 3e is the average of 120 separate spectra acquisitions respectively, and the shaded area is the standard deviation of the 120 spectra. The characteristic 4-MBN signals can be distinguished in both curves, especially the peaks at 1067 cm⁻¹ and 1574 cm⁻¹ that can be assigned to ring modes of the reporter molecule and the 2226 cm⁻¹ band, which originates from the C≡N-stretch mode.^48–50 To evaluate the SERS signal intensity increase for the transition from the expanded to the contracted state of the clusters, four distinct peaks (Fig. 3e) were considered, and an intensity ratio was calculated respectively (for details, see ESI Fig. S6 and Table S2†). The intensity increase upon temperature change obtained is roughly one order of magnitude, on average around 30, and up to 67 for the 2220 cm⁻¹ band from the C≡N-stretch mode (Table 2). Notably, thermally-induced noise does not seem to impair the signal amplification, as the spectrum shows distinct features that are significantly above the background, i.e. a sufficient signal-to-noise ratio.

Table 2 Peaks from SERS spectra (Fig. 3e) with assigned Raman modes^48–50 and intensity ratio between heated and room temperature measurement calculated from the recorded spectra

Peak	Mode	Intensity ratio
1	ν(C–S) stretching/ν(C–C–C) bending mode	7
2	ν(C–H)in-plane ring bending mode	16
3	ν(C–C)in-plane ring stretching mode	29
4	ν(C≡N) stretching mode	66

---

To study the hot-spot activation above the critical temperature and ensuing SERS enhancement, the electrical field around the clusters in the contracted and expanded states was simulated using the FDTD method. For a ‘core–shell–satellite’ model with an 80 nm AuNP core, 16 nm AuNP satellite and a poly(NIPAM) shell with a temperature-dependent variable shell thickness, the effect of the shell thickness towards field enhancements is evaluated for two different polarization configurations. The FDTD model corresponds to the experimental realization with 3 to 4 satellites per planet particle. The poly(NIPAM) layer of varying thickness can serve as a plasmonic hot-spot^51,52 to enable local field enhancements. However, the polarization direction plays an essential role in this enhancement; electric fields parallel to the nanometric gap can allow confining of the plasmonic modes. Due to the random distribution of such ‘core–shell–satellite’ systems, experimental outcomes under the unpolarized excitation (785 nm SERS laser excitation) can have the incident polarization vector in all possible directions. To cover the orientation dependence, we systematically study the two principal cases where the electric field vector is either collinear or non-collinear with the core and satellites. For a simplified model, the core and the satellites are arranged in the same X–Y plane with the core at the origin (0, 0) and the four satellites at (+X, 0), (−X, 0), (+Y, 0), (−Y, 0) coordinates. Because of the spherically symmetric core, the X and Y take the same value, given by ‘r_C + r_S + t’, where r_C and r_S are the radius of the core and satellite AuNPs, and t is the poly(NIPAM) shell thickness. In the expanded state, the planet–satellite distance was estimated to be t_{25 °C} = 14 nm based on the molar mass of the polymer and established distance-scaling behavior.²⁶ Above the critical phase transition temperature, the polymer is dense, so the known density of poly(NIPAM) (d_P = 1.1 g cm⁻³)⁵³ was assumed and the shell thickness calculated following simple stoichiometry and geometry considerations (ESI†). With a grafting density of ∼0.1 nm⁻¹ estimated based on previous results,^26,54 a distance of t_{40 °C} = 4 nm was calculated and this value used in the FDTD simulation. This variation in the shell thickness leads to two different configurations of plasmonic nanocavities with varying cavity length that has also been reflected in the experimental SERS intensity enhancement. The effect of varying the shell thickness for the situation where the electric field vector is kept parallel to the X axis, with the incident beam propagating along the ‘−Z’ direction is shown in Fig. 4(a, i and ii). To estimate the SERS intensity increase, we measure the electric field and the corresponding light-intensity enhancements 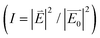; is the incident electric field, and is the resultant field after the plasmonic interaction. According to the color contour plots (Fig. 4(a, i and ii)), plasmonic hot-spots are created only between the core and the two satellites lying collinearly with the AuNP core and the electric field direction. Nodes with intensity minima can be found for the two other satellites, placed orthogonally with the X-axis. Such nodes are generally formed perpendicular to the electric field vector.⁵⁵ For a quantitative analysis of the electromagnetic field enhancement, we define the REF as the ratio between the intensity for the two different thicknesses, here REF = I_{t_40 °C}/I_{t_25 °C}. Comparing the maximum intensity (I_max) from the two cases, we obtain a REF = 266/79 = 3.4. However, for SERS activity, the electric field associated with the core surface is of higher importance. Thus, using a magnified plot (given in the inset), we calculate REF_surf = 99.3/19.3 = 5.0. Since the SERS enhancement scales with the fourth power of the associated electric field,^56,57 the SERS intensity ratio can be approximated as REF²_surf ∼ 25.0. Further, to estimate the random orientation of the incident electric field, the non-collinear model is studied in Fig. 4(b, i and ii). For an incident polarization of 45°, the electric field along X and Y axis can now be estimated as E_0x = E₀cos 45° = E₀/√2 and E_0y = E₀sin 45° = E₀/√2. This leads to the simultaneous excitation of plasmonic hot-spot for all four satellites; the nodes can still be found perpendicular to the electric field vector orientation. The reduced electric field (by a factor of 1/√2) interacting with the core-satellite has resulted in reduced I_max (by a factor of ∼1/2), leading to an almost similar REF = 138/41 = 3.4, REF_surf = 49.7/9.9 = 5.0 and a corresponding SERS intensity ratio of again ∼25.0.

Fig. 4 FDTD calculated intensity-enhancements at λ_SERS = 785 nm: (a, i and ii) Plasmonic core–shell-satellite models (AuNP-poly(NIPAM)@AuNP) with varied shell thickness (t) excited with electric field vector (red arrow) parallel to the X-axis. (b, i and ii) Similar plasmonic configurations for excitation with electric field vectors having components along both X- and Y-axis. The intensity maxima for the colour plots (in logarithmic scale) are inscribed along with the insets showing intensity values on the surface of the AuNP core.

Thus, one can conclude that for different non-collinear interactions (even if there is an additional Z component due to the asymmetric orientation of satellites around the core), the REF² – representing the SERS signal intensity increase upon heating above the LCST – can be expected to always be in the same range that is in reasonable agreement with the experimentally obtained value of ∼one order of magnitude.

Conclusions

We fabricated Au-poly(NIPAM)@Au planet–satellite clusters using an increase in the ionic strength of the solution and achieved a quantitative understanding of involved interactions in the framework of DLVO theory. The employed poly(NIPAM) linker and spacer allowed for reversible, temperature-mediated switching of the dimension of planet–satellite clusters based on the swelling state of the employed polymeric linker, associated with a modulation of their plasmonic signature. We demonstrate that this mechanism can be used to achieve an order of magnitude SERS signal intensity increase above the polymer's LCST, i.e. in the contracted non-swollen state. These experimental findings align well with calculations of electromagnetic field enhancement.

In conclusion, we have established a concept for the “on-demand” activation of local electromagnetic hot-spot sites in functional hybrid nanostructures, as demonstrated by the capability to boost SERS capability through external activation. The developed approach features the advantage of facilitated analyte access in an initial solvent-swollen state, combined with high SERS signal intensity after switching to a contracted state. The described in situ hot-spot activation is mediated by a polymeric linker, the critical phase transition temperature of which could be fine-tuned based on the intended application via co-polymerization. Given the significant signal increase in response to critical temperature change, the investigated supracolloidal SERS markers also exhibit potential as highly sensitive messenger materials.⁵⁸ These markers can report local overheating above a critical threshold temperature in complex environments, with the option to synthetically alter the LCST. Because of the underlying modular design, the hot-spot sites could as well be dynamically manipulated by macromolecular linkers that respond to different external parameters, like for example pH. This provides further prospects in biosensing, for example as nano-pH-sensor for tumor detection.⁵⁹

Author contributions

Conceptualization: D.C.-M. and C.R.; methodology: S.J., C.L., S.S., Q.A.B. Formal analysis: S.J., C.L., S.S., Q.A.B. Investigation: S.J., C.L., R.W., S.S., Q.A.B. Data curation: S.J., C.L., R.W., S.S., Q.A.B. writing—original draft preparation: S.J., C.L., S.S., Q.A.B., C.R. writing—review and editing: S.J., C.L., R.W., S.S., Q.A.B., T.A.F.K., J.P, D.C.-M., C.R. visualization: S.J., S.S., Q.A.B., D.C.-M. supervision: T.A.F.K., J.P., D.C.-M., C.R.; funding acquisition: Q.A.B., T.A.F.K., D.C.-M., C.R. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) supported this work under grants 496201730 (Q. A. B.), 465289819 (D. C. M.), and 466182523 (C. R.). The Volkswagen Foundation financially supported T. A. F. K. through a Freigeist Fellowship. C. R. acknowledges receipt of a Liebig fellowship (Fonds der Chemischen Industrie).

References

1. M. A. Garcia, J. Phys. D: Appl. Phys., 2011, 44, 283001.
2. K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677.
3. C. Rossner, T. A. F. König and A. Fery, Adv. Opt. Mater., 2021, 9, 2001869.
4. M. Blanco-Formoso, N. Pazos-Perez and R. A. Alvarez-Puebla, Nanoscale, 2020, 12, 14948–14956.
5. V. Tran, B. Walkenfort, M. König, M. Salehi and S. Schlücker, Angew. Chem., Int. Ed., 2019, 58, 442–446.
6. H. Dang, S.-G. Park, Y. Wu, N. Choi, J.-Y. Yang, S. Lee, S.-W. Joo, L. Chen and J. Choo, Adv. Funct. Mater., 2021, 31, 2105703.
7. R. Wang, P. Zimmermann, D. Schletz, M. Hoffmann, P. Probst, A. Fery, J. Nagel and C. Rossner, Nano Sel., 2022, 3, 1502–1508.
8. F. L. Yap, P. Thoniyot, S. Krishnan and S. Krishnamoorthy, ACS Nano, 2012, 6, 2056–2070.
9. S.-G. Park, X. Xiao, J. Min, C. Mun, H. S. Jung, V. Giannini, R. Weissleder, S. A. Maier, H. Im and D.-H. Kim, Adv. Funct. Mater., 2019, 29, 1904257.
10. D. Caprara, F. Ripanti, A. Capocefalo, A. Sarra, F. Brasili, C. Petrillo, C. Fasolato and P. Postorino, Colloids Surf., A, 2020, 589, 124399.
11. R. W. Taylor, R. Esteban, S. Mahajan, J. Aizpurua and J. J. Baumberg, Optimizing SERS from Gold Nanoparticle Clusters, J. Phys. Chem. C, 2016, 120, 10512–10522.
12. N. Pazos-Perez, J. M. Fitzgerald, V. Giannini, L. Guerrini and R. A. Alvarez-Puebla, Nanoscale Adv., 2019, 1, 122–131.
13. C. Kuttner, R. P. M. Höller, M. Quintanilla, M. J. Schnepf, M. Dulle, A. Fery and L. M. Liz-Marzán, Nanoscale, 2019, 11, 17655–17663.
14. S.-Y. Chen and A. A. Lazarides, J. Phys. Chem. C, 2009, 113, 12167–12175.
15. R. P. M. Höller, M. Dulle, S. Thomä, M. Mayer, A. M. Steiner, S. Förster, A. Fery, C. Kuttner and M. Chanana, ACS Nano, 2016, 10, 5740–5750.
16. P. Dey, S. Zhu, S. Zhu, K. J. Thurecht, P. M. Fredericks and I. Blakey, J. Mater. Chem. B, 2014, 2, 2827–2837.
17. R. P. M. Höller, I. J. Jahn, D. Cialla-May, M. Chanana, J. Popp, A. Fery and C. Kuttner, ACS Appl. Mater. Interfaces, 2020, 12, 57302–57313.
18. L. Xu, H. Kuang, C. Xu, W. Ma, L. Wang and N. A. Kotov, J. Am. Chem. Soc., 2012, 134, 1699–1709.
19. D. Radziuk, R. Schuetz, A. Masic and H. Moehwald, Phys. Chem. Chem. Phys., 2014, 16, 24621–24634.
20. M. Schütz and S. Schlücker, Phys. Chem. Chem. Phys., 2015, 17, 24356–24360.
21. M. Gellner, D. Steinigeweg, S. Ichilmann, M. Salehi, M. Schütz, K. Kömpe, M. Haase and S. Schlücker, Small, 2011, 7, 3445–3451.
22. N. Gandra, A. Abbas, L. Tian and S. Singamaneni, Nano Lett., 2012, 12, 2645–2651.
23. N. Gandra and S. Singamaneni, Chem. Commun., 2012, 48, 11540–11542.
24. J. H. Yoon, J. Lim and S. Yoon, ACS Nano, 2012, 6, 7199–7208.
25. A. M. T. S. Juan, S. R. Chavva, D. Tu, M. Tircuit, G. Coté and S. Mabbott, Nanoscale Adv., 2021, 4, 258–267.
26. C. Rossner, Q. Tang, O. Glatter, M. Müller and P. Vana, Langmuir, 2017, 33, 2017–2026.
27. G. Moad, Polym. Chem., 2016, 8, 177–219.
28. C. Rossner, O. Glatter and P. Vana, Macromolecules, 2017, 50, 7344–7350.
29. J. Chiefari, Y. K. Chong, F. Ercole, J. Krstina, J. L. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559–5562.
30. F. Han, S. R. C. Vivekchand, A. H. Soeriyadi, Y. Zheng and J. J. Gooding, Nanoscale, 2018, 10, 4284–4290.
31. F. Han, T. Armstrong, A. Andres-Arroyo, D. Bennett, A. Soeriyadi, A. A. Chamazketi, P. Bakthavathsalam, R. D. Tilley, J. J. Gooding and P. J. Reece, Nanoscale, 2020, 12, 1680–1687.
32. C. Rossner and P. Vana, Angew. Chem., Int. Ed., 2014, 53, 12639–12642.
33. C. Rossner, V. Roddatis, S. Lopatin and P. Vana, Macromol. Rapid Commun., 2016, 37, 1742–1747.
34. N. G. Bastús, J. Comenge and V. Puntes, Langmuir, 2011, 27, 11098–11105.
35. G. Trefalt, F. J. M. Ruiz-Cabello and M. Borkovec, J. Phys. Chem. B, 2014, 118, 6346–6355.
36. J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, Amsterdam, 3rd edn, 2011.
37. P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379.
38. Y. Brasse, M. B. Müller, M. Karg, C. Kuttner, T. A. F. König and A. Fery, ACS Appl. Mater. Interfaces, 2018, 10, 3133–3141.
39. L. Scarabelli, A. Sánchez-Iglesias, J. Pérez-Juste and L. M. Liz-Marzán, J. Phys. Chem. Lett., 2015, 6, 4270–4279.
40. R. T. A. Mayadunne, J. Jeffery, G. Moad and E. Rizzardo, Macromolecules, 2003, 36, 1505–1513.
41. B. Ebeling and P. Vana, Macromolecules, 2013, 46, 4862–4871.
42. R. M. Pashley and M. E. Karaman, in Applied Colloid and Surface Chemistry, John Wiley & Sons, Ltd, 2004, pp. 93–125.
43. Q. A. Besford, A. J. Christofferson, M. Liu and I. Yarovsky, J. Chem. Phys., 2017, 147, 194503.
44. Q. A. Besford, A. J. Christofferson, J. Kalayan, J.-U. Sommer and R. H. Henchman, J. Phys. Chem. B, 2020, 124, 6369–6375.
45. G. Zhang and C. Wu, J. Am. Chem. Soc., 2001, 123, 1376–1380.
46. S. Murphy, S. Jaber, C. Ritchie, M. Karg and P. Mulvaney, Langmuir, 2016, 32, 12497–12503.
47. S. E. J. Bell, G. Charron, E. Cortés, J. Kneipp, M. Lamy de la Chapelle, J. Langer, M. Procházka, V. Tran and S. Schlücker, Angew. Chem., Int. Ed., 2019, 59, 5454–5462.
48. S. Zhu, C. Fan, J. Wang, J. He and E. Liang, Appl. Phys. A, 2014, 117, 1075–1083.
49. S. Wang, L.-L. Tay and H. Liu, Analyst, 2016, 141, 1721–1733.
50. M. F. Mrozek, S. A. Wasileski and M. J. Weaver, J. Am. Chem. Soc., 2001, 123, 12817–12825.
51. S. Sarkar, V. Gupta, T. Tsuda, J. Gour, A. Singh, O. Aftenieva, A. M. Steiner, M. Hoffmann, S. Kumar, A. Fery, J. Joseph and T. A. F. König, Adv. Funct. Mater., 2021, 31, 2011099.
52. V. Gupta, S. Sarkar, O. Aftenieva, T. Tsuda, L. Kumar, D. Schletz, J. Schultz, A. Kiriy, A. Fery, N. Vogel and T. A. F. König, Adv. Funct. Mater., 2021, 31, 2105054.
53. H. G. Schild, Prog. Polym. Sci., 1992, 17, 163–249.
54. Q. Tang, C. Rossner, P. Vana and M. Müller, Biomacromolecules, 2020, 21, 5008–5020.
55. D. Radziuk and H. Moehwald, Phys. Chem. Chem. Phys., 2015, 17, 21072–21093.
56. Y. S. Yamamoto, Y. Ozaki and T. Itoh, J. Photochem. Photobiol., C, 2014, 21, 81–104.
57. S. Franzen, J. Phys. Chem. C, 2009, 113, 5912–5919.
58. Q. A. Besford, C. Rossner and A. Fery, Adv. Funct. Mater., 2023, 33, 2214915.
59. P. Mi, F. Wang, N. Nishiyama and H. Cabral, Macromol. Biosci., 2017, 17, 1600305.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05121h

---