Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding Yb3+-sensitized photon avalanche in Pr3+ co-doped nanocrystals: modelling and optimization†
Magdalena
Dudek
 *a,
Zuzanna
Korczak
*a,
Zuzanna
Korczak
 a,
Katarzyna
Prorok
a,
Katarzyna
Prorok
 a,
Oleksii
Bezkrovnyi
a,
Oleksii
Bezkrovnyi
 a,
Lining
Sun
a,
Lining
Sun
 b,
Marcin
Szalkowski
b,
Marcin
Szalkowski
 ac and
Artur
Bednarkiewicz
ac and
Artur
Bednarkiewicz
 *a
*a
aInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, ul. Okólna 2, 50-422 Wroclaw, Poland. E-mail: a.bednarkiewicz@intibs.pl; m.dudek@intibs.pl
bDepartment of Chemistry, College of Sciences, Shanghai University, Shanghai 200444, China
cNanophotonics Group, Institute of Physics, Faculty of Physics Astronomy and Informatics, Nicolaus Copernicus University in Toruń, ul. Grudziądzka 5, 87-100 Toruń, Poland
First published on 13th November 2023
Abstract
Among different upconversion processes where the emitted photon has higher energy than the one absorbed, photon avalanche (PA) is unique, because the luminescence intensity increases by 2–3 orders of magnitude in response to a tiny increase in excitation intensity. Since its discovery in 1979, PA has been observed in bulk materials but until recently, obtaining it at the nanoscale has been a significant challenge. In the present work, the PA phenomenon in β-NaYF4 colloidal nanocrystals co-doped with Pr3+ and Yb3+ ions was successfully observed at 482 nm (3P0 → 3H4) and 607 nm (3P0 → 3H6) under excitation at 852 nm. The impact of Pr3+ ion concentration and pump power dependence on PA behavior was investigated, i.e. PA non-linearity slopes of luminescence intensity curves as a function of pump power density as well as PA thresholds. The highest slopes, namely 8.6 and 9.0, and the smallest thresholds equal to 286 kW cm−2 and 281 kW cm−2, observed for emission bands at 607 nm and 482 nm, respectively, were obtained for NaYF4:0.5%Pr3+,15%Yb3+@NaYF4 colloidal nanocrystals. Besides experimental research, simulations of PA behavior in Pr3+, Yb3+ co-doped materials were performed based on differential rate equations describing the phenomena that contribute to the existence of PA. The influence of different processes leading to PA, e.g. the rates of nonradiative and radiative transitions as well as energy transfers, on PA performance was simulated aiming to understand their roles in this complex sensitized system.
Introduction
Photon avalanche (PA) is a highly non-linear upconversion process during which the luminescence intensity increases rapidly with a minute pump power density increase. In consequence, the characteristic s-shape curve of luminescence intensity (IL) as a function of pump power density (IP) is obtained and could be described by the following power law:| IL = ISP, | (1) |
There are some key conditions required to obtain PA. Firstly, the excitation wavelength has to be resonant with excited state absorption (ESA) and simultaneously far from resonance with ground state absorption (GSA). Additionally, the absorption cross section from the excited state (σESA) has to be much higher than from the ground state (σGSA), which is described as 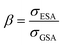 and should be above 104. In order to populate the metastable state, from which ESA can occur, cross-relaxation (CR) processes are necessary. CR relays on the exchange of energy between two ions, one of which is in a higher excited state and the other in a basic energy state. These two ions average their energies and thus produce two ions in an excited, metastable state. Consequently, the population of the metastable level increases in a loop, and absorption occurs more efficiently, which translates into PA emission. The characteristic features of PA are also slow luminescence rise times. Furthermore, to quantify the dynamics of relative changes of the luminescence intensity for the pump power changes, we introduce the parameter DAV, which is the PA luminescence intensity enhancement in response to doubling the excitation power densities, i.e.:
and should be above 104. In order to populate the metastable state, from which ESA can occur, cross-relaxation (CR) processes are necessary. CR relays on the exchange of energy between two ions, one of which is in a higher excited state and the other in a basic energy state. These two ions average their energies and thus produce two ions in an excited, metastable state. Consequently, the population of the metastable level increases in a loop, and absorption occurs more efficiently, which translates into PA emission. The characteristic features of PA are also slow luminescence rise times. Furthermore, to quantify the dynamics of relative changes of the luminescence intensity for the pump power changes, we introduce the parameter DAV, which is the PA luminescence intensity enhancement in response to doubling the excitation power densities, i.e.:
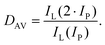 | (2) |
The subject of the present work is SPA in β-NaYF4 nanocrystals co-doped with Pr3+ and Yb3+ ions. Multicolor PA emission at 482 nm (3P0 → 3H4 transition) and 607 nm (3P0 → 3H6 transition) was successfully observed under excitation at 852 nm wavelength in samples co-doped with 15%Yb3+ ions and 0.1, 0.3, 0.5 or 0.7% of Pr3+ ions. The impacts of the concentration of Pr3+ ions and nanocrystal architecture on PA properties have been studied. In particular, the essential parameters describing the avalanching system, like S, PATH, rise times and DAV were investigated in detail. Additionally, β-NaYF4 nanocrystals singly doped with Pr3+, i.e. 0.1%, 0.5%, 1% and 3% ions, were synthesized and investigated, aiming to understand the role of CR and sensitization by Yb3+ ions. Moreover, another motivation behind our work was to critically evaluate the origin of red Pr3+ emission, as a discrepancy exists in the literature about the energy level (either 3P0 or 1D2) responsible for this transition. Furthermore, simulations of the PA process in Pr3+, Yb3+ co-doped crystals were performed. Based on the supposed PA mechanisms and relatively low phonon tetrafluoride materials, differential rate equations (DREs) were rationalized as compared to previous reports. Additionally, we have adopted a ‘knock-out’-like approach in DRE modelling, aiming to understand the influence of different individual phenomenological parameters on the PA process, i.e. the role of the rates of all the important nonradiative and radiative transitions as well as energy transfers was investigated. This knowledge is essential to further optimize the performance (e.g. decrease the PA threshold, increase PA gain or PA slopes) of these avalanching materials for numerous future photonic applications, and likewise to qualitatively understand the generic mechanisms behind sensitization in photon avalanching by other co-dopants.
Results and discussion
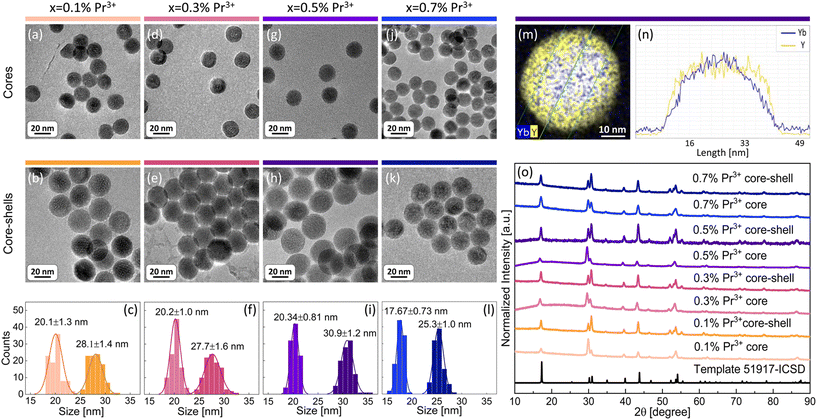
The aim of the present work was to understand the origin and mechanism of PA emission of Pr3+ ions at the nanoscale. Therefore, a set of β-NaYF4 colloidal nanocrystals singly doped with 0.1%, 0.5%, 1% and 3% of Pr3+ ions was synthesized. Additionally, based on earlier reported MPA in Pr3+, Yb3+ co-doped β-NaYF4 nanoparticles,8 a set of samples co-doped with 15% of Yb3+ ions in a wide range of concentrations of Pr3+ ions, i.e. 0.1%, 0.3%, 0.5% and 0.7%, was synthesized. All materials were synthesized by thermal decomposition of lanthanide salts in a core and core–shell architecture. Morphology and structural characterization was carried out for all prepared nanocrystals (Fig. 1 and Fig. S1, S2†). X-ray powder diffraction (XRD) reflexes of the investigated samples are compatible with the XRD pattern of the hexagonal (β) structure of NaYF4 crystals (Fig. 1o and Fig. S2†), which confirms a pure β-NaYF4 phase of the synthesized nanomaterials. The sizes of the nanocrystals were estimated based on transmission electron microscopy (TEM) images. Exemplary TEM pictures and histograms with average dimensions of the synthesized nanocrystals are presented in Fig. 1 and panels (a–l) in Fig. S1.† The diameters of the core nanoparticles are in the range of 16–20 nm and the core–shell dimensions are within 18–31 nm. Most of the crystals feature narrow size distribution, except for core–shell nanocrystals doped with 0.5% of Pr3+ ions, where, next to bigger core–shell particles (21 nm), smaller ones (around 10 nm) are observed (Fig. S1b†). We suppose that the shell material, besides crystallization on core nanoparticles, crystallized also as smaller undoped NaYF4 nanocrystals, as we discussed later on the basis of core and core–shell dimensions. An indirect proof of shell deposition is the bigger size of core–shell nanoparticles than that of core nanocrystals. Additionally, undoped shell deposition is directly evidenced by the exemplary energy dispersive X-ray spectroscopy (EDS) map and the profile of Yb3+ and Y3+ ions prepared for core–shell NaYF4:0.5%Pr3+,15%Yb3+@NaYF4 nanocrystals (Fig. 1m and n). The thicknesses of shells were calculated based on the average dimensions of nanocrystals. For most of the spherical core–shell nanoparticles, the shell thickness is around 4 nm (Table 1) with the exception of 0.5%Pr3+-doped ones, which have a shell thickness of around 2 nm (Table S1†). It is evidence that part of the shell material in this sample crystallized as smaller, undoped β-NaYF4 particles. In the case of ellipsoidal core–shell nanocrystals, the shell thickness is around 2 nm in width and between 4 nm and 6 nm in length (Table S1†).| Dopants x%Pr3+, 15%Yb3+ | Average core diameter [nm] | Average core–shell diameter [nm] | Average shell thickness [nm] |
|---|---|---|---|
| 0.1%Pr3+ | 20.1 ± 1.3 | 28.1 ± 1.4 | 4.0 ± 1.4 |
| 0.3%Pr3+ | 20.2 ± 1.0 | 27.7 ± 1.6 | 3.8 ± 1.3 |
| 0.5%Pr3+ | 20.34 ± 0.81 | 30.9 ± 1.2 | 5.3 ± 1.0 |
| 0.7%Pr3+ | 17.67 ± 0.73 | 25.3 ± 1.0 | 3.80 ± 0.86 |
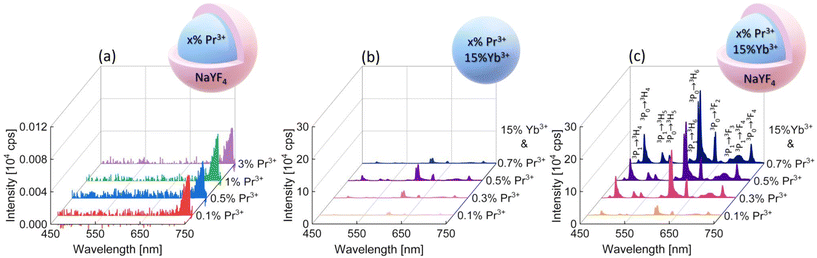
To determine the PA luminescence parameters, the 852 nm wavelength as the excitation one was used,8 which is resonant with Pr3+ ESA (1G4 → 3P1) and simultaneously far from resonance with the GSA of these ions, as is required for PA. Measurements were performed at room temperature (RT). At the beginning, singly Pr3+-doped samples were investigated. The range of ion concentrations was deliberately chosen starting with a very low content, namely 0.1% of Pr3+ ions, ending at 3%. It can be expected that a high concentration of ions would lead to the concentration quenching of luminescence intensity. However, even nanocrystals with low Pr3+ ion concentrations showed no emission under these excitation conditions (Fig. 2a). The peak at around 725 nm is an artifact resulting from a laser diode and no emission was observed from singly Pr3+-doped nanocrystals. Therefore, nanocrystals co-doped with Pr3+ and Yb3+ ions were investigated. The 852 nm wavelength can excite Yb3+ ions, and then, by energy transfer (ET) processes, the absorbed energy can be further transferred to Pr3+ ions. The core and core–shell samples co-doped with 15%Yb3+ ions and 0.1%, 0.3%, 0.5% or 0.7% of Pr3+ ions successfully showed multicolor emission in the range from 450 nm to 700 nm (Fig. 2b and c). Comparing the emission spectra of the core and core–shell samples, the core–shell nanocrystals feature significantly higher luminescence intensity, confirming the role of the inert passive shell, which protects optically active ions from environment impacts. Furthermore, for the sample singly doped with 0.5%Pr3+ ions, no avalanche emission was observed, and the sample co-doped with 0.5%Pr3+ and 15%Yb3+ ions exhibited multicolor emission, which proves that Yb3+ ions play a key role as a sensitizer of PA emission.
The emission bands of the samples co-doped with Pr3+ and Yb3+ ions were assigned to the following transitions: 3P1 → 3H4 (468 nm), 3P0 → 3H4 (482 nm), 3P1 → 3H5 (522 nm), 3P0 → 3H5 (538 nm), 3P1 → 3H6 (583 nm), 3P0 → 3H6 (607 nm), 3P0 → 3F2 (641 nm), 3P1 → 3F3 (672 nm), 3P1 → 3F4 (693 nm), and 3P0 → 3F4 (720 nm) (Fig. 2c). In the literature, the assignment of emission bands in the 580–620 nm range is ambiguous, as in some reports, they are interpreted as emission from the 3P1 level, while others are from the 1D2 level.8,12–17 Here, as also earlier,10 we assigned the emission at 607 nm to the 3P0 → 3H6 transition. Considering the emission at 607 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475 cm−1), the energy mismatch is lower for the 3P0 → 3H6 transition (ΔE = 16
475 cm−1), the energy mismatch is lower for the 3P0 → 3H6 transition (ΔE = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1) than for the 1D2 → 3H4 transition (ΔE = 16
400 cm−1) than for the 1D2 → 3H4 transition (ΔE = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1). Additionally, to prove that the emission at 607 nm comes from the same level as 482 nm, fluorescence lifetime decay curves for these wavelengths were measured in a wide range of temperatures. Luminescence lifetime curves measured at RT are presented in Fig. S3.† The values of the short and long components of the decay time curves and
800 cm−1). Additionally, to prove that the emission at 607 nm comes from the same level as 482 nm, fluorescence lifetime decay curves for these wavelengths were measured in a wide range of temperatures. Luminescence lifetime curves measured at RT are presented in Fig. S3.† The values of the short and long components of the decay time curves and  as a function of temperature are shown in Fig. S4a–d.† The average values of the lifetimes were calculated using the formula:
as a function of temperature are shown in Fig. S4a–d.† The average values of the lifetimes were calculated using the formula:
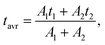 | (3) |
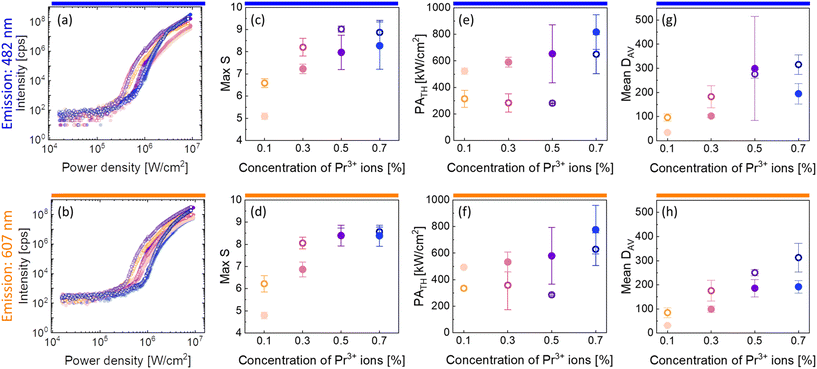 | ||
| Fig. 3 Characteristic of PA emission in the core and core–shell β-NaYF4 nanocrystals co-doped with 15%Yb3+ and 0.1%, 0.3%, 0.5% or 0.7% of Pr3+ ions. Subsequent columns: (a and b) pump-power dependence of PA luminescence; (c and d) maximum values of S, which are a measure of nonlinearity of the PA process (eqn (1)); (e and f) PATH pump powers as a function of the concentration of Pr3+ ions. (g and h) Mean values of DAV parameters indicating the efficiency of the PA process. These properties were recorded for core (●) and core–shell (○) nanoparticles at 482 nm (top row) and at 607 nm (bottom row). Average values and standard deviations for (c–h) were calculated based on a few (2–4) measurements. | ||
There were calculated DAV values (Fig. 3g and h), which, according to eqn (2), describe how much the luminescence intensity increases upon doubling the power density. The core–shell nanocrystals turned out to be more sensitive to the changes and the most sensitive was the β-NaYF4:15%Yb3+,0.7%Pr3+@NaYF4 sample. Another characteristic PA feature is the slowing down of the emission rise time for power densities close to the threshold. Here, parameters τ50% and τ80% were adopted to describe the time needed to obtain 50% and 80% of maximum luminescence intensity (at an infinitely long excitation time), respectively. The average values of τ50% and τ80% are presented in Fig. S5.† The highest values of rise times were observed for β-NaYF4:15%Yb3+,0.1%Pr3+@NaYF4 nanocrystals.
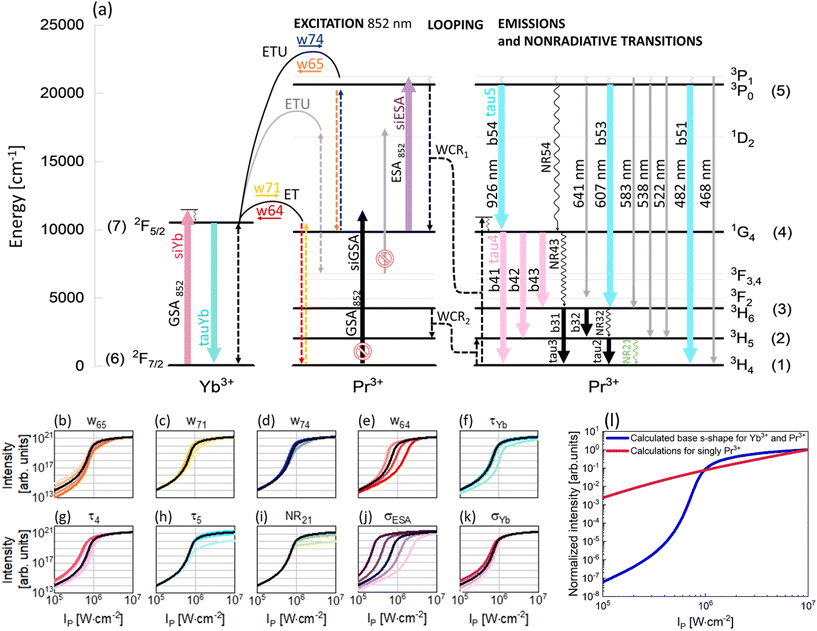
To understand the PA mechanism, besides experimental investigations, simulations of the PA process in the Pr3+, Yb3+ co-doped system and in singly Pr3+-doped nanocrystals were performed. Compared with earlier studies,8 here a significantly simpler energy diagram of the Pr3+, Yb3+ system was adopted for modeling. The supposed PA mechanism in the Pr3+, Yb3+ ion co-doped system is demonstrated in Fig. 4a and, excluding gray elements, was used to write DREs (eqn (S1)–(S7)†). The correspondence of the properties measured at 607 and 482 nm indicates that the emissions come from the same level and therefore the 1D2 level can be excluded from analysis. This feature allowed us to rationalize the rate equation model as compared to earlier studies, perform the next computational studies in a more effective way and draw general and more clear conclusions about the origin of PA in the PrYb system studied here. As expected, the 852 nm wavelength, thanks to its resonance with the ESA [1G4 → 3P1] transition in Pr3+ ions as well as its incompatibility with the GSA of Pr3+ (Fig. 4a), turned out to be appropriate for PA. Absorption cross sections from the ground and excited states in Pr3+ were indicated in modeling as σESA and σGSA, respectively. As was experimentally evidenced, the Yb3+ ions are necessary for the existence of PA. Thus, the absorption cross section in Yb3+ was also taken into consideration (σYb).
The metastable level (starting with ESA) should be initially populated to provide efficient ESA. Here, three energy transfer processes populating the metastable 1G4 level in Pr3+ ions were considered. First, CR between Pr3+ ions [3P1, 3H4] → [1G4, 1G4] (WCR1), second, w65 indicating energy transfer upconversion (ETU) from Pr3+ to Yb3+ ions [Yb3+: 2F7/2, Pr3+: 3P1] → [Yb3+: 2F5/2, Pr3+: 1G4] and finally, w71 energy transfer (ET) from Yb3+ to Pr3+ ions [Yb3+: 2F5/2, Pr3+: 3H4] → [Yb3+: 2F7/2, Pr3+: 1G4]. These ETU and ET were also considered as energy transfer processes going in opposite directions and indicated as w74 and w64, respectively. Additionally, CR populating the 3H5 level in Pr3+ ions (WCR2) was considered. This process was the basis for obtaining PA in Pr3+ for the first time by Jay S. Chivian,1 therefore, it should not be overlooked in the first approximation, despite the fact that the ESA occurs from 1G4 and not 3H5. Consequently, radiative and nonradiative emission processes from 3H6 and 3H5 levels were taken into consideration, namely τ3, τ2, NR32 and NR21. Other two nonradiative processes, i.e. NR54 and NR43, were also considered. Because both PA emissions (482 nm and 607 nm) originate from the same 3P0 level, we could disregard the 1D2 level from further analysis and thus simplify the description of the phenomenological energy transfer DRE model and speed up the data simulation presented in Fig. 4. Simultaneously, emissions from 3P1 are weaker compared with emissions from 3P0 (Fig. 2c). This is because of a small energy break between levels 3P1 and 3P0 (<600 cm−1), which can be easily bridged by matrix phonons (energy of one phonon in NaYF4 ∼350 cm−1). Thus, in the modeling, the 3P1 level has been disregarded. Emission bands from 3P0, 1G4 and Yb3+ ions were characterized by lifetimes at these levels: τ5, τ4 and τYb, respectively. Based on the supposed PA mechanism and analyzing the emission spectra of PA nanocrystals, the processes illustrated as gray in Fig. 4a have been omitted from the modeling. Finally, the DRE (eqn (S1)–(S7)†) model was designed to evaluate and qualitatively understand the PA phenomenon and its susceptibility to other material properties. The parameters utilized to solve the DREs were mostly adopted from the literature on LiYF4 matrix-based luminescent materials and are summarized in Table S3.† The rates of nonradiative transition were estimated on the basis of the chart of probabilities of nonradiative transitions of Ln3+ ions in a tetragonal LiYF4 laser crystal as a function of energy gap at T = 0.21 The probability of nonradiative transitions from the starting level, J, to the end level, J′, is described as WJJ′ (eqn (S9)†). These calculations are presented in the ESI.†
The prepared DREs were resolved and the characteristic s-shape curve illustrating luminescence intensity as a function of pump power density was obtained, which is presented in Fig. 4 in all small panels (b–k) as a black curve. All the other color s-shaped curves indicate how the increase (more intense color) or decrease (paler shade) of individual parameters influences the features of PA, what will be discussed later. It is important to notice that the prepared DREs were resolved also for the singly Pr3+-doped system (i.e. by zeroing all processes describing Yb3+ and Pr3+ interactions, namely w74, w65, w71, w64 and σYb). The model excluding Yb3+ ions (Fig. 4l) clearly showed that singly Pr3+ ions under 852 nm excitation are not sufficient to obtain PA emission, and energy transfer processes between the two selected ions play a key role.
The original DREs (eqn (S1)–(S7))† were then used to experimentally evaluate how the individual parameters influence the features of PA. To understand their roles, the values of these individual parameters of DREs were artificially and purposefully increased and decreased around the literature values. The changes were not uniform for each of the parameters, but particular parameters were tuned individually, and specific values are presented in Table S4.† The results obtained from these calculations are presented in Fig. 4(b–k) and Fig. S6.† Not all parameters affect PA in a significant way, thus, only those parameters that substantially influence the shape of the pump power dependence or slope are presented here. Although WCR1 seems to be the key process for PA performance, it does not influence PA features, because there exist other more intense processes that populate the metastable 1G4 level. The Pr3+ concentration is low, thus CR processes, including WCR2, are not efficient enough to power the avalanching. Here, w65 plays a role of CR and populates the 1G4 metastable level, which is necessary for ESA.22 Moreover, the value of w65 is higher than that of WCR1, which supports the hypothesis that Yb3+, not WCR1, is responsible for PA. Yb3+ ions not only support avalanching, but are also essential components of the system, which enables PA emission in this configuration. To obtain PA in a single Pr3+-doped material, there will be necessary excitation conditions used by Chivian.1 An increase of w65 enables more efficient ESA, which causes a steeper slope and shifts the PATH to higher values (Fig. 4b and Fig. S6a†). Similarly to w65, w71 populates the 1G4 level of Pr3+ ions and for more intense w71, the slopes are higher (Fig. S6b†). The w74 process could be assigned to ESA and its higher values increase slopes (Fig. S6c†). The w64 transfers energy from Pr3+ to Yb3+ ions, picking up the energy from the metastable state. The greater the share of w64, the more difficult it is to achieve PA (Fig. 4e) and the slope decreases (Fig. S6d†). However, w64 pumps Yb3+, which is necessary for PA, but Yb3+ can get entangled in energy migration to the surface. It is widely known that Yb3+ ions are very susceptible to surface quenching by the overtones of water vibrations (3300 cm−1); therefore, surface effects also have a vital impact. Thus, the role of Yb3+ is twofold. First, Yb3+ enables PA, but facilitates quenching on the surface, which may not be prevented by a passive shell even for the thicknesses studied here. Decreasing the radiative lifetime of Yb3+ ions (τYb), for example, due to surface quenching, increases PATH by up to one order of magnitude (Fig. 4f). Also, the saturation of the curve is smoother. The shorter lifetime of Yb3+ ions may indicate that w64 and w65 processes are more intense and consequently PATH also increases. Let us consider the other radiative lifetimes. First, the τ4, which is a radiative lifetime of the 1G4 metastable level, is considered. A longer τ4 facilitates the more efficient occurrence of ESA. Consequently, PATH is lower (Fig. 4g) but also slopes decrease (Fig. S6f†). For τ5, only minute variation was observed (Fig. S6g†). In the cases of τ2 and τ3, insignificant changes have been observed. These lifetimes determine the population of levels (2) and (3), which are necessary for cross-relaxation described by WCR2. These processes will be critical for excitation based on the 3H5 → 3P1 transition applied by Jay S. Chivian, but here, under 852 nm photoexcitation wavelength, are not significant. If these lifetimes were very long, respective levels could store electrons and reduce the ground state population, thus hindering the CR processes. But here, their impact is negligible, which in turn suggests that the ET between Yb3+ and Pr3+ is more important than the CR within the Pr3+ ion couples. The lifetimes considered here are radiative, thus nonradiative transitions were additionally taken into account in the model. Here, to make the model easier, some Pr3+ levels were overlooked and NR54 and NR43 were adopted to describe nonradiative transitions between levels 3P0 → 1G4 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1) and 1G4 → 3H4 (9850 cm−1), respectively. The energy gaps of these transitions are wide; therefore the probabilities of the processes are not high. However, it is important to remember that under experimental conditions, these transitions could be more efficient than how they appear in the numerical considerations. Calculations for increased and decreased NR54 and NR43 were performed, but no clear differences in the s-shape were observed for values up to three orders of magnitude smaller or larger than the original values. The other two nonradiative processes are closely connected with WCR2 and here do not change too much; however the impact of NR21 was observed (Fig. 4i and Fig. S6h†), indicating the importance of having Pr3+ ions in the ground state to initiate PA emission.
800 cm−1) and 1G4 → 3H4 (9850 cm−1), respectively. The energy gaps of these transitions are wide; therefore the probabilities of the processes are not high. However, it is important to remember that under experimental conditions, these transitions could be more efficient than how they appear in the numerical considerations. Calculations for increased and decreased NR54 and NR43 were performed, but no clear differences in the s-shape were observed for values up to three orders of magnitude smaller or larger than the original values. The other two nonradiative processes are closely connected with WCR2 and here do not change too much; however the impact of NR21 was observed (Fig. 4i and Fig. S6h†), indicating the importance of having Pr3+ ions in the ground state to initiate PA emission.
Ending the description of modeling, let's come back to the key conditions necessary to obtain PA emission. One of these conditions is a significantly high value of cross section for absorption from the excited state and a simultaneously negligible cross section for absorption from the ground state. The 852 nm excitation wavelength fulfills these conditions. As expected, σGSA has not influenced the features of PA, while σESA has the biggest impact on the PATH values. Higher values of σESA facilitate PA, shifting the PATH to smaller values, and conversely, lower values of σESA increase the threshold value (Fig. 4j). Moreover, the slopes increase for bigger σESA (Fig. S6f†). It confirms that ESA plays a key role in being necessary in the PA process and higher values of σESA positively influence PA. In the case of σYb, the changes are negligible. A decrease of the parameter impedes PA by moving PATH to higher power densities (Fig. 4k); however, the slopes increase (Fig. S6j†). Yb3+ ions take part in two processes populating 1G4. For w65, Yb3+ ions in the ground state are required, while for w71, Yb3+ ions in the excited state are necessary. From these two processes, w65 is found to be more intense; therefore, in this case Yb3+ ions in the ground state could help to increase a slope.
Besides PA measurements, basic spectroscopy studies of the synthesized samples has been carried out, including measurements of the absorption, emission and excitation spectra as well as luminescence lifetimes. These results are presented in the ESI.† In all cases, the amounts of the investigated samples were the same to enable a quantitative comparison. Considering the samples co-doped with Pr3+ and Yb3+ ions, where the amount of Yb3+ ions was constant (15%), one can see that it is reflected in the absorption spectra (Fig. S7a†) because the absorption values coming from Yb3+ ions are at the same level. Simultaneously, the absorption of Pr3+ ions increases with an increase of Pr3+ amount, as illustrated in the inset of Fig. S7a†. A similar situation is observed in the case of singly Pr3+-doped NaYF4 nanocrystals, where absorption also increases with Pr3+ ion concentration (inset in Fig. S7b†). Insets were prepared based on the integral area of the peak at 444 nm corresponding to the 3H4 → 3P2 transition. Excitation spectra (Fig. S8a and S8c†) were recorded for the samples co-doped with Pr3+, Yb3+ ions and singly Pr3+ doped, by monitoring emission at 980 nm and 607 nm, respectively. In all cases the most intensive peaks were obtained at 444 nm. For the core–shell nanocrystals co-doped with Pr3+ and Yb3+ ions, the integral area under the peak at 444 nm decreases with an increasing concentration of Pr3+ ions (Fig. S8a†). It means that the absorbed energy is less effectively transferred to Yb3+ ions when the Pr3+ concentration is higher, which is due to the increased concentration quenching between neighboring Pr3+ ions (i.e. increasing Pr3+ concentration from 0.1 to 0.7% quenched the emission intensity by ca. 2 fold). It is astonishing to see that the concentration quenching is not that strong in singly Pr3+-doped samples, as the integral area under the peak at the same wavelength (444 nm, monitoring Pr3+ emission at 607 nm) initially increases with Pr3+ ion concentration up to 1%, and then decreases slowly by ca.30% for samples doped with 1 and 8% Pr3+. This can only be explained by the larger amounts of lanthanides (>10%), the cooping of large23 and small ions, i.e. 1.179 Å and 1.042 Å Pr3+ and Yb3+ ions, respectively, for 9-fold coordination positions and/or the role of Yb3+ ions, which most probably cluster dopants more effectively than for dopant levels of 1%. It is well known that low concentrations of optically active ions minimize luminescence quenching relative to high dopants. However, the arrangement of atoms in the lattice is also important. It is worth mentioning here studies on nanocrystals with orthorhombic crystallographic structures, in which lanthanide ions were arranged in tetrahedral arrays.24 Such an arrangement of ions resulted in minimizing the migration of excitation energy to defects by preserving the excitation energy within the sublattice domain. The lack of control over the organization of nanomaterials at the atomic scale is one of the reasons limiting their optical performance. Providing control over the mixing of cations at the core–shell interface can provide a dramatic improvement in quantum efficiency.18
Considering that the most intense peak in the absorption spectra was obtained at 444 nm, emission spectra (Fig. S8b and d†) were recorded under excitation at 444 nm and multicolor emission was observed. Insets for emission spectra were prepared on the basis of the integral area under the peak at 482 nm assigned to the 3P0 → 3H4 emission. For small amounts of Pr3+ ions, namely 0.1%, 0.3%, 0.5%, and 0.7%, the emission intensity increased with the concentration of Pr3+ ions (inset in Fig. S8b†). Moreover, the core–shell samples, where the inert shell protects optically active ions from the environment, have shown more intense luminescence in comparison with the cores, as was expected. In the case of singly Pr3+-doped samples, where the range of concentrations of Pr3+ ions was wider (from 0.1% to 8%), initially the luminescence intensity increases with the concentration of Pr3+ ions up to the sample doped with 3% of Pr3+. Subsequently, for samples doped with 5% and 8% of Pr3+ ions, the luminescence intensity decreases. It is connected with the concentration quenching effect, which occurs for highly doped nanocrystals.
Experimental
Materials and methods
β-NaYF4 nanocrystals doped with praseodymium as well as co-doped with praseodymium and ytterbium ions were synthesised. The selected crystal matrix is appropriate for the PA phenomenon due to its low phonon energy. Additionally, compared with a cubic α-NaYF4 structure, a hexagonal one is brighter. All nanocrystals were prepared in a core and core-undoped shell architecture.Synthesis methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in a Teflon vessel. The prepared mixture was kept at 200 °C for 60 minutes to form acetates. The final precursor was obtained by evaporation of residual acetic acid and water using a rotary evaporator in a pre-vacuum (<8 hPa) and drying at 140 °C for 12 hours.
1) in a Teflon vessel. The prepared mixture was kept at 200 °C for 60 minutes to form acetates. The final precursor was obtained by evaporation of residual acetic acid and water using a rotary evaporator in a pre-vacuum (<8 hPa) and drying at 140 °C for 12 hours.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. After that, the prepared nanocrystals were dispersed in a minimal amount of n-hexane and again precipitated with ethanol at 14
000 rpm for 10 minutes. After that, the prepared nanocrystals were dispersed in a minimal amount of n-hexane and again precipitated with ethanol at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. The resulting nanoparticles were dispersed in 10 mL of chloroform.
000 rpm for 10 minutes. The resulting nanoparticles were dispersed in 10 mL of chloroform.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. Afterwards, the nanoparticles were washed with n-hexane, once more precipitated with ethanol, centrifuged at 14
000 rpm for 10 minutes. Afterwards, the nanoparticles were washed with n-hexane, once more precipitated with ethanol, centrifuged at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes and finally dispersed in chloroform (10 mL).
000 rpm for 10 minutes and finally dispersed in chloroform (10 mL).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. Then, the precipitated nanoparticles were dispersed in n-hexane and once more precipitated with ethanol and then centrifuged at 14
000 rpm for 10 minutes. Then, the precipitated nanoparticles were dispersed in n-hexane and once more precipitated with ethanol and then centrifuged at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. Finally, the nanocrystals were dispersed in chloroform (5 mL).
000 rpm for 10 minutes. Finally, the nanocrystals were dispersed in chloroform (5 mL).
Conclusions
In summary, SPA emission at 482 nm (3P0 → 3H4) and 607 nm (3P0 → 3H6) under excitation at 852 nm in β-NaYF4 colloidal nanocrystals co-doped with 15%Yb3+ and a small (0.1 to 0.7%) amount of Pr3+ ions was successfully observed and studied. We have clearly demonstrated the critical role of undoped shell passivation in the PA emission characteristics, which is obviously beneficial and diminishes the impact of the local chemical environment (quenchers, solvent) on both the emitting (Pr3+) and sensitizing–migrating (Yb3+) ions. Under the same experimental conditions no emission from singly Pr3+ ion-doped β-NaYF4 nanocrystals was observed under 852 nm photoexcitation. It emphasizes the key role of Yb3+ ions, which are necessary to obtain PA emission under chosen experimental conditions. During experimental investigations, the highest S of 8.6 and 9.0 as well as the smallest PATH of 286 kW cm−2 and 281 kW cm−2 were observed for the core–shell sample co-doped with 15%Yb3+ and 0.5%Pr3+ ions for emissions at 607 nm and 482 nm, respectively. Therefore, the optimal sample composition for SPA NaYF4:0.5%Pr3+,15%Yb3+@NaYF4 was confirmed.8 Both Stokes emission and photon avalanche emission let us clearly confirm that the 1D2 level does not take part in energy transfer, and thus can be excluded, unlike in some other existing reports, from the analysis. In consequence, elimination of processes related to 1D2 level this let us simplify the phenomenological set of rate equations and ultimately enablws to simulate the behavior, mechanism and performance of the sensitized photon avalanche emission, indicating the critical role of the Yb3+ sensitizer in this system under 852 nm photoexcitation. Moreover, the simulations of SPA allowed us to understand the impact of energy transfer parameters on PA features. These calculations confirmed that PA emissions from Pr3+ ions under excitation at 852 nm are possible only with the assistance of Yb3+ ions; thus, crystals singly doped with Pr3+ ions do not exhibit PA features at such a photoexcitation wavelength. The obtained experimental and theoretical results have shown and allowed us to understand the important role of Yb3+ ions, which are necessary to obtain PA emission from Pr3+ ions under excitation at 852 nm.Author contributions
MD: conceptualization, synthesis, data curation, data analysis, investigation, visualization, and writing the original draft; ZK: data analysis, investigation, visualization, and writing – review & editing; KP: data analysis and writing – review & editing; OB: investigation and data analysis; LS: writing – review & editing; MS: investigation, methodology, software, and writing – review & editing; AB: conceptualization, funding acquisition, methodology, software, project administration, resources, supervision, validation, writing the original draft, review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded in whole or in part by the following projects 2018/31/B/ST5/01827 (M. D., Z. K., M. S., A. B.) and 2021/43/B/ST5/01244 (A. B.). K. P. acknowledges the financial support from NCN, Poland, grant number 2018/31/D/ST5/01328. Calculations have been carried out using the resources provided by the Wroclaw Centre for Networking and Supercomputing (https://wcss.pl), grant no. 529.References
- J. S. Chivian, W. E. Case and D. D. Eden, Appl. Phys. Lett., 1979, 35, 124–125 CrossRef CAS.
- A. Bednarkiewicz, E. M. Chan, A. Kotulska, L. Marciniak and K. Prorok, Nanoscale Horiz., 2019, 4, 881–889 RSC.
- C. Lee, E. Xu, Y. Liu, A. Teitelboim, K. Yao, A. Fernandez-Bravo, A. Kotulska, S. H. Nam, Y. D. Suh, A. Bednarkiewicz, B. E. Cohen, E. M. Chan and P. J. Schuck, Nature, 2021, 589, 230–235 CrossRef CAS PubMed.
- M. Dudek, M. Szalkowski, M. Misiak, M. Ćwierzona, A. Skripka, Z. Korczak, D. Piątkowski, P. Woźniak, R. Lisiecki, P. Goldner, S. Maćkowski, E. M. Chan, P. J. Schuck and A. Bednarkiewicz, Adv. Opt. Mater., 2022, 2201052 CrossRef CAS.
- K. W. C. Kwock, C. Lee, A. Teitelboim, Y. Liu, K. Yao, S. B. Alam, B. E. Cohen, E. M. Chan and P. J. Schuck, J. Phys. Chem. C, 2021, 125, 23976–23982 CrossRef CAS.
- Z. Zhang, A. Skripka, J. C. Dahl, C. Dun, J. J. Urban, D. Jaque, P. J. Schuck, B. E. Cohen and E. M. Chan, Angew. Chem., Int. Ed., 2023, 62, e202212549 CrossRef CAS PubMed.
- C. Lee, E. Z. Xu, K. W. C. Kwock, A. Teitelboim, Y. Liu, H. S. Park, B. Ursprung, M. E. Ziffer, Y. Karube, N. Fardian-Melamed, C. C. S. Pedroso, J. Kim, S. D. Pritzl, S. H. Nam, T. Lohmueller, J. S. Owen, P. Ercius, Y. D. Suh, B. E. Cohen, E. M. Chan and P. J. Schuck, Nature, 2023, 618, 951–958 CrossRef CAS PubMed.
- Y. Liang, Z. Zhu, S. Qiao, S. Qiao, X. Guo, R. Pu, H. Tang, H. Liu, H. Dong, T. Peng, L.-D. Sun, J. Widengren and Q. Zhan, Nat. Nanotechnol., 2022, 2022, 1–7 Search PubMed.
- A. Skripka, M. Lee, X. Qi, J.-A. Pan, H. Yang, C. Lee, P. J. Schuck, B. E. Cohen, D. Jaque and E. M. Chan, Nano Lett., 2023, 23, 7100–7106 CrossRef CAS PubMed.
- Z. Korczak, M. Dudek, M. Majak, M. Misiak, Ł. Marciniak, M. Szalkowski and A. Bednarkiewicz, Low Temp. Phys., 2023, 49, 322–329 CrossRef CAS.
- M. Szalkowski, M. Dudek, Z. Korczak, C. Lee, Ł. Marciniak, E. M. Chan, P. J. Schuck and A. Bednarkiewicz, Opt. Mater.: X, 2021, 12, 100102 CAS.
- M. F. Joubert, Opt. Mater., 1999, 11, 181–203 CrossRef CAS.
- P. Boutinaud, R. Mahiou, N. Martin and M. Malinowski, J.Lumin., 1997, 72–74, 809–811 CrossRef CAS.
- S. Kuck, A. Diening, E. Heumann, E. Mix, T. Sandrock, K. Sebald and G. Huber, J. Alloys Compd., 2000, 300–301, 65–70 CrossRef CAS.
- S. Hao, W. Shao, H. Qiu, Y. Shang, R. Fan, X. Guo, L. Zhao, G. Chen and C. Yang, RSC Adv., 2014, 4, 56302–56306 RSC.
- M. Y. Tsang, P. Fałat, M. A. Antoniak, R. Ziniuk, S. J. Zelewski, M. Samoć, M. Nyk, J. Qu, T. Y. Ohulchanskyy and D. Wawrzyńczyk, Nanoscale, 2022, 14, 14770–14778 RSC.
- H. Liang, S. Zhang and C. Li, J. Phys. Chem. C, 2013, 117, 2216–2221 CrossRef.
- F. A. Cardona, N. Jain, R. Popescu, D. Busko, E. Madirov, B. A. Arús, D. Gerthsen, A. De Backer, S. Bals, O. T. Bruns, A. Chmyrov, S. Van Aert, B. S. Richards and D. Hudry, Nat. Commun., 2023, 14, 4462 CrossRef.
- D. Hudry, I. A. Howard, R. Popescu, D. Gerthsen and B. S. Richards, Adv. Mater., 2019, 31, 1900623 CrossRef.
- D. Hudry, A. De Backer, R. Popescu, D. Busko, I. A. Howard, S. Bals, Y. Zhang, A. Pedrazo-Tardajos, S. Van Aert, D. Gerthsen, T. Altantzis and B. S. Richards, Small, 2021, 17, 2104441 CrossRef CAS.
- A. A. Kaminskii, Crystlline Lasers: Physical Processes and Operating Schemes, 1996 Search PubMed.
- V. Lupei, Spectrochim. Acta, Part A, 1998, 54, 1615–1632 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. Wang, R. Deng, M. A. MacDonald, B. Chen, J. Yuan, F. Wang, D. Chi, T. S. A. Hor, P. Zhang, G. Liu, Y. Han and X. Liu, Nat. Mater., 2014, 13, 157–162 CrossRef CAS PubMed.
- K. A. Abel, J. C. Boyer and F. C. J. M. van Veggel, J. Am. Chem. Soc., 2009, 131, 14644–14645 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04409b |
| This journal is © The Royal Society of Chemistry 2023 |