A step towards rational design of carbon nanobelts with tunable electronic properties

Abstract

Belt-shaped aromatic compounds are among the most attractive classes of radial π-conjugated nanocarbon molecules with unique physical and chemical properties. In this work, we computationally studied a number of all-carbon and heteroatom-bridged nanobelts, as well as their inclusion complexes with fullerene C₆₀. Our results provide a useful guide for modulating the electronic properties of the nanobelts. An in-depth analysis of the ground and excited state properties of their complexes has allowed us to establish structure–property relationships and propose simple principles for the design of nanobelts with improved electron-donating properties suitable for photovoltaic applications.

---

1. Introduction

Design and synthesis of cyclic molecular nanocarbons has been a longstanding challenge and remains a platform for extensive research in chemistry. The synthesis of curved π-conjugated nanocarbons remained elusive for many years. Following breakthroughs in this field by the Bertozzi,¹ Itami,² and Yamago³ groups, cycloparaphenylenes (CPPs) ranging from 5 to 16, 18, and 20 phenylene units have emerged.^4,5

Carbon nanobelts (CNBs) are segments of carbon nanotubes that require the cleavage of at least two C–C bonds to open their cylindrical framework.⁶ They have been of great interest to scientists for several decades because of their unique structure and promising applications as functional materials.^7,8 The double-stranded carbon skeleton and radial π-conjugation make CNBs attractive candidates for optoelectronic applications^9–12 due to their high photoluminescence efficiency^13,14 and remarkable charge transport properties.⁹ CNBs exhibit similar electronic coupling to CPPs but significantly lower reorganization energy.^15,16 This leads to faster hole mobility within the material, as seen in the simulated values: 0.36 cm² V⁻¹ s⁻¹ for [6,6]CNB and 0.056 cm² V⁻¹ s⁻¹ for [6]CPP.

The first synthesis and isolation of the armchair [6,6]CNB consisting exclusively of fully fused six-membered rings (6-MRs) was reported by Itami and co-workers in 2017.¹⁷ In 2018, the same authors reported the synthesis of larger [8,8] and [12,12]CNBs.¹⁸ Thereafter, chiral and zigzag CNBs were also successfully obtained.^19–22 The progress made in these years attracted even more scientists and contributed to the subsequent rapid growth of this area.^23–25

Nowadays, there are several main directions for expanding the CNB family. One of the directions is associated with the synthesis of aromatic belts containing nonhexagonal rings. An example of such a system is methylene-bridged cycloparaphenylenes ([n]MCPP).^26,27 Very recently, Itami and co-workers synthesized [8]MCPP and [10]MCPP.²⁸ They found some differences in the optical properties of MCPPs and CPPs as a function of size, caused by the holding of adjacent phenylene rings by the methylene bridge. In addition, significant attention was paid to the synthesis of CNBs with unique geometries such as twisted,²⁹ bowl-shaped,^30,31 and Möbius topologies,³² as well as to the inclusion of heteroatoms into the CNB structure.^30,33–36 The addition of oxygen, sulfur or selenium heteroatoms lowers the HOMO energy level, suggesting that the modified CNBs are stable in air.³⁷

It is well known that CPPs can accommodate fullerenes and other guest molecules due to their unique concave structure.³⁸ Starting from the original example of [10]CPP⊃C₆₀ by Iwamoto et al. in 2011, hundreds of CPP-based complexes have already been reported. The semiconductor properties of such host–guest complexes make them appealing for organic electronic devices like organic photovoltaics (OPVs) and organic field-effect transistors (OFETs), where fullerenes usually act as electron acceptors.^39,40 Although host molecules have shown good electrical conductivity by themselves, encapsulation of C₆₀ makes it even higher.^41,42 Moreover, the complexation between nanocarbons and fullerenes, which are complementary in shape and size, can protect fullerenes from water and oxygen, known to disrupt the electron transfer process.

Since [10]MCPP has a diameter of 13.1 Å,²⁸ which is similar to the diameter of [10]CPP (13.7 Å),⁴³ the C₆₀ fullerene can be placed inside its cavity. Currently, only a limited number of examples of all-carbon or heteroatom-doped nanobelts with encapsulated fullerenes are known,^22,31 and their photophysical properties have not yet been studied. By modeling these complexes in both the ground and excited states, a possible relationship between the structure and characteristics of photoinduced electron transfer can be revealed.

In this work, we investigate the effects of the bridge between phenylene units on the properties of all-carbon and heteroatom-bridged nanobelts and their inclusion complexes with fullerenes. Based on the structure–property relationships, we propose several useful rules for designing nanobelts with desired electronic properties.

2. Computational methods

Optimization of geometries was performed using the B3LYP hybrid functional^44–46 with Ahlrichs’ def2-SVP basis set^47,48 and empirical D3 dispersion correction with Becke–Johnson damping⁴⁹ using the ORCA 5.0.1 program.^50,51 Orbital energies and vertical excitation energies (the latter using TDA formalism⁵²) were calculated with the range-separated CAM-B3LYP functional⁵³ and def2-SVP basis set,^47,48 using Gaussian 16 (rev. A03).⁵⁴ The same program was used to study the charge distribution according to the Mulliken,⁵⁵ Hirshfeld,⁵⁶ iterative Hirshfeld,⁵⁷ CM5,⁵⁸ NPA,⁵⁹ and Merz–Singh–Kollman⁶⁰ schemes. The interaction energies and their decomposition analysis (EDA)^61,62 were calculated at the B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-SVP level of theory, using the Amsterdam Density Functional (ADF) program.⁶³

3. Results and discussion

3.1. Methylene- vs. ethene-bridged carbon nanobelts

First, we will compare the geometrical structures and electronic properties of [10]CPP and two CNBs with methylene and ethene bridges. Formally, the mentioned CNBs differ from the “parent” CPP only in the type of bridges between phenylene units. The Kohn–Sham highest occupied molecular orbitals (HOMOs) and lowest unoccupied molecular orbitals (LUMOs) for the ground-state geometries of the mentioned molecules are given in Fig. 1. In all molecules, these orbitals are of the same nature and are delocalized over the phenylene units but not over the bridges. In the HOMO, between the phenylene units, there is an out-of-phase combination of p-orbitals of the C atoms, while in the LUMO this combination is in-phase.

Fig. 1 Structure of [10]CPP and two CNBs (top), their frontier molecular orbitals (bottom left) and selected geometrical parameters (bottom right).

Comparison of the orbitals of [10]CPP with the orbitals of [10]MCPP (methylene-bridged) and [10]ECPP (ethene-bridged) revealed significant differences in their energies. For [10]MCPP, the HOMO energy is 0.7 eV higher compared to [10]CPP, while the difference in the LUMO energy is practically negligible. In contrast, [10]ECPP and [10]CPP show very similar HOMO energies, but the LUMO in [10]ECPP has an energy of about 0.3 eV lower compared to [10]CPP. To explain the observed difference in orbital energies, we compared the structural parameters of [10]CPP and the corresponding CNBs. We considered two types of deformation – out-of-plane twisting (dihedral angle D) and in-plane scissoring (angle α) of phenylene units. The first obvious difference between [10]CPP and both CNBs is the dihedral angle D between the phenylene units. In [10]CPP, this angle is about 32°, while in nanobelts the angle between the planes of two 6-MRs is close to zero. Reduced twisting of adjacent aromatic units improves conjugation in CNBs compared to [10]CPP due to the increase in the orbital overlap. The HOMO is destabilized due to increased out-of-phase orbital interactions, while the LUMO stabilizes because of increased in-phase interactions. Another notable difference is the bending angle α, defined as the angle between the two carbon atoms attached to the bridge and the center of the bond between the phenyl rings. The value of the angle α is maximal in [10]CPP (ca. 104°), and then gradually decreases to 97° in [10]ECPP and 82.5° in [10]MCPP. This is directly related to the disparity between the distances d1 and d2 in CNBs. As seen in Fig. 1, d1 and d2 are almost equal in [10]CPP, while d1 is significantly shorter (by ca. 0.89 Å) than d2 in [10]MCPP. Such bending increases the strain of the belt and destabilizes the HOMO and LUMO.

The geometrical distortion caused by the methylene or ethene bridges certainly contributes to the modulation of the electronic properties of CNBs. However, such a significant difference in the orbital energies of [10]ECPP and [10]MCPP suggests that the structural changes are not the only factor affecting these values. The electronic nature of the bridge also has a significant impact. To confirm this, we calculated partial charges on the bridges using the Merz–Singh–Kollman scheme.⁴⁷ Despite the similar non-polar character of the methylene and ethene fragments, the calculation predicts a different charge distribution (Fig. 2). In particular, the average charge on each methylene bridge turned out to be 0.08e, while the charge on each ethene bridge was found to be negative and equal to −0.14e. Note that in phenanthrene, which is structurally similar to [10]ECPP, the charge on this fragment is −0.19e.

Fig. 2 Structure, interaction energies (in kcal mol⁻¹), and HOMO/LUMO energies of [10]CPP⊃C₆₀, [10]MCPP⊃C₆₀, and [10]ECPP⊃C₆₀ complexes and their subunits, as well as the average charge on each bridge.

Thus, a significant shift in the orbital energies of the nanobelts compared to [10]CPP seems to be due to two main factors: pronounced structural deformation (bending and reduced twisting) and partial charge separation within the nanobelt.

An appropriate size of the [10]CPP cavity makes it an ideal host for the C₆₀ fullerene.⁶⁴ The similar sizes of [10]MCPP and [10]ECPP with the original [10]CPP prompted us to investigate their complexes with C₆₀. Taking into account the different electronic nature of the studied carbon nanostructures, we expect to find notably different behaviors of their inclusion complexes in the ground and excited states.

Comparing the orbital energies of the [10]CPP⊃C₆₀, [10]MCPP⊃C₆₀, and [10]ECPP⊃C₆₀ complexes, as well as their individual fragments, we see that fullerene binding has a rather weak effect on the HOMO and LUMO energies of individual fragments. Important to note is that, in the complexes, the HOMO is always localized on the host unit, while the LUMO remains on the C₆₀ fullerene. Thus, the nanobelts act as an electron donor in complex with the fullerene, similar to CPP. The changes in the HOMO energies observed during the complex formation are less than 0.1 eV. The LUMO energy shifts by 0.3–0.4 eV, depending on the specific complex. Small changes in orbital energies upon complexation indicate that there is no or very little charge separation in the ground state (GS). This result was confirmed by the population analysis. For all complexes, the charge separation between the host and guest molecules does not exceed 0.1e (Table S1 in the ESI†).

We calculated the interaction energy (ΔE_int) between the host molecules and fullerene to assess the relative stability of the complexes. To increase the accuracy of results, we performed single-point energy calculations at the B3LYP-D3(BJ)/TZ2P level for the B3LYP-D3(BJ)/def2-SVP optimized structures. As shown in Table S2,† increasing the basis set significantly affects the interaction energy values. For [10]CPP⊃C₆₀, [10]MCPP⊃C₆₀, and [10]ECPP⊃C₆₀ systems, ΔE_int was found to be −51.9, −66.9 and −65.3 kcal mol⁻¹, respectively, at the B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-SVP level of theory. The ΔE_int value for [10]CPP⊃C₆₀ is in good agreement with the values obtained using the B97-D2 and TPSS-D3(BJ) functionals and def2-TZVP basis set.⁶⁵ As can be seen, C₆₀ forms stronger non-covalent interactions with nanobelts than with [10]CPP by more than 10 kcal mol⁻¹. Previously, we showed that dispersion interactions play an important role in the stability of nanoring complexes with fullerenes.^66–69 To understand the nature of interactions in nanobelt-based complexes, a Morokuma-type energy decomposition analysis (EDA) was performed for the interaction energy and compared with the EDA data for [10]CPP⊃C₆₀ (Table 1).

Table 1 EDA results for [10]CPP⊃C₆₀, [10]MCPP⊃C₆₀ and [10]ECPP⊃C₆₀ complexes obtained at B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-SVP

Complex	Energy terms,^a kcal mol^−1
	ΔEPauli	ΔEelstat	ΔEoi	ΔEdisp	ΔEint
a The percentage contributions to the sum of all attractive energy terms (ΔEelstat + ΔEoi + ΔEdisp) are listed in parentheses.
[10]CPP⊃C60	74.07	−36.43 (29%)	−15.02 (12%)	−74.56 (59%)	−51.94
[10]MCPP⊃C60	107.24	−54.54 (31%)	−23.00 (13%)	−96.63 (55%)	−66.94
[10]ECPP⊃C60	62.99	−31.12 (24%)	−13.05 (10%)	−84.09 (66%)	−65.26

---

The analysis revealed that among the binding forces (electrostatic, orbital, and dispersion), the dispersion term is dominant with a contribution from 55 to 66%. The absolute values of ΔE_disp in nanobelt-based complexes are much higher than those in [10]CPP⊃C₆₀, which is explained by the more extended structure of nanobelts. The second important term is electrostatic interactions. Contribution of this term was between 24 and 31%, depending on the system. The orbital interactions provide 12, 13, and 10% for the [10]CPP⊃C₆₀, [10]MCPP⊃C₆₀, and [10]ECPP⊃C₆₀ complexes, correspondingly. The destabilizing term ΔE_Pauli for [10]MCPP⊃C₆₀ is much larger than those for [10]CPP⊃C₆₀ and [10]ECPP⊃C₆₀ (107.2 vs. 74.1 and 63.0 kcal mol⁻¹). This difference is directly related to the geometrical structure of the complexes. The diameter of [10]MCPP is about 0.4 Å smaller than that of [10]CPP and [10]ECPP (Fig. 1).

The topology of non-covalent interactions in the complexes was studied using QTAIM and NCI tools and is shown in Figs. S1–S3, ESI.† As expected, π⋯π interactions between the host and guest molecules are dominant. For [10]ECPP⊃C₆₀, bond critical points (BCPs) were found only between the carbon atoms of subunits, while for [10]MCPP⊃C₆₀, BCPs were also detected between the hydrogen atoms of the methylene bridge and the carbon atoms of fullerenes. Thus, the [10]MCPP⊃C₆₀ complex is characterized by more number of BCPs than [10]ECPP⊃C₆₀ (30 vs. 24), which is in agreement with its stronger ΔE_oi. The electron density, its Laplacian, and other topological parameters at BCPs related to non-covalent interactions are given in Table S3, ESI.† The NCI isosurfaces demonstrate similar weak attractive dispersion interactions between the fragments in the [10]MCPP⊃C₆₀ and [10]ECPP⊃C₆₀ complexes. The reduced density gradient (RDG) plots and NCI isosurfaces are shown in Figs. S2 and S3, ESI.†

Different orbital energies observed in the studied inclusion complexes suggest their different behaviors upon photoexcitation. We studied 80 lowest singlet excited states of each complex using the TDA-DFT method at the CAM-B3LYP-D3(BJ)/def2-SVP//B3LYP-D3(BJ)/def2-SVP level of theory. The CAM-B3LYP functional is highly suitable for modeling charge transfer processes in fullerene-based complexes.⁷⁰ The complexes were divided into 2 fragments: guest C₆₀ and host nanoring/nanobelts. All excited states were classified into three groups: (1) locally excited (LE) states with excitation on one of the fragments and very low charge separation, CS < 0.1e; (2) charge transfer (CT) states with CS > 0.8e between fragments, and (3) mixed states with 0.1e < CS < 0.8e. Table 2 contains the characteristics of the lowest excited states of each type.

Table 2 Excitation energy (E_x, eV), main singly excited configuration (HOMO(H)–LUMO(L)) with the largest squared coefficient in the configuration-interaction (CI coef.), oscillator strength (f), extent of charge transfer (CT, e) or localization of exciton (X) computed for [10]CPP⊃C₆₀ in equilibrium and modified geometries, as well as for [10]ECPP⊃C₆₀ and [10]MCPP⊃C₆₀ in equilibrium geometries. All calculations were performed in the gas phase

	Supramolecular system
	[10]CPP⊃C60			[10]ECPP⊃C60	[10]MCPP⊃C60
	Equilibrium	Generated from [10]ECPP⊃C60	Generated from [10]MCPP⊃C60
	LE^Guest (C60)
E x (S0 → Sn)	2.546	2.559	2.519	2.562	2.523
Transition (CI coef.)	H−3 → L+1 (0.58)	H−3 → L+2 (0.67)	H−3 → L (0.60)	H−4 → L (0.23)	H−3 → L+1 (0.30)
f	<0.001	<0.001	<0.001	<0.001	<0.001
X	0.952	0.966	0.940	0.960	0.929
	LE^Host ([10]XCPP)
E x (S0 → Sn)	3.493	2.789	3.146	3.274	3.009
Transition (CI coef.)	H → L+6 (0.26)	H → L+3 (0.71)	H → L+7 (0.41)	H−1 → L+3 (0.35)	H → L+3 (0.31)
f	<0.001	<0.001	1.581	0.006	<0.001
X	0.943	0.963	0.947	0.968	0.948
	Most intense absorption band
E x (S0 → Sn)	3.885	3.385	3.146	3.937	3.556
Transition (CI coef.)	H → L+7 (0.29)	H → L+7 (0.42)	H → L+7 (0.41)	H → L+10 (0.18)	H → L+7 (0.32)
f	1.586	2.761	1.581	3.998	1.897
Localization	[10]CPP	[10]CPP	[10]CPP	[10]ECPP	[10]MCPP
X	0.801	0.936	0.947	0.818	0.850
	CT ([10]XCPP → C60)
E x (S0 → Sn)	2.759	2.400	2.153	2.816	2.183
Transition (CI coef.)	H → L+1 (0.95)	H → L+2 (0.95)	H → L (0.93)	H → L+2 (0.88)	H → L (0.66)
f	0.007	0.001	0.002	<0.001	<0.001
CT	0.982	0.987	0.981	0.984	0.976

---

The energy of the lowest LE^Guest state in [10]CPP⊃C₆₀, [10]MCPP⊃C₆₀ and [10]ECPP⊃C₆₀ complexes is almost the same and lies at the range of 2.52–2.56 eV (Table 2). In turn, the energy of the lowest LE^Host is higher in energy in all cases and its value strongly depends on the complex. For [10]CPP⊃C₆₀, this value is 3.49 eV, while for the [10]ECPP⊃C₆₀ and [10]MCPP⊃C₆₀ complexes, the energy of this state is lower by 0.22 and 0.48 eV, respectively. The LE^Host energy correlates with the energy difference between the occupied and unoccupied orbitals of the host for the corresponding transition (Table 3). The greater the difference between these orbitals, the higher the energy of the LE^Host state. The oscillator strength for the lowest LE states of both types is very weak; however, excited states with high probability of light absorption were found within the studied energy range. In each case, this state is localized on the host unit.

Table 3 Energies of frontier molecular orbitals participating in LE^Host and CT states for [10]XCPP⊃C₆₀ and [10]CPP⊃C₆₀ in non-equilibrium ([10]CPP^≠) and equilibrium ([10]CPP⁼) geometries

Complex	E(HOMO), eV	E(LUMO), eV	E(H–L), eV	E(LE^Host/CT), eV
	LE^Host ([10]XCPP)
[10]MCPP⊃C60 ^=	−6.02	−1.09	4.93	3.01
[10]ECPP⊃C60 ^=	−6.56	−1.28	5.28	3.27
[10]CPP⊃C60 ^=	−6.59	−1.16	5.43	3.49
	CT ([10]XCPP → C60)
[10]MCPP⊃C60 ^=	−6.02	−2.33	3.69	2.18
[10]ECPP⊃C60 ^=	−6.54	−2.26	4.28	2.82
[10]CPP⊃C60 ^=	−6.59	−2.37	4.22	2.76
	LE^Host ([10]XCPP)
[10]CPP⊃C60 ^≠ (M)	−5.92	−0.80	5.12	3.15
[10]CPP⊃C60 ^≠ (E)	−6.12	−1.42	4.70	2.79
	CT ([10]XCPP → C60)
[10]CPP⊃C60 ^≠ (M)	−5.92	−2.26	3.66	2.15
[10]CPP⊃C60 ^≠ (E)	−6.12	−2.26	3.86	2.40

---

Among the analyzed excited states, only one type of CT states was found. This corresponds to the electron transfer from the HOMO of the host to one of the three-fold degenerate LUMOs of the guest. The energy of the CT state is 2.76 eV for [10]CPP⊃C₆₀. This is about 0.21 eV above the lowest excited state. When considering the complex with the methylene-bridged nanobelt, a significant decrease in the energy of the CT state by almost 0.6 eV was observed. This stabilization of the CT state in [10]MCPP⊃C₆₀ makes it the lowest excited state. Interesting to note is that for the [10]ECPP⊃C₆₀ complex, the bridge has an opposite effect, increasing the energy of the CT state compared to the original [10]CPP⊃C₆₀. This adversely affects the population of such a state through the decay of the lowest LE state. The opposite effect of the bridge on the energy of the CT state is consistent with the increase and decrease in the HOMO–LUMO gap compared to the [10]CPP⊃C₆₀ complex (Table 3). The gap change is mainly caused by a shift in the host HOMO. Thus, the methylene-bridged nanobelt with a more destabilized HOMO is more attractive for photoinduced electron transfer in the complex with C₆₀. The frontier molecular orbitals representing the LE and CT states in the studied complexes are shown in Figs. S4–S6, ESI.†

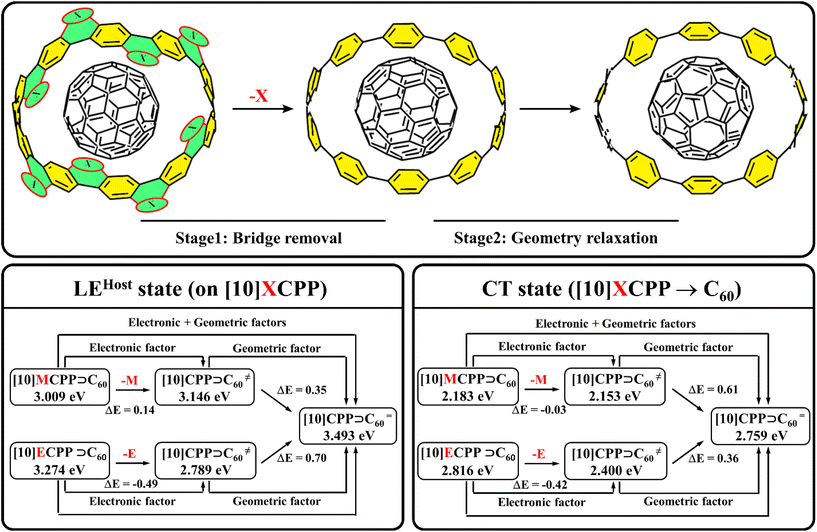
Additional calculations were performed to semi-quantitatively evaluate the electronic effect as well as the effect of geometric distortion caused by the bridge. In particular, we transformed [10]MCPP⊃C₆₀ and [10]ECPP⊃C₆₀ into two corresponding [10]CPP⊃C₆₀, where the host geometry was preserved and all bridge fragments were replaced by hydrogen atoms with a fixed C–H distance of 1.09 Å (Fig. 3). As expected, such transformation almost did not affect the lowest LE^Guest states – its energy changed by less than 0.01 eV. However, the changes that were made affected the LE^Host states. The removal of the methylene bridge led to the destabilization of the corresponding LE state by 0.14 eV, while removal of the ethene bridge caused a strong stabilization of the LE state; its energy shifted from 3.27 to 2.79 eV. Similar changes were observed for CT states. In particular, the removal of the methylene bridge caused only minor changes in the CT state energy, but for [10]ECPP⊃C₆₀, the removal of the bridge led to stabilization of the CT state by 0.42 eV (Fig. 3). Thus, the ethene bridge with partial negative charge destabilizes both the LE and CT states mainly due to the significant stabilization of the HOMO and increase in the orbital energy difference. In turn, the effect of the methylene bridge is less pronounced. Bearing in mind that this analysis was done without geometry relaxation, we assume that the observed changes characterize the electronic effect of the bridges.

Fig. 3 Representative structure of [10]XCPP⊃C₆₀ and [10]CPP⊃C₆₀ in their non-equilibrium ([10]CPP^≠) and equilibrium ([10]CPP⁼) geometries (top), as well as comparison of the LE^Host (left) and CT state (right) energies for different geometries.

Relaxation of the non-equilibrium complexes obviously leads to the equilibrium [10]CPP⊃C₆₀ structure. Thus, a comparison of the energies of the LE and CT states in non-equilibrium and equilibrium complexes will indicate geometric distortion effects. The data presented in Fig. 3 clearly show that the twisting of the phenylene units and the opening of the angle α observed during relaxation lead to destabilization of both the LE and CT states due to an increase in the energy difference between orbitals associated with the excitation. Geometry relaxation causes stabilization of both occupied and unoccupied orbitals of CPP, but the effect is more pronounced at the HOMO. Interesting to note is that changing the geometry affects the LE and CT states of [10]MCPP⊃C₆₀ and [10]ECPP⊃C₆₀ differently. In particular, structural changes have a stronger effect on the LE^Host states in [10]ECPP⊃C₆₀ (ΔE = 0.70 eV) and on the CT states in [10]MCPP⊃C₆₀ (ΔE = 0.61 eV).

Summing up, we have successfully distinguished the electronic and geometric factors that affect the energies of the LE^Host and CT states of the complexes based on CPP and CNBs. The electronic effects in CNBs are in good agreement with the partial charge on the bridge. Negative charge stabilizes the HOMO of the electron donor, thereby destabilizing both the LE^Host and CT states. Small positive charge weakly affects the CT state and stabilizes the LE^Host. At the same time, geometry change upon introduction of bridges leads to the stabilization of the LE and CT states in all cases, mainly due to destabilization of the donor HOMO. Since we are interested in the process of electron transfer, which depends on the energy of the nanobelt HOMO, the changes caused by methylene bridges are more favorable than those of ethene bridges.

3.2. Heteroatom-bridged nanobelts

In the previous section, we demonstrated that the electron-donating properties of the methylene-bridged nanobelt in the complex with fullerene are better that those of [10]CPP and the ethene-bridged nanobelt. The inclusion of heteroatoms instead of the methylene bridge can further modify both the geometrical structure and electronic properties of nanobelts, as well as improve the electron transfer characteristics of their fullerene inclusion complexes. Taking into account the recent advances in the synthesis of heteroatom-embedded carbon nanobelts,^23,25,26 we constructed the N, O, and S analogs of [10]MCPP⊃C₆₀, and studied their excited state properties.

As can be seen in Fig. 4, the studied complexes can be divided into two main groups depending on the HOMO energy. The first group consists of the [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀ complexes, in which the HOMO energy is higher than that in the original [10]CPP⊃C₆₀ (HOMO = −6.59 eV). The second group consists of the [10]OCPP⊃C₆₀ and [10]SCPP⊃C₆₀ complexes, in which the HOMO lies lower than that in [10]CPP⊃C₆₀. We compared some selected characteristics of the complexes to find the reason for their different orbital energies (Table 4).

Fig. 4 Structure, interaction energies (in kcal/mol), and HOMO/LUMO energies (in eV) of [10]MCPP⊃C₆₀, [10]NCPP⊃C₆₀, [10]OCPP⊃C₆₀, and [10]SCPP⊃C₆₀ complexes. HL corresponds to the HOMO–LUMO gap.

Table 4 Selected characteristics of the [10]MCPP⊃C₆₀, [10]NCPP⊃C₆₀, [10]OCPP⊃C₆₀, and [10]SCPP⊃C₆₀ complexes and unbridged, undistorted [10]CPP⊃C₆₀ as a reference

Parameter	[10]CPP⊃C60	[10]MCPP⊃C60	[10]NCPP⊃C60	[10]OCPP⊃C60	[10]SCPP⊃C60
a The average Merz–Singh–Kollman charge on each bridge.
∠α, °	103.6	82.6	79.1	77.7	87.0
∠D, °	28.82	0.04	0.02	0.02	0.03
d1, Å	2.982	2.365	2.268	2.208	2.511
d2, Å	2.981	3.238	3.299	3.340	3.147
|d2 − d1|, Å	0.001	0.872	1.031	1.132	0.635
Radius, Å	6.890	6.676	6.630	6.588	6.734
q (bridge), e^a	n/a	0.09	−0.10	−0.30	−0.10

---

The comparison of the data for the complexes of the first group shows that the similar values of the HOMO energy were caused by different effects. As we mentioned earlier, the electronic properties of [10]MCPP⊃C₆₀ are determined by two factors – geometrical distortion and partial positive charge on the methylene bridge (both push the HOMO up). In the [10]NCPP⊃C₆₀ complex, the geometry deformation is even stronger (smaller ∠α and bigger |d2 − d1| difference), but the bridge in this case is negatively charged. Thus, the geometrical effect destabilizes the HOMO, while the partial negative charge on the NH-bridge acts oppositely and reduces the HOMO energy.

In the second group, both O- and S- bridges are negatively charged. As expected, the negative charge on the O-bridge is significantly higher than that on the S-bridge (−0.30e vs. −0.10e), suggesting stronger HOMO stabilization in the case of [10]OCPP⊃C₆₀. Although geometrical distortion in [10]OCPP⊃C₆₀, which causes destabilization of the HOMO, is the largest among the studied complexes, the electronic effect of the O-bridge dominates and its HOMO lies lower than that in [10]CPP⊃C₆₀. In [10]SCPP⊃C₆₀, the negative charge on the S-bridge is less than that on the O-bridge and geometry deformation is also less pronounced: ∠α is equal to 77.7° and 87.0°, and |d2 − d1| is 1.132 and 0.635 Å for the [10]OCPP⊃C₆₀ and [10]SCPP⊃C₆₀ complexes, respectively. The HOMO of this complex is the lowest among all the complexes, therefore [10]SCPP is the worst donor among the studied nanobelts.

Important to note is that the interaction energy in [10]OCPP⊃C₆₀ is about 10 kcal mol⁻¹ less than those in other heteroatom-bridged nanobelts. Energy decomposition analysis showed that the stronger Pauli repulsion caused by a smaller diameter of the [10]OCPP nanobelt is the main factor for this finding. The EDA results for the heteroatom-bridged nanobelts are given in Table S4, ESI.†

To describe the photoinduced electron transfer properties of these complexes, we analyzed the lowest 80 singlet excited states (Table 5). In all complexes, the lowest LE state is localized on the C₆₀ fullerene. The lowest LE^Host state is 0.50–0.65 eV higher in energy compared to the lowest LE^Guest. Despite the different geometric characteristics, all complexes have relatively close values of the LE^Host energy. This agrees well with the observation made for [10]MCPP⊃C₆₀, namely, that the geometric distortion caused by the bridge affects the LE states less than the CT states.

Table 5 Excitation energy (E_x, eV), main singly excited configuration (HOMO(H)–LUMO(L)) with the largest squared coefficient in the configuration-interaction (CI coef.), oscillator strength (f), extent of charge transfer (CT, e) or localization of exciton (X) computed for [10]MCPP⊃C₆₀, [10]NCPP⊃C₆₀, [10]OCPP⊃C₆₀ and [10]SCPP⊃C₆₀ in the gas phase

	Supramolecular system
	[10]MCPP⊃C60	[10]NCPP⊃C60	[10]OCPP⊃C60	[10]SCPP⊃C60
a Mixed state with significant contributions of both LE and CT.
	LE^Guest (C60)
E x (S0 → Sn)	2.523	2.514	2.526	2.539
Transition (CI coef.)	H−3–L+1 (0.30)	H−9–L+1 (0.39)	H−2–L (0.21)	H−5–L (0.47)
f	<0.001	<0.001	<0.001	<0.001
X	0.929	0.837	0.926	0.949
	LE^Host ([10]XCPP)
E x (S0 → Sn)	3.009	3.174	3.037	3.154
Transition (CI coef.)	H–L+3 (0.31)	H−1–L+3 (0.59)	H–L+3 (0.73)	H–L+3(0.71)
f	<0.001	0.139	<0.001	<0.001
X	0.948	0.938	0.964	0.968
	Most intense absorption band
E x (S0 → Sn)	3.556	3.480	3.627^a	3.717
Transition (CI coef.)	H–L+7 (0.32)	H–L+7 (0.24)	H–L+6 (0.21)	H–L+6 (0.38)
f	1.897	1.194	0.703	1.852
Localization	[10]MCPP	[10]NCPP/C60	[10]OCPP/C60	[10]SCPP
X	0.850	0.55/0.35	0.48/0.27	0.893
	CT ([10]XCPP → C60)
E x (S0 → Sn)	2.183	2.101	2.684	2.859
Transition (CI coef.)	H–L (0.66)	H–L+1 (0.61)	H–L (0.74)	H–L (0.75)
f	<0.001	0.001	0.002	0.001
CT	0.976	0.972	0.975	0.976

---

In the [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀ complexes, the CT states corresponding to the electron transfer from the nanobelt to C₆₀ are the lowest excited states and can be experimentally observed. This CT state is 0.34 and 0.41 eV more stable than the lowest LE states of [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀. In turn, for [10]OCPP⊃C₆₀ and [10]SCPP⊃C₆₀ complexes, the CT states with 0.98e transferred lie 0.16 and 0.32 eV higher in energy than the lowest LE states. No other types of CT states were found within the studied number of excited states. The frontier MOs representing the LE and CT states for all complexes are shown in Figs. S7–S9, ESI.†

3.3. Environmental effects and electron transfer rates

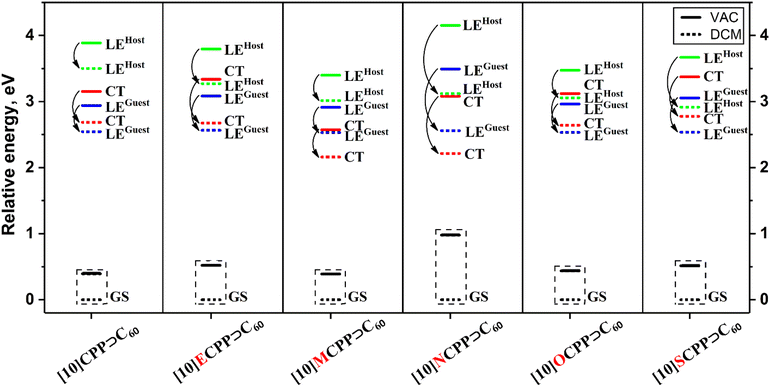
The COSMO-like model with dichloromethane (DCM) as a solvent was used to study the effect of the polar environment on electronic excitation.^71,72 The application of this model previously showed a good agreement between the results of calculations and experimental data for the CPP-based inclusion complexes and other donor–acceptor conjugates.^67,73–75 The dipole moment of all studied complexes was calculated to be smaller than 0.1 D. Low dipole moment of the complexes can be explained by the high symmetry of the units (nanobelts and C₆₀) and their symmetric mutual arrangement. The GS solvation energies of [10]CPP⊃C₆₀, [10]ECPP⊃C₆₀, [10]MCPP⊃C₆₀, [10]OCPP⊃C₆₀ and [10]SCPP⊃C₆₀ range from −0.39 to −0.52 eV. However, the solvation energy of [10]NCPP⊃C₆₀ was estimated to be −0.98 eV. To explain this difference, we compared the molecular electrostatic potentials (MEP) of the complexes (Fig. S10, ESI†). In the [10]CPP⊃C₆₀, [10]ECPP⊃C₆₀, [10]MCPP⊃C₆₀, and [10]SCPP⊃C₆₀ complexes, the MEP isosurface is almost evenly distributed over the host unit, therefore, certain charged regions cannot be distinguished. At the same time, the [10]OCPP⊃C₆₀ and [10]NCPP⊃C₆₀ complexes clearly show spots, in which the negative charge is localized. Important to note is that, in contrast to [10]NCPP⊃C₆₀, in [10]OCPP⊃C₆₀, the negatively charged regions are surrounded by the zones with opposite charges. As expected, a close location of positively and negatively charged regions on the MEP of [10]OCPP⊃C₆₀ reduces its solvation energy compared to [10]NCPP⊃C₆₀.

Changes in the dipole moment during the transition from the GS to any of the LE states are quite small and does not exceed 0.2 D; thus, the solvation energies of these states are very close to each other. The solvation energies of the CT states do not differ much from the solvation energies of the GS and LE states due to the high symmetry of the complexes and the extensive charge delocalization in C₆₀ and the nanobelt. Details of solvation in DCM are given in Table S5, ESI.† Important to note is that the CT state is the lowest excited state in DCM only in [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀, as in the gas phase. In all other cases, the stabilization of the CT state by the solvent is not enough to reorder the CT and LE states. The energies of the LE and CT states of all complexes in a vacuum and DCM are shown in Fig. 5.

Fig. 5 Relative energies of the LE and CT states (in eV) for [10]CPP⊃C₆₀, [10]ECPP⊃C₆₀, [10]MCPP⊃C₆₀, [10]NCPP⊃C₆₀, [10]OCPP⊃C₆₀, and [10]SCPP⊃C₆₀ complexes calculated under vacuum (VAC) and in dichloromethane (DCM).

Similar to the complexes of all-carbon nanobelts, the CT states of the complexes with heteroatom-bridged nanobelts have a very low probability of light absorption, and therefore cannot be directly populated. Thus, a decay of the lowest LE state (LE^Guest) was considered as the main channel for generating states with election transfer. The semi-classical method of Ulstrup and Jortner^76,77 was used to calculate the rates of electron transfer (k_ET) and charge recombination (k_CR) processes. The rates were estimated using an effective frequency of 1600 cm⁻¹, corresponding to the C=C bond stretching. Earlier, it was established that varying the effective frequency from 1400 to 1800 cm⁻¹ does not significantly affect the electron transfer rate for similar systems.^75,78,79 Our assessment on selected complexes, [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀, confirms the negligible impact of the effective frequency on the calculated ET rate (Table S6, ESI†). Important parameters controlling the k_ET and k_CR rates in DCM are listed in Table 6.

Table 6 Gibbs energy (ΔG°, eV), electronic coupling (|V_ij|, eV), reorganization energy (λ, eV), Huang–Rhys factor (S_eff), activation energy (E_a, eV) and rates (k_x, s⁻¹) of ET and CR processes in [10]CPP⊃C₆₀, [10]ECPP⊃C₆₀, [10]MCPP⊃C₆₀, [10]NCPP⊃C₆₀, [10]OCPP⊃C₆₀, and [10]SCPP⊃C₆₀ calculated in DCM

Complex	ΔG°^a	|Vij|	λ		E a	S eff	k x
			λ int	λ solv
a ΔG° is approximated by the difference in the solvated electronic energies of the corresponding states. b Activation energy for the LE^Guest → CT reaction. c Effective value of the Huang–Rhys factor Seff = λI/ħωeff, where ħωeff is set to 1600 cm^−1.
	Electron transfer (LE ^Guest → CT)
[10]CPP⊃C60	0.140	1.31 × 10^−4	0.170	0.147	0.140	0.857	1.37 × 10^6
[10]ECPP⊃C60	0.111	1.01 × 10^−4	0.204	0.135	0.112	1.028	2.13 × 10^6
[10]MCPP⊃C60
GS geometry	−0.370	2.87 × 10^−4	0.215	0.128	0.011	1.084	1.37 × 10^9
LE relaxed geometry	−0.477	3.30 × 10^−4	0.207	0.138	0.018	1.043	1.20 × 10^9
[10]NCPP⊃C60
GS geometry	−0.344	3.14 × 10^−4	0.220	0.143	0.012	1.109	1.76 × 10^9
LE relaxed geometry	−0.447	1.42 × 10^−4	0.213	0.139	0.019	1.074	2.48 × 10^9
[10]OCPP⊃C60	0.110	9.24 × 10^−5	0.208	0.160	0.114	1.049	1.49 × 10^6
[10]SCPP⊃C60	0.239	8.86 × 10^−5	0.140	0.152	0.251	0.706	4.14 × 10^4
	Charge recombination (CT → GS)
[10]MCPP⊃C60
GS geometry	−2.160	1.79 × 10^−4	0.163	0.128	0.019	0.822	2.48 × 10^2
CT relaxed geometry	−1.898	2.17 × 10^−4	0.161	0.150	0.032	0.812	1.21 × 10^3
[10]NCPP⊃C60
GS geometry	−2.215	2.50 × 10^−4	0.175	0.143	0.022	0.882	6.02 × 10^2
CT relaxed geometry	−1.950	3.72 × 10^−4	0.170	0.152	0.029	0.857	3.26 × 10^3

---

Table 6 shows that the electron transfer reactions in the complexes are characterized by moderate reorganization energies ranging from 0.29 to 0.37 eV. The LE^Guest → CT charge separation process in the [10]CPP⊃C₆₀, [10]ECPP⊃C₆₀, [10]OCPP⊃C₆₀, and [10]SCPP⊃C₆₀ complexes is unlikely due to the positive Gibbs energy. Such states are barely populated and therefore hard to detect. At the same time, the electron transfer in the [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀ complexes is favorable and proceeds almost barrier-free in the normal Marcus regime (|ΔG°| ≤ λ). The calculated rate constants indicate sub-nanosecond charge separation between C₆₀ and [10]MCPP/[10]NCPP nanobelts. Considering that the electronic coupling values for the studied complexes exhibit fairly similar values, the rate of the charge separation process correlates well with the activation energies. In particular, the [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀ complexes, with the fastest electron transfer rates, are characterized by the smallest activation energy values. On the other hand, the activation energies for the [10]CPP⊃C₆₀, [10]ECPP⊃C₆₀, [10]OCPP⊃C₆₀, and [10]SCPP⊃C₆₀ complexes are more than an order of magnitude higher, resulting in significantly slower electron transfer.

The generated CT states usually decay to the ground state in the charge recombination process. We considered this process only for [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀, since other complexes are characterized by a low probability of the CT generation. The charge recombination proceeds in the deep inverted Marcus region (|ΔG°| ≫ λ) and its rates are dramatically lower (by more than 5 orders of magnitude) compared to the charge separation rates.

Internal geometry reorganization can be an important factor that affects the lifetime of the CT state.⁸⁰ Thus, we studied the effect of geometry relaxation of the LE^Guest and CT states on the rates of charge separation and recombination in the [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀ complexes (Table 6). For the charge separation, this effect is rather small. The changes in ΔG° values are about 0.1 eV, while the k_ET rates change insignificantly. In turn, for the charge recombination, the relaxation of the CT state geometry leads to an increase in k_CR. The CR rates for the relaxed geometries are about 5 times higher than the rates estimated for the GS geometries. Since the CR rates are always much slower than the corresponding ET rates, regardless of the geometry relaxation effect, this suggests a sufficient lifetime of the CT state for efficient charge separation.

4. Conclusions

In this work, we considered a series of nanobelts with different bridges between phenylene units, as well as their host–guest complexes with fullerene. To estimate the effect of the bridge, we compared the properties of the CNB-based complexes with those of the CPP-based ones. As a result, we successfully distinguished the electronic and geometric components of the bridge effect on the HOMO energy of the belts. From our results, we can formulate the following basic principles for the design of novel nanobelts with better electron-donating properties:

(1) Given that the electronic effect of the bridge depends on its charge, nanobelts with a partially positive charged bridge will have a more destabilized HOMO and therefore will be better donors of electrons.

(2) Given that the geometric distortion of CPP leads to energetic destabilization of its HOMO, nanobelts with reduced out-of-plane twisting and increased in-plane bending of adjacent phenylene units will be the best option.

(3) When designing nanobelts, both electronic and geometric components should be taken into account, since the overall effect on the electronic properties of nanobelts is additive to some extent.

Destabilization of the HOMO of nanobelts facilitates the electron transfer from the nanobelt to fullerene and makes the CT state the most stable among the excited states. Analysis of the excited states revealed the sub-nanosecond charge separation and slow charge recombination in [10]MCPP⊃C₆₀ and [10]NCPP⊃C₆₀, confirming that [10]MCPP and [10]NCPP are the best donors among the studied nanobelts. These two nanobelts are illustrative examples of the usefulness of the proposed rules.

Conflicts of interest

There are no conflicts to declare.

Author contributions

G. G.: investigation and formal analysis. O. A. S.: investigation, formal analysis, writing – original draft, and writing – review and editing. A. J. S.: investigation, supervision, and writing – review and editing. M. S.: supervision, writing – review and editing, and funding acquisition.

Acknowledgements

We are grateful for financial support from the Spanish Ministerio de Ciencia e Innovación (Network RED2018-102815-T, project PID2020-113711GB-I00, and Juan de la Cierva contract IJC2019-039846-I to A. J. S.), the Catalan Conselleria de Recerca i Universitats of the Generalitat de Catalunya (project 2021SGR623 and contract 2020 FISDU 00345 to G. G.) and the University of Girona (María Zambrano fellowship REQ2021_C_31 to O. A. S.). A. J. S. gratefully acknowledges Poland's high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) for providing computer facilities and support within computational grant no. PLG/2022/015756.

References

1. R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647.
2. H. Takaba, H. Omachi, Y. Yamamoto, J. Bouffard and K. Itami, Angew. Chem., Int. Ed., 2009, 48, 6112–6116.
3. S. Yamago, Y. Watanabe and T. Iwamoto, Angew. Chem., Int. Ed., 2010, 49, 757–759.
4. E. S. Hirst and R. Jasti, J. Org. Chem., 2012, 77, 10473–10478.
5. S. E. Lewis, Chem. Soc. Rev., 2015, 44, 2221–2304.
6. K. Y. Cheung, Y. Segawa and K. Itami, Chem. – Eur. J., 2020, 26, 14791–14801.
7. Y. Segawa, D. R. Levine and K. Itami, Acc. Chem. Res., 2019, 52, 2760–2767.
8. M. Hermann, D. Wassy and B. Esser, Angew. Chem., Int. Ed., 2021, 60, 15743–15766.
9. J. Lin, S. Wang, F. Zhang, B. Yang, P. Du, C. Chen, Y. Zang and D. Zhu, Sci. Adv., 2022, 8, eade4692.
10. L. Jones, L. Lin and T. W. Chamberlain, Nanoscale, 2018, 10, 7639–7648.
11. G. Aydın, O. Koçak, C. Güleryüz and I. Yavuz, New J. Chem., 2020, 44, 15769–15775.
12. L. O. Jones, M. A. Mosquera, G. C. Schatz and M. A. Ratner, Chem. Mater., 2019, 31, 6506–6518.
13. D. H. Ahn and J. W. Song, J. Comput. Chem., 2021, 42, 505–515.
14. V. M. Freixas, N. Oldani, R. Franklin-Mergarejo, S. Tretiak and S. Fernandez-Alberti, J. Phys. Chem. Lett., 2020, 11, 4711–4719.
15. J. B. Lin, E. R. Darzi, R. Jasti, I. Yavuz and K. N. Houk, J. Am. Chem. Soc., 2019, 141, 952–960.
16. G. Aydın, O. Koçak, C. Güleryüz and I. Yavuz, New J. Chem., 2020, 44, 15769–15775.
17. G. Povie, Y. Segawa, T. Nishihara, Y. Miyauchi and K. Itami, Science, 2017, 356, 172–175.
18. G. Povie, Y. Segawa, T. Nishihara, Y. Miyauchi and K. Itami, J. Am. Chem. Soc., 2018, 140, 10054–10059.
19. Y. Han, S. Q. Dong, J. W. Shao, W. Fan and C. Y. Chi, Angew. Chem., Int. Ed., 2021, 60, 2658–2662.
20. K. Y. Cheung, K. Watanabe, Y. Segawa and K. Itami, Nat. Chem., 2021, 13, 255.
21. K. Y. Cheung, S. J. Gui, C. F. Deng, H. F. Liang, Z. M. Xia, Z. Liu, L. F. Chi and Q. Miao, Chem, 2019, 5, 838–847.
22. H. Chen, Z. M. Xia and Q. Miao, Chem. Sci., 2022, 13, 2280–2285.
23. Y. Li, H. Kono, T. Maekawa, Y. Segawa, A. Yagi and K. Itami, Acc. Mater. Res., 2021, 2, 681–691.
24. Q. H. Guo, Y. Y. Qiu, M. X. Wang and J. F. Stoddart, Nat. Chem., 2021, 13, 402–419.
25. H. Chen and Q. Miao, J. Phys. Org. Chem., 2020, 33, e4145.
26. Y. Li, Y. Segawa, A. Yagi and K. Itami, J. Am. Chem. Soc., 2020, 142, 12850–12856.
27. N. Kai, H. Kono, A. Yagi and K. Itami, Synlett, 2023, 34, 1433–1436.
28. H. Kono, Y. Li, R. Zanasi, G. Monaco, F. F. Summa, L. T. Scott, A. Yagi and K. Itami, J. Am. Chem. Soc., 2023, 145, 8939–8946.
29. W. Fan, T. Matsuno, Y. Han, X. Wang, Q. Zhou, H. Isobe and J. Wu, J. Am. Chem. Soc., 2021, 143, 15924–15929.
30. J. Xie, X. Li, S. Wang, A. Li, L. Jiang and K. Zhu, Nat. Commun., 2020, 11, 3348.
31. X. Lu, T. Y. Gopalakrishna, Y. Han, Y. Ni, Y. Zou and J. Wu, J. Am. Chem. Soc., 2019, 141, 5934–5941.
32. Y. Segawa, T. Watanabe, K. Yamanoue, M. Kuwayama, K. Watanabe, J. Pirillo, Y. Hijikata and K. Itami, Nat. Synth., 2022, 1, 535–541.
33. J. Zhu, Y. Han, Y. Ni, G. Li and J. Wu, J. Am. Chem. Soc., 2021, 143, 2716–2721.
34. F. Zhang, X.-S. Du, D.-W. Zhang, Y.-F. Wang, H.-Y. Lu and C.-F. Chen, Angew. Chem., Int. Ed., 2021, 60, 15291–15295.
35. H. Chen, S. J. Gui, Y. Q. Zhang, Z. F. Liu and Q. Miao, CCS Chem., 2021, 3, 613–619.
36. M.-L. Tan, Q.-H. Guo, X.-Y. Wang, T.-H. Shi, Q. Zhang, S.-K. Hou, S. Tong, J. You and M.-X. Wang, Angew. Chem., Int. Ed., 2020, 59, 23649–23658.
37. L. Jones, L. Lin and T. W. Chamberlain, Nanoscale, 2018, 10, 7639–7648.
38. T. Kawase, K. Tanaka, N. Fujiwara, H. R. Darabi and M. Oda, Angew. Chem., Int. Ed., 2003, 42, 1624–1628.
39. Q. Huang, G. Zhuang, H. Jia, M. Qian, S. Cui, S. Yang and P. Du, Angew. Chem., Int. Ed., 2019, 58, 6244–6249.
40. Y. Xu, B. Wang, R. Kaur, M. B. Minameyer, M. Bothe, T. Drewello, D. M. Guldi and M. von Delius, Angew. Chem., Int. Ed., 2018, 57, 11549–11553.
41. J. C. Barnes, E. J. Dale, A. Prokofjevs, A. Narayanan, I. C. Gibbs-Hall, M. Juríček, C. L. Stern, A. A. Sarjeant, Y. Y. Botros, S. I. Stupp and J. F. Stoddart, J. Am. Chem. Soc., 2015, 137, 2392–2399.
42. S. Wang, X. Li, X. Zhang, P. Huang, P. Fang, J. Wang, S. Yang, K. Wu and P. Du, Chem. Sci., 2021, 12, 10506–10513.
43. J. Xia, J. W. Bacon and R. Jasti, Chem. Sci., 2012, 3, 3018–3021.
44. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
46. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
47. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
48. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
49. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
50. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
51. ORCA – an ab initio density functional, and semiempirical program package, version 5.0.3.
52. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
53. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
55. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
56. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
57. P. Bultinck, C. V. Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111.
58. A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541.
59. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
60. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145.
61. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
62. K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300.
63. ADF 2018, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com.
64. T. Iwamoto, Y. Watanabe, T. Sadahiro, T. Haino and S. Yamago, Angew. Chem., Int. Ed., 2011, 50, 8342–8344.
65. I. González-Veloso, J. Rodríguez-Otero and E. M. Cabaleiro-Lago, Phys. Chem. Chem. Phys., 2019, 21, 16665–16675.
66. G. George, O. A. Stasyuk, A. A. Voityuk, A. J. Stasyuk and M. Solà, Nanoscale, 2023, 15, 1221–1229.
67. O. A. Stasyuk, A. J. Stasyuk, M. Solà and A. A. Voityuk, J. Nanostruct. Chem., 2022 DOI:10.1007/s40097-022-00518-w.
68. O. A. Stasyuk, A. J. Stasyuk, M. Solà and A. A. Voityuk, Chem. – Eur. J., 2021, 27, 8737–8744.
69. O. A. Stasyuk, A. J. Stasyuk, M. Solà and A. A. Voityuk, ChemPhysChem, 2022, 23, e202200226.
70. P. Besalú-Sala, A. A. Voityuk, J. M. Luis and M. Solà, Phys. Chem. Chem. Phys., 2021, 23, 5376–5384.
71. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
72. A. Klamt, J. Phys. Chem., 1996, 100, 3349–3353.
73. A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, J. Phys. Chem. B, 2020, 124, 9095–9102.
74. A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Chem. Commun., 2019, 55, 11195–11198.
75. A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Chem. Commun., 2020, 56, 12624–12627.
76. J. Ulstrup and J. Jortner, J. Chem. Phys., 1975, 63, 4358–4368.
77. J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867.
78. T. Liu and A. Troisi, J. Phys. Chem. C, 2011, 115, 2406–2415.
79. O. A. Stasyuk, A. J. Stasyuk, M. Solà and A. A. Voityuk, Chem. – Eur. J., 2021, 27, 8737–8744.
80. O. A. Stasyuk, A. J. Stasyuk, M. Solà and A. A. Voityuk, Nanoscale Adv., 2022, 4, 2180–2188.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04045c

---