Destructive quantum interference in meta-oligo(phenyleneethynylene) molecular wires with gold–graphene heterojunctions†
Yinqi
Fan
 ab,
Shuhui
Tao
ac,
Sylvain
Pitié
d,
Chenguang
Liu
e,
Chun
Zhao
ab,
Shuhui
Tao
ac,
Sylvain
Pitié
d,
Chenguang
Liu
e,
Chun
Zhao
 e,
Mahamadou
Seydou
f,
Yannick J.
Dappe
g,
Paul J.
Low
e,
Mahamadou
Seydou
f,
Yannick J.
Dappe
g,
Paul J.
Low
 h,
Richard J.
Nichols
h,
Richard J.
Nichols
 b and
Li
Yang
b and
Li
Yang
 *ab
*ab
aDepartment of Chemistry, Xi'an-Jiaotong Liverpool University, Suzhou, 215123, China. E-mail: li.yang@xjtlu.edu.cn
bDepartment of Chemistry, University of Liverpool, Liverpool, L69 7ZD, UK
cNUS (Chongqing) Research Institute, Chongqing, China
dApplied Quantum Chemistry Group, E4, IC2MP, UMR 7285 Poitiers University CNRS, 86073 Poitiers, France
eDepartment of Electrical and Electronic Engineering, Xi'an-Jiaotong Liverpool University, Suzhou, 215123, China
fUniversité de Paris, ITODYS, CNRS, Paris F-75006, France
gSPEC, CEA, CNRS, Université Paris-Saclay, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
hSchool of Molecular Sciences, University of Western Australia, 35 Stirling Highway, 6009 Crawley, Australia
First published on 20th November 2023
Abstract
Quantum interference (QI) is well recognised as a significant contributing factor to the magnitude of molecular conductance values in both single-molecule and large area junctions. Numerous structure–property relationship studies have shown that para-connected oligo(phenyleneethynylene) (OPE) based molecular wires exemplify the impact of constructive quantum interference (CQI), whilst destructive quantum interference (DQI) effects are responsible for the orders of magnitude lower conductance of analogous meta-contacted OPE derivatives, despite the somewhat shorter effective tunnelling distance. Since molecular conductance is related to the value of the transmission function, evaluated at the electrode Fermi energy, T(EF), which in turn is influenced by the presence and relative energy of (anti)resonances, it follows that the relative single-molecule conductance of para- and meta-contacted OPE-type molecules is tuned both by the anchor group and the nature of the electrode materials used in the construction of molecular junctions (gold|molecule|gold vs. gold|molecule|graphene). It is shown here that whilst amine-contacted junctions show little influence of the electrode material on molecular conductance due to the similar electrode–molecule coupling through this anchor group to both types of electrodes, the weaker coupling between thiomethyl and ethynyl anchors and the graphene substrate electrode results in a relative enhancement of the DQI effect. This work highlights an additional parameter space to explore QI effects and establishes a new working model based on the electrode materials and anchor groups in modulating QI effects beyond the chemical structure of the molecular backbone.
Introduction
Both experimental and theoretical studies of single molecular junctions (SMJs) have greatly contributed to the understanding of charge transport through single molecular wires and given great impetus to the field of molecular electronics.1–5 Over the last decade, these studies have allowed direct elucidation of coherent transport phenomena in charge transport through molecules and the identification of quantum interference (QI) effects.6–9 The various features arising from QI can be broadly classified as constructive quantum interference (CQI) and destructive quantum interference (DQI) effects. CQI is observed in molecular junctions (MJs) with linearly conjugated backbones, such as para-connected phenylene rings,10 including examples where two such systems are connected in parallel.11 In contrast, DQI occurs in molecular systems containing electron transport channels that result in emergent de Broglie waves arriving at the drain electrode with phase differences; prominent examples arise in molecular backbones based on meta-substituted phenylene rings12,13 and cross-conjugated systems.14,15 The experimentally determined conductance of SMJs impacted by DQI can be several orders of magnitude smaller than that of SMJs without DQI.12,13,16,17DQI can often be recognised by a characteristic sharp dip in the plot of the theoretically computed transmission function, T(E), against the electron energy, E.13,18 As the position of this DQI-induced dip in the transmission function relative to the electrode Fermi level, EF, can be tuned through heteroatom substitution in the backbone19,20 or via selectively positioned substituents,21,22 it is possible to use DQI features as a further degree of chemical-design induced control over the electrical properties of a SMJ. In addition, electrochemical gating can be used to control the energetic position of the DQI feature, since the characteristic dip in electronic transmission can be shifted in energy, which facilitates tuning of the molecular junction conductance. This has enabled electrochemically-modulated control of the junction conductance by two orders of magnitude.23–25 It has also been reported that molecular layers showing DQI exhibit significant rectification under electrochemical control.26 Peng et al. have shown that the magnitude of the effect of DQI on single-molecule junction conductance is sensitive to the composition of the (metal) electrodes.27 Similarly, the alignment of the DQI dip with respect to the electrode Fermi level is sensitive to the nature of the anchor groups contacting the molecule within the junction to the electrode; however, these changes in the electrode composition or anchor group do not disturb the fundamental properties of DQI induced by the backbone structure.28
Beyond tuning the electrical conductance, the impact of DQI in SMJs on other material properties has also been demonstrated. For example, the thermopower of a molecular junction is related to the first derivative of the transmission function evaluated at the Fermi level (EF) i.e. S(EF) ≈ −S0(dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T(E)/dE)E=EF, where E is in eV and S0 = αT (α is the Lorentz number, T is temperature in K). Therefore, molecular junctions showing DQI can exhibit significantly enhanced thermopower when compared with molecular junctions without the sharply sloped features in T(E) induced by the DQI feature.29 These combined results show the potential of molecular targets exhibiting DQI to be used in a variety of scenarios to modulate the electrical and material properties of molecular-based molecular devices.30–33
T(E)/dE)E=EF, where E is in eV and S0 = αT (α is the Lorentz number, T is temperature in K). Therefore, molecular junctions showing DQI can exhibit significantly enhanced thermopower when compared with molecular junctions without the sharply sloped features in T(E) induced by the DQI feature.29 These combined results show the potential of molecular targets exhibiting DQI to be used in a variety of scenarios to modulate the electrical and material properties of molecular-based molecular devices.30–33
Although many ‘large area’ molecular junctions are often constructed with different materials comprising the substrate and top electrodes by experimental necessity,34 the majority of studies of the electrical characteristics of SMJs have used “symmetric” anchoring of the molecular target in the junction. In other words, the molecule within the junction has been in contact with the left and right electrodes of the same type, EL and ER, via the same anchoring group, X, at each terminus (e.g. EL|X-backbone-X|ER). By contrast, the electrical properties of “asymmetric” SMJs, where the left and right contacts are differentiated by the nature of the electrode materials or contacting groups, are less commonly examined. However, there is an emerging body of evidence that highlights the opportunities that asymmetric SMJs offer for exploring and optimising electrical effects. For example, indium tin oxide (ITO)|molecule|gold SMJs exhibit an excellent selectivity and control over molecular orientation when forming molecular junctions with “asymmetric” anchoring groups (different groups at either end of the molecule).35 Beyond wire-like conductance, graphite|molecule|Au junctions featuring α,ω-diamino oligo(phenylene)s exhibit rectifying properties due to asymmetric coupling to the two electrodes,36 whilst gold|molecule|graphene heterojunctions induce a reduction of the attenuation factors (β) of symmetrically functionalised alkanes and oligo(phenylene ethynylene)-based SMJs.37,38
In this work, the electrical properties of para- and meta-connected oligo(phenylene ethynylene) (OPE) molecules contacted within symmetric (gold|molecule|gold) SMJs and asymmetric gold|molecule|graphene single molecule heterojunctions by one of three different anchoring groups (amine, methyl sulfide and ethynyl) have been determined. Whilst as noted above, the anchoring group and electrode material have been used to tune the relative energies of the electrode Fermi level and the DQI induced dip in T(E) in symmetric SMJs, here comparison of the respective single molecule conductances from gold|molecule|gold and gold|molecule|graphene SMJs allows exploration of these effects in asymmetric junctions. It has been previously reported that amine and methyl sulfide groups are connected with gold electrodes through dative bonds, while they connect with graphene by van der Waals forces.39–43 The interest in an ethynyl anchoring group lies in the spontaneous formation of a covalent bond with gold and concomitant loss of a hydrogen atom.44,45 The use of ethynyl contacts has resulted in SMJs displaying higher conductance than the equivalent molecules anchored through thiol chemisorption chemistry, and as such this provides additional interest in extending the use of this anchor group here.46 To the best of our knowledge, this is the first report of heterojunctions influenced by destructive quantum interference. The theoretical study shows that the different couplings between electrodes and anchoring groups shift the relative position of the dip in the transmission spectrum, resulting in conductance changes of the molecules studied.
Experimental and computational section
Compounds
The compounds 1,4-bis(4-aminophenylethynyl)benzene (PN), 1,4-bis(4-thiomethylphenylethynyl)benzene (PS), 1,4-bis(4-ethynylphenylethynyl)benzene (PC), 1,3-bis(4-aminophenylethynyl)benzene (MN), 1,3-bis(4-thiomethylphenylethynyl)benzene (MS), and 1,3-bis(4-ethynylphenylethynyl)benzene (MC) (Fig. 1) were prepared by literature methods47–50 or minor variations, and characterised as detailed in the ESI.†Single-molecule conductance
Molecular conductance measurements were made using the STM-I(s) technique.51 The STM tip, which is used as the top contact, was fabricated from a gold wire (Tianjin Lucheng Metal) with a diameter of 0.25 mm and a purity of 99.99% using an electrochemical etching method.52 1 × 1 cm gold on borosilicate glass and graphene on nickel substrates were purchased from Arrandee® (Germany) and the Graphene Supermarket (USA), respectively. All conductance measurements were performed in mesitylene (Sigma Aldrich, 99%) solutions containing 0.1 mM of the target molecule. In the measurement process, the gold tip was held above the substrate at an initial vertical distance (4 nm) and then gradually approached to the substrate until the tunneling current reached the set point current. After that, the tip was retracted to zero tunneling current and further retracted for 4 nm to ensure that the tip was sufficiently retracted from the substrate. During this process, the molecular target could be captured between the electrode pair, thereby forming a single molecule junction (SMJ). The set point current is adjusted to control the distance between the tip and the substrate, ensuring that there is no direct contact between the upper and lower electrodes during the extension and retraction cycles. The tip bias was set to +0.3 V for all the measurements. Over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 current–distance I–(s) curves were collected for each analysis. The I–(s) curves with conductance plateaus were collected through a fully automatic sorting program developed locally and plotted as 1D conductance histograms.53 The most probable single molecule conductance of each molecule was obtained by Gaussian fitting to the prominent feature in these histograms.
000 current–distance I–(s) curves were collected for each analysis. The I–(s) curves with conductance plateaus were collected through a fully automatic sorting program developed locally and plotted as 1D conductance histograms.53 The most probable single molecule conductance of each molecule was obtained by Gaussian fitting to the prominent feature in these histograms.
Computational methods
In order to support the experimental measurements, density functional theory (DFT) calculations have been performed using the Fireball code,54 following the same procedure as detailed elsewhere for oligophenylene ethynylene-based molecular junctions.38 This approach is based on a self-consistent version of the Harris–Foulkes LDA functional,55 instead of the traditional Kohn–Sham functional. The potential is calculated by approximating the total charge by a superposition of spherical charges around each atom. The Fireball simulation package also uses a localized optimized minimal basis set,56 and self-consistency is achieved over the occupation numbers through the Harris functional.57 Besides, the LDA exchange–correlation energy is calculated using the efficient multi-center weighted exchange–correlation density approximation (McWEDA).58,59 The cut-off radii (in atomic units) of the optimised numerical orbitals (sp3d5) used for the present calculations are s = 4.6, p = 5.2, d = 4.2 (gold), s = 4.1, p = 4.5 (C), s = 4.2, p = 4.2 (N), s = 3.1, p = 3.9 (S), and s = 4.1 (H). This basis set has been used to determine the structural and electronic properties of the molecular junctions.20,60 For the molecular junctions, we considered the meta-structured molecules presented in Fig. 1, sandwiched between gold electrodes or gold and graphene electrodes. In these simulations, the gold electrodes are represented by pyramids of 35 atoms and the graphene substrate by a 5 × 5 graphene supercell in the XY plane. The structural properties have been determined by optimising the corresponding geometry until the forces fall below 0.1 eV Å−1. Finally, we determine the electronic transmission and conductance by using a non-equilibrium green function (NEGF) formalism within a fast Fisher-Lee approach.61 As is well-known, the determination of the Fermi level is of crucial importance for electronic transport calculations in molecular junctions. Here, it is even more important in the case of meta junctions, since the position of the DQI dip with respect to the Fermi level changes the value of the calculated conductance dramatically. Here, the Fermi level is determined as the minimum of the density of states (DOS) between the HOMO and LUMO levels.61 This determination is obviously not perfect, but has been found to give results in rather good agreement with the experiment.61Results and discussion
The compounds PN, PC, PS, MN, MC, and MS each feature one of two distinct backbone geometries with linearly conjugated (para-OPE) or non-linear meta-connected (meta-OPE) π-electronic structures and one of three functional groups of varying inductive electron-donating and -withdrawing properties that can serve as electrode contacting groups. The UV-vis spectra of these molecules were measured using a UV-vis spectrophotometer (Agilent, Cary 300 UV-VIS analyser). In dichloromethane solution, the absorption spectra of members of the para- (P) (Fig. 2a) and meta- (M) (Fig. 2b) series are similar to the low energy absorption edge of the para series, exhibiting greater sensitivity to the electronic character of the substituents. However, to eliminate solvation effects and thus to better estimate the HOMO–LUMO gap, the spectra were also recorded in the solid state using an integrating sphere (Agilent, DRA-CA-301) and data analysed through the Tauc method, commonly used to determine the optical band gap in organic semiconductors.62 The relationship between the optical band gap and absorption coefficient (α) follows the equation: (αhv)2 = B(hv − Eg), where h is Planck's constant, ν is the frequency of the incident photons, B is a constant and Eg is the band gap;63 for organic semiconductors, Eg can be approximated as a HOMO–LUMO gap.64–66 | ||
| Fig. 2 (a) and (b) Normalised absorption spectra of target molecules; (c) and (e) solid UV-vis spectra and (d) and (f) Tauc plots of target molecules. | ||
As shown in Fig. 2d and f, the band gaps of the target molecules are determined as the intersection of the respective tangents derived for each peak with the horizontal coordinate. The resulting estimates gave similar HOMO–LUMO gaps for molecules within each family (PN (2.7 eV), PS (2.8 eV), and PC (2.8 eV); MN (3.1 eV), MS (3.2 eV), and MC (3.2 eV)), with the meta-connected OPEs giving larger HOMO–LUMO gaps than the linearly para-connected compounds as might be reasonably expected.67,68 These data further demonstrate that the electronic structures of each member of a series are similar and little perturbed by the anchor groups. Consequently, any differences in the electronic behaviour of members of a series within a molecular junction likely arise from the nature of the molecule–electrode contact and the associated molecule–electrode coupling.
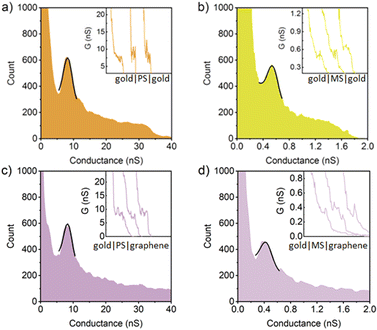
To explore the various individual and combined effects of electrode materials and anchor groups on the electrical characteristics of these molecules, the single-molecule conductance of each member of both series was determined within single-molecule gold|molecule|gold homo-junctions and gold|molecule|graphene heterojunctions using the I(s) technique.69 The resulting 1D conductance histograms together with representative G–s traces are given in Fig. 3–5 and summarised in Table 1. In each case, the most probable molecular conductance was determined by fitting the Gaussian distribution (black lines) to the peak in the conductance histogram. The error bar of each most probable molecular conductance was calculated from the half-peak width of the conductance peak. The most probable molecular conductance value of PN in a gold–gold junction was measured as 13 ± 1.8 nS, in good agreement with the values reported by Ferradás et al.70 and Lu et al.71 An essentially identical value (13 ± 2.8 nS) was also determined for the molecular conductance of PN in a gold|molecule|graphene junction (Fig. 3 and Table 1). The molecular conductance of the analogous meta-OPE MN is approximately an order of magnitude lower in both gold|molecule|gold (1.1 ± 0.21 nS) and gold|molecule|graphene (1.1 ± 0.23 nS) junctions due to the pronounced DQI dip near the electrode Fermi level in the transmission functions of meta-phenylene structures.72 It is apparent that the changes in the electrode material have little to no measurable effects on the most probable molecular conductance of these amine contacted compounds.
| Molecule | Conductance (nS) | Conductance ratio | ||
|---|---|---|---|---|
| Gold–gold | Gold–graphene | Gold–gold | Gold–graphene | |
| a A value at the noise floor is assumed here as no current histogram peak was observed. The junction may not form or the single-molecule conductance was below the current sensitivity limit of the equipment. | ||||
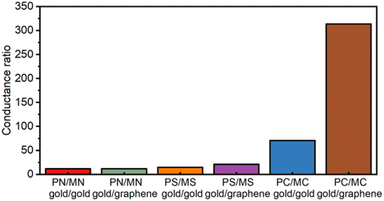
| PN | 13 ± 1.8 | 13 ± 2.8 | 12 | 12 |
| MN | 1.1 ± 0.21 | 1.1 ± 0.23 | ||
| PS | 8.2 ± 1.6 | 8.2 ± 1.5 | 15 | 21 |
| MS | 0.56 ± 0.09 | 0.39 ± 0.10 | ||
| PC | 19 ± 3.7 | 9.4 ± 1.3 | 70 | 400a |
| MC | 0.27 ± 0.11 | 0.03a | ||
In a similar manner, the 1D conductance histograms of thioether anchored para-OPE contain conductance peaks corresponding to an essentially identical most probable conductance in gold–gold (8.2 ± 1.6 nS) and gold–graphene (8.2 ± 1.5 nS) single-molecule junctions. As expected, the molecular conductance of the meta-connected analogue, MS, in gold|molecule|gold and gold|molecule|graphene junctions are substantially lower, being 0.56 ± 0.09 nS and 0.39 ± 0.10 nS, respectively (Fig. 4 and Table 1).
In single-molecule gold|molecule|gold junctions, the conductance of the ethynyl-contacted PC is found to be around 19 ± 3.7 nS, which is higher than those of both the amine (PN) and thiomethyl (PS) contacted analogues, but comparable to those of other ethynyl-contacted three-ring OPEs,73 reflecting the stronger molecule–electrode electronic coupling (Fig. 5 and Table 1). This difference in coupling arises from the fact that, in contrast to the amine and thioether anchors which bind to both gold and graphene through a combination of dative and electrostatic interactions and van der Waals forces, the terminal alkyne undergoes a dehydrogenation reaction at gold surfaces to create a strong covalent gold|–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C interaction.45,74–76 Compared to the interactions of the studied molecules with gold electrodes, the stronger interaction between gold and the ethynyl anchor leads the gold|PC|gold junction to exhibit higher conductance values than the gold|PN|gold junction and the gold|PS|gold junction. In the gold|PC|graphene heterojunctions, whilst the ethynyl anchor contacts through gold|–C
C interaction.45,74–76 Compared to the interactions of the studied molecules with gold electrodes, the stronger interaction between gold and the ethynyl anchor leads the gold|PC|gold junction to exhibit higher conductance values than the gold|PN|gold junction and the gold|PS|gold junction. In the gold|PC|graphene heterojunctions, whilst the ethynyl anchor contacts through gold|–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C with a direct Au–C bond from the deprotonated acetylene44,45 the molecule contacts to the graphene electrode through a C
C with a direct Au–C bond from the deprotonated acetylene44,45 the molecule contacts to the graphene electrode through a C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H|graphene like structure, with a much weaker van der Waals interaction. This weaker contact between the ethyne anchor and graphene is associated with a decrease in electrode|molecule coupling. The resulting shift in the alignment of the position of electrode Fermi levels decreases the most probable molecular conductance of PC by a factor of approximately two (9.4 ± 1.3 nS, Fig. 5 and Table 1).
C–H|graphene like structure, with a much weaker van der Waals interaction. This weaker contact between the ethyne anchor and graphene is associated with a decrease in electrode|molecule coupling. The resulting shift in the alignment of the position of electrode Fermi levels decreases the most probable molecular conductance of PC by a factor of approximately two (9.4 ± 1.3 nS, Fig. 5 and Table 1).
Rather strikingly, despite the strong coupling induced by the ethynyl gold|–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C contacts, the most probable single-molecule conductance of MC in the gold|molecule|gold junction was found to be 0.27 ± 0.11 nS, which is the lowest of all the meta-connected compounds in these homo-junctions (Fig. 5 and Table 1). In the gold–graphene heterojunction, the single-molecule conductance of MC lies below the limits of detection of the instrument used in this study (ca. 10 pA per sample bias, or 0.03 nS). To facilitate the discussion that follows, an upper estimate of the single-molecule conductance value is taken as 0.03 nS; true values may be far lower.
C contacts, the most probable single-molecule conductance of MC in the gold|molecule|gold junction was found to be 0.27 ± 0.11 nS, which is the lowest of all the meta-connected compounds in these homo-junctions (Fig. 5 and Table 1). In the gold–graphene heterojunction, the single-molecule conductance of MC lies below the limits of detection of the instrument used in this study (ca. 10 pA per sample bias, or 0.03 nS). To facilitate the discussion that follows, an upper estimate of the single-molecule conductance value is taken as 0.03 nS; true values may be far lower.
The anticipated effects of the chemical structure of the molecular backbones on molecular conductance regardless of the electrode materials used in the construction of the junction are clear (Table 1). Thus, whilst the linearly conjugated para-series (PN,38,70,71 PS,38 PC73) display CQI and relatively high single-molecule conductance, the emergence of DQI features in the transmission functions at the Fermi levels results in a 1–2 order of magnitude decrease in the single-molecule conductance of the meta-structured analogues (MN, MS, MC).13,20,77 For any given pair of electrodes, changes in the anchor group result in a small variation in the most probable conductance. This observation demonstrates both the robustness of the QI features imposed by the chemical structure of the molecular backbone28 and the influence of small changes in the electrode–molecule coupling on the molecular conductance. The relative effects of electrode–molecule coupling, quantum interference and Fermi energy alignment with the (anti) resonance features of the transmission functions that describe charge transport through the junction are collectively expressed within the conductance ratios summarised numerically in Table 1 and graphically in Fig. 6. The increasing single-molecule conductance PS < PN < PC observed in the gold|molecule|gold homo-junctions illustrates the role played by electrode–molecule coupling in tuning molecular conductance.78 A different trend in the magnitude of single-molecule conductance values is found for the meta-series in gold|molecule|gold single-molecule junctions (MC < MS < MN), clearly indicating the dominant effect of the position of the DQI induced dip in the transmission function relative to the electrode Fermi levels on the electronic characteristics of the junction.79
In the gold|molecule|graphene heterojunctions, the variation in conductance is somewhat less distinct with the anchor group due to the common electrostatic interaction of the anchor groups to the graphene electrode. The data indicate that it is only the carbon contacted compounds PC and MC that show any significant decrease in conductance in the heterojunctions. The single-molecule conductance values of the meta series are low and more sensitive to the anchor group, spanning some two orders of magnitude (1.1–0.03 ns). As with the para-structure compounds, variations in the electrode–molecule coupling must undoubtedly play some role in this observation, but the greater magnitude of variation points to a key role in the position of the DQI feature relative to the electrode Fermi levels.
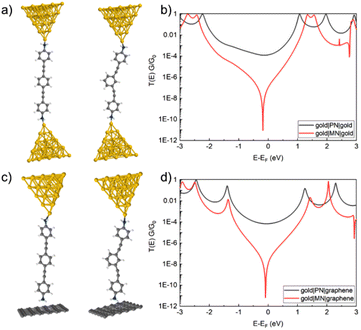
To gain further insight into these various factors on the electrical conductance of the SMJs investigated here, model junctions were constructed and explored using DFT-based calculations (Fig. 7–9 and Table 2). Taking the amine-contacted compounds PN and MN within the gold–gold homo-junctions as a point of reference, the calculated transmission curves demonstrate the expected features. The transmission functions for PN feature well-separated HOMO and LUMO resonances, which are further separated in the comparable plot for MN, consistent with the greater HOMO–LUMO gap obtained from the optical measurements. As a result of CQI, between the HOMO and LUMO resonances of PN, the transmission function describes a broad, relatively flat and rather high conductance region. In contrast, the transmission function for MC features a strong, sharp dip near the calculated Fermi energy. As is now well-appreciated in the literature,13,18 this dip explains the strong difference in magnitude between the conductance values in the PN and MN configurations.
| Molecule | Conductance (nS) | Conductance ratio | ||
|---|---|---|---|---|
| Gold–gold | Gold–graphene | Gold–gold | Gold–graphene | |
| PN | 10.46 | 7.53 | 1162 | 7530 |
| MN | 0.009 | 0.001 | ||
| PS | 16.03 | 3.9 | 133 | 260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| MS | 0.12 | 0.000015 | ||
| PC | 5.57 | 1.27 | 51 | 8466 |
| MC | 0.11 | 0.00015 | ||
Moving to the gold|molecule|graphene heterojunctions formed from PN and MN, remarkably similar transmission curves are obtained, a consequence of the similar mechanism of electrode–molecule coupling through the amine group to both gold and graphene.38 These results are therefore consistent with the experimentally observed single-molecule conductances (Table 1).
For the thioether contacted compounds PS and MS, we observe a greater shift of the molecular levels between gold|molecule|gold and gold|molecule|graphene junctions, which can be attributed to a difference in electrostatic dipoles as observed in an earlier work (Fig. 8).80 Consequently, the DQI dip lies below the Fermi level for the gold|molecule|gold configuration, whereas it is centred at the Fermi level for gold|molecule|graphene configuration, leading to a very small conductance value for MC in the heterojunction. However, as in the calculations, the dip corresponds to a mathematical singularity; the value obtained is not well suited for comparison with the experimental results.
To the best of our knowledge, no theoretical study of alkyne adsorption on graphene has been performed. The adsorption energy of the molecules PC and MC on graphene as a function of the molecule–graphene distance was first explored to estimate the stability of the resulting junctions (Fig. S5†). The adsorption energy varies as a function of the position of the terminal hydrogen, but the equilibrium position lies around 2–2.5 Å, with an energy of 0.12–0.17 eV per molecule. Consequently, we can assume that this configuration, which has some analogy to the T-shape configuration of a benzene dimer,81 is stable and allows the formation of a molecular junction.
The results from electronic transmission calculations with PC and MC in gold|molecule|gold and gold|molecule|graphene junctions are shown in Fig. 9. For PC, there is a small shift of the electronic transmission function in response to the change in the electrode material, which is consistent with the experimental observation. However, for MC, there is a far more significant shift of the position of the DQI dip, leading to the substantial difference in the single-molecule conductance values of MC in the homo- and heterojunctions.
From these calculations, several general trends can be illustrated. At the minimised energy configurations, the molecule is somewhat “stretched” in the junction. One can observe a correlation between how stretched the molecule is in the meta configuration and the position of the DQI dip. Indeed, when considering the gold–graphene junction, due to the weaker van der Waals interaction at the molecule–graphene interface, the molecule is less stretched and the DQI dip is located very close to the Fermi level. Oppositely, for the gold–gold junction, the molecular junction is more stretched which increases the angle between the two halves of the molecule, resulting in a DQI dip located further away from the Fermi level. Obviously, this stretched configuration is related to the intrinsic potentials used in the DFT calculations, which might induce some differences between the computed and measured conductance values. In addition, this specific property might also be exploited for electro-mechanical devices, as the degree of stretching of the molecule in the junction has a strong influence on the electronic conductance.
Conclusions
In this work, the conductance of para- and meta-OPE molecular wires tethered between gold–gold and gold–graphene electrodes has been measured using the STM-I(s) method. For all the molecular junctions, the meta-connection leads to a low conductance value, which is associated with the DQI induced dip in the transmission function which falls near the electrode Fermi level. To study the effects of electrode type on the relative position of the Fermi level and the DQI dip, amine, methyl sulfide and ethynyl anchoring groups were used to link para- and meta-structured OPEs into gold|molecule|gold and gold|molecule|graphene single molecular junctions. The electrode material has little effect on the electrical properties of the amine anchored OPEs, due to the similar electrode–molecule contacting chemistry in each case. However, for methyl sulfide and ethynyl anchored OPEs, gold–graphene electrode contacting shows a clear impact on DQI. In particular, for ethynyl-ethynye anchored OPE molecules with gold–graphene electrodes, the conductance ratio of PC/MC is greater than 400. Our study indicates that the conductance change resulting from DQI can be tuned through the connection between electrodes and anchoring groups as well as through the mechanical stress applied to the junction. The influence of electrode materials and anchoring groups on the DQI effect is clearly complex and further study is required.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC Grants 21503169), the Suzhou Industrial Park Initiative Platform Development for Suzhou Municipal Key Lab for New Energy Technology (RR0140), the Key Program Special Fund in XJTLU (KSF-E-38) and the XJTLU Research Development Fund (RDF-16-01-33 and REF-19-01-05). P.J.L. gratefully acknowledges support from the Australian Research Council (DP220100790).References
- X. Li, W. Ge, S. Guo, J. Bai and W. Hong, Angew. Chem., Int. Ed., 2023, 62, e202216819 CrossRef CAS PubMed.
- L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 10668–10711 RSC.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002 CrossRef CAS.
- H. Song, M. A. Reed and T. Lee, Adv. Mater., 2011, 23, 1583–1608 CrossRef CAS PubMed.
- L. Sun, Y. A. Diaz-Fernandez, T. A. Gschneidtner, F. Westerlund, S. Lara-Avila and K. Moth-Poulsen, Chem. Soc. Rev., 2014, 43, 7378–7411 RSC.
- D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur, T. Wandlowski, M. R. Bryce and C. J. Lambert, Nat. Commun., 2015, 6, 6389 CrossRef CAS PubMed.
- C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- T. Markussen, R. Stadler and K. S. Thygesen, Nano Lett., 2010, 10, 4260–4265 CrossRef CAS PubMed.
- C. M. Guedon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 305–309 CrossRef CAS PubMed.
- A. Borges, J. Xia, S. H. Liu, L. Venkataraman and G. C. Solomon, Nano Lett., 2017, 17, 4436–4442 CrossRef CAS.
- H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. S. Hybertsen, Nat. Nanotechnol., 2012, 7, 663–667 CrossRef CAS PubMed.
- G. Yang, H. Wu, J. Wei, J. Zheng, Z. Chen, J. Liu, J. Shi, Y. Yang and W. Hong, Chin. Chem. Lett., 2018, 29, 147–150 CrossRef CAS.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. Woerde, R. Eelkema, F. C. Grozema and H. S. van der Zant, Angew. Chem., Int. Ed., 2013, 52, 3152–3155 CrossRef CAS.
- G. C. Solomon, D. Q. Andrews, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17301–17308 CrossRef CAS.
- G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Nat. Chem., 2010, 2, 223–228 CrossRef CAS PubMed.
- S. V. Aradhya, J. S. Meisner, M. Krikorian, S. Ahn, R. Parameswaran, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2012, 12, 1643–1647 CrossRef CAS.
- M. Kiguchi, H. Nakamura, Y. Takahashi, T. Takahashi and T. Ohto, J. Phys. Chem. C, 2010, 114, 22254–22261 CrossRef CAS.
- C. J. Lambert, Quantum Transport in Nanostructures and Molecules, IOP Publishing, 2021 Search PubMed.
- W. Chen, H. Li, J. R. Widawsky, C. Appayee, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2014, 136, 918–920 CrossRef CAS.
- X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z. Y. Xiao, W. Hong, C. J. Lambert and S. X. Liu, Angew. Chem., Int. Ed., 2016, 56, 173–176 CrossRef.
- F. Jiang, D. I. Trupp, N. Algethami, H. Zheng, W. He, A. Alqorashi, C. Zhu, C. Tang, R. Li, J. Liu, H. Sadeghi, J. Shi, R. Davidson, M. Korb, A. N. Sobolev, M. Naher, S. Sangtarash, P. J. Low, W. Hong and C. J. Lambert, Angew. Chem., Int. Ed., 2019, 58, 18987–18993 CrossRef CAS.
- M. H. Garner, M. Koerstz, J. H. Jensen and G. C. Solomon, ACS Phys. Chem. Au, 2022, 2, 282–288 CrossRef CAS.
- J. Bai, A. Daaoub, S. Sangtarash, X. Li, Y. Tang, Q. Zou, H. Sadeghi, S. Liu, X. Huang, Z. Tan, J. Liu, Y. Yang, J. Shi, G. Meszaros, W. Chen, C. Lambert and W. Hong, Nat. Mater., 2019, 18, 364–369 CrossRef CAS PubMed.
- Y. Li, M. Buerkle, G. Li, A. Rostamian, H. Wang, Z. Wang, D. R. Bowler, T. Miyazaki, L. Xiang, Y. Asai, G. Zhou and N. Tao, Nat. Mater., 2019, 18, 357–363 CrossRef CAS PubMed.
- B. Huang, X. Liu, Y. Yuan, Z. W. Hong, J. F. Zheng, L. Q. Pei, Y. Shao, J. F. Li, X. S. Zhou, J. Z. Chen, S. Jin and B. W. Mao, J. Am. Chem. Soc., 2018, 140, 17685–17690 CrossRef CAS.
- M. Famili, C. Jia, X. Liu, P. Wang, I. M. Grace, J. Guo, Y. Liu, Z. Feng, Y. Wang, Z. Zhao, S. Decurtins, R. Häner, Y. Huang, S.-X. Liu, C. J. Lambert and X. Duan, Chem, 2019, 5, 474–484 CAS.
- L. L. Peng, J. R. Huang, J. F. Zheng, Y. Shao, Z. J. Niu, J. F. Li, S. M. Xu and X. S. Zhou, J. Nanosci. Nanotechnol., 2019, 19, 2794–2798 CrossRef CAS.
- Y. Tsuji, T. Stuyver, S. Gunasekaran and L. Venkataraman, J. Phys. Chem. C, 2017, 121, 14451–14462 CrossRef CAS.
- H. Chen, Y. Chen, H. Zhang, W. Cao, C. Fang, Y. Zhou, Z. Xiao, J. Shi, W. Chen, J. Liu and W. Hong, Chin. Chem. Lett., 2022, 33, 523–526 CrossRef CAS.
- Z.-C. Pan, J. Li, L. Chen, Y. Tang, J. Shi, J. Liu, J.-L. Liao and W. Hong, Sci. China: Chem., 2019, 62, 1245–1256 CrossRef CAS.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- A. Bellec, J. Lagoute and V. Repain, C. R. Chim., 2018, 21, 1287–1299 CrossRef CAS.
- M. Kiguchi, Proc. Jpn. Acad., Ser. B, 2018, 94, 350–359 CrossRef CAS PubMed.
- E. Gorenskaia, K. L. Turner, S. Martín, P. Cea and P. J. Low, Nanoscale, 2021, 13, 9055–9074 RSC.
- I. J. Planje, R. J. Davidson, A. Vezzoli, A. Daaoub, S. Sangtarash, H. Sadeghi, S. Martin, P. Cea, C. J. Lambert, A. Beeby, S. J. Higgins and R. J. Nichols, ACS Sens., 2021, 6, 530–537 CrossRef CAS PubMed.
- T. Kim, Z.-F. Liu, C. Lee, J. B. Neaton and L. Venkataraman, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10928–10932 CrossRef CAS PubMed.
- Q. Zhang, S. Tao, R. Yi, C. He, C. Zhao, W. Su, A. Smogunov, Y. J. Dappe, R. J. Nichols and L. Yang, J. Phys. Chem. Lett., 2017, 8, 5987–5992 CrossRef CAS.
- Y. Fan, S. Pitie, C. Liu, C. Zhao, C. Zhao, M. Seydou, Y. J. Dappe, R. J. Nichols and L. Yang, J. Phys. Chem. C, 2022, 126, 3635–3645 CrossRef CAS.
- W. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304 CrossRef CAS PubMed.
- K. Yoshida, I. V. Pobelov, D. Z. Manrique, T. Pope, G. Mészáros, M. Gulcur, M. R. Bryce, C. J. Lambert and T. Wandlowski, Sci. Rep., 2015, 5, 9002 CrossRef CAS PubMed.
- R. Frisenda, S. Tarkuç, E. Galán, M. L. Perrin, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Beilstein J. Nanotechnol., 2015, 6, 1558–1567 CrossRef CAS.
- Y. S. Park, J. R. Widawsky, M. Kamenetska, M. L. Steigerwald, M. S. Hybertsen, C. Nuckolls and L. Venkataraman, J. Am. Chem. Soc., 2009, 131, 10820–10821 CrossRef CAS.
- S. Tao, Q. Zhang, C. He, X. Lin, R. Xie, C. Zhao, C. Zhao, A. Smogunov, Y. J. Dappe, R. J. Nichols and L. Yang, ACS Appl. Nano Mater., 2018, 2, 12–18 CrossRef.
- P. Pla-Vilanova, A. C. Aragonès, S. Ciampi, F. Sanz, N. Darwish and I. Diez-Perez, Nanotechnology, 2015, 26, 381001 CrossRef.
- L. Herrer, A. González-Orive, S. Marqués-González, S. Martín, R. J. Nichols, J. L. Serrano, P. J. Low and P. Cea, Nanoscale, 2019, 11, 7976–7985 RSC.
- W. Hong, H. Li, S.-X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431 CrossRef CAS.
- K. Sonogashira, Y. Tohda and N. Hagihara, Tetrahedron Lett., 1975, 16, 4467–4470 CrossRef.
- G. Casotti, G. Fusini, M. Ferreri, L. F. Pardini, C. Evangelisti, G. Angelici and A. Carpita, Synthesis, 2020, 52, 1795–1803 CrossRef CAS.
- M. Guo, Z. Wei, J. Yang, Z. Xie and W. Zhang, Catalysts, 2020, 10, 302 CrossRef CAS.
- F. Luo, C. Pan, L. Li, F. Chen and J. Cheng, Chem. Commun., 2011, 47, 5304–5306 RSC.
- W. Haiss, H. van Zalinge, S. J. Higgins, D. Bethell, H. Höbenreich, D. J. Schiffrin and R. J. Nichols, J. Am. Chem. Soc., 2003, 125, 15294–15295 CrossRef CAS PubMed.
- B. Ren, G. Picardi and B. Pettinger, Rev. Sci. Instrum., 2004, 75, 837 CrossRef CAS.
- Q. Zhang, C. Liu, S. Tao, R. Yi, W. Su, C. Zhao, C. Zhao, Y. J. Dappe, R. J. Nichols and L. Yang, Nanotechnology, 2018, 29, 325701 CrossRef.
- J. P. Lewis, P. Jelínek, J. Ortega, A. A. Demkov, D. G. Trabada, B. Haycock, H. Wang, G. Adams, J. K. Tomfohr, E. Abad, H. Wang and D. A. Drabold, Phys. Status Solidi B, 2011, 248, 1989–2007 CrossRef CAS.
- J. Harris, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 1770–1779 CrossRef CAS PubMed.
- M. A. Basanta, Y. J. Dappe, P. Jelínek and J. Ortega, Comput. Mater. Sci., 2007, 39, 759–766 CrossRef CAS.
- A. A. Demkov, J. Ortega, O. F. Sankey and M. P. Grumbach, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1618–1630 CrossRef CAS.
- P. Jelínek, H. Wang, J. P. Lewis, O. F. Sankey and J. Ortega, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 235101 CrossRef.
- O. F. Sankey and D. J. Niklewski, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3979–3995 CrossRef PubMed.
- S. Tao, Q. Zhang, C. He, X. Lin, R. Xie, C. Zhao, C. Zhao, A. Smogunov, Y. J. Dappe, R. J. Nichols and L. Yang, ACS Appl. Nano Mater., 2018, 2, 12–18 CrossRef.
- S. Pitié, M. Seydou, Y. J. Dappe, P. Martin, F. Maurel and J. C. Lacroix, Chem. Phys. Lett., 2022, 787, 139273 CrossRef.
- J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637 CrossRef CAS.
- R. H. Ramprasath, M. S. Kajamuhideen, B. Tiwari and K. Sethuraman, J. Mater. Sci.: Mater. Electron., 2023, 34, 620 CrossRef CAS.
- M. C. Scharber and N. S. Sariciftci, Adv. Mater. Technol., 2021, 6, 2000857 CrossRef CAS.
- J. C. S. Costa, R. J. S. Taveira, C. F. R. A. C. Lima, A. Mendes and L. M. N. B. F. Santos, Opt. Mater., 2016, 58, 51–60 CrossRef CAS.
- B.-G. Kim, X. Ma, C. Chen, Y. Ie, E. W. Coir, H. Hashemi, Y. Aso, P. F. Green, J. Kieffer and J. Kim, Adv. Funct. Mater., 2013, 23, 439–445 CrossRef CAS.
- F. Barrière, B. Fabre, E. Hao, Z. M. LeJeune, E. Hwang, J. C. Garno, E. E. Nesterov and M. G. H. Vicente, Macromolecules, 2009, 42, 2981–2987 CrossRef.
- N. El Guesmi, ChemistrySelect, 2023, 8, e202203963 CrossRef CAS.
- W. Haiss, H. van Zalinge, S. J. Higgins, D. Bethell, H. Höbenreich, D. J. Schiffrin and R. J. Nichols, J. Am. Chem. Soc., 2003, 125, 15294–15295 CrossRef CAS.
- R. R. Ferradás, S. Marqués-González, H. M. Osorio, J. Ferrer, P. Cea, D. C. Milan, A. Vezzoli, S. J. Higgins, R. J. Nichols, P. J. Low, V. M. García-Suárez and S. Martín, RSC Adv., 2016, 6, 75111–75121 RSC.
- Q. Lu, K. Liu, H. Zhang, Z. Du, X. Wang and F. Wang, ACS Nano, 2009, 3, 3861–3868 CrossRef CAS PubMed.
- C. Huang, M. Jevric, A. Borges, S. T. Olsen, J. M. Hamill, J. T. Zheng, Y. Yang, A. Rudnev, M. Baghernejad and P. Broekmann, Nat. Commun., 2017, 8, 15436 CrossRef CAS.
- W. Hong, H. Li, S. X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431 CrossRef CAS.
- I. J. Olavarria-Contreras, M. L. Perrin, Z. Chen, S. Klyatskaya, M. Ruben and H. S. J. van der Zant, J. Am. Chem. Soc., 2016, 138, 8465–8469 CrossRef CAS.
- H. M. Osorio, P. Cea, L. M. Ballesteros, I. Gascón, S. Marqués-González, R. J. Nichols, F. Pérez-Murano, P. J. Low and S. Martín, J. Mater. Chem. C, 2014, 2, 7348–7355 RSC.
- L. M. Ballesteros, S. Martín, C. Momblona, S. Marqués-González, M. C. López, R. J. Nichols, P. J. Low and P. Cea, J. Phys. Chem. C, 2012, 116, 9142–9150 CrossRef CAS.
- R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. L. Pedersen, M. Leijnse, F. Pauly, K. Warnmark, E. Meyhofer, P. Reddy and H. Linke, Nano Lett., 2018, 18, 5666–5672 CrossRef CAS.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002 CrossRef CAS.
- M. H. Garner, G. C. Solomon and M. Strange, J. Phys. Chem. C, 2016, 120, 9097–9103 CrossRef CAS.
- Q. Zhang, L. Liu, S. Tao, C. Wang, C. Zhao, C. Gonzalez, Y. J. Dappe, R. J. Nichols and L. Yang, Nano Lett., 2016, 16, 6534–6540 CrossRef CAS PubMed.
- R. A. DiStasio, G. von Helden, R. P. Steele and M. Head-Gordon, Chem. Phys. Lett., 2007, 437, 277–283 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04012g |
| This journal is © The Royal Society of Chemistry 2024 |