A physics rule to design aperiodic width-modulated waveguides for minimum phonon transmission with Bayesian optimization

Abstract

Aperiodic nano-waveguides (nWVGs) and superlattices (SLs) limit phonon transmission and heat conduction much more efficiently than periodic ones. They could block parasitic heat conduction that restricts heat management and energy conversion at the nanoscale. Aperiodicity can be realized in multiple ways and with variable degrees of complexity. Machine learning optimization of hetero-SLs for minimum coherent phonon conduction showed optimal aperiodicity for moderate disorder against physics intuition. Here, we report on optimal aperiodicity in width-modulated nWVGS for maximum disorder as expected by physics. Optimizing aperiodic geometry modulation is particularly challenging due to the enormous possible configurations. We set up a feasible optimization problem removing unnecessary complexity and we demonstrate efficient Bayesian optimization. Our results confirm the predicted physics rule that minimum thermal conductance occurs for the most disordered arrays of modulation units; the degree of disorder being quantified by the number of non-identical modulation units. Our work opens a route to design geometrical aperiodicity and control transmission across metamaterials.

---

1 Introduction

Heat transfer plays a critical role in the efficiency of many applications such as high-power electronics, thermal insulation, thermoelectric, and photovoltaic energy conversion. To manipulate it requires controlling phonons and their transport. The possibility of engineering phonons in low-dimensional structures and superlattices of semiconductors stimulated extensive research activity.^1–5 Quantum confinement and periodicity modify bulk phonons and affect the thermal transport properties of the material. The physics principle lies in the wave nature of phonons. Phonon waves scattered at boundaries and interfaces interfere and their energy spectrum is modified. Low-dimensional structures and periodic superlattices (SLs) have been proposed to limit parasitic heat conduction and enhance thermoelectric energy conversion efficiency.^6–9 The progress of fabrication technology and characterization techniques oriented the research interest to more advanced metamaterials such as artificial periodic nanostructures, the so-called ‘phononic crystals’,^10–12 and geometry-modulated nano-waveguides (nWVGs).¹³ For the past two decades, research outcomes support that these classes of metamaterials are promising for breakthroughs in nanoscale thermal management, insulation, waveguiding, and energy conversion.^13–22 Their good properties are attributed to coherent phonon effects. Such effects are expected in nanostructures with high-quality interfaces, boundaries, and characteristic dimensions shorter than the dominant phonon wavelength.^23–25 Coherent phonon transport has been confirmed in SLs, nanomeshes, holey nanobeams, and width-modulated nWVGs at low temperatures.^26–29 The signature of coherent phonon transport up to room temperature has been also supported by recent experiments.^30–32 These findings call for further investigation and make research on phonon transmission across metamaterials timely.

Theoretical and experimental studies typically aimed to decrease thermal conduction in periodic SLs.^33–35 Effects of deviation from periodicity on electron and phonon transport were first addressed in Fibonacci and Thue–Morse SLs in the eighties.^36–39 The impact of aperiodicity on coherent heat conduction was addressed more recently in width-modulated nWVGs.^40,41 It was shown that coherent thermal transport was greatly reduced in aperiodic arrays compared to the corresponding periodic ones. The same behavior was found in aperiodic hetero-SLs.⁴² In both types of structures, aperiodicity (also referred to as disorder or randomness) in the modulation profile enhances destructive interference and decreases phonon transmission. Aperiodicity could thus play an important role in heat management and energy conversion at the nanoscale. It would be important to identify optimization rules for minimum heat conduction. Evidence shows that this is not trivial. Optimization of aperiodic hetero-SLs showed that coherent phonon conduction is minimized for moderate rather than maximum disorder against physics intuition.^43–49 Systematic investigation concluded that optimization could not reveal the underlying physics rule in hetero-SLs.⁴⁷ Notably, a physics rule was indicated in width-modulated nWVGs by the monotonic decrease of thermal conductance with increasing disorder in aperiodic modulation profiles.^40,41 Optimal aperiodicity was predicted to occur for maximum disorder in width-modulated nWVGs as expected by physics. This physics rule was concluded based on selected calculations and intuitive analysis. Here, we validate it with calculations on full populations of nWVGs and apply it to design aperiodic width-modulated nWVGs with Bayesian optimization.

Optimization of aperiodicity could be addressed with the aid of machine learning (ML) which has been successfully used to design materials and nanostructures with optimal properties.⁵⁰ In the last years, ML has been intensively used in the design of thermal properties.^51–54 It has been applied to optimize coherent phonon transport in aperiodic hetero-SLs of two constituent materials.^43–49 ML has not been so far applied to optimize aperiodic width-modulated nWVGs, although they have been adequately investigated with the same computational physics techniques as hetero-SLs in the last decade.¹³ Such optimization is very challenging because of the enormous number of possible configurations.

Aperiodicity in the width modulation can be realized in multiple ways and with variable complexity. This makes the number of configurations so big that the optimization problem seems impossible to tackle. We addressed this challenge by developing a methodology guided by physics experience from previous findings. We managed to set up a feasible optimization problem using physics insight to reduce complexity to the level required to address the physics problem. We selected the simplest yet representative sets of nWVGs to optimize and defined suitable descriptors for them. We demonstrate efficient optimization which we validate by calculations on the full sets of candidates. Phonon transmission and thermal conductance are interpreted in terms of the underlying physics, phonon wave interference at width discontinuities. The identified optimal aperiodic configurations are the most extended arrays of non-identical modulation units in agreement with the predicted physics rule. We confirm that phonon transmission and thermal conductance are minimized for maximum disorder in the aperiodic width-modulation profile. The degree of disorder is quantified by the number of non-identical modulation units. Comparison with optimized aperiodic hetero-SLs shows that our findings although intuitive are not trivial. We support that geometric aperiodicity can be unambiguously optimized according to a physics rule and with a quantitative tool to design disorder.

2 System and methodology

We consider three-dimensional (3D) nWVGs (1D propagation and 2D quantum confinement) with modulated width along the direction of propagation (Fig. 1a). We adopt the simplest representative geometry of the class of width-modulated nWVGs.¹³ The nWVGs consist of arrays of N layers of the same material with variable widths. Each layer has a fixed length. Layers are either wide (‘openings’) or thin (‘constrictions’). Openings separated by constrictions form modulation units referred to as quantum dots (QDs) (Fig. 1c). Wide leads are assumed at the two endings of the width-modulated nWVGs. As highlighted in Fig. 1c, QDs of variable size are formed in the array of N layers with different widths. It is straightforward to determine the number of non-identical modulation units in a configuration. This number provides a well-defined measure of the degree of disorder of the configuration.

Fig. 1 Width-modulated nWVGs and thermal conductance (a) schematics of width-modulated nWVGs of interest, (b) calculated thermal conductance of periodic and aperiodic nWVGs (adapted from ref. 40), and (c) reference aperiodic nWVGs modulated by non-identical modulation units (QDs). Examples of three QD sizes highlighted with dashed-line frames of different colors (grey, red, and blue).

We know⁴⁰ that the decrease of the thermal conductance of a modulated nWVG depends on the number and the sizes of the QDs in the modulation profile and that thermal conductance is smaller for aperiodic modulation profiles (Fig. 1b). The number of QDs in the modulation profile varies depending on the number N of layers and the array configuration. The number N of layers needs to be fixed to set up the optimization problem. We selected to optimize sets of nWVGs with different values of N in the range from 8 to 14, considering physics and computational requirements as detailed below. The size of a QD can vary by changing its width to one, two, or three dimensions. Arbitrarily changing these widths would add enormous though unnecessary complication (Fig. 1a). We avoided that by varying the size of QDs changing only their length along the nWVG axis and fixing their widths in the two lateral dimensions (Fig. 1c). QDs of different sizes were formed for different numbers of subsequent wide layers separated by subsequent layers of constrictions. This enabled us to define binary descriptors to represent the modulated nWVGs and efficiently perform the optimization. Thermal conductance was calculated within elastic wave transmission theory^55,56 as detailed in ref. 40, 57 and 58. The effect of the length scale of disorder in the width-modulation on the phonon wavelengths is taken into account by the energy dependent transmission coefficient. The transmission coefficient is calculated for the defined modulation geometry for each wavelength. Phonons with different wavelengths contribute to thermal conductance according to phonon distribution at the actual temperature. One should be aware that the spatial scale of disorder has distinct effects to phonon waves in the ballistic transport regime and to phonons treated as particles and transport dominated by scattering effects.⁵⁹ The dimensions and material properties are continuous values parameters. Here, we refer to representative nWVGs shown in Fig. 1c. Calculations are shown for GaAs nWVGs with layers of 10 nm constrictions and 100 nm openings.

ML requires input descriptors that are digital representations of the nWVGs. The choice of the descriptor is important for successful ML optimization. We used binary flag numbers that represent aperiodic arrays of QDs and constrictions according to our system described above. We denote constriction layers with the binary flag ‘0’ and opening layers with the binary flag ‘1’ (Fig. 2). A QD is formed by a sequence of ‘1s’ surrounded by ‘0’ layers at opposite endings. QDs of different sizes are formed by different numbers of subsequent layers ‘1’. Similarly, constrictions with different lengths are formed by different numbers of subsequent layers ‘0’. Following this scheme, the descriptor for a periodic SL with N = 14 layers would be 01010101010101. An example of a descriptor for an aperiodic SL with 14 layers would be the array: 01110100101111.

Fig. 2 Flowchart of the optimization methodology. Aperiodicity optimization for minimum coherent phonon heat conduction is achieved by coupling Bayesian optimization and physics property calculator in an iterative loop.

The ML optimization is performed using the open-source Bayesian optimization library COMBO,⁶⁰ which was previously tested for optimizations in various energy transport problems.^43–45 The Bayesian optimization employs Gaussian processes that are suitable for black-box optimizations. The objective function is the value of the thermal conductance. The ML algorithm is integrated with the property calculator in a closed-loop iterative optimization (Fig. 2). At the beginning of the process, thermal conductance is calculated for n candidates that have been selected randomly. Then, the next one to calculate is chosen. The goal is to train the Bayesian optimization process to find the candidate with minimum thermal conductance using a small number of training candidates as possible. This number upon convergence determines the efficiency of the optimization. A Bayesian regression function is learned from n pairs of descriptors and the corresponding calculated values of thermal conductance. A Gaussian process provides a Bayesian posterior probability distribution that describes the potential thermal conductance values for each of the remaining candidates. The best candidates are chosen based on the expected improvement criterion of the acquisition function. Next, the exact thermal conductance value is calculated for the chosen candidate and is added to the training set. The procedure is repeated until convergence to the candidate with minimum thermal conductance is achieved. This is the nWVG with the optimal modulation profile.

3 Results and discussion

We set up our optimization problem based on the findings of a previous theoretical study on coherent phonon transport in width-modulated nWVGs⁴⁰ that are summarized in Fig. 1b. A significant decrease of the thermal conductance below the uniform overlapping and core nWVGs values is shown even for a low modulation degree of a few modulation units (QDs). The thermal conductance decreases with an increasing number of identical QDs reaching a limit for the periodic superlattice (p-SL) configuration. Increasing the number of identical QDs in the modulation profile beyond this number does not decrease any further the thermal conductance. The p-SL value is approached for a small number of identical QDs: three QDs were sufficient approximation, while the infinite p-SL-limit was reached for five QDs. It was revealed that thermal conductance decreases below the p-SL value for aperiodic arrays of non-identical modulation units, QDs. It was shown a monotonic decrease of thermal conductance with an increasing degree of modulation in more disordered arrays of non-identical QDs.^40,41

Based on the above findings, we selected three sets of nWVGs with different numbers of layers N to perform the optimization (Table 1): (a) nWVG-8 with N = 8 layers and three QD p-SL, (b) nWVG-12 with N = 12 layers and five QD p-SL and (c) nWVG-14 with N = 14 layers with six QD p-SL. We aimed to optimize aperiodicity, and we used the periodic structure, the p-SL, as our reference. We fixed the modulation composition to 50% QDs as in the p-SL for which the number of constriction layers is the same as the number of opening layers. Translating this constraint into our digital descriptor notation would mean that the number of ‘0s’ is equal to the number of ‘1s’ in all arrays. The descriptors of the p-SLs for the three sets of nWVGs are 10101010 (N = 8), 101010101010 (N = 12), and 10101010101010 (N = 14). Under the constraint, the total number of candidates (2^N) 256, 4096, and 16 384 reduces to 70, 924, and 3432 for N = 8, 12 and 14 respectively. With that, the computational load was affordable, and we calculated the thermal conductance of all candidates of the reduced sets of nWVGs to validate and evaluate the Bayesian optimization.

Table 1 Results of the Bayesian optimization. Periodic and optimal aperiodic configurations for three sets of nWVGs with number of layers N = 8, 12, and 14

---

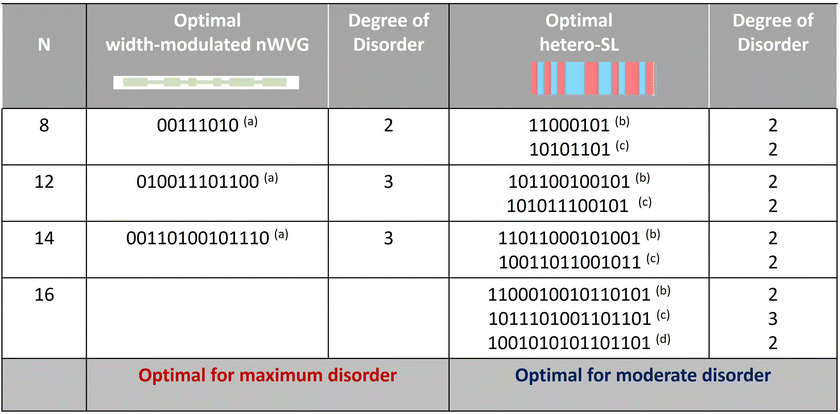
The results of the optimization are listed in Table 1. The descriptors of the optimal configurations for the three sets of nWVGs are accompanied by the corresponding modulation profiles. The descriptors are 00111010 (N = 8), 010011101100 (N = 12), and 00110100101110 (N = 14). They all denote aperiodic configurations. The optimal configurations are aperiodic for the three sets of nWVGs, as expected by physics. Even more importantly, they are arrays of the non-identical QDs 010, 0110, and 01110 as predicted.⁴⁰Fig. 3 plots the thermal conductance versus temperature for the three optimal nWVGs. Temperature is kept at low values, below 10 K, so that coherence effects are not screened by scattering or thermal broadening effects.^23–25,40 The thermal conductance is expressed relative to the p-SL value. It is smaller than 1 for all three sets of nWVGs in the whole temperature range. This was to be expected because aperiodic configurations have smaller thermal conductance than periodic ones (Fig. 1b). The optimal aperiodic nWVGs have significantly lower thermal conductance than the p-SL. Their relative thermal conductance ranges from 0.3 to 0.6 at T = 2 K and from 0.5 to 0.8 at T = 10 K. Among the three optimal nWVGs, the one with N = 14 shows the maximum decrease of thermal conductance which is 30–50% of the p-SL value depending on temperature. This is because it is the longest optimal nWVG and thus the most extended array of non-identical QDs. It is the aperiodic configuration with the highest degree of disorder and the minimum thermal conductance in agreement with the physics prediction. This holds in the whole temperature range as temperature only affects quantitatively thermal conductance through thermal broadening of wave effects on transport. It is also interesting to notice that the optimal aperiodic configuration is not the one with maximum interfacial density. The p-SL has maximum interfacial density and higher thermal conductance than the optimal aperiodic configuration.

Fig. 3 Temperature dependence of thermal conductance of the optimal nWVGs. The thermal conductance of the optimal aperiodic nWVGs is significantly lower than the p-SL value in the whole temperature range. The lowest thermal conductance is for the most extended array of non-identical QDs.

Bayesian optimization identified the aperiodic configuration with the minimum thermal conductance out of a vast pool of aperiodic candidates for each set of nWVGs. The optimal configurations are arrays of the maximum number of non-identical QDs, i.e., with the modulation profile's maximum disorder (note: ‘maximum disorder’ is in this definition finite and well-defined for each N and should not be confused with maximum disorder for infinitely large systems). This finding is not trivial as makes evident the comparison with findings in aperiodic hetero-SLs presented below. It agrees with the physics rule predicted based on selective calculations in an intuitive physics analysis.^40,41 The physics rule, validated here by extensive calculations and Bayesian optimization, can serve as a quantitative design tool for the optimal set of non-identical modulation units. Bayesian optimization identifies the optimal array out of several possible combinations of the optimal set of non-identical QDs for each N. The optimization process is very efficient (Fig. 4). The optimal configuration is identified after optimization experiments with a small percentage of candidates in the 3–10% range. Representative results are shown in Fig. 4 for N = 14 which is the set with the largest population (3432 candidates). The optimal configuration was searched in multiple tests with rounds of 10–20 candidates starting with different initial choices of random candidates. The same optimal configurations were always detected. There was a dispersion in the convergence time for the various optimization experiments. Analysis showed that this dispersion is due to that the optimal can be approached through different paths. Two such paths with different convergence times are shown in Fig. 4. The optimization evolution paths consist of different sequences of candidates. Notably, the candidates of the different sequences have a common feature: they are all arrays of the same set of non-identical QDs. In all paths, the optimization process identifies the optimal set of non-identical QDs after just a small percentage of initial trial candidates and proceeds by searching the optimal configuration among permutations of these QDs until it converges to the optimal one.

Fig. 4 Performance of the Bayesian optimization for two paths (I and II) starting with different sets of random candidates. The sequences of the candidates for the corresponding evolution paths are shown on the right.

The Bayesian optimization was validated by calculating the thermal conductance of all candidates for the three sets of nWVGs. The distribution of the thermal conductance among the candidates is shown in Fig. 5 for the three modulation lengths N = 8, 12 and 14. The corresponding histograms have been constructed for a fixed number of zones between the maximum and minimum values of thermal conductance. In all cases, there is a maximum and a minimum thermal conductance. This confirms that the problem is suitable for Bayesian optimization. The maximum thermal conductance corresponds to the single constriction configuration: 11000011 for N = 8, 111000000111 for N = 12, and 111110000000111 for N = 14. The corresponding profiles are shown in Fig. 5 together with the profiles of the periodic SLs and the optimal aperiodic nWVGs. Characteristic features of the distribution can be clearly distinguished in the three histograms. The distribution is sparse for N = 8 because the number of candidates is small (70). It becomes clearer for N = 12 with 924 candidates and clear for N = 14 with 3432 candidates. In all cases, there is a gap between the maximum thermal conductance corresponding to the single-constriction modulation and the thermal conductance of candidates modulated by one or more QDs. The distribution of QD-modulated candidates shows a tail, a peak, and a sharp low-edge threshold. The tail comprises configurations deviating from the p-SL in the number of identical QDs in their profile. As the number of non-identical modulation QDs increases, the thermal conductance decreases below that of the p-SL. The peak of the envelope corresponds to configurations with identical and non-identical QDs in their profile. The occurrence of a peak denotes the vast number of permutations of identical and non-identical QDs with similar thermal conductance. Configurations of non-identical QDs have thermal conductance in the lower part of the distribution. The number of combinations of non-identical QDs is smaller and the distribution drops rapidly after the peak towards the low-edge threshold. The process rapidly converges to configurations within this part of the distribution and identifies the one with the minimum thermal conductance, as the optimal one. The existence of an optimal configuration relies on the physics mechanism, namely quantum interference. The transmission coefficients of different configurations with the same degree of disorder show different energy fluctuation patterns and thus they have different thermal conductances that are ordered. This effect is related to wave phase matching at geometrical discontinuities, it is purely geometrical and takes place irrespectively of the total mass of the configuration. The optimal calculated configurations are shown in Fig. 5 for the three sets of nWVGs. Each of them is degenerate to its reverse. In all cases, the optimal configurations identified by the Bayesian optimization was the one with the minimum calculated thermal conductance. This validates the Bayesian optimization.

Fig. 5 Calculated distribution histograms. The distribution of the calculated thermal conductance among the candidates is shown in histograms constructed for a fixed number of zones between the maximum and minimum values of thermal conductance for each set of nWVGs. The profiles of the single constriction modulated nWVGs with maximum thermal conductance are shown together with the profiles of the corresponding periodic SLs and the optimal aperiodic nWVGs.

Additional insight into the optimization process and the optimization rule can be gained in terms of the transmission coefficient. The energy dependence of the transmission coefficient of width-modulated nWVGs shows characteristic wave interference fluctuations. Fluctuations are due to destructive interference at width-discontinuities that decrease the transmission probability of phonon waves. The transmission coefficient of a uniform nWVG has a staircase structure where a new step of height 1 enters for each additional subband. The step-like structure is shown to be gradually distorted with increasing disorder and is completely lost in the case of the optimal configuration with maximum disorder. Fig. 6a shows the transmission coefficient for a single constriction modulation, the periodic SL, and the optimal aperiodic nWVG. Even a single constriction significantly restricts the propagation of phonon waves. The perfect steps of the transmission coefficient of the uniform nWVG are distorted by fluctuations throughout the energy spectrum. As a result, thermal conductance decreases significantly below that of the uniform nWVG (Fig. 6b). The decrease is dominated by destructive interference at the two sides of the constriction, and it is comparable for the three lengths N. Destructive interference gets more extended for periodic modulation by a sequence of identical QDs. The step-like subband structure of the uniform nWVG is replaced by propagation subbands separated by propagation gaps that are formed in the presence of periodicity. The overall transmission probability decreases, and the thermal conductance of the p-SL is significantly lower than in the uniform nWVG. The thermal conductance decreases rapidly with an increasing number of QDs reaching the infinite p-SL limit for about five QDs. The thermal conductance of the periodic array of three QDs (N = 8) is larger than that of the periodic array of five QDS (N = 12) (Fig. 6b). The thermal conductance of the periodic array of six QDs (N = 14) is identical to that of five QDS (N = 12). The low limit of the infinite p-SL thermal conductance is reached for N = 12. In the presence of aperiodicity, the SL propagation bands shrink and the transmission coefficient decreases. This explains that the thermal conductance of the optimal aperiodic nWVGs is smaller than that of the p-SL. Remarkably, the thermal conductance of the optimal aperiodic nWVGs decreases for increasing N. This is because destructive interference is more significant for more extended aperiodicity. The decrease occurs gradually with an increasing degree of disorder in longer arrays of non-identical QDs. The optimal aperiodic configuration with the longest extent and the highest modulation degree is for N = 14 and has the global minimum thermal conductance. It becomes evident that the validity of the physics optimization rule lies in the underlying physics, the dominance of quantum interference in decreasing thermal conductance.

Fig. 6 The underlying physics. (a) The energy dependence of the transmission coefficient for single-constriction- (grey), periodic- (green), and optimal aperiodic (orange) modulations. (b) The corresponding thermal conductance of modulated nWVGs relative to the uniform nWVGs for the three sets of nWVGs with N = 8, 12, and 14.

According to the physics rule coherent phonon transmission and thermal conductance are minimized for the maximum degree of disorder in the modulation profile, i.e. for maximum number of non-identical modulation units, QDs in width-modulated nWVGs or layer thicknesses in SLs. This dependence although intuitive is not trivial as shows a comparison with findings on hetero-SLs. Optimization of aperiodic hetero-SLs showed minimum coherent phonon conduction for a moderate disorder rather than for the maximum. This conclusion is supported by different studies based on atomistic calculations, atomistic Green's function (AGF), non-equilibrium Green's function (NEGF), molecular dynamics, and different machine learning optimization techniques such as Bayesian optimization,^43–45 genetic algorithms,^46,47,49 Monte Carlo tree search⁴⁸ and pattern analysis.⁴⁸Table 2 compares optimal width-modulated nWVGs and hetero-SLs of the same number of unit multilayers and makes evident that nWVGs are optimized by maximum disorder as expected by the underlying physics whereas hetero-SLs are optimized by moderate disorder against physics intuition.^46,49 The unexpected behavior found in hetero-SLs was attributed to thermal boundary resistance⁴⁶ and interface thermal resistance.⁴⁶ The optimal moderate disorder was not quantified explicitly. It was concluded that even though ML can help to predict thermal conductance, it cannot explicitly reveal the underlying physics.⁴⁷ It was proposed to guess the optimal aperiodic configuration with pattern analysis based on a statistical analysis of configurations.⁴⁹ Optimal aperiodic hetero-SL configurations were though not unambiguously determined as different studies found different optimal configurations for the same type of hetero-SLs (Table 2). Importantly, our work reveals geometry-modulated nWVGs as a class of aperiodic metamaterials where optimal disorder can be unambiguously determined as the maximum disorder, the disorder being quantified by the number of non-identical modulation units.

Table 2 Comparison between optimal width-modulated nWVGs and optimal hetero-SLs

a Width-modulated nWVGs in the present work (Fig. 1c). b Si–Ge SLs.⁴³ c Si–Ge SLs.⁴⁸ d GaAs–AlAs SLs.⁴⁵ The degree of disorder is quantified by the number of non-identical modulation units, QDs (nWVGs), or layer thicknesses (SLs). Maximum disorder optimizes width-modulated nWVGs. Moderate disorder optimizes hetero-SLs.

---

4 Overview and concluding remarks

We reported on optimization of aperiodicity in width-modulated nWVGs for minimum phonon transmission with calculations and Bayesian optimization. Our work contributes to the current effort of the research community to progress beyond ‘that disorder is good at reducing thermal conduction’ and understanding and quantifying the effects of disorder/aperiodicity on nanoscale heat transfer. Non-trivial, against physics intuition, results have already been revealed. Our work provides new insight that could contribute to understanding the non-trivial role of disorder in non-uniform nanostructures.

We addressed the problem of optimizing aperiodicity in width-modulated nWVGs for minimum phonon transmission and thermal conductance. This was particularly challenging because of the enormous number of possible realizations of geometrical aperiodicity. We detailed how we set up a feasible optimization problem guided by experience from previous findings to apply physics arguments to remove unnecessary complexity in the modulation profile and efficiently tackle the problem. We defined suitable descriptors and selected representative sets of nWVGs to perform the optimization. The optimal configurations were efficiently identified with the developed methodology and were validated with calculations on the full populations. Optimal aperiodicity has been interpreted in terms of a predicted physics rule. Our outcomes confirm that the optimal width-modulated nWVGs are aperiodic arrays with the maximum disorder, the disorder being quantified by the number of non-identical modulation units (QDs). The validated physics rule serves as a quantitative tool to unambiguously design the optimal set of non-identical modulation units. Bayesian optimization identifies the optimal combination of this set for each N. Our work indicates a new route to control transmission across metamaterials designing geometrical aperiodicity.

Author contributions

A. D. S. investigation; formal analysis; data curation, X. Z. conceptualization; methodology; investigation; formal analysis; visualization; writing; supervision.

Conflicts of interest

There are no conflicts to declare.

References

1. R. W. Morse, Dispersion of Compressional Waves in Isotropic Rods of Rectangular Cross Section, J. Acoust. Soc. Am., 1948, 20, 833–838.
2. S. Yip and Y. C. Chang, Theory of phonon dispersion relations in semiconductor superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 7037–7059.
3. B. K. Ridley, Electrons and Phonons in Semiconductor Multilayers, Cambridge University Press, 1996.
4. S. Lepri, R. Livi, A. Politi and D. K. Campbell, Thermal conduction in classical low-dimensional lattices, Phys. Rep., 2003, 377, 1–80.
5. A. A. Balandin, Nanophononics: phonon engineering in nanostructures and nanodevices, J. Nanosci. Nanotechnol., 2005, 5, 1015–1022.
6. L. D. Hicks and M. Dresselhaus, Effect of quantum-well structures on the thermoelectric figure of merit, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 12727.
7. L. D. Hicks and M. Dresselhaus, Thermoelectric figure of merit of a one-dimensional conductor, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16631.
8. D. G. Cahill, et al., Nanoscale thermal transport, J. Appl. Phys., 2003, 93, 793–818.
9. D. G. Cahillet, et al., Nanoscale thermal transport. II. 2003–2012, Appl. Phys. Rev., 2014, 1, 011305.
10. A. A. Balandin and D. L. Nika, Phononics in low-dimensional materials, Mater. Today, 2012, 15, 266–275.
11. Y. Pennec and B. Djafari-Rouhani, Fundamental properties of phononic crystal, in Phononic Crystals: Fundamentals and Applications, ed. A. Khelif and A. Adibi, Springer, New York, 2016, pp. 23–50.
12. Y. Xiao, Q. Chen, D. Ma, N. Yang and Q. Hao, Phonon transport within periodic porous structures—from classical phonon size effects to wave effects, ES Mater. Manuf., 2019, 5, 2–18.
13. X. Zianni, Thermoelectric Metamaterials: Nano-Waveguides for Thermoelectric Energy Conversion and Heat Management at the Nanoscale, Adv. Electron. Mater., 2021, 7, 2100176.
14. Y. Pennec, J. Q. Vasseur, B. Djafari-Rouhani, L. Dobrzynski and P. A. Deymier, Two-dimensional phononic crystals: examples and applications, Surf. Sci. Rep., 2010, 65, 229–291.
15. J. Tang, H.-T. Wang, D.-H. Lee, M. Fardy, Z. Huo, T. P. Russell and P. Yand, Holey Silicon as an Efficient Thermoelectric Material, Nano Lett., 2010, 10(10), 4279–4283.
16. X. Zianni, Diameter-modulated nanowires as candidates for high thermoelectric energy conversion efficiency, Appl. Phys. Lett., 2010, 97, 233106.
17. J.-K. Yu, S. Mitrovic, D. Tham, J. Varghese and J. R. Heath, Reduction of thermal conductivity in phononic nanomesh structures, Nat. Nanotechnol., 2010, 5, 718–721.
18. D. Nika, A. I. Cocemasov, D. V. Crismari and A. A. Balandin, Thermal conductivity inhibition in phonon engineered core-shell cross-section modulated Si/Ge nanowires, Appl. Phys. Lett., 2013, 102, 213109.
19. R. Lucklum, Phononic crystals and metamaterials—Promising new sensor platforms, Procedia Eng., 2014, 87, 40–45.
20. R. Anufriev, A. Ramiere, J. Maire and M. Nomura, Heat guiding and focusing using ballistic phonon transport in phononic nanostructures, Nat. Commun., 2017, 8, 15505.
21. M. An, Q. Song, X. Yu, H. Meng, D. Ma, R. Li, Z. Jin, B. Huang and N. Yang, Generalized Two-Temperature Model for Coupled Phonons in Nanosized Graphene, Nano Lett., 2017, 17, 5805.
22. R. Anufriev and M. Nomura, Ray phononics: thermal guides, emitters, filters, and shields powered by ballistic phonon transport, Mater. Today Phys., 2020, 15, 100272.
23. G. Chen, Thermal conductivity and ballistic-phonon transport in the cross-plane direction of superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 14958.
24. J. Ziman, Electrons and Phonons, Oxford University Press, 2001.
25. J. S. Heron, T. Fournier, N. Mingo and O. Bourgeois, Nano Lett., 2009, 9, 1861.
26. G. Chen, Non-Fourier phonon heat conduction at the microscale and nanoscale, Nat. Rev. Phys., 2021, 3, 555.
27. X. Wan, D. Ma, D. Pan, L. Yang and N. Yang, Optimizing thermal transport in graphene nanoribbon based on phonon resonance hybridization, Mater. Today Phys., 2021, 20, 100445.
28. L. Yang, X. Wan, D. Ma, Y. Jiang and N. Yang, Maximization and minimization of interfacial thermal conductance by modulating the mass distribution of the interlayer, Phys. Rev. B, 2021, 103, 155305.
29. M. Nomura, et al., Review of thermal transport in phononic crystals, Mater. Today Phys., 2022, 22, 100613.
30. Y. Achaoui, A. Khelif, S. Benchabane, L. Robert and V. Laude, Experimental observation of locally-resonant and Bragg band gaps for surface guided waves in a phononic crystal of pillars, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 104201.
31. M. N. Luckyanova, et al., Coherent phonon heat conduction in superlattices, Science, 2012, 338, 936–939.
32. S. Alaie, D. F. Goettler, M. Su, Z. C. Leseman, C. M. Reinke and I. El-Kady, Thermal transport in phononic crystals and the observation of coherent phonon scattering at room temperature, Nat. Commun., 2015, 6, 7228.
33. R. Venkatasubramanian, Lattice thermal conductivity reduction and phonon localization like behavior in superlattice structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3091–3097.
34. B. Yang and G. Chen, Partially Coherent Phonon Heat Conduction in Superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 195311.
35. K. Termentzidis, P. Chantrenne and P. Keblinski, Nonequilibrium molecular dynamics simulation of the in-plane thermal conductivity of superlattices with rough interfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 214307.
36. F. Nori and J. Rodriguez, Acoustic and Electronic Properties of One-Dimensional Quasicrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 2207–2211.
37. S. Tamura and J. Wolfe, Acoustic-Phonon Transmission in Quasiperiodic Superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 3491–3494.
38. R. Merlin, Structural and Electronic Properties of Nonperiodic Superlattices, IEEE J. Quantum Electron., 1988, 24, 1791–1798.
39. S. Tamura and F. Nori, Transmission and Frequency Spectra of Acoustic Phonons in Thue-Morse Superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 9790–9801.
40. X. Zianni, The effect of the modulation shape in the ballistic thermal conductance of modulated nanowires, J. Solid State Chem., 2012, 193, 53–57.
41. X. Zianni, Disorder-induced enhancement of the thermoelectric efficiency in diameter- modulated nanowires, Microelectron. Eng., 2013, 112, 235–240.
42. B. Qiu, G. Chen and Z. Tian, Effects of Aperiodicity and Roughness on Coherent Heat Conduction in Superlattices, Nanoscale Microscale Thermophys. Eng., 2015, 19, 272–278.
43. S. Ju, T. Shiga, L. Feng, Z. Hou, K. Tsuda and J. Shiomi, Designing Nanostructures for Phonon Transport via Bayesian Optimization, Phys. Rev. X, 2017, 7, 021024.
44. S. Ju and J. Shiomi, Materials informatics for heat transfer: recent progresses and perspectives, Nanoscale Microscale Thermophys. Eng., 2019, 23, 157–172.
45. R. Hu, et al., Machine-Learning-Optimized Aperiodic Superlattice Minimizes Coherent Phonon Heat Conduction, Phys. Rev. X, 2020, 10, 021050.
46. R. Chowdhury, C. Reynolds, A. Garrett, T. Feng, S. P. Adiga and X. Ruan, Machine learning maximized Anderson localization of phonons in aperiodic superlattices, Nano Energy, 2020, 69, 104428.
47. P. Chakraborty, Y. Liu, T. Ma, X. Guo, L. Cao, R. Hu and Y. Wang, Quenching thermal transport in aperiodic superlattices: a molecular dynamics and machine learning study, ACS Appl. Mater. Interfaces, 2020, 12, 8795–8804.
48. Y. Liu, R. Hu, Y. Wang, J. Ma, Z. Yang and X. Luo, Big-data-accelerated aperiodic Si/Ge superlattice prediction for quenching thermal conduction via pattern analysis, Energy AI, 2021, 3, 100046.
49. S. Lin, Y. Liu, Z. Cai and C. Zhao, High-Throughput Screening of Aperiodic Superlattices Based on Atomistic Simulation-Informed Effective Medium Theory and Genetic Algorithm, Int. J. Heat Mass Transfer, 2023, 202, 123694.
50. R. Ramprasad, et al., Machine learning in materials informatics: recent applications and prospects, npj Comput. Mater., 2017, 3, 54.
51. R. Juneja, G. Yumnam, S. Satsangi and A. K. Singh, Coupling the high-throughput property map to machine learning for predicting lattice thermal conductivity, Chem. Mater., 2019, 31, 5145–5151.
52. L. Chen, H. Tran, R. Batra, C. Kim and R. Ramprasad, R. Machine learning models for the lattice thermal conductivity prediction of inorganic materials, Comput. Mater. Sci., 2019, 170, 109155.
53. D. Visaria and A. Jain, A. Machine-learning-assisted space-transformation accelerates discovery of high thermal conductivity alloys, Appl. Phys. Lett., 2020, 117, 202107.
54. H. Wei, H. Bao and X. Ruan, Perspective: Predicting and optimizing thermal transport properties with machine learning methods, Energy AL, 2022, 8, 100153.
55. M. C. Cross and R. Lifshitz, Elastic wave transmission at an abrupt junction in a thin plate with application to heat transport and vibrations in mesoscopic systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 085324.
56. A. Weisshaar, J. Lary, S. M. Goodnick and V. K. Tripathi, Analysis and modeling of quantum waveguide structures and devices, J. Appl. Phys., 1991, 70, 355.
57. W.-X. Li, K.-Q. Chen, W. Duan, J. Wu and B.-L. Gu, Acoustic phonon transport through a T-shaped quantum waveguide, J. Phys.: Condens. Matter, 2004, 16, 5049–5059.
58. W.-X. Li, T. Liu and C. Liu, Phonon transport through a three-dimensional abrupt junction, Appl. Phys. Lett., 2006, 89, 163104.
59. N. Mingo, D. Hauser, N. P. Kobayashi, M. Plissonnier and A. Shakouri, Nanoparticle-in-Alloy” Approach toEfficient Thermoelectrics: Silicides in SiGe, Nano Lett., 2009, 9(2), 711–715.
60. T. Ueno, T.-D. Rhone, Z. Hou, T. Mizoguchi and K. Tsuda, COMBO: An efficient Bayesian optimization library for materials science, Mater. Discovery, 2016, 4, 18–21.

---