Efficient second- and higher-order harmonic generation from LiNbO3 metasurfaces
Yun
Zhao
a,
Zhaoxi
Chen
b,
Cheng
Wang
*b,
Yuanmu
Yang
 *a and
Hong-Bo
Sun
*a and
Hong-Bo
Sun
 *a
*a
aState Key Laboratory of Precision Measurement Technology and Instruments, Department of Precision Instrument, Tsinghua University, Beijing 100084, China. E-mail: ymyang@tsinghua.edu.cn; hbsun@tsinghua.edu.cn
bDepartment of Electronical Engineering and State Key Laboratory of Terahertz and Millimeter Waves, City University of Hong Kong, Hong Kong 999077, China. E-mail: cwang257@cityu.edu.hk
First published on 10th July 2023
Abstract
Lithium niobate (LiNbO3) is a material that has drawn great interest in nonlinear optics because of its large nonlinear susceptibility and wide transparency window. However, for complex nonlinear processes such as high-harmonic generation (HHG), which involves frequency conversion over a wide frequency range, it can be extremely challenging for a bulk LiNbO3 crystal to fulfill the phase-matching conditions. LiNbO3 metasurfaces with resonantly enhanced nonlinear light–matter interaction at the nanoscale may circumvent such an issue. Here, we experimentally demonstrate efficient second-harmonic generation (SHG) and HHG from a LiNbO3 metasurface enhanced by guided-mode resonance. We observe a high normalized SHG efficiency of 5.1 × 10−5 cm2 GW−1. Moreover, with the alleviated above-gap absorption of the material, we demonstrate HHG up to the 7th order with the shortest generated wavelength of 226 nm. This work may provide a pathway towards compact coherent white-light sources with frequency spanning into the deep ultraviolet region for applications in spectroscopy and imaging.
Introduction
Lithium niobate (LiNbO3) is a widely used material for nonlinear optics. It is transparent over a broad spectral range from ultraviolet (UV) to mid-infrared. Due to the lack of centrosymmetry of its crystal structure, LiNbO3 exhibits both even- and odd-order nonlinear responses. Most notably, the large second-order nonlinear susceptibility (χ(2)) allows it to be used for efficient second-order nonlinear optical processes such as second-harmonic generation (SHG),1,2 sum- and difference-frequency generation,3,4 and spontaneous parametric down-conversion (SPDC).5,6 In addition, LiNbO3 can also be appealing in third-order nonlinear interactions, including four-wave mixing7 and Kerr-based optical frequency comb generation.8,9To allow efficient nonlinear light–matter interaction in a bulk LiNbO3 crystal or a LiNbO3 waveguide, the phase-matching conditions must be met.10 Nonetheless, conventional phase-matching techniques, including birefringent phase-matching and quasi-phase-matching, typically only work for a limited bandwidth and do not perform well for nonlinear processes such as high-harmonic generation (HHG), which involves frequency conversion over many octaves. To tackle this challenge, it was recently shown that a stringently engineered chirped periodically poled LiNbO3 (CPPLN) crystal can allow HHG up to the 10th order,11–13 generating a supercontinuum white light source spanning an extremely wide wavelength range from 350 nm to 2500 nm. However, HHG into the deep ultraviolet (DUV) spectral range is yet to be observed due to the strong absorption of the above-gap harmonics when propagating inside such a bulk LiNbO3 crystal.
The abovementioned issues of phase mismatch and above-gap absorption may be partly addressed using LiNbO3 metasurfaces with a subwavelength thickness. With the rapid development of lithium niobate on insulator (LNOI)14 technology over the last few years, LiNbO3 thin films can now be patterned into metasurfaces15 that support a variety of Mie resonances, including electric- or magnetic-dipole resonance,16–18 Fano resonance,19,20 anapole resonance,21,22 bound states in the continuum (BIC) resonance,23–27 and guided-mode resonance.28–30 For SHG, LiNbO3 metasurfaces with resonantly enhanced nonlinear light–matter interaction have been demonstrated, yet with relatively low conversion efficiency, which may be due to the relatively low Q-factors limited by design or fabrication constraints. For HHG, reports from LiNbO3 metasurfaces remain elusive. HHG from the Si metasurface,31,32 GaP metasurface,33 and sub-wavelength-thick epsilon-near-zero thin film34 has been demonstrated, yet the relatively strong above-gap absorption loss in the UV region still poses an issue.
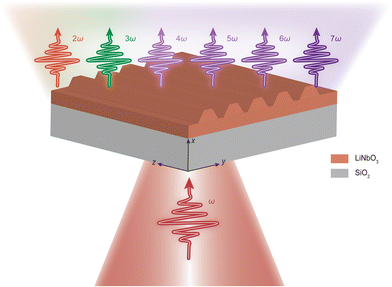
In this work, we demonstrate efficient SHG and HHG up to the 7th order, with the shortest generated wavelength of 226 nm in the DUV regime, from a LiNbO3 metasurface that supports a guided-mode resonance. When the metasurface is resonantly driven by a transverse electric (TE) polarized femtosecond laser, we observed a high SHG conversion efficiency of 8.6 × 10−3 at a peak pump intensity of 0.17 TW cm−2. We further observed the 7th harmonic generation in the DUV region.
Results
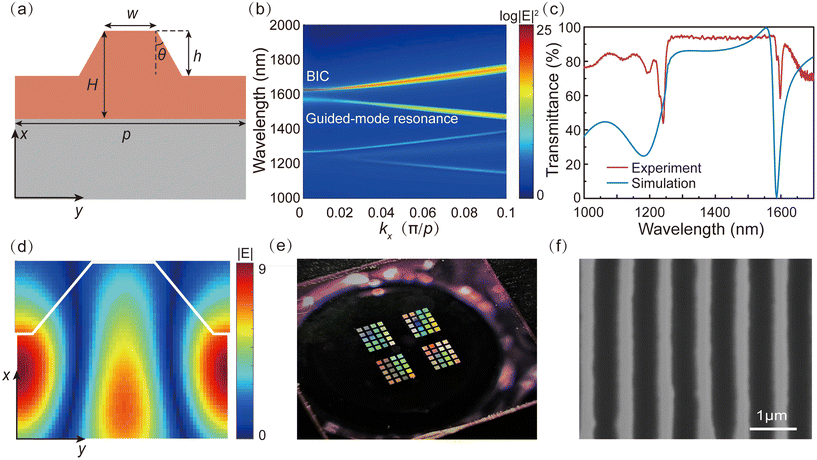
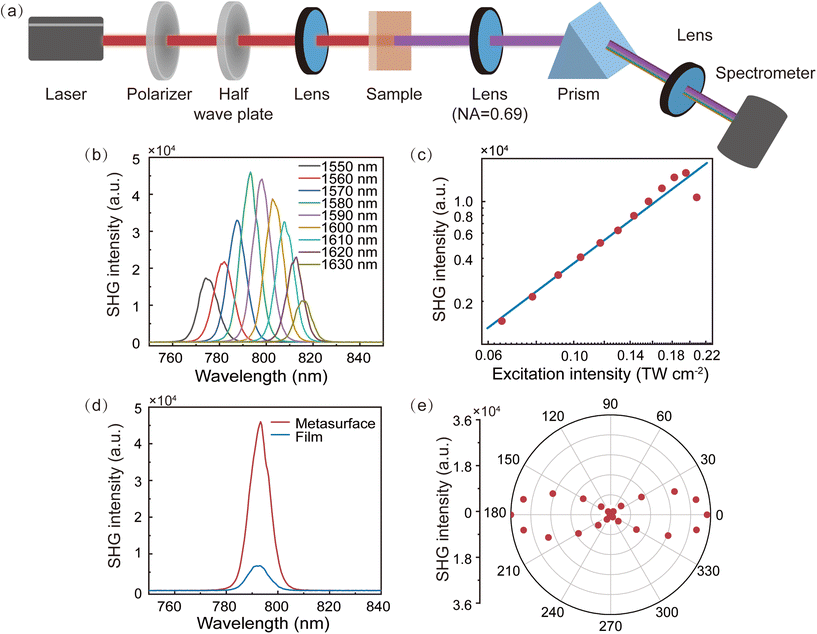
The metasurface supporting guided-mode resonance, composed of a partially-etched 1D LiNbO3 grating, is fabricated on an x-cut LNOI wafer. The wafer has a 600-nm-thick LiNbO3 thin-film layer on a 2-μm-thick SiO2 box layer placed on a 500-μm-thick transparent quartz substrate, and the schematic is shown in Fig. 1. The optical axis of the LiNbO3 thin-film is along the z-direction and the pump laser is polarized along the TE direction to utilize LiNbO3's largest second-order nonlinear tensor component d33. The harmonic signals from the 2nd to 7th order spanning the near-infrared to DUV wavelength range are generated in the transmission direction with a femtosecond pump laser incident in the normal direction.Fig. 2a depicts the geometry of the grating which is designed to support high-Q guided-mode resonance. We calculate the eigenmodes and the transmission spectrum of the metasurface for TE polarization using the commercial software Lumerical FDTD (see Numerical simulations in the Methods section for more details). The photonic band structure of the 1D subwavelength grating is shown in Fig. 2b, which reveals two strong resonances in the first Brillouin zone, corresponding to a guided-mode resonance and a BIC resonance, respectively. Though the BIC resonance can have an extremely large Q-factor approaching infinity, it is prohibited to couple with normally incident light due to symmetry constraints.35 In contrast, the guided-mode resonance can be excited under normal incidence, occurring at a wavelength of 1580 nm. The simulated normal-incident transmittance spectrum of the metasurface, as shown in Fig. 2c, also indicates that only the guided-mode resonance is excited. The electric field distribution at the resonant wavelength is given in Fig. 2d, which shows about 9-fold enhancement of the local electric field confined inside the LiNbO3 structure. The optical photo and scanning electron microscopy (SEM) images of the fabricated metasurface, patterned by electron beam lithography (EBL) followed by reactive ion etching (RIE), are shown in Fig. 2e and f (see Sample fabrication in the Methods section for more details). Subsequently, the linear transmittance spectrum of the fabricated metasurface is experimentally measured under TE-polarized normal incident light. As shown in Fig. 2c, the experimental result qualitatively agrees with the simulation. The lower extinction ratio and larger resonance linewidth may originate from the imperfection of fabrication as well as the finite angular range of the incident white light. To further experimentally characterize the nonlinear responses of the metasurface, we set up the nonlinear optical measurement system (see Optical characterization in the Methods section for more details) as schematically shown in Fig. 3a. The pump laser with a pulse duration of 290 fs and a repetition rate of 75 kHz is focused on the sample via a lens with a focal length of 50 mm. The polarization of the pump laser is controlled by a linear polarizer and a half-wave plate. The generated harmonic signals are collected with a high numerical aperture lens (NA = 0.69) and then spatially dispersed with a CaF2 prism before being coupled into the grating spectrometer.
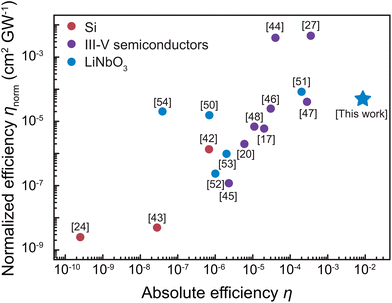
By tuning the pump wavelength from 1550 nm to 1630 nm with a step of 10 nm at a constant peak pump intensity of 1.8 GW cm−2, we observed a SHG signal peak at a pump wavelength of 1580 nm, as shown in Fig. 3b. The peak in the signal confirms the resonance enhancement of the SHG as a result of the guided-mode resonance. As the pump power increases, the SHG intensity exhibits a quadratic relationship with the excitation intensity, as depicted in Fig. 3c. The SHG intensity starts to drop at a peak pump intensity of 0.21 TW cm−2, which corresponds to the damage threshold of the metasurface. Compared with an unpatterned LiNbO3 film at an identical excitation intensity of 1.8 GW cm−2, the SHG intensity of the LiNbO3 metasurface is enhanced 7 times, as shown in Fig. 3d. Because of the polarization-sensitive nature of the GMR metasurface and the substantial difference in χ(2) tensor components along the z- and y-crystal directions, the SHG intensity of LiNbO3 gratings is strongly dependent on the polarization of the pump light, as shown in Fig. 3e. The intensity shows 80-fold enhancement in the resonant pump with TE polarization compared to the non-resonant pump with transverse magnetic (TM) polarization. At a peak pump intensity IFHpeak of 0.17 TW cm−2, we measured a high absolute conversion efficiency η = PSHavg/PFHavg of 8.6 × 10−3, where PSHavg is the average power of the second harmonic. Since the SHG efficiency is proportional to the peak pump intensity, we use the normalized SHG efficiency, defined as ηnorm = η/IFHpeak, as the criterion to benchmark the SHG efficiency of various metasurface platforms. The normalized efficiency of our LiNbO3 metasurface is 5.1 × 10−5 cm2 GW−1. We compare this value with other dielectric metasurfaces36–41 including Si,24,42,43 III–V semiconductors,17,20,27,44–49 and other LiNbO3 platforms50–54 and summarize the results in Fig. 4. The high efficiency of our LiNbO3 metasurface supporting guided-mode resonance may result from the large intrinsic second-order nonlinear coefficient of LiNbO3 as well as the high Q-factor of the metasurface with fine fabrication process control and is comparable to some III–V semiconductor metasurfaces which have a larger second-order susceptibility.
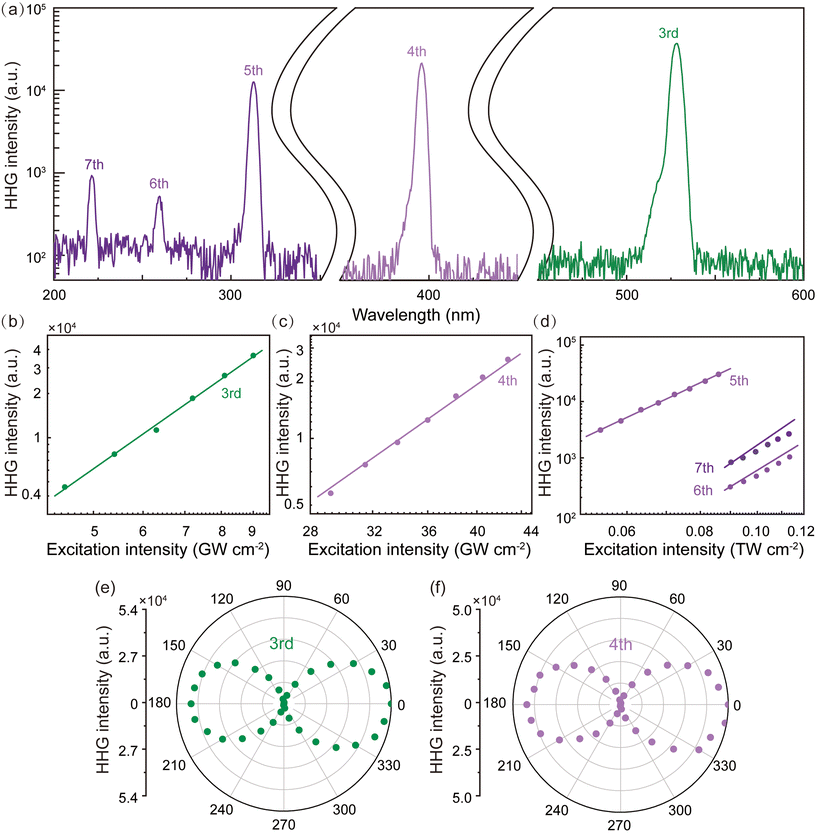
Subsequently, we measured the higher-order nonlinear optical responses of the metasurface. As shown in Fig. 5a, harmonic signals from the 3rd to 7th order are observed when pumping the metasurface at a resonant wavelength of 1580 nm. Due to the non-centrosymmetric crystal structure of LiNbO3, both even- and odd-order harmonics have been observed. Fig. 5b–d show the dependence of the nth harmonic intensity on the excitation intensity. The harmonic intensity of the 3rd–5th order as (IFHpeak)3,4,5, respectively, which indicates that the harmonic generations are in the perturbative regime. As the pump power increases further, the intensity of the 6th and 7th harmonics reaches the non-perturbative regime, which indicates that the strength of the laser field approaches the atomic bonding strength of the material.55 We finally characterized the polarization states of the output even- and odd-order harmonics respectively when pumping with a TE-polarized beam at the resonant wavelength. As shown in Fig. 5e and f, both the 3rd and 4th harmonics have good linear polarizations with the same direction as the pump light which illustrates the dominant role of the nonlinear optical tensor d33.
Conclusions and discussion
Here, we experimentally demonstrate that using a LiNbO3 metasurface supporting guided-mode resonance, one can achieve a normalized SHG conversion efficiency as high as 5.1 × 10−5 cm2 GW−1 and HHG up to the 7th order, with the shortened wavelength down to 226 nm. Unlike bulk crystals that rely on the long propagation distance, nonlinear harmonic generation in LiNbO3 metasurfaces with guided-mode resonance is not restricted by the phase-matching conditions. The LiNbO3 metasurface is transparent over a wide spectral range, and thus may allow broadband THz generation,56–58 SPDC,59 and coherent supercontinuum white-light generation down to the DUV region. Furthermore, the metasurface may be tailored to have spatially varying amplitudes and phase responses at a subwavelength resolution,60,61 thus enabling wavefront control for nonlinear harmonics of the LiNbO3 metasurface.62Methods
Numerical simulations
The simulation of the transmittance spectrum and electric field distribution of the metasurface is carried out using Lumerical FDTD. The periodic boundary conditions along the y-direction and PML boundary conditions along the x-direction are used. The light source which is a linearly polarized plane-wave pulse along the z-axis is normally incident from the substrate side. A field and power monitor is placed on the air side to calculate the transmittance. The photonic band structure of the metasurface for TE polarization is also calculated using Lumerical FDTD with Bloch boundary conditions along the y-direction and PML boundary conditions along the x-direction. A dipole cloud of 10 randomly positioned electric dipole sources is placed in each unit cell to excite the eigenmodes of TE polarization. An analysis group of 20 randomly positioned time monitors is used to calculate the band structure for an in-plane wave vector ranging from 0 to 0.1.Sample fabrication
To utilize the largest second-order susceptibility of LiNbO3, an x-cut LNOI wafer is used whose crystallographic optical axis (z-axis) is located within the film plane. The fabrication of our device starts from an LNOI chip with a 600-nm-thick LiNbO3 thin film, a 2-μm-thick SiO2 buffer layer, and a 500-μm-thick quartz substrate. To fabricate the metasurface in the LiNbO3 layer, a 150-nm-thick nichrome (NiCr) mask is first defined by EBL, thermal evaporation, and standard lift-off processes. The mask patterns are then transferred to the LiNbO3 layer by standard RIE with argon (Ar+)-based plasma. Finally, the residue of the NiCr mask is removed to reveal the metasurface array. The fabricated structure has a rib height of 240 nm, an unetched slab height of 360 nm, and a sidewall angle of ∼45°. The entire footprint of each metasurface array is 200 × 200 μm2.Optical characterization
For the measurement of the linear transmittance spectrum, white light emitted from a tungsten lamp is used as the light source. A linear polarizer and a half-wave plate are used to control the polarization of the incident light. Two pairs of diaphragms and lenses are used to achieve Köhler illumination conditions for the metasurface. The transmitted light is collected by an infrared objective (Mitutoyo, 50×, 0.42 NA) and then coupled to a camera-based grating spectrometer (Andor Kymera 328i and DU490A) through a multimode fiber.For the nonlinear harmonic generation measurement, the excitation laser beam with a 290 fs pulse duration and a 75 kHz repetition rate is generated by an optical parametric amplifier (Light Conversion Orpheus-ONE-HP) pumped by a Yb: KGW laser amplifier (Light Conversion Pharos). A linear polarizer and a half-wave plate are used to adjust the polarization of the pump laser. The laser is focused onto the sample with a spot radius of 18 μm, using a lens with a focal length of 50 mm. The generated high-harmonic signals are collected by a high numerical aperture aspheric lens with an NA of 0.69 and further spatially dispersed by a CaF2 prism (Thorlabs, PS863). The harmonic signals are finally coupled into a visible-UV grating spectrometer (Ideaoptics, PG2000-pro) for spectrum analysis through a multimode fiber.
Author contributions
Yuanmu Yang proposed the project. Yun Zhao designed the sample and performed the simulation. Zhaoxi Chen fabricated the metasurface and Yun Zhao carried out the optical characterization. Yun Zhao and Yuanmu Yang prepared the manuscript. Cheng Wang, Yuanmu Yang, and Hong-Bo Sun supervised the research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the National Natural Science Foundation of China (NSFC) (61975251 and 62135008) and the Research Grants Council, University Grants Committee (CityU 11204820).References
- T. Sugita, K. Mizuuchi, Y. Kitaoka and K. Yamamoto, Opt. Lett., 1999, 24, 1590–1592 CrossRef CAS PubMed.
- N. Uesugi and T. Kimura, Appl. Phys. Lett., 2008, 29, 572–574 CrossRef.
- D. Hofmann, G. Schreiber, C. Haase, H. Herrmann, W. Grundkötter, R. Ricken and W. Sohler, Opt. Lett., 1999, 24, 896–898 CrossRef CAS PubMed.
- W. Sohler and H. Suche, Appl. Phys. Lett., 2008, 37, 255–257 CrossRef.
- S. Tanzilli, W. Tittel, H. De Riedmatten, H. Zbinden, P. Baldi, M. DeMicheli, D. B. Ostrowsky and N. Gisin, Eur. Phys. J. D, 2002, 18, 155–160 CAS.
- H. G. de Chatellus, A. V. Sergienko, B. E. A. Saleh, M. C. Teich and G. D. Giuseppe, Opt. Express, 2006, 14, 10060–10072 CrossRef PubMed.
- R. Normandin and G. I. Stegeman, Opt. Lett., 1979, 4, 58–59 CrossRef CAS PubMed.
- Y. He, Q.-F. Yang, J. Ling, R. Luo, H. Liang, M. Li, B. Shen, H. Wang, K. Vahala and Q. Lin, Optica, 2019, 6, 1138–1144 CrossRef CAS.
- C. Wang, M. Zhang, M. Yu, R. Zhu, H. Hu and M. Loncar, Nat. Commun., 2019, 10, 978 CrossRef PubMed.
- R. W. Boyd, Nonlinear optics, Academic press, 2020 Search PubMed.
- B.-Q. Chen, C. Zhang, C.-Y. Hu, R.-J. Liu and Z.-Y. Li, Phys. Rev. Lett., 2015, 115, 083902 CrossRef PubMed.
- B. Chen, L. Hong, C. Hu and Z. Li, Research, 2021, 2021, 1539730 CAS.
- M. Li, L. Hong and Z.-Y. Li, Research, 2022, 2022, 9871729 CAS.
- P. Rabiei, J. Ma, S. Khan, J. Chiles and S. Fathpour, Opt. Express, 2013, 21, 25573–25581 CrossRef PubMed.
- G. Li, S. Zhang and T. Zentgraf, Nat. Rev. Mater., 2017, 2, 17010 CrossRef CAS.
- M. R. Shcherbakov, D. N. Neshev, B. Hopkins, A. S. Shorokhov, I. Staude, E. V. Melik-Gaykazyan, M. Decker, A. A. Ezhov, A. E. Miroshnichenko, I. Brener, A. A. Fedyanin and Y. S. Kivshar, Nano Lett., 2014, 14, 6488–6492 CrossRef CAS PubMed.
- S. Liu, M. B. Sinclair, S. Saravi, G. A. Keeler, Y. Yang, J. Reno, G. M. Peake, F. Setzpfandt, I. Staude, T. Pertsch and I. Brener, Nano Lett., 2016, 16, 5426 CrossRef CAS PubMed.
- H. Jiang, Y. Cai and Z. Han, J. Opt. Soc. Am. B, 2020, 37, 3146–3151 CrossRef CAS.
- Y. Yang, W. Wang, A. Boulesbaa, I. I. Kravchenko, D. P. Briggs, A. Puretzky, D. Geohegan and J. Valentine, Nano Lett., 2015, 15, 7388–7393 CrossRef CAS PubMed.
- P. P. Vabishchevich, S. Liu, M. B. Sinclair, G. A. Keeler, G. M. Peake and I. Brener, ACS Photonics, 2018, 5, 1685 CrossRef CAS.
- G. Grinblat, Y. Li, M. P. Nielsen, R. F. Oulton and S. A. Maier, ACS Photonics, 2017, 4, 2144–2149 CrossRef CAS.
- M. Semmlinger, M. Zhang, M. L. Tseng, T.-T. Huang, J. Yang, D. P. Tsai, P. Nordlander and N. J. Halas, Nano Lett., 2019, 19, 8972–8978 CrossRef CAS PubMed.
- K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov and Y. Kivshar, Phys. Rev. Lett., 2018, 121, 193903 CrossRef PubMed.
- Z. Liu, Y. Xu, Y. Lin, J. Xiang, T. Feng, Q. Cao, J. Li, S. Lan and J. Liu, Phys. Rev. Lett., 2019, 123, 253901 CrossRef CAS PubMed.
- K. Koshelev, Y. Tang, K. Li, D. Y. Choi, G. Li and Y. Kivshar, ACS Photonics, 2019, 6, 1639 CrossRef CAS.
- A. P. Anthur, H. Zhang, R. Paniagua-Dominguez, D. A. Kalashnikov, S. T. Ha, T. W. W. Maß, A. I. Kuznetsov and L. Krivitsky, Nano Lett., 2020, 20, 8745–8751 CrossRef CAS PubMed.
- K. Koshelev, S. Kruk, E. Melik-Gaykazyan, J.-H. Choi, A. Bogdanov, H.-G. Park and Y. Kivshar, Science, 2020, 367, 288–292 CrossRef CAS PubMed.
- S. Fan and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 235112 CrossRef.
- X. Gao, C. W. Hsu, B. Zhen, X. Lin, J. D. Joannopoulos, M. Soljačić and H. Chen, Sci. Rep., 2016, 6, 31908 CrossRef CAS PubMed.
- J. Jin, X. Yin, L. Ni, M. Soljačić, B. Zhen and C. Peng, Nature, 2019, 574, 501–504 CrossRef CAS PubMed.
- H. Liu, C. Guo, G. Vampa, J. L. Zhang, T. Sarmiento, M. Xiao, P. H. Bucksbaum, J. Vučković, S. Fan and D. A. Reis, Nat. Phys., 2018, 14, 1006 Search PubMed.
- G. Zograf, K. Koshelev, A. Zalogina, V. Korolev, R. Hollinger, D.-Y. Choi, M. Zuerch, C. Spielmann, B. Luther-Davies, D. Kartashov, S. V. Makarov, S. S. Kruk and Y. Kivshar, ACS Photonics, 2022, 9, 567–574 Search PubMed.
- M. R. Shcherbakov, H. Zhang, M. Tripepi, G. Sartorello, N. Talisa, A. AlShafey, Z. Fan, J. Twardowski, L. A. Krivitsky, A. I. Kuznetsov, E. Chowdhury and G. Shvets, Nat. Commun., 2021, 12, 4185 Search PubMed.
- Y. Yang, J. Lu, A. Manjavacas, T. S. Luk, H. Liu, K. Kelley, J.-P. Maria, E. L. Runnerstrom, M. B. Sinclair, S. Ghimire and I. Brener, Nat. Phys., 2019, 15, 1022–1026 Search PubMed.
- C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos and M. Soljačić, Nat. Rev. Mater., 2016, 1, 16048 Search PubMed.
- P. Vabishchevich and Y. Kivshar, Photonics Res., 2023, 11, B50–B64 Search PubMed.
- C. Gigli, G. Marino, A. Borne, P. Lalanne and G. Leo, Front. Phys., 2019, 7, 221 Search PubMed.
- D. Rocco, R. C. Morales, L. Xu, A. Zilli, V. Vinel, M. Finazzi, M. Celebrano, G. Leo, M. Rahmani, C. Jagadish, H. Tan, D. Neshev and C. De Angelis, Adv. Phys.: X, 2022, 7, 2022992 Search PubMed.
- T. Liu, S. Xiao, B. Li, M. Gu, H. Luan and X. Fang, Front. Nanotechnol., 2022, 4, 891892 Search PubMed.
- G. Grinblat, ACS Photonics, 2021, 8, 3406–3432 Search PubMed.
- K. Koshelev and Y. Kivshar, ACS Photonics, 2021, 8, 102–112 Search PubMed.
- C. Fang, Q. Yang, Q. Yuan, L. Gu, X. Gan, Y. Shao, Y. Liu, G. Han and Y. Hao, Laser Photonics Rev., 2022, 16, 2100498 Search PubMed.
- Y. Zhao, W. Jia, X.-J. Wang, Y. Dong, H.-H. Fang, Y. Yang and H.-B. Sun, Adv. Photonics Res., 2022, 3, 2200157 Search PubMed.
- A. P. Anthur, H. Zhang, R. Paniagua-Dominguez, D. A. Kalashnikov, S. T. Ha, T. W. W. Maß, A. I. Kuznetsov and L. Krivitsky, Nano Lett., 2020, 20, 8745 CrossRef CAS PubMed.
- S. Liu, P. P. Vabishchevich, A. Vaskin, J. L. Reno, G. A. Keeler, M. B. Sinclair, I. Staude and I. Brener, Nat. Commun., 2018, 9, 2507 CrossRef PubMed.
- L. Xu, G. Saerens, M. Timofeeva, D. A. Smirnova, I. Volkovskaya, M. Lysevych, R. Camacho-Morales, M. Cai, K. Z. Kamali, L. Huang, F. Karouta, H. H. Tan, C. Jagadish, A. E. Miroshnichenko, R. Grange, D. N. Neshev and M. Rahmani, ACS Nano, 2020, 14, 1379–1389 CrossRef CAS PubMed.
- R. Camacho-Morales, M. Rahmani, S. Kruk, L. Wang, L. Xu, D. A. Smirnova, A. S. Solntsev, A. Miroshnichenko, H. H. Tan, F. Karouta, S. Naureen, K. Vora, L. Carletti, C. De Angelis, C. Jagadish, Y. S. Kivshar and D. N. Neshev, Nano Lett., 2016, 16, 7191–7197 CrossRef CAS PubMed.
- V. F. Gili, L. Carletti, A. Locatelli, D. Rocco, M. Finazzi, L. Ghirardini, I. Favero, C. Gomez, A. Lemaître, M. Celebrano, C. De Angelis and G. Leo, Opt. Express, 2016, 24, 15965–15971 CrossRef CAS PubMed.
- S. S. Kruk, R. Camacho-Morales, L. Xu, M. Rahmani, D. A. Smirnova, L. Wang, H. H. Tan, C. Jagadish, D. N. Neshev and Y. S. Kivshar, Nano Lett., 2017, 17, 3914–3918 CrossRef CAS PubMed.
- Z. Huang, K. Luo, Z. Feng, Z. Zhang, Y. Li, W. Qiu, H. Guan, Y. Xu, X. Li and H. Lu, Sci. China: Phys., Mech. Astron., 2022, 65, 104211 CAS.
- L. Qu, L. Bai, C. Jin, Q. Liu, W. Wu, B. Gao, J. Li, W. Cai, M. Ren and J. Xu, Nano Lett., 2022, 22, 9652–9657 CrossRef CAS PubMed.
- A. Fedotova, M. Younesi, J. Sautter, A. Vaskin, F. J. F. Löchner, M. Steinert, R. Geiss, T. Pertsch, I. Staude and F. Setzpfandt, Nano Lett., 2020, 20, 8608 CrossRef CAS PubMed.
- J. Ma, F. Xie, W. Chen, J. Chen, W. Wu, W. Liu, Y. Chen, W. Cai, M. Ren and J. Xu, Laser Photonics Rev., 2021, 15, 2000521 CrossRef CAS.
- S. Yuan, Y. Wu, Z. Dang, C. Zeng, X. Qi, G. Guo, X. Ren and J. Xia, Phys. Rev. Lett., 2021, 127, 153901 CrossRef CAS PubMed.
- S. Ghimire and D. A. Reis, Nat. Phys., 2019, 15, 10–16 Search PubMed.
- L. Luo, I. Chatzakis, J. Wang, F. B. P. Niesler, M. Wegener, T. Koschny and C. M. Soukoulis, Nat. Commun., 2014, 5, 3055 Search PubMed.
- S. Keren-Zur, M. Tal, S. Fleischer, D. M. Mittleman and T. Ellenbogen, Nat. Commun., 2019, 10, 1778 Search PubMed.
- Y. Tu, X. Sun, H. Wu, X. Zan, Y. Yang, N. Liu, X. Wang, C. Meng, Z. Lyu, Z. Zhu, K. Liu, D. Zhang and Z. Zhao, Front. Phys., 2022, 10, 883703 Search PubMed.
- G. Marino, A. S. Solntsev, L. Xu, V. F. Gili, L. Carletti, A. N. Poddubny, M. Rahmani, D. A. Smirnova, H. Chen, A. Lemaître, G. Zhang, A. V. Zayats, C. De Angelis, G. Leo, A. A. Sukhorukov and D. N. Neshev, Optica, 2019, 6, 1416–1422 Search PubMed.
- L. Huang, X. Chen, H. Mühlenbernd, G. Li, B. Bai, Q. Tan, G. Jin, T. Zentgraf and S. Zhang, Nano Lett., 2012, 12, 5750–5755 CrossRef CAS PubMed.
- G. Li, S. Chen, N. Pholchai, B. Reineke, P. W. H. Wong, E. Y. B. Pun, K. W. Cheah, T. Zentgraf and S. Zhang, Nat. Mater., 2015, 14, 607–612 CrossRef CAS PubMed.
- M. Sivis, M. Taucer, G. Vampa, K. Johnston, A. Staudte, A. Y. Naumov, D. M. Villeneuve, C. Ropers and P. B. Corkum, Science, 2017, 357, 303–306 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |