Open Access Article
Open Access ArticleMolecular design of a highly matched and bonded interface achieves enhanced thermal boundary conductance†
Shuting
Wang
,
LinLin
Ren
,
Meng
Han
,
Wei
Zhou
 ,
Chunyu
Wong
,
Chunyu
Wong
 ,
Xue
Bai
,
Rong
Sun
,
Xue
Bai
,
Rong
Sun
 and
Xiaoliang
Zeng
and
Xiaoliang
Zeng
 *
*
Shenzhen Institute of Advanced Electronic Materials, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China. E-mail: xl.zeng@siat.ac.cn
First published on 20th March 2023
Abstract
Interfacial binding and phonon mismatch are two crucial parameters in determining thermal boundary conductance. However, it is difficult for polymer/metal interfaces to possess both significant interfacial binding and weak phonon mismatch to achieve enhanced thermal boundary conductance. Herein, we circumvent this inherent trade-off by synthesizing a polyurethane and thioctic acid (PU-TA) copolymer with multiple hydrogen bonds and dynamic disulfide bonds. Using PU-TA/aluminum (Al) as a model interface, we demonstrate that the thermal boundary conductance of the PU-TA/Al interfaces measured by transient thermoreflectance is 2–5 times higher than that of traditional polymer/Al interfaces, which is attributed to the highly matched and bonded interface. Furthermore, a correlation analysis is developed, which demonstrates that interfacial binding has a greater impact than phonon mismatch on thermal boundary conductance at a highly matched interface. This work provides a systematic understanding of the relative contributions of the two dominant mechanisms to thermal boundary conductance by tailoring the polymer structure, which has applications in thermal management materials.
Introduction
Efficient thermal management has become highly sought-after with the rapid development of high-performance integrated devices in the information age.1 When devices come to the length scale of the mean free path of an energy carrier, thermal boundary conductance (TBC) has a preferential influence on thermal management over the intrinsic thermal conductivity of materials.2 A desirable TBC in organic/metal or organic/inorganic interfaces may have a cross-correlation with the interfacial solid bond strength and weak phonon vibrational mismatch of materials.3 Composites consisting of polymers and metals are one type of typical thermal management materials such as polydimethylsiloxane (PDMS)/metal and epoxy resin (EP)/metal. However, exhibiting a highly matched and bonded polymer/metal interface is tough. Previous work has demonstrated that although the PDMS/metal interface has a weak phonon mismatch,4 weak interfacial binding5 leads to low TBC.6 By contrast, EP/metal has excellent interfacial binding, but substantial phonon mismatch still results in low TBC, as the phonon vibration of EP is mainly distributed at the intermediate-frequency (35–65 THz) and high-frequency modes (65–100 THz), while the phonon vibration of metal is mainly distributed at low-frequency modes (0–35 THz).7Material scientists have proposed a collection of strategies to improve the TBC of organic/metal or organic/inorganic interfaces.8 For example, surface treatment based on covalent bonding has been employed to modify the interfacial bond strength.9–12 Introducing a self-assembled monolayer can insert an intermediate layer to enhance the TBC.13–15 Bionic engineering combined with thermal management has also increasingly attracted a significant amount of interest.16,17 Two typical mechanisms, including enhancing interfacial binding or bridging the vibration mismatch at the interface in the above strategies, have been recognized as the main contributions to TBC optimization in organic/metal or organic/inorganic interface. However, there are few reports on optimizing the interfacial binding and phonon mismatch simultaneously to achieve enhanced TBC in polymer/metal interfaces. The relative contribution of the two mechanisms to TBC in polymer/metal interfaces remains unclear. Furthermore, a linear regression that unifies interfacial binding and phonon mismatch on TBC in the polymer/metal interface, which would further guide promotion of heat transport at the interface is highly desirable yet continues to pose a challenge.
In this paper, we intend to synthesize a copolymer of polyurethane and thioctic acid (PU-TA) containing multiple hydrogen bonds and dynamic disulfide bonds. Three different polymer/aluminum (Al) interfaces were selected as mode systems including PDMS/Al, EP/Al, and PU-TA/Al. The shear adhesion and overlap ratio of the phonon vibrational spectra were characterized to represent the strength of interfacial binding and phonon mismatch, respectively. We found that multiple hydrogen bonds at the PU-TA/Al interface enhanced interfacial binding and dynamic disulfide bonds in the monomers of PU-TA resulted in a well matched interface. Consequently, transient thermoreflectance (TDTR) measurements showed the highest TBC for the PU-TA/Al interface among the three types of polymer/Al interfaces. A correlation analysis was further established to explore the relationships between interfacial binding, phonon mismatch, and TBC, and the results demonstrated that interfacial binding had a greater impact than phonon mismatch on the TBC at a highly matched interface. Our work systematically elucidated the mechanisms affecting TBC and provided directions for enhancing TBC from the aspect of molecular design.
Results and discussion
Synthesis and characterization
The copolymer was designed and synthesized via a nucleophilic rearrangement reaction (Fig. 1a). PU-TA copolymers with different cross-linking densities were synthesized by varying the feed ratio of adipic dihydrazide-isophorone diisocyanate (AD-NCO) and thioctic acid (TA) in a range from 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 500
1 to 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
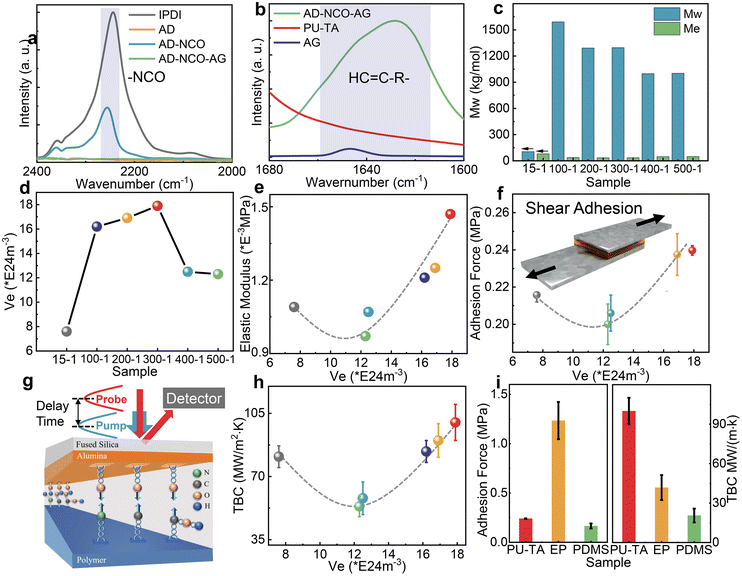
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the samples were denoted as PU-TA@15-1, PU-TA@100-1, PU-TA@200-1, PU-TA@300-1, PU-TA@400-1, and PU-TA@500-1 (see details in the Materials and synthesis section of the ESI†). The hard segments of the PU-TA copolymers comprise multiple acylsemicarbazide (ASCZ) and urethane moieties with abundant H-bond donors and acceptors. ASCZ moieties were formed via the reaction between the hydrazide groups of adipic dihydrazide and the NCO groups of isophorone diisocyanate (IPDI). The soft segments of the PU-TA copolymers comprise regularly arranged carboxyl groups formed by ring-opening polymerization in a solvent-free melting state (Fig. S1, ESI†). Compared with those synthesized from the commonly used diol or diamine chain extenders, the resultant PU-TA copolymers possess abundant numbers of H-bonding sites (Fig. 1b and c). A typical thermal interface was constructed by spin-coating the PU-TA copolymers on the Al substrate (Fig. 1d). H-bonding interactions would be hence formed between the hydroxyl groups on the surface of the Al layer and the ASCZ, the urethane moieties, and the carboxyl groups in the PU-TA copolymers (Fig. 1e). The interfacial bonding force between the PU-TA copolymers and Al changes by varying the cross-linking densities of the PU-TA copolymers, hence realizing the regulation of the interface bonding force.
1, and the samples were denoted as PU-TA@15-1, PU-TA@100-1, PU-TA@200-1, PU-TA@300-1, PU-TA@400-1, and PU-TA@500-1 (see details in the Materials and synthesis section of the ESI†). The hard segments of the PU-TA copolymers comprise multiple acylsemicarbazide (ASCZ) and urethane moieties with abundant H-bond donors and acceptors. ASCZ moieties were formed via the reaction between the hydrazide groups of adipic dihydrazide and the NCO groups of isophorone diisocyanate (IPDI). The soft segments of the PU-TA copolymers comprise regularly arranged carboxyl groups formed by ring-opening polymerization in a solvent-free melting state (Fig. S1, ESI†). Compared with those synthesized from the commonly used diol or diamine chain extenders, the resultant PU-TA copolymers possess abundant numbers of H-bonding sites (Fig. 1b and c). A typical thermal interface was constructed by spin-coating the PU-TA copolymers on the Al substrate (Fig. 1d). H-bonding interactions would be hence formed between the hydroxyl groups on the surface of the Al layer and the ASCZ, the urethane moieties, and the carboxyl groups in the PU-TA copolymers (Fig. 1e). The interfacial bonding force between the PU-TA copolymers and Al changes by varying the cross-linking densities of the PU-TA copolymers, hence realizing the regulation of the interface bonding force.
Fourier transform infrared spectrometer (FTIR) spectra were used to determine whether the chemical reaction had taken place completely. The asymmetric stretching vibration peak of –NCO at 2280 and 2260 cm−1 was observed in the raw materials IPDI and AD-NCO,18 yet disappeared in adipic dihydrazide-isophorone diisocyanate-allyl glycol (AD-NCO-AG) indicating that IPDI had reacted (Fig. 2a and Fig. S2a†). The peaks in the range from 1620 to 1680 cm−1 were the stretching vibration peaks of the carbon–carbon double bond, and they were observed in AD-NCO-AG, finally disappearing in the PU-TA copolymers, indicating that AD-NCO-AG completely reacted (Fig. 2b and Fig. S2b†).19 Rheology was used to determine the platform modulus of a series of PU-TA copolymers (see details in the Experimental methods and Fig. S3†). The molecular weight between cross-linking points (Me) and cross-linking density (Ve) was derived from the platform modulus (see details in the Experimental methods).20,21 As the molar ratio of TA and AD-NCO-AG gradually increased, the Me of the PU-TA copolymers decreased to a minimum at PU-TA@200-1 and then gradually increased (Fig. 2c). The weight-average molecular weight (Mw) of the PU-TA copolymers was investigated via gel permeation chromatography (GPC). The lowest one was PU-TA@15-1, and its weight-average molecular weight reached 104.71 kg mol−1. In comparison, the value of the others was kept within the range from 1000 to 1600 kg mol−1 (Fig. 2c). The PU-TA copolymers exhibited different Ve values with the different feed molar ratios of TA and AD-NCO-AG (Fig. 2d). The structure characterization not only deepens the understanding of polymer configuration, but also provides a basis for the subsequent study of structure–activity relationships including bonding force, thermal boundary conductance, and phonon matching.
Adhesion properties
Depending on the way an adhesion joint is stressed, the adhesion strength can be measured by a variety of different methods, and the shear adhesion test is one of the typical methods. The shear adhesion was measured by the lap shear test (see details in the Experimental methods). The surface energy of six different samples of the Al layer was in the range of 25.0 to 26.6 mJ m−2, which is a highly similar value excluding the influence of the hydroxyl concentration at the Al layers on adhesion (Tables S1 and S2†). The high consistency of roughness of the PU-TA copolymers with various Ve values at the interface excludes the influence of this factor on the test of TBC, and the Al layer being prepared in the same batch by the physical vapor deposition equipment ensures the consistency of roughness as well (Fig. S4 and Table S3†). For the PU-TA copolymers with different Ve values, the concentration of ASCZ, urethane moieties, and carboxyl groups in the polymer that can generate hydrogen bonds with the Al interface is different, and thus the strength of the hydrogen bond interaction force at the interface varies as well. Besides the strength of the interfacial bonding force, the Young's modulus of the PU-TA copolymers also plays a significant role in shear adhesion (Fig. S5† and Fig. 2e).22 The shear adhesion strength first decreased and then rose in the range from 0.2 to 0.24 MPa at different Ve values, and the maximal adhesion strength was achieved at the Ve of 17.9 × 1024 m−3 in the sample PU-TA@300-1 (Fig. 2f).Thermal boundary conductance
Thermal boundary conductance was further measured using time-domain thermoreflectance (TDTR) and the sample configuration is shown in Fig. 2g. Two types of materials including silicon with high thermal conductivity and fused silica with low thermal conductivity were tested to verify the accuracy of the TDTR (Fig. S7a and b†). The thermal conductivities of the PU-TA copolymers with various Ve values range between 0.12 W m−1 K−1 and 0.27 W m−1 K−1. The TBC of the PU-TA copolymers was obtained by fitting the phase signals of TDTR (see details in the Experimental methods; Fig. S6, S8, S9, S10; and Table S4†). The main error in fitting TBC came from the uncertainties in the thicknesses of the Al layer, and their values were 7.2% to 25.6% (Fig. S11†). As shown in Fig. 2h, the TBC of PU-TA decreases from 81.0 MW m−2 K−1 to 57.9 MW m−2 K−1 when the Ve rises from 7.6 × 1024 m−3 to 12.3 × 1024 m−3 and then increases to 99.9 MW m−2 K−1 when the Ve rises from 12.2 × 1024 m−3 to 17.9 × 1024 m−3. Among the three types of materials including PU-TA, PDMS, and EP, PDMS has the weakest adhesion properties corresponding to the lowest TBC with Al (20.5 MW m−2 K−1). The adhesion properties of EP were the strongest, while its TBC is 41.8 MW m−2 K−1 which is lower than that of the PU-TA copolymers with Al (99.9 MW m−2 K−1) (Fig. 2i). However, the PU-TA copolymers with medium adhesion forces exhibited the highest TBC among the three types of polymers. This may be attributed to the effect of phonon mismatch on the TBC. Hence, phonon transport at the interface needs to be further investigated.Phonon mismatch
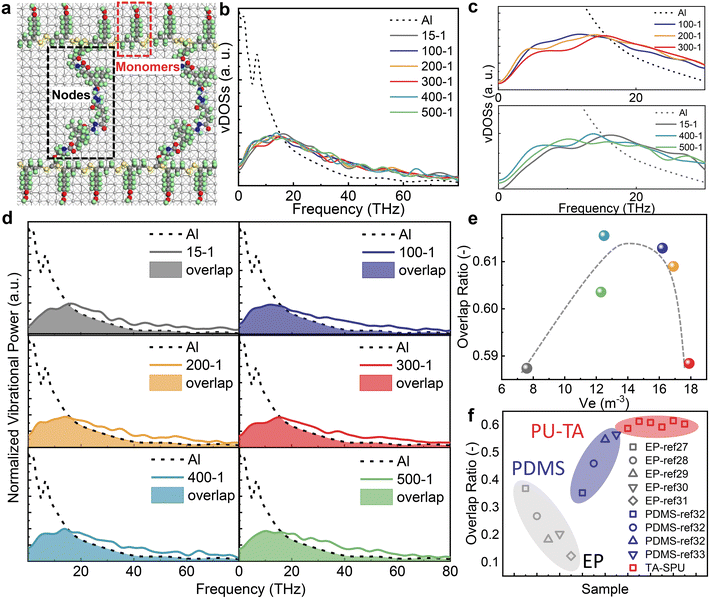
To reveal the role of phonon transport in TBC, molecular dynamics (MD) simulations of the PU-TA/Al system were performed (see details in the Simulation section in Theoretical methods). Theoretical models were obtained by scaling down the Mw and Me of the PU-TA copolymers and keeping their density consistent with the experimental value (1.26 g ml−1), and then placed on Al to form a thermal interfacial model. Chemical crosslinks were defined as nodes, and repeating units on the chain between crosslinks were labeled as monomers (Fig. 3a). The corresponding numbers of nodes and monomers and a schematic diagram of sample PU-TA@400-1 as an example are shown in Table S5 and Fig. S13.† We calculated the lattice vibrational spectrum (vDOS) of Al and the PU-TA copolymers with distinct Ve values (see the parameters used in MD in Table S6†). The vDOS of Al showed two sharp peaks at 3 and 7 THz corresponding to longitudinal and transversal vibrations respectively (Fig. 3b), which is consistent with previous reports.23,24 The vDOS of the PU-TA copolymers showed a principal peak at approximately 19 THz and distributed over a wide frequency range from 0 to 60 THz.From PU-TA@100-1 to PU-TA@300-1, the phonon vibrational frequency shifted toward higher wavenumbers. For PA-TA@400-1 and PU-TA@500-1, phonon vibrational frequency shifted toward higher wavenumbers while nodes remained the same and nodes ascended from 7 to 8. Phonon matching at the interface is a leading contributor to TBC and it is generally believed that that a stronger mismatch in the phonon vibrational distributions will result in lower TBC and less efficient energy transfer on the interface between materials.25,26 The degree of phonon matching for Al and the PU-TA copolymers was quantitatively assessed by their overlap ratio (Fig. 3d; see details in the Simulation section in Theoretical methods). The overlap ratio from the perspective of the PU-TA copolymers configuration indicated that increases in Ve firstly benefited phonon matching and then caused phonon mismatch (Fig. 3e). The phonon vibrational spectra of EP27–31 and PDMS32,33 in the literature were normalized and employed to calculate the overlap ratio with that of Al (Fig. 3f). As the polymer increases from a single chain to bulk crystalline configuration, its vDOS shifts to higher frequencies and its phonon overlap with Al decreases. The result indicated that EP has a substantial phonon mismatch with Al while PU-TA is relatively highly matched with Al. The harmonic oscillator spring model can explain this. Compared with PDMS and EP, a large proportion of sulfur atoms in PU-TA results in a heavier atomic mass than in PDMS and EP. What is more, dynamic disulfide bonds in the PU-TA monomers are weaker than the covalent bonds in PDMS and EP. Therefore, the low frequencies of the PU-TA copolymers can be attributed to both a heavier inter-atomic mass and a weaker effective force constant of the whole PU-TA copolymers than that of PDMS and EP. Hence, the TBC of PU-TA/Al is higher than that of EP/Al even though its binding properties are better than that of PU-TA/Al.
Correlation analysis
Furthermore, using mathematical language, we developed a linear fit to describe the relationship of the TBC (see more details in the theoretical analysis in Theoretical methods). Linear regressions between the adhesion force and overlap ratio (R12) and the TBC and overlap ratio (R22) both show a weak relevance (Fig. 4a and b), however linear fitting between TBC and adhesion force (R32) exhibits a strong relevance (Fig. 4c). In Fig. 4b, a counterintuitive result was obtained that a stronger phonon mismatch results in a higher TBC. The adjusted R-square (R2) in Fig. 4d shows a more visual indication of the same trends. The value of R12, R22, and R32 are in the order of −0.194, 0.00177, and 0.900, indicating a weak to strong correlation between the two different factors. This indicated that the negative effect on TBC caused by the phonon mismatch was offset by the positive effect caused by adhesion forces. Correlation analysis also demonstrates that the interfacial binding has a greater impact than the phonon mismatch on the TBC at a highly matched interface, and this conclusion is consistent with that of others reported previously.34,35 Such a phenomenon appears in the system when the overall phonon mismatch is low, i.e., the overlap ratio in the PU-TA/Al interface ranges from 0.58 to 0.62 which is a relatively high value. Highly mismatched interfaces in previous literature reports showed the opposite behavior. By controlling the SAM structure for metal/diamond systems, a weak phonon mismatch is more critical in determining the TBC and can offset the negative effect of the low adhesion force.36 This linear regression thus shows that interfacial binding has a higher impact than phonon mismatch on the TBC at a highly matched interface.Conclusions
In summary, we succeeded in synthesizing a series of PU-TA copolymers containing multiple hydrogen bonds and dynamic disulfide bonds. Owing to their highly matched and bonded interfaces, the TBC of the PU-TA/Al interfaces showed a remarkable increase 2–5 times higher than that of traditional polymers/Al interfaces. Using mathematical language, we developed a correlation analysis to describe the relationship among the TBC values. In the correlation analysis, TBC showed a higher correlation with adhesion than with phonon mismatch at the PU-TA/metal interfaces. The results enable us to give vital practical advice when optimizing thermal transport in polymer/metal composites. For polymers exhibiting low phonon vibrational frequencies because of their heavy inter-atomic mass and weak effective force constants, regulation of adhesion force under the binding effect has a greater impact than phonon mismatch under the bridge effect on enhancing the TBC. From the perspective of molecular design, the polymer's modulus can be adjusted to optimize the interfacial binding and further enhance the TBC of the polymers/Al interface bonded by hydrogen bonds. This study put forward an exhaustive model for strengthening heat transport at polymers/metal interfaces and is suitable for a wide range of applications at highly matched interfaces.Experimental and theoretical section
Synthesis
(1) Synthesis of the PU-TA elastomers: the PU-TA polymers were synthesized in four steps. In the first step, a nucleophilic substitution reaction occurred between adipic dihydrazide (AD) and isophorone diisocyanate (IPDI) to obtain adipic dihydrazide-isophorone diisocyanate (AD-NCO). Next, a nucleophilic substitution reaction occurred again between AD-NCO and allyl glycol (AG) to produce adipic dihydrazide-isophorone diisocyanate-allyl glycol (AD-NCO-AG). In the third step, thioctic acid (TA) was heated at a high temperature and a ring-opening reaction occurred to obtain poly (TA). Finally, an additional reaction occurred between poly (TA) and AD-NCO-AG to produce PU-TA. When the theoretical molar ratio of TA and AD-NCO-AG was 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, PU-TA was denoted as PU-TA@500-1. The naming method of PU-TA@400-1, PU-TA@300-1, PU-TA@200-1, PU-TA@100-1, and PU-TA@15-1 was the same as the method above (see details in the Materials and synthesis of the ESI†).
1, PU-TA was denoted as PU-TA@500-1. The naming method of PU-TA@400-1, PU-TA@300-1, PU-TA@200-1, PU-TA@100-1, and PU-TA@15-1 was the same as the method above (see details in the Materials and synthesis of the ESI†).
(2) Synthesis of the PU-TA thermal interface: physical vapor deposition (PVD) technology was employed to deposit the Al layer on the surface of the quartz glass surface. Polymethyl methacrylate (PMMA) ether solution was used to form a protective layer on the surface of the Al layer to prevent metal oxidation. PMMA can be removed by acetone before the next use. PU-TA was spin-coated at the Al layer to obtain the PU-TA/Al interface (see details in the Synthesis section of the ESI†).
(3) Synthesis of the PDMS/Al and EP/Al: a Sylgard™ 184 silicone elastomer kit was spin-coated on the Al layer to obtain the PDMS/Al interface. EP was synthesized by mixing CYD-128, methylhexahydrophthalic anhydride, and N-dimethylacetamide, and then spin-coated on the Al layer to form the EP/Al interface.
Experimental methods
(1) Material characterization: Fourier transform infrared spectroscopy (FTIR) was recorded using an Invenio R (BRUKER OPTICS) spectrometer. Permeation chromatography (GPC) was tested using Waters 1515. Rheology was carried out by Anton Paar MCR 302. Wu et al. proposed that the storage modulus (G′) corresponding to the frequency of the minimum loss factor (tan(δ)) was the plateau modulus (G0Nexp) (eqn (1)).37,38 The entangled molecular weight (Me) was derived from the platform modulus in the pipeline model shown in eqn (2). Permanent cross-linking density (Ve) was calculated from the platform modulus in eqn (3). In the equation, kB and T are the Boltzmann constant (1.38 × 10–23 J K−1) and the absolute temperature (297.15 K), respectively. R is the molar gas constant (8.314 J mol−1 K−1) and ρ is the density of PU-TA (1.26 × 103 kg m−3).G0Nexp = G′(ω)tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ→min δ→min | (1) |
 | (2) |
 | (3) |
(2) Mechanical properties: the Young's modulus was obtained from the stress–strain curves tested by AGX-10Knvd (Fig. S5†). The stretch rate was 10 mm min−1. The ratio of stress to strain within 10% strain was denoted as the Young's modulus (see the inset in Fig. S5†). Shear adhesion tests were performed on the PU-TA samples and Al surface using DAGE STELLAR 4000 with a conospherical diamond tip. PU-TA with different Ve values in the molten state was placed directly on top of the Al surface. Then, another Al surface was put on top, held together for 1 min and dried at 80 °C for 12 hours; then the shear adhesion was measured. The tip was brought into contact with the sample at a rate of 100 μm s−1 until it reached a prescribed indentation depth: 300 μm. In order to exclude the influence of roughness on the measurement of shear adhesion and thermal boundary conductance, the roughness of the PU-TA and Al surface were characterized by Keyence VK-X1100 and Thermo Fisher Scientific Apreo 2 SEM. The results are shown in Table S3 and Fig. S4.† The arithmetic mean height (Sa), maximum height (Sz), aspect ratio of surface features (Str), arithmetic mean curvature of peak apex (Spc), and interface expansion area ratio (Sdr) are listed in Table S3† in sequence. The Al layer in Fig. S4† possessed a thickness of 46 ± 1 nm.
(3) Surface energy of Al layers: the surface energy of the Al layers was determined using the method developed by van Oss et al.39 When three probe liquids (liquid 2) including diiodomethane, ethylene glycol, and water form a contact angle θ on the surface of the Al layers (γAl) in air, the interfacial energies of the probe liquids (γ2) are related by the Young's equation:
 | (4) |
| γ = γLW + γAB | (5) |
 | (6) |
According to the van Oss method, the surface energy (γ) is comprised of two terms that consider the contributions from Lifshitz-van der Waals (γLW) and Lewis acid–base (γAB) interactions. The Lewis acid–base (γAB) component of the surface energy comprises the electron-acceptor (γ−) and electron-donor (γ+) interactions. By measuring the contact angle of the three probe liquids and using the above equations, we can calculate the surface energy of six different samples of the Al layer. The results are shown in Tables S1 and S2.†
(4) Time-domain thermoreflectance: thermal boundary conductance was further measured using time-domain thermoreflectance (TDTR) through the reflectance change with temperature. In order to verify the accuracy of the TDTR, we tested two materials including silicon with high thermal conductivity and fused silica with low thermal conductivity, respectively. In Fig. S7a,† by fitting the amplitude signal, the thermal conductivity of silicon was calculated as 139.10 W m−1 K−1 and the thermal boundary conductance of Si/Al was calculated as ∼105.20 MW m−2 K−1. This value is consistent with the results of Stevens.40 In Fig. S7b,† by fitting the phase signal, the thermal conductivity of fused silica was calculated as 1.30 W m−1 K−1 and the thermal boundary conductance of fused silica/Al was calculated as 59.50 MW m−2 K−1. This value is consistent with the results of Hopkins41 and can also be used as a known parameter in the following experiments. In summary, for the sample with high thermal conductivity, both amplitude and phase signals can be used for fitting calculations. But for the samples with low thermal conductivity, the phase signal is much better than the amplitude signal, and it will be commonly used for fitting calculations.
The sample configuration is shown schematically, in which the Al layer was deposited on a carefully cleaned fused silica substrate using physical vapor deposition and subsequently PU-TA was spin-coated at the Al layer. Fused silica not only acted as a support material for an extremely thin Al layer of approximately 46 nm but also its low thermal conductivity (1.30 W m−1 K−1) can force the heat generated at the Al layer to flow to the polymer side, hence improving the measurement sensitivity of TBC. The Al layer was employed as a transducer and a thermometer considering its high thermal response in pump–probe measurements. The TDTR measurement data were fitted using a multilayer thermal conduction model.42 To calculate the thermal boundary conductance of Al/PU-TA, the thickness, thermal conductivity, and heat capacity for all materials and TBC of fused silica/Al in the system must be known. The thickness of PU-TA was set as −1 in the multilayer thermal conduction model representing the semi-infinite thickness of substrate. The thickness of the fused silica and Al layer were 200 μm and 46 nm, respectively. The heat capacity of Al and fused silica were taken from literature values. The heat capacity of PU-TA was tested by differential scanning calorimetry (DSC) using TA Instruments DSC2500. The thermal conductivity of Al and fused silica were 237.00 W m−1 K−1 and 1.30 W m−1 K−1 according to the literature.43 The thermal conductivities of the PU-TA copolymers, PDMS, and EP were measured on an LW-9389, according to the ASTMD5470 standard. The samples for tests were square in shape with an initial length of 25.4 mm and a width of 25.4 mm. The tests were performed at 80 °C with an initial pressure of 10 psi (Fig. S8†). All these modeling parameters are summarized in Table S4.† In Fig. S8,† the thermal conductivity of PU-TA@300-1 is the lowest among all the samples. From PU-TA@15-1 to PU-TA@500-1, the content of chemical cross-linker decreases and the chemical cross-linking density also reduces. However, the Ve increases from PU-TA@15-1 to PU-TA@300-1 and then decreases from PU-TA@300-1 to PU-TA@500-1. The trapped entanglement density is defined as the difference between the Ve and chemical cross-linking density. Hence, we can infer that PU-TA@300-1 exbibits the largest trapped entanglements. The trapped entanglements can dramatically reduce the thermal conductivity for two reasons. On the one hand, chain–chain spacing and configuration disorder will inhibit the heat transfer between chains. On the other hand, phonon transport trapped entanglement is a typical defect that can scatter phonons significantly. What is more, thermal boundary conductance of fused silica/Al was recorded as 59.50 MW m−2 K−1. All these values were known in TDTR data analysis, only the TBC of polymers/Al was an unknown parameter. The TBC of PU-TA/Al, PDMS/Al, and EP/Al were fitted via phase signals using the multilayer thermal conduction model (Fig. S9 and 10†). Each sample was measured at three different locations.
We provided the sensitivity affected by the thermal properties and thickness of the constituent materials (Fig. S11†). The following factors were analyzed: the thermal conductivity of Al (Fig. S11a†), thermal conductivity of fused silica (SiO2) (Fig. S11b†), thermal conductivity of PU-TA (Fig. S11c†), thermal capacity of SiO2 (Fig. S11d†), thermal capacity of the Al layer (Fig. S11e†), the thickness of the Al layer (Fig. S11f†), thickness of SiO2 (Fig. S11g†), thermal boundary conductance of Al/SiO2 (Fig. S11h†), and the thermal boundary conductance of Al/PU-TA (Fig. S11i†). The largest errors of the extracted thermal boundary conductance were from the thickness of Al layer. However, the minimum sensitivity of the extracted thermal boundary conductance (value equals 0) was achieved at the thickness of SiO2 in Fig. S12.† This indicates that the thickness of SiO2 has no effect on the TBC in the PU-TA/Al/SiO2 system.
Theoretical methods
(1) Molecular dynamics simulation: All MD simulations in the present study were performed using a large-scale atomic/molecular massively parallel simulator (LAMMPS) package.44 The density of PU-TA was determined by the fully automatic true density analyzer UltraPYC 1200e and its value was 1.26 g ml−1. The density of the polymer in MD was kept the same as the experimental value. An ideal PU-TA polymer model was built by scaling down the weight-average molecular weight (Mw) and entanglement molecular weight (Me). Nodes and monomers in PU-TA with different Ve values are listed in Table S5.† Taking PU-TA@400-1 as an example, the schematic diagram of the PU-TA model is shown in Fig. S13.† The CVFF force field was employed to describe interatomic interactions between polymers.45 For aluminum, an embedded atom model (EAM) potential of Zhakhovskii was used, which is a good approximation that accounts for both a pair-wise interaction and a contribution of the electron charge density from the nearest neighbors of an atom under consideration.46,47 In addition, the geometric mixing rule was applied to describe the van der Waals (VdW) interactions between the alumina and the polymers, and the detailed parameters are shown in Table S6.† The initial structures we constructed were minimized using the conjugate gradient algorithm, followed by the relaxation in NVT at 300 K for 10 ns. The timestep size was set to be 0.1 fs in equilibration and subsequent production runs. When the total energy reached equilibrium, the NVE ensemble was applied to the system for the calculation of the phonon vibration.(2) The overlap of vDOS: The phonon transport across two interface materials can be obtained by the overlap of the vDOS between them. To analyze the mechanism of the Al and polymers, the lattice vibrational spectrum (vDOS) can be calculated via a Fourier transform of the atomic velocity autocorrelation function (VACF) of atoms at the equilibrium state (eqn (7)),48 where ω, D(ω), τ and Γ(t) are the angular frequency, vibration density of states at frequency ω, the total time and the velocity autocorrelation function of atoms, respectively, and it is given in eqn (8), where v(t) is the atom velocity at time t and v(0) denotes the time and atom number-averaged velocity autocorrelation function. The overlap ratio (R) was defined as the ratio of the overlap area between the phonon vibrational spectrum of Al and PU-TA (SAl/PU-TA) and the area of the phonon vibrational spectrum of Al (SAl) (eqn (9)).
 | (7) |
| Γ(t) = 〈v(t)v(0)〉 | (8) |
 | (9) |
Author contributions
Xiaoliang Zeng: conceptualization (lead); investigation (lead); project administration (equal); resources (equal); supervision (equal); writing – review & editing (equal). Shuting Wang: methodology (lead); formal analysis (lead); writing – original draft (lead). LinLin Ren: conceptualization (equal); formal analysis (equal); writing – review & editing (equal). Meng Han: methodology (equal); writing – review & editing (equal). Wei Zhou: conceptualization (equal); methodology (equal); writing – review & editing (equal). Zhenyu Wang: methodology (equal). Xue Bai: methodology (equal). Rong Sun: project administration (equal); resources (equal); supervision (equal).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 52073300 and 62104161), Guangdong Province Key Field R&D Program Project (No. 2020B010190004), Guangdong Basic and Applied Basic Research Funding (No. 2019A1515110845), Youth Innovation Promotion Association of the Chinese Academy of Sciences (2019354), Shenzhen Science and Technology Research Funding (No. JCYJ20200109114401708), and the Key Project of Science and Technology of Changsha (kq2102005).References
- A. L. Moore and L. Shi, Mater. Today, 2014, 17, 163–174 CrossRef CAS.
- B. Gotsmann and M. A. Lantz, Nat. Mater., 2013, 12, 59–65 CrossRef CAS PubMed.
- X. Qian, J. Zhou and G. Chen, Nat. Mater., 2021, 20, 1188–1202 CrossRef CAS PubMed.
- T. Luo, K. Esfarjani, J. Shiomi, A. Henry and G. Chen, J. Appl. Phys., 2011, 109, 074321 CrossRef.
- X. Z. Niu, S. L. Peng, L. Y. Liu, W. J. Wen and P. Sheng, Adv. Mater., 2007, 19, 2682–2686 CrossRef CAS.
- S. Jasmee, G. Omar, S. S. C. Othaman, N. A. Masripan and H. A. Hamid, Polym. Compos., 2021, 1–24 Search PubMed.
- F. F. T. Araujo and H. M. Rosenberg, J. Phys. D: Appl. Phys., 1976, 9, 665 CrossRef.
- J. Chen, X. Xu, J. Zhou and B. Li, Rev. Mod. Phys., 2022, 94, 025002 CrossRef CAS.
- S. Kaur, N. Raravikar, B. A. Helms, R. Prasher and D. F. Ogletree, Nat. Commun., 2014, 5, 3082 CrossRef PubMed.
- P. Yasaei, Z. Hemmat, C. J. Foss, S. J. Li, L. Hong, A. Behranginia, L. Majidi, R. F. Klie, M. W. Barsoum, Z. Aksamija and A. Salehi-Khojin, Adv. Mater., 2018, 30, 1801629 CrossRef PubMed.
- Z. Liu, J. Li and X. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 6503–6515 CrossRef CAS PubMed.
- C. Guo, Y. Li, J. Xu, Q. Zhang, K. Wu and Q. Fu, Mater. Horiz., 2022, 9, 1690–1699 RSC.
- P. J. O′Brien, S. Shenogin, J. Liu, P. K. Chow, D. Laurencin, P. H. Mutin, M. Yamaguchi, P. Keblinski and G. Ramanath, Nat. Mater., 2013, 12, 118–122 CrossRef PubMed.
- M. D. Losego, M. E. Grady, N. R. Sottos, D. G. Cahill and P. V. Braun, Nat. Mater., 2012, 11, 502–506 CrossRef CAS PubMed.
- Y. Zhang, T. Liang, Z. Ye, S. Gao, M. Han, X. Zeng and P. Zhang, Compos. Sci. Technol., 2022, 229, 109690 CrossRef CAS.
- M. Jiang, Q. Shen, J. Zhang, S. An, S. Ma, P. Tao, C. Song, B. Fu, J. Wang, T. Deng and W. Shang, Adv. Funct. Mater., 2020, 30, 1910481 CrossRef CAS.
- P. Xue, Y. Chen, Y. Xu, C. Valenzuela, X. Zhang, H. K. Bisoyi, X. Yang, L. Wang, X. Xu and Q. Li, Nano-Micro Lett., 2023, 15, 1 CrossRef CAS PubMed.
- Y. Yao, B. Liu, Z. Xu, J. Yang and W. Liu, Mater. Horiz., 2021, 8, 2742–2749 RSC.
- L. D. S. Yadav, in Organic Spectroscopy, ed. L. D. S. Yadav, Springer Netherlands, Dordrecht, 2005, pp. 52–106, DOI:10.1007/978-1-4020-2575-4.
- M. Doi and S. F. Edwards, J. Chem. Soc., Faraday Trans. 2, 1979, 75, 38–54 RSC.
- K. Cui, Y. N. Ye, T. L. Sun, C. Yu, X. Li, T. Kurokawa and J. P. Gong, Macromolecules, 2020, 53, 5116–5126 CrossRef CAS.
- M. A. Rahman, C. Bowland, S. Ge, S. R. Acharya, S. Kim, V. R. Cooper, X. C. Chen, S. Irle, A. P. Sokolov, A. Savara and T. Saito, Sci. Adv., 2021, 7, eabk2451 CrossRef CAS PubMed.
- G. G. Rusina, S. V. Eremeev, S. D. Borisova, I. Y. Sklyadneva, P. M. Echenique and E. V. Chulkov, J. Phys.: Condens. Matter, 2007, 19, 266005 CrossRef CAS PubMed.
- D. V. Minakov, P. R. Levashov and V. B. Fokin, Comput. Mater. Sci., 2017, 127, 42–47 CrossRef CAS.
- H. Peer-Mohammadi, A. Rajabpour and M. Khanaki, Comput. Mater. Sci., 2018, 149, 348–353 CrossRef CAS.
- K. Wu, J. Wang, D. Liu, C. Lei, D. Liu, W. Lei and Q. Fu, Adv. Mater., 2020, 32, 1906939 CrossRef CAS PubMed.
- M. Li, H. Zhou, Y. Zhang, Y. Liao and H. Zhou, Carbon, 2018, 130, 295–303 CrossRef CAS.
- X. Shen, Z. Wang, Y. Wu, X. Liu and J.-K. Kim, Carbon, 2016, 108, 412–422 CrossRef CAS.
- J. Zeng, J. Li, P. Yuan and P. Zhang, Macromol. Res., 2018, 26, 978–983 CrossRef CAS.
- F. M. Bellussi, C. Sáenz Ezquerro, M. Laspalas and A. Chiminelli, Nanomaterials, 2021, 11(7), 1709 CrossRef CAS PubMed.
- Z. Liu, X. Sun, J. Xie, X. Zhang and J. Li, Int. J. Heat Mass Transfer, 2022, 195, 123031 CrossRef CAS.
- T. Luo, K. Esfarjani, J. Shiomi, A. Henry and G. Chen, J. Appl. Phys., 2011, 109, 074321 CrossRef.
- W. Xu and X. Liang, Chin. Phys. Lett., 2020, 37, 046601 CrossRef CAS.
- M. Jeong, J. P. Freedman, H. J. Liang, C. Chow, V. M. Sokalski, J. A. Bain and J. A. Malen, Phys. Rev. Appl., 2016, 5, 014009 CrossRef.
- J. C. Duda, C. P. Yang, B. M. Foley, R. Cheaito, D. L. Medlin, R. E. Jones and P. E. Hopkins, Appl. Phys. Lett., 2013, 102, 081902 CrossRef.
- B. Xu, S. Hu, S.-W. Hung, C. Shao, H. Chandra, F.-R. Chen, T. Kodama and J. Shiomi, Sci. Adv., 2021, 7, eabf8197 CrossRef CAS PubMed.
- S. Wu, J. Polym. Sci., Part B: Polym. Phys., 1989, 27, 723–741 CrossRef CAS.
- S. Wu and R. Beckerbauer, Polymer, 1992, 33, 509–515 CrossRef CAS.
- C. J. van Oss, M. K. Chaudhury and R. J. Good, Adv. Colloid Interface Sci., 1987, 28, 35–64 CrossRef CAS PubMed.
- R. J. Stevens, A. N. Smith and P. M. Norris, J. Heat Transfer, 2005, 127, 315–322 CrossRef CAS.
- P. E. Hopkins, B. Kaehr, L. M. Phinney, T. P. Koehler, A. M. Grillet, D. Dunphy, F. Garcia and C. J. Brinker, J. Heat Transfer, 2011, 133, 061601 CrossRef.
- J. Zhu, D. Tang, W. Wang, J. Liu, K. W. Holub and R. Yang, J. Appl. Phys., 2010, 108, 094315 CrossRef.
- C. P. Dillon, Chem. Eng., 2015, 109, 10–12 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Proteins: Struct., Funct., Bioinf., 1988, 4, 31–47 CrossRef CAS PubMed.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443–6453 CrossRef CAS.
- N. A. Inogamov, V. V. Zhakhovskii, S. I. Ashitkov, V. A. Khokhlov, Y. V. Petrov, P. S. Komarov, M. B. Agranat, S. I. Anisimov and K. Nishihara, Appl. Surf. Sci., 2009, 255, 9712–9716 CrossRef CAS.
- L. T. Kong, Comput. Phys. Commun., 2011, 182, 2201–2207 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr00627a |
| This journal is © The Royal Society of Chemistry 2023 |