Open Access Article
Open Access ArticleBacterial lipids drive compartmentalization on the nanoscale†
Antonio
De Nicola
 ag,
Costanza
Montis
*b,
Greta
Donati‡
c,
Antonio
Molinaro
*d,
Alba
Silipo
ag,
Costanza
Montis
*b,
Greta
Donati‡
c,
Antonio
Molinaro
*d,
Alba
Silipo
 d,
Arianna
Balestri
b,
Debora
Berti
d,
Arianna
Balestri
b,
Debora
Berti
 b,
Flaviana
Di Lorenzo
d,
You-Liang
Zhu
b,
Flaviana
Di Lorenzo
d,
You-Liang
Zhu
 e and
Giuseppe
Milano
*f
e and
Giuseppe
Milano
*f
aScuola Superiore Meridionale, Via Largo San Marcellino 10, 80132 Napoli, Italy
bDipartimento di Chimica “Ugo Schiff”, Università degli Studi di Firenze and CSGI, 50019 Firenze, Italy. E-mail: costanza.montis@unifi.it
cDepartment of Chemistry and Biology, University of Salerno, Via Giovanni Paolo II 132, 84084 Fisciano, SA, Italy
dDepartment of Chemical Sciences, University of Napoli Federico II, Complesso Universitario Monte Santangelo, Via Cintia 4, 80126 Napoli, Italy. E-mail: antonio.molinaro@unina.it
eState Key Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun 130021, China
fUniversity of Naples Federico II, Department of Chemical, Materials and Production Engineering, Piazzale V. Tecchio, 80, 80125 Napoli, Italy. E-mail: giuseppe.milano@unina.it
gGraduate School of Organic Materials Science, Yamagata, University, Jonan 4-3-16, Yonezawa, Yamagata, 992-8510, Japan
First published on 24th April 2023
Abstract
The design of cellular functions in synthetic systems, inspired by the internal partitioning of living cells, is a constantly growing research field that is paving the way to a large number of new remarkable applications. Several hierarchies of internal compartments like polymersomes, liposomes, and membranes are used to control the transport, release, and chemistry of encapsulated species. However, the experimental characterization and the comprehension of glycolipid mesostructures are far from being fully addressed. Lipid A is indeed a glycolipid and the endotoxic part of Gram-negative bacterial lipopolysaccharide; it is the moiety that is recognized by the eukaryotic receptors giving rise to the modulation of innate immunity. Herein we propose, for the first time, a combined approach based on hybrid Particle-Field (hPF) Molecular Dynamics (MD) simulations and Small Angle X-Ray Scattering (SAXS) experiments to gain a molecular picture of the complex supramolecular structures of lipopolysaccharide (LPS) and lipid A at low hydration levels. The mutual support of data from simulations and experiments allowed the unprecedented discovery of the presence of a nano-compartmentalized phase composed of liposomes of variable size and shape which can be used in synthetic biological applications.
Introduction
The study and characterization of the supramolecular structure of bacterial lipids is a complex and challenging area of research. The last two decades have witnessed the real blossoming of the study of the structural and supramolecular properties of bacterial glycolipids, many of which play key roles in bacterial interactions with eukaryotes, in which they either elicit or suppress the innate immunity of the host.1,2 Much effort has been made to implement cellular functions in synthetic systems using a ‘bottom-up’ approach based on synthetic biology.3,4 Inspired by the internal partitioning of living cells, several multi-compartment systems using bottom-up assemblies have been proposed. In particular, the varied hierarchies of these internal compartments have been explored by employing different types of interfaces, including liposomes, polymersomes, protein capsules, emulsions, and membranes.5–7 The creation of compartments using different building blocks is paving the way towards new and challenging applications, such as highly functional systems that can regulate the chemistry of encapsulated reactant species.5,8–11 An exhaustive disentanglement of self-assembled structures and the ability to compartmentalize and control them are pivotal to the development of suitable building blocks for bottom-up synthesis of living organisms.3,4From the simulation point of view, these systems give rise to multiple challenges because accurate descriptions of the complex ensembles of interactions involved in the self-assembly processes at the molecular level are required.12 Moreover, if the assembling molecules are charged, the long-range nature of their electrostatic interactions poses further challenges.13,14
Given these facts, detailed knowledge of the nature and nanostructure of supramolecular assemblies will need to be based on studies combining both experiments and simulations for mutual validation and support. Indeed, using this approach, successful results have already been obtained for the slaved diffusion and lateral phase separation of charged lipids induced by cationic nanoparticles, as characterized by length scales ranging from nanometres to microns via the combination of several experimental techniques (confocal microscopy, fluorescence correlation spectroscopy, X-ray reflectivity) and coarse-grained molecular dynamics (CG-MD) simulations.15 Electrostatic co-assembly of nanoparticles with different small molecules of opposing charges into interesting supramolecular structures has been studied by combining CG-MD simulations with several experimental techniques.16 Moreover, combining X-ray/neutron scattering studies with CG-MD simulations of sodium dodecyl sulfate (SDS) nanostructures over a broad range of concentrations and ionic strengths has led to a detailed understanding of the effect of long-range electrostatic interactions on the morphology of charged supramolecular assemblies.17 Different types of CG models have been developed for both charged and uncharged biological phospholipids.18–23 A comprehensive overview of this subject area can be gained by referring to a number of recent reviews.24–32 A largely explored example of this CG approach, applied to several lamellar lipid phases and able to model cell membranes, is the Martini model developed by Marrink et al.33,34 Using this approach, some attention has been devoted to low-hydration phases, as characterized by reverse micelles of dipalmitoylphosphatidylcholine (DPPC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC).35–37 Van Oosten38 and Khalid39–41 introduced CG models for the outer membrane of Gram-negative bacteria using the Martini representation. Similarly, Nangia42 used an analogous representation to model lipid A bilayers from different bacteria. More recently, Ayappa and co-workers developed a CG model of peptidoglycan.43 A recent CG model parametrized to reproduce reference results for bilayers and able to show non-lamellar phases of lipid A from Pseudomonas aeruginosa (Pseudomonas) and IV-A at low levels of hydration has been described by two of us.44
In this study, we report novel nano-compartmentalized supramolecular structures obtained by self-assembly of lipid A bilayers at low levels of hydration. Lipid A bilayers are ubiquitous constituents of Gram-negative bacterial outer membranes. The first experimental studies of the phase behaviour of lipid A date back to the 1990s: Brandenburg and co-workers made several efforts to disentangle the phase diagram of lipid A derived from different sources and under different experimental conditions.45,46 By employing the pioneering small-angle X-ray scattering (SAXS) experiments, they discovered that the phase diagram of lipid A is particularly rich and is characterized by the presence of lamellar and non-lamellar phases with different symmetries and arrangements.45,46 The complexity of supramolecular self-assembled structures, coupled with the limits of available techniques, strongly limited the formulation of more robust and comprehensive hypotheses regarding the aggregate morphologies, such as the hypothesized presence, at low levels of hydration, of coexisting lamellar and non-lamellar phases. Thanks to a combination of hybrid particle-field (hPF) MD simulation47,48 and SAXS, we herein report a detailed description of the morphology of lipid A assemblies from Escherichia coli (E. coli) and Pseudomonas under low-hydration conditions, which have unveiled new, ordered, and previously unrecognized nano-compartmentalized supramolecular structures.
Methods
hybrid Particle-Field (hPF) simulation method
This section serves as a brief introduction to the hPF approach. The main advantage of the hPF method is the huge reduction in the computational cost for the calculation of non-bonding interactions, which is the most expensive part of a standard MD simulation. This is possible because the non-bonded pair interactions are replaced by the evaluation of forces between a single molecule in an external potential field. In fact, the main feature of the hPF method is the derivation of the partition function of a single molecule in an external field and the obtaining of a suitable expression for the external potential Vk(ri) and its spatial derivatives. A complete derivation of Vk(ri) starting from the partition function is given in ref. 49. It can be demonstrated that the density-dependent external potential can be written as: | (1) |
 | (2) |
Then, the force acting on particle A at position r is:
 | (3) |
Bridging the particle and field models is necessary to obtain a smooth coarse grained density function directly from the particle positions. To this aim, a mesh-based approach able to give the density derivatives needed for the force calculation is used. Further details about the derivation of eqn (2) and the implementation of the hPF approach are reported in ref. 49–52. Details about the OCCAM code used to perform all the hPF simulations in this work are reported in ref. 50.
Electrostatic interaction treatments in the hPF approach
The electrostatic interactions between charged particles are evaluated through an electric field E – the field that depends on the spatially inhomogeneous distributions of charge densities.51,53 The E-field can be represented by dividing the simulation box (L1, L2, L3) into N1 × N2 × N3 cells (Nα = number of cells in the direction Lα for α = 1, 2, 3). The location of lattice points is given by l = l1L1/N1, l2L2/N2, l3L3/N3, where lα is an integer number 0 ≤ lα ≤ Nα.The total Coulomb energy can be written as:
 | (4) |
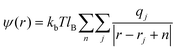 | (5) |
The outer sum over n is a sum, with periodic boundary conditions, over the vectors n – n1L1 + n2L2 + n3L3.  is the Bjerrum length and e is the elementary charge. The terms ε0 and εr are the vacuum permittivity and the relative dielectric constant of the medium. The ψ(r) can be split into two contributions, long and short ranges by using the Ewald summation:
is the Bjerrum length and e is the elementary charge. The terms ε0 and εr are the vacuum permittivity and the relative dielectric constant of the medium. The ψ(r) can be split into two contributions, long and short ranges by using the Ewald summation:
 | (6) |
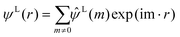 | (7) |
The term 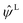 on the right hand of eqn (7) is the long-range contribution of the electrostatic potential in the reciprocal space. Considering the Gaussian distribution of charge density, it is possible to solve the Poisson's equation in the reciprocal space and to obtain
on the right hand of eqn (7) is the long-range contribution of the electrostatic potential in the reciprocal space. Considering the Gaussian distribution of charge density, it is possible to solve the Poisson's equation in the reciprocal space and to obtain 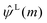 :
:
 | (8) |
The long-range contribution of the electrostatic potential at the lattice point of the special position (l) can be written, by using the discrete Fourier transform (DFT), in the following way:
 | (9) |
In the spirit of the hPF approach where only mean field parameters are applicable, the short-range electrostatic interactions (usually considered as pairwise interactions in standard MD) can be evaluated in the following way. Using the Flory–Huggins approach for the lattice model, it is possible to evaluate the χe parameter for the short-range part of electrostatic interactions:
 | (10) |
| ψS(l) = χeQ(l1, l2, l3)kBT | (11) |
hPF coarse-grained (CG) lipid-A models
The models of lipid A used here are based on a recent CG model44 validated to reproduce, against an all-atom reference model, the lamellar phase of a mixture of lipid A and water. Particularly, the area per lipid, membrane thickness and mass density profiles, which are fundamental properties to characterize the lamellar-like phase, are qualitatively and quantitatively reproduced by the hPF CG model. Additional details of the CG model, including the mapping scheme for both lipids A, bonded and non-bonded interaction parameters and details about sample preparation are reported in the ESI.†Computational details
hPF-MD simulations were performed using the OCCAM MD software50 modifying the more recent optimized version able to efficiently handle large-scale systems54 including the evaluation of electrostatic interactions as implemented by some of the authors in the GALAMOST code.53 A time step of 0.03 ps was used for all simulations. The NVT ensemble with a temperature T = 300 K, kept constant by using the Andersen thermostat55 with a collision frequency of 5 ps−1, was used for all systems. A constant mesh size of l = 0.57 nm was used for all simulations. The density field was updated every hundred time steps. Both the density update time and the mesh size were chosen to give a good reproduction of the reference atomistic simulations, as reported in our previous works.44,56–60 The composition of all simulated systems is reported in Table S4 of the ESI.† hPF-MD simulations started from homogeneous mixtures obtained by randomly placing all the species (lipid-A, water, and counter-ions) in the simulation box. Systems have been prepared under the experimental conditions of lipid and counterion concentrations. Divalent counterions (Ca2+) have been added to assure electroneutrality.Results and discussion
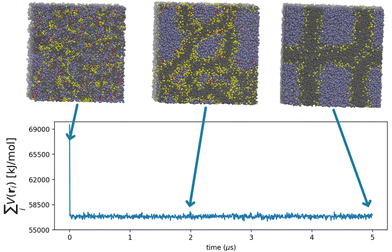
The processes governing the self-assembly of the homogeneous mixtures were simulated until equilibrium structures were reached. The equilibrium conditions were confirmed by the behaviour of the intermolecular particle-field potential, initially decreasing and then oscillating stably about a constant value, and by the formation of stable structures (Fig. 1). The equilibrated morphology of lipid A from E. coli (see the snapshots in Fig. 1) shows a stable supramolecular structure formed approximately at 5 μs with a highly organized and periodic structure.With the aim of obtaining experimental data to confirm these results, a suitable quantity of purified lipid A was required for SAXS characterization, a step that has hitherto proved to be a serious bottleneck for these kinds of studies. Therefore, we isolated and purified LPS from E. coli and Pseudomonas. Briefly, the LPS was exhaustively purified using an iterative chromatography and ultracentrifugation cycle, and afterwards, the purified lipid A was obtained by mild acid hydrolysis of the LPS, exploiting the acid lability of the linkage between the Kdo monosaccharide, the first sugar of the saccharide portion of the LPS and the glucosamine of the lipid A backbone. In this way, following centrifugation, a suitable quantity of lipid A was obtained. Further details about the LPS purification are reported in the ESI.†
The SAXS profiles of both E. coli and Pseudomonas lipid A under the same conditions as employed in the MD simulations were acquired. Sample preparation and the experimental conditions used for the measurements are reported in the ESI.† The computed and experimental SAXS profiles (see Fig. S5 in the ESI†) were comparable in the range from 0.05 Å−1 to higher values of q. In particular, the two Bragg-like peaks at ∼0.08 and ∼0.16 Å−1 were well reproduced. The intensity decay, and on the other hand, the local minimum at ∼0.05 Å−1, due to the limited system size of the simulated system (17 nm cubic box length), were absent in the calculated profile.
From these results, it can be argued that the characteristic periodicity of the 3D compartmentalized structures obtained from the simulation could be of the same order of magnitude as the periodicity of the simulation box. To overcome this limitation, large-scale systems were simulated. In particular, a double-sized box (more than 430![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 beads) was obtained for both systems (lipid A from E. coli and Pseudomonas) by replicating the system in all three directions. Long simulations were then performed, where the non-bonded particle-field potential time evolution was used to check that the equilibrium state had been reached. Thanks to the intrinsically faster dynamics of the hPF method61–66 and its computational efficiency,54,67 the equilibrium structures of lipid A were gained in approximately 6.5 × 108 MD cycles. Considering a dynamic speed-up factor of ∼5, the total simulated time corresponded to ∼0.1 ms.61 In Fig. 2, the time evolution of the self-assembly process and the equilibrium configurations reached by both lipid A systems are shown in a sequence of snapshots. Similar morphologies were found for both lipid A systems at equilibrium (Fig. 2), showing a well-defined multi-lamellar pattern for E. coli and Pseudomonas. Minor morphological differences arising from the two assemblies were essentially ascribed to defective lamellae located in regions where lamellae adhere to each other.
000 beads) was obtained for both systems (lipid A from E. coli and Pseudomonas) by replicating the system in all three directions. Long simulations were then performed, where the non-bonded particle-field potential time evolution was used to check that the equilibrium state had been reached. Thanks to the intrinsically faster dynamics of the hPF method61–66 and its computational efficiency,54,67 the equilibrium structures of lipid A were gained in approximately 6.5 × 108 MD cycles. Considering a dynamic speed-up factor of ∼5, the total simulated time corresponded to ∼0.1 ms.61 In Fig. 2, the time evolution of the self-assembly process and the equilibrium configurations reached by both lipid A systems are shown in a sequence of snapshots. Similar morphologies were found for both lipid A systems at equilibrium (Fig. 2), showing a well-defined multi-lamellar pattern for E. coli and Pseudomonas. Minor morphological differences arising from the two assemblies were essentially ascribed to defective lamellae located in regions where lamellae adhere to each other.
Fig. 3 shows the measured SAXS profiles for the two systems (circular points) compared against those calculated by averaging molecular configurations obtained from large-scale MD simulations (continuous lines, systems of 34 nm box length). The intensity (I) of the calculated profiles has been shifted to make comparison with the measured ones easier. The SAXS comparison clearly shows that E. coli and Pseudomonas possess similar patterns, in agreement with the similarities found in the morphologies obtained from the MD simulations, suggesting that the modelled systems were representative of their experimental counterparts. In the range of q values accessible to the simulations, the main features of the computed SAXS profiles reproduce the measured patterns extremely well. Particularly, from the SAXS profiles shown in Fig. 3, it can be seen that there is a similar decay of I(q) in the range of q values 0.003–0.05 Å−1 for both E. coli and Pseudomonas; this behaviour is well reproduced by the calculated profiles. Two main peaks, at q = ∼0.008 and q = ∼0.16 Å−1, characterize the E. coli and Pseudomonas meso-structures. Both peaks can be attributed to a lamellar structure of approximately 8 nm spacing (see Fig. S4 in the ESI†). This is compatible with the multiplicity of the observed structures contributing to the complex morphologies; for example, a periodicity of ∼10 nm characterizes the packing of the largest oblate vesicle in the y direction (see Fig. 4B and E). Moreover, molecular organization on the scale of 8–10 nm is compatible with the dimension of non-spherical shapes (Fig. 4B and D) or with the sizes of adjacent multiple layers (Fig. 4C and D). An additional peak at ∼0.11 Å−1 is clearly visible in the E. coli profile, while it is less evident in the case of Pseudomonas. Considering the strong asymmetry of the first structure peak arising from the convolution of two separated peaks, this signal would be considered to be a hallmark of a multiphase structure, with coexisting lamellar and non-lamellar mesophases.45 Even this fine detail is well reproduced in the simulated profile, which correctly describes the entire set of experimental SAXS curves. This highlights that MD simulations are key to structurally resolving such systems, which historically were investigated only experimentally by means of small-angle scattering methods.46 The amount of disorder in lipids A in the dense phase can be qualitatively estimated by analyzing the α exponent of a power law I(q) = qα in the MD-based SAXS profile. Particularly, we found more than a single α exponent characterizing decays of the intensity I(q) in different ranges of q. In the log–log plot of Fig. 3, q regions with different α are shown. In Table S5 of the ESI,† estimated α exponents are reported. As can be seen from the figure, larger deviation of α is found at very low q values, corresponding to the limit of q accessible by the sizes of simulated systems. However, semi-quantitative agreement of α values confirms a similar amount of disorder in lipids A at different investigated length scales. For simple systems of multi-lamellar lipid vesicles, composed of concentric lipid layers, the variation in α is related to the number of layers and their packing, as estimated from the analytical models used to calculate the SAXS profiles.68,69 In particular, as the number of layers increases and the multi-lamellar vesicles become more densely packed, the exponent α approaches −4.68 It must be stressed that those models were developed for simple systems quite different from the conditions of high lipid concentrations and low hydration levels investigated in this study. However, we found comparable α values (from −3 to −4) in the range of q values 0.003–0.05 Å−1, which were found to be rich in compact nanostructures of the order of 10–20 nm in size.
 | ||
| Fig. 4 (A) Equilibrium supramolecular structure of lipid-A including the water molecules (in light blue). Representative snapshots of E. coli (C and E) and Pseudomonas (B and D) in different orientations. Water molecules are omitted for clarity. CG beads of lipid A heads are reported in yellow and red, while the hydrophobic tails are reported in black. (F) Classification of the water aggregates confined in the compartments formed by the lipid-A condensed phase. Two views of the representative water aggregate type are reported next to the semi-axis lengths (a, b, c) and the volume (V) of the aggregate. On the panel left side, graphical representation of semi-axes is reported. The volume of each aggregate is estimated assuming an ellipsoidal shape and by using the equation V = 4/3π × a × b × c. Numbers in brackets have the meaning of standard error. Distribution of semi-axis lengths are reported in the ESI.† | ||
Looking at the equilibrium morphologies of the lipid-A phase from the hPF-MD simulations, we observe a rich collection of densely packed compartments of different shapes and sizes in which the hydrophilic heads of lipids A (in yellow) are in contact with the confined water molecules inside the cavity (Fig. 4A). We found large compartments that can have prolate or oblate shapes, both with the largest length of the order of ∼16–24 nm (see Fig. 4B–E). Quasi-spherical nanocompartments, with a diameter of ∼10 nm, fused with other adjacent ones have also been found and are shown in the snapshots of Fig. 4B–E. The stacking and dense packing of all these hydrophobic compartments are clearly visible in the lateral view of all reported snapshots in Fig. 4B–E. A way to identify and classify the different compartments is to extract geometrical information from the aggregates of water molecules confined in each of them. Once water aggregates were identified and isolated, the directions of minor, medium, and major axes of each aggregate were detected by using the principal component analysis (PCA).70 Using PCA, we calculated the three eigenvectors and the corresponding eigenvalues of the covariant matrix for the particle positions. The eigenvector with the largest eigenvalue corresponds to the basis vector of the major axis direction, while basis vectors in the minor axes are obtained from the other two remaining eigenvectors. Because we are considering only water CG beads, the axes detected from PCA correspond to the inertia axes of water aggregates. The lengths of inertia semi-axes are used as geometrical descriptors to classify the water aggregates and the corresponding hydrophilic compartments. In total, 150 different configurations taken from the last microsecond of both hPF-MD simulations (E. coli and Pseudomonas) were used to calculate the three semi-axes (a, b, and c) and the volume of the aggregate (in Fig. S6 of the ESI,† distributions of a, b, and c lengths are reported). According to the ratios between semi-axis lengths, we identified three shapes (oblate, prolate and quasi-spherical) and four sizes of the water aggregates. In Fig. 4F, representative configurations of the aggregates (P1–P4) and their geometrical characteristics are reported. As can be seen, the volume (V) of the nano-compartments ranges from about 750 to 1800 nm3. Overall, this result represents a new milestone in the physicochemical investigation of lipid-condensed mesophases. The perfect agreement between simulated and experimental data, where SAXS and simulated curves overlap in the investigated region, allows for the first time to completely reveal the organization of lipid A under low hydration conditions, which was previously unrecognized. The importance of this result is multifold: first, the correspondence between the simulated and experimental SAXS spectra provides a clear validation of the lipid A meso-structures obtained for the first time from the MD simulations, opening up new perspectives on the investigation of lipid A phase behaviour by means of computational techniques; second, it suggests that the lipid A phase under the conditions of low hydration could be characterized by richer and more complex mesophases than those hypothesized so far.45,46 Finally, it reveals a completely new arrangement of lipid A under low hydration conditions, previously unknown and/or unrecognized. This completely new, highly organized, structure opens up new perspectives for several biological strategies, such as the so-called bottom-up approach employing synthetic biology in order to implement cellular functions in synthetic systems.3,4
Conclusions
Our study has shown, for the first time, how self-assembly of glycolipids derived from bacteria under some conditions can lead to nano-compartmentalization. The compartmentalized structures were characterized by a combination of MD and SAXS studies. The proposed molecules and their self-assembled nanostructures have great potential for use as tools in synthetic biology applications for several reasons. First, these systems are derived from natural and renewable sources, and fermentation plant technologies can enable them to be prepared via suitable scale-up schemes. Second, the large degree of ‘natural’ variability among such molecules, furnished by a multitude of different microbes, makes them very flexible tools for synthetic biology.Further studies are planned, aimed at understanding, in a systematic way, the role of lipid chemical structures, the concurrent presence of synthetic or natural surfactants, and the effect of ionic strength on the resulting self-assembled nanostructures.
Author contributions
A. D. N. and G. D. built the coarse-grained model configurations. Y.-L. Z. helped with and supervised the implementation of the electrostatic force calculation in the Occam computer source code. G. M. conceived the molecular dynamics simulations and data analysis, and A. D. N. and G. D. performed them. F. D. L., A. S., and A. M. carried out the LPS purification. C. M., A. B., and D. B. carried out the X-ray characterization of the LPS. A. M., D. B., and G. M. designed the study and wrote the manuscript. All of the authors contributed to scientific discussions of the results.Conflicts of interest
There are not conflicts to declare.Acknowledgements
We would like to offer our special thanks to Prof. Zhong-Yuan Lu of the State Key Laboratory of Theoretical and Computational Chemistry, Jilin University, China for useful discussions regarding the implementation of electrostatic interactions in the Occam computer source code.G. M. and A. D. N. wish to thank the HPC team of Enea (https://www.enea.it) for use of the ENEA-GRID and HPC CRESCO facilities (https://www.cresco.enea.it) in Portici. F. D. L. acknowledges European Research Council (ERC) under the Horizon Europe program under grant agreement No 101039841 (DEBUGGING LPS).
References
- F. Di Lorenzo, K. A. Duda, R. Lanzetta, A. Silipo, C. De Castro and A. Molinaro, Chem. Rev., 2022, 122, 15767–15821 CrossRef CAS PubMed.
- C. Di Carluccio, M. C. Forgione, S. Martini, F. Berti, A. Molinaro, R. Marchetti and A. Silipo, Carbohydr. Res., 2021, 503, 108313 CrossRef CAS PubMed.
- Synthetic Biology, ed. M. Ryadnov, L. Brunsveld and H. Suga, Royal Society of Chemistry, Cambridge, 2014, vol. 1, pp. P001–P005 Search PubMed.
- Synthetic Biology, ed. M. Ryadnov, L. Brunsveld and H. Suga, Royal Society of Chemistry, Cambridge, 2017, vol. 2, pp. P001–P004 Search PubMed.
- H. R. Marsden and A. Kros, Synthetic Biology, ed. M. Ryadnov, L. Brunsveld and H. Suga, Royal Society of Chemistry, Cambridge, 2014, vol. 1, pp. 253–274 Search PubMed.
- D. E. Discher and F. Ahmed, Annu. Rev. Biomed. Eng., 2006, 8, 323–341 CrossRef CAS PubMed.
- J. U. Bowie, Nature, 2005, 438, 581–589 CrossRef CAS PubMed.
- S. Okushima, T. Nisisako, T. Torii and T. Higuchi, Langmuir, 2004, 20, 9905–9908 CrossRef CAS PubMed.
- H. C. Shum, D. Lee, I. Yoon, T. Kodger and D. A. Weitz, Langmuir, 2008, 24, 7651–7653 CrossRef CAS PubMed.
- J. A. Hanson, C. B. Chang, S. M. Graves, Z. Li, T. G. Mason and T. J. Deming, Nature, 2008, 455, 85–88 CrossRef CAS PubMed.
- I. Marzuoli, C. H. B. Cruz, C. D. Lorenz and F. Fraternali, Nanoscale, 2021, 13, 10342–10355 RSC.
- G. Milano, I. Marzuoli, C. D. Lorenz and F. Fraternali, Synthetic Biology, ed. M. Ryadnov, L. Brunsveld and H. Suga, Royal Society of Chemistry, Cambridge, 2017, vol. 2, pp. 35–64 Search PubMed.
- P. Koehl, Curr. Opin. Struct. Biol., 2006, 16, 142–151 CrossRef CAS PubMed.
- C. Sagui and T. A. Darden, Annu. Rev. Biophys. Biomol. Struct., 1999, 28, 155–179 CrossRef CAS PubMed.
- T. Pfeiffer, A. De Nicola, C. Montis, F. Carlà, N. F. A. van der Vegt, D. Berti and G. Milano, J. Phys. Chem. Lett., 2019, 10, 129–137 CrossRef CAS PubMed.
- T. Bian, A. Gardin, J. Gemen, L. Houben, C. Perego, B. Lee, N. Elad, Z. Chu, G. M. Pavan and R. Klajn, Nat. Chem., 2021, 13, 940–949 CrossRef CAS PubMed.
- K. Schäfer, H. B. Kolli, M. K. Christensen, S. L. Bore, G. Diezemann, J. Gauss, G. Milano, R. Lund and M. Cascella, Angew. Chem., Int. Ed., 2020, 59, 18591–18598 CrossRef PubMed.
- B. Różycki and R. Lipowsky, J. Chem. Phys., 2015, 142, 054101 CrossRef PubMed.
- R. Lipowsky, Advances in Biomembranes and Lipid Self-Assembly, Elsevier, 2019, vol. 30, pp. 105–157 Search PubMed.
- S. Seo and W. Shinoda, J. Chem. Theory Comput., 2019, 15, 762–774 CrossRef CAS PubMed.
- Y. Miyazaki, S. Okazaki and W. Shinoda, J. Chem. Theory Comput., 2020, 16, 782–793 CrossRef PubMed.
- W. Shinoda, R. DeVane and M. L. Klein, Soft Matter, 2008, 4, 2454 RSC.
- S. Izvekov and G. A. Voth, J. Phys. Chem. B, 2005, 109, 2469–2473 CrossRef CAS PubMed.
- M. Muller, K. Katsov and M. Schick, Phys. Rep., 2006, 434, 113–176 CrossRef.
- S. J. Marrink, A. H. de Vries and D. P. Tieleman, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 149–168 CrossRef CAS PubMed.
- G. S. Ayton and G. A. Voth, Curr. Opin. Struct. Biol., 2009, 19, 138–144 CrossRef CAS PubMed.
- M. Venturoli, M. Maddalenasperotto, M. Kranenburg and B. Smit, Phys. Rep., 2006, 437, 1–54 CrossRef CAS.
- A. P. Lyubartsev and A. L. Rabinovich, Soft Matter, 2011, 7, 25–39 RSC.
- B. Smit, P. A. J. Hilbers, K. Esselink, L. A. M. Rupert, N. M. van Os and A. G. Schlijper, Nature, 1990, 348, 624–625 CrossRef CAS.
- R. Goetz and R. Lipowsky, J. Chem. Phys., 1998, 108, 7397–7409 CrossRef CAS.
- K. V. Pinigin, Membranes, 2022, 12, 1149 CrossRef CAS PubMed.
- C. Lorenz and N. L. Doltsinis, Handbook of Computational Chemistry, ed. J. Leszczynski, A. Kaczmarek-Kedziera, T. Puzyn, M. G. Papadopoulos, H. Reis and M. K. Shukla, Springer International Publishing, Cham, 2017, pp. 337–396 Search PubMed.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef CAS.
- S. J. Marrink, L. Monticelli, M. N. Melo, R. Alessandri, D. P. Tieleman and P. C. T. Souza, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2023, 13, e1620 Search PubMed.
- M. Ceccarelli and M. Marchi, Biochimie, 1998, 80, 415–419 CrossRef CAS PubMed.
- Y. G. Smirnova, S.-J. Marrink, R. Lipowsky and V. Knecht, J. Am. Chem. Soc., 2010, 132, 6710–6718 CrossRef CAS PubMed.
- S.-J. Marrink and A. E. Mark, Biophys. J., 2004, 87, 3894–3900 CrossRef CAS PubMed.
- B. Van Oosten and T. A. Harroun, J. Mol. Graphics Modell., 2016, 63, 125–133 CrossRef CAS PubMed.
- P.-C. Hsu, D. Jefferies and S. Khalid, J. Phys. Chem. B, 2016, 120, 11170–11179 CrossRef CAS PubMed.
- D. Jefferies, P.-C. Hsu and S. Khalid, Biochemistry, 2017, 56, 1672–1679 CrossRef CAS PubMed.
- S. Khalid, C. Schroeder, P. J. Bond and A. L. Duncan, Microbiology, 2022, 168, 001165 CrossRef CAS PubMed.
- H. Ma, D. D. Cummins, N. B. Edelstein, J. Gomez, A. Khan, M. D. Llewellyn, T. Picudella, S. R. Willsey and S. Nangia, J. Chem. Theory Comput., 2017, 13, 811–824 CrossRef CAS PubMed.
- R. Vaiwala, P. Sharma, M. Puranik and K. G. Ayappa, J. Chem. Theory Comput., 2020, 16, 5369–5384 CrossRef CAS PubMed.
- A. De Nicola, T. A. Soares, D. E. S. Santos, S. L. Bore, G. J. A. Sevink, M. Cascella and G. Milano, Biochim. Biophys. Acta, Gen. Subj., 2020, 129570 Search PubMed.
- K. Brandenburg, U. Seydel, A. B. Schromm, H. Loppnow, M. H. J. Koch and E. Th. Rietschel, J. Endotoxin Res., 1996, 3, 173–178 CrossRef CAS.
- K. Brandenburg, W. Richter, M. H. J. Koch, H. W. Meyer and U. Seydel, Chem. Phys. Lipids, 1998, 91, 53–69 CrossRef CAS PubMed.
- G. Milano and T. Kawakatsu, J. Chem. Phys., 2009, 130, 214106 CrossRef PubMed.
- G. Milano and T. Kawakatsu, J. Chem. Phys., 2010, 133, 214102 CrossRef PubMed.
- G. Milano and T. Kawakatsu, J. Chem. Phys., 2009, 130, 214106 CrossRef PubMed.
- Y. Zhao, A. De Nicola, T. Kawakatsu and G. Milano, J. Comput. Chem., 2012, 33, 868–880 CrossRef CAS PubMed.
- Y.-L. Zhu, Z.-Y. Lu, G. Milano, A.-C. Shi and Z.-Y. Sun, Phys. Chem. Chem. Phys., 2016, 18, 9799–9808 RSC.
- H. B. Kolli, A. De Nicola, S. L. Bore, K. Schäfer, G. Diezemann, J. Gauss, T. Kawakatsu, Z. Lu, Y.-L. Y. Zhu, G. Milano and M. Cascella, J. Chem. Theory Comput., 2018, 14, 4928–4937 CrossRef CAS PubMed.
- Y.-L. Zhu, H. Liu, Z.-W. Li, H.-J. Qian, G. Milano and Z.-Y. Lu, J. Comput. Chem., 2013, 34, 2197–2211 CrossRef CAS PubMed.
- S. Caputo, V. Hristov, A. D. Nicola, H. Herbst, A. Pizzirusso, G. Donati, G. Munaò, A. R. Albunia and G. Milano, J. Chem. Theory Comput., 2021, 17, 1755–1770 CrossRef CAS PubMed.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- A. De Nicola, Y. Zhao, T. Kawakatsu, D. Roccatano and G. Milano, J. Chem. Theory Comput., 2011, 7, 2947–2962 CrossRef CAS PubMed.
- A. De Nicola, T. Kawakatsu and G. Milano, Macromol. Chem. Phys., 2013, 214, 1940–1950 CrossRef CAS.
- A. De Nicola, T. Kawakatsu, C. Rosano, M. Celino, M. Rocco and G. Milano, J. Chem. Theory Comput., 2015, 11, 4959–4971 CrossRef CAS PubMed.
- A. De Nicola, S. Hezaveh, Y. Zhao, T. Kawakatsu, D. Roccatano and G. Milano, Phys. Chem. Chem. Phys., 2014, 16, 5093 RSC.
- E. Sarukhanyan, A. De Nicola, D. Roccatano, T. Kawakatsu, G. Milano, A. De Nicola, D. Roccatano, T. Kawakatsu and G. Milano, Chem. Phys. Lett., 2014, 595–596, 156–166 CrossRef CAS.
- A. De Nicola, Y. Zhao, T. Kawakatsu, D. Roccatano and G. Milano, J. Chem. Theory Comput., 2011, 7, 2947–2962 CrossRef CAS PubMed.
- A. De Nicola, Y. Zhao, T. Kawakatsu, D. Roccatano and G. Milano, Theor. Chem. Acc., 2012, 131, 1167 Search PubMed.
- A. De Nicola, T. Kawakatsu, C. Rosano, M. Celino, M. Rocco and G. Milano, J. Chem. Theory Comput., 2015, 11, 4959–4971 CrossRef CAS PubMed.
- E. Sarukhanyan, A. De Nicola, D. Roccatano, T. Kawakatsu and G. Milano, Chem. Phys. Lett., 2014, 595–596, 156–166 CrossRef CAS.
- A. Pizzirusso, A. De Nicola, G. J. A. Sevink, A. Correa, M. Cascella, T. Kawakatsu, M. Rocco, Y. Zhao, M. Celino and G. Milano, Phys. Chem. Chem. Phys., 2017, 19, 29780–29794 RSC.
- W. Murakami, A. De Nicola, Y. Oya, J.-I. Takimoto, M. Celino, T. Kawakatsu and G. Milano, ACS Appl. Nano Mater., 2021, 4, 4552–4561 CrossRef CAS.
- Y. Zhao, A. De Nicola, T. Kawakatsu and G. Milano, J. Comput. Chem., 2012, 33, 868–880 CrossRef CAS PubMed.
- H. Frielinghaus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051603 CrossRef PubMed.
- F. Nallet, R. Laversanne and D. Roux, J. Phys. II France, 1993, 3, 487–502 CrossRef CAS.
- I. T. Jolliffe and J. Cadima, Philos. Trans. R. Soc., A, 2016, 374, 20150202–20150202 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Protocol for the purification of LPS, the small angle X-ray scattering method and details. Description of the CG model and additional analyses. See DOI: https://doi.org/10.1039/d3nr00559c |
| ‡ Current address: Department of Pharmacy, University of Napoli Federico II, Via Domenico Montesano 49, 80131 Napoli, Italy. |
| This journal is © The Royal Society of Chemistry 2023 |