Interfacial thermal resonance in an SiC–SiC nanogap with various atomic surface terminations

Abstract

Quasi-Casimir coupling can induce phonon heat transfer across a sub-nanometer vacuum gap between monoatomic solid walls without electromagnetic fields. However, it remains unclear how the atomic surface terminations in diatomic molecules contribute to phonon transmission across a nanogap. Herein, we study the thermal energy transport across an SiC–SiC nanogap with four pairs of atomic surface terminations using classical nonequilibrium molecular dynamics simulations. In the case of identical atomic surface terminations, the net heat flux and thermal gap conductance are much greater than those in the nonidentical cases. Thermal resonance occurs between identical atomic terminated layers, whereas it vanishes between nonidentical ones. A notable heat transfer enhancement in the identical case of C–C is due to optical phonon transmission, with thermal resonance between the C-terminated layers. Our findings deepen the understanding of phonon heat transfer across a nanogap and provide insights into thermal management in nanoscale SiC power devices.

---

Silicon carbide (SiC) has shown great potential in high-power devices because of its outstanding properties, such as high thermal conductivity, wide band gap, and high electric breakdown field.^1–5 The polytypes of SiC that are most widely employed in micro- and nanoelectronics include 3C-SiC, 4H-SiC, and 6H-SiC, of which the cubic crystallization of SiC is unique to 3C-SiC.⁶ With the increasing miniaturization and integration of electronic devices, heat dissipation is now an essential issue restricting their development. In previous investigations, 3C-SiC has been commonly utilized to study thermal energy transport at solid–solid and solid–liquid interfaces because of its relatively simple crystal structure in molecular dynamics (MD) simulations.^7–10

Nanoscale heat transfer has been the focus of much attention over the past decade.^11–16 The scale of the gap distance is dominant in the heat transfer between two separated objects at different temperatures.^17,18 Near-field heat transfer plays a crucial role in the transition regime between conventional heat conduction and thermal radiation because phonons transport thermal energy more efficiently than photons across a gap with few nanometers.^19–23 When the gap distance is smaller than Wien's wavelength (λ ≅ 10⁻⁵ m), radiative heat transfer can break the blackbody limit by orders of magnitude,^24,25 which is called near-field radiative heat transfer (NFRHT). This heat transfer phenomenon has attracted increasing interest in advanced applications of thermal rectification,^26–29 nanogap near-field thermophotovoltaics,^30–32 and thermal transistors.^33,34 Continuous efforts have been made to clarify the mechanism of NFRHT experimentally and theoretically when the gap distance is approximately 20 nm^35,36 and even down to 2 nm.^37–40 Phonons can be transmitted across a vacuum nanogap mediated by the electric field between two solids.^41–44 Furthermore, Casimir force has been found to induce phonon heat transfer across a vacuum gap owing to the quantum fluctuations in electromagnetic fields.^45–47 A generalization of Casimir force based on fluctuating electromagnetic fields has been proposed by Lifshitz for large separations, rather than molecular-scale separations, between two bodies.⁴⁸

In previous studies, quasi-Casimir heat transfer could be induced by intermolecular interactions for a molecular-scale separation between two solid walls without an electromagnetic field.¹⁷ The intermolecular force for molecular-scale separation was calculated using the Lennard-Jones potential, including the London dispersion interaction, which stems from quantum fluctuations in electron density.⁴⁹ By manipulating the gap distance between the two solid walls, the significant phonon heat transfer enhancement was confirmed to be attributed to thermal resonance between interfacial solid layers of monoatomic molecules. Additionally, thermal resonance was found to exist between adsorbed monoatomic liquid layers on a superhydrophilic solid surface induced by quasi-Casimir coupling in a nanogap;¹⁷ compared with the vacuum gap case, an enhanced thermal energy transport was achieved due to the thermal resonance between adsorbed monoatomic liquid layers.

Moreover, solid–liquid interfacial heat transfer has attracted increasing interest in nanoscale thermal management. Thermal energy transport at a solid–liquid interface can be affected by the atomic surface terminations of diatomic molecules.^7,8,50 It is well known that surface wettability is a critical factor in solid–liquid interfacial heat transfer. Using classical MD simulations, the wetting behaviour of a 3C-SiC solid surface was shown to suffer from atomic surface terminations.⁷ Crystallographic planes (100 and 111) with Si or C atomic surface termination were built to study the thermal transport across SiC–water interfaces. The Si-terminated surfaces showed a higher attraction to the liquid phase compared with C-terminated surfaces, resulting in a larger thermal boundary conductance.⁸ To understand the mechanism of solid–liquid interfacial heat transfer, the phonon density of states at the interface was observed with different atomic surface terminations.⁵⁰ Interfacial heat transfer was dominated by low-frequency modes for the C- and Si-terminated SiC (100) planes and the C-terminated SiC (111) plane, whereas it was considerably dominated by high-frequency modes for the Si-terminated SiC (111) plane.

The atomic surface termination of diatomic molecules could manipulate the thermal energy transport at solid–liquid interfaces; however, its contribution to phonon heat transfer across a solid–vacuum–solid nanogap is still not well understood. In the study reported herein, the effects of atomic surface terminations on phonon heat transfer across an SiC–SiC nanogap were examined using nonequilibrium molecular dynamics (NEMD) simulations. A (111) crystallographic plane with Si and C atomic surface terminations of SiC diatomic molecules was simulated to verify the thermal energy transport between two separated SiC solid walls. The temperature profiles of the solid walls, the net heat flux, and the thermal gap conductance were investigated for the various atomic surface terminations. The existence of thermal resonance between identical atomic terminated layers was verified based on analyses of atomic vibrational displacements and vibrational density of states (VDOSs). Consequently, it was determined that the phonon heat transfer across the SiC–SiC nanogap with various atomic surface terminations is vital for revealing the mechanism of nanoscale thermal energy transport between the regimes of heat conduction and NFRHT.

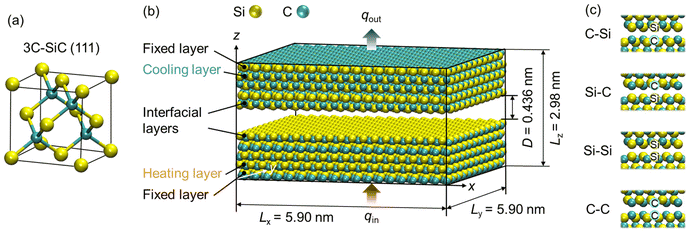
The thermal resonance induced by the quasi-Casimir coupling across a vacuum gap between the two separated monoatomic solid walls has been verified previously.¹⁷ Herein, we investigate the effects of atomic surface terminations on phonon heat transfer across the SiC–SiC nanogap using NEMD simulations.^51–53Fig. 1 shows the crystal structure of cubic 3C-SiC with the (111) crystallographic plane, the simulation system of two 3C-SiC solid walls separated by a nanogap distance D, and four pairs of atomic surface terminations at the interfacial layers built by LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator). The Vashishta potential was applied to simulate the Si–Si, Si–C, and C–C interactions for the SiC molecules;^54,55 see the ESI† for a detailed description of the modelling approach.

Fig. 1 (a) The crystal structure of cubic 3C-SiC with the (111) crystallographic plane. (b) NEMD simulation system of two separated SiC solid walls with a constant gap distance, where the yellow spheres represent Si atoms, and the cyan spheres represent C atoms. (c) Four pairs of atomic surface terminations at interfacial layers: C–Si, Si–C, Si–Si, and C–C.

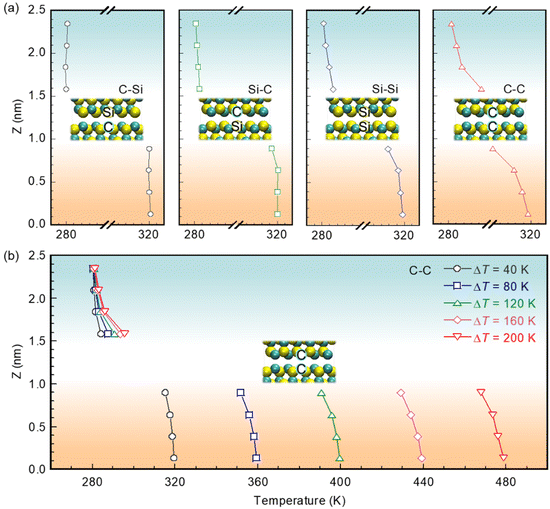
Fig. 2(a) shows the temperature profiles (except for the fixed solid layers) obtained at the end of the steady state for 20 ns under a temperature difference, ΔT (= T_H − T_C), of 40 K between the heating (T_H) and cooling (T_C) layers. Each temperature profile contains a schematic of the relevant pair of atomic surface terminations. As can be seen, the temperature gradient in the solid walls changes depending on the choice of atomic surface terminations. As given in Table 1, the interfacial temperature difference, ΔT_i ( = T_Hi − T_Ci), between the heating (T_Hi) and cooling (T_Ci) interfacial layers satisfies the following order: C–Si > Si–C > Si–Si > C–C. Specifically, ΔT_i is smallest in the identical case of C–C and largest in the nonidentical case of C–Si. These results indicate that atomic surface terminations play a dominant role in thermal energy transport across the vacuum nanogap.

Fig. 2 Temperature profiles of solid walls in steady NEMD simulations along the z direction: (a) four pairs of atomic surface terminations at interfacial layers (C–Si, Si–C, Si–Si, and C–C); (b) identical atomic surface terminations of C–C under various temperature differences ΔT between heating and cooling layers.

Table 1 Simulation results for the four pairs of atomic surface terminations at the interfacial layers

Atomic surface terminations	C–Si	Si–C	Si–Si	C–C
ΔTi (K)	39.98	39.04	36.44	31.64
q (GW m^−2)	0.22	0.43	1.64	2.36
G (MW m^−2 K^−1)	5.58	11.10	45.00	74.60

---

To study the heat exchange between two solid walls under various temperature differences, ΔT, temperature profiles of solid walls with identical atomic surface terminations of C–C are shown in Fig. 2(b). The temperature gradient of the heating wall is nearly the same as that of the cooling wall, and that of each wall increases with increasing ΔT. Meanwhile, the temperature difference between the interfacial layers, ΔT_i, increases with increasing ΔT, showing the enhanced heat transfer across the SiC–SiC nanogap. The temperature profiles of the solid walls in the cases of C–Si, Si–C, and Si–Si are available in the ESI.†

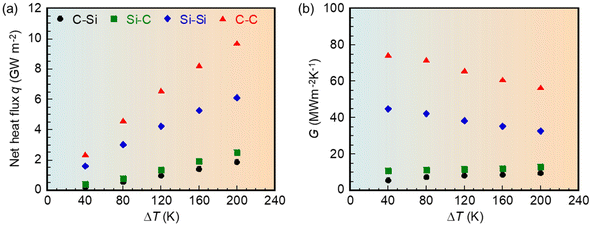
The thermal energy transport across a vacuum nanogap can be affected by atomic surface terminations due to the different strengths of quasi-Casimir coupling between the interfacial layers. Therefore, the net heat flux q and thermal gap conductance G under various temperature differences ΔT were acquired through 20 ns of data sampling in the steady NEMD simulations, as presented in Fig. 3 and Table 1. As shown in Fig. 3(a), q increases linearly with ΔT; however, as shown in Fig. 3(b), G decreases with ΔT in the identical cases of Si–Si and C–C but increases in the nonidentical cases of C–Si and Si–C. The atomic vibrational displacements along the z direction in the cases of Si–Si and C–Si at the heating (orange) and cooling (green) interfacial layers under various ΔT are shown in Fig. S2 and S4 (see ESI†). As shown in Fig. S2,† the mismatch of vibrational displacements for Si atomic surface terminations between the heating and cooling interfacial layers increases with ΔT. Fig. S3† shows the VDOSs at the atomic terminated layers in the identical case of Si–Si under various temperature differences ΔT. The VDOSs at atomic terminated layers in the heating and cooling walls agree well when ΔT = 40 K, whereas the mismatch between the VDOSs increases as increasing ΔT. The peaks of VDOSs at atomic terminated layers in the heating wall under the higher temperature shift toward the lower frequency band, thus the thermal gap conductance decreases as increasing ΔT. As shown in Fig. S4,† the peak amplitudes for Si atomic surface terminations are almost the same, whereas those for C atomic surface terminations increase with increasing ΔT, which is the underlying reason for the increased G in the nonidentical cases with ΔT. Moreover, q and G in the case of identical atomic surface terminations are 3.81–10.73 and 4.05–13.37 times greater than those in the nonidentical case as ΔT = 40 K, respectively.

Fig. 3 Effects of ΔT on (a) net heat flux q and (b) thermal gap conductance G for various atomic surface terminations.

To understand the mechanism of heat transfer across the SiC–SiC nanogap with various atomic surface terminations, atomic vibrational characteristics were analysed in the steady NEMD simulations under a constant ΔT of 40 K. As shown in Fig. 4(a)–(d), the peak amplitudes for the Si atomic surface terminations are significantly larger than those for the C atomic surface terminations. However, the vibrational frequencies for the Si atomic surface terminations are much smaller than those for the C atomic surface terminations because of their different atomic physical properties.

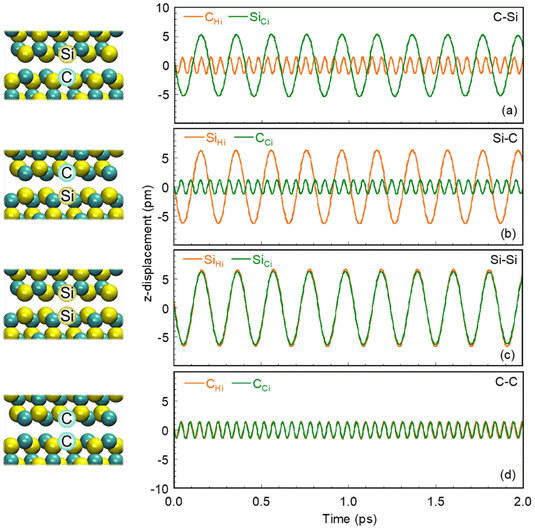Fig. 4 Vibrational displacements of (a and b) nonidentical atomic surface terminations and (c and d) identical atomic surface terminations in the heating and cooling interfacial layers.

Note that the vibrational displacements for the identical atomic surface terminations agree perfectly, as shown in Fig. 4(c) and (d). This is because the identical atomic surface terminations are subjected to strong molecular interactions across the nanogap, which results in thermal resonance between atomic terminated layers induced by quasi-Casimir coupling.^17,18 However, the vibrational displacements for the nonidentical atomic surface terminations are completely mismatched, as shown in Fig. 4(a) and (b). Table 2 summarizes the vibrational characteristics of nonidentical and identical atomic surface terminations in the heating and cooling interfacial layers. The differences in peak amplitude Am between atomic surface terminations at heating and cooling interfacial layers of the identical cases are one order of magnitude lower than those of the nonidentical cases. Meanwhile, the differences in the dominant frequency f of the identical cases are two orders of magnitude lower than those of the nonidentical cases. As a result, the normalized cross-correlation coefficient⁵⁶ between atomic vibrational displacements in the identical cases is close to 1 (i.e., with thermal resonance), whereas those in the nonidentical cases are close to 0 (i.e., without thermal resonance). Consequently, the much larger q and G in Fig. 3 are the result of thermal resonance between the identical atomic surface terminations. Furthermore, the vibrational frequency of C atomic termination is much larger than that of Si atomic termination, resulting in the greater q and G in the identical case of C–C.

Table 2 Vibrational characteristics of nonidentical and identical atomic surface terminations in the heating and cooling interfacial layers at T_H = 320 K, T_C = 280 K

Atomic surface terminations	Heating interfacial layers	Cooling interfacial layers			Cross-correlation coefficient between atomic vibrational displacements
	Am (pm)	f (THz)	Am (pm)	f (THz)
C–Si	1.451	18.384	5.361	4.959	0.013
Si–C	6.323	4.969	1.230	18.239	0.015
Si–Si	6.652	4.855	6.342	4.839	0.971
C–C	1.530	18.959	1.382	18.889	0.999

---

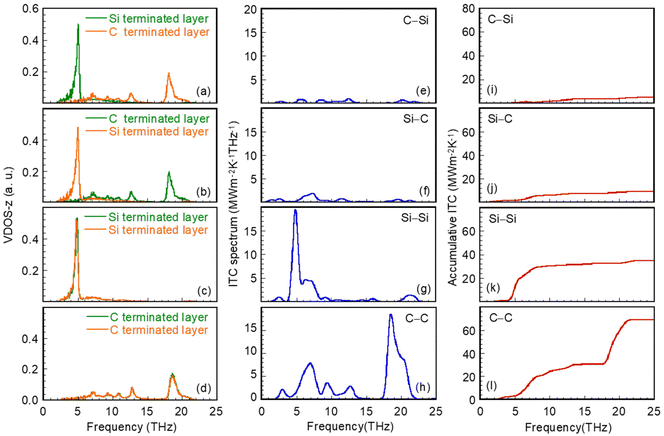
Phonon heat transfer across the SiC–SiC nanogap can be analyzed further by means of the VDOSs of the atomic terminated layers. In Fig. 5, the orange and green solid lines represent the VDOSs of the atomic terminated layers at the heating and cooling walls, respectively. The phonons of the Si-terminated layers are transmitted across the nanogap in the low-frequency band of 4.0–5.5 THz, whereas those of the C-terminated layers are transmitted in the high-frequency band of 18–22 THz. In a previous study, the heat transfer across the sub-nanometer vacuum gap between two planar Pt walls was verified as being due to the acoustic phonon transmission in the low-frequency band.¹⁷ As is known, the frequency of acoustic phonons ranges from zero to 10 THz, whereas higher-frequency phonons are called optical phonons.⁵⁷ That is, in addition to acoustic phonons, even optical phonons can contribute to heat transfer across the SiC–SiC nanogap.^58–61

Fig. 5 VDOSs in the z direction at interfacial layers with atomic surface terminations: (a) C–Si; (b) Si–C; (c) Si–Si; (d) C–C. Spectral thermal conductance for: (e) C–Si; (f) Si–C; (g) Si–Si; (h) C–C. Accumulative thermal conductance for: (i) C–Si; (j) Si–C; (k) Si–Si; (l) C–C.

For the nonidentical cases of C–Si and Si–C, the VDOSs of the atomic terminated layer in the heating wall are mismatched with those in the cooling wall, as shown in Fig. 5(a) and (b). For the identical cases of Si–Si and C–C in Fig. 5(c) and (d), the VDOSs of the atomic terminated layers in the heating and cooling walls are perfectly overlapped. In other words, thermal resonance exists between identical atomic terminated layers but vanishes between nonidentical ones.

Fig. 5(e)–(h) quantifies the relationship between the atomic surface termination and spectral thermal conductance calculated by a spectral heat current decomposition scheme.^62–67 The spectral thermal conductance of the nonidentical cases is much lower than that of the identical cases, owing to the phonon mismatch between the heating and cooling interfacial layers in the nonidentical cases (Fig. 5(a) and (b)). In the identical cases, the acoustic phonons are dominant for Si–Si (4–8 THz), while optical phonons are the main heat carriers for C–C (18–22 THz). Moreover, Fig. 5(i)–(l) quantifies the effect of the surface termination on the accumulative thermal conductance. The accumulative thermal conductance in the identical cases is 3.85–14.34 times larger than those in the nonidentical cases, coinciding with Table 1 quantitatively. It is noted that the considerable thermal energy transport in the identical case of C–C is attributed to the enhanced thermal resonance between the identical C-terminated layers (Fig. 4(d)) and the higher vibrational frequency of optical phonons (18–22 THz, Fig. 5(h)).

In conclusion, NEMD simulations were performed to characterize the phonon heat transfer across an SiC–SiC vacuum nanogap, with a special focus on four pairs of atomic surface terminations at the interfacial layers. We found that the temperature differences between the interfacial layers in the cases of identical atomic surface terminations were smaller than those in the nonidentical cases. The net heat flux and thermal gap conductance across the nanogap in the cases of identical atomic surface terminations were remarkably larger than those in the nonidentical cases. Thermal resonance existed between the identical atomic terminated layers but vanished between the nonidentical ones. The optical phonon transmission enhanced the thermal energy transport across the SiC–SiC nanogap in the identical case of C–C with thermal resonance between C-terminated layers. It is noteworthy that the quantum effect on phonon heat transfer across a nanogap is significant (see Fig. S6†), and further quantum correction is necessary in future works. The present findings provide a fundamental understanding of the thermal energy transport across the SiC–SiC nanogap, with potential benefits for the thermal management of nanoscale SiC power devices.

Author contributions

Xiangrui Li: investigation, methodology, data curation, formal analysis, writing – original draft. Wentao Chen: investigation, methodology, data curation, formal analysis, writing – review & editing, funding acquisition. Gyoko Nagayama: conceptualization, methodology, supervision, writing – review & editing, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Ministry of Education, Science and Culture of the Japanese Government through the Grant-in-Aid for Scientific Research, Project No. 22K18773 & 22K20412, the research supercomputing services by the Research Institute for Information Technology, Kyushu University, and the Initiative for Realizing Diversity in the Research Environment by Ministry of Education, Culture, Sports, Science and Technology, Japan.

References

1. J. Wu, Z. Xu, J. Zhao, M. Rommel, K. Nordlund, F. Ren and F. Fang, J. Nucl. Mater., 2021, 557, 153313.
2. Q. Wang, N. Gui, X. Huang, X. Yang, J. Tu and S. Jiang, Int. J. Heat Mass Transfer, 2021, 180, 121822.
3. Y. Xu, G. Wang and Y. Zhou, Int. J. Heat Mass Transfer, 2022, 187, 122499.
4. B. Szpunar, L. Malakkal, J. Rahman and J. A. Szpunar, J. Am. Ceram. Soc., 2018, 101, 4753–4762.
5. V. T. Nguyen and T. Fang, Ceram. Int., 2020, 46, 21578–21595.
6. K. H. J. Buschow, Encyclopedia of materials: Science and technology, Elsevier, Oxford, 1st edn, 2001.
7. C. U. Gonzalez-Valle, S. Kumar and B. Ramos-Alvarado, J. Phys. Chem. C, 2018, 122, 7179–7186.
8. C. U. Gonzalez-Valle, S. Kumar and B. Ramos-Alvarado, ACS Appl. Mater. Interfaces, 2018, 10, 29179–29186.
9. Q. Wang, C. Wang, Y. Zhang and T. Li, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 328, 42–47.
10. R. Li, K. Gordiz, A. Henry, P. E. Hopkins, E. Lee and T. Luo, Phys. Chem. Chem. Phys., 2019, 21, 17029–17035.
11. Y. Xu, H. Fan, Z. Li and Y. Zhou, Int. J. Heat Mass Transfer, 2023, 201, 123628.
12. W. Liu, X. Huang and Y. Yue, Int. J. Heat Mass Transfer, 2023, 201, 123673.
13. H. Han, S. Merabia and F. Müller-Plathe, Nanoscale, 2017, 9, 8314–8320.
14. F. Li, J. Wang, G. Xia and Z. Li, Nanoscale, 2019, 11, 13051–13057.
15. Y. Kim, T. Kodama, Y. Kim, B. S. Kim, C. Ko, J. Lim and W. Park, NPG Asia Mater., 2022, 14, 1–7.
16. W. Park, T. Kodama, J. Park, J. Cho, A. Sood, M. T. Barako and K. E. Goodson, ACS Appl. Mater. Interfaces, 2017, 9, 30100–30106.
17. W. Chen and G. Nagayama, Int. J. Heat Mass Transfer, 2021, 176, 121431.
18. W. Chen and G. Nagayama, Phys. Chem. Chem. Phys., 2022, 24, 11758–11769.
19. L. Tranchant, S. Hamamura, J. Ordonez-Miranda, T. Yabuki, A. Vega-Flick, F. Cervantes-Alvarez, J. J. Alvarado-Gil, S. Volz and K. Miyazaki, Nano Lett., 2019, 19, 6924–6930.
20. O. Ilic, N. H. Thomas, T. Christensen, M. C. Sherrott, M. Soljačic, A. J. Minnich, O. D. Miller and H. A. Atwater, ACS Nano, 2018, 12, 2474–2481.
21. M. Nomura, Nat. Nanotechnol., 2016, 11, 496–497.
22. S. Shen, A. Narayanaswamy and G. Chen, Nano Lett., 2009, 9, 2909–2913.
23. A. Alkurdi, C. Adessi, F. Tabatabaei, S. Li, K. Termentzidis and S. Merabia, Int. J. Heat Mass Transfer, 2020, 158, 119963.
24. B. Song, A. Fiorino, E. Meyhofer and P. Reddy, AIP Adv., 2015, 5, 053503.
25. K. Kim, B. Song, V. Fernández-Hurtado, W. Lee, W. Jeong, L. Cui, D. Thompson, J. Feist, M. T. H. Reid, F. J. García-Vidal, J. C. Cuevas, E. Meyhofer and P. Reddy, Nature, 2015, 528, 387–391.
26. H. Liu, H. Wang and X. Zhang, Appl. Sci., 2019, 9, 344.
27. S. Zhao, Y. Zhou and H. Wang, Int. J. Heat Mass Transfer, 2022, 195, 123218.
28. A. Fiorino, D. Thompson, L. Zhu, R. Mittapally, S. Biehs, O. Bezencenet, N. El-Bondry, S. Bansropun, P. Ben-Abdallah, E. Meyhofer and P. Reddy, ACS Nano, 2018, 12, 5774–5779.
29. G. Xu, J. Sun, H. Mao and T. Pan, J. Appl. Phys., 2018, 124, 183104.
30. A. Fiorino, L. Zhu, D. Thompson, R. Mittapally, P. Reddy and E. Meyhofer, Nat. Nanotechnol., 2018, 13, 806–811.
31. H. Yu, D. Liu, Y. Duan and Z. Yang, J. Quant. Spectrosc. Radiat. Transfer, 2018, 217, 235–242.
32. R. Mittapally, B. Lee, L. Zhu, A. Reihani, J. W. Lim, D. Fan, S. R. Forrest, P. Reddy and E. Meyhofer, Nat. Commun., 2021, 12, 1–8.
33. P. Ben-Abdallah and S. A. Biehs, Phys. Rev. Lett., 2014, 112, 044301.
34. E. Moncada-Villa and J. C. Cuevas, Phys. Rev. Appl., 2021, 15, 024036.
35. R. Liu, C. Zhou, Y. Zhang, Z. Cui, X. Wu and H. Yi, Int. J. Extreme Manuf., 2022, 4, 032002.
36. B. Song, Y. Ganjeh, S. Sadat, D. Thompson, A. Fiorino, V. Fernández-Hurtado, J. Feist, F. J. Garcia-Vidal, J. C. Cuevas, P. Reddy and E. Meyhofer, Nat. Nanotechnol., 2015, 10, 253–258.
37. K. Kloppstech, N. Könne, S. A. Biehs, A. W. Rodriguez, L. Worbes, D. Hellmann and A. Kittel, Nat. Commun., 2017, 8, 1–5.
38. L. Cui, W. Jeong, V. Fernández-Hurtado, J. Feist, F. J. García-Vidal, J. C. Cuevas, E. Meyhofer and P. Reddy, Nat. Commun., 2017, 8, 1–9.
39. A. I. Volokitin, J. Phys.: Condens. Matter, 2020, 32, 215001.
40. A. Fiorino, D. Thompson, L. Zhu, R. Mittapally, S. A. Biehs, O. Bezencenet, N. El-Bondry, S. Bansropun, P. Ben-Abdallah, E. Meyhofer and P. Reddy, ACS Nano, 2018, 12, 5774–5779.
41. V. Chiloyan, J. Garg, K. Esfarjani and G. Chen, Nat. Commun., 2015, 6, 6755.
42. T. Tokunaga, A. Jarzembski, T. Shiga, K. Park and M. Francoeur, Phys. Rev. B, 2021, 104, 25–30.
43. G. Domingues, S. Volz, K. Joulain and J. J. Greffet, Phys. Rev. Lett., 2005, 94, 2–5.
44. S. Xiong, K. Yang, Y. A. Kosevich, Y. Chalopin, R. D'Agosta, P. Cortona and S. Volz, Phys. Rev. Lett., 2014, 112, 114301.
45. K. Y. Fong, H. K. Li, R. Zhao, S. Yang, Y. Wang and X. Zhang, Nature, 2019, 576, 243–247.
46. K. Sasihithlu, Nature, 2019, 576, 216–217.
47. J. A. Macken, Research Gate, 2021, preprint, DOI:10.13140/RG.2.2.20007.68003.
48. E. M. Lifshitz, J. Exp. Theor. Phys., 1956, 2, 73.
49. P. Atkins and J. Paula, Elements of physical chemistry, Oxford University Press, New York, 5th edn, 2009.
50. C. U. Gonzalez-Valle and B. Ramos-Alvarado, Int. J. Heat Mass Transfer, 2019, 131, 645–653.
51. W. Chen, M. Sedighi and A. P. Jivkov, Nanoscale, 2021, 13, 1696–1716.
52. C. Herrero, G. Tocci, S. Merabia and L. Joly, Nanoscale, 2020, 12, 20396–20403.
53. T. Kodama, N. Shinohara, S. W. Hung, B. Xu, M. Obori, D. Suh and J. Shiomi, ACS Appl. Mater. Interfaces, 2021, 13, 17404–17411.
54. P. Vashishta, R. K. Kalia, A. Nakano and J. P. Rino, J. Appl. Phys., 2007, 101, 103515.
55. B. Yang, Q. Deng, Y. Su, X. Peng, C. Huang, A. Lee and N. Hu, Comput. Mater. Sci., 2022, 203, 111114.
56. J. L. Rodgers and W. A. Nicewander, Am. Stat., 1988, 42, 59–66.
57. Z. M. Zhang, Nano/microscale heat transfer, Springer, Switzerland, 2nd edn, 2020.
58. E. Lee and T. Luo, Phys. Chem. Chem. Phys., 2017, 19, 18407–18415.
59. T. Wang, Z. Gui, A. Janotti, C. Ni and P. Karandikar, Phys. Rev. Mater., 2017, 1, 034601.
60. D. N. Talwar, Mater. Sci. Eng., B, 2017, 226, 1–9.
61. Z. Tong, L. Liu, L. Li and H. Bao, Phys. B, 2018, 537, 194–201.
62. K. Sääskilahti, J. Oksanen, J. Tulkki and S. Volz, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 134312.
63. K. Sääskilahti, J. Oksanen, S. Volz and J. Tulkki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115426.
64. K. Xu, S. Deng, T. Liang, X. Cao, M. Han, X. Zeng, Z. Zhang, N. Yang and J. Wu, Nanoscale, 2022, 14, 3078–3086.
65. Y. Yao, G. Ren, Y. Yu, J. Che, T. Liang, L. Li, Y. Liu, F. Yang and X. Zhao, J. Am. Ceram. Soc., 2022, 105, 4360–4374.
66. Y. Xu, G. Wang and Y. Zhou, Int. J. Heat Mass Transfer, 2022, 187, 122499.
67. Y. Guo, C. Adessi, M. Cobian and S. Merabia, Phys. Rev. B, 2022, 106, 085403.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr00533j

‡ These authors contributed equally to this work.

---