Theoretical screening of single atom doping on β-Ga2O3 (100) for photoelectrochemical water splitting with high activity and low limiting potential†
Abstract
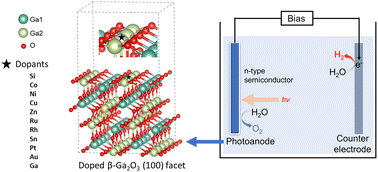
Photoelectrochemical (PEC) water splitting combined with renewable energy is an appealing approach for solar energy conversion and storage. Monoclinic gallium oxide (β-Ga2O3) has been identified as a promising photoelectrode for PEC because of its good electrical conductivity and chemical and thermal stability. However, the wide bandgap (around 4.8 eV) and the recombination of photogenerated electrons and holes inside β-Ga2O3 limit its performance. Doping β-Ga2O3 is a practical strategy to enhance photocatalytic activity, but studies on doped β-Ga2O3 based photoelectrodes are lacking. In this study, we evaluate the doping effect of ten different dopants for β-Ga2O3 photoelectrode at the atomic level using density functional theory calculations. In addition, the oxygen evolution performance is evaluated on doped structures as it is considered the bottleneck reaction in water slitting on the anode of the PEC cell. Our results suggest that rhodium doping is optimal as it demonstrated the lowest overpotential for oxygen evolution reaction. We performed further electronic structure analysis, indicating the narrower bandgap and enhanced photogenerated electron–hole transfer comparing with β-Ga2O3 are the main reasons for the improved performance after Rh doping. This study demonstrates that doping is an attractive strategy for the development of efficient Ga2O3-based photoanodes and it will be of great importance in helping the design of other semiconductor-based photoelectrodes for practical application.
- This article is part of the themed collections: Celebrating International Women’s day 2024: Women in Nanoscience and Nanoscale 2023 Emerging Investigators


 Please wait while we load your content...
Please wait while we load your content...