Open Access Article
Open Access ArticleLanthanide metal–organic network featuring strong perpendicular magnetic anisotropy†
Sofia O.
Parreiras‡
 *a,
Daniel
Moreno‡
*a,
Daniel
Moreno‡
 a,
Shanmugasibi K.
Mathialagan
a,
Shanmugasibi K.
Mathialagan
 a,
Beatriz
Muñiz-Cano
a,
Beatriz
Muñiz-Cano
 a,
Cristina
Martín-Fuentes
a,
María
Tenorio
a,
Cristina
Martín-Fuentes
a,
María
Tenorio
 a,
Lenka
Černa
b,
José I.
Urgel
a,
Lenka
Černa
b,
José I.
Urgel
 a,
Koen
Lauwaet
a,
Koen
Lauwaet
 a,
Manuel
Valvidares
c,
Miguel A.
Valbuena
a,
Manuel
Valvidares
c,
Miguel A.
Valbuena
 a,
José M.
Gallego
a,
José M.
Gallego
 ad,
José I.
Martínez
ad,
José I.
Martínez
 d,
Pierluigi
Gargiani
c,
Rodolfo
Miranda
ae,
Julio
Camarero
ae and
David
Écija
d,
Pierluigi
Gargiani
c,
Rodolfo
Miranda
ae,
Julio
Camarero
ae and
David
Écija
 *a
*a
aInstituto Madrileño de Estudios Avanzados en Nanociencia (IMDEA Nanoscience), Madrid 28049, Spain. E-mail: sofia.oliveira@imdea.org; david.ecija@imdea.org
bBrno University of Technology, 601 90, Czech Republic
cALBA Synchrotron Light Source, Cerdanyola del Vallès 08290, Spain
dInstituto de Ciencia de Materiales de Madrid (ICMM-CSIC), Cantoblanco, Madrid 28049, Spain
eDepartamento de Física de la Materia Condensada and Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, Madrid 28049, Spain
First published on 6th April 2023
Abstract
The coordination of lanthanides atoms in two-dimensional surface-confined metal–organic networks is a promising path to achieve an ordered array of single atom magnets. These networks are highly versatile with plenty of combinations of molecular linkers and metallic atoms. Notably, with an appropriate choice of molecules and lanthanide atoms it should be feasible to tailor the orientation and intensity of the magnetic anisotropy. However, up to now only tilted and almost in-plane easy axis of magnetizations were reported in lanthanide-based architectures. Here we introduce an Er-directed two-dimensional metallosupramolecular network on Cu(111) featuring strong out-of-plane magnetic anisotropy. Our results will contribute to pave avenues for the use of lanthanides in potential applications in nanomagnetism and spintronics.
Molecular magnetism is an emerging field with potential for technological applications such as high density information storage, molecular spin qubits and spintronics devices.1,2 In the frontier of this field shines the design of low dimensional magnetic materials, in which exotic physical phenomena emerge.1 From a fundamental point of view, lanthanides have high potential for the development of magnetic devices. Lanthanide atoms present higher magnetic moments, anisotropy and spin lifetimes than 3d elements, which can lead to an augmented magnetic stability and is essential to develop practical applications.3 Lanthanides are also ideal candidates for single atom magnets.4–6
Some attention has already been set on lanthanide molecular magnetic systems, particularly on the double-decker phthalocyanine family (LnPc2),7–13 and with some insights in alternative single molecule magnets.14–18 However, the investigation of the magnetism of lanthanides embedded in metal–organic networks remains underexplored.19,20 This is surprising since the engineering of 2D metal–organic networks exploiting lanthanides as single atom magnets,4–6 represents a promising path to design nanoarchitectures for information storage at the smallest scale.
We have pioneered this field with the investigation of the magnetic properties of Dy atoms coordinated with p-terphenyl-4,4′-dicarboxylic acid (TDA) and benzene-1,4-dicarboxylic acid (TPA) molecular linkers on Cu(111).19 For both TDA and TPA molecules a nearly in-plane magnetization axis was observed. More recently, we have inspected the magnetism of a different molecular linker, [1,4-bis(4-pyridyl)-biphenyl] (DPBP), coordinated with Dy and Er on Au(111).20 Dy- and Er-DPBP molecular networks present the same structure with dinuclear metallic centers, but there is a significant change in the electronic and magnetic properties. While Dy-DPBP has close to in-plane anisotropy, Er-DPBP presents a tilted magnetization easy axis. This demonstrates that it is possible to tailor the orientation and intensity of the magnetic anisotropy by metal–organic coordination.
On the other side, materials featuring perpendicular magnetic anisotropy are particularly interesting for the development of spintronic applications, as high density storage devices.21,22 These materials usually exhibit larger magnetic anisotropy, more uniform magnetization and improved thermal stability.21 Coordination chemistry has revealed that it is feasible for lanthanide molecular magnets on surfaces to display out-of-plane magnetic anisotropy.9–12 However, to the best of our knowledge a lanthanide-directed metal–organic network displaying perpendicular magnetic anisotropy has remained elusive.
In this work we report an investigation of the structural, electronic and magnetic properties of a metal–organic network based on Er atoms coordinated with deprotonated TDA species. We have performed scanning tunnelling microscopy (STM) and spectroscopy (STS), X-ray absorption spectroscopy (XAS), X-ray linear dichroism (XLD) and X-ray magnetic circular dichroism (XMCD). The experimental results are complemented with density functional theory (DFT) and multiplet calculations. Our results demonstrate the feasibility of accomplishing strong out-of-plane magnetic anisotropy by on-surface synthesis of a lanthanide metal–organic network.
The metal–organic network was prepared by the deposition of TDA molecules on a clean Cu(111) surface heated at 370 K to afford full deprotonation, followed by the deposition of Er atoms with the sample still heated at 370 K and a post-annealing at 430 K. The result is a mononuclear square network, analogous to the one observed for Dy- and Gd-TDA nanoarchitectures.19,23,24
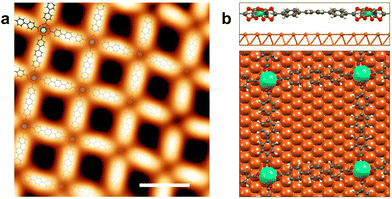
Fig. 1a presents a representative high resolution STM image of the network with a superimposed atomistic model. The network has an experimental internodal distance of (20.3 ± 0.5) Å, an Er–O distance of (2.4 ± 0.1) Å, and the average angle between the molecules is (90 ± 4)°. In order to get a commensurate lattice, the structure used in the DFT calculations diverges slightly from a square lattice and there are two different internodal distances, 20.4 Å in one direction and 20.9 Å in the other (see Fig. 1b). For the angles between molecules the theoretical values are 94° and 86°. The Er–O bond length ranges between 2.35 Å and 2.50 Å, in good agreement with the experimental values. This excellent match between the structure observed by STM and calculated by DFT for a mononuclear network confirms that the network has a single Er atom at the coordination nodes. According to the DFT calculations, the crystal field coordination is a distorted square antiprism, close to a D4d symmetry, similar to the Dy-TDA network.19
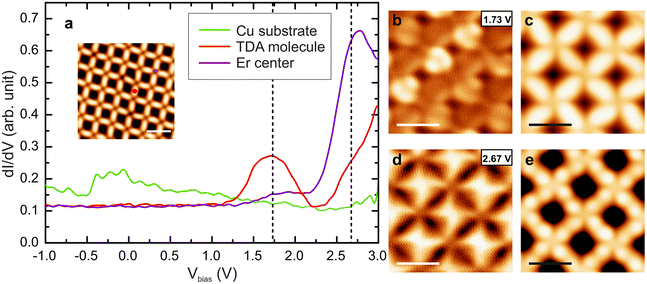
An inspection of the electronic properties by means of STS measurements reveals a resonance at 1.7 V for the Er-coordinated molecules (see Fig. 2a), that is attributed to the lowest unoccupied molecular orbital (LUMO). This resonance is at the same energy than the resonance observed for Dy-coordinated TDA molecules.19 A dI/dV map of the LUMO state (Fig. 2b) shows the presence of two lobes at the molecular backbone, being more intense in one direction of the network, which is attributed to the registry with the substrate. The main molecular resonance appears at ∼1.7 V, just like in the Dy-TDA case.19 The Er centers, on the other hand, show a resonance around 2.8 V, which is visualized in the dI/dV map as a bright protrusion (Fig. 2d). A resonance at approximately the same energy was observed in the Er-DBDP case.20
In order to interrogate the nature of the bonds and the plausible emergence of a delocalized band (not expected) we performed angle-resolved photoemission spectroscopy (ARPES) on this sample (see ESI†). Our results only indicate the confinement of the surface state, with no fingerprint of the presence of a band that could be assigned to the network. In fact, high resolution STS close to the Fermi level reveals two distinct peaks at −0.18 V and 0.14 V in the pores (see Fig. S3†), corroborating such confinement of the surface state. Altogether, we suggest that our results could be in line with the expected dominant ionic character of the bond,19,23,24 precluding the measurement of such a band (if at all existing).
The investigation of the magnetic properties of the Er-TDA network was performed at BOREAS beamline of ALBA synchrotron25 (see ESI†). The network was prepared following the same procedures described previously and the structure was checked with STM (Fig. 3a and b). The experimental results of XAS, XMCD and XLD measurements are presented in Fig. 3d and e together with multiplet calculations performed using the MultiX code.26 The peak's structure of XAS spectra indicates a Er3+ oxidation state,27 which was confirmed by the multiplet calculations. The differences between the experimental and simulated spectra are attributed to the difficulty in reproducing the exact symmetry of the real system in the simulations, as previously observed and discussed in the related Dy-TDA network on Cu(111).19
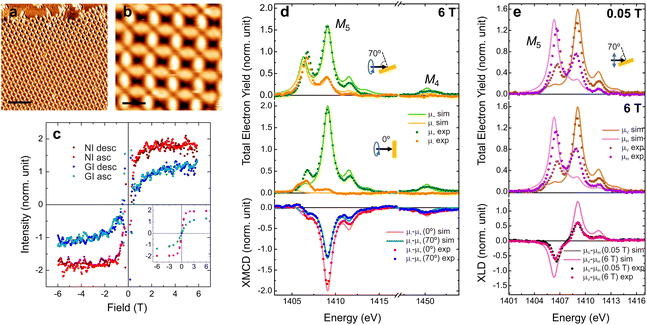 | ||
| Fig. 3 Characterization of the magnetic properties of the Er-TDA network on Cu(111). (a and b) STM images of the Er-TDA network on Cu(111). Scanning parameters: (a) Vb = 500 mV, It = 300 pA, T = 90 K, scale bar: 10 nm; (b) Vb = 500 mV, It = 300 pA, T = 90 K, scale bar: 2 nm. (c) Magnetization curves constructed by measuring the XMCD intensity at the most intense peak of the M5-edge at NI (red) and GI (blue). Dark (light) dots represent the descending (ascending) branches. The inset shows field dependent measurements of the XMCD intensity for some selected fields (T = 1.7 K). See the ESI† for more details. (d) XAS spectra acquired with positive (μ+, green dots) and negative (μ−, orange dots) circularly polarized light and XMCD (μ−–μ+) taken at the Er M4,5-edges at NI (red dots) and GI (blue dots) (B = 6 T, T = 1.7 K). (e) XAS spectra acquired with vertical (μV, brown dots) and horizontal (μH, purple dots) linearly polarized light and XLD (μV–μH) taken at the Er M5-edge at GI at 0.05 T (black dots) and 6 T (pink dots) (T = 1.7 K). Multiplet calculations are presented in (d and e) together with the experimental data with brighter lines. | ||
Regarding the magnetic properties, the higher intensity of the XMCD spectrum (see Fig. 3d) measured at normal incidence (NI, 0°) when compared to grazing incidence (GI, 70° respect to the surface normal) indicates an out-of-plane magnetization easy axis, in opposition to the nearly in-plane observed for Dy-TDA.19 The perpendicular anisotropy is confirmed by the magnetization curves (Fig. 3c). Besides the higher intensity, at NI the curve is squarer, saturating at a lower field than at GI. These results confirm that it is possible to tailor the magnetic anisotropy of metal–organic networks by metal exchange. Out-of-plane anisotropy was observed previously for Er trimers on Cu(111), while Er single atoms and dimers have in-plane anisotropy.28 However, to our knowledge, this is the first report of a lanthanide metal–organic network with a magnetization easy axis perpendicular to the surface plane. Expectation values of spin (〈Sz〉), orbital (〈Lz〉) and total (〈Jz〉) magnetic moments (in units of ħ) are presented in Table 1, as also the total magnetic moment (mT in units of μB), and the moment anisotropy (mT = mT(70°) − mT(0°), as defined in the ESI†), obtained using the sum rules29,30 for an Er3+ ion. The experimental value of Jz at NI indicates that the quantum number is Jz = 15/2, the maximum possible value for Er3+. According to the multiplet calculations the quantum numbers for this system are Sz = 3/2, Lz = 6 and Jz = 15/2, in agreement with the values obtained from the XMDC spectra measured at NI. The moment anisotropy of (−4.8 ± 1.5)μB is even higher (and of opposite sign) than the one measured in the Dy-TDA network.19
| Incidence angle (°) | 0 | 70 |
|---|---|---|
| 〈Sz〉 (ħ) | 1.8(2) | 1.0(1) |
| 〈Lz〉 (ħ) | 6.0(6) | 3.4(3) |
| 〈Jz〉 (ħ) | 7.8(8) | 4.4(4) |
| m T (μB) | 9.7(1.0) | 5.4(5) |
| ΔmT (μB) | −4.8(1.5) | |
Fig. 3e shows that the XLD spectra feature a strong anisotropy due to the crystal field generated by the molecular network. XLD spectra measured with low and high applied magnetic fields (at 0.05 T and 6 T, respectively) are similar, both in shape and intensity. The XLD orientation is inverted when compared to Dy-TDA,19 as it can be expected for the different charge density of Er3+ ions with large Jz (prolate charge) when compared to Dy3+ (oblate charge).3 These charge densities are linked with the orientation and intensity of the magnetic moments. According to previous results for Dy-directed networks, the oblate charge of Dy3+ ions is associated with close to in-plane magnetic anisotropy.19,20 In the case of Er3+ ions the prolate charge density can be related to an out-of-plane orientation of the magnetic anisotropy.20 Accordingly, for the case of Er-TDA network the multiplet calculations indicate that the magnetic anisotropy is uniaxial and totally out-of-plane with a maximum Jz as expected for prolate Er3+ ions,3 which is further confirmed by the sum rule analysis.
In summary, we have investigated the structural, electronic and magnetic properties of an on-surface synthesized metal–organic network directed by Er atoms that are coordinated with TDA molecular linkers. Although the structure is analogous to the Dy-TDA nanoarchitecture, we observe a modification in the electronic and magnetic properties as a consequence of the metal exchange. The energy level alignment of the frontier states in Er-TDA is distinct from the Dy-TDA network. Moreover, the Er atoms present +3 oxidation state with strong charge anisotropy and high perpendicular magnetic anisotropy. The moment anisotropy is also significantly larger when compared to the Dy-TDA network.
Our results demonstrate that it is feasible to tune the magnetic anisotropy in isostructural supramolecular networks by metal exchange, increasing its magnitude and switching the magnetic easy axis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work received funding from the European Research Council (ERC, grant 766555), Marie Sklodowska-Curie Actions (MSCA, project 894924) under the European Union's Horizon 2020 Research and Innovation Programme, and the EMPIR Programme co-financed by the Participating States and the European and Union's Horizon 2020 Research and Innovation Programme (grant EMPIR 20FUN03 COMET). IMDEA Nanociencia acknowledges support from the “Severo Ochoa” Programme for Centres of Excellence in R&D (MINECO, Grant SEV-2016-0686). The ALBA synchrotron is acknowledged for providing beam time at BOREAS beamline (proposal number 2021025028).References
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350–364 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- F. Donati, S. Rusponi, S. Stepanow, C. Wäckerlin, A. Singha, L. Persichetti, R. Baltic, K. Diller, F. Patthey, E. Fernandes, J. Dreiser, Ž. Šljivančanin, K. Kummer, C. Nistor, P. Gambardella and H. Brune, Science, 2016, 352, 318–321 CrossRef CAS PubMed.
- F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Nature, 2017, 543, 226–228 CrossRef CAS PubMed.
- F. Donati and A. J. Heinrich, Appl. Phys. Lett., 2021, 119, 160503 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- N. Ishikawa, Polyhedron, 2007, 26, 2147–2153 CrossRef CAS.
- M. Studniarek, C. Wäckerlin, A. Singha, R. Baltic, K. Diller, F. Donati, S. Rusponi, H. Brune, Y. Lan, S. Klyatskaya, M. Ruben, A. P. Seitsonen and J. Dreiser, Adv. Sci., 2019, 6, 1901736 CrossRef CAS PubMed.
- L. Ruan, J. Tong, F. Luo, Y. Wu, G. Qin, X. Jiao and X. Zhang, Appl. Surf. Sci., 2022, 585, 152445 CrossRef CAS.
- C. Wäckerlin, F. Donati, A. Singha, R. Baltic, S. Rusponi, K. Diller, F. Patthey, M. Pivetta, Y. Lan, S. Klyatskaya, M. Ruben, H. Brune and J. Dreiser, Adv. Mater., 2016, 28, 5195 CrossRef PubMed.
- V. Corradini, A. Candini, D. Klar, R. Biagi, V. De Renzi, A. Lodi Rizzini, N. Cavani, U. del Pennino, S. Klyatskaya, M. Ruben, E. Velez-Fort, K. Kummer, N. B. Brookes, P. Gargiani, H. Wende and M. Affronte, Nanoscale, 2018, 10, 277 RSC.
- H. Wang, K. Wang, J. Tao and J. Jiang, Chem. Commun., 2012, 48, 2973–2975 RSC.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- P. Stoll, M. Bernien, D. Rolf, F. Nickel, Q. Xu, C. Hartmann, T. R. Umbach, J. Kopprasch, J. N. Ladenthin, E. Schierle, E. Weschke, C. Czekelius, W. Kuch and K. J. Franke, Phys. Rev. B, 2016, 94, 224426 CrossRef.
- F. Habib, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242–13245 CrossRef CAS PubMed.
- J. J. Le Roy, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2014, 136, 8003–8010 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- S. O. Parreiras, D. Moreno, B. Cirera, M. A. Valbuena, J. I. Urgel, M. Paradinas, M. Panighel, F. Ajejas, M. A. Niño, J. M. Gallego, M. Valvidares, P. Gargiani, W. Kuch, J. I. Martínez, A. Mugarza, J. Camarero, R. Miranda, P. Perna and D. Écija, Small, 2021, 17, 2102753 CrossRef CAS PubMed.
- D. Moreno, S. O. Parreiras, J. I. Urgel, B. Muñiz-Cano, C. Martín-Fuentes, K. Lauwaet, M. Valvidares, M. A. Valbuena, J. M. Gallego, J. I. Martínez, P. Gargiani, J. Camarero, R. Miranda and D. Écija, Small, 2021, 18, 2107073 CrossRef PubMed.
- R. Sbiaa, H. Meng and S. N. Piramanayagam, Phys. Status Solidi RRL, 2011, 5, 413–419 CrossRef CAS.
- S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami and S. N. Piramanayagam, Mater. Today, 2017, 20, 530–548 CrossRef.
- J. I. Urgel, B. Cirera, Y. Wang, W. Auwärter, R. Otero, J. M. Gallego, M. Alcamí, S. Klyatskaya, M. Ruben, F. Martín, R. Miranda, D. Ecija and J. V. Barth, Small, 2015, 11, 6358 CrossRef CAS PubMed.
- B. Cirera, L. Dordevic, R. Otero, J. M. Gallego, D. Bonifazi, R. Miranda and D. Ecija, Chem. Commun., 2016, 52, 11227 RSC.
- A. Barla, J. Nicolas, D. Cocco, S. M. Valvidares, J. Herrero-Martın, P. Gargiani, J. Moldes, C. Ruget, E. Pellegrin and S. Ferrer, J. Synchrotron Radiat., 2016, 23, 1507 CrossRef CAS PubMed.
- A. Uldry, F. Vernay and B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125133 CrossRef.
- A. Singha, R. Baltic, F. Donati, C. Wackerlin, J. Dreiser, L. Persichetti, S. Stepanow, P. Gambardella, S. Rusponi and H. Brune, Phys. Rev. B, 2017, 96, 224418 CrossRef.
- A. Singha, F. Donati, C. Wäckerlin, R. Baltic, J. Dreiser, M. Pivetta, S. Rusponi and H. Brune, Nano Lett., 2016, 16, 3475–3481 CrossRef CAS PubMed.
- B. T. Thole, P. Carra, F. Sette and G. van der Laan, Phys. Rev. Lett., 1992, 68, 1943–1946 CrossRef CAS PubMed.
- P. Carra, B. T. Thole, M. Altarelli and X. Wang, Phys. Rev. Lett., 1993, 70, 694–697 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr07189d |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |