Tuning the carrier injection barrier of hybrid metal–organic interfaces on rare earth-gold surface compounds

Abstract

Magnetic hybrid metal–organic interfaces possess a great potential in areas such as organic spintronics and quantum information processing. However, tuning their carrier injection barriers on-demand is fundamental for the implementation in technological devices. We have prepared hybrid metal–organic interfaces by the adsorption of copper phthalocyanine CuPc on REAu₂ surfaces (RE = Gd, Ho and Yb) and studied their growth, electrostatics and electronic structure. CuPc exhibits a long-range commensurability and a vacuum level pinning of the molecular energy levels. We observe a significant effect of the RE valence of the substrate on the carrier injection barrier of the hybrid metal–organic interface. CuPc adsorbed on trivalent RE-based surfaces (HoAu₂ and GdAu₂) exhibits molecular level energies that may allow injection carriers significantly closer to an ambipolar injection behavior than in the divalent case (YbAu₂).

---

1. Introduction

Organic semiconducting molecules are an excellent and promising alternative for the development of molecular spintronic based devices.¹ They show unique properties, such as strong responses to electrical and optical stimuli, and intrinsic physical and chemical functionality,^2–4 which are not usually present in inorganic materials. Organic spintronics pave the way for the development of cleaner, cheaper and efficient technological devices with novel and versatile capabilities. The functionality of such devices is based on the generation, transport and detection of spin-polarized carriers across the hybrid interface between a ferromagnetic metal and an organic semiconductor. That is the so-called spinterface, which is key for the spin injection into the organic molecules. There are two possible scenarios of ferromagnetic metal–organic interaction at the interface. On the one hand, a strong electron hybridization can produce a new interfacial spin-polarized hybrid electronic state that facilitates spin selectivity. 3d transition metal phthalocyanines (Pc),^5–7 Alq₃,⁸ as well as C₆₀ on 3d ferromagnetic surfaces^9,10 are representative systems featuring such type of spinterface. On the other hand, a weak interaction between the organic and ferromagnetic components, namely physisorption driven by van der Waals forces, can leave the electronic properties of the molecule almost intact. This latter case is an advantageous scenario for more versatile devices that integrate spintronics and optoelectronics functionalities, where optimized injection barriers and carrier mobilities need to be taken into consideration during the design process.^11,12

In this work, we study the interfacial electronic structure between a long-range ordered copper phthalocyanine (CuPc) monolayer (ML) and the family of two-dimensional (2D) REAu₂ surface compounds, where RE is a rare earth species.^13–15 The adsorbed molecule CuPc is a chemically stable prototypical p-type semiconductor. It is known to have an unpaired electron leading to an open-shell electronic structure on many different surfaces, such as noble metals,^16–21 graphene,²² topological insulators^21,23 and some semimetals.^21,24 Over the recent years, REAu₂ and REAg₂ surface alloys have become highly valued for their rich magnetic behavior, which originates from the interplay of 4f magnetism, substrate-mediated ferromagnetism, spin–orbit interaction and valence state effects on their characteristic 2D electron band structure.^25–32 Moreover, REAu₂ surfaces have been probed as excellent templates of several materials from monodomain ferromagnetic nanodots^25,26,28 to molecules,^27,33 including on-surface polymerized organic complexes.^34,35 Nevertheless, their performance in spinterfaces remains unknown.

We adsorb CuPc monolayers on YbAu₂, GdAu₂ and HoAu₂ surfaces as case studies and analyze the structural properties by scanning tunneling microscopy (STM) and low energy electron diffraction (LEED). Furthermore, by means of photoemission techniques we obtain direct information on the metal-band/molecular orbital alignment, work functions and surface dipoles. These properties turn out to non-trivially depend on the RE species of the substrate. Particularly, the RE valence (divalent Yb, trivalent Gd and Ho³¹) seems to be key for the energy level alignment of metal and organic molecule. This situation opens up the design of hybrid interfaces on demand using the RE valence as tuning factor. Indeed the valence may influence in the type of carriers injected (electrons/holes) or even approximate to an ambipolar carrier injection, i.e. the simultaneous injection of electrons and holes, which facilitates an effective recombination of the carriers in the active organic layer and the further production of light.^36–38

In order to characterize comprehensively our interfaces and the effect of the RE atoms on their electronic structure, we resort to density-functional theory (DFT) calculations. This method confirms the physisorption of CuPc on REAu₂, despite the relatively high amount of RE atoms in these surface compounds. Usually, the energy alignment of the organic molecular orbitals with the metal bands at the interface is subject to charge transfer, hybridization and metal substrate polarization effects. However, in the absence of a net charge transfer, like in the present studied case, the surface dipole developed upon adsorption is ascribed to the so-called push-back effect,^39–41 which is related to polarization and can be interpreted as the Pauli repulsion between the electron clouds of the metallic surface and the molecule.^42–45 The interaction with the substrate, even if it is weak, leads to the renormalization of the molecular levels, inducing a reduction of the ionization potential, electron affinity, and the HOMO–LUMO gap.^46,47 While such electronic structure changes are detectable by photoemission, they are a challenge for DFT-based theoretical methods. In the latter case, corrections are required to overcome self-interaction errors (SIE)⁴⁸ to approximately account for the many-body dynamical polarization effects⁴⁹ that take place at the CuPc/REAu₂ interfaces.

2. Experimental and theory section

2.1. Experimental

Samples have been prepared in an ultra-high vacuum (UHV) chamber at a base pressure of 2 × 10⁻¹⁰ mbar. A Au(111) single crystal was used as substrate, that was cleaned by cycles of Ar⁺ ion sputtering (E_kin = 1 keV) and annealing to 500 °C. The different REAu₂ surface compounds were grown in situ by evaporation of small amounts of RE atoms on the Au(111) surface, held at a fixed temperature. The optimal growth temperature of the substrate is of 300 °C for YbAu₂ and varies between 400–450 °C for GdAu₂ and HoAu₂. Below these temperatures the characteristic moiré pattern was not well formed, and above them the RE metals diffuse into the bulk or re-evaporate from the surface. CuPc molecules have been evaporated on the REAu₂ surface with deposition rates of 0.05 ML min⁻¹. The completion of one monolayer (ML) is probed carefully using LEED and STM. The substrate temperature during CuPc evaporation was set to room temperature.

Preparation and sample analysis was mainly performed in the laboratories of the Material Physics Center of San Sebastian. X-ray photoelectron spectroscopy measurements were carried out at room temperature, illuminating the sample with monochromatized Al K_α light from a microfocus setup (SPECS Focus 600). The excited photelectrons were collected with a SPECS 150 analyzer at an emission angle of 40°. The overall experimental resolution was extracted from a fit of the Fermi edge and resulted in 0.4 eV. UPS laboratory data were acquired using Helium Iα and IIα excitation lines (hν = 21.2 eV and 40.8 eV, respectively). Complementary ultra-violet photoemission (UPS) measurements were performed at the VUV Photoemission beamline of the Elettra Synchrotron in Trieste. In San Sebastian and Trieste a channel plate-based display type hemispherical analyzer was used with angular and energy resolution set to 0.1° and 40 meV, respectively. At the synchrotron, p-polarized light was used and the sample temperature during measurements was 17 K. In San Sebastian the work function Φ was evaluated by UPS in the laboratory, by measuring the difference in energy between the Fermi level E_F and the photoemission cutoff for several extracting voltages (5 V, 10 V and 15 V).⁵⁰ Scanning tunneling microscopy (STM) experiments were done at 300 K using an Omicron VT Setup.

2.2. DFT calculations

Density functional theory (DFT) calculations were carried out with the projector augmented waves formalism for the ion cores and a basis of plane waves, as implemented in VASP.^51,52 The surface was modelled in the supercell approach with up to three atomic planes in the substrate, leaving a vaccum distance of 12.5 Å between slab replicas. The experimental lattice constant and superperiodicty was used for the CuPc layer. REAu₂, with RE = Yb and Gd, free-standing flat monolayers as well as relaxed ones on 2 ML Au(111) were used. In this case, the moiré pattern is disregarded and instead a fcc stacked (√3 × √3)R30° structure is used as in previous works. The plane-wave basis was set from a Brillouin zone sampling⁵³ 3 × 3 × 1 and an energy cut-off of 400 eV (a finer grid 6 × 6 × 1 was used to obtain densities of states). Tolerances were 10⁻⁵ eV in the total energies and 10⁻⁴ eV in the ionic relaxation, together with forces on the atoms smaller than 0.05 eV Å⁻¹. First, the atomic positions of the isolated layer of CuPc were allowed to relax. This structure was then rigidly placed on the flat REAu₂ monolayers at three different registries (top RE, top Au and bridge between Au atoms), with molecules oriented as indicated by the STM images (see Fig. 1), and adsorption heights z to obtain a first approximation of the adsorption potential V_ads(z). The same procedure was applied to REAu₂/Au(111) slabs, where the alloy monolayer had been previously optimized. Finally, at the obtained minima, the CuPc were allowed to relax.

Fig. 1 Structural investigations of 1 ML CuPc on HoAu₂ surface compound. (a) LEED diffraction pattern taken at kinetic energy of 11.5 eV. One of the three rotational domains of the CuPc arrays is marked with a solid rhomboid in red, the other two domains by dashed lines. (b) STM image of CuPc on HoAu₂ (scanning parameters: I = 0.2 nA; U = 0.7 V). The rhomboidal surface unit cell for CuPc is marked in black. (c) Model of growth of CuPc on REAu₂ alloys. Again the molecular unit cell is marked.

In the geometry optimization and charge density distribution analyses, the generalized gradient approximation PBE functional⁵⁴ was used, together with the DFT+U approach⁵⁵ for electron correlations in the Cu(d) and RE(f) orbitals. Here the Dudarev parameters⁵⁶U–J = 7.5, 3.5, and 3.5 eV for Gd, Yb and Cu were selected based on previous experience,^18,25,27 and occupation matrix control⁵⁷ was used to initialize the electron distributions with the actual CuPc configuration. The 4f electrons were considered both as valence and core states in the calculations with free-standing REAu₂ monolayers. After confirmation that this does not significantly alter the main results (adsorption heights and charge density distributions), the calculations with an Au(111)-2 ML substrate were carried out with the 4f orbital in the ion cores. Additionally, van der Waals (vdW) dispersion forces were accounted for with the cx-13 functional.^58,59 At the so-obtained equilibrium geometries, the z-dependence of the carrier density difference (CDD) at the interface upon physisorption is calculated according to the definition

Here, the ρ_S(z) terms are the plane-integrated charge densities of each system S, where atomic coordinates are fixed at the optimized positions in the CuPc/REAu₂/Au(111) structures found in the PBE+U+vdW calculations.

The effect of self-interaction corrections on the densities of states of these structures was examined using range-separated hybrid functionals (HSE,^60,61 as implemented in VASP⁶²), perturbatively: the eigenenergies of a PBE calculation were corrected to first order by applying the exact Hartree–Fock contribution non-selfconsistently to the corresponding wavefunctions. In addition, the DFT+∑_axc method^63,64 was used to determine the HOMO level alignment in CuPc/REAu₂/Au(111). Further details^65–70 can be found in the ESI.†

3. Results and discussion

3.1. Structure and adsorption energetics

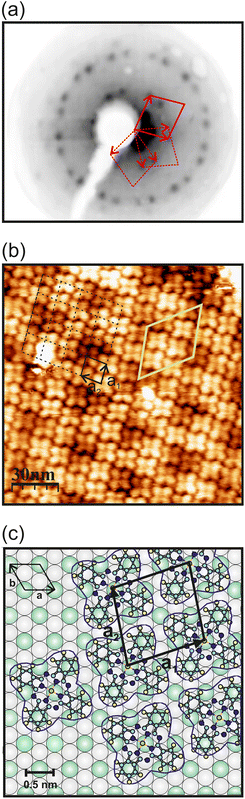
The growth of the monolayer CuPc adsorbed on GdAu₂, HoAu₂ and YbAu₂ surfaces was studied with low-energy electron diffraction (LEED) and scanning tunneling microscopy (STM) at room temperature. It is worth noting that REAu₂ surfaces are characterized by a hexagonal surface structure and a long-range moiré periodicity that extends over the whole surface.^13,15 Depending on the RE ion, the lattice parameters of the compounds show tiny differences, but these become amplified in the moiré periodicities.³¹ However, the growth of CuPc shows identical adsorption geometries with analogous LEED patterns on all three REAu₂ substrates studied here. Fig. 1(a) displays the LEED pattern of 1 ML of CuPc on HoAu₂. CuPc grows with three different rotational domains, as many Pc overlayers on hexagonal surfaces.^19,71,72 The surface unit cell of CuPc in this particular case results to be rhomboidal with a lattice parameter a = 1.43 nm and θ = 80°, and it appears marked by a solid red line in Fig. 1(a). The dashed red lines represent the unit cells of the other two rotational domains rotated at 60° with respect to each other. Similar LEED patterns have been measured on 1 ML of CuPc/GdAu₂ and CuPc/YbAu₂ (Fig. S1 in the ESI†). The complex epitaxy of CuPc (four-fold symmetry) on hexagonal REAu₂ surfaces can be expressed in matrix notation⁷³ as , which points out the commensurability of CuPc on these substrates. Considering this arrangement, the packing density of the CuPc overlayer is 0.49 molecule per nm², very close to the value obtained in CuPc on Au(111) (0.5 molecule per nm²).¹⁹ The high degree of commensurability between the molecules and the surface is confirmed by STM measurements. Fig. 1(b) displays a STM micrograph of CuPc grown on HoAu₂ and shows one of the three rotational domains of the CuPc ML. The surface unit cells of CuPc monolayer is marked in black, while the moiré periodicity of the substrates underneath is marked in yellow. Fig. 1(c) illustrates the structural model extracted from LEED pattern analysis. In this particular case, it is assumed that CuPc molecules are adsorbed with the Cu ion centered on top of a RE atom of the substrate. Nevertheless, the coincidence between the molecular lattice and the REAu₂ surface alloys allows other adsorption sites on the substrate that preserve the same molecular arrangement and LEED pattern. From the LEED measurements one can only evaluate the lattice but not the surface adsorption site of the molecule (Cu atom). In order to further investigate the structure and energetics of the system, we resort to first-principles calculations in the DFT+U approach, including a van der Waals (vdW) functional (see Methods section). The vdW correction is needed to obtain meaningful adsorption wells. CuPc molecular arrays on REAu₂ MLs with divalent Yb²⁺ and trivalent Gd³⁺ were studied with this approach. Fig. 2(a) shows the adsorption potential energies as a function of the height z_Cu of the central Cu atom inside the CuPc molecule landing rigidly on free-standing REAu₂ MLs. For the three studied adsorption sites (top RE, top Au and bridge site between two Au atoms), the adsorption minima are located at around 3 and 3.25 Å for YbAu₂ and GdAu₂, respectively, which are characteristic of vdW physisorbed systems. The main observation is that the interaction of CuPc with GdAu₂ is stronger than with YbAu₂. The adsorption minima on GdAu₂ are deeper (E_ads ≃ 4 eV) than on YbAu₂ (≃3 eV) and there are larger differences between the E_ads at the different adsorption sites on GdAu₂. Moreover, a larger E_ads on GdAu₂ is also obtained in the absence of vdW corrections (pink curves), with a shallow adsorption well at 3.25 Å, while interaction of CuPc on YbAu₂ results to be much weaker. The Cu–Gd magnetic exchange interaction, absent in YbAu₂, is another factor to be considered in the adsorption stability. The largest magnetic effect is found on free-standing GdAu₂ at the top Gd site, where antiferromagnetic (AFM) interaction is favored by 0.18 eV over the ferromagnetic (FM) one. At the other sites, the AFM–FM energy differences are one order of magnitude smaller. The same calculation performed on CuPc on supported REAu₂ on a Au(111)-2 ML thick layer shows important vdW dispersion forces, which are introduced by the Au(111) layers, dominating the adsorption energetics on GdAu₂, as it is shown in Fig. 2(b). Here, E_ads values are reduced by up to 2 eV and adsorption becomes slightly more stable on YbAu₂. In this case a further energy reduction of ≃0.2 eV is achieved by allowing the CuPc geometry to relax, specially at the Au top and bridge sites.

Fig. 2 Potential of CuPc interaction as a function of the molecule height above the surface, measured at the Cu position, with free-standing REAu₂ (left panels) and supported REAu₂/Au(111)-2 ML (right panels) for RE = Yb and Gd. For the supported cases, the empty symbols represent the potential values for the optimized geometries.

The adsorption geometry at top RE and top Au configurations implies a coincidence of five RE atoms with CuPc, while at bridge site configuration the coincidence is reduced to four atoms. This is shown by the spatial dependence of carrier density difference (CDD) Δρ(r) (see Methods section). The mapping of Δρ(x,y) discloses clear electron accumulation regions that are localized at the coincidence points between the RE atoms of the substrate and the organic ligand, as shown in Fig. 3(a). The charge accumulation areas, represented in red, are clearly localized underneath the Cu and C atoms. These points are hotspots that act as anchoring points for CuPc on both free-standing and supported REAu₂ MLs. Δρ(x,y) for all three adsorption sites are represented in Fig. S2 in the ESI.† This larger coincidence would explain the slightly stronger interaction observed in the V_ads(z) curves upon CuPc adsorption on top RE and top Au sites compared with Au bridge sites of Fig. 2.

Fig. 3 (a and b) Carrier density difference Δρ(r) in the CuPc/GdAu₂/Au(111)-2 ML interface with Cu at the Gd atop site. (a) Map of the Δρ(x,y) section at the z value corresponding to the intermediate distance between the surface and the CuPc layer. The grid points indicate the RE atoms positions. The coincidence of the molecule atoms with the RE atoms induces a charge accumulation that appears as red areas. (b) Side view, with view point in the Y direction, of the Δρ(r) isosurface 0.01 n_e Å⁻³. (c) Plane-averaged Δρ(z) at the CuPc/REAu₂/Au(111)-2 ML interfaces for RE = Yb and Gd. The vertical solid lines represent the atomic plane positions. Curve colors indicate the Cu adsorption site.

The CDD in the side-view representation of Fig. 3(b) reveals that these areas of charge accumulation (red) are clearly localized at the interface near the CuPc layer. Moreover, such effect induces a certain defect of charge (blue) at the CuPc layer and a slight polarization of the corresponding RE atoms. The CDD topography at the CuPc/REAu₂/Au(111) interface qualitatively differs from those at CuPc/Au(111) and CuPc/Ag(111). For CuPc on Au(111) the Δρ(r) distribution is uniform, whereas it is very corrugated throughout the interface with Ag(111), rapidly shifting between positive and negative values.⁷⁴ In contrast, here Δρ(r) is markedly localized above the RE atomic positions.

3.2. Electrostatics at the interface

Experimental work function (Φ) measurements were performed by photoemission spectroscopy from the cutoff of the secondary emitted electrons (see Methods section) on pristine REAu₂ substrates and upon adsorption of 1 ML CuPc on top. Both results were systematically compared, detecting a change in the work function ΔΦ that is related with the surface dipole induced by the evaporation of CuPc (see Table 1). This effect can be assigned to the Pauli push-back effect, which is commonly observed in metal–organic interfaces.^39–41 The highest ΔΦ values are found in the samples of CuPc/HoAu₂ and CuPc/GdAu₂. On the pristine alloys Φ displays similar values for both GdAu₂ (4.89 eV) and HoAu₂ (4.88 eV) surfaces. However, the highest Φ is measured in YbAu₂ (4.98 eV). This is an unexpected result, considering that Yb as pure element is divalent and exhibits smaller values than the trivalent Ho and Gd.^42,43

Table 1 Experimental (UPS) and theoretical work functions Φ for 1 ML of CuPc on REAu₂ surfaces, and the variation ΔΦ with respect to the pristine surfaces. The calculated values for the CuPc/REAu₂/Au(111)-2 ML slab with RE = Yb and Gd, together with the dipole p_z and vacuum level shift ΔV_vac, are given for three different adsorption sites of the molecule, namely Cu-atom on top-RE, top-Au, and bridge-Au, respectively. The theoretical ΔΦ values are given with respect to the values calculated on the clean substrates (Φ = 3.39 and 3.76 eV for Yb and Gd, respectively)

		Φ (eV)	ΔΦ (eV)	ΔVvac (eV)	pz (e Å)
CuPc/YbAu2	UPS(exp)	4.54	−0.44
	Top-Yb	3.08	−0.31	−0.84	0.54
	Top-Au	2.99	−0.40	−0.61	0.33
	Bridge-Au	3.12	−0.28	−0.66	0.33
CuPc/GdAu2	UPS(exp)	4.35	−0.54
	Top-Gd	2.96	−0.79	−1.24	0.85
	Top-Au	3.20	−0.56	−0.90	0.64
	Bridge-Au	3.15	−0.61	−0.98	0.69
CuPc/HoAu2	UPS(exp)	4.35	−0.53
CuPc/Au(111)	Exp.^75	4.81	−0.99

---

Furthermore, DFT+U has been used to calculate Φ from the electrostatic potentials along the perpendicular direction Z in the supercells. This calculation was carried out for the CuPc/GdAu₂ and CuPc/YbAu₂ systems. The corresponding Φ and ΔΦ values upon CuPc adsorption are included in Table 1. The values are reasonably close to the measured ones and, in particular, the trend of a stronger work function reduction in GdAu₂ is confirmed. However, a disagreement with the experimental Φ values of the pristine surfaces exists. This discrepancy, of around 1.5 eV, can be attributed in part to the finite slab size effect, which adds to a loss in accuracy at the surface electrostatic potential tail. In any case, an error of 0.4 eV is estimated for the calculated Φ,‡ which is smaller than the obtained Φ values and vacuum level downward shifts ΔV_vac upon CuPc adsorption shown in Table 1. The plane-integrated CDD curves Δρ(z) (eqn (1) in the Methods section), disclosed in Fig. 3(c), shows a similar sharp-peaked profile across the interface for all adsorption sites on both substrates GdAu₂ and YbAu₂. The main features are a clear electron depletion in the CuPc and REAu₂ planes and a strong accumulation at intermediate, slightly closer to the CuPc plane. The peaks in the YbAu₂ case are more intense. The fact that the peaks in the Δρ(z) curves are placed at the same z value for the three sites reflects that the physisorption is mostly governed by the molecule height, rather than by the Cu atom registry with the surface (see Fig. S4 in the ESI†). Table 1 shows the dipoles p_z at the CuPc/REAu₂ interface, obtained by integration of Δρ(z). The larger induced surface dipole on GdAu₂ is consistent with larger ΔV_vac and ΔΦ values on this substrate.⁷⁶ The curve of the plane-averaged accumulated dipole p_z across the interface of CuPc/GdAu₂ and CuPc/YbAu₂ is shown in Fig. S3 in the ESI.†

3.3. Electronic structure

The valence band of adsorbed CuPc MLs on REAu₂ surfaces has been investigated by angle resolved photoemission spectroscopy (ARPES). The characteristic dispersing bands of the REAu₂ surfaces, already discussed in previous publications^14,15,31 can still be observed in the CuPc-covered surface, although with a strongly reduced intensity due to the high surface sensitivity of the photoemission measurements (hν = 21.2 eV, 30 eV). The growth of CuPc introduces new non-dispersing bands that are assigned to the highest occupied orbital (HOMO) levels of the adsorbed molecule. Fig. 4(a) displays in the top panel the photoemission intensity mapping of electronic bands of YbAu₂ and at the bottom the same measurement after 1 ML CuPc adsorption (hν = 30 eV). One can distinguish the YbAu₂ dispersing bands and two strong non-dispersive emission peaks that arise from the spin–orbit split Yb 4f levels. These features are related with the divalent character of Yb in the YbAu₂ surface compound. However, the RE 4f levels are not observed in the band structure measured by ARPES on Ho and Gd alloys (Fig. S6 in the ESI†), because their 4f core levels are detected at much higher binding energies with photoemission.³¹

Fig. 4 Representative ARPES band structure of REAu₂ surfaces compounds before and after CuPc adsorption. (a) Photoemission intensity mapping taken along the indicated [capital Gamma, Greek, macron]M̄ directions of YbAu₂ (top) and 1 ML CuPc on YbAu₂. The non-dispersing HOMO levels of CuPc add to the substrate bands after adsorption (hν = 30 eV). (b) Upshift of the A band upon adsorption of 1 ML of CuPc on YbAu₂, HoAu₂ and GdAu₂. The largest shift has been detected in the YbAu₂ surface compound (θ = 0, hν = 30 eV [YbAu₂], 21.2 eV [other]).

At first glance, upon CuPc adsorption the band structure of REAu₂ surfaces generally appears unaffected. However, an exception is found in the A band. This band, common to all REAu₂ surfaces, is characterized by a free-electron-like parabolic dispersion around the [capital Gamma, Greek, macron]-point of the surface Brillouin zone. After CuPc deposition an upward shift toward the Fermi level (smaller binding energy E_B) is detected at [capital Gamma, Greek, macron]. This effect reveals the surface-state character of the A band and its sensitivity to the presence of adlayers. Fig. 4(b) shows the energy dispersion curves at an emission angle of 0° ([capital Gamma, Greek, macron]-point). In the case of YbAu₂, E_B shifts from binding energy values of 0.92 eV to 0.84 eV upon CuPc adsorption (δE_B = 80 meV). However, for HoAu₂ and GdAu₂E_B is shifted from 1.03 eV to 0.99 eV (δE_B = 35 meV). ARPES studies performed on noble-gas/Au(111) and organic molecules/Au(111) interfaces have ascribed a similar shift of the surface-state band to the pushback effect.⁷⁷ Moreover, models have been developed to account for the surface state energy shift in the cases of graphene/metal^78,79 and noble-gas/metal⁸⁰ interfaces. Thus, it has been established an universal curve that relates the shift with the adlayer height above the metal surface, while the substrate work function plays a minor role.⁸¹ For the case studied here, the A band is formed upon REAu₂ interaction with the Au(111) support.^27,31 Therefore, it is expected to interact with CuPc more weakly than the usual Shockley-like surface states in noble metals, which are localized at the outer regions of the surface. Indeed, the observed δE_B values are lower than other typical shifts. In comparison, the Shockley state shift caused by PTCDA physisorption ranges from 0.164 eV on Au(111)⁸² to 0.95 eV on Ag(100).⁸³

Fig. 5(a) shows the photoemission results at higher emission angles θ of 1 ML of CuPc on YbAu₂, HoAu₂ and GdAu₂ as well as on pure Au(111). Higher emission angles are usually better suited for the detection of the molecular levels like the HOMO levels. This is related to the symmetry and band character of the molecules and is explored in detail in molecular orbital tomography.^84–87 Here, the inclusion of CuPc/Au(111) is used as a reference to estimate and compare energy shifts of the valence band structures among the CuPc/REAu₂ samples. The emissions from a possible former lowest unoccupied molecular level (F-LUMO) below the Fermi energy is not detected in any of the four systems, which is in contrast to some chemisorbed systems like CuPc/Ag(111)⁷¹ or TiOPc/Ag(111),^88,89 where the F-LUMO gets occupied. However, the HOMO related features are readily seen, as previously mentioned above, and present different shifts with respect to the reference CuPc/Au(111) system. In the case of YbAu₂, this shift amounts to 0.26 eV, while in the other two cases this value increases to approximately 0.5 eV. The exact HOMO positions have been obtained after peak fit analysis using Lorentzian curves and taking into account the vibrational couplings of CuPc.^90–92 These values are presented in Table 2.

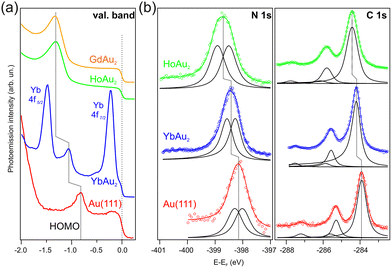Fig. 5 Photoemission measurements for CuPc/REAu₂ samples in comparison to CuPc/Au(111).⁷⁵ (a) Valence bands measured on CuPc ML grown on GdAu₂, HoAu₂ and YbAu₂ MLs. For comparison the valence band of 1 ML of CuPc/Au(111) is given. (hν = 44 eV and 50 eV, θ = (20 ± 7)° for Au(111) and YbAu₂ and hν = 21.22 eV and θ = (50 ± 7)° for HoAu₂ and GdAu₂ substrates, respectively.) (b) N 1s and C 1s core levels of 1 ML CuPc grown on Au(111), HoAu₂ and YbAu₂ (hν = 520 eV and 390 eV, θ = (0 ± 7)°).

Table 2 Binding energies and core level shifts of N 1s and C 1s measured on 1 ML CuPc grown on REAu₂ surface compounds for RE = Yb, Gd and Ho. The first column is the HOMO position with respect to E_F. The difference of these quantities with respect to the values measured on 1 ML of CuPc on Au(111) are given as ΔE. All values in eV

	HOMO/ΔE^H	E B ^N 1s/ΔE^N 1s	E B ^C 1s/ΔE^C1s
CuPc/YbAu2	1.08/0.26	398.42/0.20	284.18/0.24
CuPc/GdAu2	1.32/0.50	398.74/0.50	284.47/0.53
CuPc/HoAu2	1.32/0.50	398.74/0.52	284.42/0.48
CuPc/Au(111)	0.82/—	398.22/—	283.94/—

---

In addition, the interaction strength of CuPc with the different REAu₂ surfaces was studied by X-ray photoelectron spectroscopy (XPS). Fig. 5(b) shows N 1s and C 1s core levels measured on CuPc/HoAu₂ and CuPc/YbAu₂. For both N 1s and C 1s, core level shifts to higher binding energies with respect to the CuPc/Au(111) emissions (see Table 2) were detected. In order to disentangle both contributions, a peak fit analysis was carried out using individual Doniach-Sunjic peaks⁹³ of the same width, asymmetry, and Shirley background.⁹⁴ As in other works, the broad N 1s peak was explained by the contribution of two non-equivalent nitrogen atoms within the Pc ligand that cannot be resolved due to peak width.⁹⁵ For the fits, constraints for identical width, asymmetry and background were set for both features. The C 1s spectrum of CuPc is composed of three visible peaks, in CuPc/YbAu₂ at approximately 284.2 eV, 285.6 eV, and 287.5 eV with approximate area ratios of 3 : 1 : 0.15, respectively. For the latter case, the width (FWHM) associated with these positions is quite similar (0.4 ± 0.05) eV and there is a small asymmetry of 0.11 in all cases. These values, including the asymmetry, are very similar to those of CuPc/Au(100) results.⁹⁶ The asymmetry partially results from molecular vibrations^96,97 as well as from the reduced molecular layer thickness associated with a metallic substrate interaction. The highest emission peak was originally associated to C–C interaction of the carbon benzene ring atoms, the second peak to the C–N contribution from the pyrole structure and the high binding energy peak to a shake-up satellite, originally associated to the main C 1s peak originating from the π → π* transition.^96,98 Later works on H₂Pc, CuPc and FePc^97,99–102 have shown, however, that there should be two shake-up's with identical shake-up/main peak distances. As a result, the shake-up of the C–C emission overlaps with the C–N emission and is not distinguishable by eyes. With a peak fitting procedure taking into account these four emissions, the intensity relation of the carbon atoms of C–C : C–N = 24 : 8 including both shake-ups was then correctly fullfilled for the phthalocyanine molecules. Also in our cases here, the peak fitting results confirm the correct intensity relation (see ESI for details, Fig. S7†). More importantly, however, a rigid multiplet shift from CuPc/Au(111) to CuPc/YbAu₂ by approximately 0.25 eV and from CuPc/Au(111) to HoAu₂ by 0.5 eV is obtained. These values are very similar to the N 1s core level shifts and, as explained before, to the HOMO level shifts. These results indicate that YbAu₂ surfaces show a slightly weaker interaction than GdAu₂ and HoAu₂ with the CuPc molecules, taking Au(111) as reference. The exact positions of the core levels are again included in Table 2.

From all the photoemission results we extract that the Fermi level is located well inside the HOMO–LUMO molecular gap, far from the edges. In such scenario we do not expect a significant amount of charge flowing to align E_F to the molecular levels. In fact, we observe an almost rigid shift of the spectrum in the three cases, i.e. a very similar energy shift for all HOMO, core and vacuum levels at the three interfaces. This demonstrates a weak molecule/metal surface interaction, with vacuum level pinning of molecular electronic states.^45,75 This indicates that the behavior of the metal–organic interfaces is close to the Schottky–Mott limit¹⁰³ with a notable interface dipole, as it has been previously discussed.

The experimetal HOMO values of Table 2 obtained by photoemision are equivalent to the hole injection barrier (HIB) of the metal–organic interfaces. Likewise, the electron injection barrier (EIB) is given by the LUMO level. In order to estimate a possible LUMO energy and hence an EIB for our samples, we consider a molecular gap of 3 eV, obtained from a combination of normal and inverse photoemission measured on CuPc/Au(111)¹⁰⁴ CuPc on both REAu₂ and Au(111) is physisorbed, though on REAu₂ it reveals a slightly stronger electrostatic interaction. Therefore, the predicted bandgap for CuPc/REAu₂ should be close to, or even somewhat smaller than 3 eV. This argument is based on the fact that the bandgap of molecules adsorbed on surfaces becomes smaller in case of stronger interactions.^45,105 Hence, we extract for our samples the following LUMO/EIB energies (LUMO : bandgap-HOMO) of 1.67 eV (HoAu₂), 1.73 eV (GdAu₂), 1.92 eV (YbAu₂) and 2.18 eV for Au(111). It is worth to note that the smallest difference EIB-HIB is found in GdAu₂ and HoAu₂ (approx. 0.4 eV), while it doubles in YbAu₂ (0.84 eV). This means that in the interface CuPc/GdAu₂ and CuPc/HoAu₂, E_F is located much closer to the middle of the molecular gap, allowing an ambipolar injection of electrons and holes into the active organic layer.^36–38

Fig. 6 shows the projected densities of states (PDOS) on the molecular orbitals (MO) calculated by DFT+U+vdW (see Methods section) for CuPc adsorbed at the top Yb and top Gd geometries. The a_1u and e_g MOs corresponds to the HOMO and LUMO of CuPc, respectively and have a marginal contribution from the Cu 3d states. b_1g MO is the characteristic singly-occupied molecular orbital (SOMO) of CuPc, which has a strong d-character due to the hybridization between a Cu d_x²−y² state with the N p_x,y orbital.¹⁸ Two features in the PDOS of both substrates are not consistent with the experimental observations, pointing to the so-called self-interaction error (SIE)⁴⁸ effect in the calculation: (i) the theoretical HOMO levels (a_1u) lie 0.2–0.4 eV deeper than the experimental ones (see Table 2) and (ii) the LUMO levels lie at the Fermi level, while workfunctions and photoemission indicate that they should lie above. A better agreement with the experimental HOMO binding energies is obtained by means of the DFT+∑_axc approach,^63,64 which provides renormalized eigenvalues using an electrostatic image potential model for the substrate. This procedure, described in the ESI,† results in 1.1 and 1.2 eV for the HOMO levels of CuPc on YbAu₂ and GdAu₂, close to the values of Table 2. However, the LUMO pinning at the Fermi energy is a persistent feature even when using hybrid functionals, which partially correct the SIE. This is shown in the ESI and in Fig. S11.† The performance of these functionals is, nevertheless, conditioned by the occupation of the PBE reference calculation.¹⁰⁶ Therefore, the LUMO pinning may be interpreted as an artifact of the calculation and it is manifested by the highly localized interfacial charge density above the RE atoms (anchoring points), as shown by the spectral analysis of the CDDs. This means that the SIE is highly inhomogeneous in CuPc/REAu₂ systems, a qualitatively different scenario to that of CuPc physisorbed on pure noble metals.

Fig. 6 PDOS projected on atomic orbital groups of CuPc in CuPc/REAu₂/Au(111), RE = Yb and Gd, which account for relevant CuPc frontier molecular orbitals, obtained with the PBE+U+vdW correlation functional. Spin majority and minority states correspond to positive and negative PDOS values, respectively. The Cu in-plane (IP) orbitals are d_x²−y²,d_xy; Cu out-of-plane (OOP) are d_xz,d_yz,d_z²; organic IP are p_x,p_y of C and N; and organic OOP are p_z of C and N.

4. Conclusions

Hybrid metal–organic interfaces have been prepared by adsorption of CuPc on 2D REAu₂ surfaces (RE = Gd, Ho and Yb). We observe that CuPc forms a commensurate superstructure with densely packed molecules that differs from the clean CuPc/Au(111) case. Moreover, we see that there is not a clear preference for adsorption sites concerning the central Cu atom of CuPc. By means of photoemission experiments and DFT calculations, we have performed an extensive study on the electrostatics and electronic structure of the interface. Our study clearly reveals that CuPc is physisorbed on all the REAu₂ surfaces tried here. The electronic structure of these hybrid interfaces displays characteristic features that are not seen in other physisorbed molecules on pure metals. The interfacial charge density distribution is strongly corrugated and mainly localized on the RE atoms of the substrate.

Importantly, photoemission experiments show quantitative differences depending on the CuPc adsorption on divalent or trivalent REAu₂ substrates. In all cases the LUMO level of CuPc/REAu₂ remains empty as on other noble metals, but the HOMO binding energy values are significantly larger (≃0.3 eV) on trivalent substrates (HoAu₂ and GdAu₂) than on a divalent one (YbAu₂). The DFT+∑_axc approach allows to explain the renormalization of the CuPc HOMO level upon adsorption as an interaction with the substrate Coulomb-like potential. This is, in essence, the Pauli push-back effect. Furthermore, it is found that the physisorption of CuPc induces an upward shift of the distinctive surface state of the REAu₂ substrate, which is larger in YbAu₂ (80 meV) than in HoAu₂ and GdAu₂ (35 meV). Interestingly, unlike in other noble metals, this state is confined below the REAu₂ atomic plane and appears upon its interaction with the Au(111) substrate underneath.

All in all, the REAu₂ substrates preserve the CuPc properties, as it occurs on the widely used noble metal substrates, but with the fingerprints of a singular interaction with the RE atoms and the REAu₂ band structure. The significant dependence of the HOMO binding energy on the RE valence opens the door to a feasible fine tuning of the carrier injection barriers for organic electronic devices. Remarkably, it is found that hybrid interfaces prepared with trivalent substrates (HoAu₂ and GdAu₂) exhibit molecular level energies that may allow carrier injection barriers closer to an ambipolar behavior. Such results and the unique ferromagnetic properties of the subtrates reveal a large potential for the design of new organic spintronic devices with extensive functionalities that combine the use of light with electric and magnetic fields.

Author contributions

L. F., F. S. and M. B.-R. conceptualized the work. R. C.-B., K. A., L. F. and F. S. carried out experimental photoemission investigations. The formal analysis of the photoemission measurements was carried out by F. S. STM and LEED investigations were carried out by R. C.-B. and L. F. The experimental investigations were supervised by L. F. and F. S. DFT investigations were performed by M. B.-R. The article was original drafted by L. F. and M. B.-R., and reviewed and edited by all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financial supported by Spanish Ministerio de Ciencia e Innovación (grants No. MAT-2017-88374-P, PID2020-116093RB-C44, PID2019-103910GB-I00 and PTA2019-018134-I funded by MCIN/AEI/10.13039/501100011033/ and by “ESF investing in your future”), and the Basque Government (grants No. IT-1591-22, IT-1527-22). L. F. acknowledges funding from the European Union's Horizon 2020 research and innovation programme through the Marie Skłodowska-Curie Grant Agreement MagicFACE No. 797109. Computational resources were provided by DIPC. Part of the research leading to this results has been supported by the project CALIPSOplus under Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. We further aknowledge Polina M. Sheverdyaeva and Paolo Moras for the assistance in the VUV-Photoemission beam line of Elettra Synchrotron in Trieste.

References

1. M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502.
2. M. J. Comstock, N. Levy, A. Kirakosian, J. Cho, F. Lauterwasser, J. H. Harvey, D. A. Strubbe, J. M. J. Fréchet, D. Trauner, S. G. Louie and M. F. Crommie, Phys. Rev. Lett., 2007, 99, 038301.
3. T. D. Nguyen, E. Ehrenfreund and Z. V. Vardeny, Science, 2012, 337, 204–209.
4. X. Sun, S. Vélez, A. Atxabal, A. Bedoya-Pinto, S. Parui, X. Zhu, R. Llopis, F. Casanova and L. E. Hueso, Science, 2017, 357, 677–680.
5. M. Cinchetti, K. Heimer, J.-P. Wüstenberg, O. Andreyev, M. Bauer, S. Lach, C. Ziegler, Y. Gao and M. Aeschlimann, Nat. Mater., 2009, 8, 115–119.
6. S. Lach, A. Altenhof, K. Tarafder, F. Schmitt, M. E. Ali, M. Vogel, J. Sauther, P. M. Oppeneer and C. Ziegler, Adv. Funct. Mater., 2012, 22, 989–997.
7. S. Javaid, M. Bowen, S. Boukari, L. Joly, J.-B. Beaufrand, X. Chen, Y. J. Dappe, F. Scheurer, J.-P. Kappler, J. Arabski, W. Wulfhekel, M. Alouani and E. Beaurepaire, Phys. Rev. Lett., 2010, 105, 077201.
8. A. Droghetti, P. Thielen, I. Rungger, N. Haag, N. Großmann, J. Stöckl, B. Stadtmüller, M. Aeschlimann, S. Sanvito and M. Cinchetti, Nat. Commun., 2016, 7, 12668.
9. F. Al Ma'Mari, T. Moorsom, G. Teobaldi, W. Deacon, T. Prokscha, H. Luetkens, S. Lee, G. E. Sterbinsky, D. A. Arena, D. A. MacLaren, M. Flokstra, M. Ali, M. C. Wheeler and B. Gavin Burnell, Nature, 2015, 524, 69–74.
10. T. Moorsom, M. Wheeler, T. Mohd Khan, F. Al Ma'Mari, C. Kinane, S. Langridge, D. Ciudad, A. Bedoya-Pinto, L. Hueso, G. Teobaldi, V. K. Lazarov, D. Gilks, G. Burnell, B. J. Hickey and O. Cespedes, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125311.
11. R. Geng, T. T. Daugherty, K. Do, H. M. Luong and T. D. Nguyen, J. Sci.: Adv. Mater. Devices, 2016, 1, 128–140.
12. T. Arnold, A. Atxabal, S. Parui, L. E. Hueso and F. Ortmann, Adv. Funct. Mater., 2018, 28, 1706105.
13. M. Corso, L. Fernández, F. Schiller and J. E. Ortega, ACS Nano, 2010, 4, 1603–1611.
14. M. Corso, M. J. Verstraete, F. Schiller, M. Ormaza, L. Fernández, T. Greber, M. Torrent, A. Rubio and J. E. Ortega, Phys. Rev. Lett., 2010, 105, 016101.
15. M. Ormaza, L. Fernández, S. Lafuente, M. Corso, F. Schiller, B. Xu, M. Diakhate, M. J. Verstraete and J. E. Ortega, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125405.
16. S. Stepanow, A. Mugarza, G. Ceballos, P. Moras, J. C. Cezar, C. Carbone and P. Gambardella, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014405.
17. A. Mugarza, N. Lorente, P. Ordejón, C. K. S. Stepanow, M.-L. Bocquet, J. Fraxedas, G. Ceballos and P. Gambardella, Phys. Rev. Lett., 2019, 105, 115702–115705.
18. A. Mugarza, R. Robles, C. Krull, R. Korytár, N. Lorente and P. Gambardella, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155437.
19. B. Stadtmüller, I. Kröger, F. Reinert and C. Kumpf, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 085416–085425.
20. D. G. de Oteyza, A. El-Sayed, J. M. Garcia-Lastra, E. Goiri, T. N. Krauss, A. Turak, E. Barrena, H. Dosch, J. Zegenhagen, A. Rubio, Y. Wakayama and J. E. Ortega, J. Chem. Phys., 2010, 133, 214703–214708.
21. R. Sk and A. Deshpande, Mol. Syst. Des. Eng., 2019, 4, 471–483.
22. P. Järvinen, S. K. Hämäläinen, M. Ijäs, A. Harju and P. Liljeroth, J. Phys. Chem. C, 2014, 118, 13320–13325.
23. T. Bathon, P. Sessi, K. A. Kokh, O. E. Tereshchenko and M. Bode, Nano Lett., 2015, 15, 2442–2447.
24. K. Sun, M. L. Tao, Y. B. Tu and J. Z. Wang, Molecules, 2017, 22, 740–747.
25. L. Fernández, M. Blanco-Rey, M. Ilyn, L. Vitali, A. Magaña, A. Correa, P. Ohresser, J. E. Ortega, A. Ayuela and F. Schiller, Nano Lett., 2014, 14, 2977–2981.
26. L. Fernández, M. Ilyn, A. Magaña, L. Vitali, J. Ortega and F. Schiller, Adv. Sci., 2016, 14, 1600187–1600192.
27. M. Ormaza, L. Fernández, M. Ilyn, A. Magaña, B. Xu, M. J. Verstraete, M. Gastaldo, M. A. Valbuena, P. Gargiani, A. Mugarza, A. Ayuela, L. Vitali, M. Blanco-Rey, F. Schiller and J. E. Ortega, Nano Lett., 2016, 16, 4230–4235.
28. L. Fernández, M. Corso, F. Schiller, M. Ilyn, M. Holder and J. E. Ortega, Appl. Phys. Lett., 2010, 96, 013107.
29. B. Feng, R.-W. Zhang, Y. Feng, B. Fu, S. Wu, K. Miyamoto, S. He, L. Chen, K. Wu, K. Shimada, T. Okuda and Y. Yao, Phys. Rev. Lett., 2019, 123, 116401.
30. Y. Que, Y. Zhuang, Z. Liu, C. Xu, B. Liu, K. Wang, S. Du and X. Xiao, J. Phys. Chem. Lett., 2020, 11, 4107–4112.
31. L. Fernandez, M. Blanco-Rey, R. Castrillo-Bodero, M. Ilyn, K. Ali, E. Turco, M. Corso, M. Ormaza, P. Gargiani, M. A. Valbuena, A. Mugarza, P. Moras, P. M. Sheverdyaeva, A. K. Kundu, M. Jugovac, C. Laubschat, J. E. Ortega and F. Schiller, Nanoscale, 2020, 12, 22258–22267.
32. M. Blanco-Rey, R. Castrillo-Bodero, K. Ali, P. Gargiani, F. Bertran, P. M. Sheverdyaeva, J. E. Ortega, L. Fernandez and F. Schiller, Phys. Rev. Res., 2022, 4, 013237.
33. M. Farnesi Camellone, A. Correa, A. Barragán, M. Pedio, S. Fabris, C. Cepek and L. Vitali, J. Phys. Chem. C, 2019, 123, 6496–6501.
34. M. Abadía, M. Ilyn, I. Piquero-Zulaica, P. Gargiani, C. Rogero, J. E. Ortega and J. Brede, ACS Nano, 2017, 11, 12392–12401.
35. M. Elsebach, Ph.D. thesis, Fakultät für Mathematik, Informatik und Naturwissenschaften im Fachbereich Physik der Universität Hamburg, 2021.
36. A. Risteska and D. Knipp, Handbook of Visual Display Technology, 2016, pp. 1–21.
37. S. Z. Bisri, T. Takenobu, Y. Yomogida, H. Shimotani, T. Yamao, S. Hotta and Y. Iwasa, Adv. Funct. Mater., 2009, 19, 1728–1735.
38. T. Kanagasekaran, H. Shimotani, R. Shimizu, T. Hitosugi and K. Tanigaki, Nat. Commun., 2017, 8, 999.
39. N. Koch, J. Phys.: Condens. Matter, 2008, 20, 184008.
40. L. Yan, N. J. Watkins, S. Zorba, Y. Gao and C. W. Tang, Appl. Phys. Lett., 2002, 81, 2752–2754.
41. G. Witte, S. Lukas, P. S. Bagus and C. Wöll, Appl. Phys. Lett., 2005, 87, 263502.
42. J. Ziroff, P. Gold, A. Bendounan, F. Forster and F. Reinert, Surf. Sci., 2009, 603, 354–358.
43. H. Yamane and N. Kosugi, J. Phys. Chem. C, 2016, 120, 24307–24313.
44. H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605.
45. E. Goiri, P. Borghetti, A. El-Sayed, J. E. Ortega and D. G. de Oteyza, Adv. Mater., 2016, 28, 1340–1368.
46. K. S. Thygesen and A. Rubio, Phys. Rev. Lett., 2009, 102, 046802.
47. L. Kronik and Y. Morikawa, in Understanding the Metal-Molecule Interface from First Principles, John Wiley & Sons, Ltd, 2013, ch. 3, pp. 51–89.
48. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
49. L. Hedin, Phys. Rev., 1965, 139, A796–A823.
50. J. W. Kim and A. Kim, Curr. Appl. Phys., 2021, 31, 52–59.
51. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
52. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
53. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
54. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
55. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808.
56. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
57. J. P. Allen and G. W. Watson, Phys. Chem. Chem. Phys., 2014, 16, 21016–21031.
58. K. Berland and P. Hyldgaard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035412.
59. T. Björkman, J. Chem. Phys., 2014, 141, 074708.
60. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
61. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
62. J. Paier, M. Marsman, K. Hummer and G. Kresse, J. Chem. Phys., 2006, 124, 154709.
63. J. B. Neaton, M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216405.
64. D. A. Egger, Z.-F. Liu, J. B. Neaton and L. Kronik, Nano Lett., 2015, 15, 2448–2455.
65. N. Marom, O. Hod, G. E. Scuseria and L. Kronik, J. Chem. Phys., 2008, 128, 164107.
66. N. Marom, X. Ren, J. E. Moussa, J. R. Chelikowsky and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195143.
67. D. A. Egger, S. Weissman, S. Refaely-Abramson, S. Sharifzadeh, M. Dauth, R. Baer, S. Kümmel, J. B. Neaton, E. Zojer and L. Kronik, J. Chem. Theory Comput., 2014, 10, 1934–1952.
68. Q. Zhou, Z.-F. Liu, T. J. Marks and P. Darancet, J. Phys. Chem. A, 2021, 125, 4055–4061.
69. L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, J. Chem. Theory Comput., 2012, 8, 1515–1531.
70. S. Refaely-Abramson, S. Sharifzadeh, N. Govind, J. Autschbach, J. B. Neaton, R. Baer and L. Kronik, Phys. Rev. Lett., 2012, 109, 226405.
71. I. Kröger, B. Stadtmüller, C. Stadler, J. Ziroff, M. Kochler, A. Stahl, F. Pollinger, T.-L. Lee, J. Zegenhagen, F. Reinert and C. Kumpf, New J. Phys., 2010, 12, 083038.
72. L. Fernandez, S. Thussing, A. Mänz, G. Witte, A. X. Brion-Rios, P. Cabrera-Sanfelix, D. Sanchez-Portal and P. Jakob, J. Phys. Chem. C, 2017, 121, 1608–1617.
73. D. E. Hooks, T. Fritz and M. D. Ward, Adv. Mater., 2001, 13, 227–241.
74. Y. L. Huang, E. Wruss, D. A. Egger, S. Kera, N. Ueno, W. A. Saidi, T. Bucko, A. T. Wee and E. Zojer, Molecules, 2014, 19, 2969.
75. P. Borghetti, A. El-Sayed, E. Goiri, C. Rogero, J. Lobo-Checa, L. Floreano, J. E. Ortega and D. G. de Oteyza, ACS Nano, 2014, 8, 12786–12795.
76. T. C. Leung, C. L. Kao, W. S. Su, Y. J. Feng and C. T. Chan, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195408.
77. T. Andreev, I. Barke and H. Hövel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205426.
78. P. L. de Andres, P. M. Echenique, D. Niesner, T. Fauster and A. Rivacoba, New J. Phys., 2014, 16, 023012.
79. N. Armbrust, J. Güdde and U. Höfer, New J. Phys., 2015, 17, 103043.
80. T. Andreev, I. Barke and H. Hövel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205426.
81. N. Armbrust, F. Schiller, J. Güdde and U. Höfer, Sci. Rep., 2017, 7, 46561.
82. N. Nicoara, J. Méndez and J. M. Gómez-Rodríguez, Nanotechnology, 2016, 27, 475707.
83. M. C. E. Galbraith, M. Marks, R. Tonner and U. Höfer, J. Phys. Chem. Lett., 2014, 5, 50–55.
84. P. Puschnig, S. Berkebile, A. J. Fleming, G. Koller, K. Emtsev, T. Seyller, J. D. Riley, C. Ambrosch-Draxl, F. P. Netzer and M. G. Ramsey, Science, 2009, 326, 702–706.
85. P. Puschnig, E.-M. Reinisch, T. Ules, G. Koller, S. Soubatch, M. Ostler, L. Romaner, F. S. Tautz, C. Ambrosch-Draxl and M. G. Ramsey, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235427.
86. M. Dauth, T. Körzdörfer, S. Kümmel, J. Ziroff, M. Wiessner, A. Schöll, F. Reinert, M. Arita and K. Shimada, Phys. Rev. Lett., 2011, 107, 193002.
87. S. Weiß, D. Lüftner, T. Ules, E. M. Reinisch, H. Kaser, A. Gottwald, M. Richter, S. Soubatch, G. Koller, M. G. Ramsey, F. S. Tautz and P. Puschnig, Nat. Commun., 2015, 6, 8287.
88. I. Kröger, B. Stadtmüller and C. Kumpf, New J. Phys., 2016, 18, 113022.
89. A. Lerch, L. Fernandez, M. Ilyn, M. Gastaldo, M. Paradinas, M. A. Valbuena, A. Mugarza, A. B. M. Ibrahim, J. Sundermeyer, U. Höfer and F. Schiller, J. Phys. Chem. C, 2017, 121, 25353–25363.
90. N. Ueno, S. Kera, K. Sakamoto and K. K. Okudaira, Appl. Phys. A, 2008, 92, 495–504.
91. S. Kera, H. Yamane, I. Sakuragi, K. K. Okudaira and N. Ueno, Chem. Phys. Lett., 2002, 364, 93–98.
92. S. Kera, H. Yamane, I. Sakuragi, K. K. Okudaira and N. Ueno, J. Electron Spectrosc. Relat. Phenom., 2007, 156–158, 135–138.
93. S. Doniach and M. Šunjic, J. Phys. C: Solid State Phys., 1970, 3, 285.
94. D. A. Shirley, Phys. Rev. B: Solid State, 1972, 5, 4709–4714.
95. Y. Zhang, T. Learmonth, S. Wang, A. Y. Matsuura, J. Downes, L. Plucinski, S. Bernardis, C. O'Donnell and K. E. Smith, J. Mater. Chem., 2007, 17, 1276–1283.
96. K. T. Park, A. Miller, K. Klier, R. L. Opila and J. E. Rowe, Surf. Sci., 2003, 529, L285–L292.
97. B. Brena, Y. Luo, M. Nyberg, S. Carniato, K. Nilson, Y. Alfredsson, J. Åhlund, N. Mårtensson, H. Siegbahn and C. Puglia, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195214.
98. Y. Niwa, H. Kobayashi and T. Tsuchiya, J. Chem. Phys., 1974, 60, 799–807.
99. L. Ottaviano, S. Di Nardo, L. Lozzi, M. Passacantando, P. Picozzi and S. Santucci, Surf. Sci., 1997, 373, 318–332.
100. H. Peisert, M. Knupfer and J. Fink, Surf. Sci., 2002, 515, 491–498.
101. T. Schwieger, H. Peisert, M. S. Golden, M. Knupfer and J. Fink, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155207.
102. K. Greulich, A. Belser, T. Basova, T. Chassé and H. Peisert, J. Phys. Chem. C, 2022, 126, 716–727.
103. Y. Liu, J. Guo, E. Zhu, L. Liao, S.-J. Lee, M. Ding, I. Shakir, V. Gambin, Y. Huang and X. Duan, Nature, 2018, 557, 696–700.
104. J. Xiao and P. A. Dowben, J. Phys.: Condens. Matter, 2008, 21, 052001.
105. I. F. Torrente, K. J. Franke and J. I. Pascual, J. Phys.: Condens. Matter, 2008, 20, 184001.
106. O. T. Hofmann, V. Atalla, N. Moll, P. Rinke and M. Scheffler, New J. Phys., 2013, 15, 123028.

---

Footnotes

† Electronic supplementary information (ESI) available: Further experimental and theoretical details. See DOI: https://doi.org/10.1039/d2nr06440e

‡ The error in the calculated work function Φ can be estimated from the clean Au(111) bottom faces of the model slabs, which shows work function differences up to 0.4 eV (Fig. S5 in the ESI†).

---